Assessment of Direct Normal Irradiance Forecasts Based on IFS/ECMWF Data and Observations in the South of Portugal
Abstract
1. Introduction
2. Materials and Methods
2.1. DNI Observational Data
2.2. DNI Forecast Data
2.3. Statistical Indicators for Model Sssessment
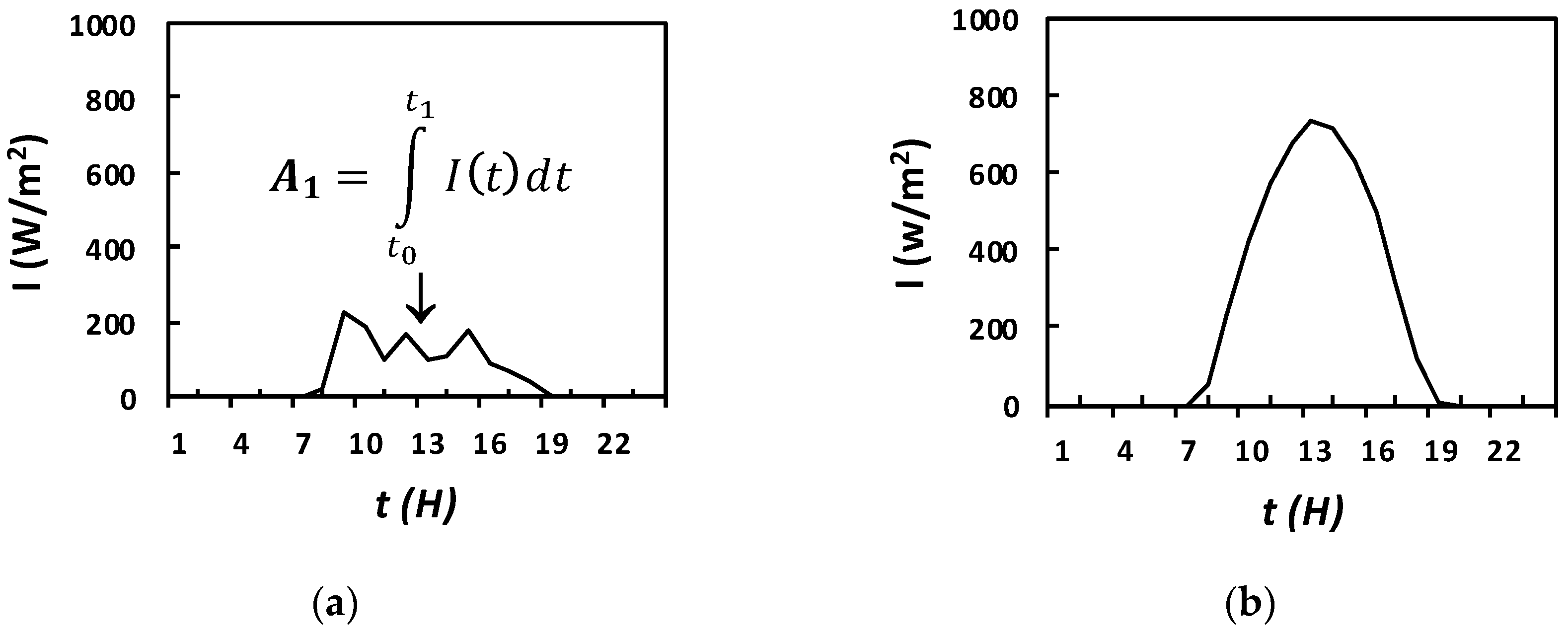
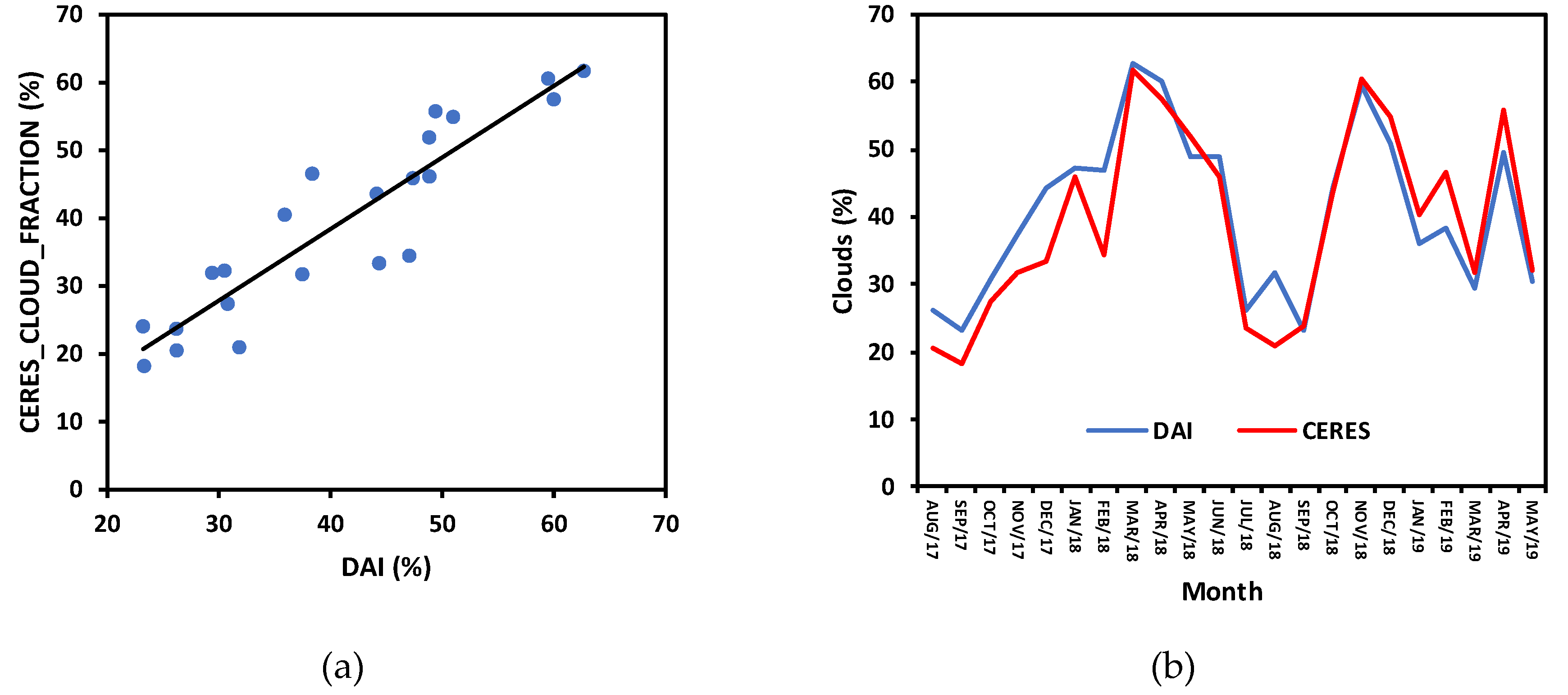
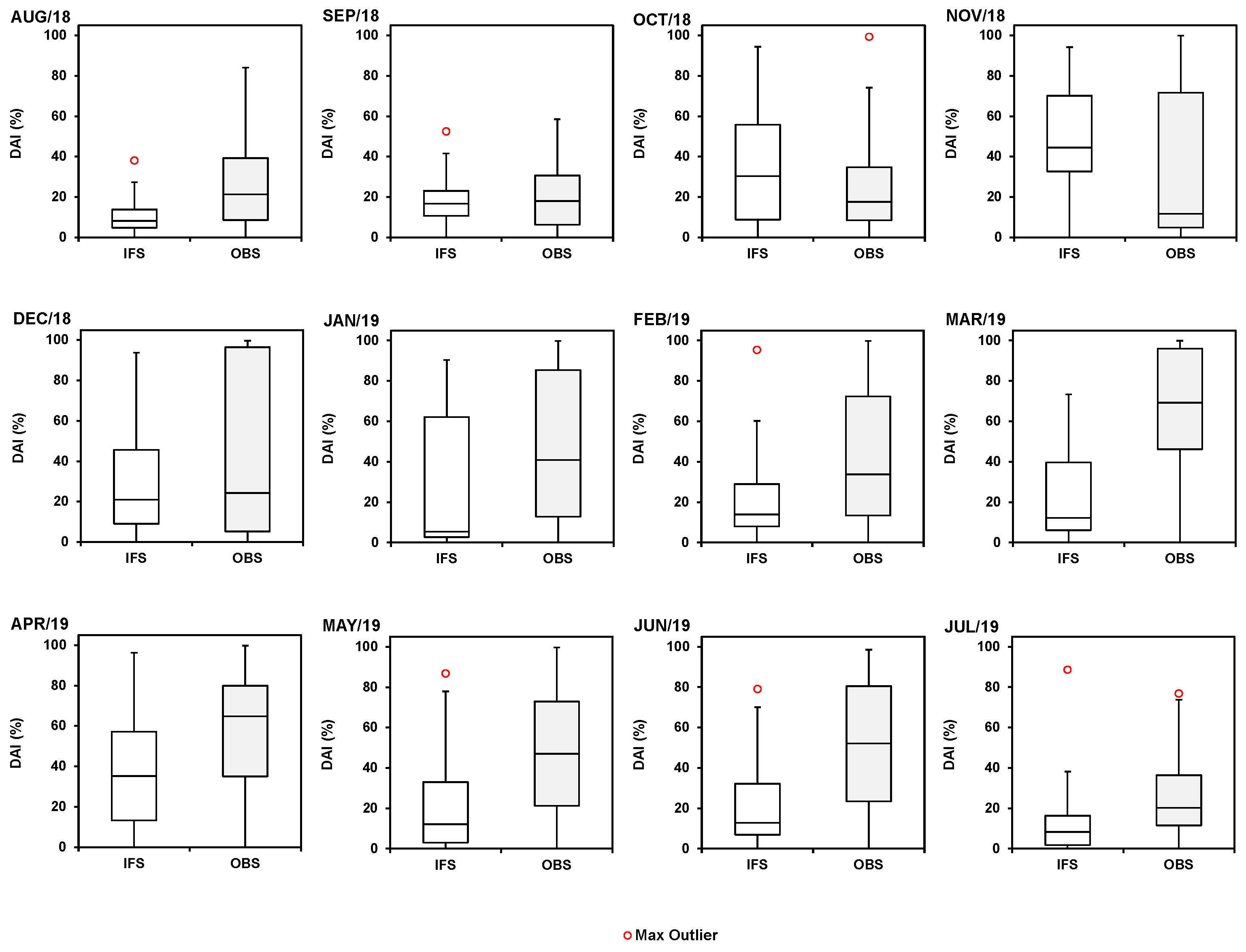
2.4. Cloud Area Fraction and DNI Attenuation Index (DAI)
2.5. Post Processing Correction
3. Results and Discussion
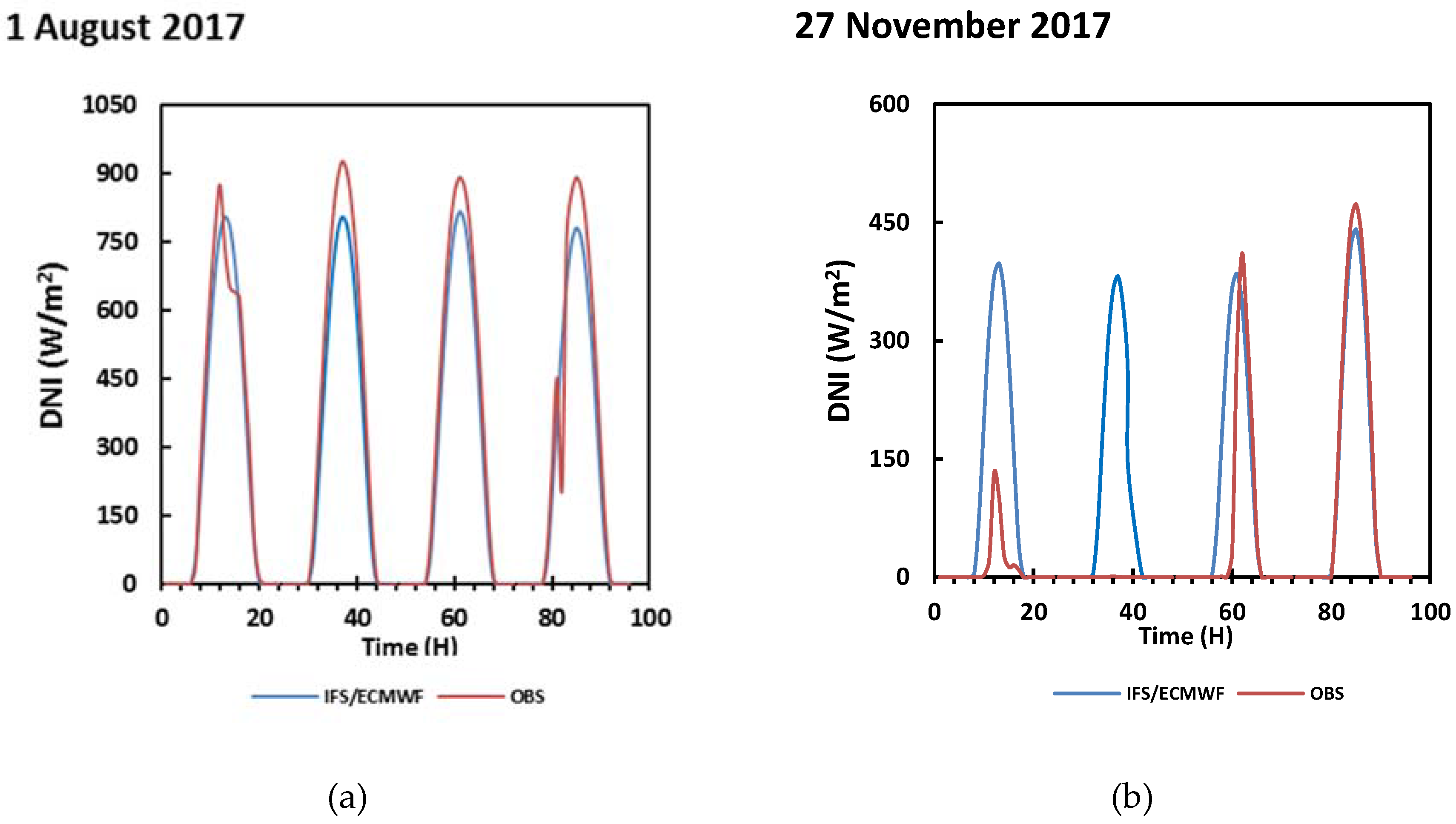
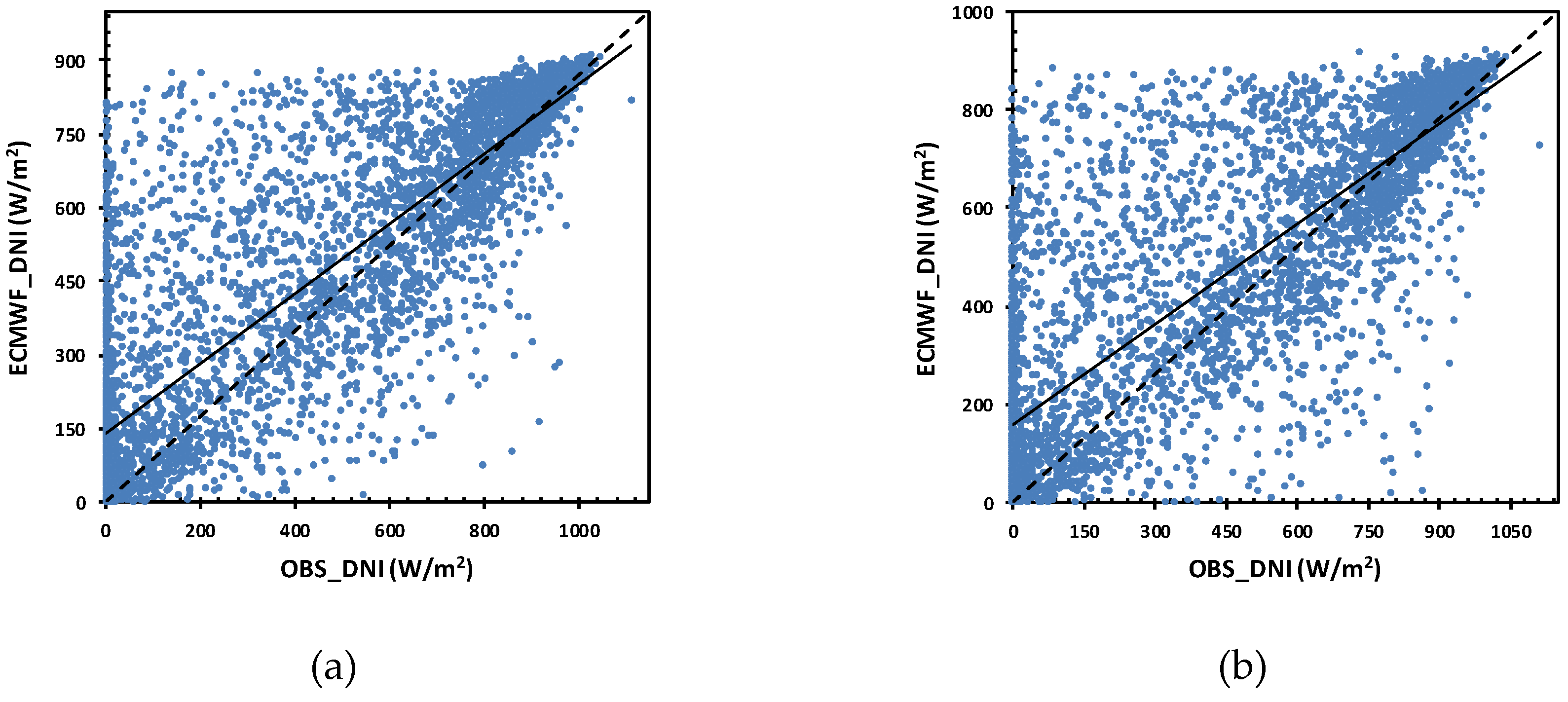
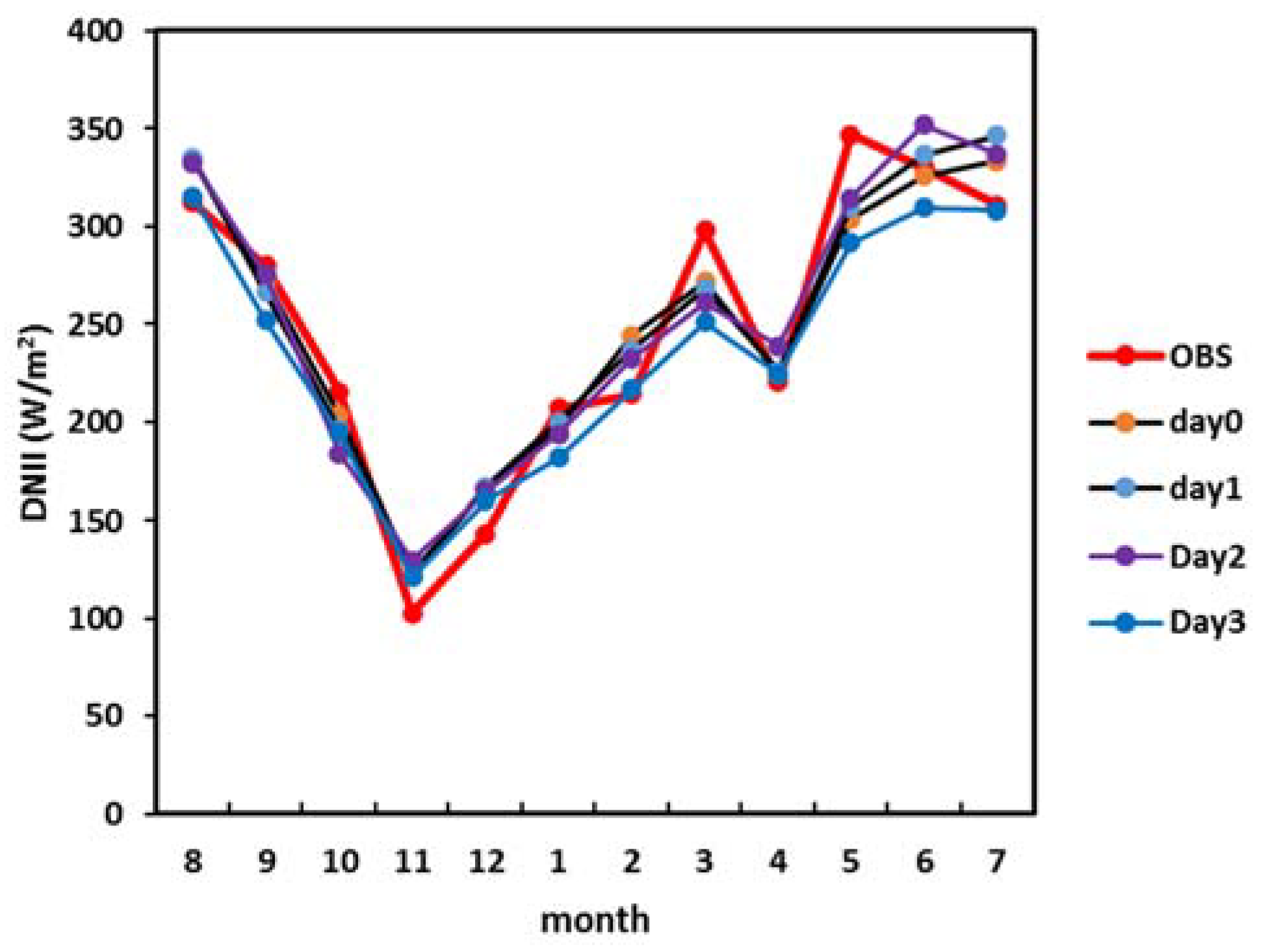
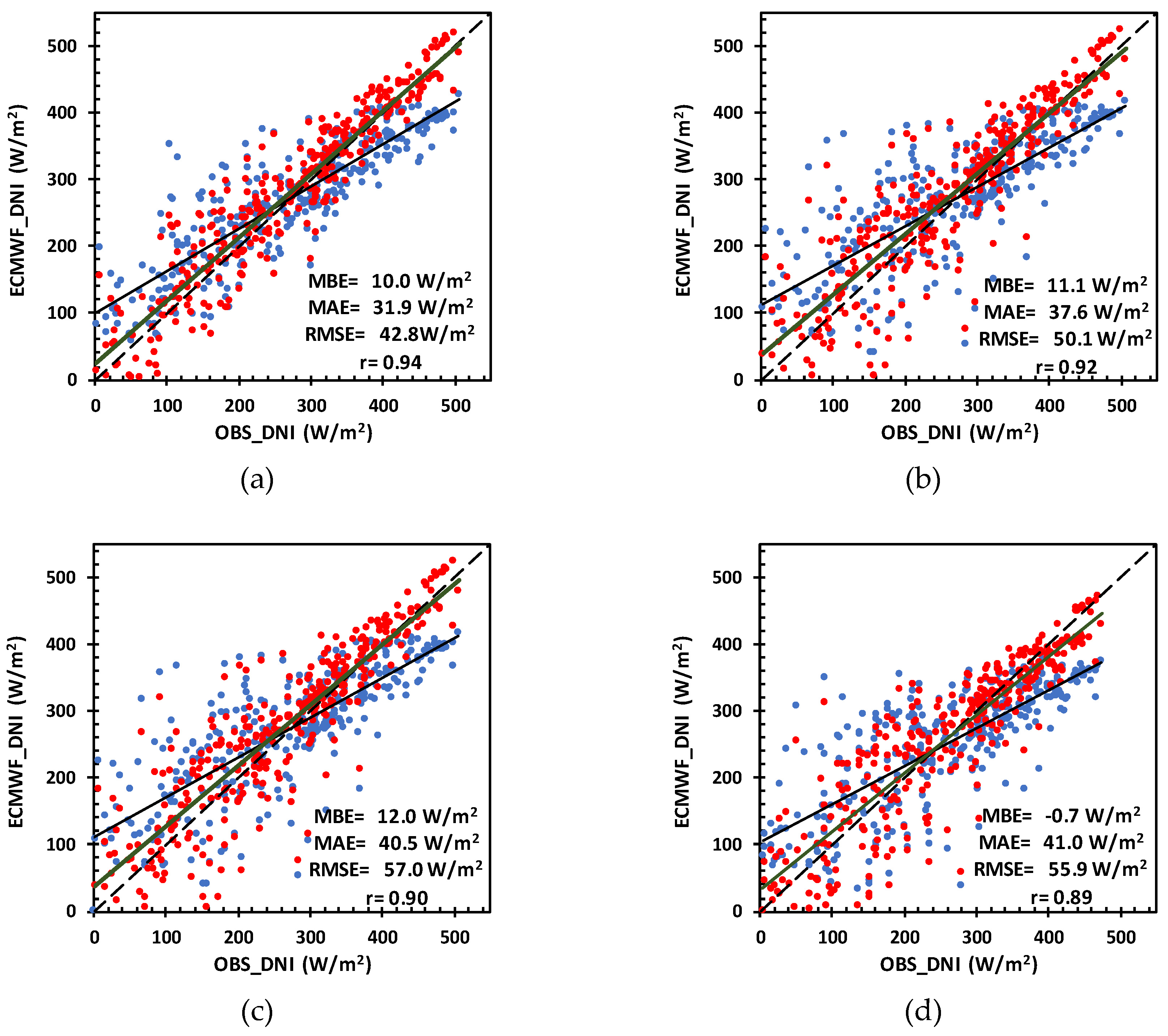
3.1. Assessment of Hourly and Daily DNI Forecasts
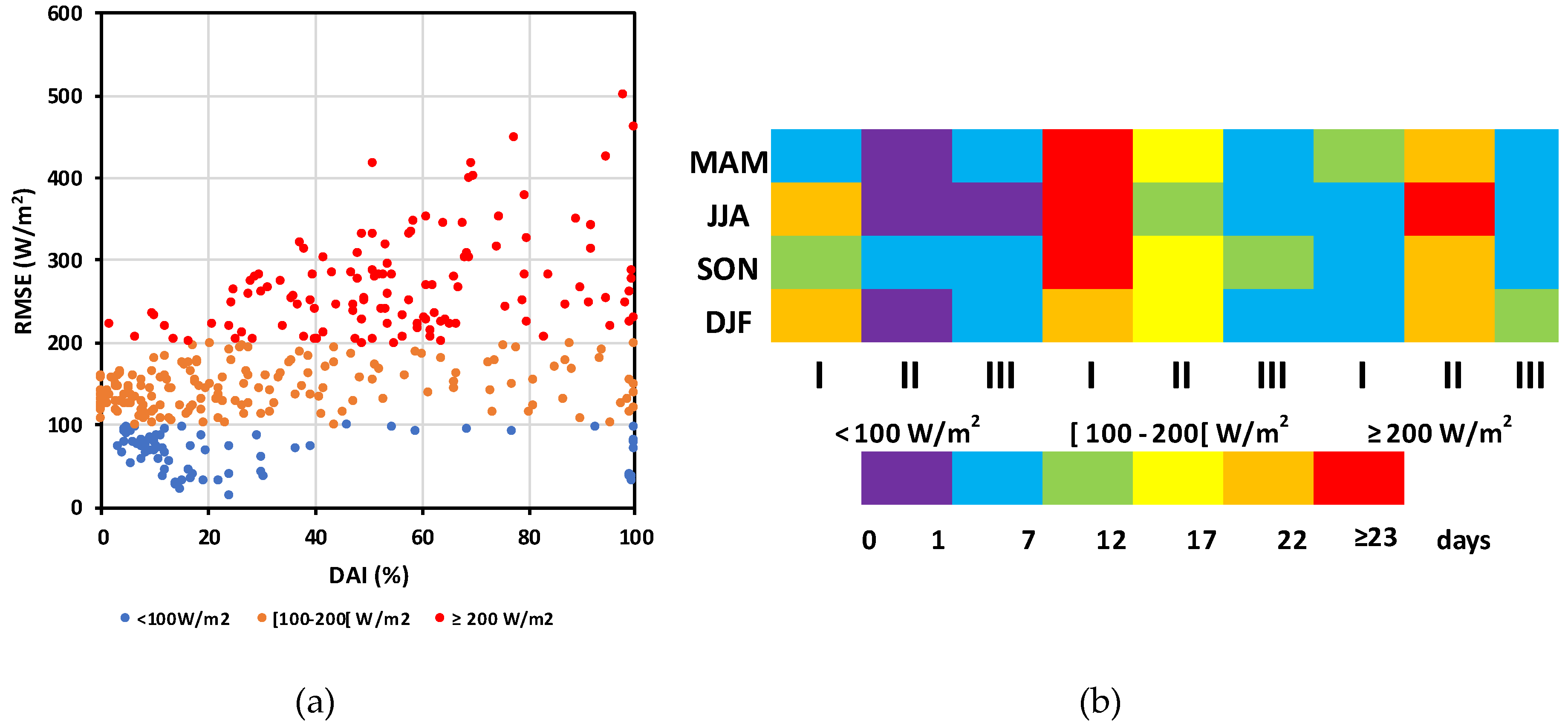
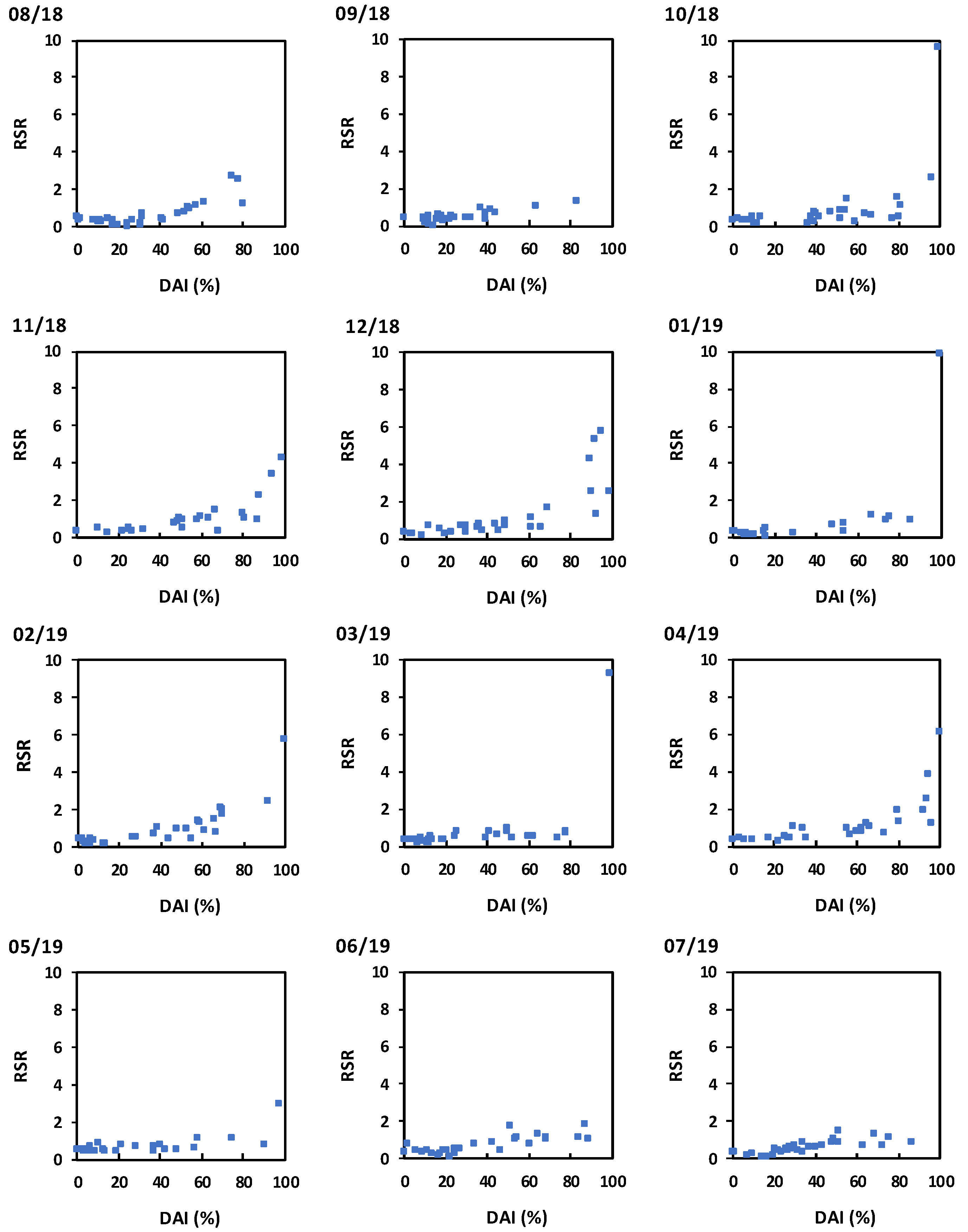
3.2. Relation between the DNI Attenuation Index (DAI) and DNI Forecasts
- (i)
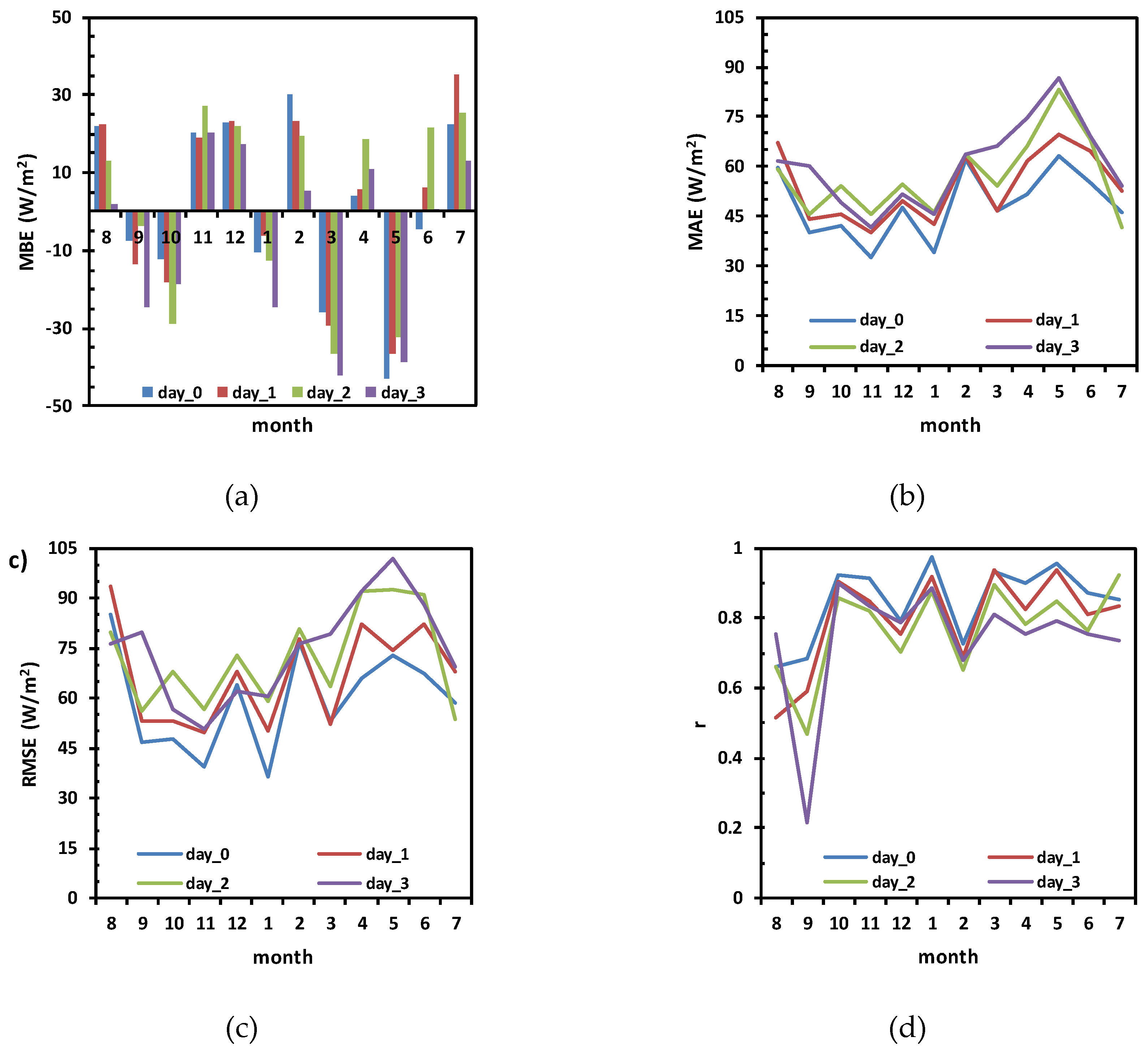
- Approximately ~19% of the days present RMSE values lower than 100 W⁄m2 (blue dots in Figure 10a). This percentage corresponds mostly to a cloud coverage lower than or equal to two oktas-clear skies days;
- (ii)
- ~47% of the days present a cloud coverage of class II type, in the range (100–200 W⁄m2);
- (iii)
- RMSE values above 200 W⁄m2 occur for ~34% of the days (red dots in Figure 10a). For this value, the majority of days are found in the cloud coverage type II category, suggesting that the model gives worst results in partially cloudy days, due to an inaccurate cloud representation or of their effects on the solar irradiance at the surface. For instance, Lopes [47] found that thin clouds (like cirrus) may cause a decrease in DNI of around 20%;
- (iv)
- The errors found in summer months can be explained by the monthly constant aerosol climatology used in IFS/ECMWF as argued by Lopes et al. [17].
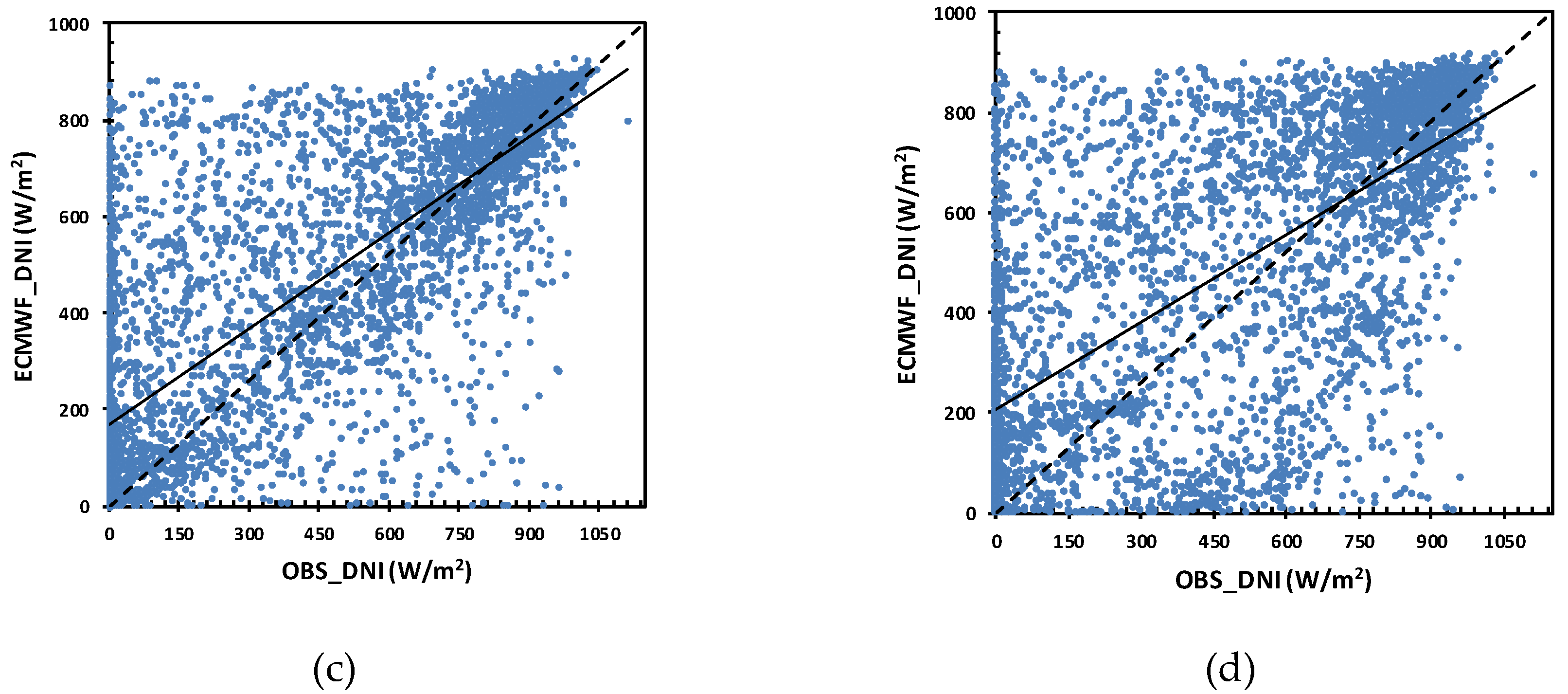
3.3. Statistical Bias Correction Analysis of Daily DNI Forecasts
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gaetani, M.; Huld, T.; Vignati, E.; Monforti-Ferrario, F.; Dosio, A.; Raes, F. The near future availability of photovoltaic energy in Europe and Africa in climate-aerosol modeling experiments. Renew. Sustain. Energy Rev. 2014, 38, 706–716. [Google Scholar] [CrossRef]
- Escobar, R.A.; Cortés, C.; Pino, A.; Salgado, M.; Pereira, E.B.; Martins, F.R.; Boland, J.; Cardemil, J.M. Estimating the potential for solar energy utilization in Chile by satellite-derived data and ground station measurements. Sol. Energy 2015, 121, 139–151. [Google Scholar] [CrossRef]
- Santos, J.A.; Rochinha, C.; Liberato, M.L.R.; Reyers, M.; Pinto, J.G. Projected changes in wind energy potentials over Iberia. Renew. Energy 2015, 75, 68–80. [Google Scholar] [CrossRef]
- Du, H.; Jones, P.J.; Lannon, S.C. Creating localised near future weather data for predicting the performance of buildings in the UK. In Proceedings of the 12th REHVA World Congress CLIMA 2016, Aalborg, Denmark, 22–25 May 2016; Heiselberg, P.K., Ed.; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2016; p. 537. [Google Scholar]
- Ruiz-Arias, J.A.; Gueymard, C.A.; Dudhia, J.; Pozo-Vazquez, D. Improvement of the weather research and forecasting (WRF) model for solar resource assessments and forecasts under clear skies. In Proceedings of the World Renewable Energy Forum, Denver, CO, USA, 13–17 May 2012. [Google Scholar]
- Perdigão, J.; Salgado, R.; Magarreiro, C.; Soares, P.M.M.; Costa, M.J.; Dasari, H. An Iberian climatology of solar radiation obtained from WRF regional climate simulations for 1950–2010 period. Atmos. Res. 2017. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Quesada-Ruiz, S.; Fernández, E.F.; Gueymard, C.A. Optimal combination of gridded and ground-observed solar radiation data for regional solar resource assessment. Sol. Energy 2015, 112, 411–424. [Google Scholar] [CrossRef]
- Šúri, M.; Huld, T.A.; Dunlop, E.D.; Ossenbrink, H.A. Potential of solar electricity generation in the European Union member states and candidate countries. Sol. Energy 2007, 81, 1295–1305. [Google Scholar] [CrossRef]
- Pereira, S.; Canhoto, P.; Salgado, R.; Costa, M.J. Development of an ANN based corrective algorithm of the operational ECMWF global horizontal irradiation forecasts. Sol. Energy 2019, 185, 387–405. [Google Scholar] [CrossRef]
- Martín, L.; Zarzalejo, L.F.; Polo, J.; Navarro, A.; Marchante, R.; Cony, M. Prediction of global solar irradiance based on time series analysis: Application to solar thermal power plants energy production planning. Sol. Energy 2010, 84, 1772–1781. [Google Scholar] [CrossRef]
- Alsamamra, H.; Ruiz-Arias, J.A.; Pozo-Vázquez, D.; Tovar-Pescador, J. A comparative study of ordinary and residual kriging techniques for mapping global solar radiation over southern Spain. Agric. For. Meteorol. 2009, 149, 1343–1357. [Google Scholar] [CrossRef]
- Kraas, B.; Schroedter-Homscheidt, M.; Madlener, R. Economic Merits of a State-of-the-Art Concentrating Solar Power Forecasting System for Participation in the Spanish Electricity Market. Sol. Energy 2013, 93, 244–255. [Google Scholar] [CrossRef]
- Law, E.W.; Prasad, A.A.; Kay, M.; Taylor, R.A. Direct normal irradiance forecasting and its application to concentrated solar thermal output forecasting—A review. Sol. Energy 2014, 108, 287–307. [Google Scholar] [CrossRef]
- Nonnenmacher, L.; Kaur, A.; Coimbra Coimbra, C. Day-ahead resource forecasting for concentrated solar power integration. Renew. Energy 2016, 86, 866–876. Available online: http://www.sciencedirect.com/science/article/pii/S0960148115302688 (accessed on 3 December 2019). [CrossRef]
- Gomez-Gil, F.J.; Wang, X.; Barnett, A. Analysis and prediction of energy production in concentrating photovoltaic (CPV) installations. Energies 2012, 5, 770–789. [Google Scholar] [CrossRef]
- Casado-Rubio, J.; Revuelta, M.; Postigo, M.; Martínez-Marco, I.; Yagüe, C.A. Postprocessing Methodology for Direct Normal Irradiance Forecasting Using Cloud Information and Aerosol Load Forecasts. J. Appl. Meteorol. Climatol. 2017, 56, 1595–1608. [Google Scholar] [CrossRef]
- Lopes, F.; Silva, H.; Salgado, R.; Cavaco, A.; Canhoto, P.; Colarres-Pereira, M. Short-term forecasts of GHI and DNI for solar energy systems operation: Assessment of the ECMWF integrated forecasting system in southern Portugal. Sol. Energy 2018, 170, 14–30. [Google Scholar] [CrossRef]
- Lara-Fanego, V.; Ruiz-Arias, J.A.; Pozo-Vázquez, A.D.; Gueymard, C.A.; Tovar-Pescador, J. Evaluation of DNI forecast based on the WRF mesoscale atmospheric model for CPV applications. AIP Conf. Proc.-Am. Inst. Phys. 2012, 1477, 317. [Google Scholar] [CrossRef]
- Troccoli, A.; Morcrette, J.J. Skill of direct solar radiation predicted by the ECMWF global atmospheric model over Australia. J. Appl. Meteorol. Climatol. 2014, 53, 2571–2588. [Google Scholar] [CrossRef]
- Vick, B.D.; Myers, D.R.; Boyson, W.E. Using direct normal irradiance models and utility electrical loading to assess benefit of a concentrating solar power plant. Sol. Energy 2012, 86, 3519–3530. [Google Scholar] [CrossRef]
- Haiden, T.; Rodwell, M.J.; Richardson, D.S.; Okagaki, A.; Robinson, T.; Hewson, T. Intercomparison of global model precipitation forecast skill in 2010/11 using the SEEPS score. Mon. Weather Rev. 2012, 140, 2720–2733. [Google Scholar] [CrossRef]
- Kipp & Zonen. Available online: http://www.kippzonen.com/ (accessed on 15 September 2019).
- World Meteorological Organization (WMO). Guide to Meteorological Instruments and Methods of Observation, (WMO-No. 8), 7th ed.; World Meteorological Organization (WMO): Geneva, Switzerland, 2008; ISBN 978-92-63-100085. [Google Scholar]
- ISO. ISO 9060:1990: Specification and Classification of Instruments for Measuring Hemispherical Solar and Direct Solar Radiation; ISO: Geneva, Switzerland, 1990. [Google Scholar]
- Long, C.N.; Dutton, E.G. BSRN Global Network recommended QC tests, V2. J. Clim. 2010, 25, 8542–8567. [Google Scholar] [CrossRef]
- Hogan, R.J.; Bozzo, A. ECRAD: A new radiation scheme for the IFS. ECMWF Tech. Memo. 2016, 787, 33p. [Google Scholar]
- Morcrette, J.-J.; Barker, H.; Cole, J.; Iacono, M.; Pincus, R. Impact of a new radiation package, mcrad, in the ecmwf integrated forecasting system. Mon. Weather Rev 2008, 136, 4773–4798. [Google Scholar] [CrossRef]
- Tegen, I.; Hoorig, P.; Chin, M.; Fung, I.; Jacob, D.; Penner, J. Contribution of different aerosol species to the global aerosol extinction optical thickness: Estimates from model results. J. Geophys. Res. 1997, 102, 23895–23915. [Google Scholar] [CrossRef]
- Flemming, J.; Benedetti, A.; Inness, A.; Engelen, R.J.; Jones, L.; Huijnen, V.; Rémy, S.; Parrington, M.; Suttie, M.; Bozzo, A.; et al. The CAMS interim reanalysis of carbon monoxide, ozone and aerosol for 2003–2015. Atmos. Chem. Phys. 2017, 17, 1945–1983. [Google Scholar] [CrossRef]
- Fu, Q. An accurate parameterization of the solar radiative properties of cirrus clouds. J. Clim. 1996, 9, 2058–2082. [Google Scholar] [CrossRef]
- European Center for Medium Time Weather Forecasting (ECMWF). Available online: www.ecmwf.int (accessed on 25 August 2019).
- Wild, M.; Schmucki, E. Assessment of global dimming and brightening in IPCC-AR4/CMIP3 models and ERA-40. Clim. Dyn. 2011, 37, 1671–1688. [Google Scholar] [CrossRef]
- Perez, R.; Lorenz, E.; Pelland, S.; Beauharnois, M.; Van Knowe, G.; Hemker, K.; Heinemann, D.; Remund, J.; Müller, S.C.; Traunmüller, W.; et al. Comparison of numerical weather prediction solar irradiance forecasts in the US, Canada and Europe. Sol. Energy 2013, 94, 305–326, ISBN 0038-092X. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Landelius, T.; Lindskog, M.; Körnich, H.; Andersson, S. Short-range solar radiation forecasts over Sweden. Adv. Sci. Res. 2018, 15, 39–44. Available online: https://www.adv-sci-res.net/15/39/2018/asr-15-39-2018.pdf (accessed on 5 December 2019). [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Jafariserajehlou, S.; Mei, L.; Vountas, M.; Rozanov, V.; Burrows, J.P.; Hollmann, R. A cloud identification algorithm over the Arctic for use with AATSR–SLSTR measurements. Atmos. Meas. Tech. 2019, 12, 1059–1076. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Louis Smith, G.; Cooper, J.E. Clouds and the Earth’s Radiant Energy System (CERES): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Polo, J.; Martin, L.; Vindel, J.M. Correcting satellite derived DNI with systematic and seasonal deviations: Application to India. Renew. Energy 2015, 80, 238–243. [Google Scholar] [CrossRef]
- Mejia, J.F.; Giordano, M.; Wilcox, E. Conditional summertime day-ahead solar irradiance forecast. Sol. Energy 2018, 163, 610–622. [Google Scholar] [CrossRef]
- Polo, J.; Wilbert, S.; Ruiz-Arias, J.A.; Meyer, R.; Gueymard, C.; Súri, M.; Martín, L.; Mieslinger, T.; Blanc, P.; Grant, I.; et al. Preliminary survey on site-adaptation techniques for satellite-derived and reanalysis solar radiation datasets. Sol. Energy 2016, 132, 25–37. [Google Scholar] [CrossRef]
- Nonnenmacher, L.; Kaur, A.; Coimbra, C.F.M. Verification of the SUNY direct normal irradiance model with ground measurements. Sol. Energy 2014, 99, 246–258. [Google Scholar] [CrossRef]
- Gala, Y.; Fernandez, A.; Dıaz, J.; Dorronsoro, J. Support vector forecasting of solar radiation values. In Hybrid Artificial Intelligent Systems; Pan, J.-S., Polycarpou, M., Wozniak, M., Carvalho, A.P.L.F., Quintian, H., Corchado, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 51–60. [Google Scholar]
- Almorox, J.; Ovando, G.; Sayago, S.; Bocco, M. Assessment of surface solar irradiance retrieved by CERES. Int. J. Remote Sens. 2017, 38, 3669–3683. [Google Scholar] [CrossRef]
- Royé, D.; Lorenzo, N.; Rasilla, D.; Martí, A. Spatio-temporal variations of cloud fraction based on circulation types in the Iberian Peninsula. Int. J. Climatol. 2019, 39, 1716–1732. [Google Scholar] [CrossRef]
- Lopes, M. Desenvolvimento de um Sistema de Baixo custo para a Previsão da Irradiância Solar a Curto Prazo. Master’s Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2015. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/281870113702447/Dissertacao_67932 (accessed on 3 December 2019).
- Sanchez-Lorenzo, A.; Calbó, J.; Brunetti, M.; Deser, C. Dimming/brightening over the Iberian Peninsula: Trends in sunshine duration and cloud cover and their relations with atmospheric circulation. J. Geophys. Res. 2009, 114, D00D09. [Google Scholar] [CrossRef]
- Freile-Aranda, M.D.; Gomez-Amo, J.L.; Utrillas, M.P.; Pedros, R.; Martínez-Lozano, J.A. Seasonal analysis of cloud characteristics and radiative effect over the Iberian Peninsula using MODIS-CERES observations. Tethys 2017, 14, 3–9. [Google Scholar] [CrossRef]
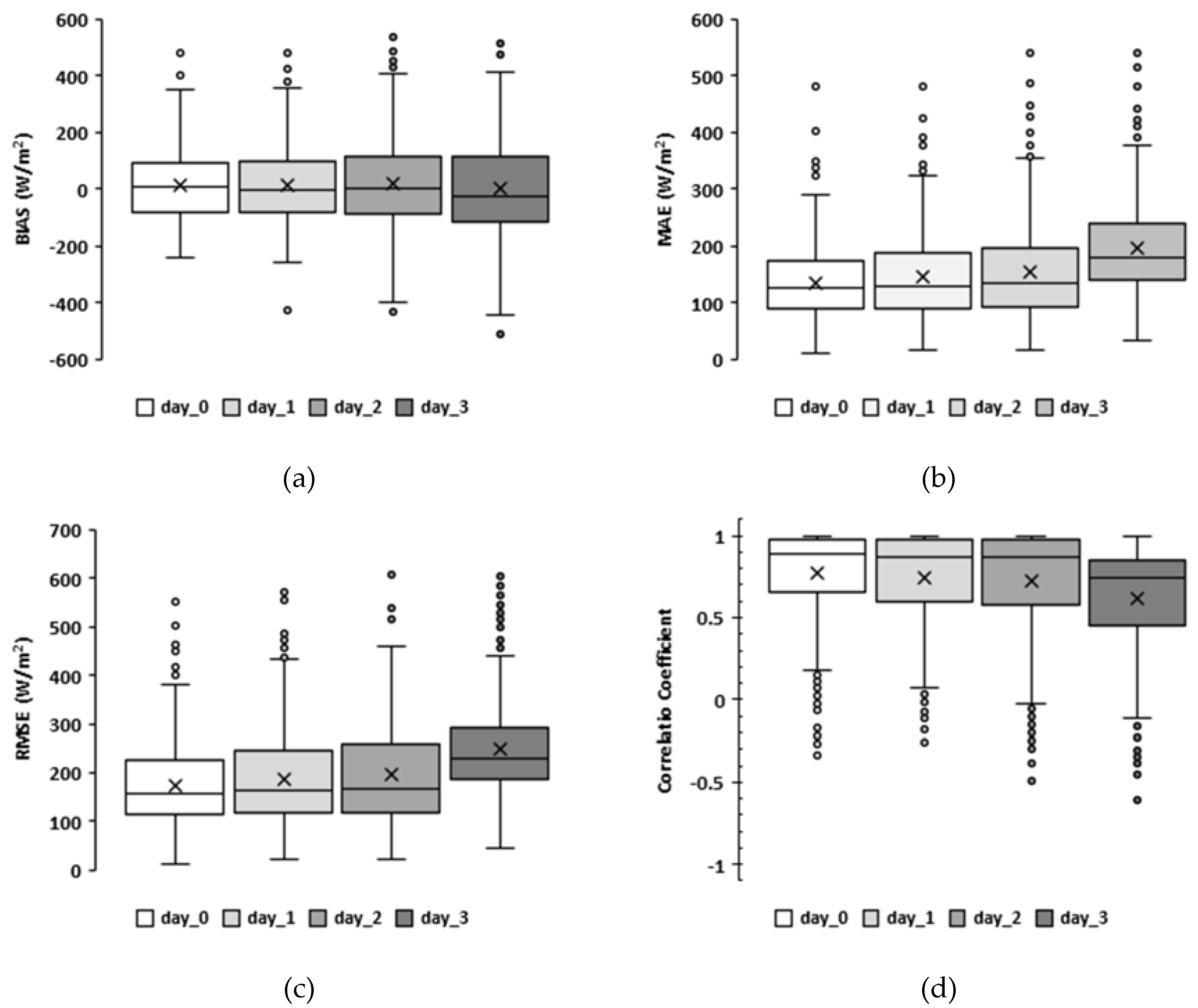
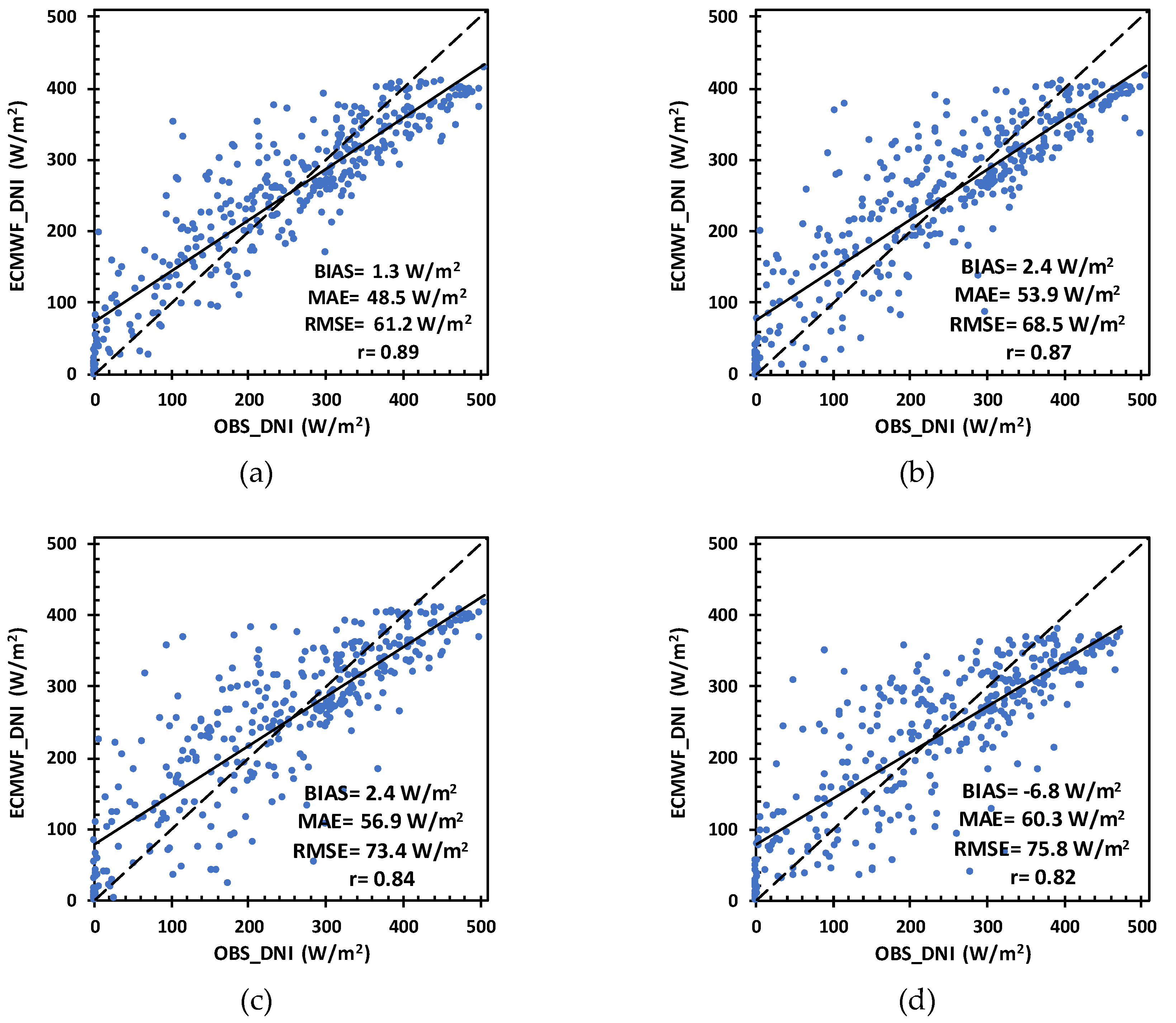
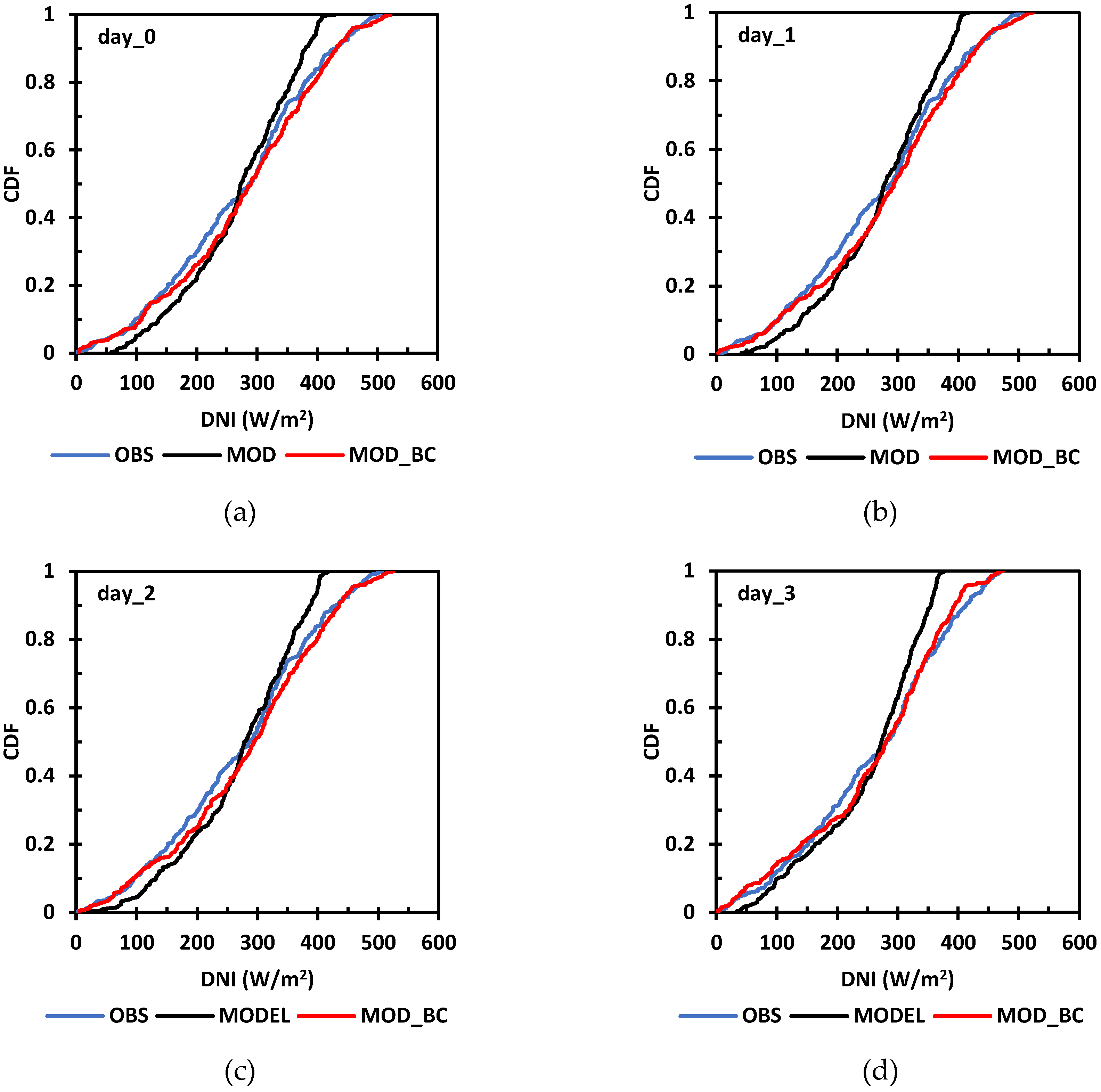
| Day | MBE (W/m2) | MAE (W/m2) | RMSE (W/m2) | |
|---|---|---|---|---|
| 0 | 13.54 | 136.80 | 195.41 | 0.84 |
| 1 | 15.03 | 146.35 | 210.60 | 0.81 |
| 2 | 17.273 | 154.97 | 224.02 | 0.78 |
| 3 | 1.048 | 197.88 | 267.25 | 0.70 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perdigão, J.; Canhoto, P.; Salgado, R.; Costa, M.J. Assessment of Direct Normal Irradiance Forecasts Based on IFS/ECMWF Data and Observations in the South of Portugal. Forecasting 2020, 2, 130-150. https://doi.org/10.3390/forecast2020007
Perdigão J, Canhoto P, Salgado R, Costa MJ. Assessment of Direct Normal Irradiance Forecasts Based on IFS/ECMWF Data and Observations in the South of Portugal. Forecasting. 2020; 2(2):130-150. https://doi.org/10.3390/forecast2020007
Chicago/Turabian StylePerdigão, João, Paulo Canhoto, Rui Salgado, and Maria João Costa. 2020. "Assessment of Direct Normal Irradiance Forecasts Based on IFS/ECMWF Data and Observations in the South of Portugal" Forecasting 2, no. 2: 130-150. https://doi.org/10.3390/forecast2020007
APA StylePerdigão, J., Canhoto, P., Salgado, R., & Costa, M. J. (2020). Assessment of Direct Normal Irradiance Forecasts Based on IFS/ECMWF Data and Observations in the South of Portugal. Forecasting, 2(2), 130-150. https://doi.org/10.3390/forecast2020007







