Quantile Regression and Clustering Models of Prediction Intervals for Weather Forecasts: A Comparative Study
Abstract
:1. Introduction and Background
2. Weather Forecast Uncertainty Modeling
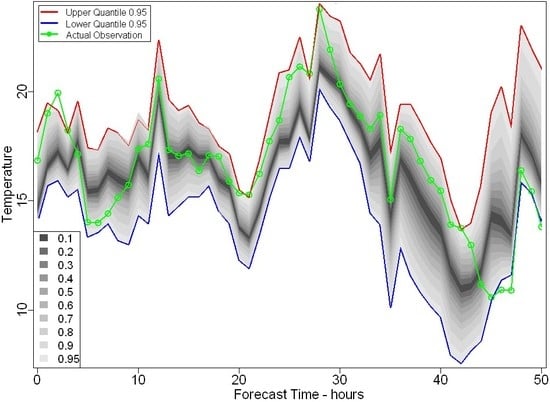
2.1. Prediction Intervals
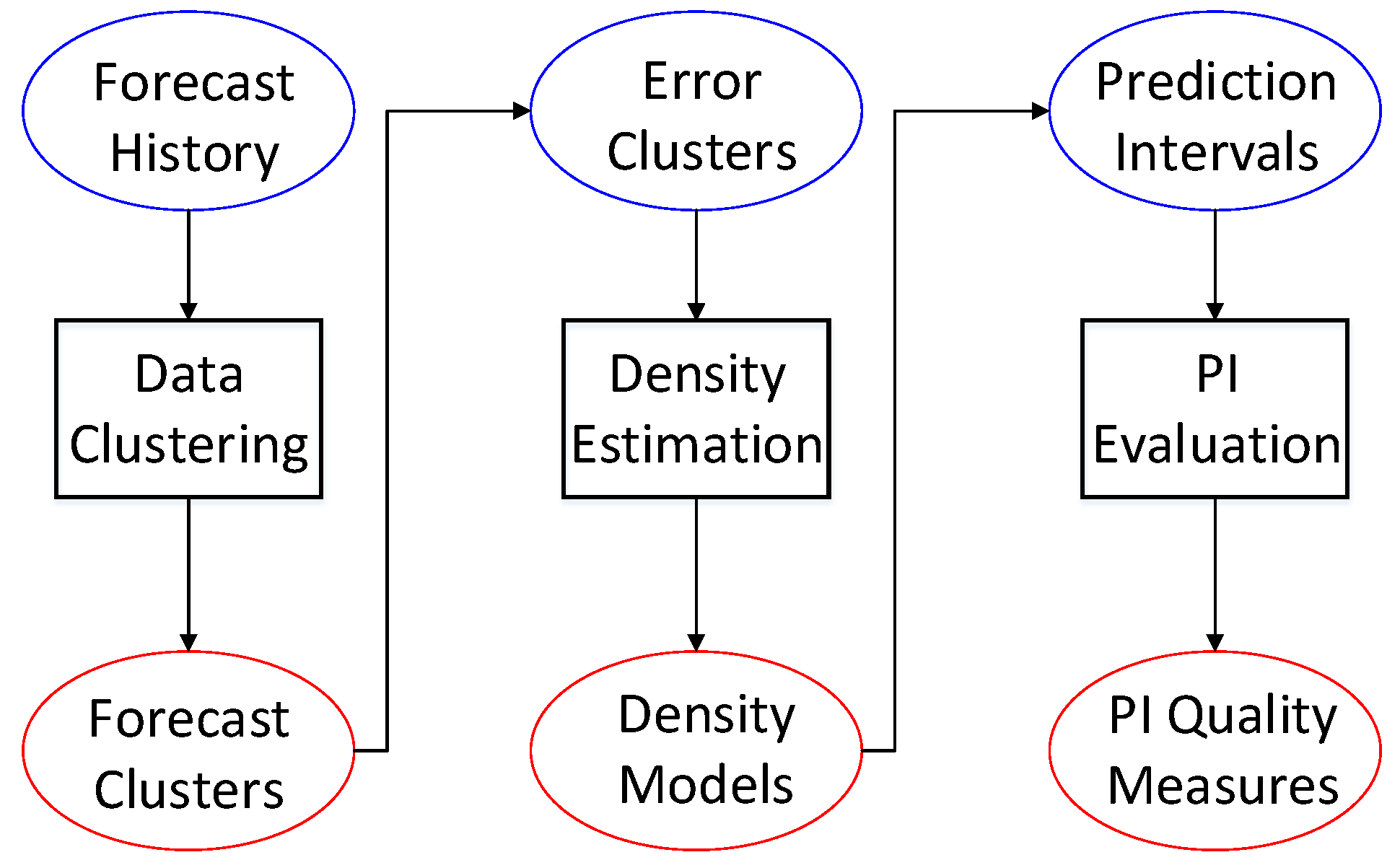
2.2. Prediction Interval Modeling Using Fuzzy Clustering
2.3. Prediction Interval Modeling Using Linear and Non-Linear Quantile Regression
2.3.1. Quantile Regression with Spline-Basis Functions
2.3.2. Local Quantile Regression
2.3.3. Kernel Quantile Regression
3. An Evaluation Framework for Prediction Interval Forecasts
3.1. Basic Verification Measures
3.2. Skill Score for Evaluating Prediction Interval Forecast Models
- when a “hit” occurs for forecast PI of case i, then ; by substituting the values in (14) we have
- in the case of a “missed” observation appearing either on the right or the left side of the PI boundaries, the values of are equal to or , respectively.
- −
- when it is on the right side, it has a positive distance of from the upper boundary ; by substituting these values we have .
- −
- when it is on the left side, an equal score is obtained.
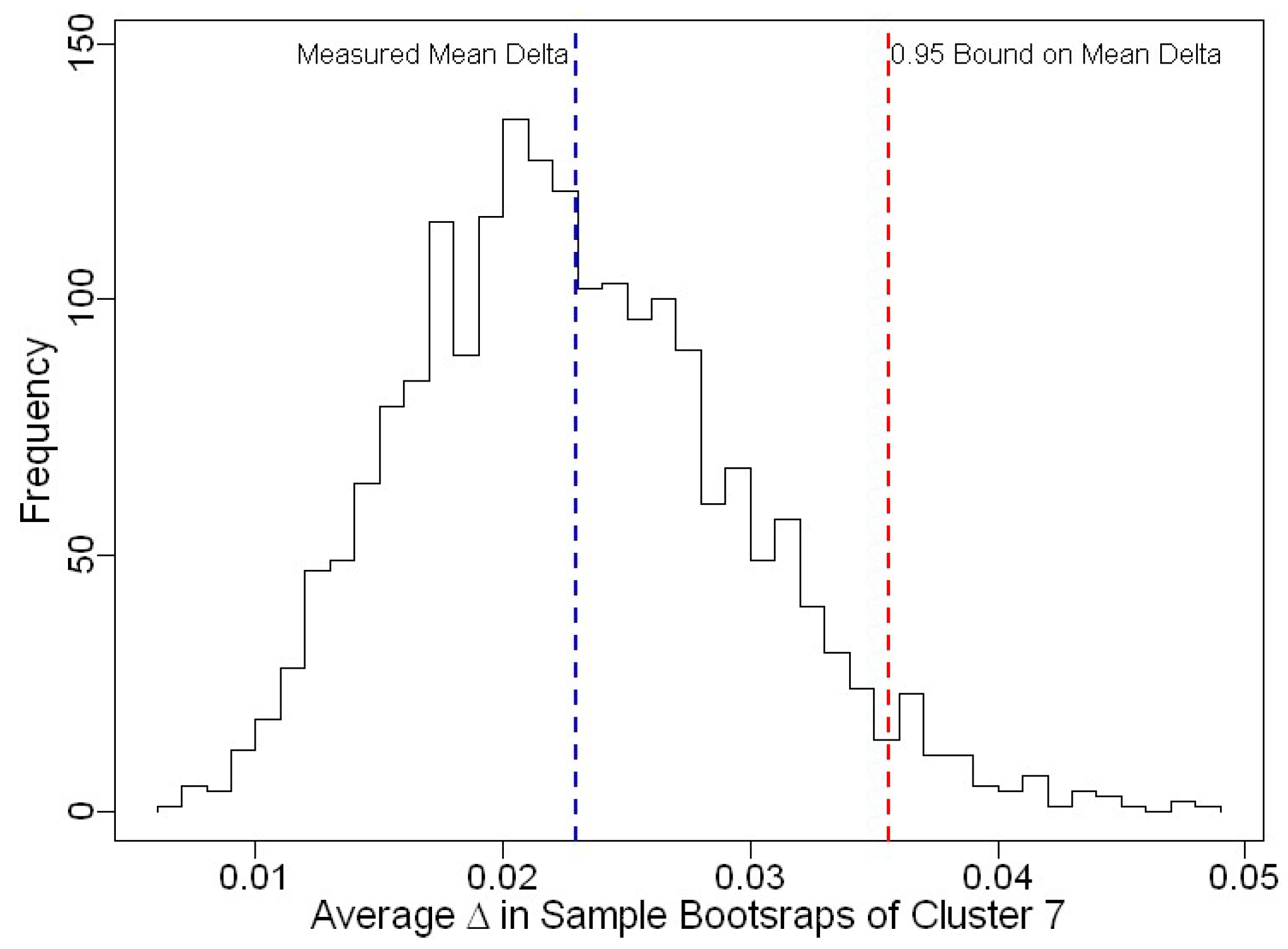
3.3. Uncertainty of Skill Score Measurements
4. Evaluation Study
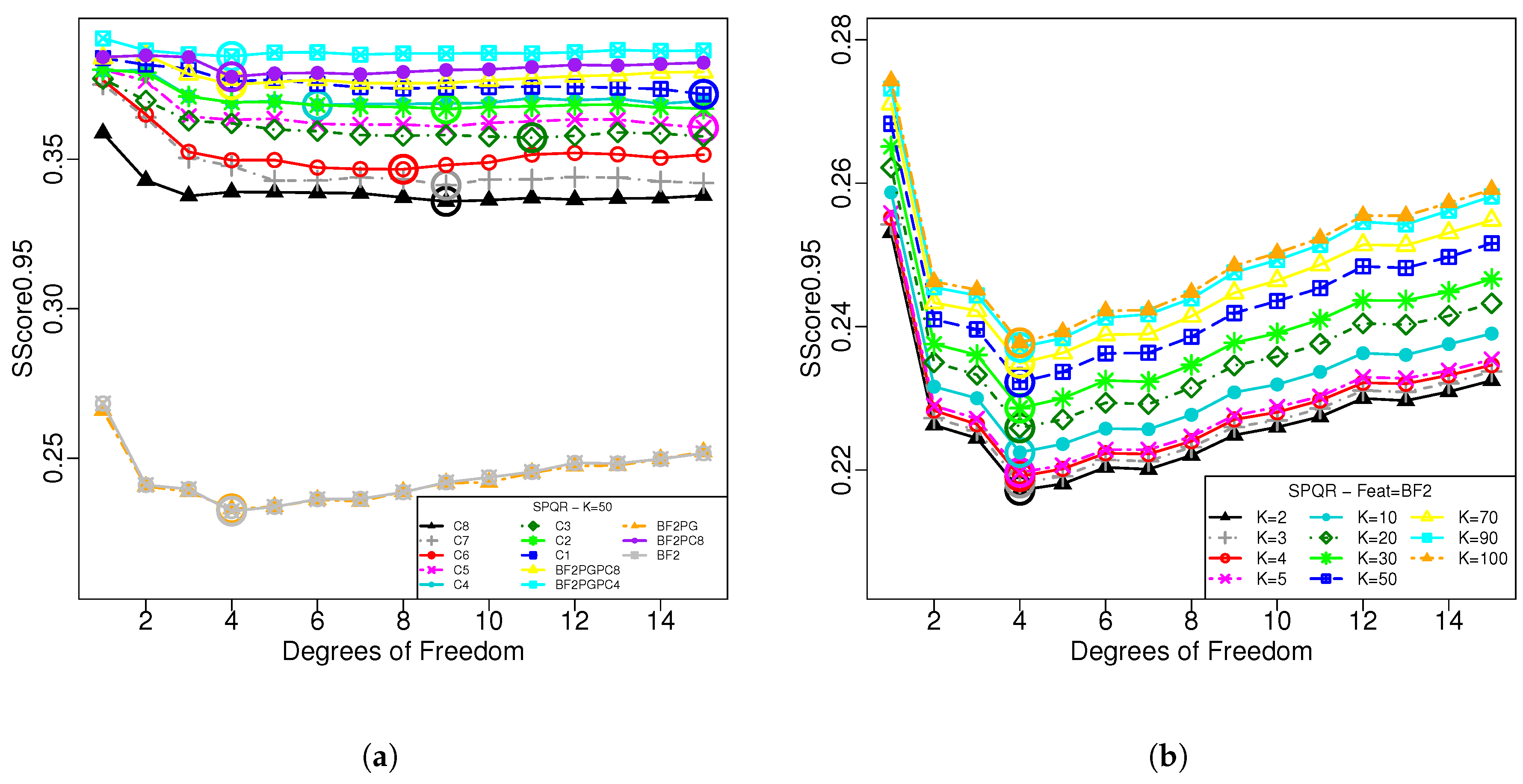
4.1. Data and Models
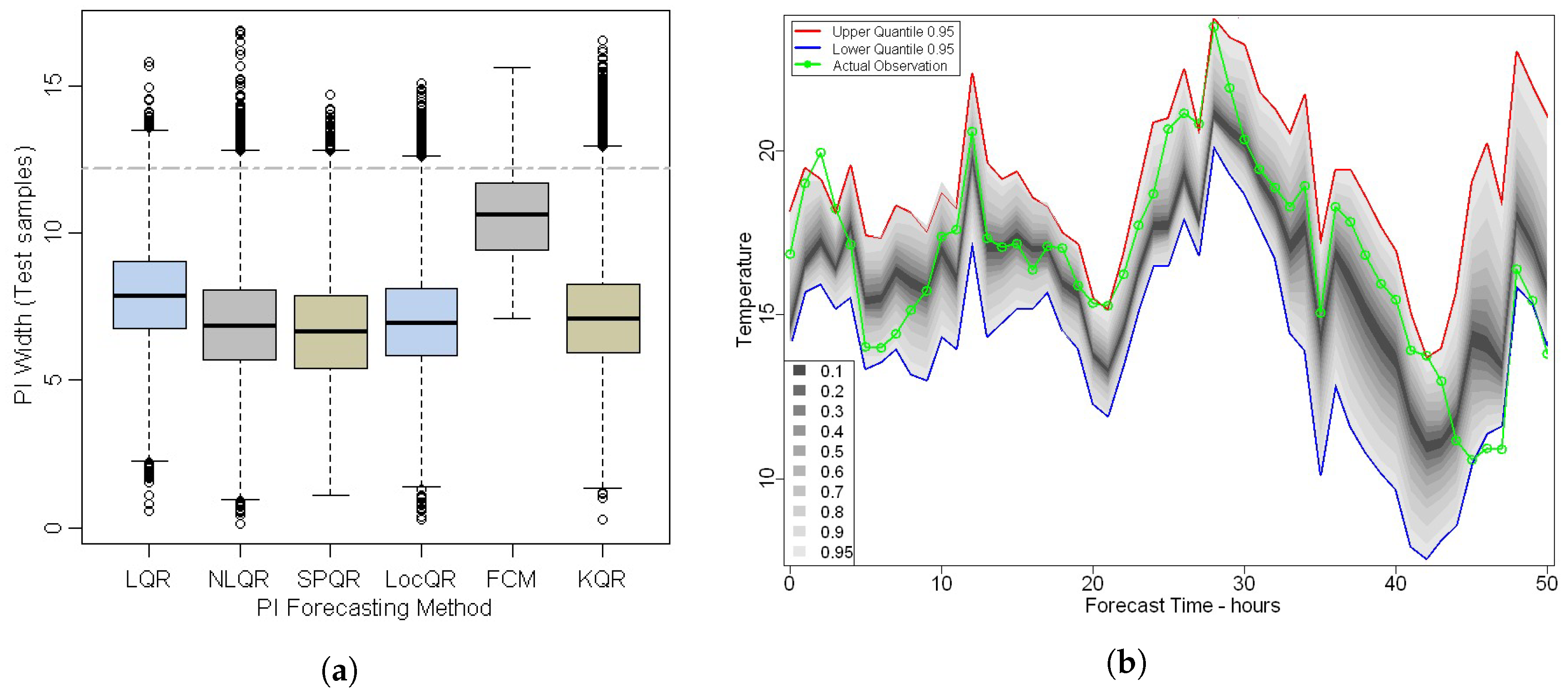
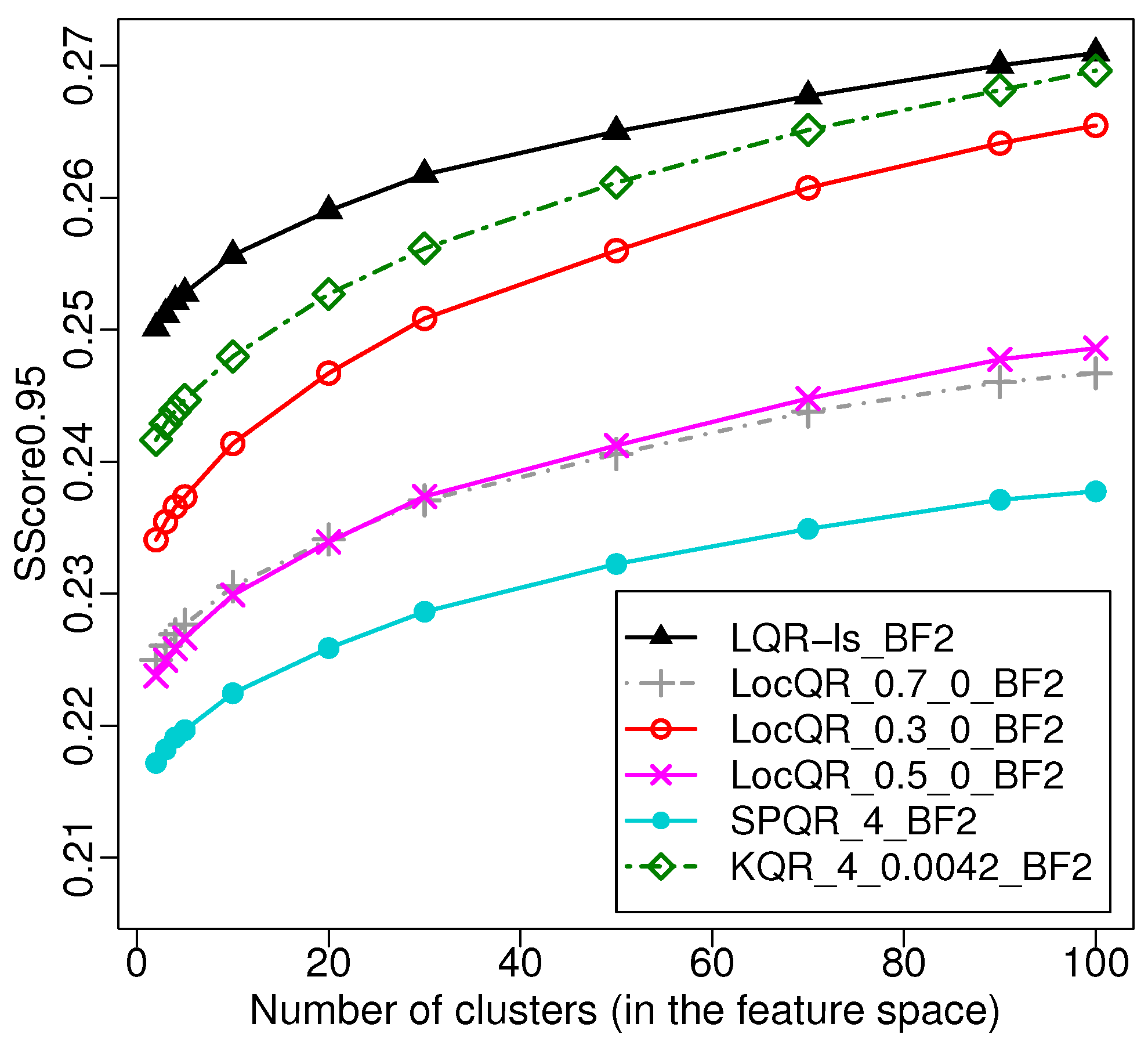
4.2. Comparative Analysis of the PI Forecast Models
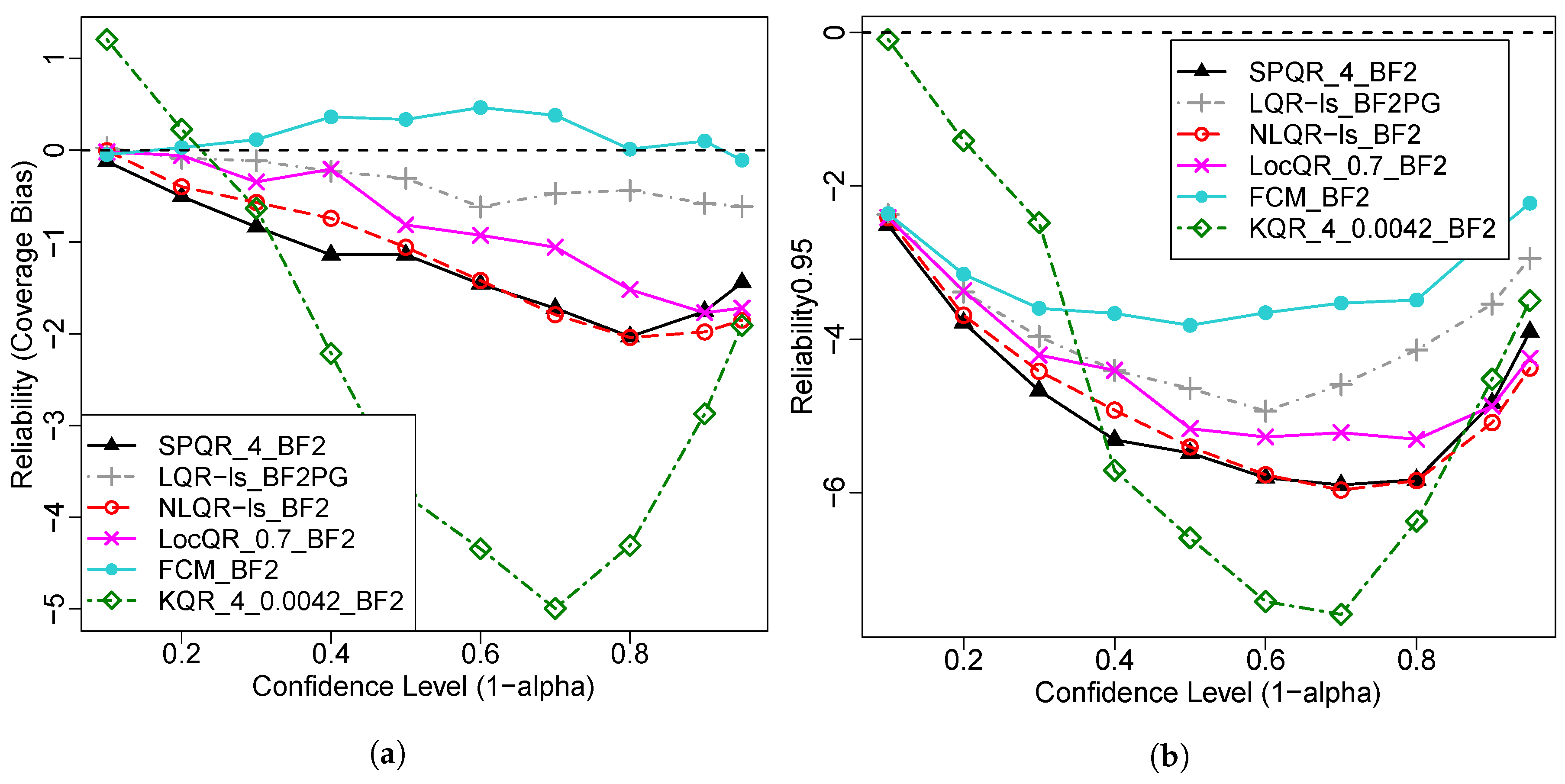
4.3. PI Forecast Evaluation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- The Weather Research and Forecasting (WRF) Model. Available online: http://www.wrf-model.org/index.php (accessed on 21 July 2017).
- Lange, M. Analysis of the Uncertainty of Wind Power Predictions. Ph.D. Thesis, Universität Oldenburg, Oldenburg, Germany, 2003. [Google Scholar]
- Pinson, P. Estimation of the Uncertainty in Wind Power Forecasting. Ph.D. Thesis, École Nationale Supérieure des Mines de Paris, Paris, France, 2006. [Google Scholar]
- Wan, C.; Lin, J.; Wang, J.; Song, Y.; Dong, Z.Y. Direct quantile regression for nonparametric probabilistic forecasting of wind power generation. IEEE Trans. Power Syst. 2017, 32, 2767–2778. [Google Scholar] [CrossRef]
- Andrade, J.R.; Bessa, R.J. Improving Renewable Energy Forecasting with a Grid of Numerical Weather Predictions. IEEE Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef]
- Huang, C.M.; Kuo, C.J.; Huang, Y.C. Short-term wind power forecasting and uncertainty analysis using a hybrid intelligent method. IET Renew. Power Gener. 2017, 11, 678–687. [Google Scholar] [CrossRef]
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Madsen, H. Short-term probabilistic forecasting of wind speed using stochastic differential equations. Int. J. Forecast. 2016, 32, 981–990. [Google Scholar] [CrossRef]
- Juban, R.; Ohlsson, H.; Maasoumy, M.; Poirier, L.; Kolter, J.Z. A multiple quantile regression approach to the wind, solar, and price tracks of GEFCom2014. Int. J. Forecast. 2016, 32, 1094–1102. [Google Scholar] [CrossRef]
- Hosek, J.; Musilek, P.; Lozowski, E.; Pytlak, P. Effect of time resolution of meteorological inputs on dynamic thermal rating calculations. IET Gener. Transm. Distrib. 2011, 5, 941–947. [Google Scholar] [CrossRef]
- Pytlak, P.; Musilek, P.; Lozowski, E.; Toth, J. Modelling precipitation cooling of overhead conductors. Electr. Power Syst. Res. 2011, 81, 2147–2154. [Google Scholar] [CrossRef]
- Shaker, H.; Fotuhi-Firuzabad, M.; Aminifar, F. Fuzzy dynamic thermal rating of transmission lines. IEEE Trans. Power Deliv. 2012, 27, 1885–1892. [Google Scholar] [CrossRef]
- Shaker, H.; Zareipour, H.; Fotuhi-Firuzabad, M. Reliability modeling of dynamic thermal rating. IEEE Trans. Power Deliv. 2013, 28, 1600–1609. [Google Scholar] [CrossRef]
- Aznarte, J.L.; Siebert, N. Dynamic line rating using numerical weather predictions and machine learning: A case study. IEEE Trans. Power Deliv. 2017, 32, 335–343. [Google Scholar] [CrossRef]
- Pytlak, P.; Musilek, P.; Lozowski, E.; Arnold, D. Evolutionary optimization of an ice accretion forecasting system. Mon. Weather Rev. 2010, 138, 2913–2929. [Google Scholar] [CrossRef]
- Jamali, A.; Ghamati, M.; Ahmadi, B.; Nariman-Zadeh, N. Probability of failure for uncertain control systems using neural networks and multi-objective uniform-diversity genetic algorithms (MUGA). Eng. Appl. Artif. Intell. 2013, 26, 714–723. [Google Scholar] [CrossRef]
- Mazloumi, E.; Rose, G.; Currie, G.; Moridpour, S. Prediction intervals to account for uncertainties in neural network predictions: Methodology and application in bus travel time prediction. Eng. Appl. Artif. Intell. 2011, 24, 534–542. [Google Scholar] [CrossRef]
- Heckenbergerová, J.; Musilek, P.; Filimonenkov, K. Quantification of gains and risks of static thermal rating based on typical meteorological year. Int. J. Electr. Power Energy Syst. 2013, 44, 227–235. [Google Scholar] [CrossRef]
- Chatfield, C. Calculating interval forecasts. J. Bus. Econ. Stat. 1993, 11, 121–135. [Google Scholar]
- Hahn, G.J.; Meeker, W.Q. Statistical Intervals: A Guide for Practitioners; John Wiley & Sons: New York, NY, USA, 2011; Volume 328. [Google Scholar]
- Pinson, P.; Kariniotakis, G. Conditional prediction intervals of wind power generation. IEEE Trans. Power Syst. 2010, 25, 1845–1856. [Google Scholar] [CrossRef]
- Ehrendorfer, M. Predicting the uncertainty of numerical weather forecasts: A review. Meteorol. Z. 1997, 6, 147–183. [Google Scholar] [CrossRef]
- Richardson, D.S. Skill and relative economic value of the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 2000, 126, 649–667. [Google Scholar] [CrossRef]
- Nipen, T.; Stull, R. Calibrating probabilistic forecasts from an NWP ensemble. Tellus A 2011, 63, 858–875. [Google Scholar] [CrossRef]
- Bach, F.R.; Jordan, M.I. Kernel independent component analysis. J. Mach. Learn. Res. 2002, 3, 1–48. [Google Scholar]
- Bessa, R.J.; Miranda, V.; Botterud, A.; Wang, J.; Constantinescu, E.M. Time adaptive conditional kernel density estimation for wind power forecasting. IEEE Trans. Sustain. Energy 2012, 3, 660–669. [Google Scholar] [CrossRef]
- Bremnes, J.B. A comparison of a few statistical models for making quantile wind power forecasts. Wind Energy 2006, 9, 3–11. [Google Scholar] [CrossRef]
- Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Using quantile regression to extend an existing wind power forecasting system with probabilistic forecasts. Wind Energy 2006, 9, 95–108. [Google Scholar] [CrossRef]
- Pinson, P.; Nielsen, H.A.; Møller, J.K.; Madsen, H.; Kariniotakis, G.N. Non-parametric probabilistic forecasts of wind power: Required properties and evaluation. Wind Energy 2007, 10, 497–516. [Google Scholar] [CrossRef]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Zarnani, A.; Musilek, P.; Heckenbergerova, J. Clustering numerical weather forecasts to obtain statistical prediction intervals. Meteorol. Appl. 2014, 21, 605–618. [Google Scholar] [CrossRef]
- Yu, K.; Lu, Z.; Stander, J. Quantile regression: Applications and current research areas. J. R. Stat. Soc. Ser. D 2003, 52, 331–350. [Google Scholar] [CrossRef]
- Bremnes, J.B. Probabilistic wind power forecasts using local quantile regression. Wind Energy 2004, 7, 47–54. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Zhu, J. Quantile regression in reproducing kernel Hilbert spaces. J. Am. Stat. Assoc. 2007, 102, 255–268. [Google Scholar] [CrossRef]
- Zarnani, A.; Musilek, P. Learning uncertainty models from weather forecast performance databases using quantile regression. In Proceedings of the 25th International Conference on Scientific and Statistical Database Management, Baltimore, MD, USA, 29–31 July 2013; p. 16. [Google Scholar]
- Zarnani, A.; Musilek, P. Modeling Forecast Uncertainty Using Fuzzy Clustering. In Soft Computing Models in Industrial and Environmental Applications; Springer: Berlin, Germany, 2013; pp. 287–296. [Google Scholar]
- Candille, G.; Talagrand, O. Evaluation of probabilistic prediction systems for a scalar variable. Q. J. R. Meteorol. Soc. 2005, 131, 2131–2150. [Google Scholar] [CrossRef]
- Candille, G.; Côté, C.; Houtekamer, P.; Pellerin, G. Verification of an ensemble prediction system against observations. Mon. Weather Rev. 2007, 135, 2688–2699. [Google Scholar] [CrossRef]
- Bröcker, J.; Smith, L.A. Scoring probabilistic forecasts: The importance of being proper. Weather Forecast. 2007, 22, 382–388. [Google Scholar] [CrossRef]
- Bröcker, J. Reliability, sufficiency, and the decomposition of proper scores. Q. J. R. Meteorol. Soc. 2009, 135, 1512–1519. [Google Scholar] [CrossRef] [Green Version]
- Weigel, A.P.; Liniger, M.; Appenzeller, C. Can multi-model combination really enhance the prediction skill of probabilistic ensemble forecasts? Q. J. R. Meteorol. Soc. 2008, 134, 241–260. [Google Scholar] [CrossRef]
- Weigel, A.P.; Mason, S.J. The generalized discrimination score for ensemble forecasts. Mon. Weather Rev. 2011, 139, 3069–3074. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Number 38 in Econometric Society Monographs; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Møller, J.K.; Nielsen, H.A.; Madsen, H. Time-adaptive quantile regression. Comput. Stat. Data Anal. 2008, 52, 1292–1303. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; CRC Press: Boca Raton, FL, USA, 1990; Volume 43. [Google Scholar]
- Yu, K.; Jones, M. Local linear quantile regression. J. Am. Stat. Assoc. 1998, 93, 228–237. [Google Scholar] [CrossRef]
- Takeuchi, I.; Le, Q.V.; Sears, T.D.; Smola, A.J. Nonparametric quantile estimation. J. Mach. Learn. Res. 2006, 7, 1231–1264. [Google Scholar]
- Casati, B.; Wilson, L.; Stephenson, D.; Nurmi, P.; Ghelli, A.; Pocernich, M.; Damrath, U.; Ebert, E.; Brown, B.; Mason, S. Forecast verification: Current status and future directions. Meteorol. Appl. 2008, 15, 3–18. [Google Scholar] [CrossRef]
- Roulston, M.S.; Smith, L.A. Evaluating probabilistic forecasts using information theory. Mon. Weather Rev. 2002, 130, 1653–1660. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: New York, NY, USA, 2011; Volume 100. [Google Scholar]
- Winkler, R.L. A decision-theoretic approach to interval estimation. J. Am. Stat. Assoc. 1972, 67, 187–191. [Google Scholar] [CrossRef]
- Gneiting, T.; Katzfuss, M. Probabilistic forecasting. Annu. Rev. Stat. Appl. 2014, 1, 125–151. [Google Scholar] [CrossRef]
- Mason, S.J. On using “climatology” as a reference strategy in the Brier and ranked probability skill scores. Mon. Weather Rev. 2004, 132, 1891–1895. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Gaba, A.; Tsetlin, I.; Winkler, R.L. Combining interval forecasts. Decis. Anal. 2017, 14, 1–20. [Google Scholar] [CrossRef]




| Feat Set | m | d | h | t2 | ws | wd | sp | pg |
|---|---|---|---|---|---|---|---|---|
| C1 | • | • | ||||||
| C2 | • | • | • | |||||
| C3 | • | • | • | • | ||||
| C4 | • | • | • | • | ||||
| C5 | • | • | • | • | ||||
| C6 | • | • | • | • | • | • | ||
| C7 | • | • | • | • | • | • | • | • |
| Feature Set | Basic Feats. | Pressure Levels Feats. | pg1, pg3, pg6, pg12 | PCA |
|---|---|---|---|---|
| BF1 | • | |||
| BF2 | • | • | ||
| BF2PG | • | • | • | |
| BF2PC8 | • | • | ||
| BF2PGPC4 | • | • | • | • |
| BF2PGPC8 | • | • | • | • |
| Algorithm | K | Features | Fit/Params | Sharpness (C) | Coverage (%) | Coverage (%) | Resolution | RMSE | SScore | SScore |
|---|---|---|---|---|---|---|---|---|---|---|
| SPQR | 50 | BF2 | ||||||||
| LocQR | 50 | BF2 | ||||||||
| NLQR | 50 | BF2 | - | |||||||
| KQR | 50 | BF2 | ||||||||
| LQR | 50 | BF2PG | - | |||||||
| FCM | 45 | BF2 | Kernel | |||||||
| Base-Month | 12 | Month | Kernel | |||||||
| Base-Temp. | 10 | Normal | Temp. | |||||||
| Base-Clim. | 1 | - | Normal |
| Algorithm | Avg. (C) | Miss (Left)% | Hit (Center)% | Miss (Right)% | Avg. (C) | Miss (Left)% | Hit (Center)% | Miss (Right)% | Avg. (C) | Miss (Left)% | Hit (Center)% | Miss (Right)% |
| SPQR | 0.70 | 3.3 | 93.6 | 3.2 | 1.06 | 25.8 | 48.9 | 25.3 | 1.35 | 45.5 | 9.9 | 44.6 |
| LocQR | 0.75 | 3.4 | 93.5 | 3.2 | 1.11 | 26.8 | 49.2 | 24.0 | 1.41 | 46.8 | 10.0 | 43.2 |
| NLQR | 0.78 | 3.4 | 93.2 | 3.4 | 1.12 | 25.8 | 48.9 | 25.3 | 1.42 | 45.3 | 10.0 | 53.7 |
| KQR | 0.82 | 3.4 | 93.1 | 3.5 | 1.20 | 28.4 | 46.2 | 25.4 | 1.55 | 46.3 | 11.2 | 42.5 |
| LQR | 0.82 | 2.8 | 94.4 | 2.9 | 1.22 | 25.2 | 49.7 | 25.1 | 1.55 | 45.1 | 10.0 | 54.0 |
| FCM | 1.08 | 2.7 | 94.9 | 2.4 | 1.62 | 24.8 | 50.3 | 24.9 | 2.03 | 44.9 | 10.0 | 45.2 |
| Base-Month | 1.11 | 2.5 | 95.1 | 2.4 | 1.82 | 24.6 | 50.7 | 26.6 | 2.32 | 44.8 | 10.3 | 44.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarnani, A.; Karimi, S.; Musilek, P. Quantile Regression and Clustering Models of Prediction Intervals for Weather Forecasts: A Comparative Study. Forecasting 2019, 1, 169-188. https://doi.org/10.3390/forecast1010012
Zarnani A, Karimi S, Musilek P. Quantile Regression and Clustering Models of Prediction Intervals for Weather Forecasts: A Comparative Study. Forecasting. 2019; 1(1):169-188. https://doi.org/10.3390/forecast1010012
Chicago/Turabian StyleZarnani, Ashkan, Soheila Karimi, and Petr Musilek. 2019. "Quantile Regression and Clustering Models of Prediction Intervals for Weather Forecasts: A Comparative Study" Forecasting 1, no. 1: 169-188. https://doi.org/10.3390/forecast1010012
APA StyleZarnani, A., Karimi, S., & Musilek, P. (2019). Quantile Regression and Clustering Models of Prediction Intervals for Weather Forecasts: A Comparative Study. Forecasting, 1(1), 169-188. https://doi.org/10.3390/forecast1010012