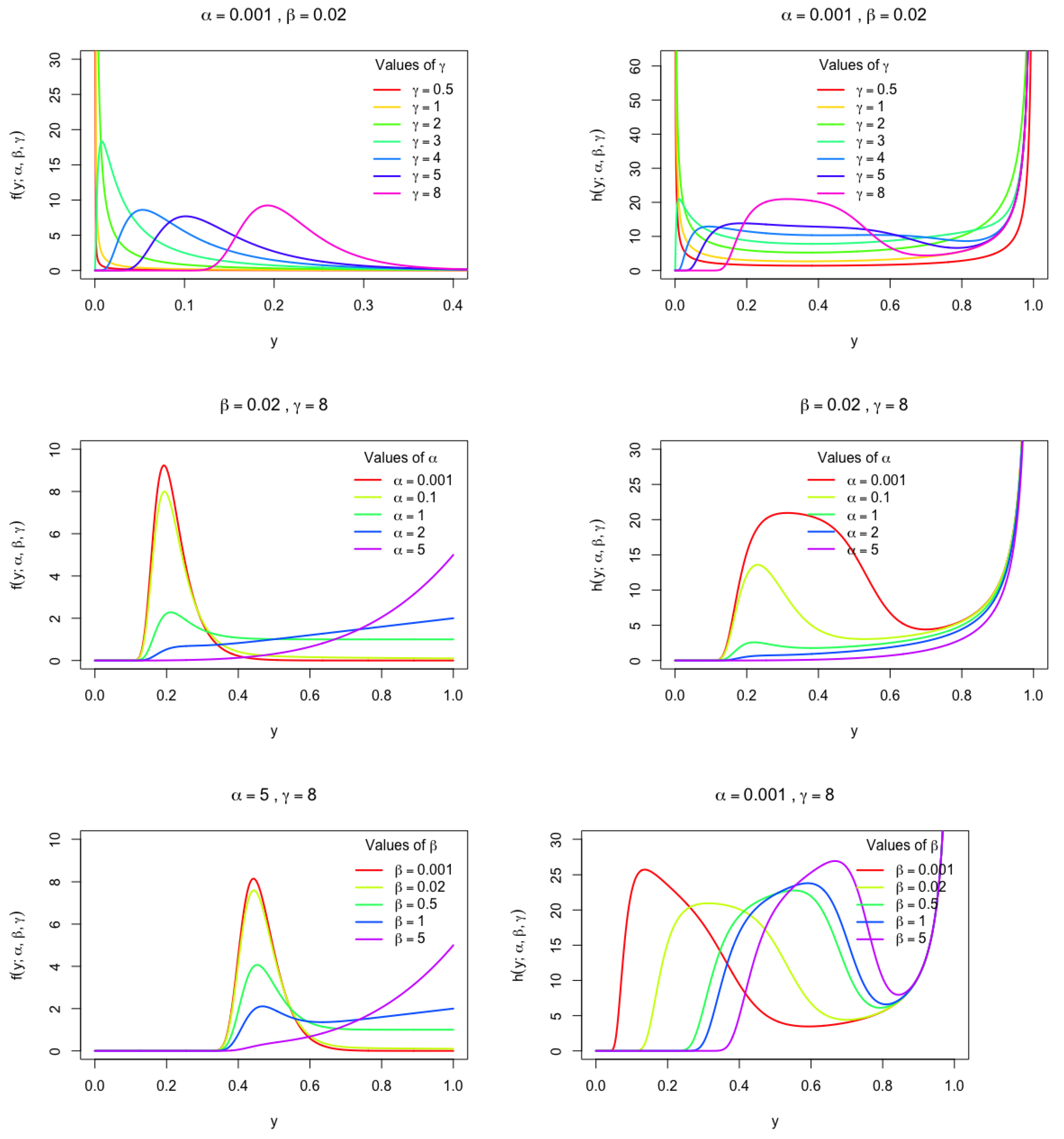
Figure 1.
The PDF and HRF of UMW distribution for different values of .
Figure 1.
The PDF and HRF of UMW distribution for different values of .
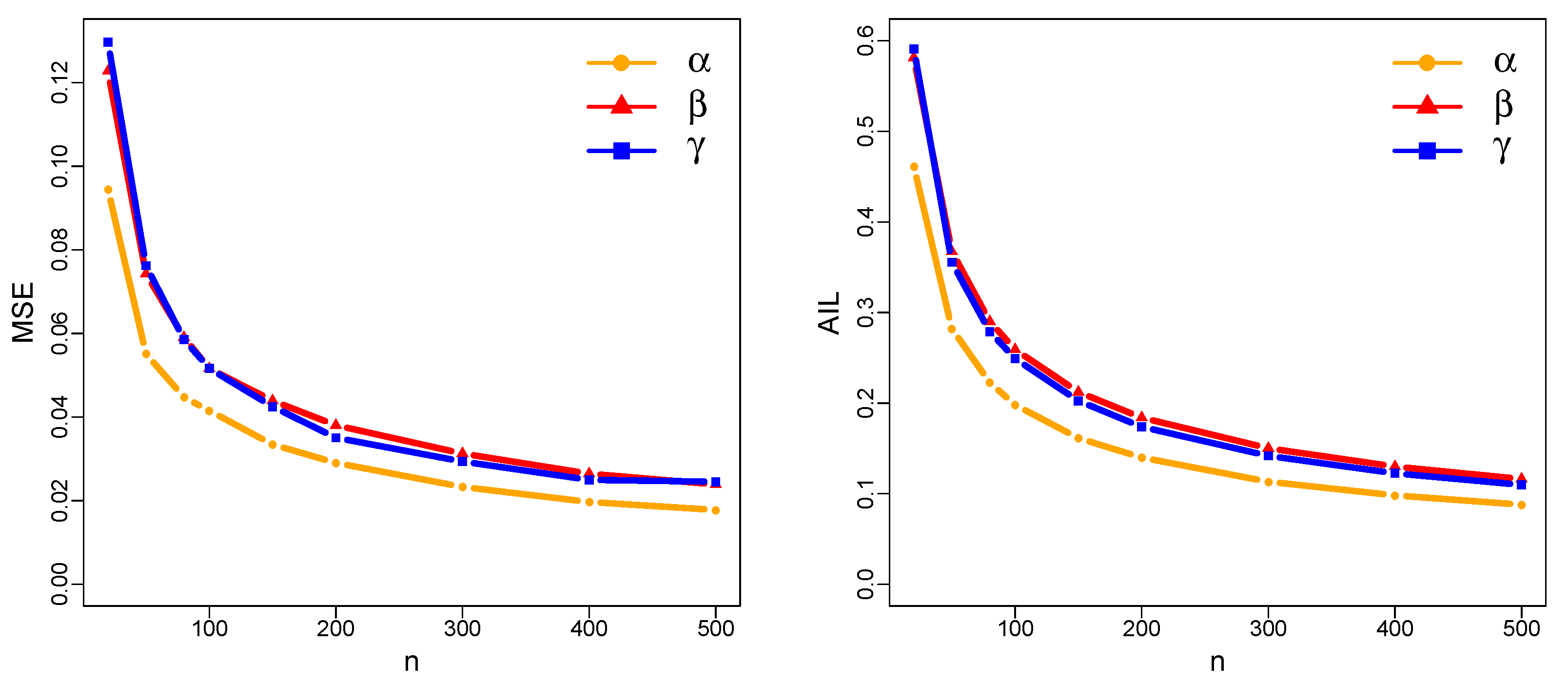
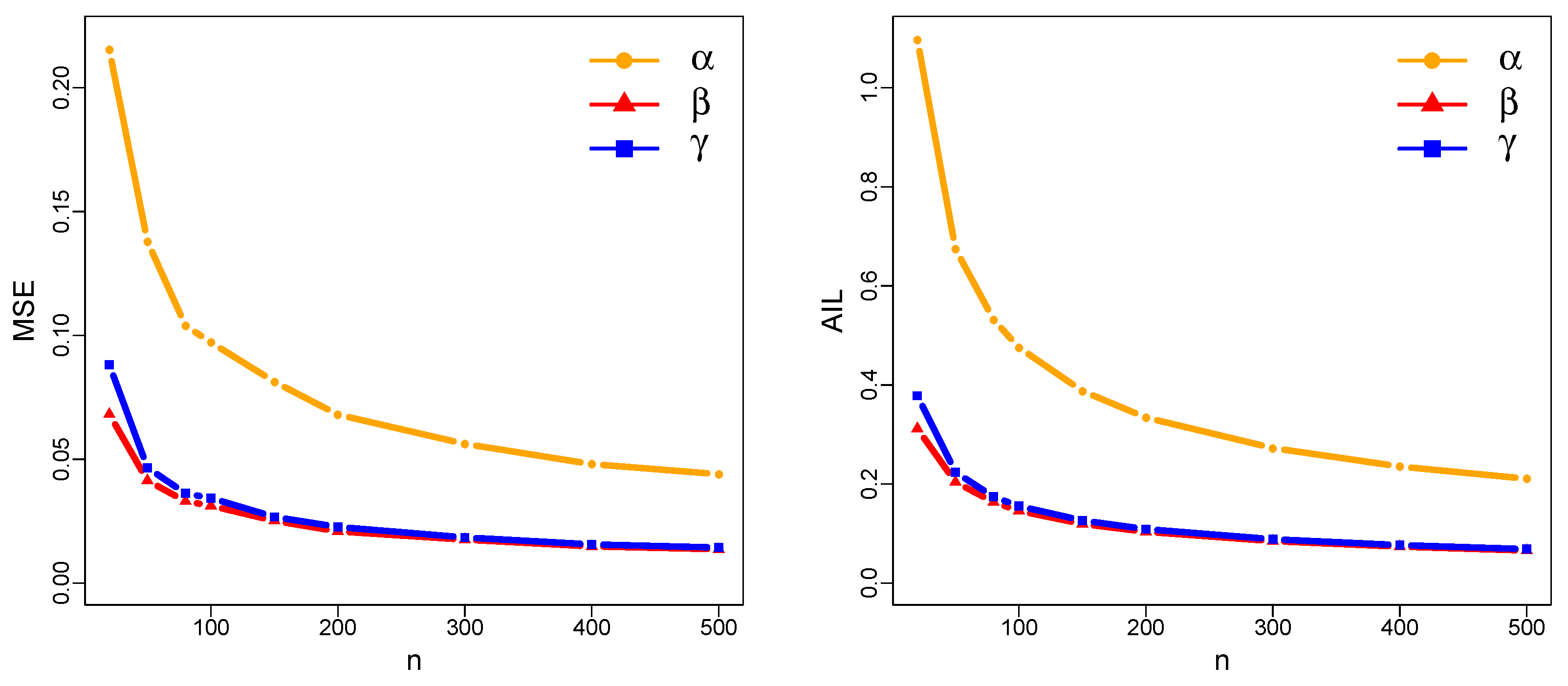
Figure 2.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
Figure 2.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
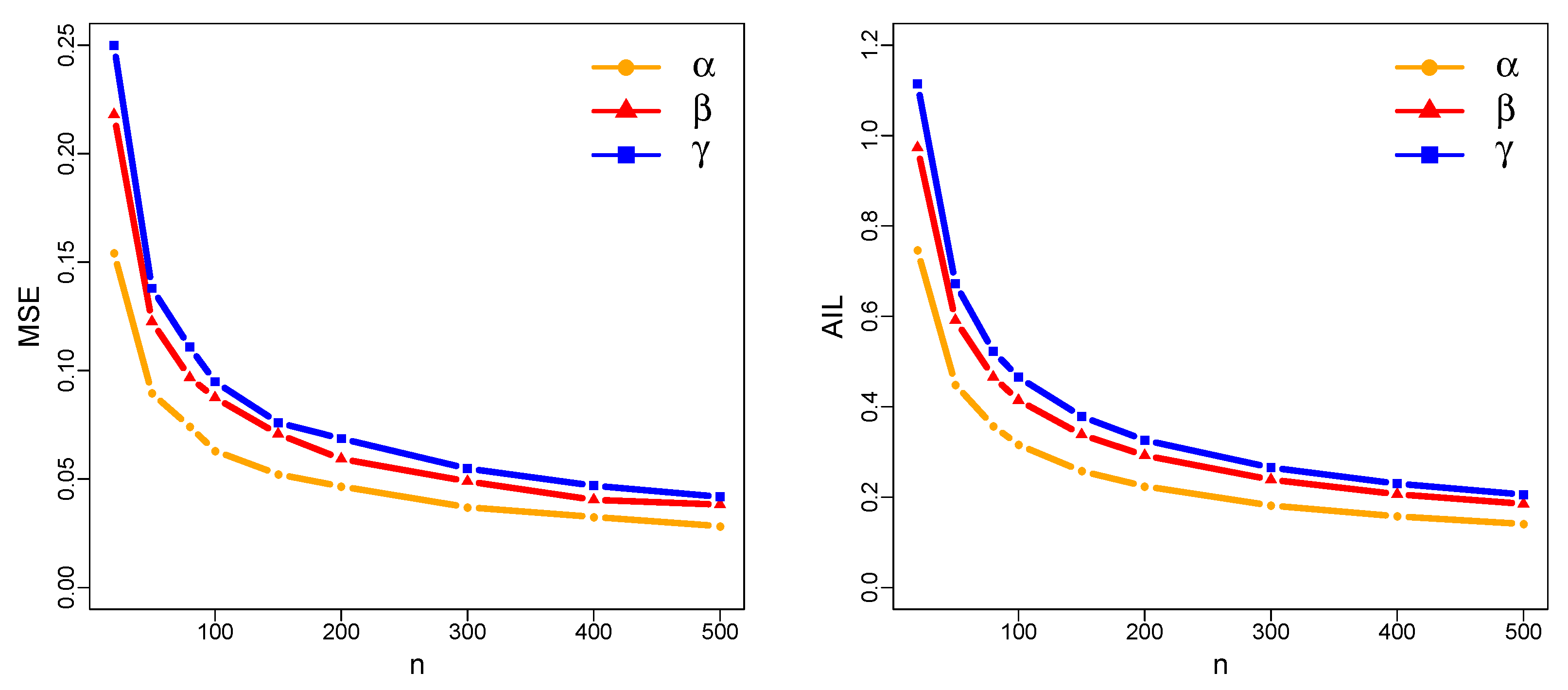
Figure 3.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
Figure 3.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
Figure 4.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
Figure 4.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
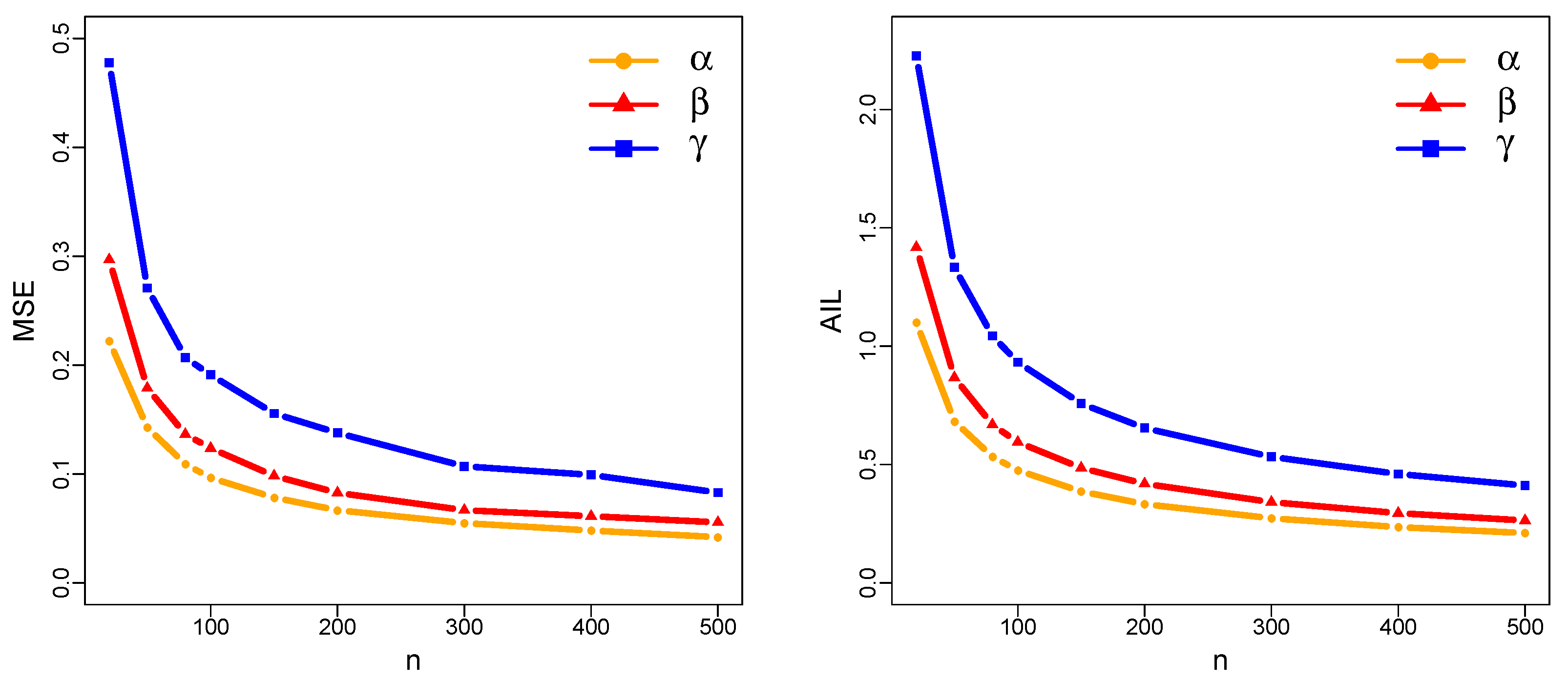
Figure 5.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
Figure 5.
The MSE of the MLE obtained via simulation, with true parameter values , , and .
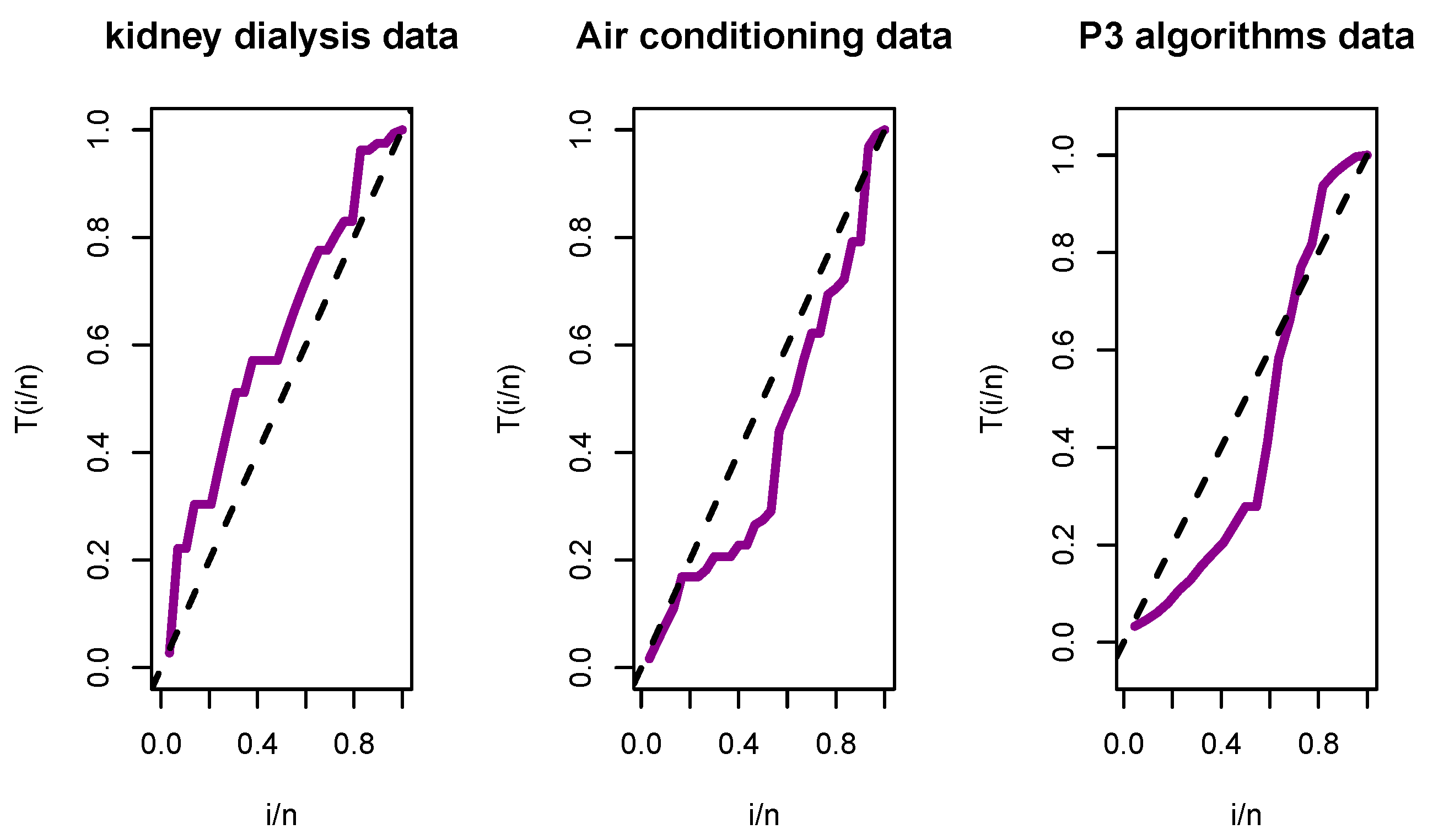
Figure 6.
TTT plot for the three data sets.
Figure 6.
TTT plot for the three data sets.
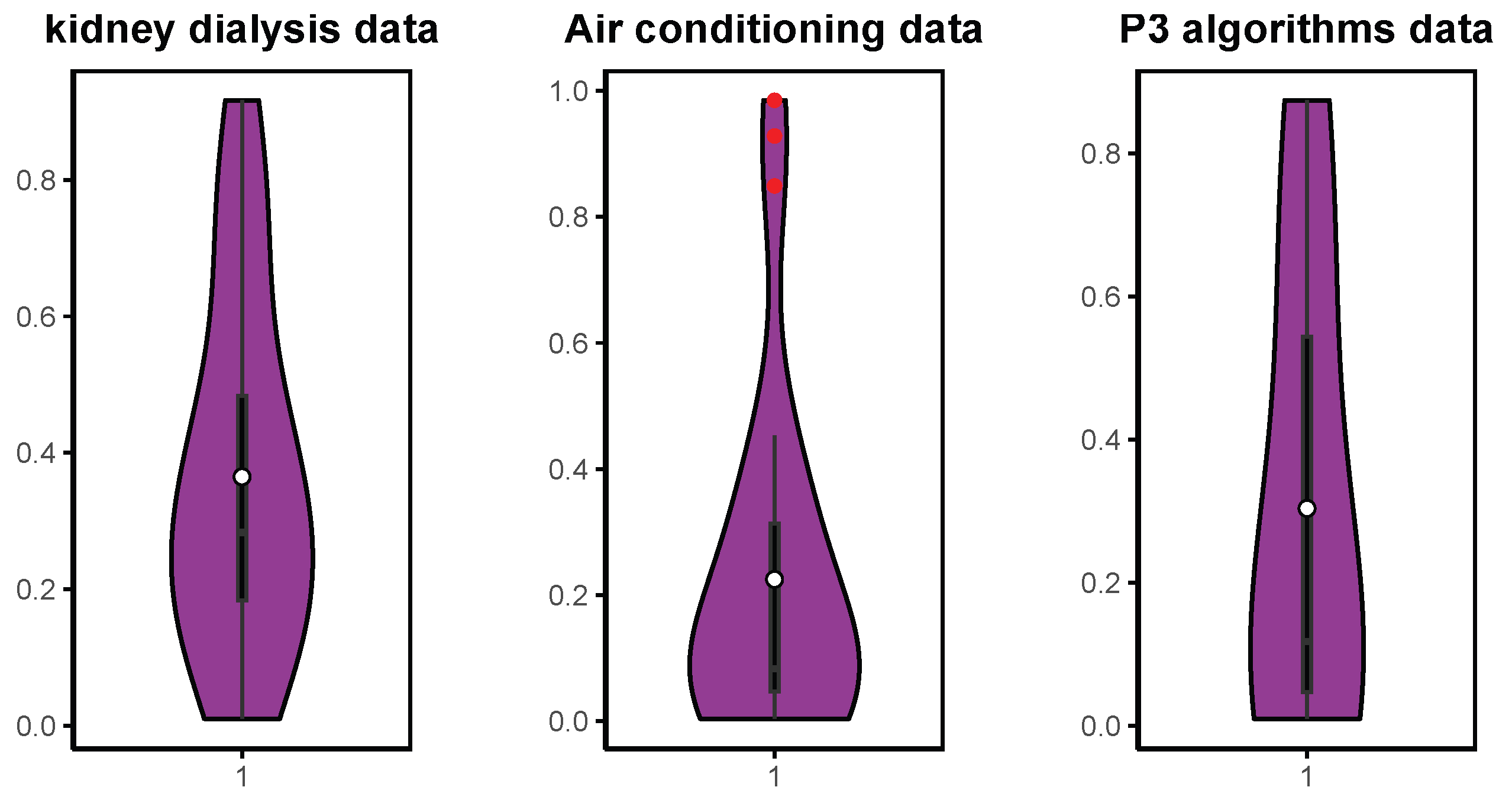
Figure 7.
The violin plots for the three data sets.
Figure 7.
The violin plots for the three data sets.
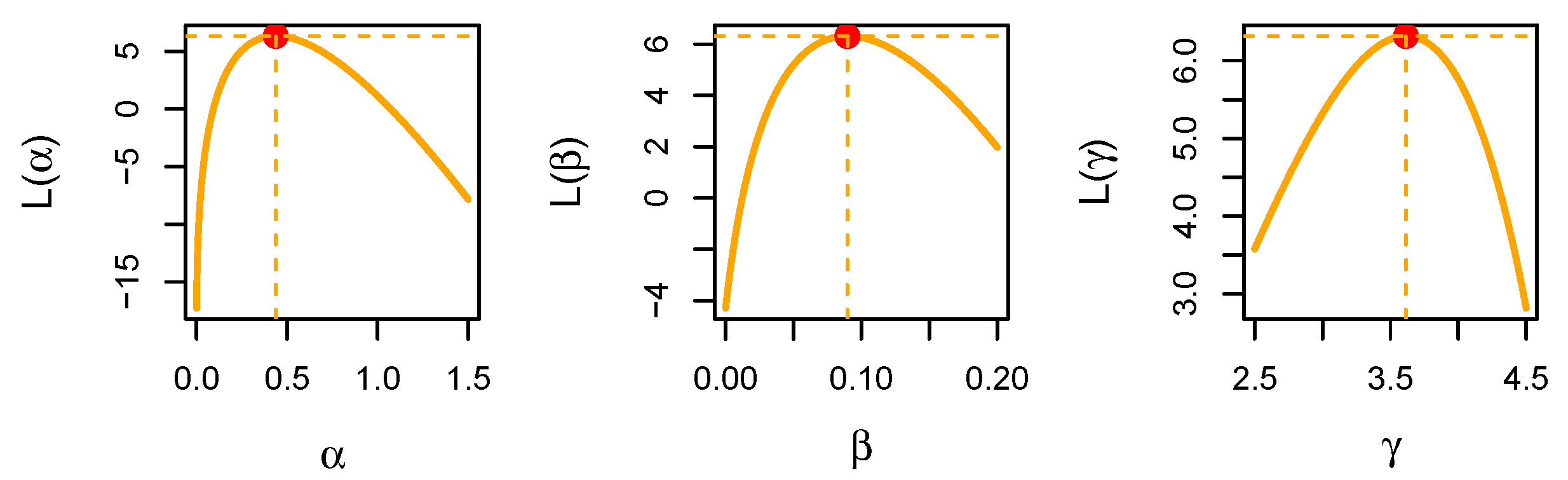
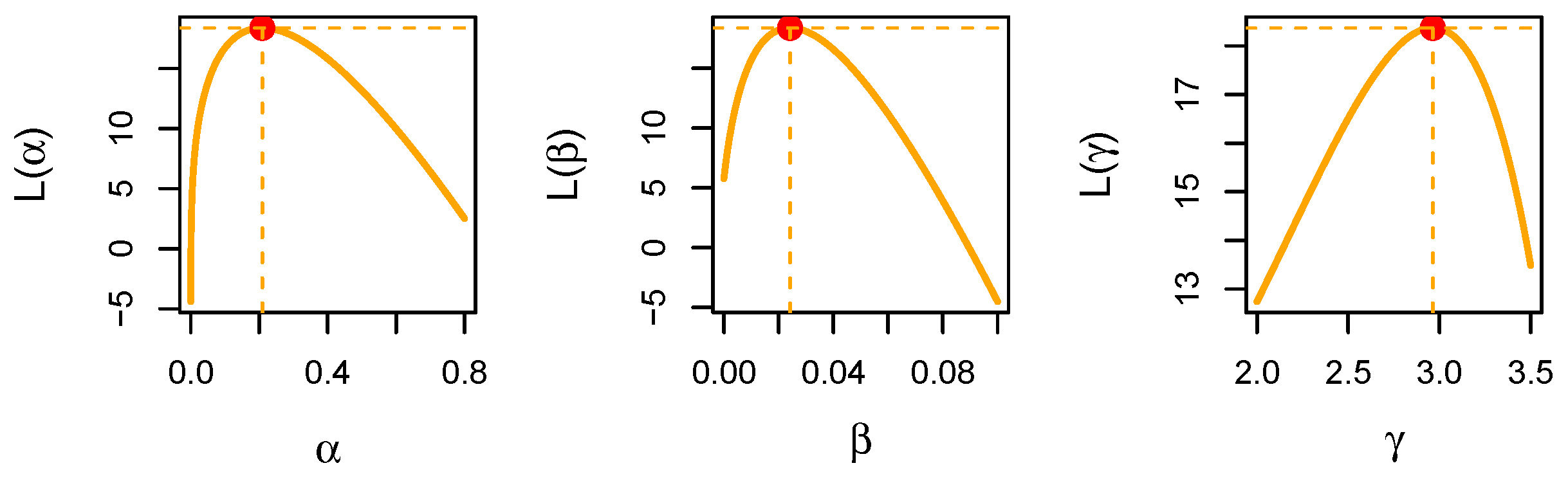
Figure 8.
Profile likelihood functions vs. the UMW’s parameters for the kidney dialysis data.
Figure 8.
Profile likelihood functions vs. the UMW’s parameters for the kidney dialysis data.
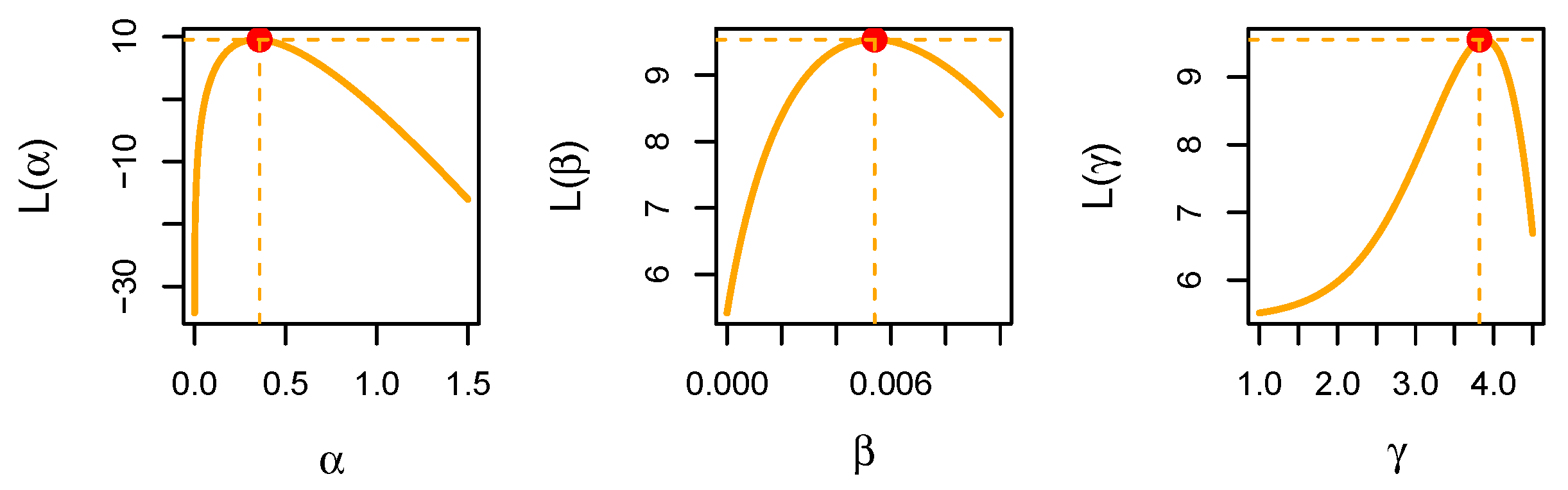
Figure 9.
Profile likelihood functions vs. the UMW’s parameters for air conditioning data.
Figure 9.
Profile likelihood functions vs. the UMW’s parameters for air conditioning data.
Figure 10.
Profile likelihood functions vs. the UMW’s parameters for P3 algorithm data.
Figure 10.
Profile likelihood functions vs. the UMW’s parameters for P3 algorithm data.
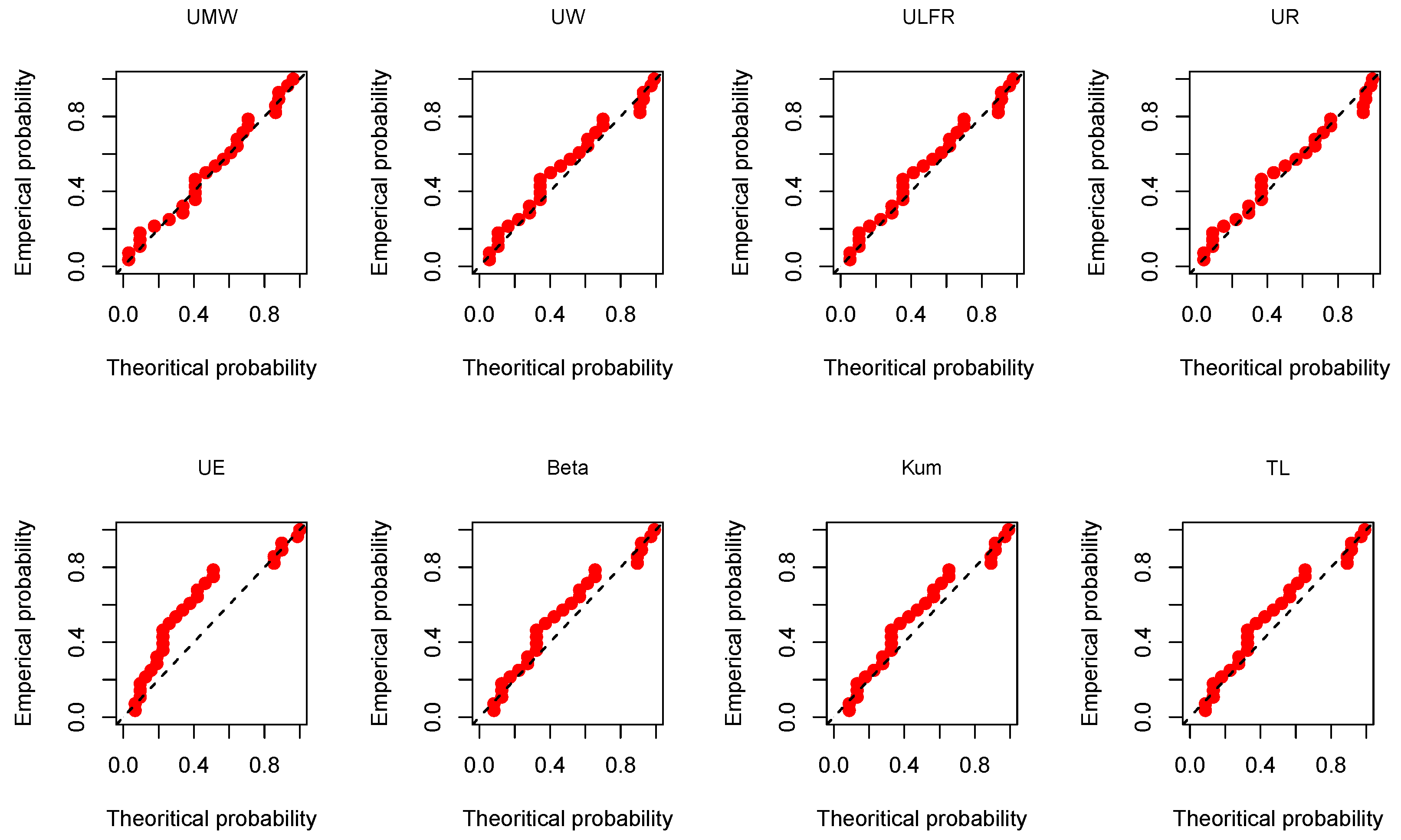
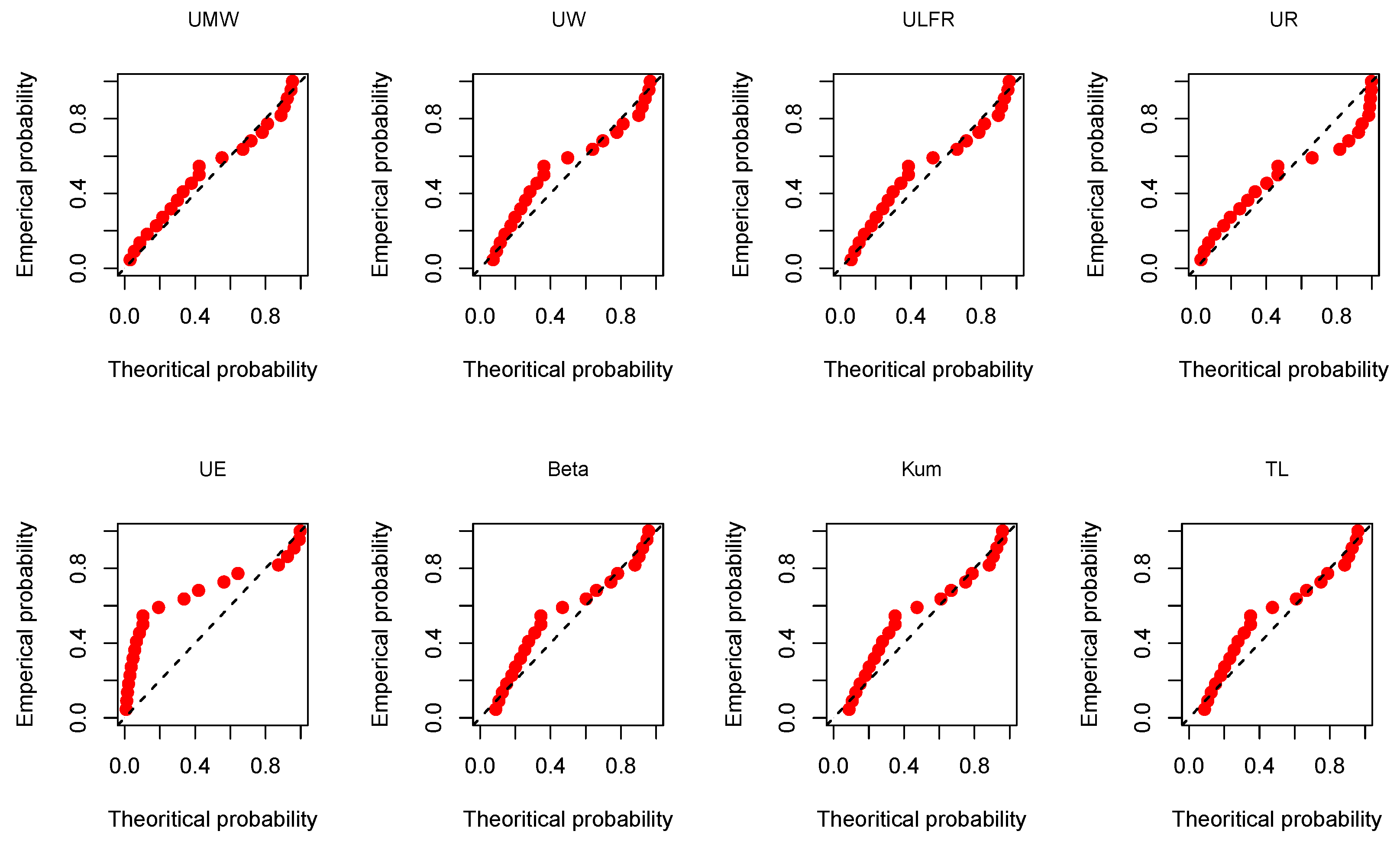
Figure 11.
The P-P plots for the kidney dialysis data using the eight competitive models.
Figure 11.
The P-P plots for the kidney dialysis data using the eight competitive models.
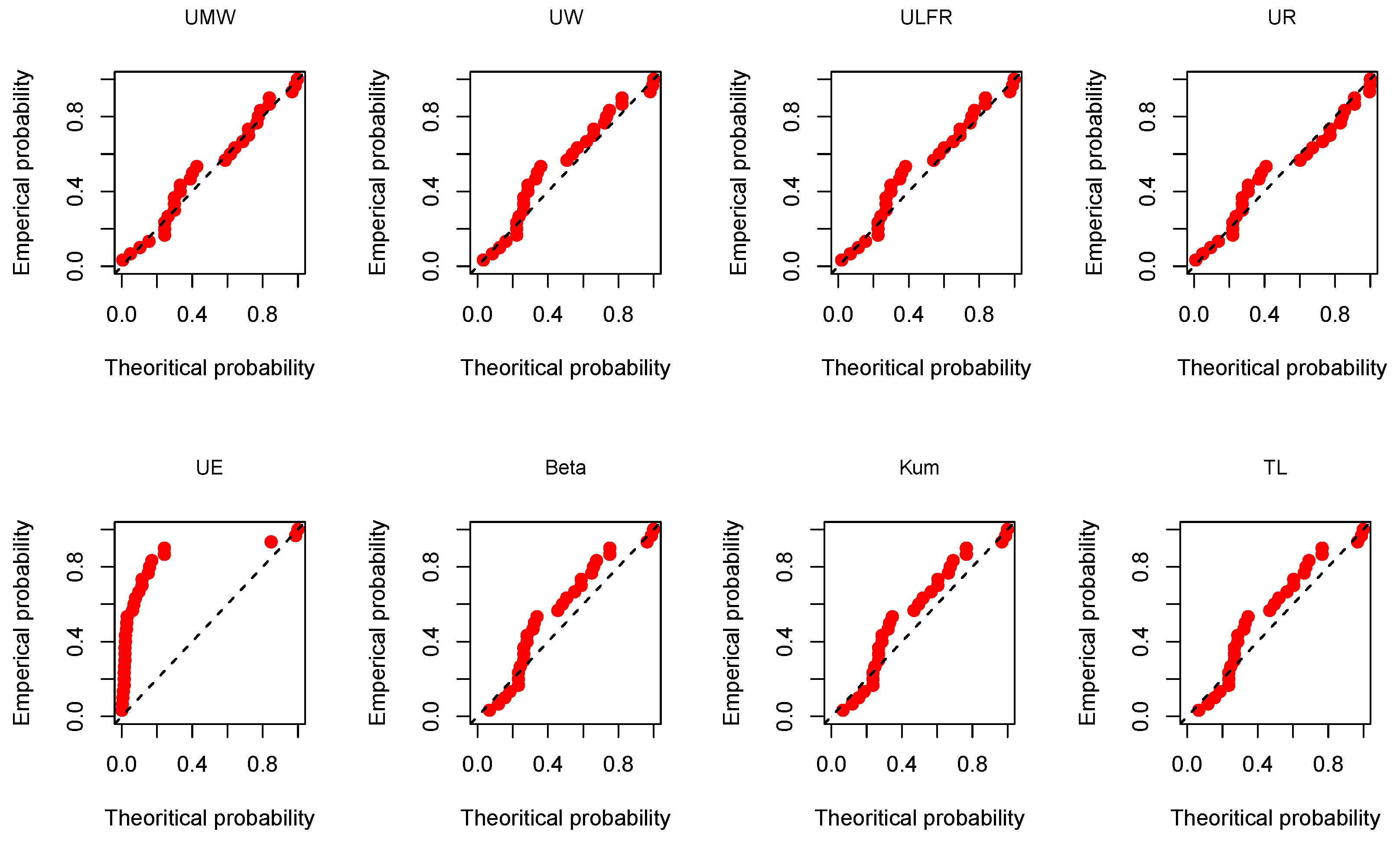
Figure 12.
The P-P plots for the air conditioning data using all used models.
Figure 12.
The P-P plots for the air conditioning data using all used models.
Figure 13.
The P-P plots for the P3 algorithm data using all models.
Figure 13.
The P-P plots for the P3 algorithm data using all models.
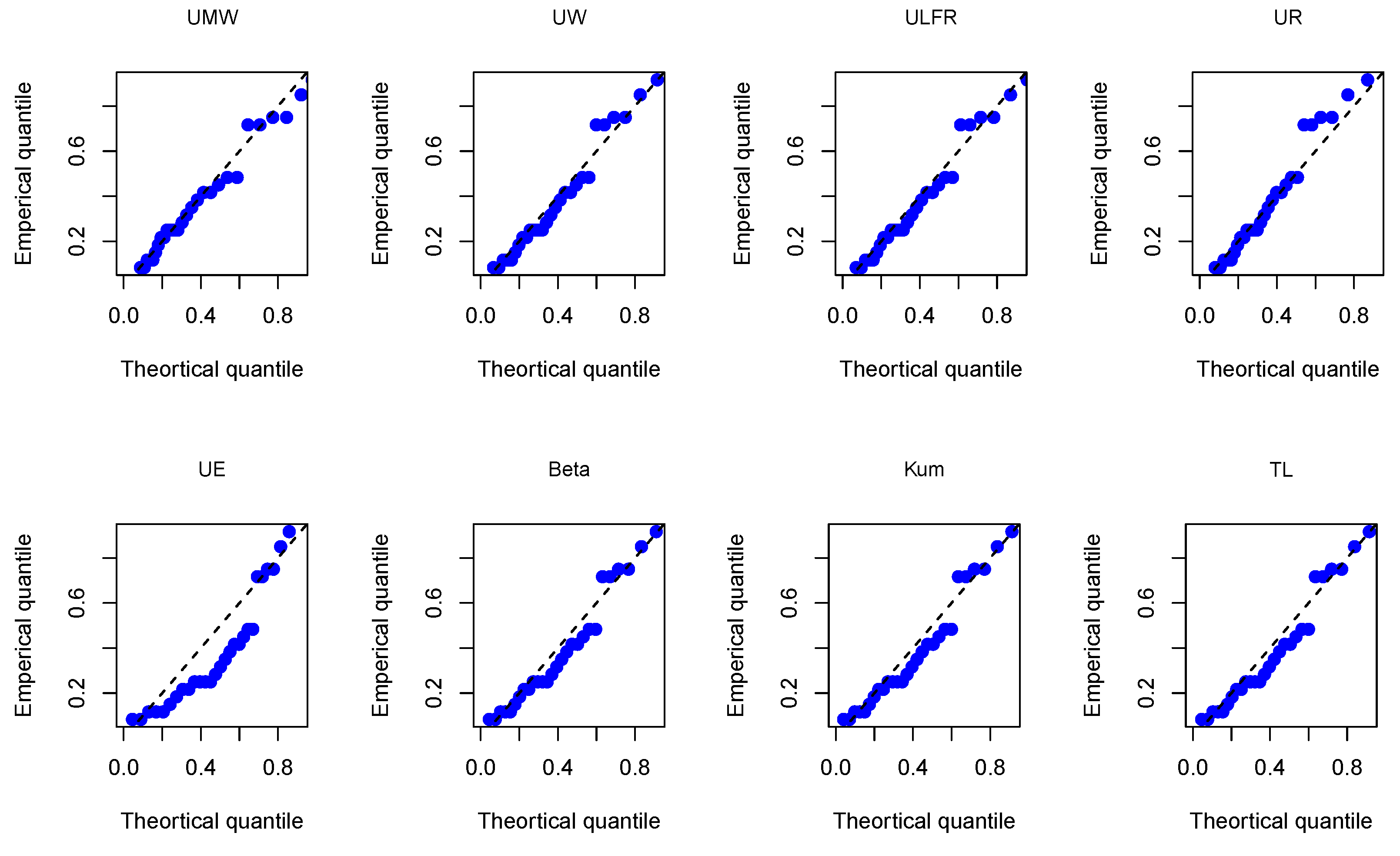
Figure 14.
The Q-Q plots for the kidney dialysis data using all models.
Figure 14.
The Q-Q plots for the kidney dialysis data using all models.
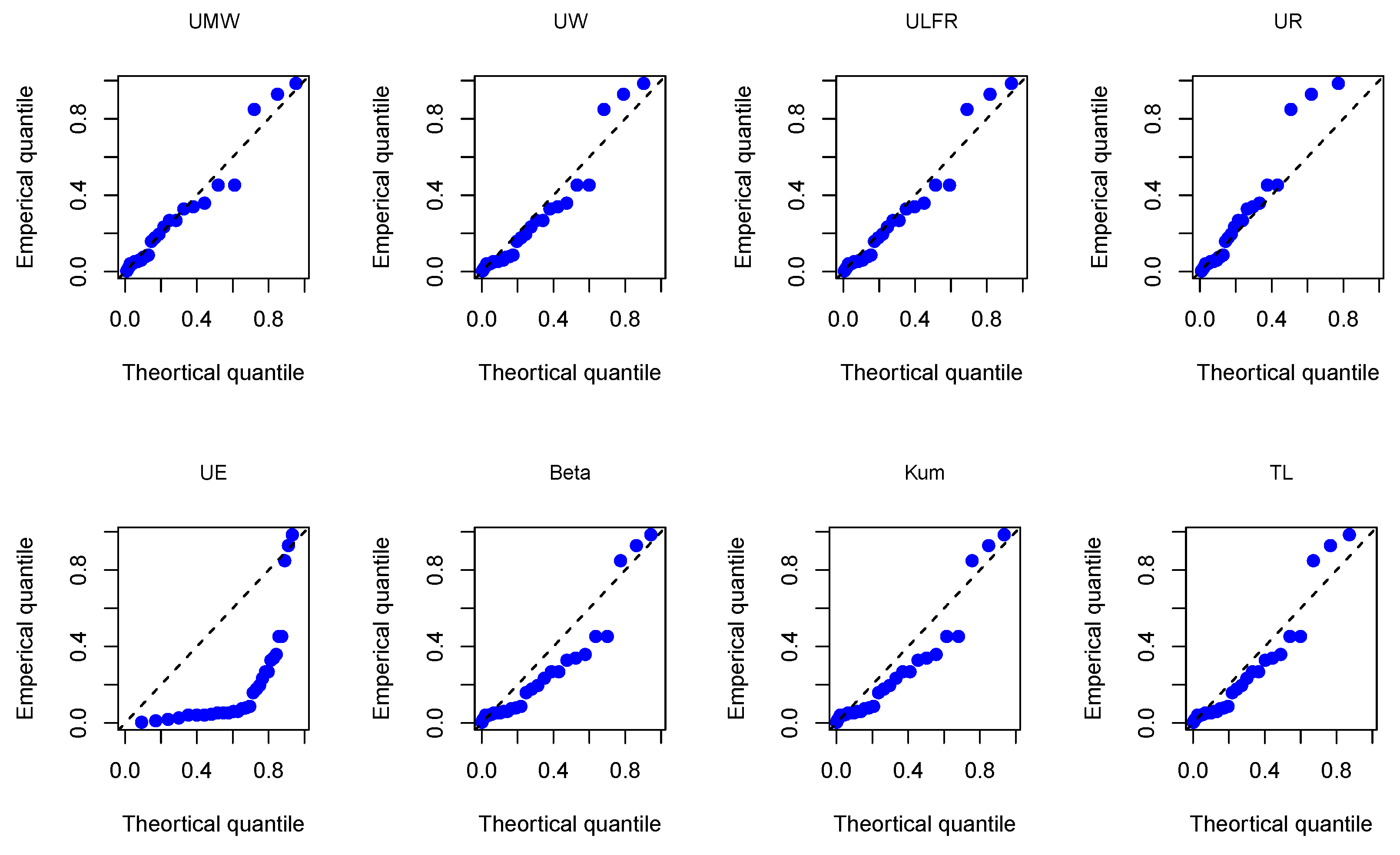
Figure 15.
The Q-Q plots for the air conditioning data using all models.
Figure 15.
The Q-Q plots for the air conditioning data using all models.
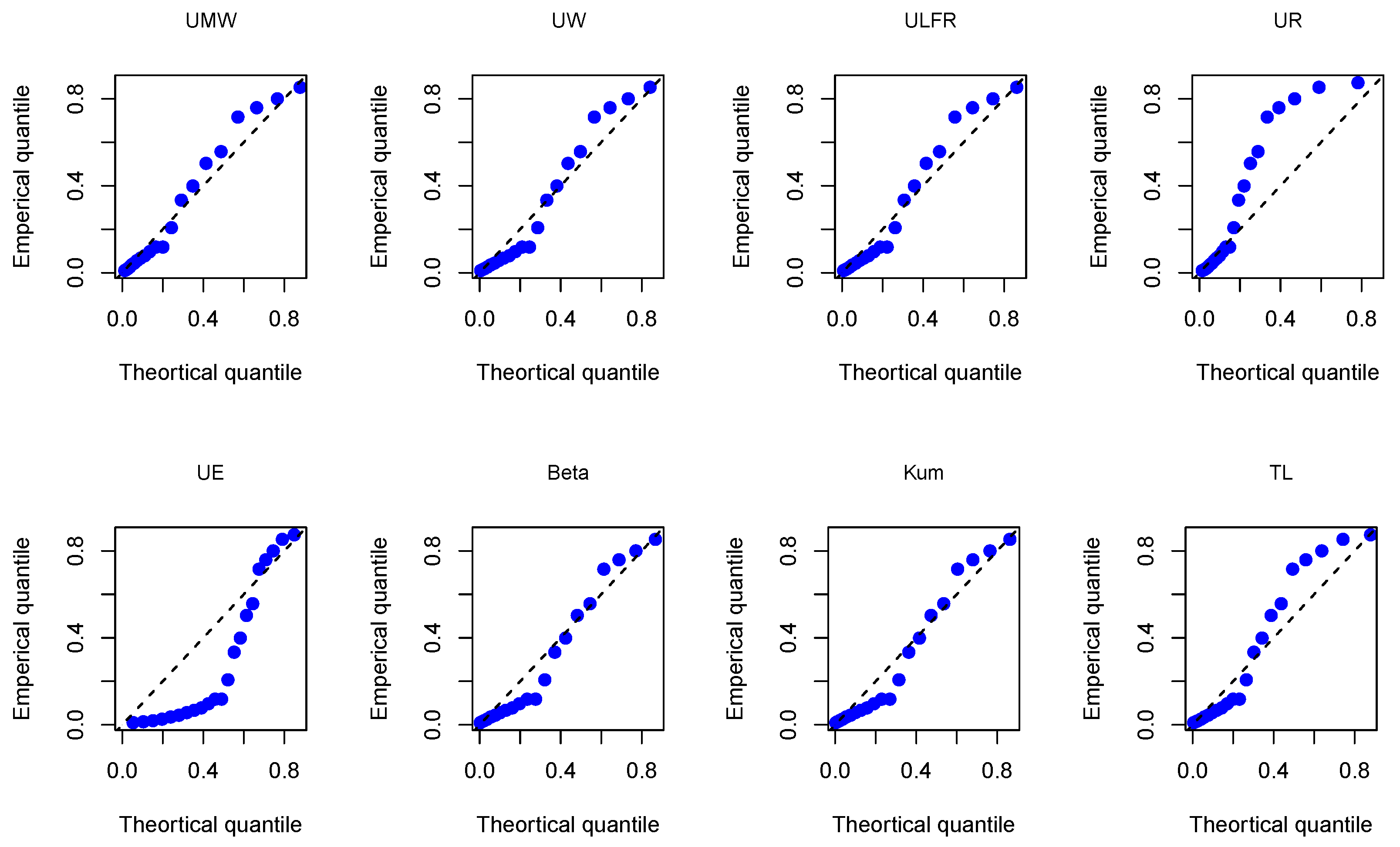
Figure 16.
The Q-Q plots for the P3 algorithm data using all models.
Figure 16.
The Q-Q plots for the P3 algorithm data using all models.
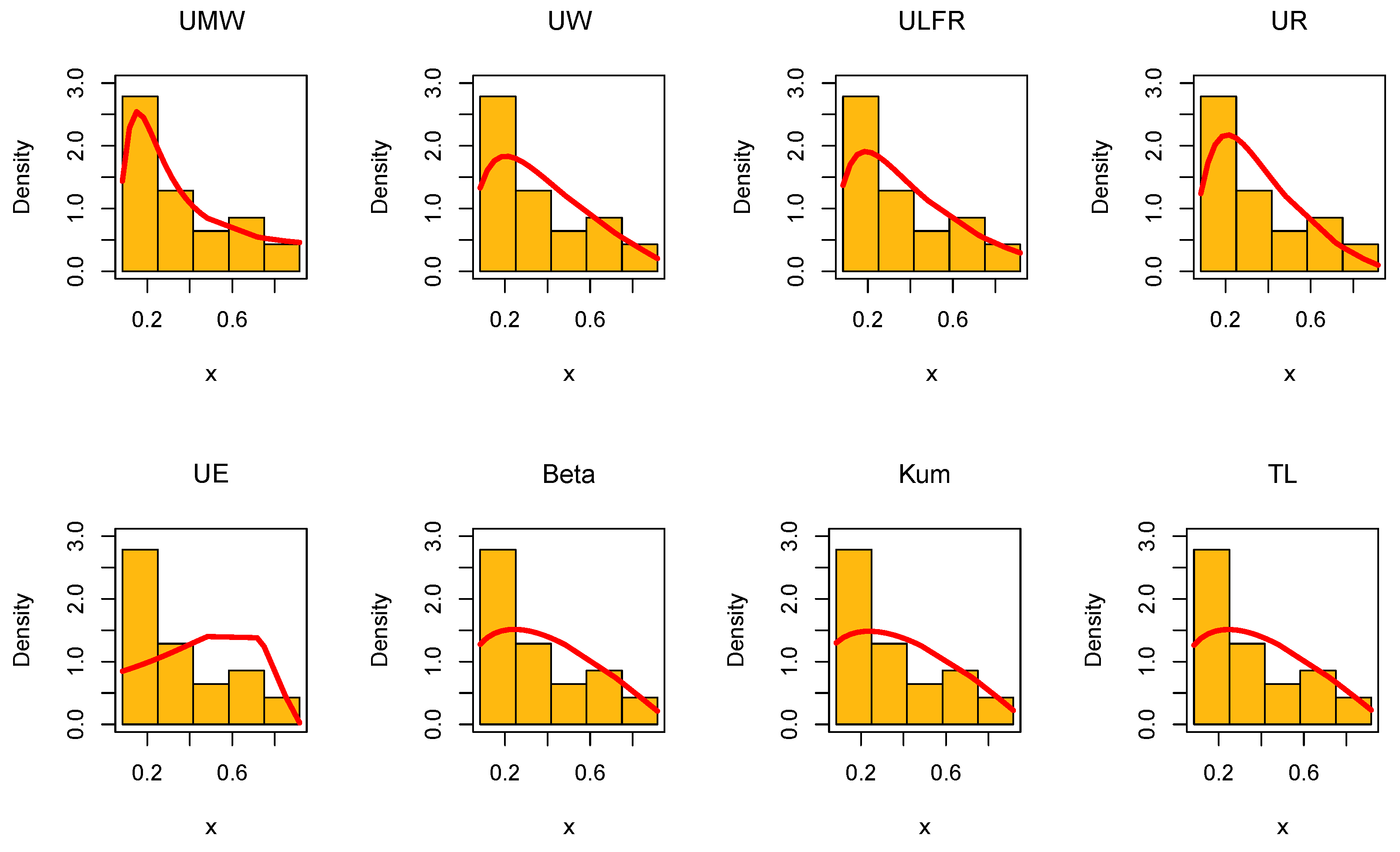
Figure 17.
Histogram of the kidney dialysis data with the fitted PDFs of all compared models.
Figure 17.
Histogram of the kidney dialysis data with the fitted PDFs of all compared models.
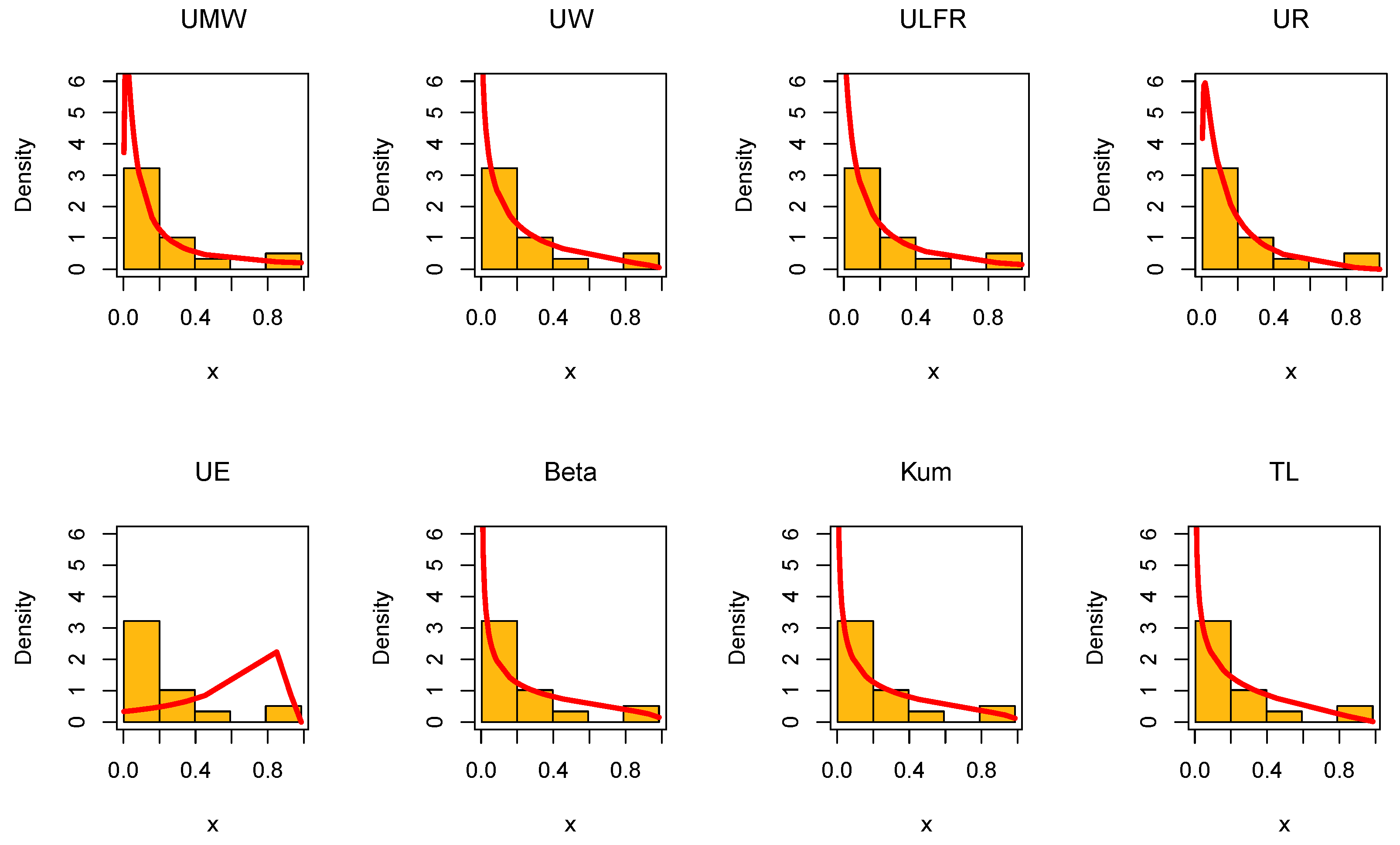
Figure 18.
Histogram of the air conditioning data with the fitted PDFs of all compared models.
Figure 18.
Histogram of the air conditioning data with the fitted PDFs of all compared models.
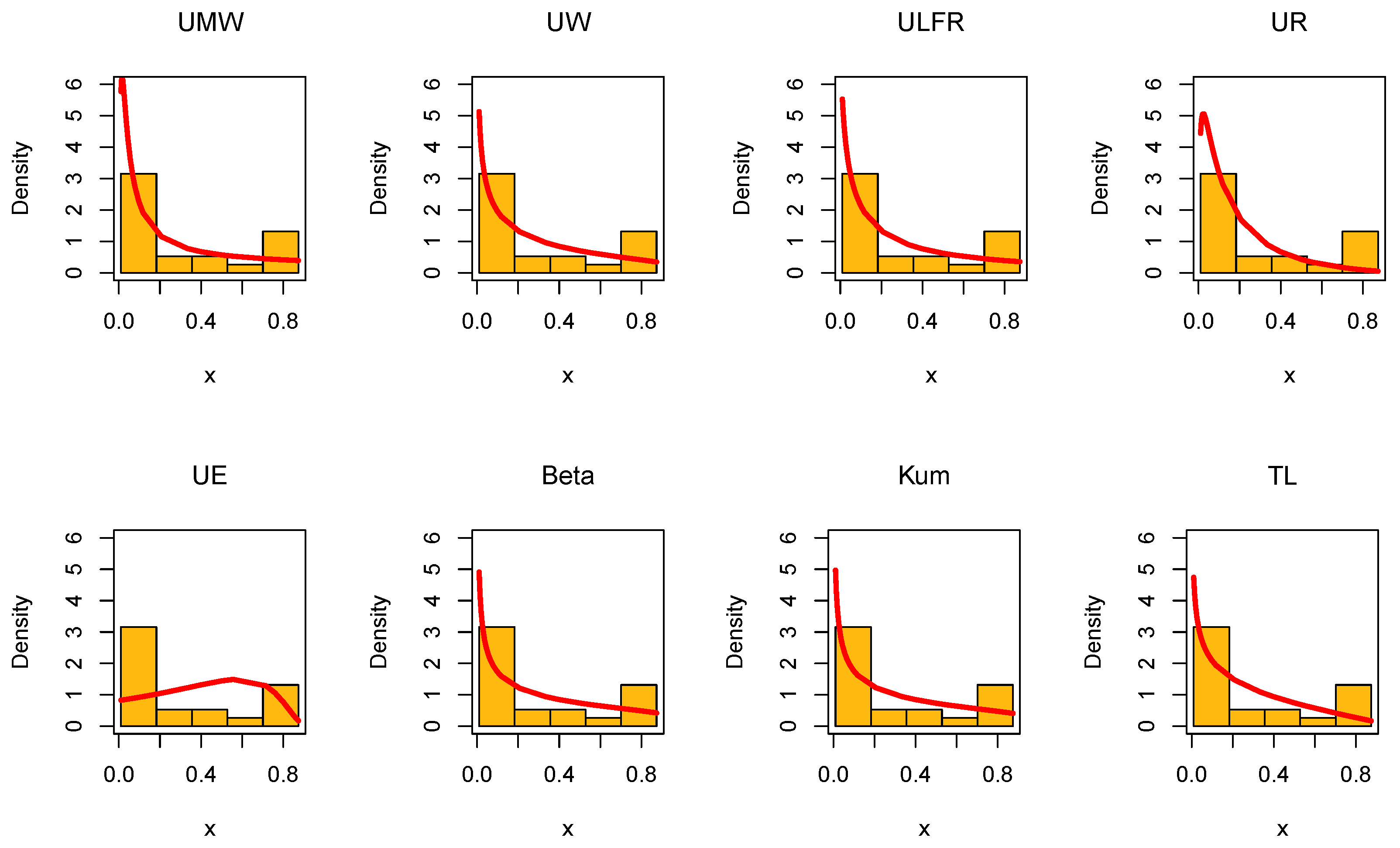
Figure 19.
Histogram of the P3 algorithm data with the fitted PDFs of all compared models.
Figure 19.
Histogram of the P3 algorithm data with the fitted PDFs of all compared models.
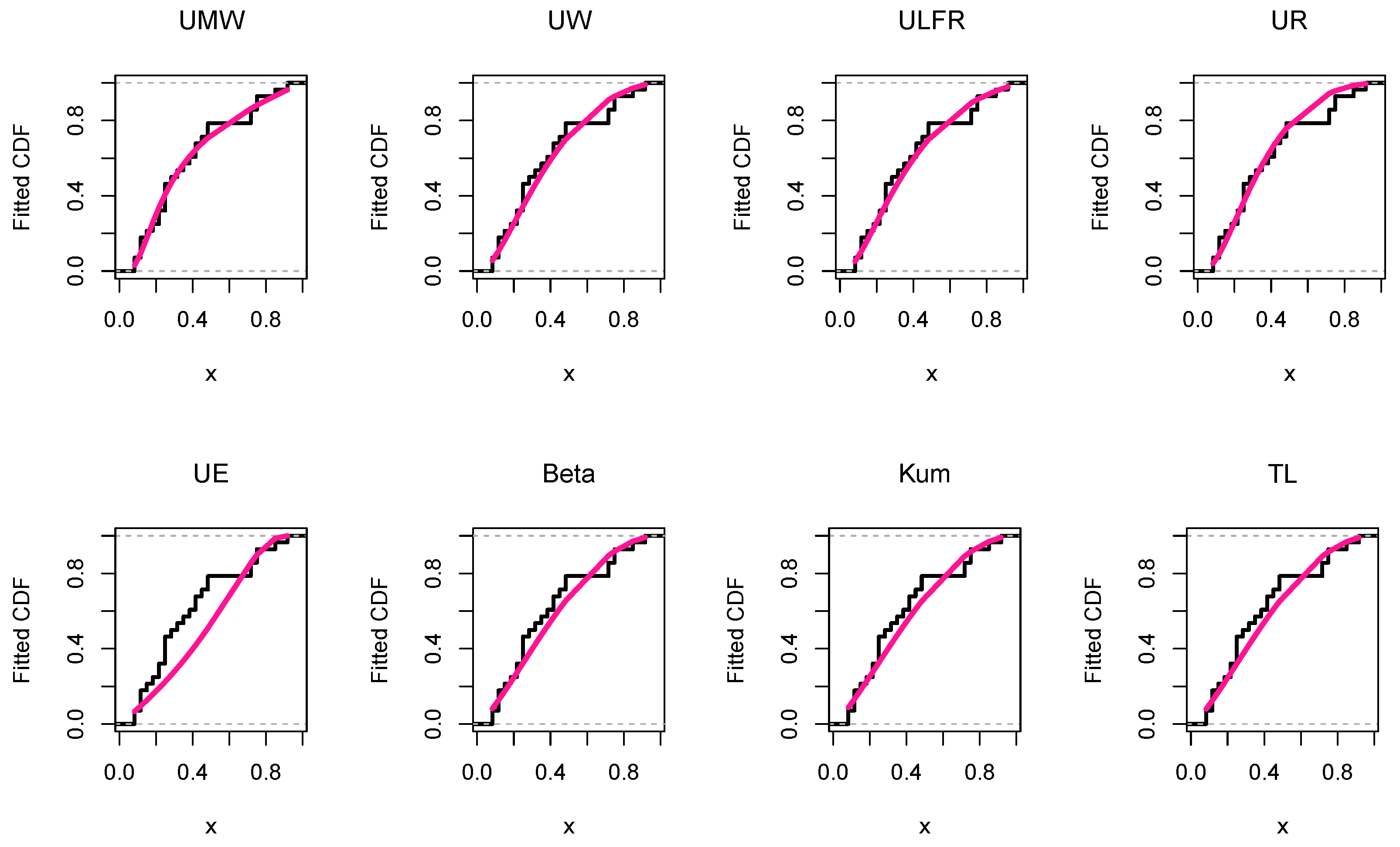
Figure 20.
The empirical and fitted CDF for the kidney dialysis data using the competitive models.
Figure 20.
The empirical and fitted CDF for the kidney dialysis data using the competitive models.
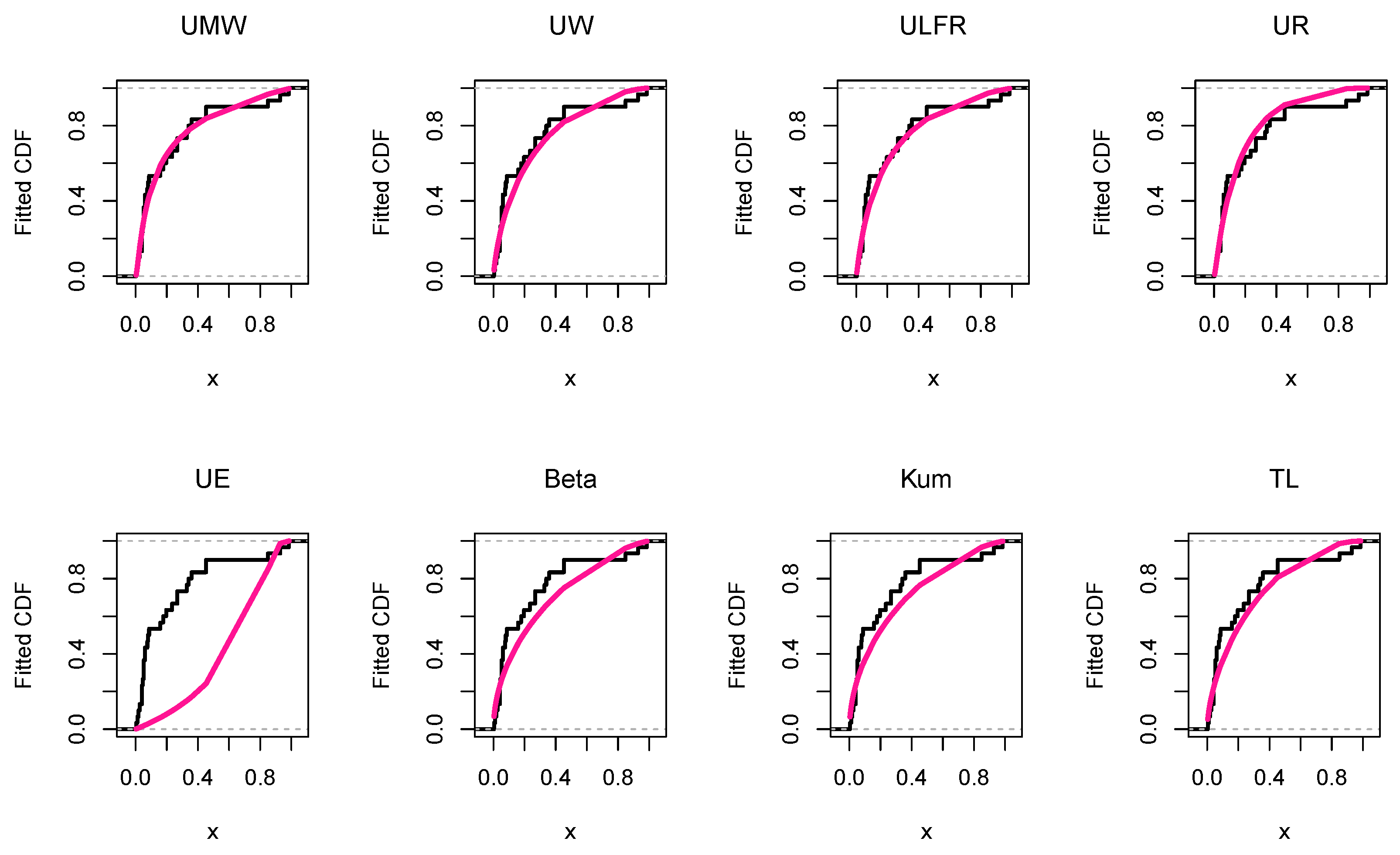
Figure 21.
The empirical and fitted CDF for the air conditioning data using the competitive models.
Figure 21.
The empirical and fitted CDF for the air conditioning data using the competitive models.
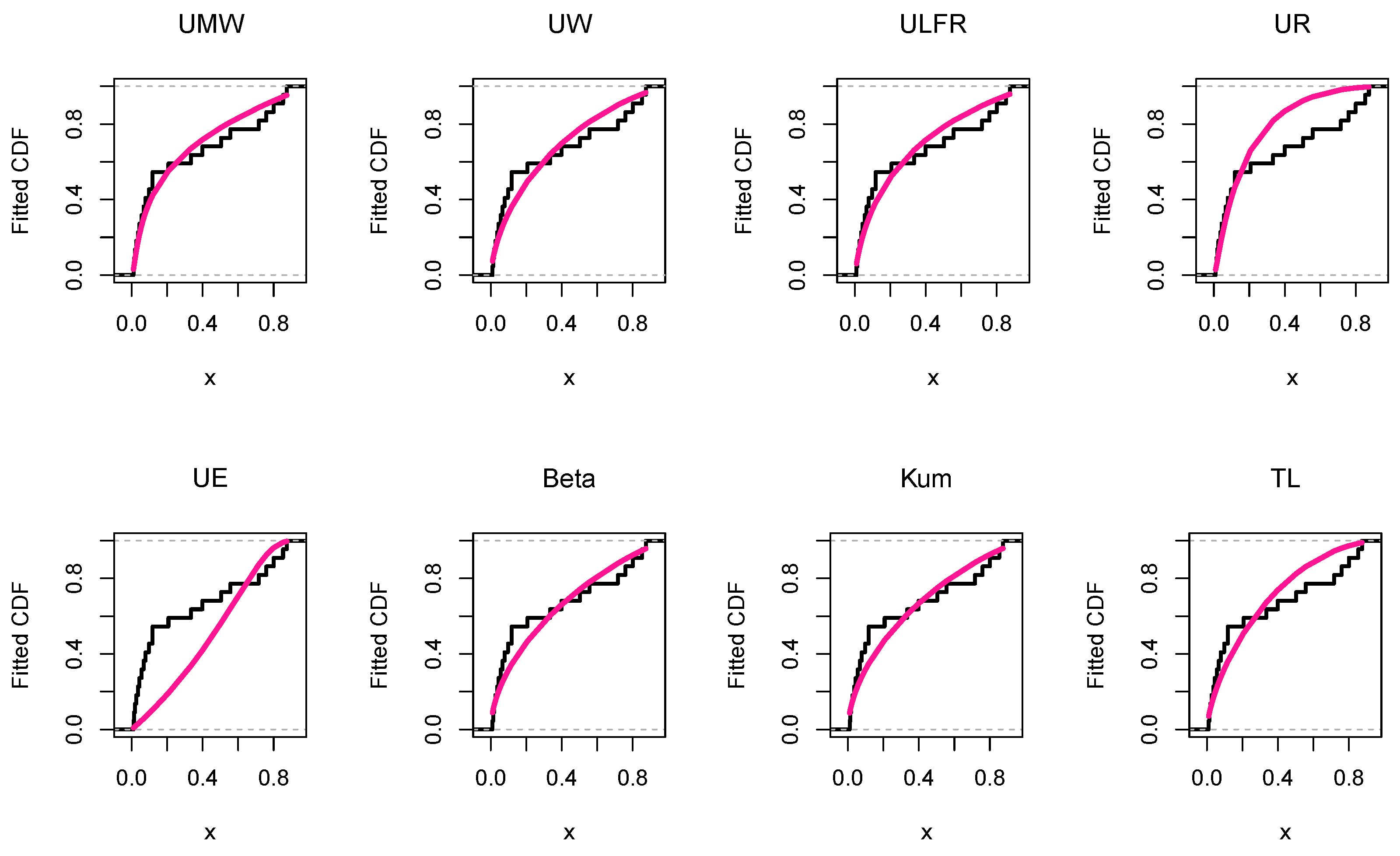
Figure 22.
The empirical and fitted CDF for the P3 algorithm data using the competitive models.
Figure 22.
The empirical and fitted CDF for the P3 algorithm data using the competitive models.
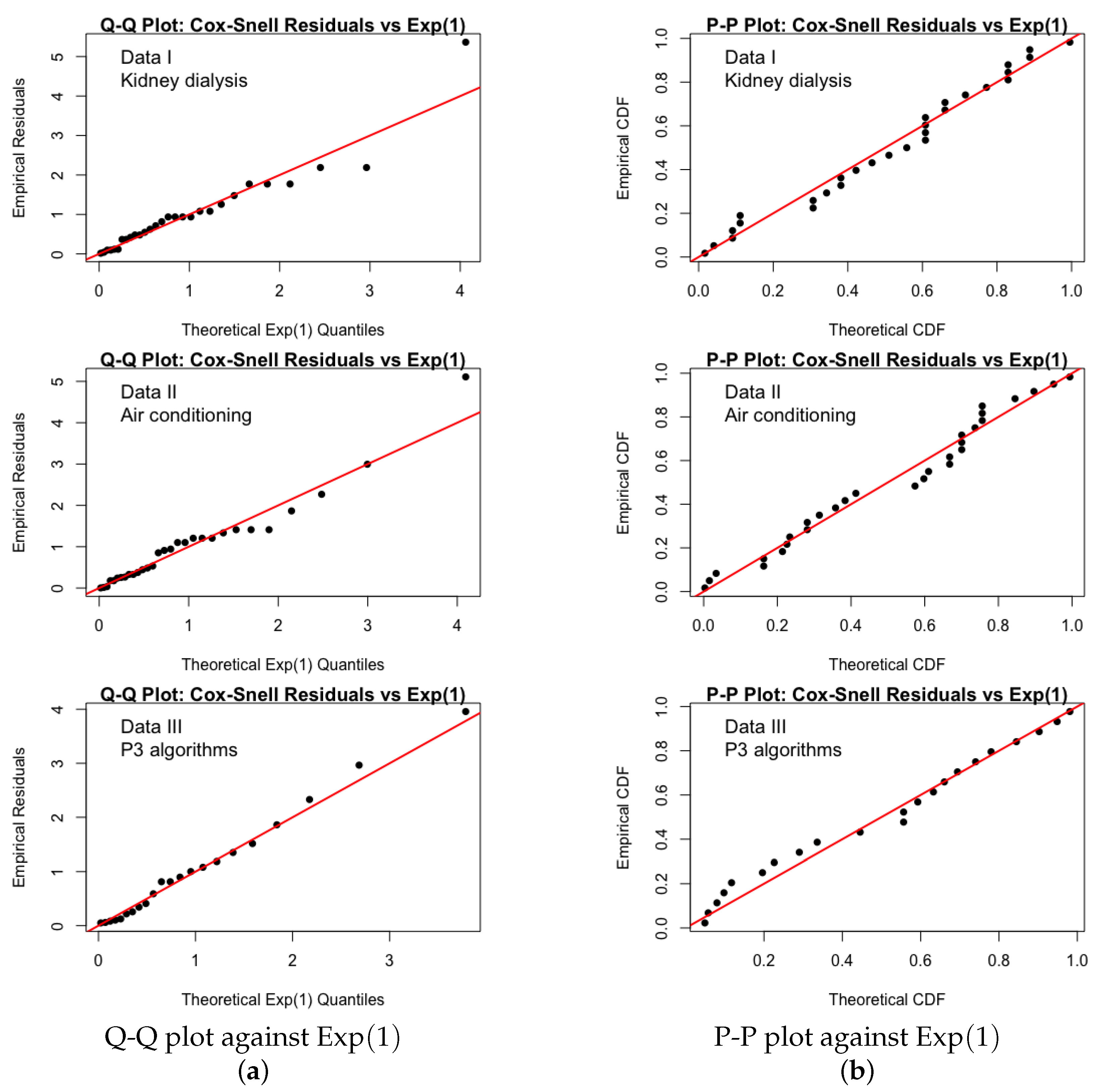
Figure 23.
(a) Q-Q plots of Cox–Snell residuals against the theoretical Exp(1) distribution for the three data sets. (b) P-P plots of the empirical CDF of the residuals against the theoretical Exp(1) CDF.
Figure 23.
(a) Q-Q plots of Cox–Snell residuals against the theoretical Exp(1) distribution for the three data sets. (b) P-P plots of the empirical CDF of the residuals against the theoretical Exp(1) CDF.
Table 1.
The sub-models of the UMW distribution.
Table 1.
The sub-models of the UMW distribution.
| Model | | | | Reference |
|---|
| Unit exponential (UE) | - | 0 | - | [14] |
| Unit exponential (UE) | - | - | 1 | [14] |
| Unit Rayleigh (UR) | 0 | - | 2 | [15] |
| Unit Weibull (UW) | 0 | - | - | [4] |
| Unit linear failure rate (ULFR) | - | - | 2 | New model |
| Uniform | 1 | 0 | - | - |
Table 2.
Descriptive statistics of the UMW distribution at .
Table 2.
Descriptive statistics of the UMW distribution at .
| Measure | | 0.1 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 7.0 |
|---|
| 0.5 | 0.1638 | 0.3794 | 0.5301 | 0.6832 | 0.7608 | 0.8077 | 0.8789 |
| 1.0 | 0.1667 | 0.3750 | 0.5238 | 0.6774 | 0.7561 | 0.8039 | 0.8765 |
| 3.0 | 0.2358 | 0.3951 | 0.5254 | 0.6729 | 0.7522 | 0.8009 | 0.8752 |
| 5.0 | 0.2875 | 0.4189 | 0.5344 | 0.6739 | 0.7519 | 0.8006 | 0.8750 |
| 7.0 | 0.3151 | 0.4337 | 0.5411 | 0.6752 | 0.7521 | 0.8006 | 0.8750 |
| 0.5 | 0.0768 | 0.0993 | 0.0853 | 0.0548 | 0.0367 | 0.0260 | 0.0119 |
| 1.0 | 0.0631 | 0.0901 | 0.0805 | 0.0533 | 0.0362 | 0.0258 | 0.0119 |
| 3.0 | 0.0353 | 0.0679 | 0.0699 | 0.0515 | 0.0361 | 0.0261 | 0.0121 |
| 5.0 | 0.0229 | 0.0549 | 0.0622 | 0.0497 | 0.0358 | 0.0261 | 0.0121 |
| 7.0 | 0.0179 | 0.0484 | 0.0576 | 0.0483 | 0.0355 | 0.0261 | 0.0121 |
| 0.5 | 1.9573 | 2.2114 | 5.8814 | 24.2264 | 61.7552 | 124.4307 | 524.0429 |
| 1.0 | 1.9502 | 2.4110 | 6.2151 | 24.8499 | 61.9803 | 124.0099 | 517.9699 |
| 3.0 | 3.6186 | 4.1253 | 7.9216 | 25.6074 | 61.2560 | 120.8403 | 503.4262 |
| 5.0 | 8.9522 | 6.5869 | 10.0574 | 27.1649 | 61.8812 | 120.4489 | 500.8145 |
| 7.0 | 15.7047 | 8.6906 | 11.7764 | 28.5983 | 62.8389 | 120.8426 | 500.2055 |
| 0.5 | 4.8107 | 1.8879 | 1.7978 | 2.4819 | 3.1959 | 3.8027 | 5.0836 |
| 1.0 | 4.7143 | 1.9469 | 1.8316 | 2.4720 | 3.1600 | 3.7509 | 5.0119 |
| 3.0 | 5.6845 | 2.3038 | 1.8365 | 2.2967 | 2.9755 | 3.5916 | 4.9244 |
| 5.0 | 8.3234 | 2.6291 | 1.7954 | 2.1157 | 2.8256 | 3.4991 | 4.9221 |
| 7.0 | 10.8684 | 2.8576 | 1.7838 | 2.0002 | 2.7164 | 3.4271 | 4.9197 |
Table 3.
Descriptive statistics of the UMW distribution at .
Table 3.
Descriptive statistics of the UMW distribution at .
| Measure | | 0.1 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 7.0 |
|---|
| 0.5 | 0.5732 | 0.6546 | 0.7191 | 0.7933 | 0.8353 | 0.8627 | 0.9074 |
| 1.0 | 0.5238 | 0.6000 | 0.6667 | 0.7500 | 0.8000 | 0.8333 | 0.8889 |
| 3.0 | 0.4532 | 0.5292 | 0.6025 | 0.7022 | 0.7649 | 0.8072 | 0.8763 |
| 5.0 | 0.4312 | 0.5103 | 0.5873 | 0.6928 | 0.7592 | 0.8037 | 0.8754 |
| 7.0 | 0.4208 | 0.5020 | 0.5811 | 0.6894 | 0.7574 | 0.8026 | 0.8752 |
| 0.5 | 0.1295 | 0.0959 | 0.0695 | 0.0414 | 0.0275 | 0.0197 | 0.0093 |
| 1.0 | 0.0805 | 0.0686 | 0.0556 | 0.0375 | 0.0267 | 0.0198 | 0.0099 |
| 3.0 | 0.0244 | 0.0369 | 0.0413 | 0.0369 | 0.0292 | 0.0227 | 0.0115 |
| 5.0 | 0.0149 | 0.0326 | 0.0406 | 0.0385 | 0.0309 | 0.0239 | 0.0119 |
| 7.0 | 0.0119 | 0.0318 | 0.0411 | 0.0395 | 0.0317 | 0.0245 | 0.0120 |
| 0.5 | 3.7079 | 8.8129 | 19.4349 | 58.1719 | 126.4021 | 231.2504 | 836.4035 |
| 1.0 | 6.2151 | 11.6898 | 22.0617 | 57.2337 | 116.5257 | 205.8796 | 714.1188 |
| 3.0 | 25.2258 | 21.4384 | 26.1952 | 48.5647 | 88.9606 | 152.5219 | 542.5166 |
| 5.0 | 45.7170 | 23.5623 | 25.1583 | 43.7877 | 80.0642 | 139.0163 | 515.6736 |
| 7.0 | 59.2981 | 23.5497 | 24.0966 | 41.5320 | 76.5179 | 134.1807 | 508.5252 |
| 0.5 | 1.5853 | 2.0753 | 2.6709 | 3.6737 | 4.4395 | 5.0365 | 6.2121 |
| 1.0 | 1.8316 | 2.0505 | 2.4000 | 3.0953 | 3.6964 | 4.2000 | 5.2841 |
| 3.0 | 3.4451 | 2.5111 | 2.0272 | 2.1180 | 2.5955 | 3.1440 | 4.5663 |
| 5.0 | 6.8218 | 3.1108 | 1.9922 | 1.8738 | 2.3729 | 2.9992 | 4.6226 |
| 7.0 | 10.4935 | 3.4000 | 1.9690 | 1.7878 | 2.3159 | 2.9831 | 4.6866 |
Table 4.
Descriptive statistics of the UMW distribution at .
Table 4.
Descriptive statistics of the UMW distribution at .
| Measure | | 0.1 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 7.0 |
|---|
| 0.5 | 0.9352 | 0.9389 | 0.9428 | 0.9490 | 0.9537 | 0.9575 | 0.9654 |
| 1.0 | 0.8361 | 0.8462 | 0.8571 | 0.8750 | 0.8889 | 0.9000 | 0.9231 |
| 3.0 | 0.6139 | 0.6503 | 0.6888 | 0.7479 | 0.7907 | 0.8223 | 0.8803 |
| 5.0 | 0.5344 | 0.5857 | 0.6386 | 0.7171 | 0.7712 | 0.8098 | 0.8764 |
| 7.0 | 0.4961 | 0.5559 | 0.6168 | 0.7053 | 0.7646 | 0.8060 | 0.8756 |
| 0.5 | 0.0126 | 0.0108 | 0.0091 | 0.0068 | 0.0054 | 0.0044 | 0.0027 |
| 1.0 | 0.0193 | 0.0174 | 0.0153 | 0.0122 | 0.0099 | 0.0082 | 0.0051 |
| 3.0 | 0.0145 | 0.0189 | 0.0216 | 0.0218 | 0.0195 | 0.0167 | 0.0099 |
| 5.0 | 0.0102 | 0.0203 | 0.0265 | 0.0281 | 0.0248 | 0.0206 | 0.0113 |
| 7.0 | 0.0087 | 0.0222 | 0.0301 | 0.0318 | 0.0274 | 0.0223 | 0.0117 |
| 0.5 | 577.0437 | 735.1459 | 960.9091 | 1511.5906 | 2203.5079 | 3047.1535 | 6589.5472 |
| 1.0 | 216.6983 | 263.6965 | 331.2708 | 498.6863 | 714.1188 | 983.5635 | 2175.9447 |
| 3.0 | 133.6461 | 106.0717 | 103.3127 | 129.5327 | 180.9329 | 257.3317 | 683.0323 |
| 5.0 | 149.8434 | 70.3439 | 60.9923 | 78.1086 | 117.3836 | 179.4241 | 557.9673 |
| 7.0 | 152.7117 | 53.1348 | 45.5499 | 61.7377 | 98.1447 | 156.8770 | 528.2465 |
| 0.5 | 15.2734 | 15.2309 | 15.1549 | 14.9684 | 14.7714 | 14.5799 | 14.0764 |
| 1.0 | 4.2456 | 4.4202 | 4.6222 | 4.9792 | 5.2841 | 5.5470 | 6.1542 |
| 3.0 | 2.8909 | 2.6179 | 2.2552 | 2.1037 | 2.3108 | 2.6577 | 3.8681 |
| 5.0 | 5.8425 | 3.4788 | 2.2556 | 1.8056 | 2.0606 | 2.5273 | 4.0928 |
| 7.0 | 9.9957 | 3.8622 | 2.1983 | 1.7097 | 2.0397 | 2.5907 | 4.3129 |
Table 5.
Simulation results for the UMW parameters.
Table 5.
Simulation results for the UMW parameters.
| n | Parameter | | |
|---|
| | | AMLE | MSE | AIL | CP | AMLE | MSE | AIL | CP |
|---|
| | | 0.5265 | 0.0945 | 0.4615 | 95.1% | 0.8515 | 0.1542 | 0.7464 | 95.4% |
| 20 | | 0.5053 | 0.1227 | 0.5812 | 92.5% | 1.0555 | 0.2180 | 0.9732 | 93.9% |
| | | 0.8573 | 0.1297 | 0.5911 | 94.8% | 1.6116 | 0.2499 | 1.1144 | 94.2% |
| | | 0.5093 | 0.0551 | 0.2823 | 95.7% | 0.8098 | 0.0895 | 0.4489 | 95.5% |
| 50 | | 0.5016 | 0.0743 | 0.3674 | 94.2 % | 1.0128 | 0.1226 | 0.5914 | 94.4% |
| | | 0.8182 | 0.0762 | 0.3555 | 94.3% | 1.5464 | 0.1379 | 0.6723 | 95.8% |
| | | 0.5079 | 0.0446 | 0.2226 | 96.4% | 1.5464 | 0.1379 | 0.6723 | 95.8% |
| 80 | | 0.4999 | 0.0591 | 0.2900 | 94.7% | 1.0098 | 0.0968 | 0.4659 | 94.4% |
| | | 0.8135 | 0.0585 | 0.2789 | 95.1% | 1.5239 | 0.1108 | 0.5224 | 94.1% |
| | | 0.5053 | 0.0415 | 0.1981 | 94.8% | 0.8056 | 0.0629 | 0.3158 | 95.7% |
| 100 | | 0.4986 | 0.0516 | 0.2591 | 95.2% | 1.0029 | 0.0875 | 0.4144 | 93.9% |
| | | 0.8135 | 0.0516 | 0.2492 | 95.7% | 1.5195 | 0.0949 | 0.4654 | 96.4% |
| | | 0.5039 | 0.0334 | 0.1613 | 94.9% | 0.8045 | 0.0522 | 0.2575 | 94.7% |
| 150 | | 0.5008 | 0.0439 | 0.2122 | 95.5% | 1.0034 | 0.0708 | 0.3382 | 95.1% |
| | | 0.8104 | 0.0425 | 0.2025 | 95.1% | 1.5131 | 0.0760 | 0.3784 | 95.4 % |
| | | 0.5048 | 0.0290 | 0.1399 | 95.2% | 0.8082 | 0.0466 | 0.2240 | 94.3% |
| 200 | | 0.5014 | 0.0380 | 0.1839 | 94.3% | 1.0005 | 0.0593 | 0.2922 | 94.9% |
| | | 0.8036 | 0.0351 | 0.1738 | 95.4% | 1.5069 | 0.0686 | 0.3261 | 95.0% |
| | | 0.5004 | 0.0233 | 0.1132 | 94.5% | 0.8016 | 0.0370 | 0.1814 | 95.1% |
| 300 | | 0.5014 | 0.0313 | 0.1502 | 95.1% | 1.0012 | 0.0489 | 0.2386 | 94.9% |
| | | 0.8034 | 0.0294 | 0.1418 | 96.1% | 1.5024 | 0.0548 | 0.2654 | 94.3% |
| | | 0.5010 | 0.0197 | 0.0982 | 94.4% | 0.8034 | 0.0325 | 0.1575 | 95.1% |
| 400 | | 0.5008 | 0.0265 | 0.1299 | 94.2% | 0.9996 | 0.0404 | 0.2064 | 95.2% |
| | | 0.8014 | 0.0249 | 0.1225 | 95.6% | 1.5031 | 0.0469 | 0.2298 | 93.8% |
| | | 0.5014 | 0.0178 | 0.0879 | 94.6% | 0.8019 | 0.0283 | 0.1406 | 95.2% |
| 500 | | 0.5002 | 0.0239 | 0.1162 | 94.7% | 1.0030 | 0.0382 | 0.1851 | 94.9% |
| | | 0.8026 | 0.0245 | 0.1098 | 94.4% | 1.5042 | 0.0418 | 0.2057 | 94.8% |
Table 6.
Simulation results for the UMW parameters.
Table 6.
Simulation results for the UMW parameters.
| n | Parameter | | |
|---|
| | | AMLE | MSE | AIL | CP | AMLE | MSE | AIL | CP |
|---|
| | | 1.2554 | 0.2222 | 1.1004 | 95.2% | 1.2515 | 0.2154 | 1.0969 | 95.8% |
| 20 | | 1.5841 | 0.2969 | 1.4175 | 94.7% | 0.1915 | 0.06817 | 0.3119 | 88.2% |
| | | 3.2173 | 0.4777 | 2.2265 | 94.6% | 0.5468 | 0.0882 | 0.3783 | 94.7% |
| | | 1.2314 | 0.1428 | 0.6826 | 94.3% | 1.2166 | 0.1379 | 0.6744 | 94.7% |
| 50 | | 1.5538 | 0.1789 | 0.8672 | 95.8% | 0.1969 | 0.0414 | 0.2039 | 92.9% |
| | | 3.0721 | 0.2708 | 1.3327 | 94.4% | 0.5156 | 0.0466 | 0.2238 | 95.0% |
| | | 1.2174 | 0.1091 | 0.5335 | 95.8% | 1.2140 | 0.1039 | 0.5321 | 95.7% |
| 80 | | 1.5188 | 0.1365 | 0.6683 | 95.2% | 0.1997 | 0.0330 | 0.1633 | 94.2% |
| | | 3.0466 | 0.2069 | 1.0438 | 95.3% | 0.5083 | 0.0362 | 0.1743 | 94.5% |
| | | 1.2127 | 0.0965 | 0.4754 | 96.3% | 1.2129 | 0.0972 | 0.4754 | 95.3% |
| 100 | | 1.5122 | 0.1237 | 0.5947 | 94.4% | 0.1991 | 0.0312 | 0.1458 | 93.5% |
| | | 3.0425 | 0.1911 | 0.9322 | 95.4% | 0.5074 | 0.0343 | 0.1554 | 94.0% |
| | | 1.2076 | 0.0784 | 0.3865 | 94.7% | 1.2117 | 0.0813 | 0.3878 | 94.8% |
| 150 | | 1.5144 | 0.0983 | 0.4857 | 96.3% | 0.1994 | 0.0251 | 0.1194 | 93.2% |
| | | 3.0277 | 0.1556 | 0.7575 | 96.2% | 0.5054 | 0.0267 | 0.1264 | 94.5% |
| | | 1.2009 | 0.0668 | 0.3329 | 95.0% | 1.2055 | 0.0680 | 0.3341 | 95.6% |
| 200 | | 1.5093 | 0.0828 | 0.4189 | 95.8% | 0.1998 | 0.0209 | 0.1036 | 93.9% |
| | | 3.0239 | 0.1378 | 0.6541 | 95.4% | 0.5038 | 0.0227 | 0.1089 | 93.9% |
| | | 1.2069 | 0.0549 | 0.2731 | 94.8% | 1.2045 | 0.0562 | 0.2726 | 95.3% |
| 300 | | 1.5067 | 0.0668 | 0.3414 | 96.4% | 0.2000 | 0.0175 | 0.0847 | 94.3% |
| | | 3.0159 | 0.1071 | 0.5327 | 94.7 % | 0.5011 | 0.0184 | 0.0885 | 94.3% |
| | | 1.2028 | 0.0481 | 0.2357 | 95.4% | 1.2008 | 0.0481 | 0.2353 | 94.7% |
| 400 | | 1.5026 | 0.0613 | 0.2948 | 93.4 % | 0.2008 | 0.0148 | 0.0736 | 94.2% |
| | | 3.0099 | 0.0992 | 0.4601 | 95.0 % | 0.5009 | 0.0156 | 0.0766 | 94.1% |
| | | 1.2018 | 0.0421 | 0.2107 | 95.2% | 1.2013 | 0.0439 | 0.2106 | 94.3% |
| 500 | | 1.5026 | 0.0556 | 0.2636 | 95.4% | 0.2002 | 0.0137 | 0.0657 | 94.7% |
| | | 3.0095 | 0.0829 | 0.4115 | 95.2% | 0.5011 | 0.0143 | 0.0685 | 94.9% |
Table 7.
Descriptive statistics of the three real data sets.
Table 7.
Descriptive statistics of the three real data sets.
| Data | Min. | Mean | Q1 | Median | Q3 | Var | Skewness | Kurtosis | Max. |
|---|
| Kidney dialysis data | 0.0833 | 0.3774 | 0.2083 | 0.3000 | 0.4833 | 0.0611 | 0.7651 | 2.4219 | 0.9167 |
| Air conditioning data | 0.0038 | 0.2249 | 0.0472 | 0.0830 | 0.3132 | 0.0736 | 1.6936 | 4.9667 | 0.9849 |
| P3 algorithm data | 0.0100 | 0.3039 | 0.0470 | 0.1180 | 0.5435 | 0.1010 | 0.7114 | 1.8838 | 0.8740 |
Table 8.
The MLE estimates and corresponding SE for the kidney dialysis data.
Table 8.
The MLE estimates and corresponding SE for the kidney dialysis data.
| Model | | | | | | |
|---|
| UMW | 0.4371 | 0.0897 | 3.6139 | 0.1960 | 0.1243 | 1.4790 |
| UW | 0.6125 | 1.6991 | - | 0.1424 | 0.2669 | - |
| ULFR | 0.2064 | 0.3931 | - | 0.1815 | 0.1334 | - |
| UR | 0.5222 | - | - | 0.0987 | - | - |
| UE | 0.7623 | - | - | 0.1441 | - | - |
| Beta | 1.3568 | 2.1058 | - | 0.3332 | 0.5497 | - |
| kum | 1.2651 | 2.0797 | - | 0.2544 | 0.5714 | - |
| TL | 1.3779 | - | - | 0.2604 | - | - |
Table 9.
The MLE estimates and corresponding SE for the air conditioning data.
Table 9.
The MLE estimates and corresponding SE for the air conditioning data.
| Model | | | | | | |
|---|
| UMW | 0.2071 | 0.0250 | 2.9426 | 0.0999 | 0.0348 | 0.8629 |
| UW | 0.2787 | 1.4561 | - | 0.0858 | 0.2262 | - |
| ULFR | 0.1485 | 0.1004 | - | 0.0886 | 0.0335 | - |
| UR | 0.1498 | - | - | 0.0274 | - | - |
| UE | 0.3351 | - | - | 0.0612 | - | - |
| Beta | 0.5142 | 1.3430 | - | 0.1118 | 0.3643 | - |
| kum | 0.5451 | 1.3837 | - | 0.1148 | 0.3362 | - |
| TL | 0.6017 | - | - | 0.1099 | - | - |
Table 10.
The MLE estimates and corresponding SE for the P3 algorithm data.
Table 10.
The MLE estimates and corresponding SE for the P3 algorithm data.
| Model | | | | | | |
|---|
| UMW | 0.3571 | 0.0054 | 3.8185 | 0.1134 | 0.0089 | 1.1726 |
| UW | 0.4003 | 1.2259 | - | 0.1263 | 0.2213 | - |
| ULFR | 0.3042 | 0.0662 | - | 0.1390 | 0.0432 | - |
| UR | 0.1672 | - | - | 0.0356 | - | - |
| UE | 0.8194 | - | - | 0.1747 | - | - |
| Beta | 0.5539 | 1.2198 | - | 0.1423 | 0.3758 | - |
| kum | 0.5718 | 1.2306 | - | 0.1478 | 0.3483 | - |
| TL | 0.6778 | - | - | 0.1445 | - | - |
Table 11.
The , AIC, BIC, CAIC, HQIC, , , , and corresponding p-values derived from using eight competitive models for the kidney dialysis data.
Table 11.
The , AIC, BIC, CAIC, HQIC, , , , and corresponding p-values derived from using eight competitive models for the kidney dialysis data.
| Model | | AIC | BIC | CAIC | HQIC | | | | p-Value |
|---|
| UMW | −6.3169 | −6.6339 | −2.6373 | −5.6339 | −5.4121 | 0.0381 | 0.2819 | 0.0879 | 0.9820 |
| UW | −5.0611 | −6.1223 | −3.4579 | −5.6423 | −5.3077 | 0.0659 | 0.4415 | 0.1240 | 0.7824 |
| ULFR | −5.4608 | −6.9215 | −4.2571 | −6.4415 | −6.1069 | 0.0483 | 0.3489 | 0.1114 | 0.8779 |
| UR | −4.4825 | −6.9650 | −5.6328 | −6.8112 | −6.5577 | 0.0557 | 0.3833 | 0.1579 | 0.4869 |
| UE | 1.8933 | 5.7866 | 7.1188 | 5.9404 | 6.1938 | 0.2606 | 1.4695 | 0.2758 | 0.0283 |
| Beta | −3.7776 | −3.5552 | −0.8908 | −3.0752 | −2.7407 | 0.1101 | 0.6859 | 0.1412 | 0.6321 |
| kum | −3.6625 | −3.3249 | −0.6606 | −2.8449 | −2.5104 | 0.1136 | 0.7049 | 0.1377 | 0.6629 |
| TL | −3.8524 | −5.7049 | −4.3727 | −5.5510 | −5.2976 | 0.1067 | 0.6679 | 0.1442 | 0.6056 |
Table 12.
The , AIC, BIC, CAIC, HQIC, , , , and corresponding p-values derived from using eight competitive models for the air conditioning system data.
Table 12.
The , AIC, BIC, CAIC, HQIC, , , , and corresponding p-values derived from using eight competitive models for the air conditioning system data.
| Model | | AIC | BIC | CAIC | HQIC | | | | p-Value |
|---|
| UMW | −18.3687 | −30.7375 | −26.5339 | −29.8144 | −29.3927 | 0.0754 | 0.4625 | 0.1102 | 0.8596 |
| UW | −15.1924 | −26.3847 | −23.5823 | −25.9403 | −25.4882 | 0.1593 | 1.0192 | 0.1741 | 0.3228 |
| ULFR | −17.4207 | −30.8414 | −28.0390 | −30.3969 | −29.9448 | 0.1055 | 0.6546 | 0.1515 | 0.4969 |
| UR | −12.7731 | −23.5462 | −22.1449 | −23.4033 | −23.0979 | 0.1254 | 0.7933 | 0.1262 | 0.7260 |
| UE | 35.9335 | 73.8671 | 75.2683 | 74.0099 | 74.3153 | 0.6164 | 3.4108 | 0.6626 | <0.0001 |
| Beta | −13.2463 | −22.4926 | −19.6902 | −22.0482 | −21.5961 | 0.2173 | 1.3859 | 0.1958 | 0.2003 |
| kum | −13.5389 | −23.0778 | −20.2754 | −22.6334 | −22.1813 | 0.2109 | 1.3470 | 0.1879 | 0.2403 |
| TL | −11.9802 | −21.9604 | −20.5592 | −21.8175 | −21.5121 | 0.2379 | 1.5103 | 0.1939 | 0.2095 |
Table 13.
The , AIC, BIC, CAIC, HQIC, , , , and corresponding p-values derived from using eight competitive models for the computing time of P3 algorithm data.
Table 13.
The , AIC, BIC, CAIC, HQIC, , , , and corresponding p-values derived from using eight competitive models for the computing time of P3 algorithm data.
| Model | | AIC | BIC | CAIC | HQIC | | | | p-Value |
|---|
| UMW | −9.5357 | −13.0714 | −9.7982 | −11.7380 | −11.7380 | 0.0425 | 0.2879 | 0.1228 | 0.8944 |
| UW | −7.1755 | −10.3509 | −8.1689 | −9.7194 | −9.8369 | 0.1048 | 0.6406 | 0.1833 | 0.4508 |
| ULFR | −7.9048 | −11.8096 | −9.6275 | −11.1779 | −11.2955 | 0.0827 | 0.5146 | 0.1597 | 0.6286 |
| UR | −2.7357 | −3.4713 | −2.3803 | −3.2713 | −3.2143 | 0.0795 | 0.4966 | 0.2423 | 0.1511 |
| UE | 3.0758 | 8.1516 | 9.2427 | 8.3516 | 8.4086 | 0.1621 | 0.9582 | 0.4416 | 0.0004 |
| Beta | −6.7819 | −9.5639 | −7.3818 | −8.9323 | −9.0498 | 0.1173 | 0.7123 | 0.2002 | 0.3413 |
| kum | −6.8436 | −9.6872 | −7.5052 | −9.0557 | −9.1732 | 0.1158 | 0.7037 | 0.1963 | 0.3650 |
| TL | −5.4982 | −8.9965 | −7.9055 | −8.7965 | −8.7395 | 0.1249 | 0.7557 | 0.1848 | 0.4401 |
Table 14.
Testing of hypothesis results.
Table 14.
Testing of hypothesis results.
| Full | Sub | df | Data I | Data II | Data III |
|---|
| Model | Model | | | p-Value | | p-Value | | p-Value |
|---|
| UMW | UW | 1 | 2.5116 | 0.11301 | 6.3526 | 0.0117 | 4.7204 | 0.0298 |
| | ULFR | 1 | 1.7122 | 0.1907 | 1.896 | 0.1685 | 3.2618 | 0.0709 |
| | UR | 2 | 3.6688 | 0.15971 | 11.1912 | 0.0037 | 13.6 | 0.0011 |
| | UE | 2 | 16.4204 | 0.00027 | 108.6044 | 0.0000 | 25.223 | 0.0000 |
| ULFR | UR | 1 | 1.9566 | 0.16188 | 9.2952 | 0.0023 | 10.3382 | 0.0013 |
| | UE | 1 | 14.7082 | 0.00013 | 106.7084 | 0.00000 | 21.9612 | 0.0000 |