On the Appropriateness of Fixed Correlation Assumptions in Repeated-Measures Meta-Analysis: A Monte Carlo Assessment
Abstract
1. Introduction
2. Materials and Methods
3. Results
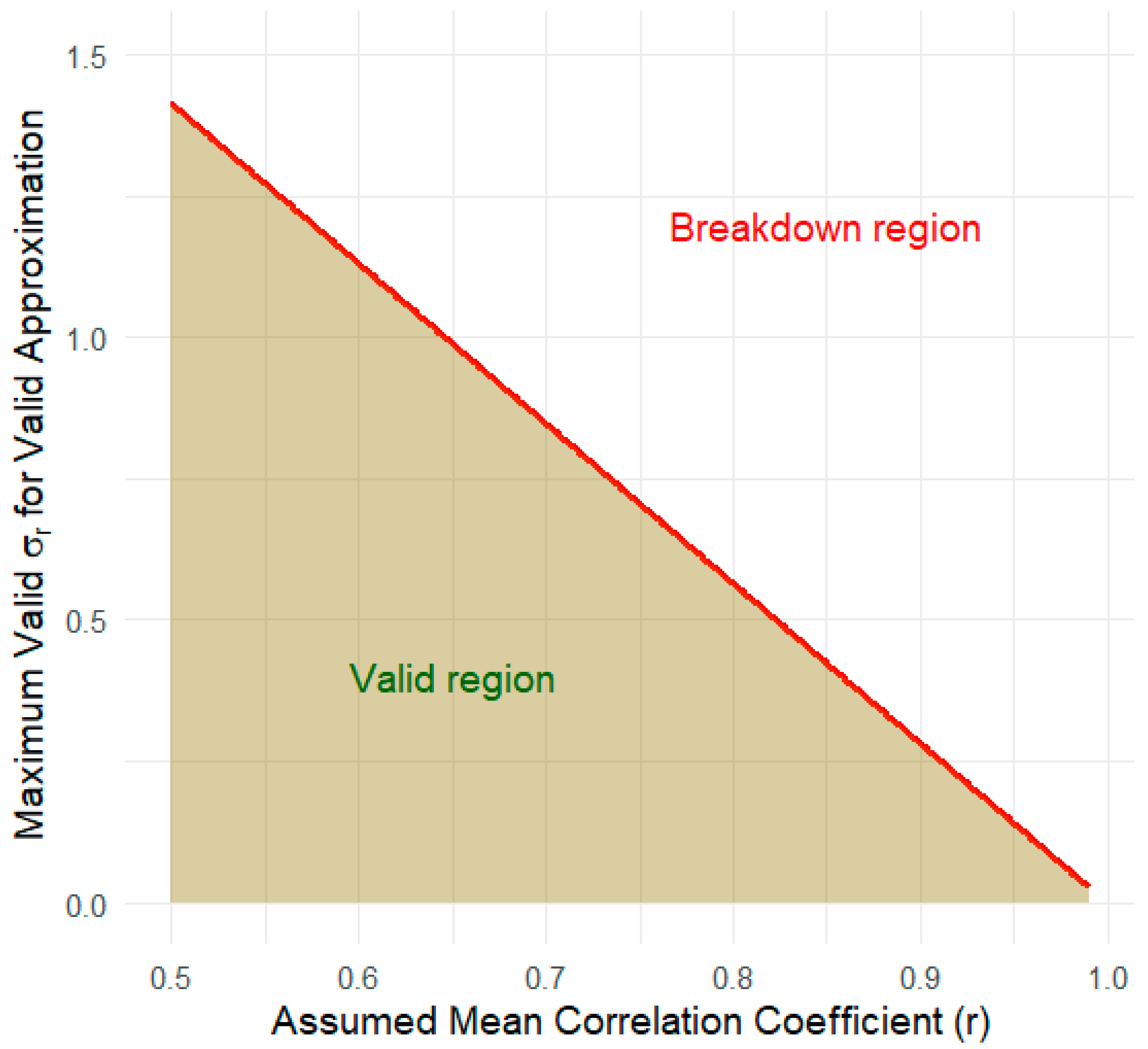
3.1. What Are the Consequences of r Uncertainty?
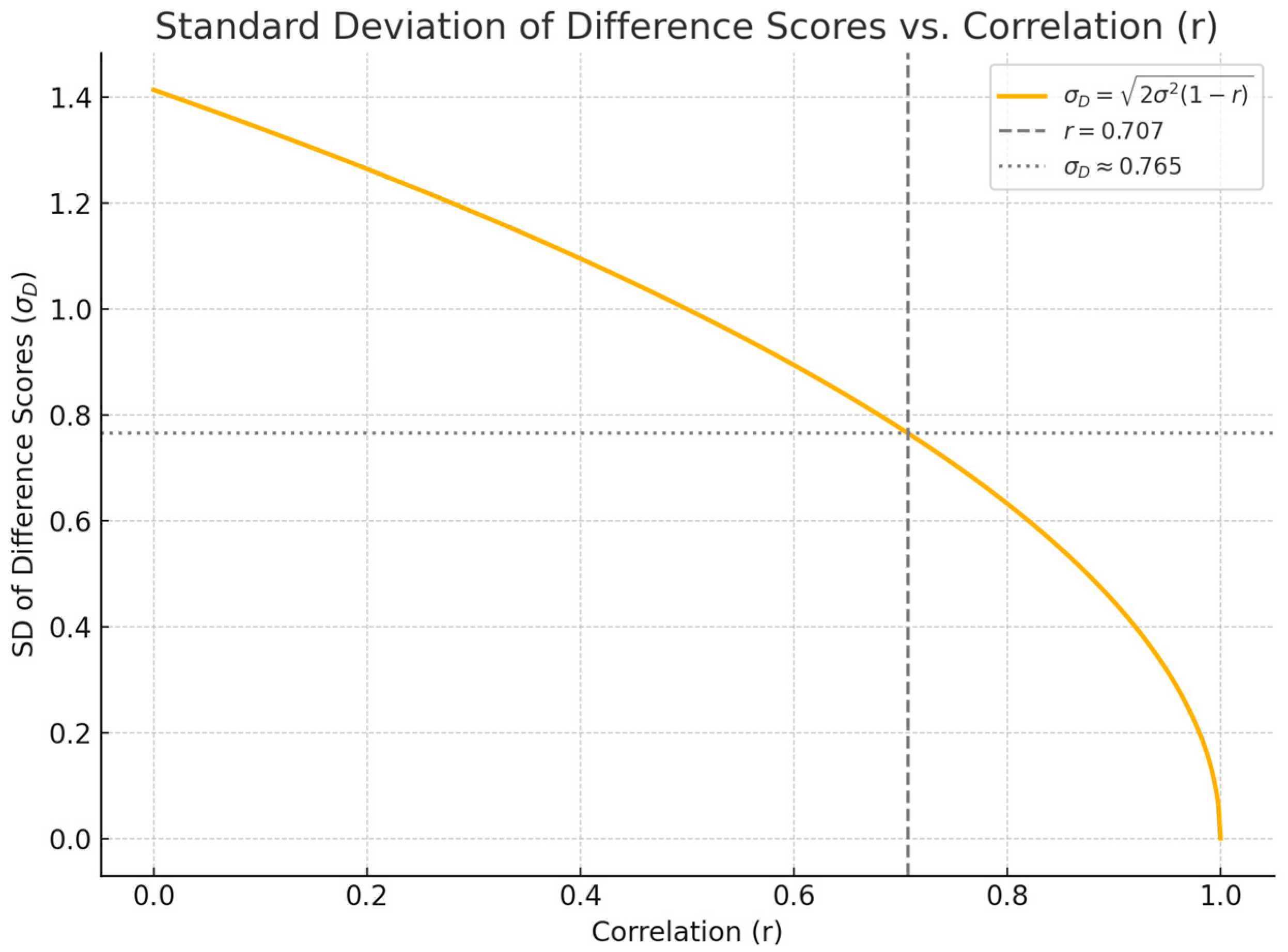
3.2. Does the r = 0.7 Heuristic Satisfy the “Midway” Hypothesis for Equal Pre/Post-Variances?
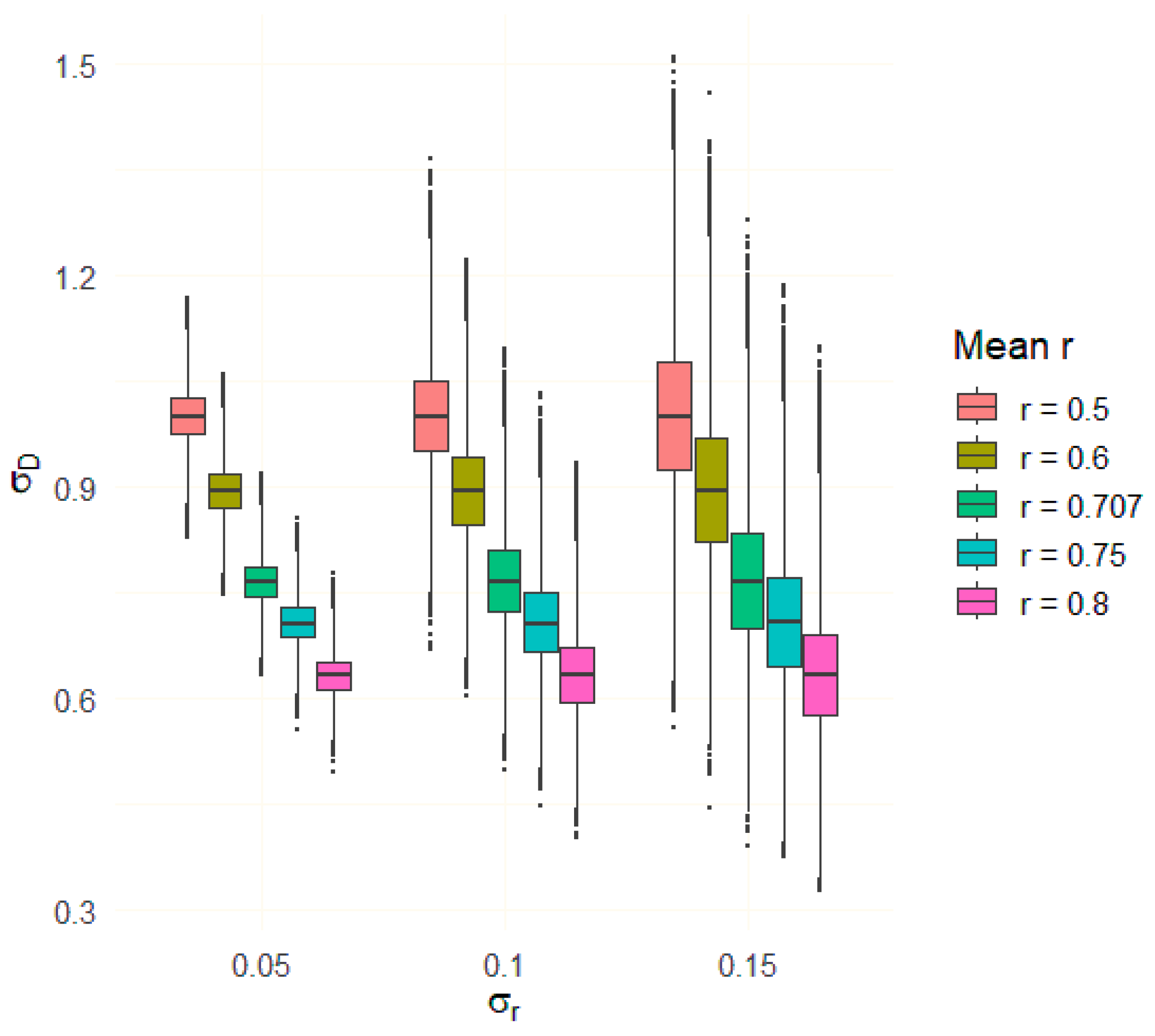
3.3. Simulation of Uncertainty of σD to Examine the Feasibility of the Proposed r = 0.75 for Equal Pre/Post-Variances
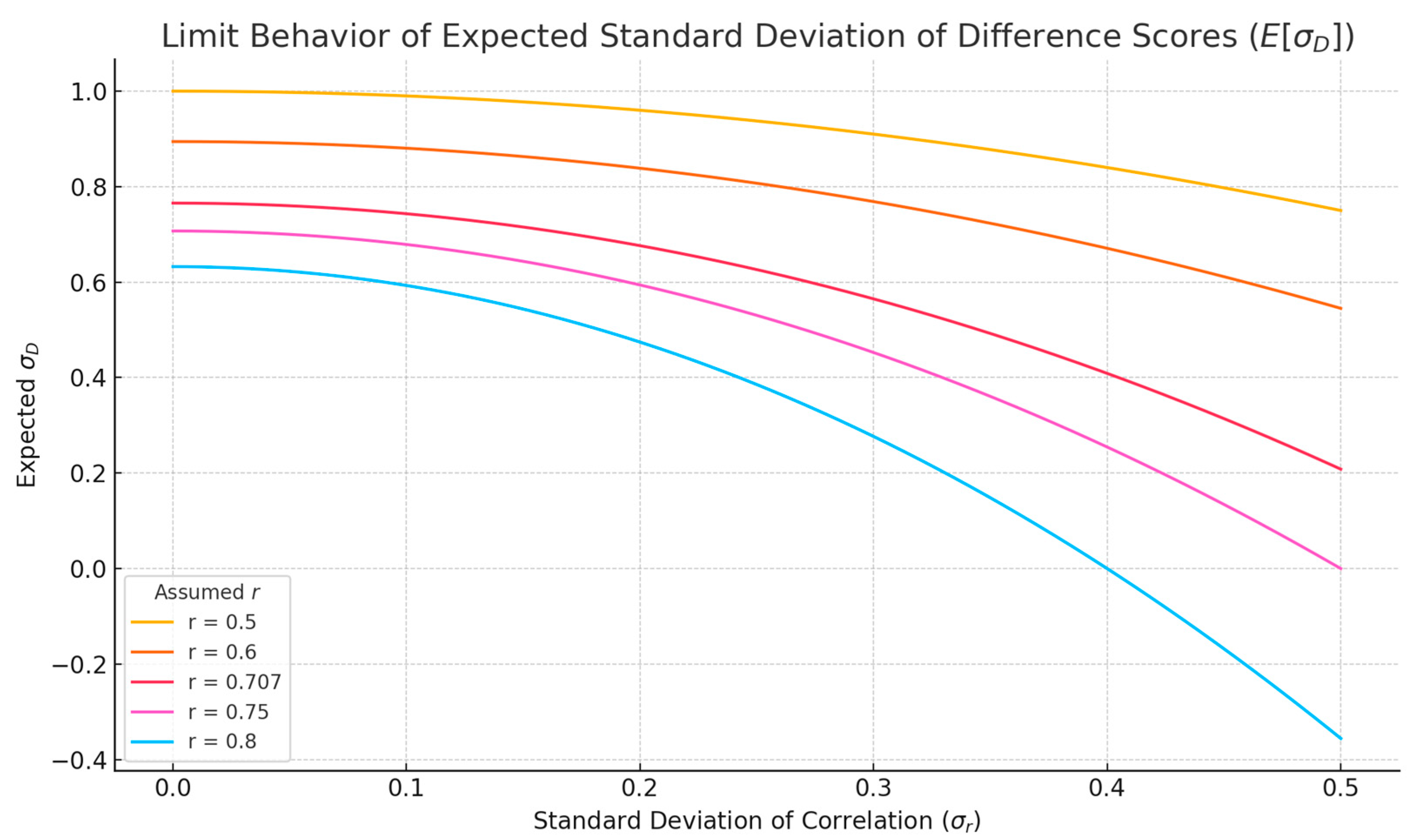
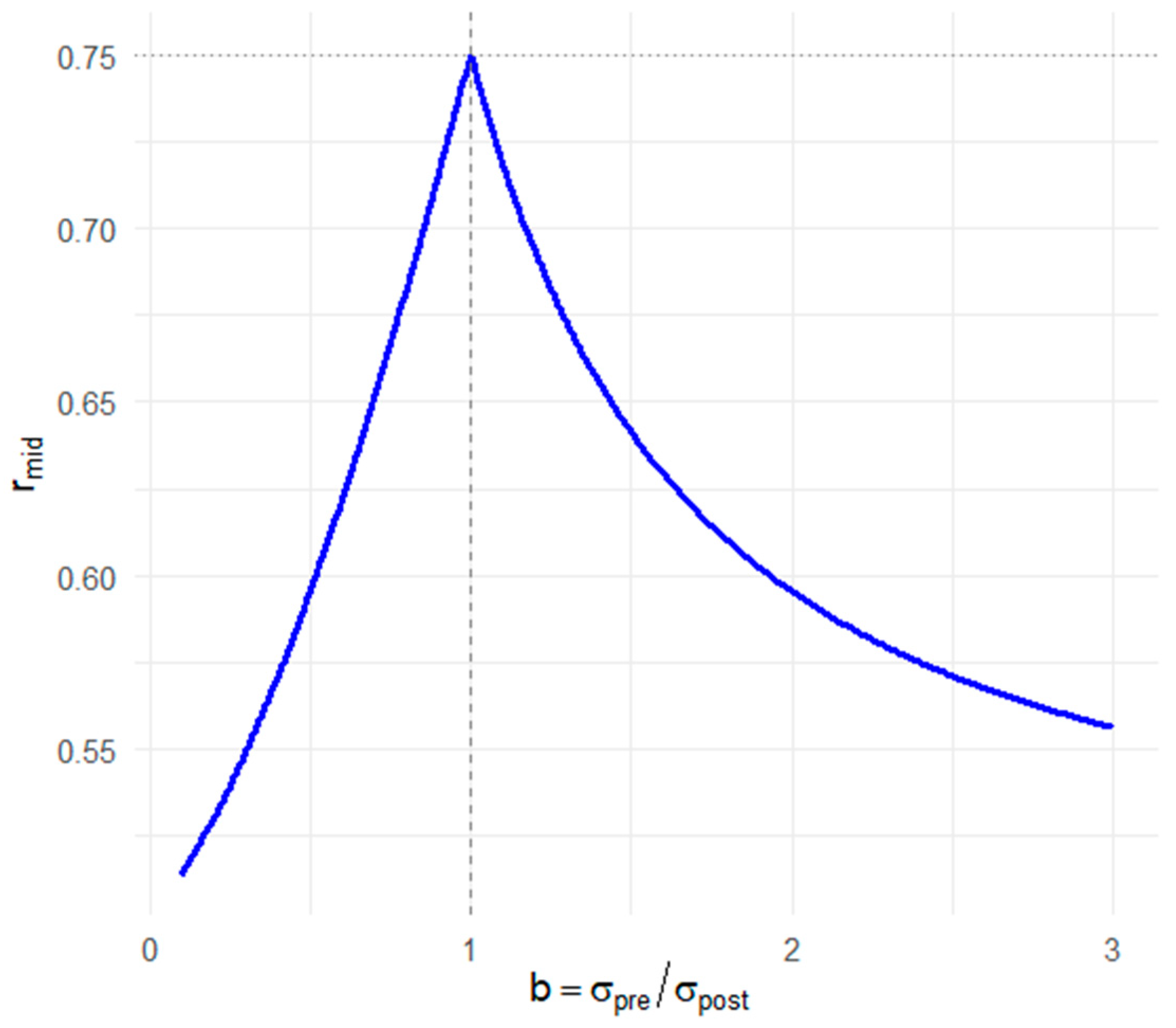
3.4. The “Midway” Hypothesis for Proposed r Under Unequal Pre/Post-Variances
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| R code for Monte Carlo simulation of σD # Load required libraries library(ggplot2) library(dplyr) # Define parameters mean_r_values <- c(0.5, 0.6, 0.707, 0.75, 0.8) sigma_r_values <- c(0.05, 0.10, 0.15) n <- 500000 # Fisher z-transform and inverse fisher_z <- function(r) 0.5 * log((1 + r) / (1 − r)) inv_fisher_z <- function(z) tanh(z) # Function to compute σD compute_sigma_D <- function(r) sqrt(2 * (1 − r)) # Initialize empty data frame results <- data.frame() # Simulation loop set.seed(123) for (r_mean in mean_r_values) { z_mean <- fisher_z(r_mean) for (sigma_r in sigma_r_values) { z_samples <- rnorm(n, mean = z_mean, sd = sigma_r) r_samples <- inv_fisher_z(z_samples) sigma_D <- compute_sigma_D(r_samples) df <- data.frame( sigma_r = as.factor(sigma_r), sigma_D = sigma_D, Group = paste0(“r = ”, r_mean) ) results <- bind_rows(results, df) } } # Boxplot visualization ggplot(results, aes(x = sigma_r, y = sigma_D, fill = Group)) + geom_boxplot(outlier.size = 0.5, coef = 2) + labs( title = expression(“Monte Carlo Simulation of” ~ sigma[D]), subtitle = “500,000 samples per group”, x = expression(sigma[r]), y = expression(sigma[D]), fill = “Mean r” ) + theme_minimal(base_size = 14) + theme(legend.position = “right”) |
References
- UNISTAT Statistics Software. 6.8.3. Summary of Effect Sizes. Available online: https://www.unistat.com/guide/meta-analysis-summary-of-effect-sizes/?utm_source=chatgpt.com (accessed on 17 June 2025).
- Socha, M.; Pietrzak, A.; Grywalska, E.; Pietrzak, D.; Matosiuk, D.; Kiciński, P.; Rolinski, J. The effect of statins on psoriasis severity: A meta-analysis of randomized clinical trials. Arch. Med. Sci. 2019, 16, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, V.P.; Apergis, N.; Filippou, D.K. Nocturia in CPAP-treated obstructive sleep apnea patients: A systematic review and meta-analysis. SN Comprehens. Clin. Med. 2020, 2, 2799–2807. [Google Scholar] [CrossRef]
- Manser, P.; Herold, F.; de Bruin, E.D. Components of effective exergame-based training to improve cognitive functioning in middle-aged to older adults—A systematic review and meta-analysis. Ageing Res. Rev. 2024, 99, 102385. [Google Scholar] [CrossRef] [PubMed]
- Chin, P.; Gorman, F.; Beck, F.; Russell, B.R.; Stephan, K.E.; Harrison, O.K. A systematic review of brief respiratory, embodiment, cognitive, and mindfulness interventions to reduce state anxiety. Front. Psychol. 2024, 15, 1412928. [Google Scholar] [CrossRef] [PubMed]
- Obomsawin, A.; Pejic, S.R.; Koziol, C. Effects of racial discrimination tasks on salivary cortisol reactivity among racially minoritized groups: A meta-analysis. Horm. Behav. 2025, 173, 105775. [Google Scholar] [CrossRef] [PubMed]
- McGirr, A.; Berlim, M.T.; Bond, D.J.; Neufeld, N.H.; Chan, P.Y.; Yatham, L.N.; Lam, R.W. A systematic review and meta-analysis of randomized controlled trials of adjunctive ketamine in electroconvulsive therapy: Efficacy and tolerability. J. Psychiatr. Res. 2015, 62, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, R. Meta-Analytic Procedures for Social Research; Applied Social Research Methods Series 6; Sage Publications: Newbury Park, CA, USA, 1991. [Google Scholar]
- Campbell Collaboration and Effect-Size Calculators. Available online: https://www.campbellcollaboration.org/calculator/equations?utm_source=chatgpt.com (accessed on 17 June 2025).
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Yagiz, G.; Akaras, E.; Kubis, H.-P.; Owen, J.A. The Effects of Resistance Training on Architecture and Volume of the Upper Extremity Muscles: A Systematic Review of Randomised Controlled Trials and Meta-Analyses. Appl. Sci. 2022, 12, 1593. [Google Scholar] [CrossRef]
- Meléndez-Oliva, E.; Martínez-Pozas, O.; Cuenca-Zaldívar, J.N.; Villafañe, J.H.; Jiménez-Ortega, L.; Sánchez-Romero, E.A. Efficacy of Pulmonary Rehabilitation in Post-COVID-19: A Systematic Review and Meta-Analysis. Biomedicines 2023, 11, 2213. [Google Scholar] [CrossRef] [PubMed]
- Herrero, P.; Val, P.; Lapuente-Hernández, D.; Cuenca-Zaldívar, J.N.; Calvo, S.; Gómez-Trullén, E.M. Effects of Lifestyle Interventions on the Improvement of Chronic Non-Specific Low Back Pain: A Systematic Review and Network Meta-Analysis. Healthcare 2024, 12, 505. [Google Scholar] [CrossRef] [PubMed]
- Higgins, J.P.T.; Thomas, J.; Chandler, J.; Cumpston, M.; Li, T.; Page, M.J.; Welch, V.A. (Eds.) Cochrane Handbook for Systematic Reviews of Interventions, version 6.5; updated August 2024; Cochrane: London, UK, 2024. Available online: www.cochrane.org/authors/handbooks-and-manuals/handbook/current/chapter-06#section-6-5-2-8 (accessed on 2 August 2025).
- Olkin, I.; Pratt, J.W. Unbiased estimation of certain correlation coefficients. Ann. Math. Stat. 1958, 29, 201–211. [Google Scholar] [CrossRef]
- Zimmerman, D.W.; Williams, R.H.; Zumbo, B.D. Effect of nonindependence of sample observations on some parametric and nonparamentric statistical tests. Commun. Stat.—Simul. Comput. 1993, 22, 779–789. [Google Scholar] [CrossRef]
- Papadimitropoulou, K.; Stijnen, T.; Riley, R.D.; Dekkers, O.M.; le Cessie, S. Meta-analysis of continuous outcomes: Using pseudo IPD created from aggregate data to adjust for baseline imbalance and assess treatment-by-baseline modification. Res. Synth. Methods 2020, 11, 780–794. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, V.P.; Mimidis, K. Corrected QT interval in cirrhosis: A systematic review and meta-analysis. World J. Hepatol. 2023, 27, 1060–1083. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadopoulos, V. On the Appropriateness of Fixed Correlation Assumptions in Repeated-Measures Meta-Analysis: A Monte Carlo Assessment. Stats 2025, 8, 72. https://doi.org/10.3390/stats8030072
Papadopoulos V. On the Appropriateness of Fixed Correlation Assumptions in Repeated-Measures Meta-Analysis: A Monte Carlo Assessment. Stats. 2025; 8(3):72. https://doi.org/10.3390/stats8030072
Chicago/Turabian StylePapadopoulos, Vasileios. 2025. "On the Appropriateness of Fixed Correlation Assumptions in Repeated-Measures Meta-Analysis: A Monte Carlo Assessment" Stats 8, no. 3: 72. https://doi.org/10.3390/stats8030072
APA StylePapadopoulos, V. (2025). On the Appropriateness of Fixed Correlation Assumptions in Repeated-Measures Meta-Analysis: A Monte Carlo Assessment. Stats, 8(3), 72. https://doi.org/10.3390/stats8030072





