A Mixture Integer GARCH Model with Application to Modeling and Forecasting COVID-19 Counts
Abstract
1. Introduction
2. Materials and Methods
2.1. Mixture INGARCH Model
- This sequence is known as a mixture INGARCH (MINGARCH) model.
- The proof is rather simple by considering the total law of expectation. It can be noticed that for the MINGARCH(1,1) process, the unconditional mean is
2.2. Covid Data
2.2.1. Descriptive Statistics
2.2.2. Data Properties
3. Results and Discussion
3.1. Model Fitting
| State | Seasonal Size | Order Size | Loglikelihood | AIC | BIC |
|---|---|---|---|---|---|
| Selangor | 34 | 3 | −10,693 | 21,395 | 21,404 |
| KL | 34 | 3 | −3462 | 6932 | 6941 |
| Johor | 24 | 1 | −17,000 | 34,004 | 34,008 |
| Penang | 34 | 3 | −13,950 | 27,909 | 27,918 |
| Sarawak | 23 | 1 | −29,690 | 59,384 | 59,388 |
| State | Mean Function |
|---|---|
| Selangor | |
| KL | |
| Johor | |
| Penang | |
| Sarawak |
| State | Seasonal Size | Order Size | Loglikelihood | AIC | BIC |
|---|---|---|---|---|---|
| Selangor | 34 | 3 | −53,140 | 106,289 | 106,300 |
| KL | 34 | 3 | −13,600 | 27,211 | 27,222 |
| Johor | 24 | 1 | −5959 | 11,924 | 11,931 |
| Penang | 34 | 3 | −13,797 | 27,603 | 27,614 |
| Sarawak | 23 | 1 | −3882 | 7769 | 7776 |
| State | Seasonal Size | Order Size | Loglikelihood | AIC | BIC |
|---|---|---|---|---|---|
| Selangor | 34 | 3 | −50,601.131 | 101,216 | 101,232 |
| KL | 34 | 3 | −13,549.302 | 27,113 | 27,128 |
| Johor | 24 | 1 | −12,907.852 | 25,826 | 25,837 |
| Penang | 34 | 3 | −14,449.323 | 28,913 | 28,928 |
| Sarawak | 23 | 1 | −2784.7142 | 5579 | 5591 |
3.2. Forecasting
3.3. Policy Implications
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cardinal, M.; Roy, R.; Lambert, J. On the application of integer-valued time series models for the analysis of disease incidence. Stat. Med. 1999, 18, 2025–2039. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Victor, S.; Dugard, L. Non-integer (or fractional) power model of a viral spreading: Application to the COVID-19. Annu. Rev. Control 2021, 51, 324–334. [Google Scholar]
- Palmer, W.R.; Davis, R.A.; Zheng, T. Count-valued time series models for COVID-19 daily death dynamics. Stat 2021, 10, e369. [Google Scholar] [CrossRef] [PubMed]
- Wamwea, C.; Mwelu, S.; Odin, M. Modelling COVID-19 cumulative number of cases in Kenya using a negative binomial INAR(1) model. Open J. Model. Simul. 2023, 11, 14–36. [Google Scholar] [CrossRef]
- Tawiah, K.; Iddrisu, W.A.; Asosega, K.A. Zero-inflated time series modelling of COVID-19 deaths in Ghana. J. Environ. Public Health 2021, 2021, 5543977. [Google Scholar] [CrossRef] [PubMed]
- Soobhug, A.D.; Jowaheer, H.; Mamode Khan, N.; Reetoo, N.; Meethoo-Badulla, K.; Musango, L. Re-analyzing the SARS-CoV-2 series using an extended integer-valued time series models: A situational assessment of the COVID-19 in Mauritius. PLoS ONE 2022, 17, e0263515. [Google Scholar] [CrossRef]
- Freeland, R.K.; McCabe, B.P.M. Analysis of low count time series data by Poisson autoregression. J. Time Ser. Anal. 2004, 25, 701–722. [Google Scholar] [CrossRef]
- Agosto, A.; Giudici, P. A Poisson autoregressive model to understand COVID-19 contagion dynamics. Risks 2020, 8, 77. [Google Scholar] [CrossRef]
- Weiss, C.H. An Introduction to Discrete-Valued Time Series; Wiley: Hoboken, NJ, USA, 2018; ISBN 978-1-119-09696-2. [Google Scholar]
- Jacobs, P.A.; Lewis, P.A.W. Discrete time series generated by mixtures. I: Correlational and runs properties. J. R. Stat. Soc. Ser. B 1978, 40, 94–105. [Google Scholar] [CrossRef]
- Biswas, A.; Song, P.X.-K. Discrete-valued ARMA processes. Stat. Probab. Lett. 2009, 79, 1884–1889. [Google Scholar] [CrossRef]
- Khoo, W.C.; Ong, S.H.; Biswas, A. Modeling time series of counts with a new class of INAR(1) model. Stat. Pap. 2017, 58, 393–416. [Google Scholar] [CrossRef]
- Khoo, W.C.; Ong, S.H.; Atanu, B. Coherent forecasting for a mixed integer-valued time series model. Mathematics 2022, 10, 2961. [Google Scholar] [CrossRef]
- Khendhiri, S. Statistical modeling of COVID-19 deaths with excess zero counts. Epidemiol. Methods 2021, 10, 20210007. [Google Scholar] [CrossRef]
- Ferland, R.; Latour, A.; Oraichi, D. Integer-valued GARCH process. J. Time Ser. Anal. 2006, 27, 923–942. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Fokianos, K.; Fried, R. Interventions in INGARCH processes. J. Time Ser. Anal. 2010, 31, 210–225. [Google Scholar] [CrossRef]
- Liboschik, T.; Fokianos, K.; Fried, R. tscount: An R package for analysis of count time series following generalized linear models. J. Stat. Softw. 2017, 82, 1–51. [Google Scholar] [CrossRef]
- Chan, S.; Chu, J.; Zhang, Y.; Nadarajah, S. Count regression models for COVID-19. Phys. A Stat. Mech. Appl. 2021, 563, 125460. [Google Scholar] [CrossRef]
- Pegram, G.G.S. An autoregressive model for multileg Markov chains. J. Appl. Probab. 1980, 17, 350–362. [Google Scholar] [CrossRef]
- Li, G.; Zhu, Q.; Liu, Z.; Li, W.K. On mixture double autoregressive time series models. J. Bus. Econ. Stat. 2017, 35, 306–317. [Google Scholar] [CrossRef]
- Low, V.J.M.; Khoo, W.C.; Khoo, H.L. A generalized Burr mixture autoregressive models for modeling non-linear time series. Commun. Stat. Theory Methods 2024, 53, 6832–6851. [Google Scholar] [CrossRef]
- Wong, C.S.; Chan, W.S.; Kam, P.L. A Student t-mixture autoregressive model with applications to heavy-tailed financial data. Biometrika 2009, 96, 751–760. [Google Scholar] [CrossRef]
- Golinski, A.; Spencer, P. Modeling the COVID-19 epidemic using time series econometrics. Health Econ. 2021, 30, 2808–2828. [Google Scholar] [CrossRef]
- Vig, V.; Kaur, A. Time series forecasting and mathematical modeling of COVID-19 pandemic in India: A developing country struggling to cope up. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 2920–2933. [Google Scholar] [CrossRef]
- Cheng, Y.; Cheng, R.; Xu, T.; Tan, X.; Bai, Y. Machine learning techniques applied to COVID-19 prediction: A systematic literature review. Bioengineering 2025, 12, 514. [Google Scholar] [CrossRef]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]

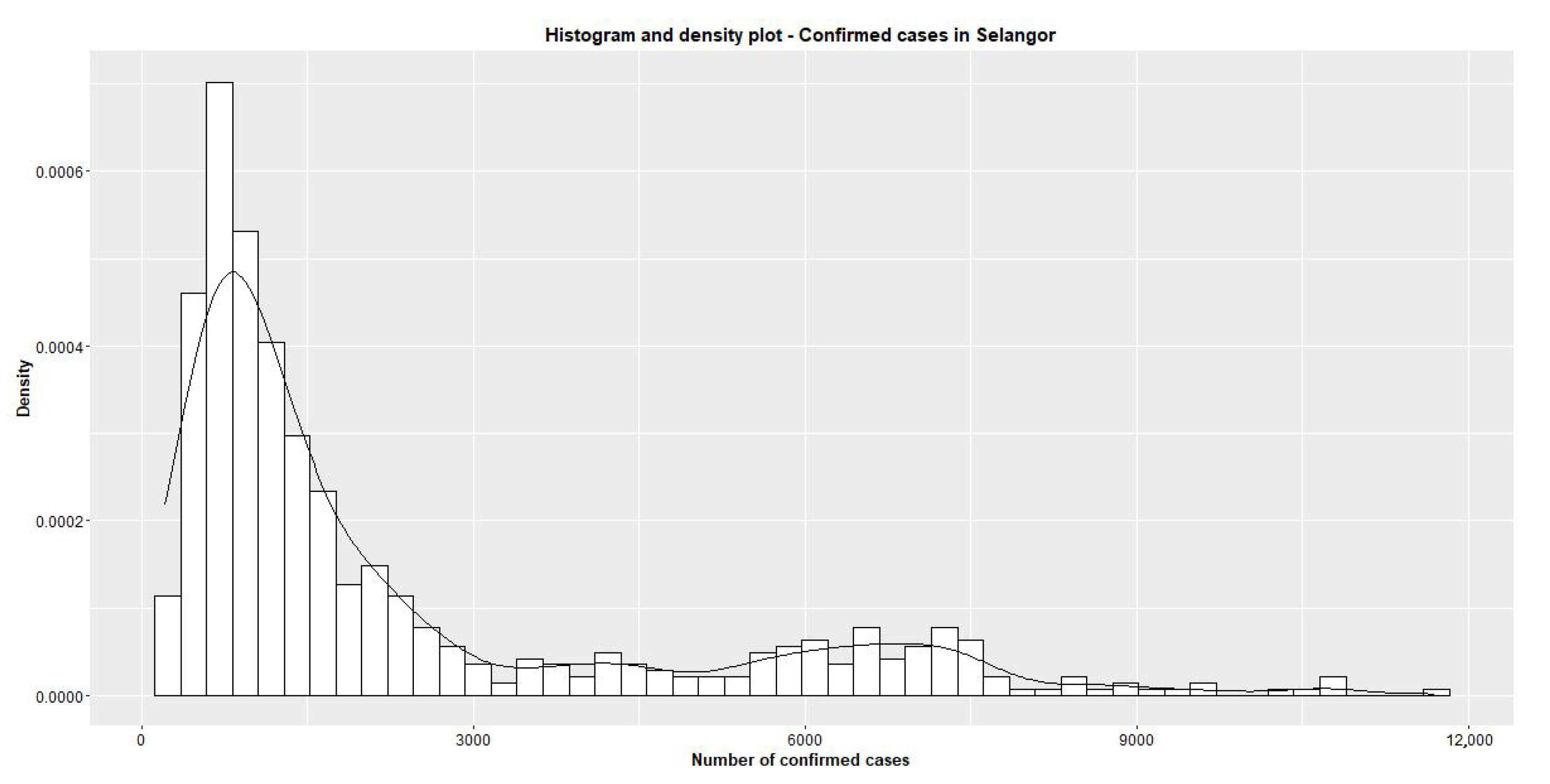
| State (Density) | Weekday | Descriptive Statistics | |||||
|---|---|---|---|---|---|---|---|
| Minimum | Q1 | Median | Mean | Q3 | Maximum | ||
| Selangor (880 km2) | Sunday | 256 | 746 | 1112 | 2192 | 2330 | 9273 |
| Monday | 213 | 613 | 884 | 1830 | 2096 | 6941 | |
| Tuesday | 242 | 663 | 1090 | 2079 | 2576 | 8095 | |
| Wednesday | 294 | 854 | 1436 | 2460 | 2809 | 10,240 | |
| Thursday | 237 | 892 | 1440 | 2537 | 2843 | 11,692 | |
| Friday | 348 | 822 | 1325 | 2600 | 2842 | 10,842 | |
| Saturday | 283 | 789 | 1394 | 2483 | 2754 | 10,790 | |
| KL (8157 km2) | Sunday | 55 | 221 | 354 | 543 | 616 | 2685 |
| Monday | 57 | 190 | 315 | 479 | 582 | 2214 | |
| Tuesday | 53 | 317 | 424 | 757 | 989 | 4527 | |
| Wednesday | 42 | 320 | 455 | 745 | 961 | 3565 | |
| Thursday | 79 | 334 | 517 | 770 | 976 | 3266 | |
| Friday | 86 | 308 | 484 | 783 | 966 | 4105 | |
| Saturday | 67 | 298 | 476 | 711 | 773 | 3603 | |
| Penang (1664 km2) | Sunday | 57 | 140 | 216 | 427 | 422 | 1961 |
| Monday | 50 | 104 | 172 | 411 | 398 | 2137 | |
| Tuesday | 53 | 115 | 199 | 473 | 421 | 2601 | |
| Wednesday | 51 | 119 | 198 | 498 | 430 | 2575 | |
| Thursday | 65 | 143 | 234 | 527 | 481 | 2773 | |
| Friday | 75 | 140 | 248 | 519 | 504 | 2750 | |
| Saturday | 74 | 134 | 218 | 494 | 407 | 2621 | |
| Johor (209 km2) | Sunday | 28 | 87.5 | 354 | 573 | 728 | 2644 |
| Monday | 36 | 92.8 | 340 | 577 | 757 | 2800 | |
| Tuesday | 29 | 91.5 | 348 | 564 | 665 | 2780 | |
| Wednesday | 33 | 103 | 384 | 606 | 700 | 2986 | |
| Thursday | 37 | 110 | 412 | 650 | 801 | 2856 | |
| Friday | 33 | 106 | 389 | 612 | 718 | 2860 | |
| Saturday | 33 | 81.2 | 403 | 592 | 710 | 3238 | |
| Sarawak (20 km2) | Sunday | 6 | 51.2 | 234 | 507 | 580 | 5291 |
| Monday | 7 | 39.2 | 213 | 464 | 521 | 3714 | |
| Tuesday | 10 | 79.8 | 211 | 505 | 605 | 3732 | |
| Wednesday | 13 | 81.2 | 212 | 513 | 549 | 4709 | |
| Thursday | 14 | 70.5 | 280 | 528 | 604 | 3660 | |
| Friday | 11 | 69 | 234 | 556 | 692 | 3734 | |
| Saturday | 13 | 56.2 | 238 | 504 | 570 | 3743 | |
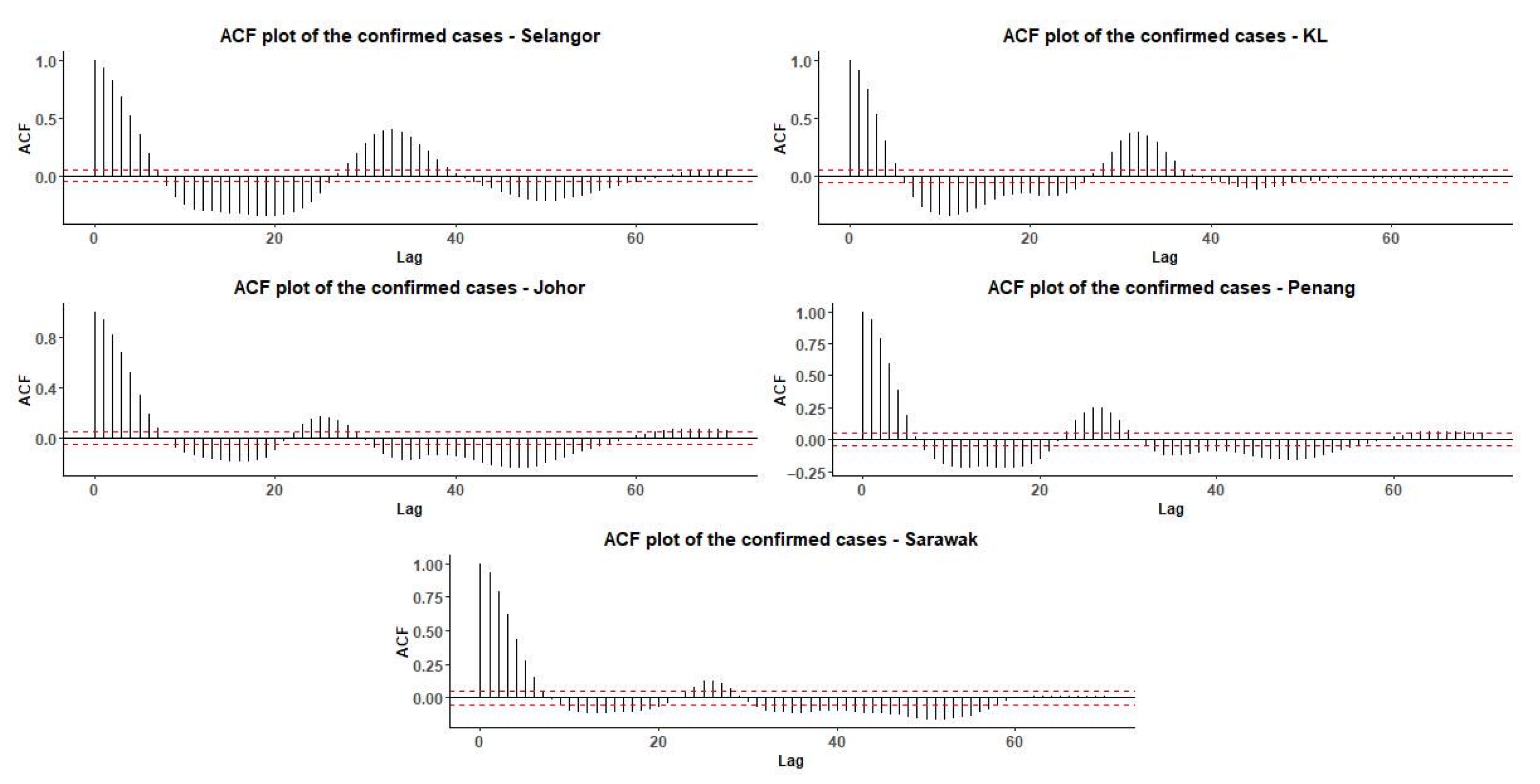
| State | Decision | Conclusion of Seasonality Indicator |
|---|---|---|
| Selangor | Reject | at lags 18, 33 to 39 |
| KL | Reject | at lags 18, 27, 28 and 34 |
| Johor | Reject | at lags 21 to 24 |
| Penang | Reject | at lags 13, 22 to 26 |
| Sarawak | Reject | at lags 21 to 27 |
| State | MINGARCH | INGARCH | INGARCH with Intervention | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | |
| Selangor | 42.75 | 292.06 | 328.79 | 203.65 | 1359.59 | 1503.41 | 346.49 | 2488.56 | 2540.63 |
| KL | 38.80 | 336.18 | 458.25 | 47.21 | 294.56 | 340.00 | 83.82 | 374.29 | 442.69 |
| Johor | 400.85 | 266.94 | 268.22 | 576.54 | 356.35 | 415.69 | 805.51 | 525.15 | 548.79 |
| Penang | 262.04 | 252.94 | 257.39 | 512.88 | 439.24 | 526.84 | 580.98 | 481.97 | 600.75 |
| Sarawak | 195.92 | 135.59 | 137.53 | 154.75 | 118.29 | 163.33 | 116.04 | 89.41 | 118.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoo, W.C.; Ong, S.H.; Low, V.J.M.; Srivastava, H.M. A Mixture Integer GARCH Model with Application to Modeling and Forecasting COVID-19 Counts. Stats 2025, 8, 73. https://doi.org/10.3390/stats8030073
Khoo WC, Ong SH, Low VJM, Srivastava HM. A Mixture Integer GARCH Model with Application to Modeling and Forecasting COVID-19 Counts. Stats. 2025; 8(3):73. https://doi.org/10.3390/stats8030073
Chicago/Turabian StyleKhoo, Wooi Chen, Seng Huat Ong, Victor Jian Ming Low, and Hari M. Srivastava. 2025. "A Mixture Integer GARCH Model with Application to Modeling and Forecasting COVID-19 Counts" Stats 8, no. 3: 73. https://doi.org/10.3390/stats8030073
APA StyleKhoo, W. C., Ong, S. H., Low, V. J. M., & Srivastava, H. M. (2025). A Mixture Integer GARCH Model with Application to Modeling and Forecasting COVID-19 Counts. Stats, 8(3), 73. https://doi.org/10.3390/stats8030073








