Unraveling Similarities and Differences Between Non-Negative Garrote and Adaptive Lasso: A Simulation Study in Low- and High-Dimensional Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Design
2.2. Data-Generating Mechanisms
2.3. Performance Measures
2.3.1. Variable Selection
Simple Matching Coefficient
False Positive Rates and False Negative Rates
Matthews Correlation Coefficient
2.3.2. Regression Estimates
Manhattan Distance
2.3.3. Prediction Accuracy
Relative Test Error
2.4. Methods
2.4.1. Adaptive Lasso
2.4.2. Non-Negative Garrote
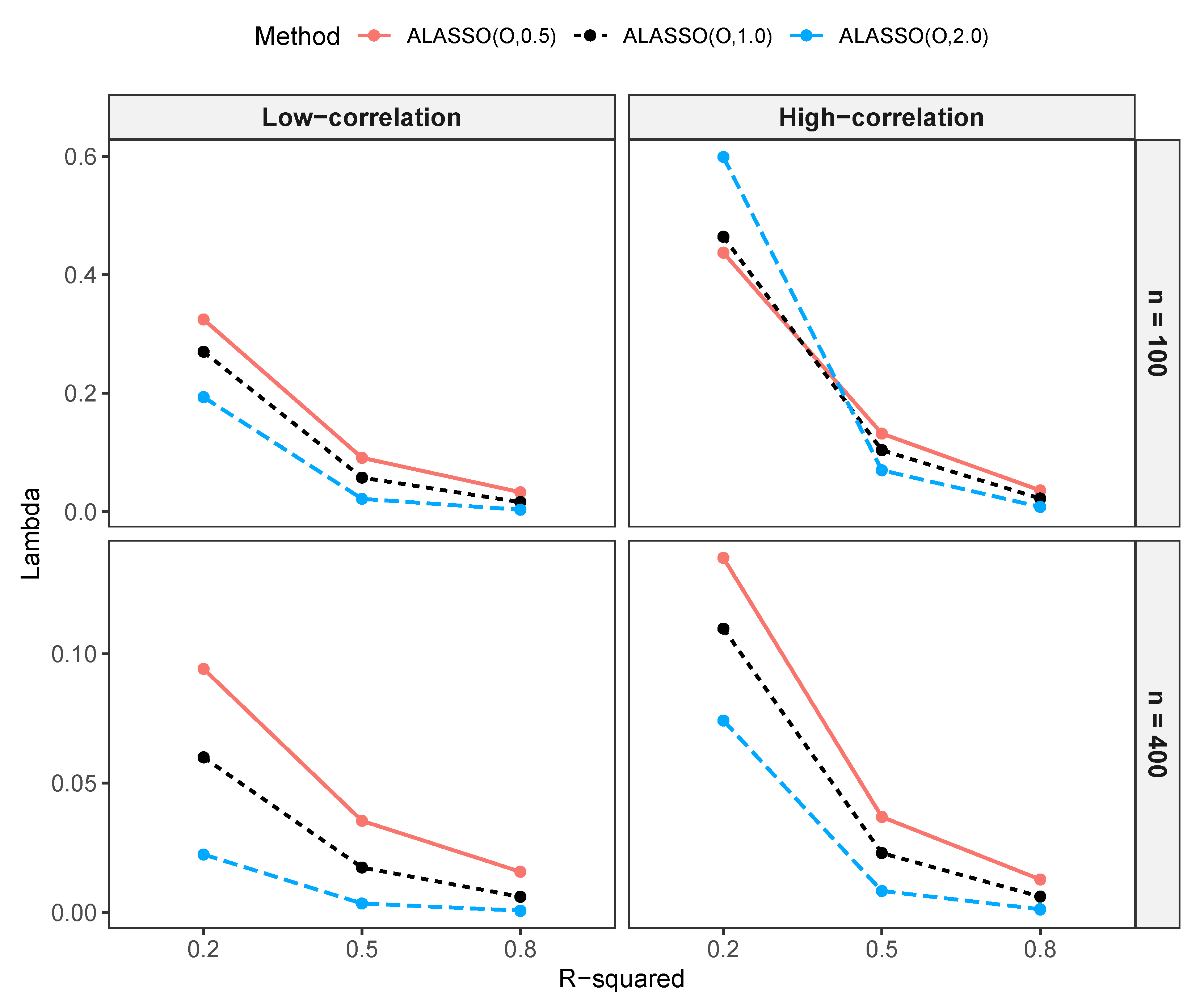
2.4.3. Adaptive Lasso Versus Non-Negative Garrote Weights
2.4.4. Orthonormal Design
A Toy Example Illustrating Orthonormal Design
2.5. Notation
3. Results
3.1. Simulation Results in Low-Dimensional Settings
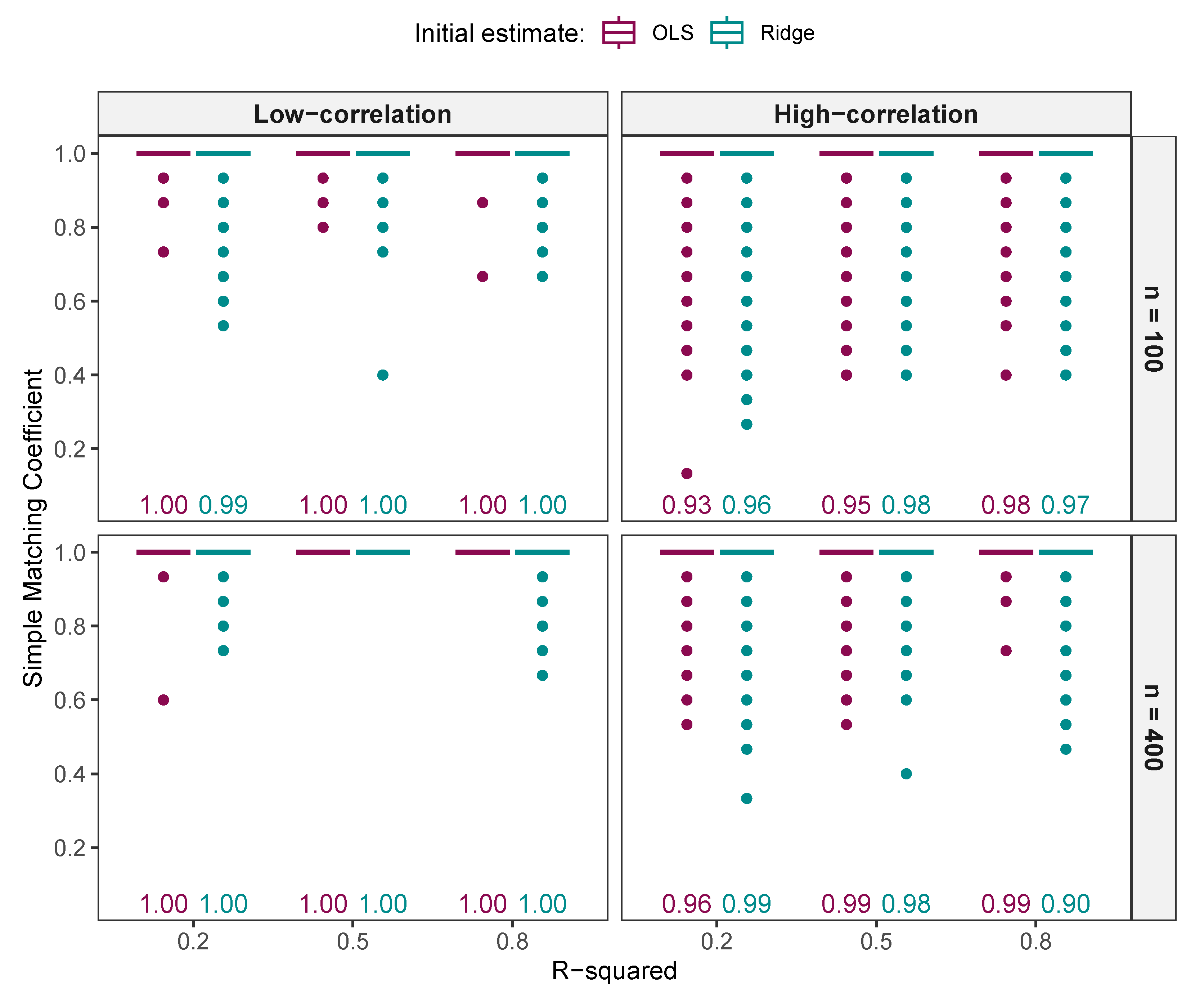
3.1.1. Example Illustrating the Impact of Initial Estimate Signs on Model Selection
3.1.2. Comparison of Variables Selected by NNG and ALASSO with Different Values
Comparison of Variables Selected by NNG and ALASSO ()
Comparison of Variables Selected by NNG and ALASSO ()
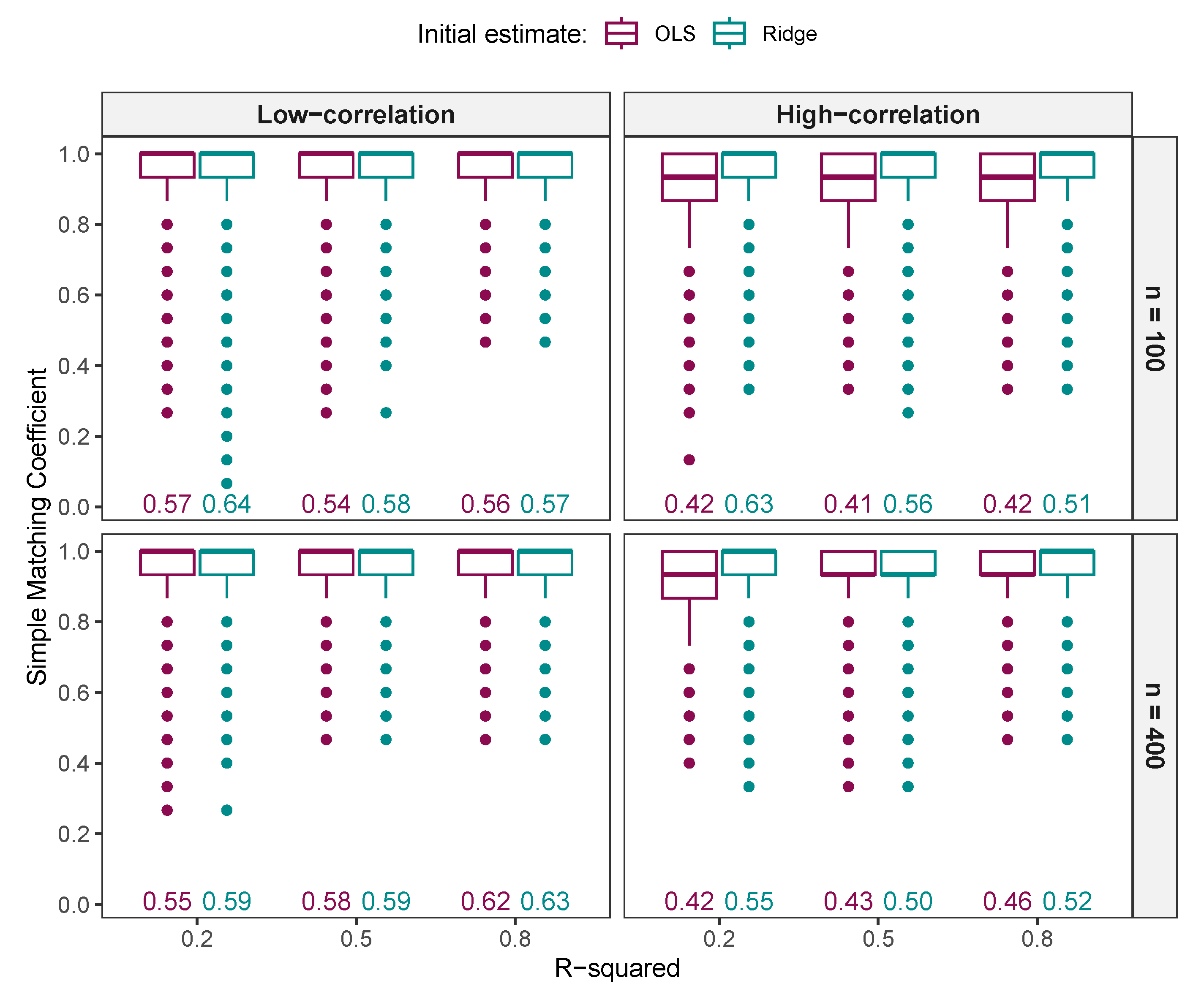
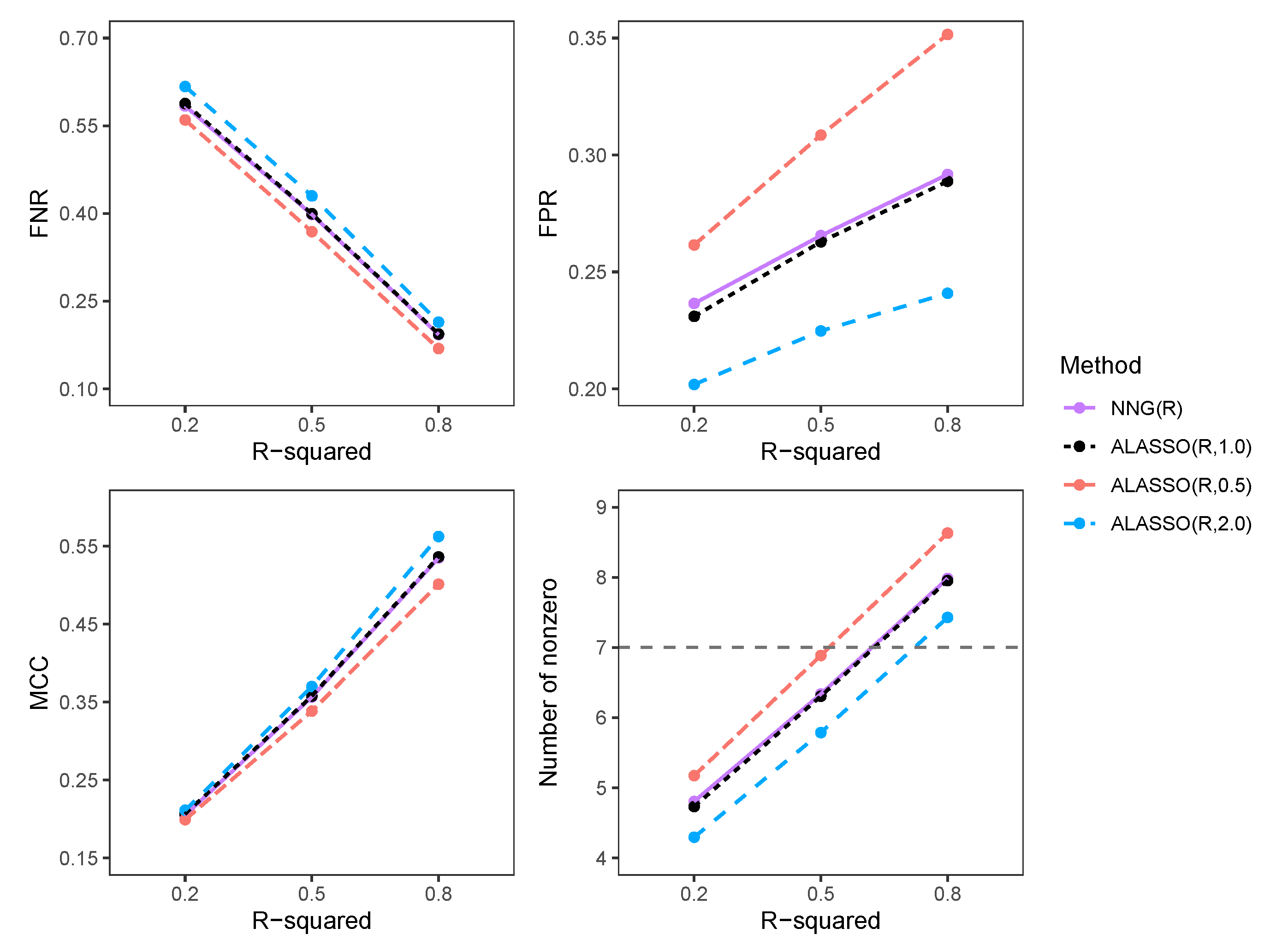
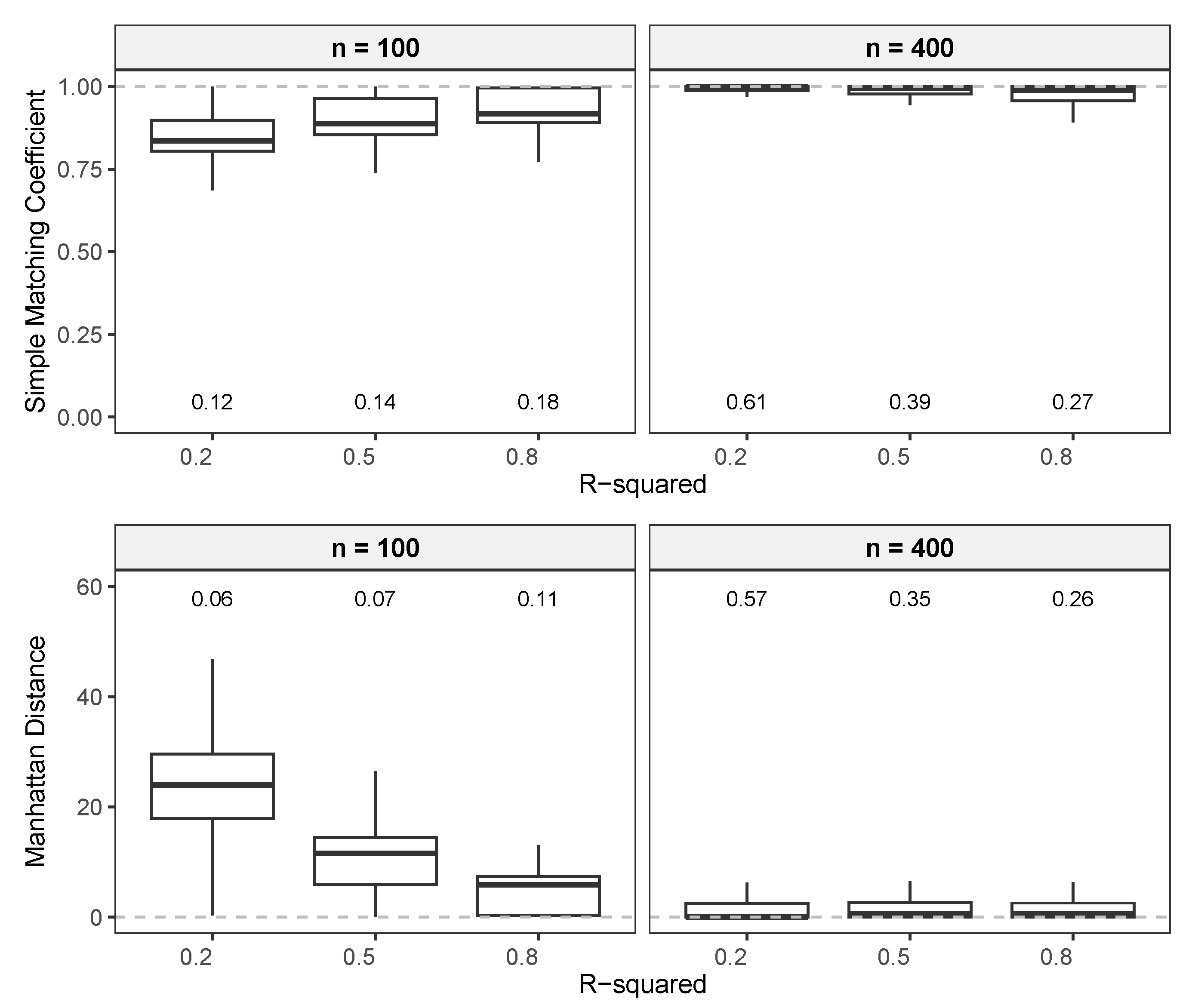
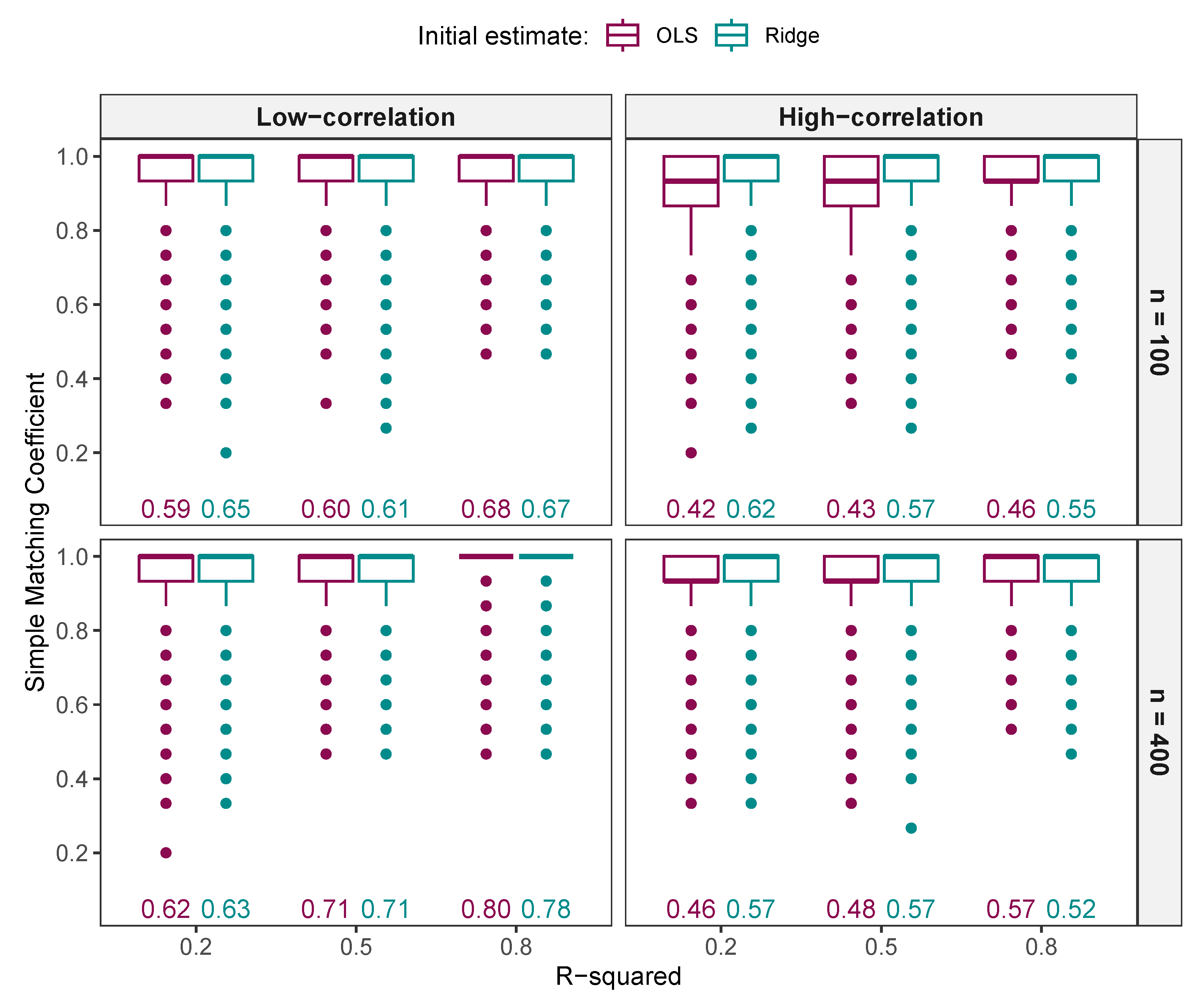
3.1.3. Comparison of FNR, FPR, and MCC
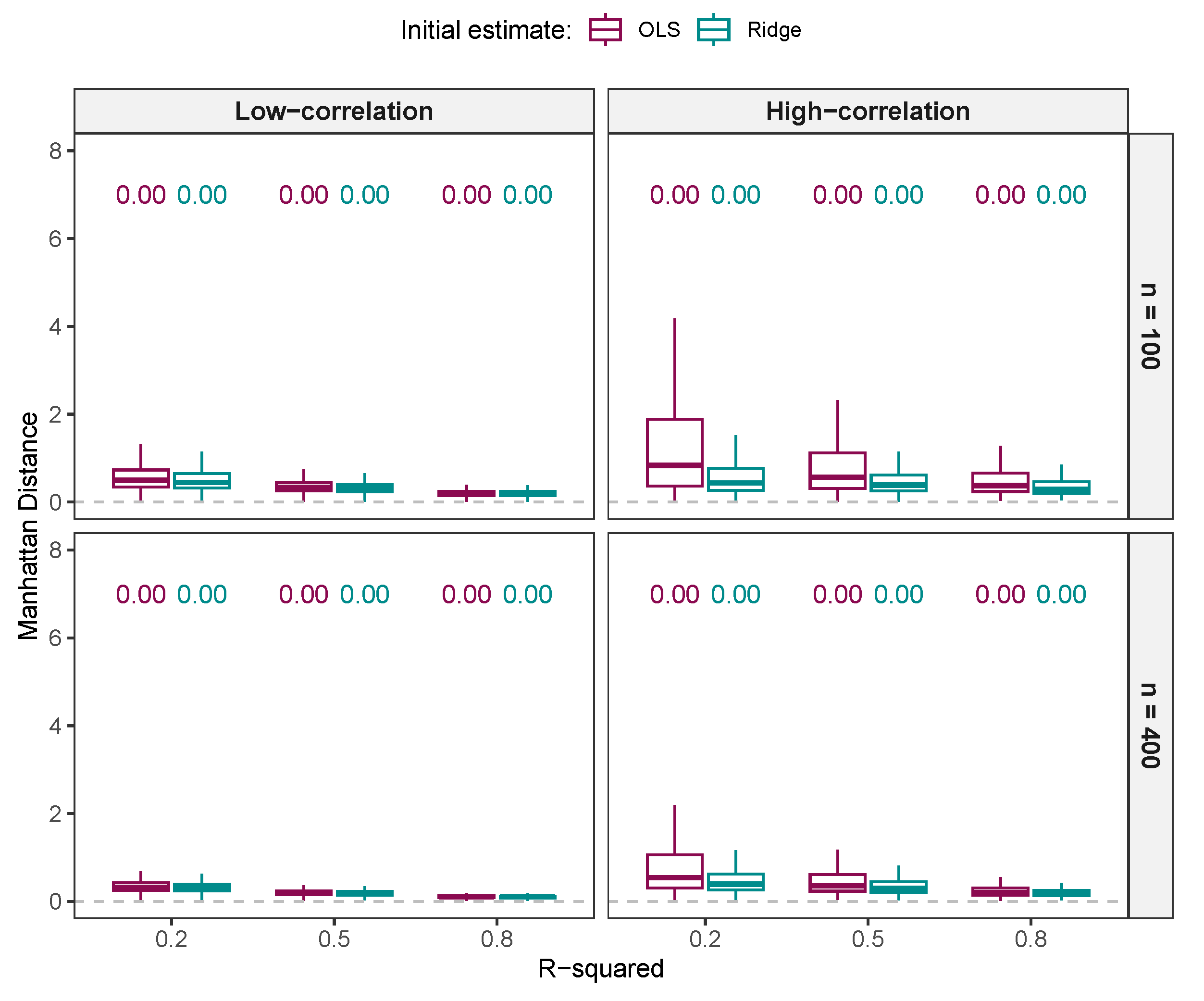
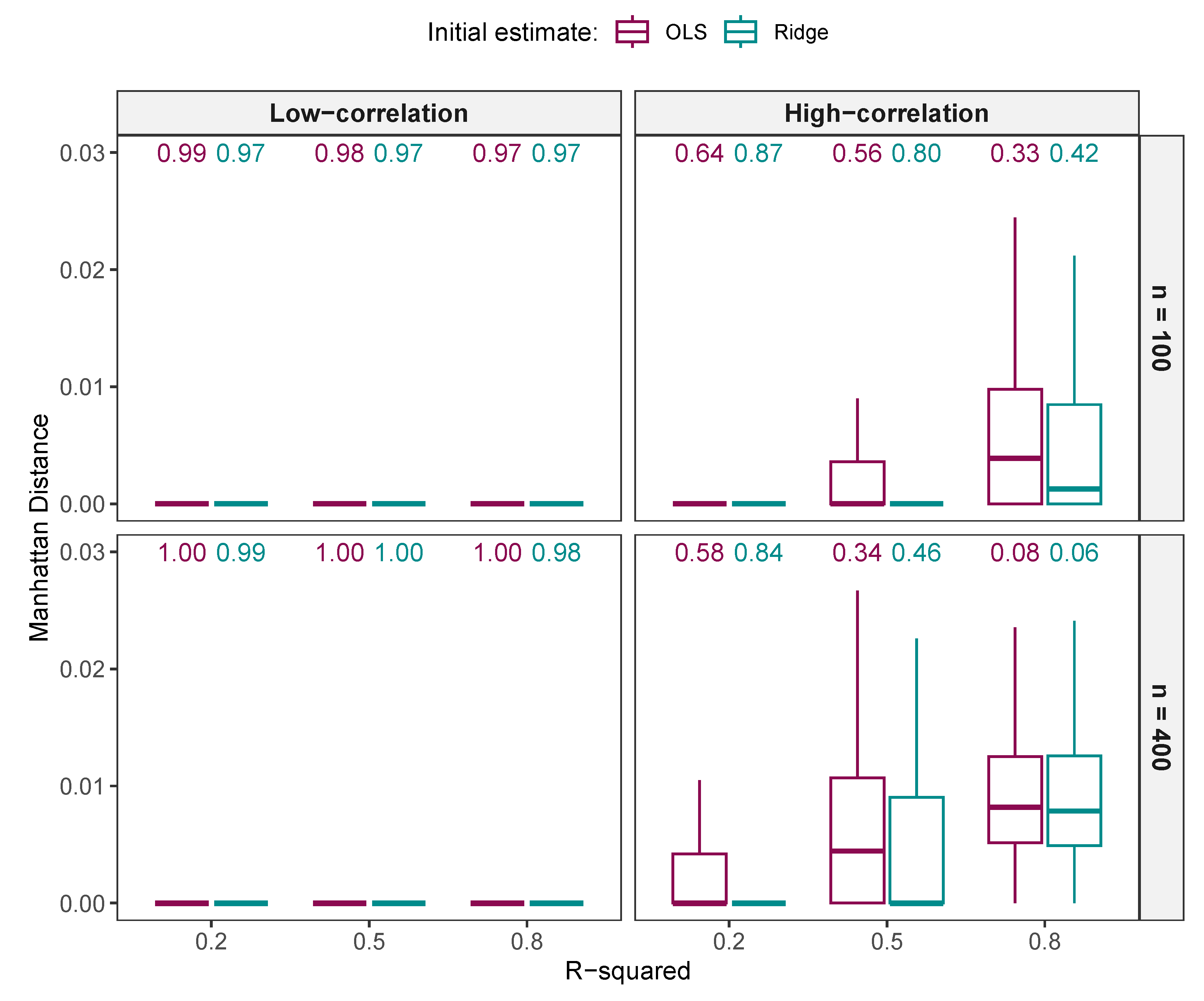
3.1.4. Comparison of Regression Estimates
Comparison of Regression Estimates from NNG and ALASSO ()
Comparison of Regression Estimates from NNG and ALASSO ()
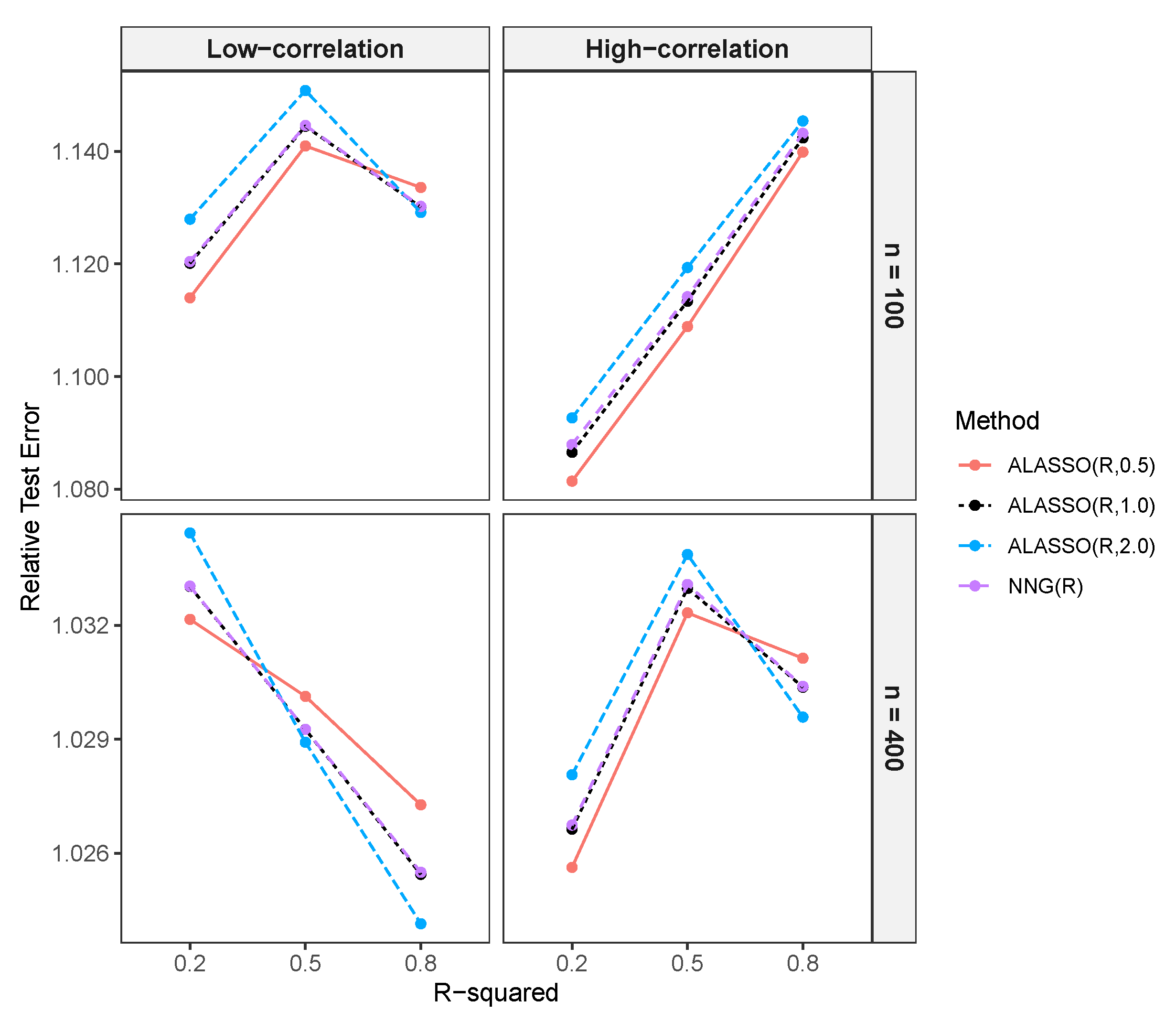
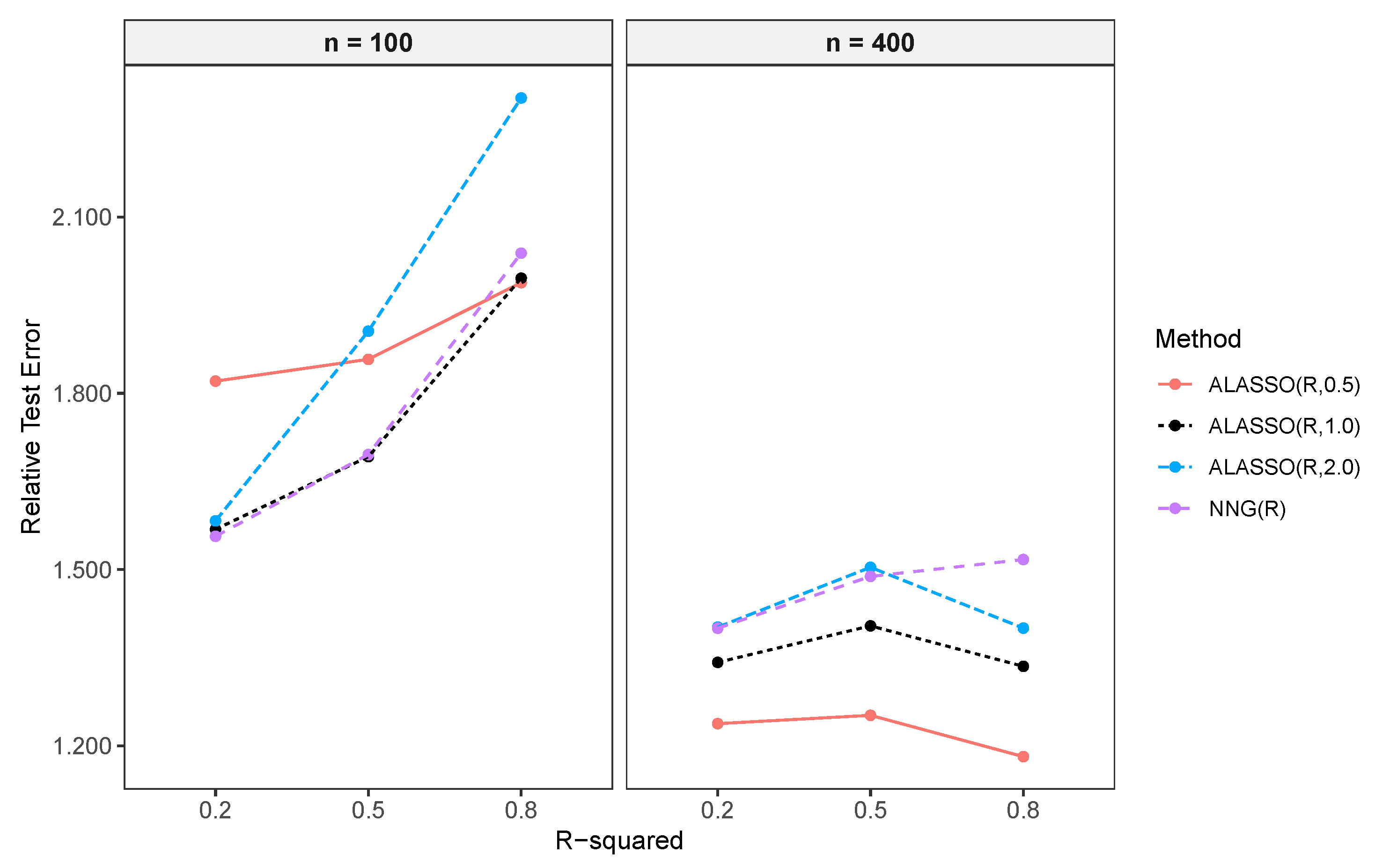
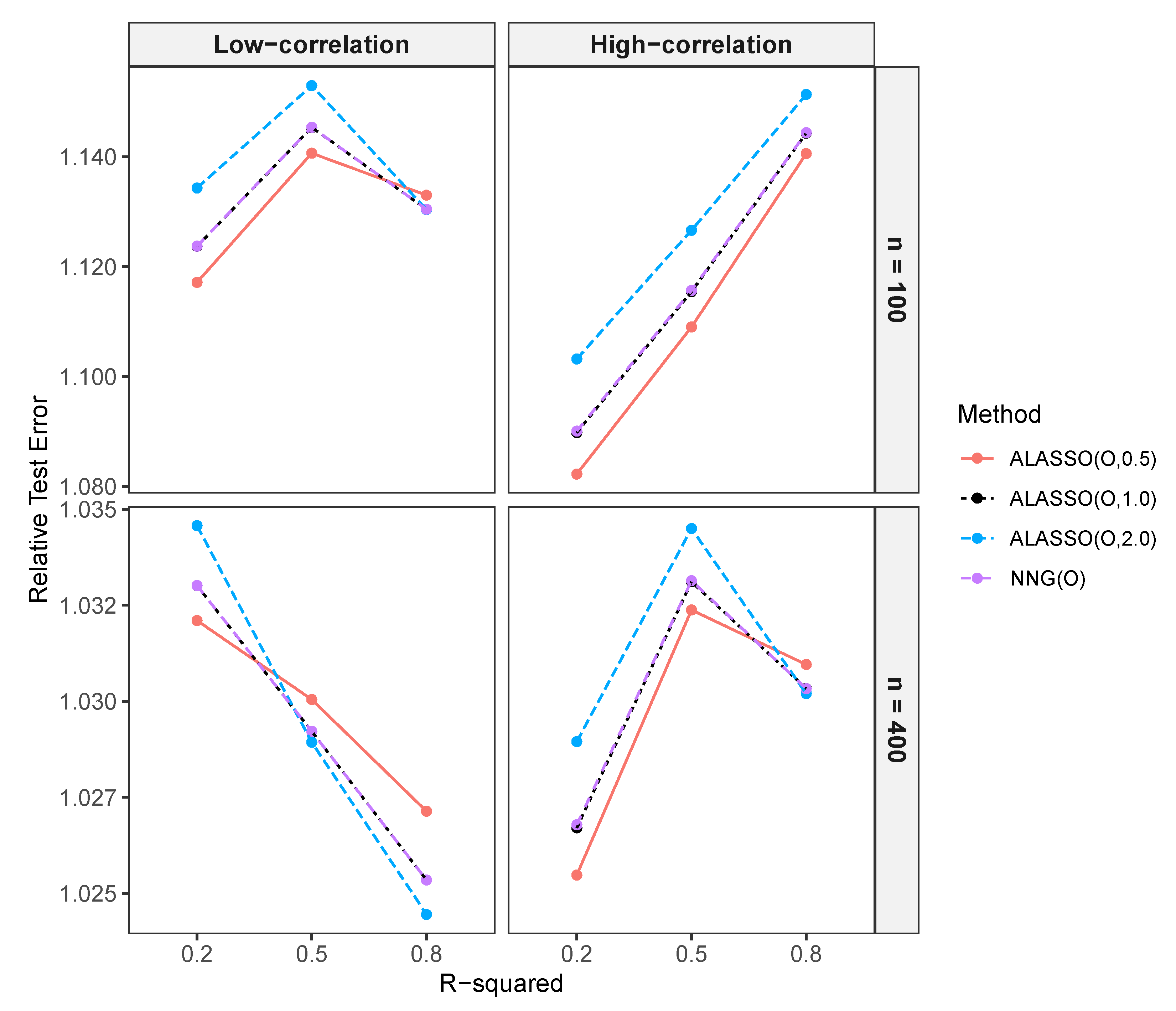
Comparison of the Prediction Performance of NNG and ALASSO ()
3.2. Simulation Results in High-Dimensional Settings
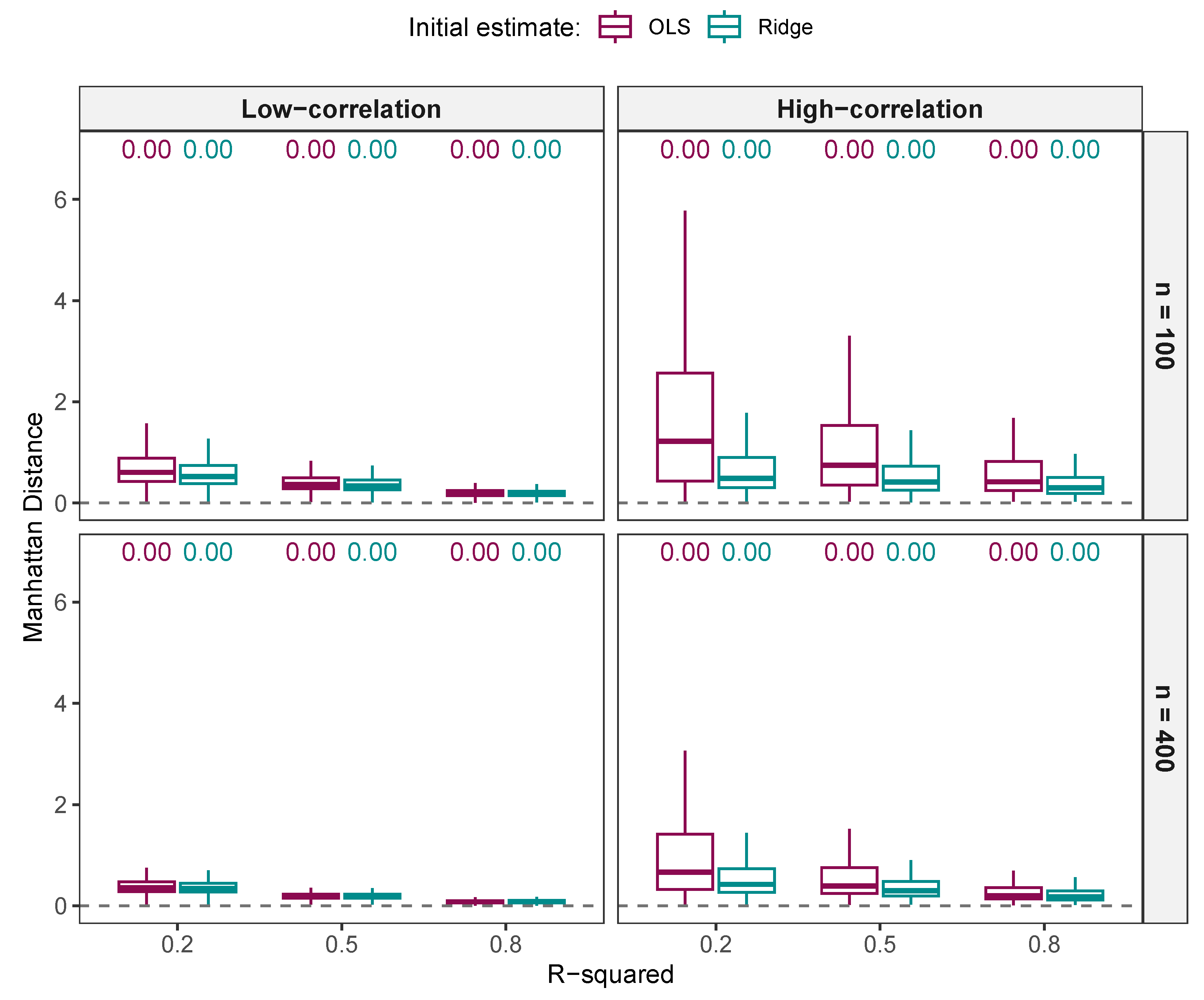
3.2.1. Comparison of Selected Variables and Regression Estimates for NNG and ALASSO () in High-Dimensional Settings
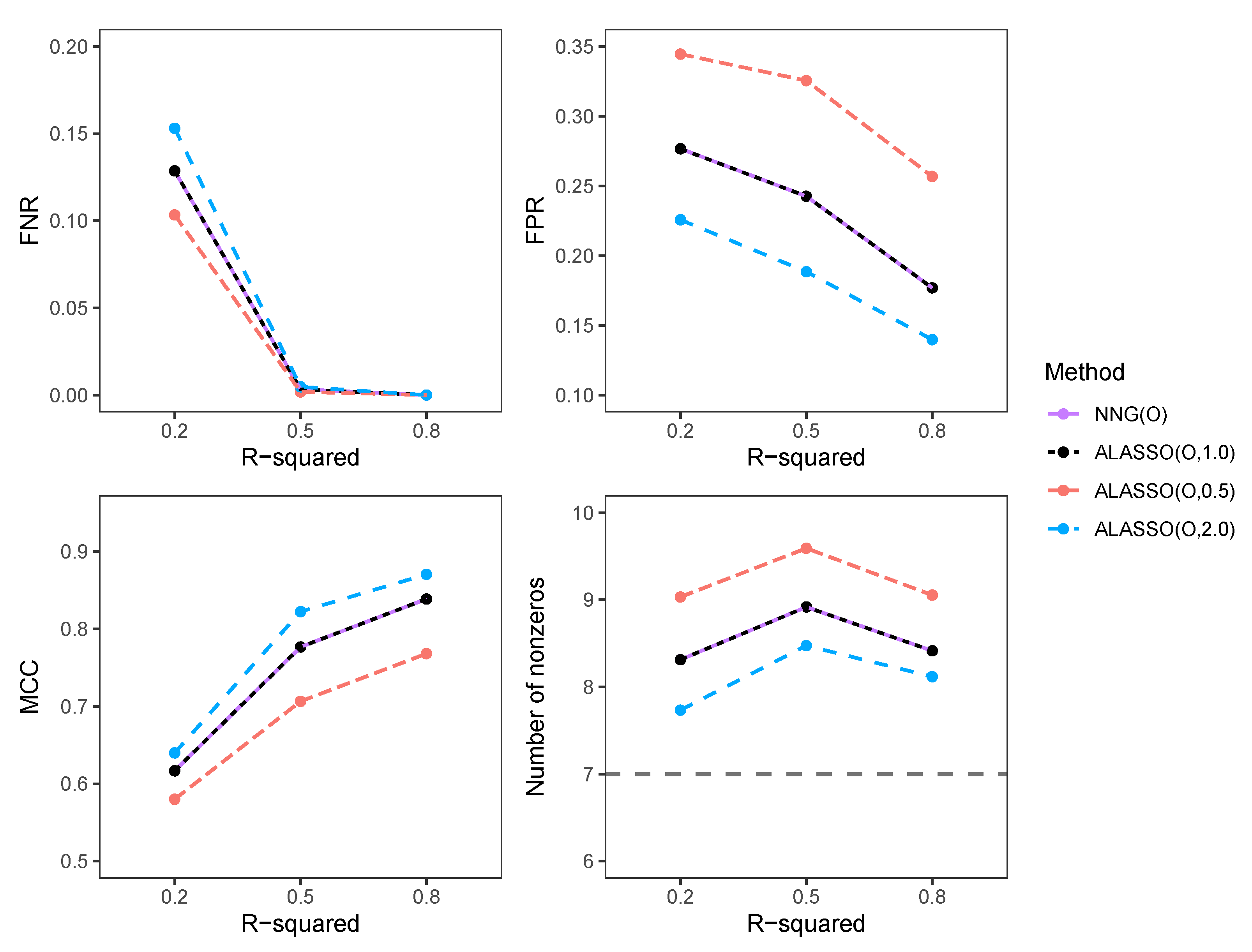
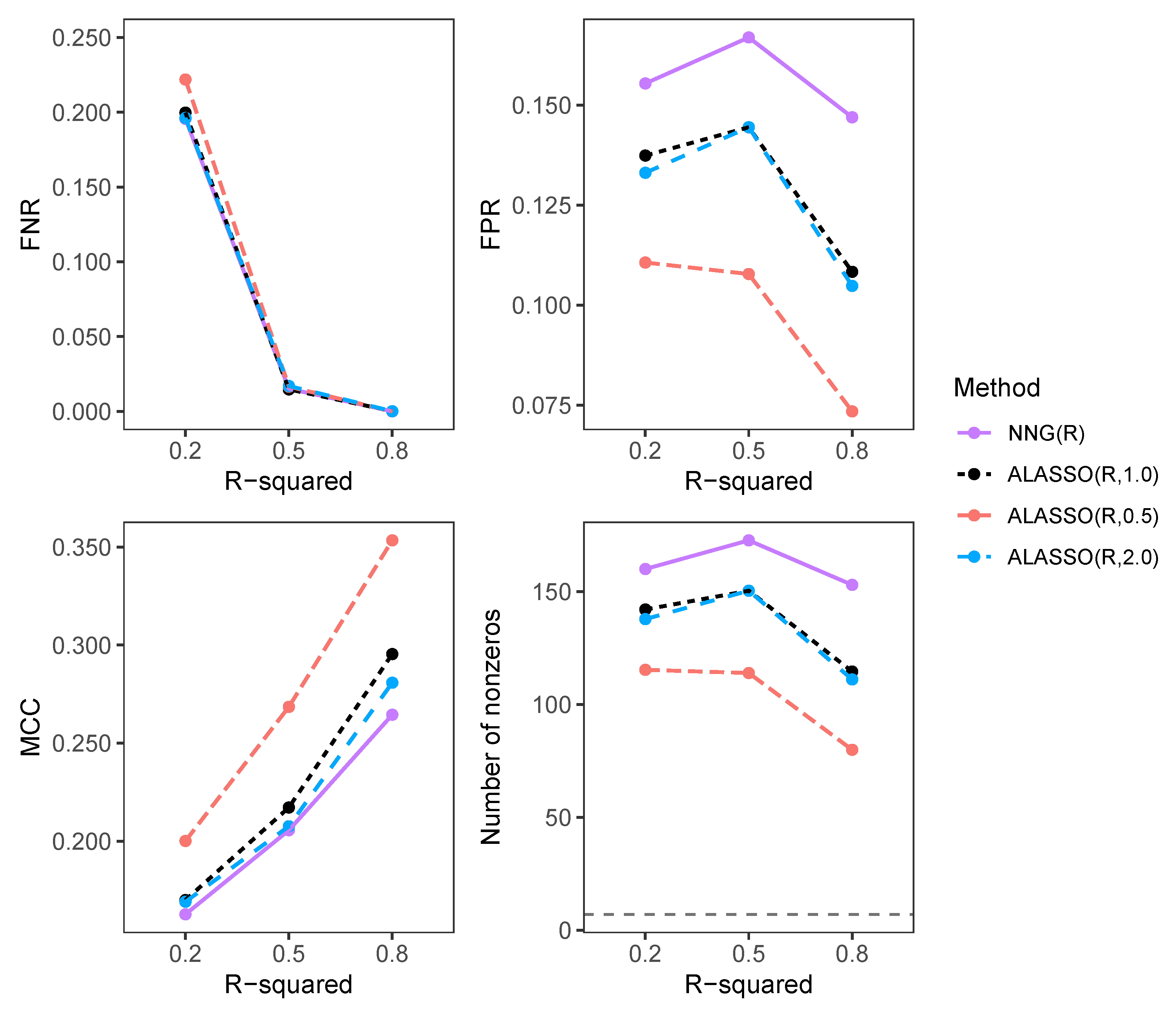
3.2.2. Comparison of FNR, FPR, MCC, and Number of Selected Variables in High-Dimensional Settings
3.2.3. Comparison of Prediction Performance in High-Dimensional Settings
3.3. Real Data Examples
3.3.1. Gene Expression Data
3.3.2. Prostate Cancer Data
4. Discussion
4.1. NNG Versus ALASSO ()
4.2. NNG Versus ALASSO ()
4.3. When to Choose NNG over ALASSO
5. Conclusions
6. Directions for Future Research
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike information criterion |
| ALASSO | Adaptive lasso |
| ALASSO() | Adaptive lasso using initial estimates from a (e.g., OLS or ridge) and . |
| BIC | Bayesian information criterion |
| CV | Cross-validation |
| FNR | False negative rate |
| FPR | False positive rate |
| MCC | Matthews correlation coefficient |
| MCSE | Monte Carlo standard error |
| MD | Manhattan distance |
| ME | Model error |
| MSE | Mean squared error |
| NNG | Non-negative garrote |
| NNG(O) | Non-negative garrote with OLS initial estimates |
| NNG(R) | Non-negative garrote with ridge initial estimates |
| OLS | Ordinary least squares |
| Coefficient of determination | |
| RTE | Relative test error |
| SMC | Simple matching coefficient |
Appendix A. Results
| Variable | NNG | ALASSO (1) | ALASSO (0.5) | ALASSO (2) |
|---|---|---|---|---|
| 0.65 | 0.65 | 0.62 | 0.64 | |
| 0.29 | 0.29 | 0.25 | 0.24 | |
| 0.26 | 0.26 | 0.24 | 0.24 | |
| −0.13 | −0.13 | −0.08 | - | |
| 0.12 | 0.12 | 0.10 | - | |
| −0.09 | −0.09 | - | - | |
| 0.11 | 0.11 | 0.06 | - | |
| - | - | - | - | |
| Adj. | 0.64 | 0.64 | 0.63 | 0.62 |
| 0.0016 | 0.0016 | 0.01121 | 0.0028 |
References
- Heinze, G.; Wallisch, C.; Dunkler, D. Variable selection—a review and recommendations for the practicing statistician. Biom. J. 2018, 60, 431–449. [Google Scholar] [CrossRef]
- Sauerbrei, W.; Perperoglou, A.; Schmid, M.; Abrahamowicz, M.; Becher, H.; Binder, H.; Dunkler, D.; Harrell, F.E.; Royston, P.; Heinze, G. On behalf of TG2 of the STRATOS initiative. State of the art in selection of variables and functional forms in multivariable analysis—Outstanding issues. Diagn. Progn. Res. 2020, 4, 1–8. [Google Scholar] [CrossRef]
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis; Springer: New York, NY, USA, 2015. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; Volume 103. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2, pp. 1–758. [Google Scholar]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Breiman, L. Better subset regression using the nonnegative garrote. Technometrics 1995, 37, 373–384. [Google Scholar] [CrossRef]
- Huang, J.; Ma, S.; Zhang, C.H. Adaptive lasso for sparse high-dimensional regression models. Stat. Sin. 2008, 18, 1603–1618. [Google Scholar]
- Makalic, E.; Schmidt, D.F. Logistic regression with the nonnegative garrote. In AI 2011: Advances in Artificial Intelligence; Walsh, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 82–91. [Google Scholar]
- Antoniadis, A.; Gijbels, I.; Verhasselt, A. Variable selection in additive models using P-splines. Technometrics 2012, 54, 425–438. [Google Scholar] [CrossRef]
- Gregorich, M.; Kammer, M.; Mischak, H.; Heinze, G. Prediction modeling with many correlated and zero-inflated predictors: Assessing the nonnegative garrote approach. Stat. Med. 2025, 44, e70062. [Google Scholar] [CrossRef]
- Meinshausen, N. Relaxed lasso. Comput. Stat. Data Anal. 2007, 52, 374–393. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. On the non-negative garrotte estimator. J. R. Stat. Soc. Ser. B Stat. Methodol. 2007, 69, 143–161. [Google Scholar] [CrossRef]
- Kipruto, E.; Sauerbrei, W. Comparison of variable selection procedures and investigation of the role of shrinkage in linear regression-protocol of a simulation study in low-dimensional data. PLoS ONE 2022, 17, e0271240. [Google Scholar] [CrossRef]
- Kipruto, E.; Sauerbrei, W. Evaluating prediction performance: A simulation study comparing penalized and classical variable selection methods in low-dimensional data. Appl. Sci. 2025, 15, 7443. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso: A retrospective. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Zhao, P.; Yu, B. On model selection consistency of lasso. J. Mach. Learn. Res. 2006, 7, 2541–2563. [Google Scholar]
- Buehlmann, P.; Van De Geer, S. Statistics for High-Dimensional Data: Methods, Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Benner, A.; Zucknick, M.; Hielscher, T.; Ittrich, C.; Mansmann, U. High-dimensional Cox models: The choice of penalty as part of the model building process. Biom. J. 2010, 52, 50–69. [Google Scholar] [CrossRef]
- Bertsimas, D.; King, A.; Mazumder, R. Best subset selection via a modern optimization lens. Ann. Stat. 2016, 44, 813–852. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Tibshirani, R. Best subset, forward stepwise or lasso? Analysis and recommendations based on extensive comparisons. Stat. Sci. 2020, 35, 579–592. [Google Scholar] [CrossRef]
- Su, W.; Bogdan, M.; Candès, E. False discoveries occur early on the lasso path. Ann. Stat. 2017, 45, 2133–2150. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Sauerbrei, W. The use of resampling methods to simplify regression models in medical statistics. J. R. Stat. Soc. Ser. C Appl. Stat. 1999, 48, 313–329. [Google Scholar] [CrossRef]
- Breiman, L. Heuristics of instability and stabilization in model selection. Ann. Statist. 1996, 24, 2350–2383. [Google Scholar] [CrossRef]
- Riley, R.D.; Snell, K.I.E.; Martin, G.P.; Whittle, R.; Archer, L.; Sperrin, M.; Collins, G.S. Penalization and shrinkage methods produced unreliable clinical prediction models especially when sample size was small. J. Clin. Epidemiol. 2021, 132, 88–96. [Google Scholar] [CrossRef]
- Morris, T.P.; White, I.R.; Crowther, M.J. Using simulation studies to evaluate statistical methods: Using simulation studies to evaluate statistical methods. Stat. Med. 2019, 38, 2074–2102. [Google Scholar] [CrossRef]
- Johnson, R.W. Fitting percentage of body fat to simple body measurements. J. Stat. Educ. 1996, 4. [Google Scholar] [CrossRef]
- Steyerberg, E.W. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Sneath, P.H.A.; Sokal, R.R. The Principles and Practice of Numerical Classification; W.H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Chinchor, N. MUC-4 evaluation metrics. In Proceedings of the 4th Conference on Message Understanding (MUC-4 ’92), Morristown, NJ, USA, 16–18 June 1992; Association for Computational Linguistics: Stroudsburg, PA, USA, 1992. [Google Scholar]
- Hand, D.; Christen, P. A note on using the F-measure for evaluating record linkage algorithms. Stat. Comput. 2018, 28, 539–547. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- Hennig, C.; Sauerbrei, W. Exploration of the variability of variable selection based on distances between bootstrap sample results. Adv. Data Anal. Classif. 2019, 13, 933–963. [Google Scholar] [CrossRef]
- Kipruto, E.; Sauerbrei, W. Post-estimation shrinkage in full and selected linear regression models in low-dimensional data revisited. Biom. J. 2024, 66, e202300368. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025; Available online: https://www.R-project.org/ (accessed on 28 June 2025).
- Boulesteix, A.-L.; Guillemot, V.; Sauerbrei, W. Use of pretransformation to cope with extreme values in important candidate features. Biom. J. 2011, 53, 673–688. [Google Scholar] [CrossRef]
- Stamey, T.A.; Kabalin, J.N.; McNeal, J.E.; Johnstone, I.M.; Freiha, F.; Redwine, E.A.; Yang, N. Prostate specific antigen in the diagnosis and treatment of adenocarcinoma of the prostate. II. Radical prostatectomy treated patients. J. Urol. 1989, 141, 1076–1083. [Google Scholar] [CrossRef]
- Ioannidis, J.P.A.; Greenland, S.; Hlatky, M.A.; Khoury, M.J.; Macleod, M.R.; Moher, D.; Schulz, K.F.; Tibshirani, R. Increasing value and reducing waste in research design, conduct, and analysis. Lancet 2014, 383, 166–175. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Yuan, M. Nonnegative garrote component selection in functional ANOVA models. In Proceedings of the Artificial Intelligence and Statistics Conference, San Juan, Puerto Rico, 21–24 March 2007; pp. 660–666. [Google Scholar]
- Jhong, J.H.; Bak, K.Y.; Shin, J.K.; Koo, J.Y. Additive regression splines with total variation and non-negative garrote penalties. Commun. Stat. Theory Methods 2021, 51, 7713–7736. [Google Scholar] [CrossRef]
- Gijbels, I.; Verhasselt, A.; Vrinssen, I. Variable selection using P-splines. Wiley Interdiscip. Rev. Comput. Stat. 2015, 7, 1–20. [Google Scholar] [CrossRef]
| Component | Description |
|---|---|
| Aims and objectives | Aim: To investigate and compare the performance of NNG and ALASSO in multivariable linear regression with respect to variable selection and prediction accuracy. |
Objectives:
| |
| Data-generating mechanism (Section 2.2) |
|
| Target of analysis |
|
| Methods (Section 2.4) |
|
| Performance measures (Section 2.3) |
|
| ALASSO: 0 | ALASSO:1 | |
|---|---|---|
| NNG: 0 | a = 1 | b = 1 |
| NNG: 1 | c = 1 | d = 2 |
| ALASSO () | ALASSO () | ALASSO () | NNG | |
|---|---|---|---|---|
| 0.01 | 10.00 | 100.00 | 10,000.00 | 100.00 |
| 0.05 | 4.47 | 20.00 | 400.00 | 20.00 |
| 1.5 | 0.82 | 0.67 | 0.44 | 0.67 |
| 4 | 0.50 | 0.25 | 0.06 | 0.25 |
| Variable | NNG | ALASSO (0.5) | ALASSO (1) | ALASSO (2) | ALASSO (10) | |
|---|---|---|---|---|---|---|
| 0.06 | – | – | – | – | – | |
| 0.12 | – | – | – | – | – | |
| 0.20 | – | – | – | – | – | |
| 0.30 | – | 0.13 | – | – | – | |
| 0.41 | 0.16 | 0.25 | 0.16 | – | – | |
| 0.91 | 0.79 | 0.80 | 0.79 | 0.78 | 0.64 | |
| 1.20 | 1.12 | 1.11 | 1.12 | 1.14 | 1.19 | |
| 1.52 | 1.45 | 1.43 | 1.45 | 1.47 | 1.51 | |
| 2.01 | 1.96 | 1.94 | 1.96 | 1.98 | 2.00 | |
| 4.01 | 3.98 | 3.96 | 3.98 | 4.01 | 4.01 |
| (1) (Original) | (2) with Reversed | (3) (All Reversed) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | NNG | ALASSO | NNG | ALASSO | NNG | ALASSO | |||
| 1.51 | 1.51 | 1.51 | −1.51 | – | 1.51 | −1.51 | – | 1.51 | |
| 0.02 | – | – | 0.02 | 0.26 | – | −0.02 | – | – | |
| 1.03 | 1.02 | 1.02 | 1.03 | 1.08 | 1.02 | −1.03 | – | 1.02 | |
| −0.01 | – | – | −0.01 | – | – | 0.01 | 0.37 | – | |
| 1.00 | 0.99 | 0.99 | 1.00 | 0.97 | 0.99 | −1.00 | – | 0.99 | |
| 0.02 | – | – | 0.02 | – | – | −0.02 | – | – | |
| 0.51 | 0.50 | 0.50 | 0.51 | 0.52 | 0.50 | −0.51 | – | 0.50 | |
| −0.05 | – | – | −0.05 | – | – | 0.05 | 0.21 | – | |
| 0.55 | 0.53 | 0.53 | 0.55 | 0.53 | 0.53 | −0.55 | – | 0.53 | |
| 0.00 | – | – | 0.00 | – | – | −0.00 | – | – | |
| 0.39 | 0.39 | 0.39 | 0.39 | 0.41 | 0.39 | −0.39 | – | 0.39 | |
| 0.04 | – | – | 0.04 | – | – | −0.04 | – | – | |
| −0.47 | −0.45 | −0.45 | −0.47 | −0.45 | −0.45 | 0.47 | – | −0.45 | |
| −0.04 | – | – | −0.04 | – | – | 0.04 | – | – | |
| 0.04 | – | – | 0.04 | – | – | −0.04 | – | – | |
| NNG | ALASSO () | ALASSO () | ALASSO () | |||
|---|---|---|---|---|---|---|
| Not Selected | Selected | Not Selected | Selected | Not Selected | Selected | |
| Not Selected | 22,072 | 70 | 22,142 | 0 | 22,134 | 8 |
| Selected | 10 | 131 | 0 | 141 | 29 | 112 |
| MD | 24.17 | 0.85 | 11.39 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kipruto, E.; Sauerbrei, W. Unraveling Similarities and Differences Between Non-Negative Garrote and Adaptive Lasso: A Simulation Study in Low- and High-Dimensional Data. Stats 2025, 8, 70. https://doi.org/10.3390/stats8030070
Kipruto E, Sauerbrei W. Unraveling Similarities and Differences Between Non-Negative Garrote and Adaptive Lasso: A Simulation Study in Low- and High-Dimensional Data. Stats. 2025; 8(3):70. https://doi.org/10.3390/stats8030070
Chicago/Turabian StyleKipruto, Edwin, and Willi Sauerbrei. 2025. "Unraveling Similarities and Differences Between Non-Negative Garrote and Adaptive Lasso: A Simulation Study in Low- and High-Dimensional Data" Stats 8, no. 3: 70. https://doi.org/10.3390/stats8030070
APA StyleKipruto, E., & Sauerbrei, W. (2025). Unraveling Similarities and Differences Between Non-Negative Garrote and Adaptive Lasso: A Simulation Study in Low- and High-Dimensional Data. Stats, 8(3), 70. https://doi.org/10.3390/stats8030070






