Archimedean Copulas: A Useful Approach in Biomedical Data—A Review with an Application in Pediatrics
Abstract
1. Introduction
2. Copula
- We consider , the unit segment, and ; then, we define the copula functions below.
- From the definition, it follows that for any copula partial derivatives and exist for almost all u, . Let and exist and be continuous on ; then, copula density is designed as
- From the definition, if and , where u and v have uniform distributions on I, then any copula is a valid bivariate distribution function. Hence, the joint probability density function of X and Y can be represented aswhere and are marginal densities of X and Y.
- The more relevant property is that every joint distribution function is a copula, as demonstrated by Sklar’s theorem below [15].
- The importance of this theorem is that every valid bivariate (or multivariate) distribution can be represented as a copula of its marginals, thus separating the marginal from the dependence modeling. Consequently, in order to define a model for a bivariate distribution with given marginals, we only need to find the proper copula which, according to Sklar’s theorem, exist and is often unique. In practical terms, they allow to model the joint behavior of variables by separately specifying their marginal distributions and their dependence structure by the Copula function (this is not trivial, as we will see later). Given the previous theorem and the observation that X and Y are independent if and only if for all x,y, we can derive the following:
2.1. Archimedean Copula
- If fulfils these conditions, it is called an Archimedean copula and the function is its additive generator. Hereafter, we state two theorems regarding the main algebraic properties of Archimedean copula.
- 1.
- C is symmetric; i.e., for all u,v ;
- 2.
- C is associative, i.e., for all u,v,w ;
- 3.
- If is any constant, then is also a generator of C.
- A useful condition to assess if an arbitrary copula is an Archimedean copula is the following:
- Finally, given that the second derivative exists, we define the density of an Archimedean copula through its generator and its derivatives as
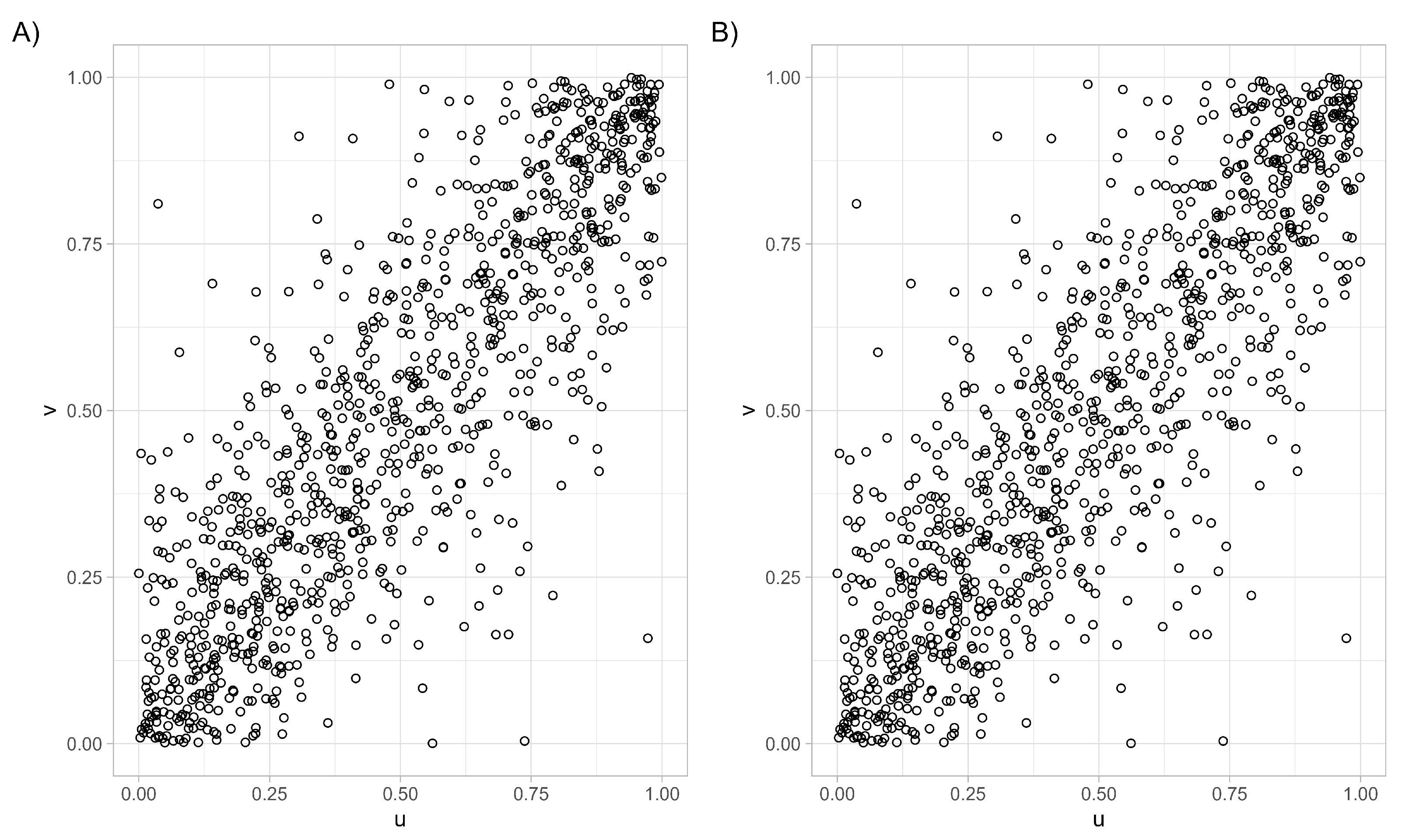
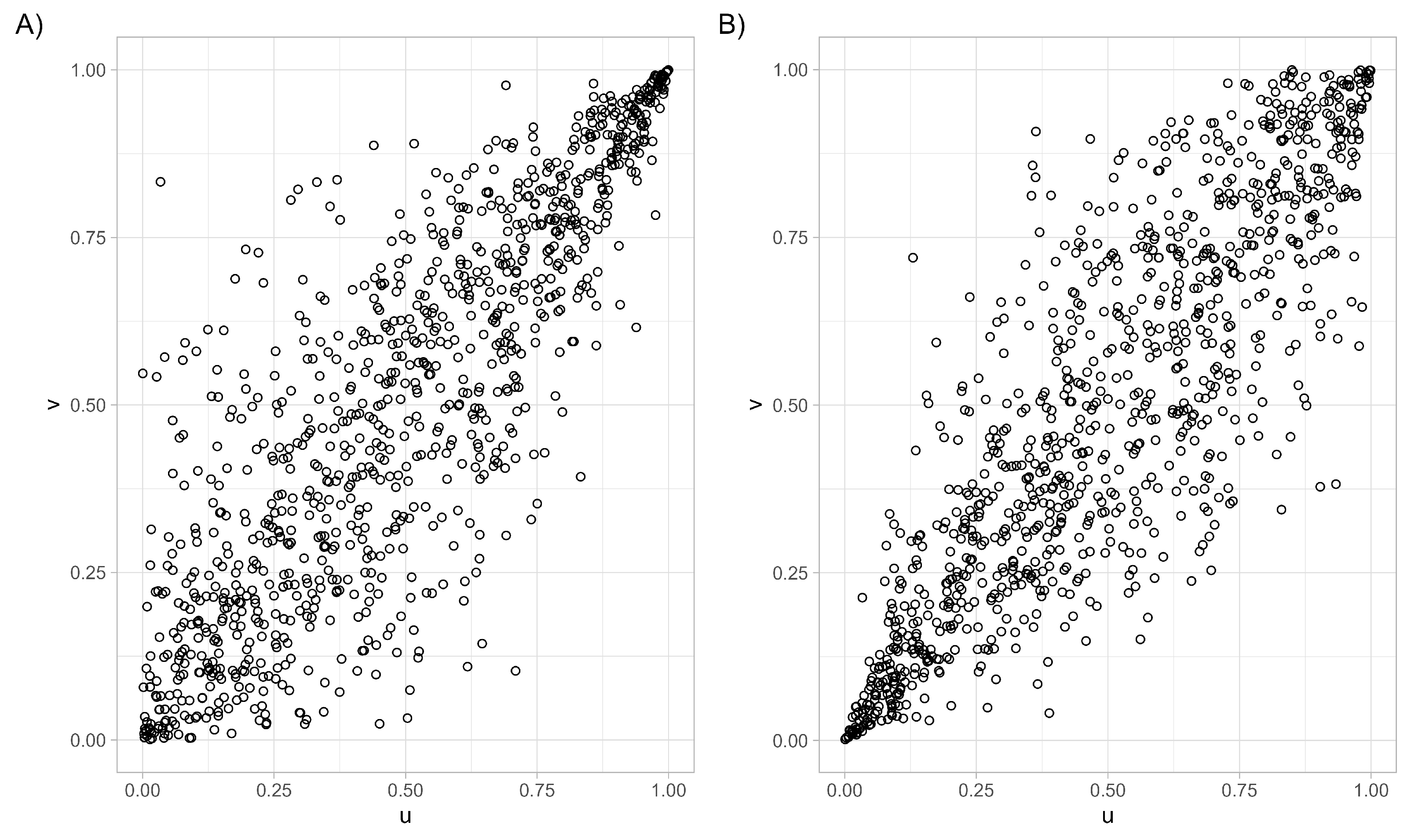
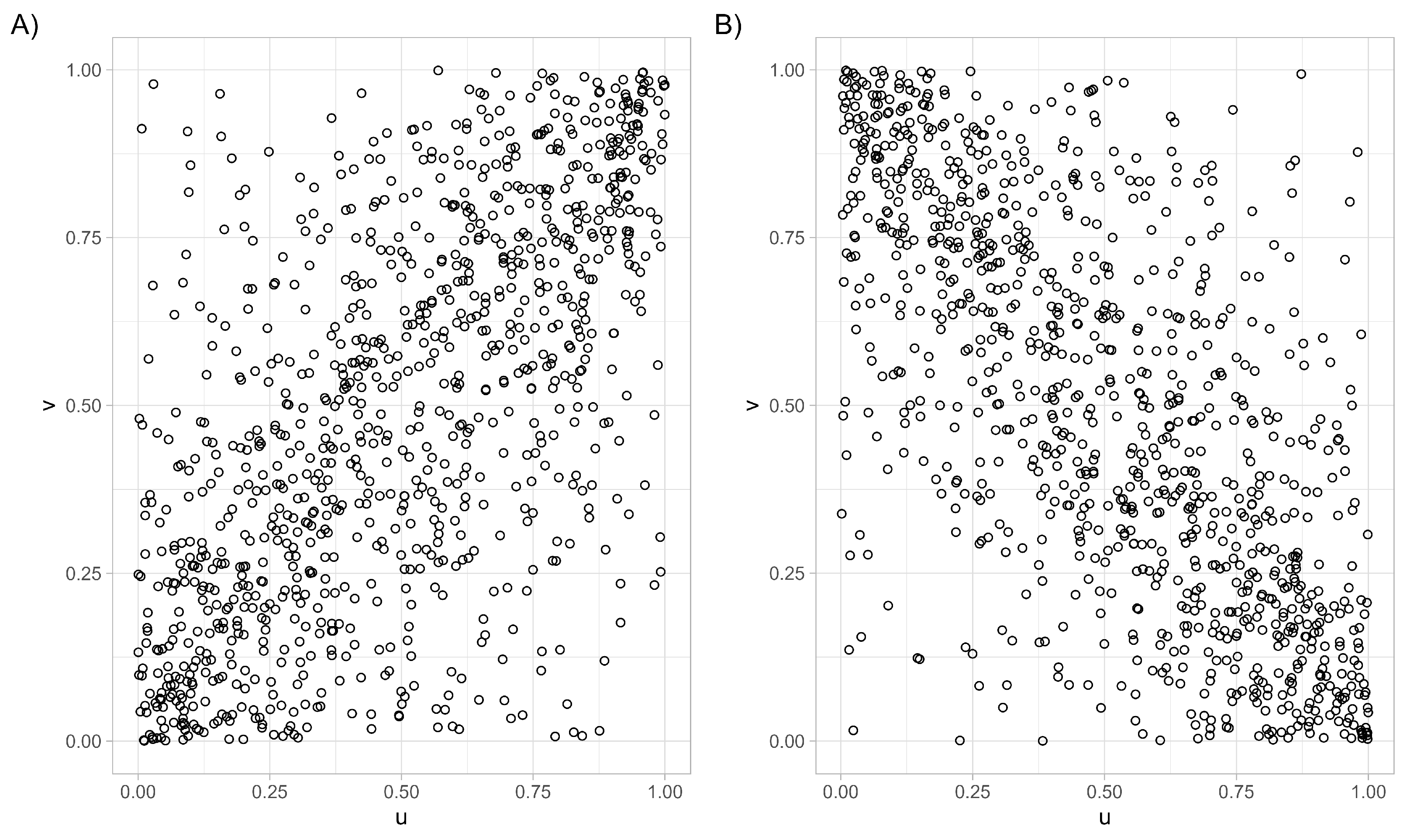
- At the moment, we are interested in three one-parameter families from the Archimedean class, namely the Clayton copula, the Gumbel–Hougaard copula, and the Frank copula.
2.2. Measures of Concordance
2.3. Rotated Copulas
- rotated (reflected) copula: , whereis the density of the copula.
- rotated copula: ,where is the density of the copula.This particular rotation defines the survival copula that we will discuss in Section 2.3.1.
- rotated (reflected) copula: , where is the density of the copula.
2.3.1. Survival Copula
- From the definition, we note thatand equivalently with respect to v.
2.3.2. Examples on Rotated Archimedean Copulas: Clayton and Hougaard
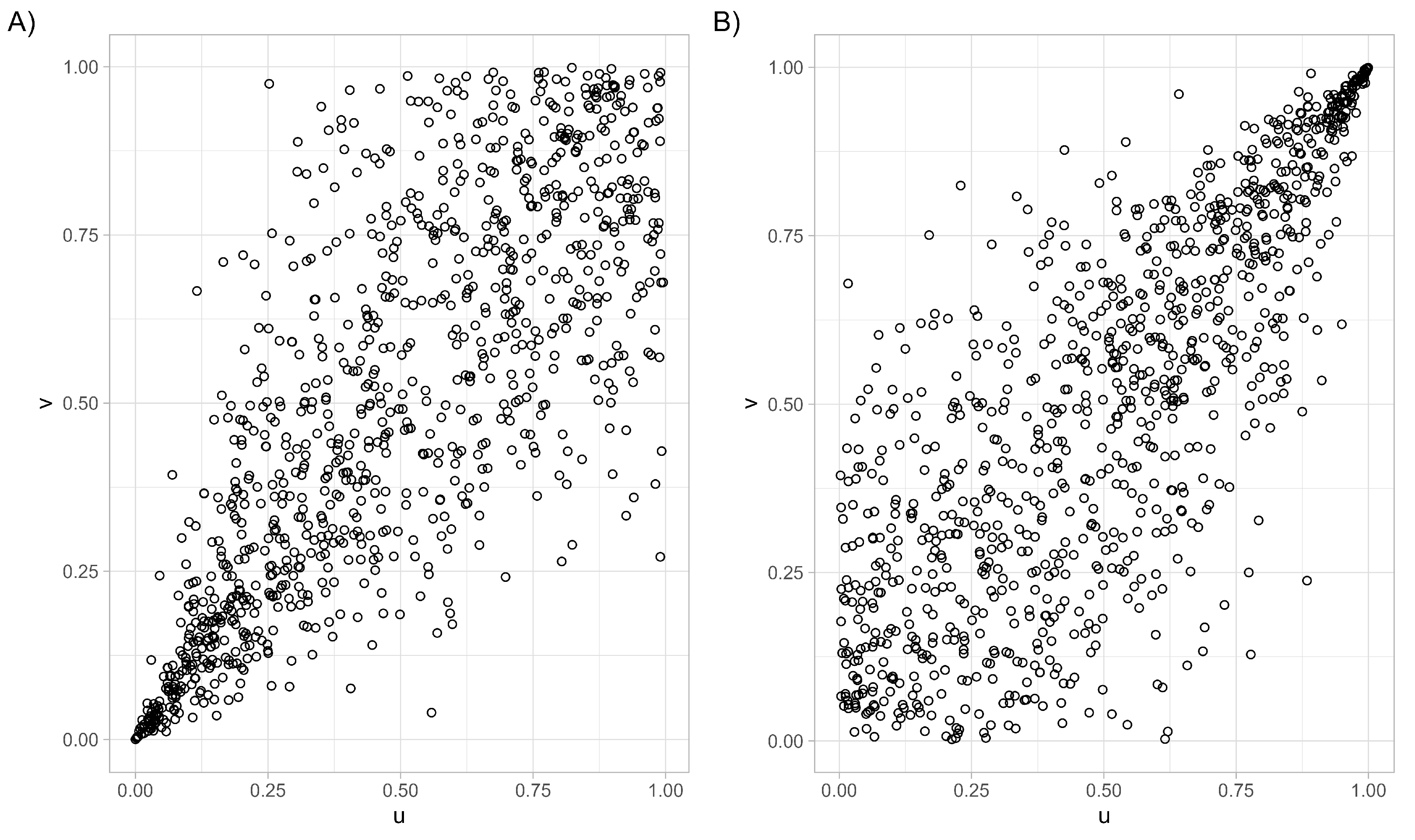
- The Clayton survival copula has the following form for :Figure 2 illustrates how the survival Clayton copula emphasizes strong upper-tail dependence, in contrast to the lower-tail dependence captured by the standard Clayton copula. In the latter, a strong association is expected near the point (0, 0), whereas in the survival copula, strong dependence is expected as approaches (1, 1).
2.4. Plackett Copula
3. Estimation Methods
4. How to Select the Bivariate Copula Functions
5. The Goodness of Fit
- Kolmogorov–Smirnov distance:
- Cramer–von Mises distance:
- Anderson and Darling distance:
- Average of Anderson and Darling distance:
6. Significant Applications of Copulas
6.1. Nonnormality and Nonlinear Dependence Assumption
6.2. Survival Data and Validation of Surrogate Endpoints
6.3. Competing Risks
6.4. Omics Data
6.5. Toxicity
6.6. Rare Diseases
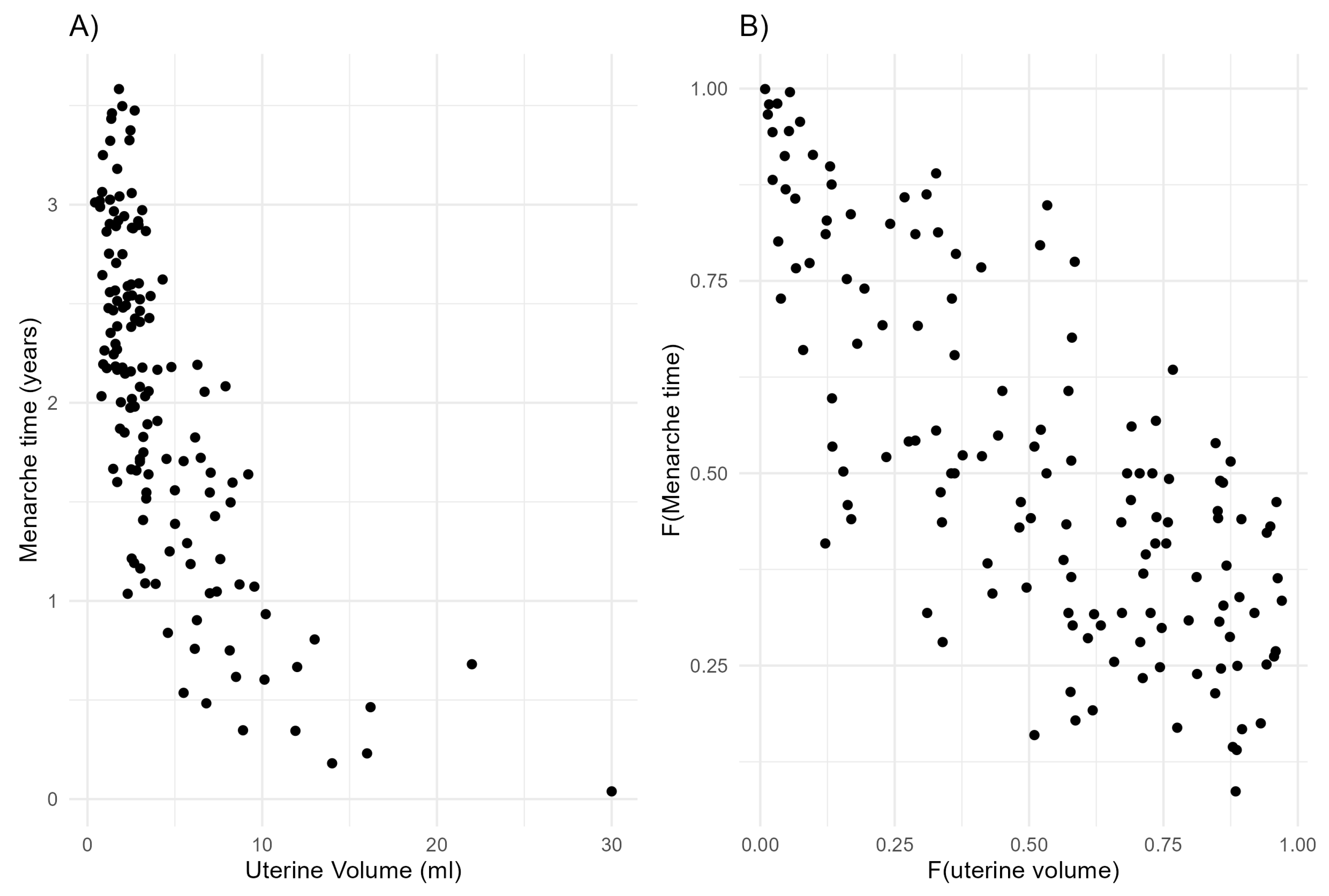
7. Application in a Pediatric Study
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IFM | Inference Function for Margins |
| MLE | Maximum Likelihood Estimation |
| MPLE | Maximum Pseudo-Likelihood method |
| CML | Canonical Maximum Likelihood |
| MD | Minimum Distance |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| CDF | Cumulative Distribution Function |
References
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Hougaard, P. Modelling Multivariate Survival. Scand. J. Stat. 1987, 14, 291–304. [Google Scholar]
- Shih, J.H.; Louis, T.A. Inferences on the Association Parameter in Copula Models for Bivariate Survival Data. Int. Biom. Soc. 1995, 51, 1384–1399. [Google Scholar] [CrossRef]
- Clementi, F.; Gianmoena, L. Chapter 9—Odeling the Joint Distribution of Income and Consumption in Italy: A Copula-Based Approach With k-Generalized Margins. In Introduction to Agent-Based Economics; Gallegati, M., Palestrini, A., Russo, A., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 191–228. [Google Scholar] [CrossRef]
- Fan, Y.; Patton, A.J. Copulas in Econometrics. Annu. Rev. Econ. 2014, 6, 179–200. [Google Scholar] [CrossRef]
- Patton, A.J. A review of copula models for economic time series. J. Multivar. Anal. 2012, 110, 4–18. [Google Scholar] [CrossRef]
- Kolev, N.; Anjos, U.D.; Mendes, B.V.D.M. Copulas: A review and recent developments. Stoch. Model. 2006, 22, 617–660. [Google Scholar] [CrossRef]
- Burzykowski, T.; Molenberghs, G.; Buyse, M.; Geys, H.; Renard, D. Validation of Surrogate End Points in Multiple Randomized Clinical Trials with Failure Time End Points. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2001, 50, 405–422. [Google Scholar] [CrossRef]
- Crommen, G.; Deresa, N.W.; D’Haen, M.; Ding, J.; Willems, I.; Keilegom, I.V. Recent advances in copula-based methods for dependent censoring. SORT 2025, 49, 3–42. [Google Scholar] [CrossRef]
- Nadarajah, S.; Afuecheta, E.; Chan, S. A compendium of Copulas. Statistica 2017, 4, 279–328. [Google Scholar] [CrossRef]
- Genest, C.; Nešlehová, J.; Ziegel, J. Inference in multivariate Archimedean copula models. Test 2011, 20, 223–256. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Wolfowitz, J. The Minimum Distance Method. Ann. Math. Stat. 1957, 28, 75–88. [Google Scholar] [CrossRef]
- Cattoni, A.; Russo, G.; Capitoli, G.; Rodari, G.; Nicolosi, M.L.; Molinari, S.; Tondelli, D.; Pelliccia, C.; Radaelli, S.; Arosio, A.M.L.; et al. Pelvic ultrasound and pubertal attainment in girls with sexual precocity: The pivotal role of uterine volume in predicting the timing of menarche. Front. Endocrinol. 2024, 15, 1417281. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Genest, C.; Mackay, J. The Joy of Copulas: Bivariate Distributions with Uniform Marginals. Am. Stat. 1986, 40, 280–283. [Google Scholar] [CrossRef]
- Clayton, D.G. A Model for Association in Bivariate Life Tables and Its Application in Epidemiological Studies of Familial Tendency in Chronic Disease Incidence. Oxf. J. 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Hougaard, P. A Class of Multivariate Failure Time Distributions. Oxf. J. 1986, 73, 671–678. [Google Scholar] [CrossRef]
- Yan, J. Enjoy the Joy of Copulas: With a Package Copula; Technical Report; University of Connecticut: Storrs, CT, USA, 2007. [Google Scholar]
- Cech, C. Copula-Based Top-Down Approaches in Financial Risk Aggregation; Working Paper Series; University of Applied Sciences of BFI Vienna: Wien, Austria, 2006; Volume 32. [Google Scholar]
- Georges, P.; Lamy, A.G.; Nicolas, E.; Quibel, G.; Roncalli, T. Multivariate survival modelling: A unified approach with copulas. SSRN Electron. J. 2001. [Google Scholar] [CrossRef]
- Renfro, L.A.; Shang, H.; Sargent, D.J. Impact of copula directional specification on multi-trial evaluation of surrogate end points. J. Biopharm. Stat. 2015, 25, 857–877. [Google Scholar] [CrossRef][Green Version]
- Plackett, R.L.; Placmett, R.L. A Class of Bivariate Distributions. J. Am. Stat. Assoc. 1965, 60, 516–522. [Google Scholar] [CrossRef]
- Tibaldi, F.; Molenberghs, G.; Burzykowski, T.; Geys, H. Pseudo-likelihood estimation for a marginal multivariate survival model. Stat. Med. 2004, 23, 947–963. [Google Scholar] [CrossRef]
- Joe, H. Asymptotic efficiency of the two-stage estimation method for copula-based models. J. Multivar. Anal. 2005, 94, 401–419. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Shemyakin, A.; Kniazev, A. Introduction to Bayesian Estimation and Copula Models of Dependence, 1st ed.; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2017; pp. 195–232. [Google Scholar]
- Genest, C.; Rivest, L.P. Statistical Inference Procedures for Bivariate Archimedean Copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Cuevas, J.R.T.; Yela, J.P.; Achcar, J.A. A method to select bivariate copula functions. Rev. Colomb. Estad. 2019, 42, 61–80. [Google Scholar]
- Pearson, K. Method of Moments and Method of Maximum Likelihood. Biometrika 1936, 28, 34–59. [Google Scholar] [CrossRef]
- Akaike, H. Likelihood of a model and information criteria. J. Econom. 1981, 16, 3–14. [Google Scholar] [CrossRef]
- Gülöksüz, C.T. Comparison of Some Selection Criteria for Selecting Bivariate Archimedean Copulas. Afyon Kocatepe Univ. J. Sci. Eng. 2016, 16, 250–255. [Google Scholar] [CrossRef]
- Frees, E.W.; Valdez, E.A. Understanding Relationships Using Copulas. N. Am. Actuar. J. 1998, 2, 1–25. [Google Scholar] [CrossRef]
- Fernandez, V. Copula-based measures of dependence structure in assets returns. Phys. Stat. Mech. Its Appl. 2008, 387, 3615–3628. [Google Scholar] [CrossRef]
- Genest, C.; Remillard, B. Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models. Ann. L’Institut Henri Poincare (B) Probab. Stat. 2008, 44, 1096–1127. [Google Scholar] [CrossRef]
- Genest, C.; Quessy, J.F.; Rémillard, B. Goodness-of-Fit Procedures for Copula Models Based on the Probability Integral Transformation. Scand. J. Stat. 2006, 33, 337–366. [Google Scholar] [CrossRef]
- Wang, W.; Wells, M.T. Model Selection and Semiparametric Inference for Bivariate Failure-Time Data. J. Am. Stat. Assoc. 2000, 95, 19. [Google Scholar] [PubMed]
- Rosenblatt, M. Remarks on a Multivariate Transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Größer, J.; Okhrin, O. Copulae: An overview and recent developments. Wiley Interdiscip. Rev. Comput. Stat. 2022, 14, e1557. [Google Scholar] [CrossRef]
- Qura, M.E.; Fayomi, A.; Kilai, M.; Almetwally, E.M. Bivariate power Lomax distribution with medical applications. PLoS ONE 2023, 18, 0282581. [Google Scholar] [CrossRef]
- Ahmad, H.H.; Ramadan, D.A. Copula-Based Bivariate Modified Fréchet–Exponential Distributions: Construction, Properties, and Applications. Axioms 2025, 14, 431. [Google Scholar] [CrossRef]
- Winkelmann, R. Copula bivariate probit models: With an application to medical expenditures. Health Econ. 2012, 21, 1444–1455. [Google Scholar] [CrossRef]
- McGovern, M.E.; Bärnighausen, T.; Marra, G.; Radice, R. On the assumption of bivariate normality in selection models. Epidemiology 2015, 26, 229–237. [Google Scholar] [CrossRef]
- Kumar, P.; Shoukri, M.M. Copula based prediction models: An application to an aortic regurgitation study. BMC Med. Res. Methodol. 2007, 7, 21. [Google Scholar] [CrossRef]
- Weber, E.M. Statistical Models to Capture the Association Between Progression-free and Overall Survival in Oncology Trials. Ph.D. Thesis, Lancaster University, Lancaster, UK, 2020. [Google Scholar]
- Burzykowski, T.; Molenberghs, G.; Buyse, M. The Evaluation of Surrogate Endpoints; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Galimberti, S.; Devidas, M.; Lucenti, A.; Cazzaniga, G.; Möricke, A.; Bartram, C.R.; Mann, G.; Carroll, W.; Winick, N.; Borowitz, M.; et al. Validation of Minimal Residual Disease as Surrogate Endpoint for Event-Free Survival in Childhood Acute Lymphoblastic Leukemia. JNCI Cancer Spectr. 2018, 2, pky069. [Google Scholar] [CrossRef]
- Petti, D.; Eletti, A.; Marra, G.; Radice, R. Copula link-based additive models for bivariate time-to-event outcomes with general censoring scheme. Comput. Stat. Data Anal. 2022, 175, 107550. [Google Scholar] [CrossRef]
- Dimier, N.; Todd, S. An investigation into the two-stage meta-analytic copula modelling approach for evaluating time-to-event surrogate endpoints which comprise of one or more events of interest. Pharm. Stat. 2017, 16, 322–333. [Google Scholar] [CrossRef] [PubMed]
- Escarela, G.; Carrière, J.F. Fitting competing risks with an assumed copula. Stat. Methods Med. Res. 2003, 12, 333–349. [Google Scholar] [CrossRef] [PubMed]
- Adatorwovor, R.; Latouche, A.; Fine, J.P. A parametric approach to relaxing the independence assumption in relative survival analysis. Int. J. Biostat. 2022, 18, 577–592. [Google Scholar] [CrossRef] [PubMed]
- Michimae, H.; Emura, T.; Miyamoto, A.; Kishi, K. Bayesian parametric estimation based on left-truncated competing risks data under bivariate Clayton copula models. J. Appl. Stat. 2024, 51, 2690–2708. [Google Scholar] [CrossRef]
- Huang, C.H.; Chen, Y.H.; Wang, J.L.; Wang, M. Semiparametric copula-based analysis for treatment effects in the presence of treatment switching. Stat. Med. 2020, 39, 2936–2948. [Google Scholar] [CrossRef]
- Sorrell, L.; Wei, Y.; Wojtyś, M.; Rowe, P. Estimating the correlation between semi-competing risk survival endpoints. Biom. J. 2021, 64, 131–145. [Google Scholar] [CrossRef]
- Choi, Y.H.; Briollais, L.; Win, A.K.; Hopper, J.; Buchanan, D.; Jenkins, M.; Lakhal-Chaieb, L. Modeling of successive cancer risks in Lynch syndrome families in the presence of competing risks using copulas. Biometrics 2017, 73, 271–282. [Google Scholar] [CrossRef]
- Emura, T.; Chen, Y.H. Gene selection for survival data under dependent censoring: A copula-based approach. Stat. Methods Med. Res. 2016, 25, 2840–2857. [Google Scholar] [CrossRef]
- Yin, G.; Yuan, Y. Bayesian dose finding in oncology for drug combinations by copula regression. Appl. Statist. 2009, 58, 211–224. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, J.; Li, Z.; Lin, J.; Lu, T.; Yan, F. Dose-finding based on bivariate efficacy-toxicity outcome using archimedean copula. PLoS ONE 2013, 8, e78805. [Google Scholar] [CrossRef]
- Owzar, K.; Pranab, K.S. Copulas: Concepts and novel applications. METRON-Int. J. Stat. 2003, LXI, 323–353. [Google Scholar]
- Alonso, A.; Bigirumurame, T.; Burzykowski, T.; Geert, M.B.; Leacky, M.; Nolen, M.; Perualila, J.; Shkedy, Z.; Elst, W.V.D. Applied Surrogate Endpoint Evaluation Methods with SAS and R; CRC Biostatistics Series; Chapman & Hall: London, UK, 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Risca, G.; Galimberti, S.; Rebora, P.; Cattoni, A.; Valsecchi, M.G.; Capitoli, G. Archimedean Copulas: A Useful Approach in Biomedical Data—A Review with an Application in Pediatrics. Stats 2025, 8, 69. https://doi.org/10.3390/stats8030069
Risca G, Galimberti S, Rebora P, Cattoni A, Valsecchi MG, Capitoli G. Archimedean Copulas: A Useful Approach in Biomedical Data—A Review with an Application in Pediatrics. Stats. 2025; 8(3):69. https://doi.org/10.3390/stats8030069
Chicago/Turabian StyleRisca, Giulia, Stefania Galimberti, Paola Rebora, Alessandro Cattoni, Maria Grazia Valsecchi, and Giulia Capitoli. 2025. "Archimedean Copulas: A Useful Approach in Biomedical Data—A Review with an Application in Pediatrics" Stats 8, no. 3: 69. https://doi.org/10.3390/stats8030069
APA StyleRisca, G., Galimberti, S., Rebora, P., Cattoni, A., Valsecchi, M. G., & Capitoli, G. (2025). Archimedean Copulas: A Useful Approach in Biomedical Data—A Review with an Application in Pediatrics. Stats, 8(3), 69. https://doi.org/10.3390/stats8030069





