A Data-Driven Approach of DRG-Based Medical Insurance Payment Policy Formulation in China Based on an Optimization Algorithm

Abstract

The diagnosis-related group (DRG) system classifies patients into different groups in order to facilitate decisions regarding medical insurance payments. Currently, more than 600 standard DRGs exist in China. Payment details represented by DRG weights must be adjusted during decision-making. After modeling the DRG weight-determining process as a parameter-searching and optimization-solving problem, we propose a stochastic gradient tracking algorithm (SGT) and compare it with a genetic algorithm and sequential quadratic programming. We describe diagnosis-related groups in China using several statistics based on sample data from one city. We explored the influence of the SGT hyperparameters through numerous experiments and demonstrated the robustness of the best SGT hyperparameter combination. Our stochastic gradient tracking algorithm finished the parameter search in only 3.56 min when the insurance payment rate was set at 95%, which is acceptable and desirable. As the main medical insurance payment scheme in China, DRGs require quantitative evidence for policymaking. The optimization algorithm proposed in this study shows a possible scientific decision-making method for use in the DRG system, particularly with regard to DRG weights.

1. Background

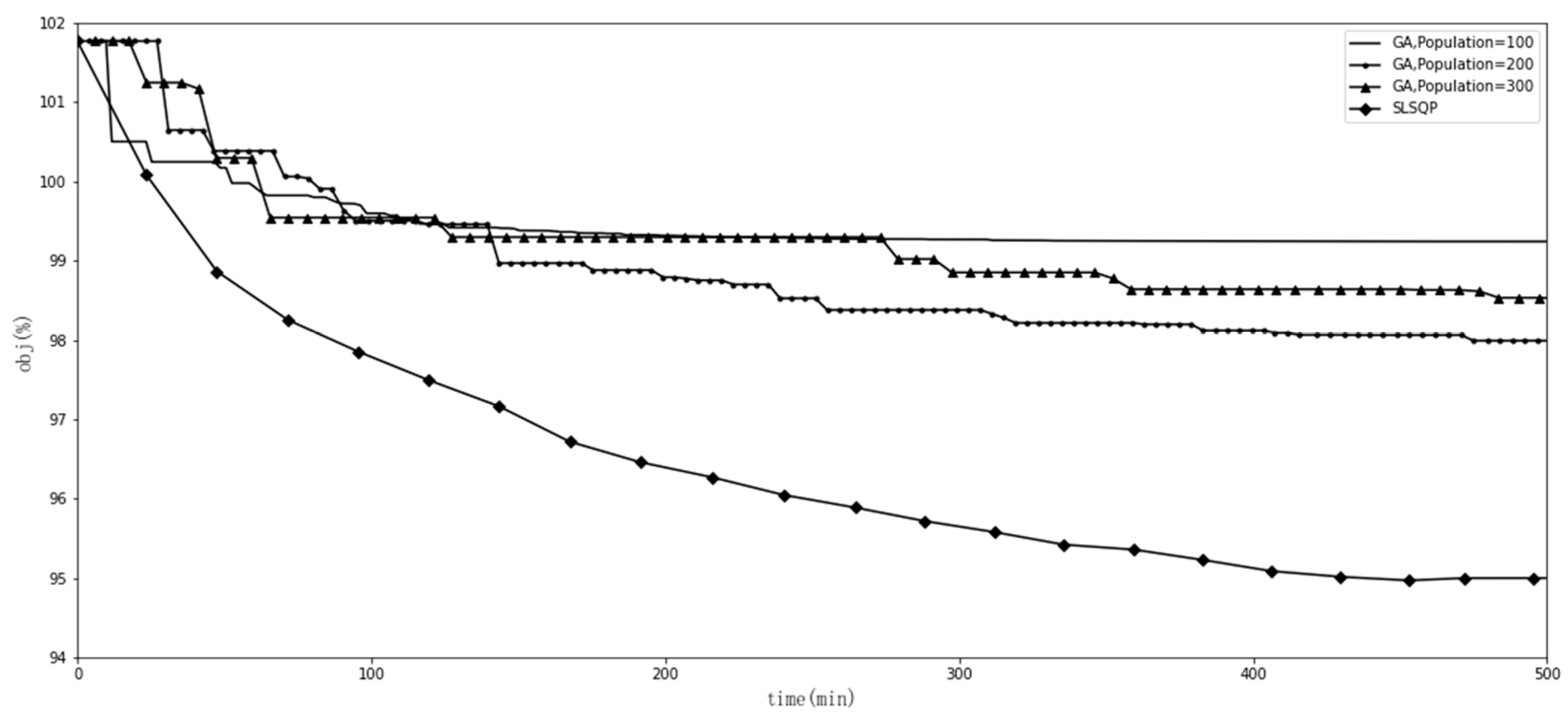
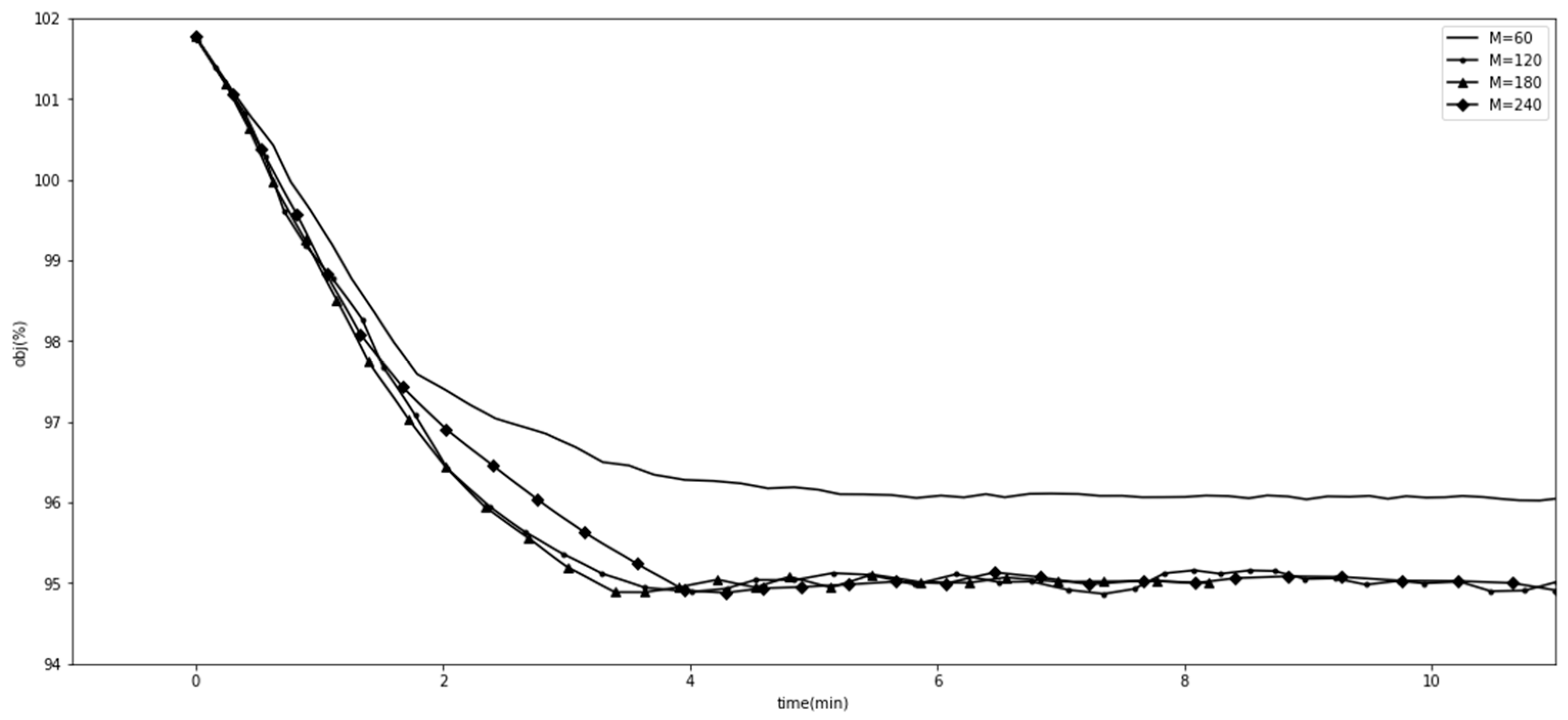
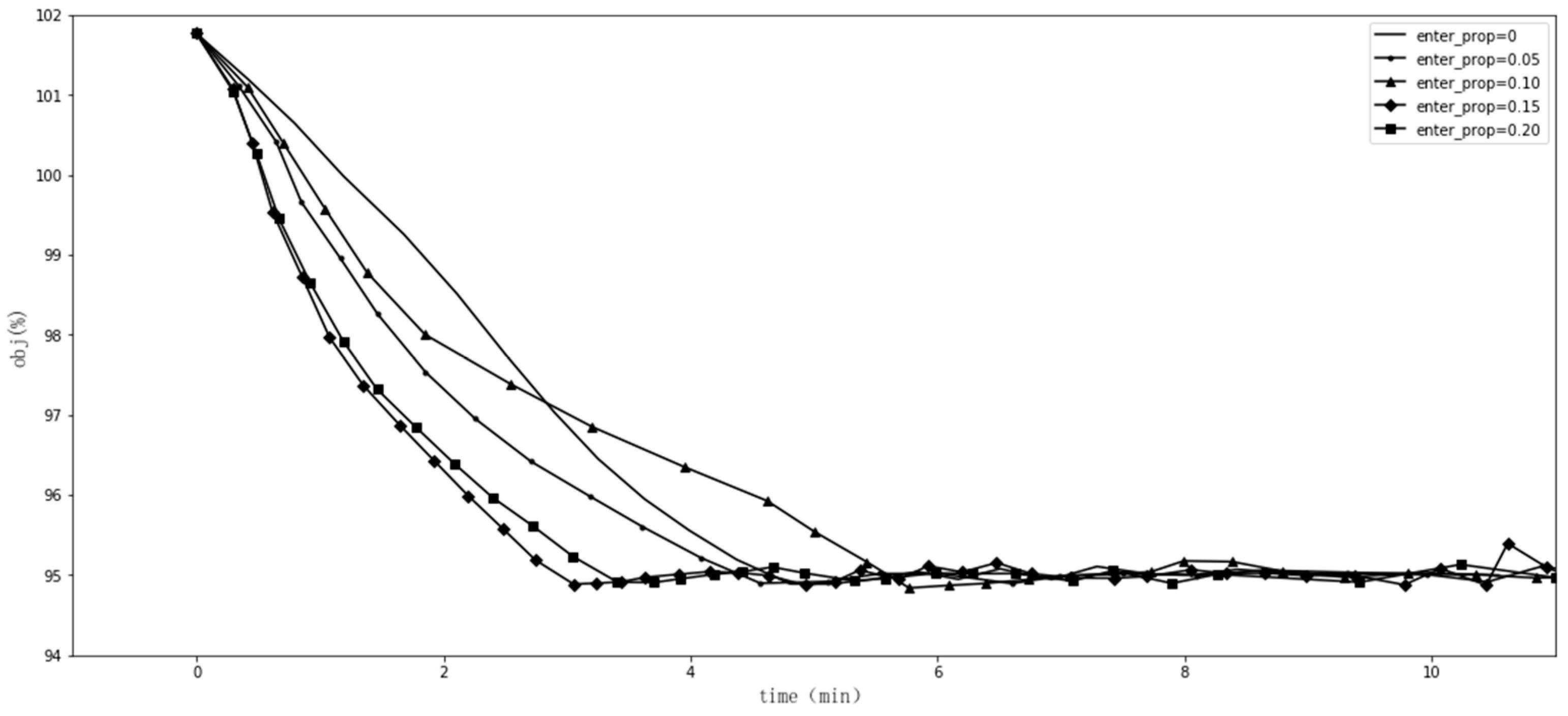
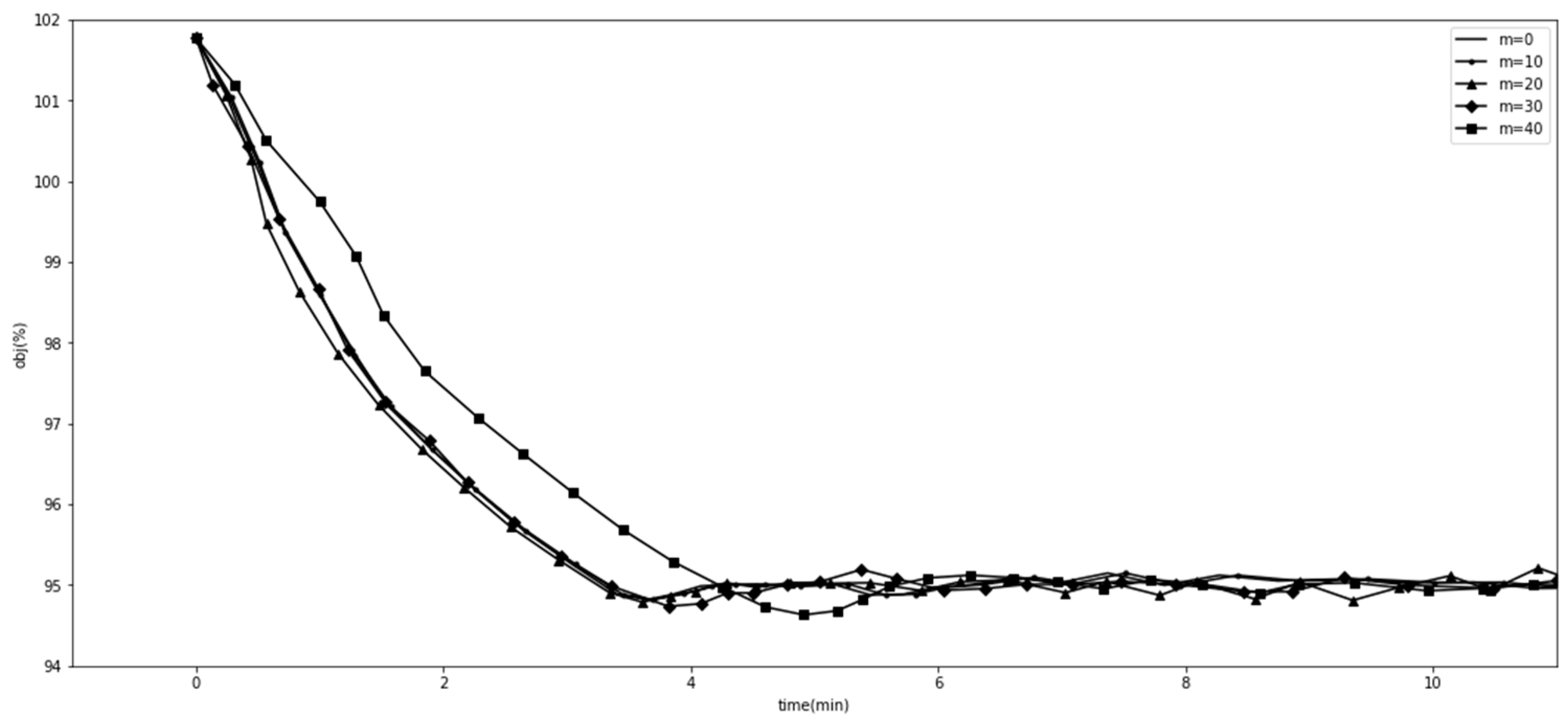
1.1. Diagnosis-Related Groups in Medical Insurance Payment

A diagnosis-related group (DRG) is a patient classification scheme that divides patients into several diagnostic groups for management based on diagnosis, treatment, complications, age, disease severity, and resource consumption. DRG works as a tool to decide medical insurance payments and measure the quality and efficiency of medical services. An efficient DRG payment system can achieve a win–win solution for insurers, doctors, and patients. It prevents medical insurance funds from being overspent, standardizes the diagnosis and treatment processes of hospitals, and provides patients with high-quality medical services and a convenient settlement at the cost of reasonably compensated medical expenses. There are two main reasons for the use of the DRG system, which are similar across various countries. First, using DRGs, countries can increase the transparency of their hospital services, which are represented by patient classification and measurements of hospital output. Second, the payment of hospital fees based on the quantity and category of cases treated could encourage the effective use of medical resources in hospitals. These two factors can help to ensure and improve the quality of national healthcare services.

Reimbursement mechanisms based on DRGs were first proposed in the United States in 1983 as an integral part of the Medicare program and were soon adopted in many other countries [1]. Healthcare policy planners and researchers from Europe launched the EuroDRG social project to pay hospitals. Although they are widely used, DRGs have different meanings across Europe [2]. Finland and Sweden use DRGs primarily to measure hospital case portfolios, while in countries such as Germany and France, DRGs are a synonym for payment. This is because the DRG application process differs among countries, and each country has adapted the DRG system based on the needs of their healthcare systems. For example, the primary objective of the early adoption of DRGs was to improve medical transparency in countries such as France and Portugal. However, countries that have introduced DRGs more recently, such as Poland and the Netherlands, have generally aimed to pay hospitals based on the DRG system [2]. In many countries, compensation mechanisms based on DRGs may face certain challenges, such as doctors’ unfamiliarity with DRGs [3,4], poor medical record-keeping [5], and confusion regarding data encoding [6]. Several solutions for this problem have been proposed: Barouni [1] emphasized the consideration of disease complexity and severity, number of complications, and type when modifying or creating DRGs, while Wild [7] suggested increasing budgets for unusual and complex groups. Furthermore, the standardization of clinical decision-making procedures requires further attention.

At present, there are more than 600 standard diagnosis-related groups in China, and payment details need to be adjusted during decision-making. Kun Zou [8] pointed out that DRG payments in China may negatively affect the quality and equity of healthcare at the cost of a mild improvement in efficiency. Therefore, policymakers should carefully design the components and weights of DRGs based on policy goals; to enable this, there is a need for comparative studies and randomized trials to provide evidence of the effects of DRGs.

The current DRG payments in China usually take average cost of diseases across one province or one city as the benchmark for DRG weights. This may cause potential non-financial effects, such as quality of care, perverse incentives, or inequality between hospitals and regions. Zhang’s research [9] shows that the implementation of diagnosis-related group reimbursement systems may mitigate excessive medical interventions and optimize resource utilization. Paradoxically, this approach coincides with emerging systemic challenges such as heightened clinician–patient communication demands, constraints on innovative medical technology adoption, strategic case fragmentation, and selective admission practices.

With the full coverage of medical insurance in China, medical costs have grown rapidly. According to the National Health Commission of the PRC, the total health expenditure in 2019 exceeded CNY 6.5 trillion, accounting for 6.6% of GDP, up 0.15% from 2018. Per capita health expenditure increased by 12.24% from 2018 to CNY 4656.7. The medical insurance fund is at risk of deficit; therefore, regularizing the intensive use of funds, such as payment standards, has become a priority in the reform of medical insurance policy. We believe that reasonable numerical simulations and efficient model optimization based on artificial intelligence and learning algorithms can introduce convenience to DRG medical insurance payment research.

1.2. Data-Driven Methods for Public Policy Formulation

Artificial intelligence (AI) and optimization techniques have greatly facilitated innovations in social systems [10]. In healthcare, AI serves as a powerful reshaping force that enables early disease detection and timely clinical treatment [11,12,13]. Furthermore, artificial intelligence and learning techniques are emerging to address public health challenges, especially those related to clinical decision-making and healthcare planning. For policy modeling, Silva [14] presented an M/M/c/K queuing model depicting an Internet of Healthcare Things infrastructure with a three-layer cloud/fog/edge computing system to improve healthcare management in hospitals during the COVID-19 pandemic; for policy planning, Tutsoy [15] developed an artificial intelligence-based algorithm for planning long-term policies and making decisions for the reopening of schools during the COVID-19 pandemic; and for policy evaluation, Yu [16] presented a method based on system dynamics to explain mechanisms and evaluate performance in the macroscopic implementation of public policy, which verified that the use of computer simulation is feasible in policy planning.

To formulate medical insurance payment policy scientifically, the national healthcare security administration of China recommends simulation before implementation, as the data accumulated in the simulation could provide a reference for policy evaluation. It is necessary to improve DRG payment optimization based on artificial intelligence and learning algorithms, as this approach has gained little attention worldwide. Patrick [17] proposed an agent-based GAP-DRG model to formulate payment standards. This model reflects the process of treatment, payment, and reimbursement to compare different reimbursement schemes in outpatient care. However, the GAP-DRG model simplifies many assumptions from reality and thus lacks practicality. Currently, complex models adapted to reality and optimized solutions obtained using learning algorithms are being developed for two reasons: first, data from both real and simulated situations can support policy planning and parameter setting, and second, increasing computing power improves efficiency while ensuring accuracy. Therefore, the conditions are right for developing a data-driven approach to DRG medical insurance payment policy based on an optimization algorithm.

2. Methods

2.1. DRG-Based Medical Insurance Payment Policy Formulation

This research focuses on formulating medical insurance payment standards and helps achieve certain policy objectives under constraints that can provide a decision support tool for experts adjusting DRG reimbursement standards. While numerous details (represented by DRG weights in the payment policy) affect the reimbursement standard and final payment effect, this decision-making process could be modeled as a parameter-searching problem based on optimization; DRG weights are the decision variable, policy goals formulate objective functions, and restrictions are transformed into constraint conditions. Ignoring the indirect impact on doctors’ behavior and patients’ welfare, this study evaluates medical insurance funds and hospital operations using budget balance rates and insurance payment rates, respectively. The budget balance rate refers to the percentage of the medical insurance budget remaining after payment, reflecting the security of the medical insurance fund. The insurance payment rate refers to the proportion of the actual payment amount to the amount applied for, which represents the operating level of the hospital.

DRG weights serve as the decision variables, reflecting the relative treatment difficulty and economic costs for each DRG. As shown in Equation (1), the weights are initialized by the ratio of the average cost from a specific group to the average cost. $w_i$ is the initial weight of DRG group $i$, $F_i$ is the average cost of DRG group $i$, and $F_{all}$ is average cost of all DRG groups.

$$w_i={\displaystyle \frac{F_i}{F_{all}}}$$

(1)

The insurance payment rate serves as the main objective function and can be formulated as Equation (2). V represents the insurance payment rate, $F\left(w\right)$ is the actual payment from the medical insurance fund, and $F_{submit}$ is the amount applied for by the hospital. In our research, $F\left(w\right)$ is simulated according to payment settlement rules and thus acts as a function of the DRG weights. $F_{submit}$ is a constant for each patient and is not affected by the medical insurance settlement rules within a specific group. Our mission is to impel the insurance payment rate $V$ close to the value $v_1$, assumed as a policy goal, so that the policy-formulating situation can be transformed into an optimization-solving problem. The objective function is set as Equation (3) and is used to minimize the difference between the actual payment rate and the payment rate set by the government.

$$V={\displaystyle \frac{F\left(w\right)}{F_{submit}}}$$

(2)

$$\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\left(\left|V-v_1\right|\right)$$

(3)

Restrictions from insurance accounts, hospitals, and regions served as constraint conditions, as listed in

Table 1. Constraint conditions.

Constraint Condition	Definition	Feasible Range
Overall Budget Balance Rate	${\displaystyle \frac{\mathrm{O}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{B}\mathrm{u}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{t}-\mathrm{O}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{P}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}{\mathrm{O}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{B}\mathrm{u}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{t}}}$	$\left[{\mathrm{l}}_1,{\mathrm{u}}_1\right]$
Insurance Payment Rate per Hospital	${\displaystyle \frac{\mathrm{A}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{P}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{H}\mathrm{o}\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{l}}{\mathrm{P}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{H}\mathrm{o}\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{l}}}$	$\left[{\mathrm{l}}_2,{\mathrm{u}}_2\right]$
Insurance Payment Rate per Insurance Account	${\displaystyle \frac{\mathrm{A}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{P}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{I}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}}{\mathrm{P}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{I}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}}}$	$\left[{\mathrm{l}}_3,{\mathrm{u}}_3\right]$
Budget Balance Rate per Region	${\displaystyle \frac{\mathrm{R}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{B}\mathrm{u}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{t}-\mathrm{R}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{P}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}{\mathrm{R}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{B}\mathrm{u}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{t}}}$	$\left[{\mathrm{l}}_4,{\mathrm{u}}_4\right]$
Weighted Average of DRG weights	$\overline{\mathrm{w}}={\sum }_{\mathrm{i}}{\mathrm{w}}_{\mathrm{i}}\times {\displaystyle \frac{{\mathrm{C}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{w}}_{\mathrm{i}}\right)}^1}{{\sum }_{\mathrm{i}}\mathrm{C}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{w}}_{\mathrm{i}}\right)}}$	1

¹ $Count\left(w_i\right)$ represents the number of cases in the diagnosis-related group $i$.

. Overall budget balance rate controls the overall payment of insurance in a city/province/country. If the payment exceeds the budget too much, future medical expenses will be affected. If it is too much lower than the budget, the guarantee of current medical services will be affected. The insurance payment rate per hospital will balance the payment for different hospitals, and if this rate for a certain hospital is too low, financial problems will be caused for that hospital. The insurance payment rate per insurance account will balance the payment for each government insurance account. The Budget balance rate per region will balance the different regions in one city. The weighted average of DRG weights should always be 1, so that the DRG weights can be used for the future payment and the total cost of all patients will be the same.

In DRG payment policy planning, we assume other parameters to be constants, including the payment rate, the upper and lower bounds of payment, and the payment ratio beyond bounds, as shown in

Table 2. Parameters of constant settings.

Parameter	Definition	Constant Setting
Payment Rate	Represents the value of DRG weight	Differs among insurance accounts
Upper Bound of Payment (U)	To avoid abnormalities caused by the high cost of individual cases, the upper bound payment is set for each group. When the medical cost of a certain case is higher than the upper bound, special payment rules will be adopted.	Set as 3 times the payment standard within a group
Lower Bound of Payment (L)	To avoid abnormalities caused by the low cost of individual cases, the lower bound payment is set for each group. When the medical cost of a certain case is lower than the lower bound, special payment rules will be adopted.	Set as 0.3 times the payment standard within a group
Payment Ratio beyond Bounds	Parameters for applying special payment rules when costs for individual cases are too high or too low	Related to local medical insurance payment level, typically set as 0.85

.

2.2. Data Description

We used 324,832 data points involving insurance payments in a city for simulation and optimization, covering 747 diagnosis-related groups and 11,644 disease categories. The type of variables used in the dataset include DRG group, original diagnosis, hospital department, hospital, type of hospital, actual payment amount, and payment applied for by the hospital. Distribution of cases by type of hospital, level of hospital, and subgroup is shown as

Table 3. Distribution of cases by type of hospital.

Types of Hospital	Levels of Hospital	Subgroups	Cases	Proportion
Traditional Chinese Medicine Hospital	Level I	Internal Medicine	10,536	3.33%
		Operation	1139	0.36%
		Surgeon without Operation	6302	1.99%
	Level III	Internal Medicine	23,556	7.45%
		Operation	1548	0.49%
		Surgeon without Operation	12,757	4.03%
Specialized Hospital	Level II	Internal Medicine	/	/
		Operation	/	/
		Surgeon without Operation	/	/
	Level III	Internal Medicine	14,630	4.62%
		Operation	744	0.24%
		Surgeon without Operation	8200	2.59%
General Hospital	Level II	Internal Medicine	6941	2.19%
		Operation	772	0.24%
		Surgeon without Operation	4365	1.38%
	Level III	Internal Medicine	120,587	38.12%
		Operation	15,008	4.74%
		Surgeon without Operation	89,262	28.22%

. Cases are mainly concentrated in general hospitals and Level III hospitals, and 66.34% of total cases fall in the physician and surgeon subgroups of Level III hospital.

Table 4. Top 10 DRGs with the largest number of cases.

DRG Code	DRG Designation	Number of Cases
RU10	Malignant hyperplastic disorders associated with chemical and/or targeted and biologic therapies, hospital stay ≤7 days	18,216
BR23	Ischemic brain disease, no death or hospital transfer within 5 days, accompanied by complications or comorbidities	12,297
RE19	Chemical and/or targeted biologic therapies for malignant proliferative disorders	10,523
ES20	Respiratory infection/inflammation, age ≤17 years	6336
JB19	Mammoplasty	4848
RW25	Malignant hyperplastic disorders, without complications or comorbidities	4634
KS13	Diabetes, no death or hospital transfer within 5 days, accompanied by complications or comorbidities	4608
FM39	Cardiac catheterization procedure	4603
GZ19	Other digestive system diagnoses	4242
ET29	Chronic respiratory obstruction disease	3929

summarizes the top ten DRGs with the largest number of cases.

Table 5. Top 10 DRGs with the highest total costs.

DRG Code	DRG Designation	Total Costs (in Thousands of CNY)
BR23	Ischemic brain disease, no death or hospital transfer within 5 days, accompanied by complications or comorbidities	1,482,719
RU10	Malignant hyperplastic disorders associated with chemical and/or targeted and biologic therapies, hospital stay ≤7 days	1,338,713
RE19	Chemical and/or targeted biologic therapies for malignant proliferative disorders	1,171,234
AH19	Tracheotomy with ventilator for more than 96 h or ECMO	1,157,519
IC29	Joint replacement of hip, shoulder, knee, elbow, or ankle	1,084,282
EB19	Major chest surgery	993,034
FM19	Percutaneous coronary stent implantation	843,867
IB39	Other operations related to the spine	793,382
IC39	Joint surgery of the hip, shoulder, knee, elbow, or ankle other than replacement/revision	741,202
IB29	Spine fusion surgery	695,619

lists the top 10 DRGs with the highest total costs, and

Table 6. Top 10 DRGs with the highest average hospitalization cost per case.

DRG Code	DRG Designation	Average Cost per Case (in CNY)
AE19	Kidney transplantation	214,623.91
AG19	Allogeneic marrow/hematopoietic stem cell transplantation	214,024.34
AG29	Autologous marrow/hematopoietic stem cell transplantation	184,981.19
BC19	Intracranial vascular surgery with diagnosis of hemorrhage	146,484.41
FB39	Heart valve surgery	135,746.43
IB19	Combined anterior and posterior spinal fusion	131,420.16
FB19	Cardiac assistance system implantation	130,936.61
QR13	Reticuloendothelial and immune disorders with complications or comorbidities	127,276.82
FB29	Cardiac valve surgery with cardiac catheterization	123,633.85
FK39	Defibrillator implantation or replacement	118,886.68

shows the top 10 DRGs with the highest average hospitalization cost per case. As can be seen, the average cost and total cost of different DRGs differ greatly. For DRGs with a higher total cost, a 1% weight change is seen, and thus the change in total cost may be up to CNY 10 million. For DRGs with a higher average cost per case, the impact of a 1% weight change on a single case can be up to CNY 1000.

2.3. Optimization Algorithm

2.3.1. Proposed Algorithm: Stochastic Gradient Tracking (SGT)

As the formulation of DRG-based medical insurance payment policy shows, the complexity of the payment policy brings challenges for decision-makers to find the perfect DRG weights to balance the interests of hospitals, patients and medical insurance.

Inspired by stochastic gradient descent [18], we propose a novel stochastic gradient tracking algorithm to anchor the target insurance payment rate $v_i$ and the search weights of the DRGs. Stochastic gradient tracking first initializes the DRG weight vector $w_i$, total step size $∆$, the gradient-updated upper bound $\delta$, and the top $M$ DRGs with the highest costs to formulate the candidate set $S$. Focusing on minimizing the objective function $L\left(w\right)=\left|V-v_1\right|$, stochastic gradient tracking attempts to find a suitable gradient descent direction and calculate the descent step size during each iteration. Both effectiveness and randomness were considered when determining the descending direction. In each iteration, in addition to the top $M$ DRGs with the highest cost, other $P$ DRGs are randomly selected as extra descending directions with the probability parameter $\mathit{enter\_prob}$. The forward and backward gradients, $g_f$ and $g_b$, are calculated using Equations (4) and (5). Updated step sizes are comprehensively restricted by three conditions: the upper or lower bound in each group, the gradient-updated upper bound $\delta$, and the total step size $∆$.

Customized constraint conditions are checked in each iteration as an optional step. For example, insurance payment rate per hospital in Table 1, is set as the balance between hospitals to avoid the DRG weight will cause a certain hospital financial problem. It is formulated in Table 1, and the algorithm will check whether insurance payment rate per hospital exceeds the feasible range in Table 1, $\left[l_2,u_2\right].$ If it exceeds the feasible range, a penalty coefficient will be added to the objective function. The hyperparameters of the stochastic gradient tracking algorithm are shown in

Table 7. Hyperparameters of stochastic gradient tracking algorithm.

Hyperparameter	Description
$\mathrm{M}$	$\mathrm{Number}\mathrm{of}\mathrm{DRGs}\mathrm{included}\mathrm{in}\mathrm{the}\mathrm{weight}\mathrm{adjustment}\mathrm{optimization}.\mathrm{DRGs}\mathrm{were}\mathrm{racked}\mathrm{based}\mathrm{on}\cos \mathrm{ts},\mathrm{and}\mathrm{the}\mathrm{highest}\mathrm{M}$ DRGs were included.
$\mathrm{m}$	Batch size, number of DRGs updated in each iteration. In each iteration, only m DRGs were randomly shuffled, and the weights of m DRGs were updated.
$\mathrm{enter\_prob}$	$\mathrm{Probability}\mathrm{of}\mathrm{the}\mathrm{random}\mathrm{sampling}\mathrm{to}\mathrm{include}\mathrm{more}\mathrm{DRGs}(\mathrm{other}\mathrm{than}\mathrm{M}$ DRGs with the highest costs) in the weight adjustment optimization.
$\mathsf{\Delta }$	$\mathrm{Total}\mathrm{step}\mathrm{size}.\mathsf{\Delta }$ is set to limit the number of DRG weights updated in each iteration.

, and the pseudo code of the algorithm is shown in

Table 8. Stochastic gradient tracking algorithm.

Step	Stochastic Gradient Tracking
Initialize:	$w=w_0$. $∆={∆}_0$, $\delta ={\delta }_0$, $S=DRG\left(M\right)$;
1:	$L\left(w\right)=\left|V-v_1\right|$;
2:	$\mathrm{Calculate}{g}_f$$,g_b$ via (4) and (5);
3:	For i = 1, …, n:
4:	$\mathrm{Update}∆={\displaystyle \frac{∆(n-i+1)}{n}}$;
5:	$\mathrm{Randomly}\mathrm{sample}P$ $\mathrm{DRGs}\mathrm{by}\mathrm{enter\_prob},\mathrm{expand}\mathrm{candidate}\mathrm{set}\mathrm{S}=\mathrm{S}+\mathrm{P}$;
6:	$\mathrm{Incrementally}\mathrm{sort}S$ $\mathrm{by}{\displaystyle \frac{g_{f_i}}{Count\left(w_i\right)}}$ $\mathrm{and}\mathrm{randomly}\mathrm{shuffle}\mathrm{the}\mathrm{first}m$ DRGs;
7:	$\mathrm{Diminishingly}\mathrm{sort}S$ $\mathrm{by}{\displaystyle \frac{g_{b_i}}{Count\left(w_i\right)}}$ $\mathrm{and}\mathrm{randomly}\mathrm{shuffle}\mathrm{the}\mathrm{first}m$ DRGs;
8:	$\mathrm{Assign}\mathrm{step}\mathrm{size}\mathrm{to}\mathrm{DRGs}\mathrm{by}\mathrm{order}\mathrm{of}{g}_{f_i}$, $\mathrm{ensure}\mathrm{not}\mathrm{to}\mathrm{exceed}\mathrm{upper}\mathrm{bound}\mathrm{in}\mathrm{each}\mathrm{group}\mathrm{and}\mathrm{keep}\delta \left(w\right)\le \delta$. $\mathrm{Stop}\mathrm{when}{\sum }_1^m\delta \left(w\right)\times m>∆$;
9:	$\mathrm{Assign}\mathrm{step}\mathrm{size}\mathrm{to}\mathrm{DRGs}\mathrm{by}\mathrm{order}\mathrm{of}{g}_{b_i}$, $\mathrm{ensure}\mathrm{not}\mathrm{to}\mathrm{exceed}\mathrm{lower}\mathrm{bound}\mathrm{in}\mathrm{each}\mathrm{group}\mathrm{and}\mathrm{keep}\mathsf{\delta }\left(\mathrm{w}\right)\le \mathsf{\delta }$. $\mathrm{Stop}\mathrm{when}{\sum }_1^m\delta \left(w\right)\times m>∆$;
10:	$\left(\mathrm{optional}\right)\mathrm{Check}\mathrm{customized}\mathrm{constraint}\mathrm{conditions}.\mathrm{Add}\mathrm{penalty}\mathrm{coefficient}\mathrm{to}L\left(w\right)$ when exceed feasible range in Table 1;
11:	$\mathrm{Update}w=w+\delta \left(w\right)$;
12:	$\mathrm{Recalculate}\mathrm{L}\left(\mathrm{w}\right)=\left|\mathrm{V}-{\mathrm{v}}_1\right|$, exit loop when converge;
13:	$\mathrm{Recalculate}{g}_f$$,g_b$ via (4) and (5);
14:	End for;
15:	$\mathrm{Return}\mathrm{w}$.

.

$$g_f={\displaystyle \frac{L\left(w_i+\delta \right)-L\left(w_i\right)}{\delta }}$$

(4)

$$g_b={\displaystyle \frac{L\left(w_i\right)-L(w_i-\delta )}{\delta }}$$

(5)

The loop and converging rate are controlled by the number of DRG groups n, and the complexity of the algorithm is O(n).

2.3.2. Genetic Algorithm (GA)

The genetic algorithm [19] is a method that searches for an optimal solution by simulating the process of biological evolution and natural selection. There are five main steps in the GA: encoding the parameter space; setting the initial population; designing the fitness function; designing genetic operations, including selection crossover and variation; and setting control parameters. The GA does not require the objective to be differentiable and continuous and shows high adaptiveness when adjusting the search direction. Our research uses the GA as a baseline for comparison with the proposed stochastic gradient tracking algorithm.

GA operates on a population of candidate solutions (termed individuals or chromosomes), iteratively improving fitness through stochastic operations. The key components of GA include:

Initialization: A population of individuals is generated randomly, each representing a potential solution encoded as a bitstring, real-valued vector, or other structures. In this research, DRG weights are initialized with Equation (1).

Fitness evaluation: Each individual’s quality is assessed via a user-defined fitness function. In this research, the objective function and constraint conditions are used as fitness function.

Selection: High-fitness individuals are probabilistically chosen for reproduction using methods like tournament selection or roulette wheel selection. In this research, DRG weights of the highest average cost will change first.

Mutation: Random alterations introduce diversity, preventing premature convergence to local optima. In this research, a random portion of DRGs will also change the weight.

Generational replacement: Offspring replace low-fitness individuals, forming a new population. This loop repeats until convergence.

2.3.3. Sequential Quadratic Programming (SQP)

Sequential quadratic programming [20,21] is efficient in nonlinear constrained optimization problems and divides the original problem into a series of quadratic programming subproblems. Our research used sequential least squares programming (SLSQP) [21] as a baseline for comparison with the proposed stochastic gradient tracking algorithm.

At every iteration, SQP follows this workflow:

Build a local model: approximate the objective function as a quadratic “bowl-shaped” curve (retains curvature information). Approximate constraints (constraint condition in Table 1) as straight lines.

Solve the QP subproblem: find the best direction to move by minimizing the quadratic model while staying within linearized constraints.

Choose a safe step size: avoid overcommitting to the QP solution (approximations might be inaccurate).

Use line search or trust-region: objective function decreases, constraints become less violated.

Update and check convergence: move to the new point. Stop if solutions barely change and constraints are satisfied. Otherwise, repeat.

3. Results

We experimented with the comparative methods GA and SLSQP, as shown in Figure 1. Furthermore, we tested the effects of different GA hyperparameter values for tracking the goal. Figure 2 shows the effect of $M$ when $\mathit{enter\_prob}$, $m=20$, $\Delta =2000$, and $\mathit{max\_step}=0.3$. Figure 3 shows the effect of $\mathit{enter\_prob}$ when $M=180$, $m=20$, $\Delta =2000$, and $\mathit{max\_step}=0.3$. Figure 4 shows the effect of $m$ when $M=180$, $\mathit{enter\_prob}=0.15$, $\Delta =2000$, and $\mathit{max\_step}=0.3$. Figure 5 shows the effect of $\Delta$ when $M=180$, $\mathit{enter\_prob}=0.15$, $m=20$, and $\mathit{max\_step}=0.3$. All experiments were conducted using a 16-core CPU and 120 G memory. The goal of all experiments was to track the insurance payment rate $v_1$, and the target was set as 95%, which corresponds with the medical insurance policy target.

4. Discussion

We first performed an experiment with the comparative methods GA and SLSQP, as shown in Figure 1. GAs with different populations were trapped in local optima and were far from the 95% target. SLSQP worked well, reaching the target of 95%, but took more than 400 min to do so.

Figure 2, Figure 3, Figure 4 and Figure 5 show the results of SGT, in which we depict the effects of the hyperparameters. The number of DRGs chosen with the highest costs had a positive effect on tracking, while marginal utility decreased as $M$ exceeded 120. After a comprehensive comparison and careful consideration, we chose 180 as the value of the hyperparameter $M$. The probability with which the descending directions were randomly selected, $\mathit{enter\_prob}$, had a slightly positive effect, so we assigned it a value of 0.15. Figure 4 shows the effect of $m$, the number of groups randomly shuffled, which we set as 20. Figure 5 shows the effect of $\Delta$, the initial total step size, which we set as 3500 for the proper value.

The insurance payment rate of 95% corresponded with the target of medical insurance policies; we also tested multiple settings to determine the robustness of SGT with the above optimal hyperparameters. As shown in

Table 9. The robustness of SGT on different insurance payment rates.

Insurance Payment Rate ${\mathit{v}}_1$ (Tracking Goal, in %)	Time Consumed (in Minutes)
93	8.82
94	4.00
95	3.56
96	3.05
97	2.79

, we assumed the insurance payment rate to be 93% to 97% (the stop criterion is a 0.1% relative error) and the running time to be consistent, which decreases when the insurance payment rate increases. Our SGT with optimal settings completed this parameter-searching task in only 3.56 min when the insurance payment rate was set at a practical 95%.

Limitations of this study include issues related to generalizability, model interpretability, and the comprehensive evaluation of the healthcare system. Regarding generalizability, the dataset utilized in this study was derived from a single city, which may limit the broader applicability of the findings. Future research should validate the proposed approach across multiple cities to enhance its generalizability. The challenges of generalizability would be customized policy constraint conditions and data availability. Concerning model interpretability, the complexity of the DRG weight optimization results may pose challenges for decision-makers in fully comprehending the outcomes. As a result, expert manual review remains necessary to ensure proper interpretation and implementation. With respect to the comprehensive evaluation of the healthcare system, the inherent complexity of healthcare systems means that adjustments to DRG weights could have wide-ranging implications across multiple dimensions. Further research is warranted to conduct a thorough assessment of the impacts resulting from changes in DRG weights.

More research on other relevant algorithms to solve medical insurance policy formulation will also be considered as future work. The hyperparameters were selected manually in this research, but an automated hyperparameter optimization procedure can be discussed with grid search, random search, Bayesian optimization, gradient-based optimization, and so on.

Healthcare policy decision-making necessitates engagement with a diverse constellation of stakeholders—including patients, clinicians, healthcare institutions, insurers, and pharmaceutical firms. While the establishment of an optimal evaluative framework remains an aspirational objective, its realization is inherently constrained by competing priorities. Future research should operationalize multi-objective optimization methodologies to systematize diagnosis-related group (DRG) weighting determinations.

5. Conclusions

Diagnosis-related groups (DRGs) provide a classification scheme for different patients and are widely used in countries all around the world. They support the rational utilization of medical insurance funds, standardize the diagnosis and treatment processes of hospitals, and provide patients with high-quality medical services at a reasonable cost.

In China, settlement details and DRG weights need to be fine-tuned in various areas. In this study, we introduced a mathematical paradigm into the detail-deciding problem and policy planning process. Based on emerging artificial intelligence and optimization techniques, we proposed a stochastic gradient tracking (SGT) algorithm and explored its hyperparameters in numerous experiments. SGT performed better than the genetic algorithm and maturely deployed sequential quadratic programming to solve the detail-deciding problem. Further, additional experiments with different insurance payment rates set as tracking targets demonstrated the robustness of the SGT algorithm and its potential use for future decision-making in medical insurance policy.

Finally, our stochastic gradient tracking algorithm determined parameters in only 3.56 min when the insurance payment rate was set to 95%. Our study provides a scientific and helpful reference for formulating medical insurance payment standards.