Distance-Based Relevance Function for Imbalanced Regression
Abstract
1. Introduction
2. Preliminaries
2.1. Previous Research
2.2. Performance Measures
3. Proposed Method
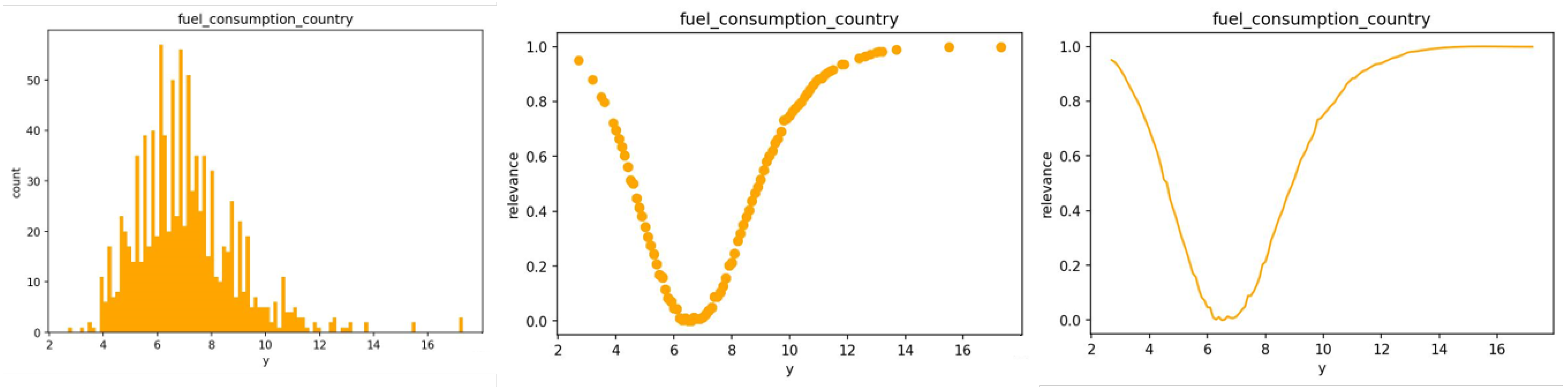
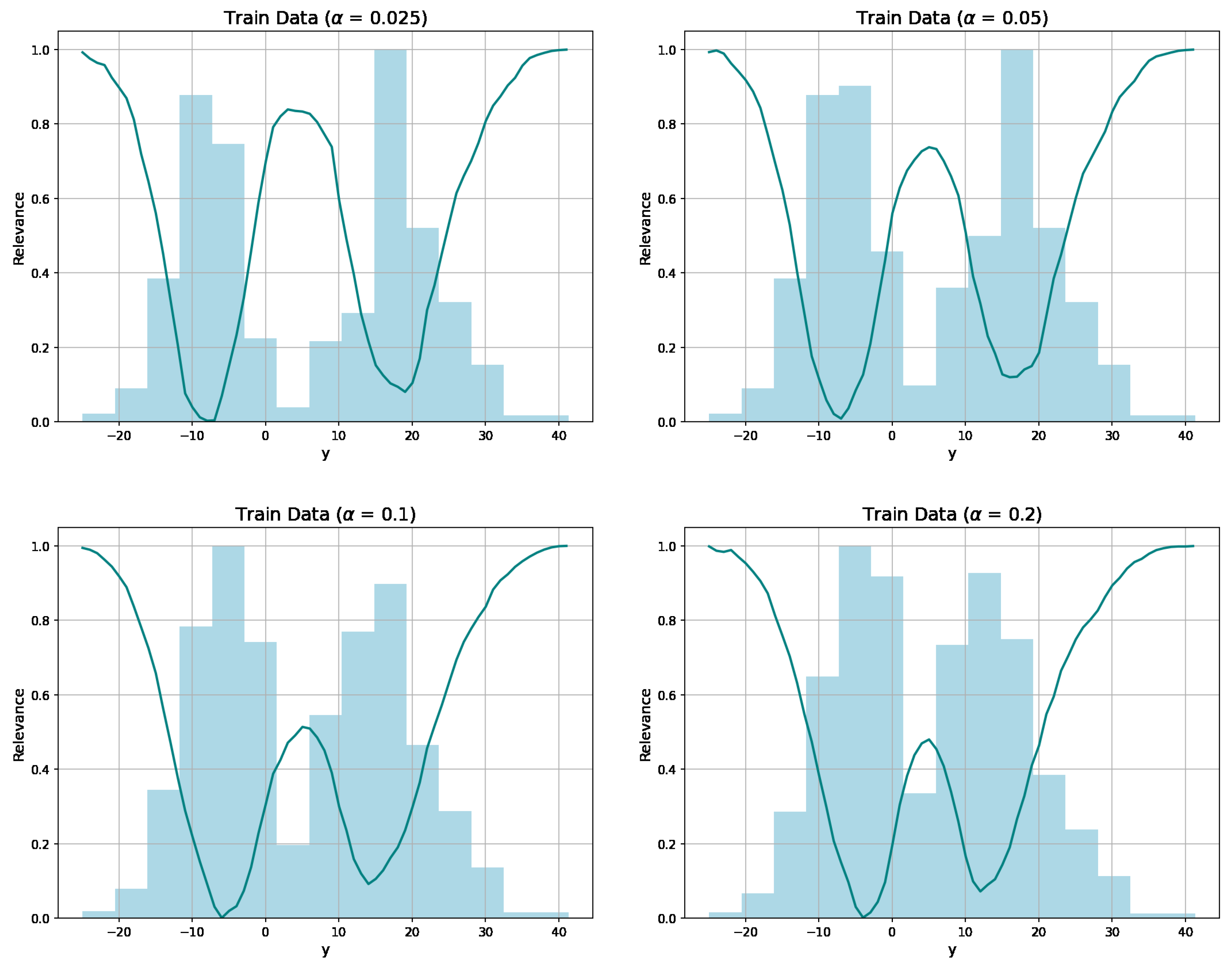
3.1. Distance-Based Relevance Function
3.2. DRF-SMOGN
4. Experimental Study
4.1. Data Description
4.1.1. Simulation Data
4.1.2. Real Data
4.2. Method
4.2.1. Relevance Threshold
4.2.2. Sampling via SMOGN
4.2.3. Experimental Setup
- Support Vector Regressor (SVR).
- Neural network (NNET).
- XGBoost Regressor (XGB).
- Random Forest Regressor (RF).
4.2.4. Evaluation Metrics
4.3. Results
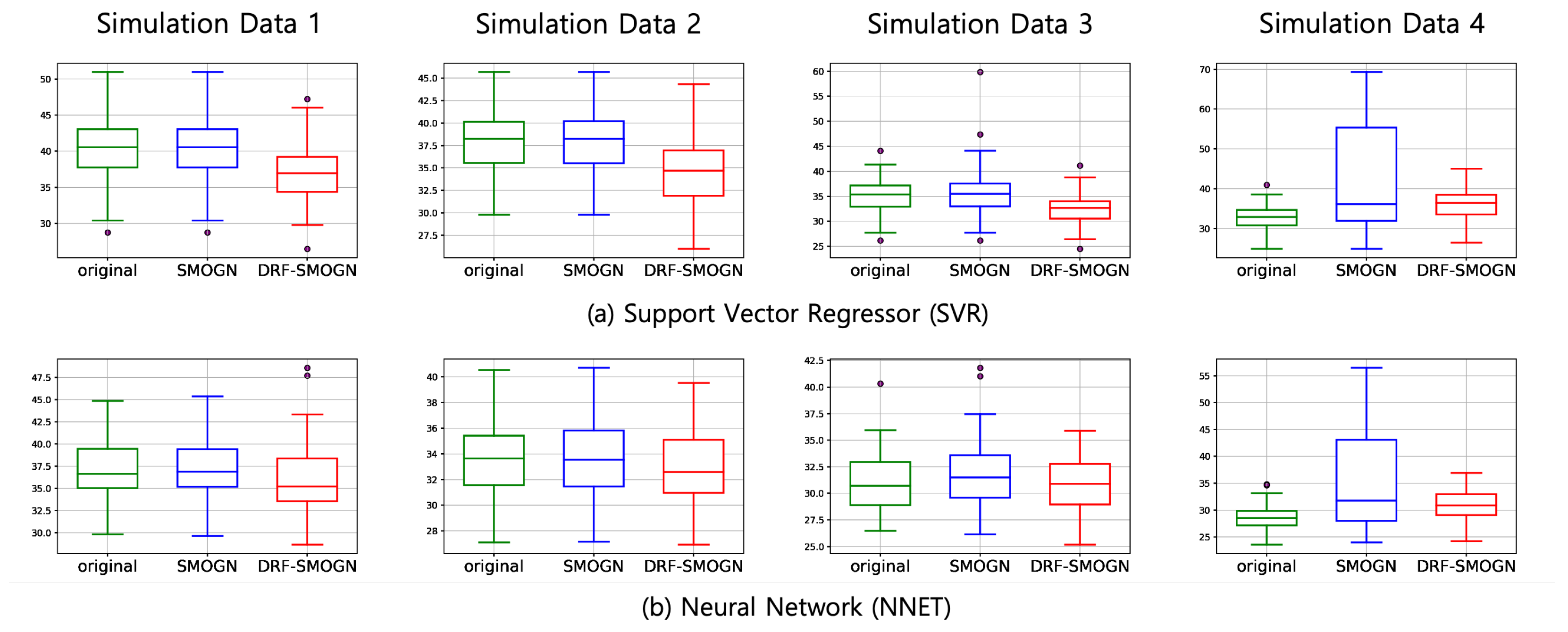
4.3.1. Simulation Data Results
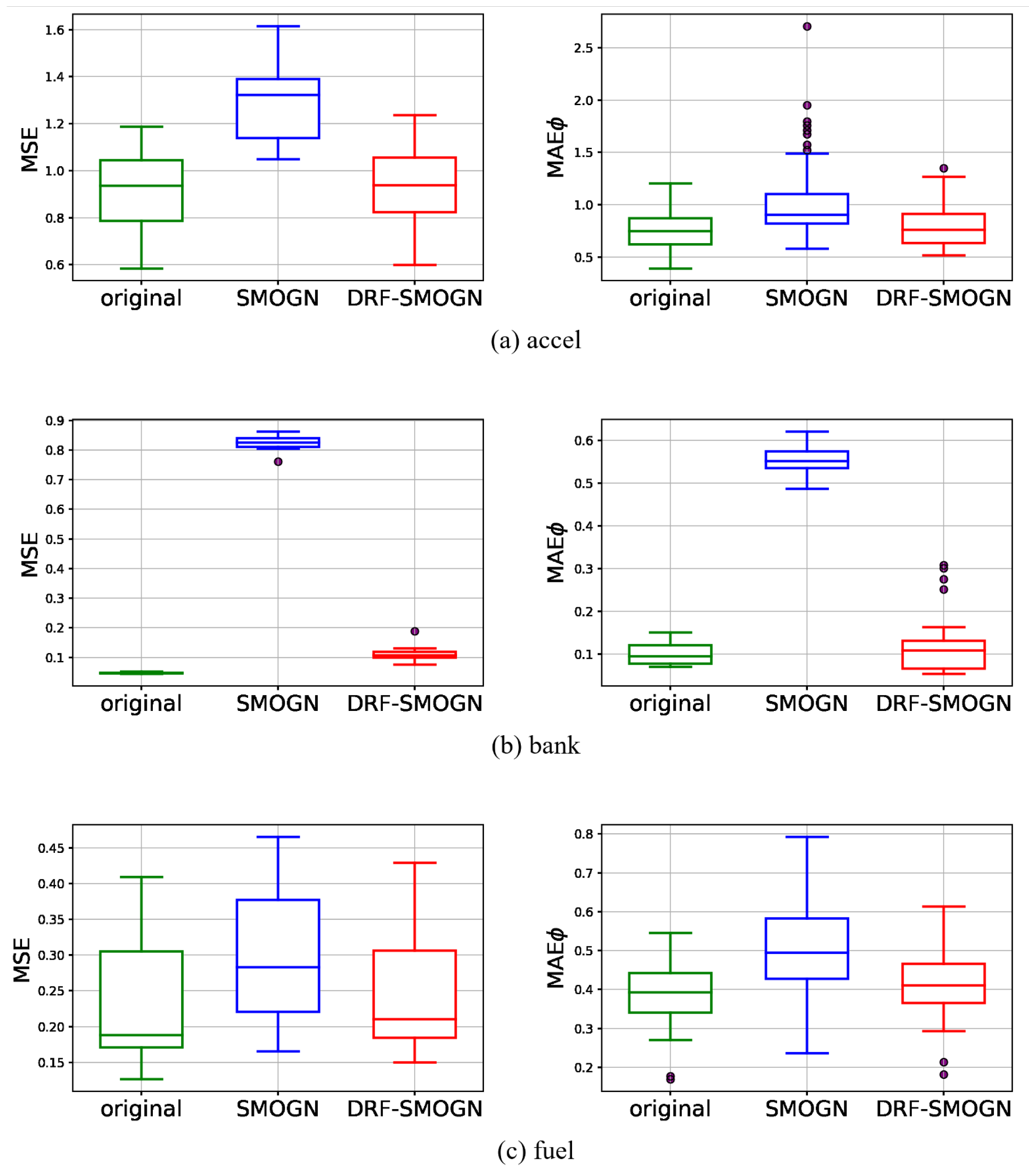
4.3.2. Real Data Results
- Nominal features: Unlike our simulations, some real datasets include up to 13 categorical predictors. HEOM handles these by treating each mismatched category as distance 1, which can overwhelm the Euclidean contributions from numerical features when categories dominate. Since DRF-SMOGN weights synthetic targets by inverse distance, overly coarse categorical distances may distort both neighbor selection and target interpolation.
- Gaussian noise sampling: SMOGN’s safety threshold rule falls back on adding Gaussian noise when neighbors are too far apart—a useful idea in principle, but one that depends on a user-defined perturbation constant. Without clear guidelines for setting this constant across diverse datasets, noise levels can vary unpredictably, undermining the stability. The systematic calibration of this parameter—or the adoption of alternative noise models—could yield more consistent results.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Algorithm A1
| Algorithm A1 Distance-based Relevance Function |
| Input: Y—sorted list of n target values (standardized) D—search radius (e.g., ) —stabilization constant (e.g., 1) Output: —relevance scores in initialize array raw_scores of length n for to n do for to n do if then end if end for raw_scores[j] end for for to n do end for return |
Appendix B. Algorithm A2
| Algorithm A2 DRF-SMOGN |
Require: Dataset with continuous targets Y
|
References
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- King, G.; Zeng, L. Logistic regression in rare events data. Political Anal. 2001, 9, 137–163. [Google Scholar] [CrossRef]
- Torgo, L.; Ribeiro, R.P. Utility-based regression. In Proceedings of the 11th European Conference on Principles and Practice of Knowledge Discovery in Databases, Warsaw, Poland, 17–21 September 2007; pp. 597–604. [Google Scholar]
- Torgo, L.; Ribeiro, R.P.; Pfahringer, B.; Branco, P. SMOTE for regression. In Proceedings of the EPIA 2013: Progress in Artificial Intelligence, Azores, Portugal, 9–12 September 2013; pp. 378–389. [Google Scholar]
- Branco, P.; Torgo, L.; Ribeiro, R.P. SMOGN: A pre-processing approach for imbalanced regression. In Proceedings of the First International Workshop on Learning with Imbalanced Domains: Theory and Applications, Skopje, Macedonia, 22 September 2017; Volume 74, pp. 36–50. [Google Scholar]
- Steininger, M.; Kobs, K.; Davidson, P.; Krause, A.; Hotho, A. Density-based weighting for imbalanced regression. Mach. Learn. 2021, 110, 2187–2211. [Google Scholar] [CrossRef]
- Son, J. KSMOTER: KDE SMOTE for Imbalanced Regression. Master’s Thesis, Yonsei University, Seoul, Republic of Korea, 2023. [Google Scholar]
- Camacho, L.; Douzas, G.; Bacao, F. Geometric SMOTE for regression. Expert Syst. Appl. 2022, 193, 116387. [Google Scholar] [CrossRef]
- Yang, Y.; Zha, K.; Chen, Y.; Wang, H.; Katabi, D. Delving into deep imbalanced regression. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 11842–11851. [Google Scholar]
- Gonzalez-Abril, L.; Guerrero-Gonzalez, A.; Torres, J.; Ortega, J.A. A review on imbalanced data preprocessing for supervised learning: Evolutionary fuzzy systems and beyond. Appl. Sci. 2020, 10, 4014. [Google Scholar]
- Branco, P.; Torgo, L.; Ribeiro, R.P. Relevance-based evaluation metrics for multi-target regression. Mach. Learn. 2017, 106, 1779–1800. [Google Scholar]
- Torgo, L.; Ribeiro, R.P. Precision and recall for regression. In Proceedings of the DS 2009: Discovery Science, Porto, Portugal, 3–5 October 2009; pp. 332–346. [Google Scholar]
- Song, X.Y.; Dao, N.; Branco, P. DistSMOGN: Distributed SMOGN for imbalanced regression problems. In Proceedings of the Fourth International Workshop on Learning with Imbalanced Domains: Theory and Applications, Grenoble, France, 23 September 2022; Volume 183, pp. 38–52. [Google Scholar]
- Wilson, D.L.; Martinez, T.R. Improved Heterogeneous Distance Functions. In Proceedings of the Fourteenth International Conference on Machine Learning (ICML). Morgan Kaufmann, Nashville, Tennessee, 8–12 July 1997; pp. 656–666. [Google Scholar]

| Dataset | N | % Rare | ||||
|---|---|---|---|---|---|---|
| a1 | 198 | 11 | 3 | 8 | 46 | 23.2 |
| a2 | 198 | 11 | 3 | 8 | 35 | 17.7 |
| a3 | 198 | 11 | 3 | 8 | 34 | 17.2 |
| a4 | 198 | 11 | 3 | 8 | 27 | 13.6 |
| a5 | 198 | 11 | 3 | 8 | 30 | 15.2 |
| a6 | 198 | 11 | 3 | 8 | 33 | 16.7 |
| a7 | 198 | 11 | 3 | 8 | 27 | 13.6 |
| abal | 4177 | 8 | 1 | 7 | 679 | 16.3 |
| accel | 1732 | 15 | 3 | 12 | 137 | 7.9 |
| avail | 1802 | 16 | 7 | 9 | 217 | 12.0 |
| bank | 4499 | 9 | 0 | 9 | 662 | 14.7 |
| bost | 506 | 13 | 0 | 13 | 76 | 15.0 |
| cpu | 8192 | 13 | 0 | 13 | 755 | 9.2 |
| dAil | 7129 | 5 | 0 | 5 | 773 | 10.8 |
| dElev | 9517 | 6 | 0 | 6 | 990 | 10.4 |
| fuel | 1764 | 38 | 12 | 26 | 248 | 14.1 |
| heat | 7400 | 12 | 8 | 4 | 802 | 10.8 |
| maxt | 1802 | 33 | 13 | 20 | 129 | 7.2 |
| Learner | Parameter Variants |
|---|---|
| SVR | |
| NNET | hidden_layer_sizes , activation , |
| solver , alpha | |
| XGB | learning_rate , n_estimators , max_depth |
| RF | n_estimators , max_depth |
| Dataset | Algorithm | MSE | SMAPE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Orig. | SMOGN | DRF | Orig. | SMOGN | DRF | Orig. | SMOGN | DRF | ||
| Data 1 ( | SVR | 40.37 | 40.37 | 36.87 * | 5.14 | 5.14 | 4.95 * | 88.28 | 88.28 | 86.55 * |
| NNET | 37.11 | 37.12 | 35.94 * | 5.41 | 5.41 | 5.26 * | 84.05 | 84.00 | 83.08 * | |
| XGB | 53.04 | 53.04 | 51.39 * | 6.42 | 6.42 | 6.29 * | 89.74 | 89.87 | 89.34 * | |
| RF | 43.49 | 43.47 * | 44.47 | 6.23 | 6.23 | 6.23 | 86.16 | 86.12 * | 86.79 | |
| Data 2 ( | SVR | 40.25 | 40.65 | 37.02 * | 5.10 | 5.12 | 4.91 * | 87.83 | 87.95 | 86.16 * |
| NNET | 33.85 | 34.09 | 33.12 * | 5.05 | 5.06 | 4.93 * | 82.41 | 82.51 | 81.95 * | |
| XGB | 50.41 | 50.26 | 50.17 * | 6.06 | 6.05 | 5.98 * | 88.96 | 89.02 | 88.90 * | |
| RF | 38.18 | 38.18 | 39.36 | 5.64 | 5.64 | 5.65 | 84.17 | 84.14 * | 84.79 | |
| Data 3 ( | SVR | 35.04 | 35.47 | 32.35 * | 4.93 | 4.95 | 4.73 * | 86.62 | 86.79 | 84.83 * |
| NNET | 31.11 | 31.59 | 28.59 * | 4.76 | 4.79 | 4.65 * | 81.42 | 81.65 | 81.08 * | |
| XGB | 45.13 | 45.17 | 43.80 * | 5.65 | 5.64 | 5.53 * | 81.42 | 81.65 | 81.08 * | |
| RF | 33.45 * | 33.58 | 34.10 | 5.10 | 5.11 | 5.06 * | 82.60 * | 82.73 | 83.15 | |
| Data 4 ( | SVR | 32.65 * | 42.77 | 35.92 | 5.00 * | 5.47 | 5.10 | 85.84 * | 88.85 | 86.78 |
| NNET | 30.74 * | 35.41 | 31.06 | 4.56 * | 4.87 | 4.63 | 80.49 * | 83.33 | 81.78 | |
| XGB | 42.56 * | 44.71 | 44.98 | 5.43 * | 5.54 | 5.51 | 80.49 * | 83.33 | 81.78 | |
| RF | 30.72 * | 33.12 | 32.77 | 4.86 | 4.94 | 4.84 * | 82.01 * | 83.07 | 82.79 | |
| Dataset | Algorithm | MSE | MAE | ||||
|---|---|---|---|---|---|---|---|
| Original | SMOGN | DRF-SMOGN | Original | SMOGN | DRF-SMOGN | ||
| a1 | SVR | 336.3 | 428.2 | 286.7 * | 21.2 | 16.7 * | 16.9 |
| NNET | 556.1 * | 581.2 | 563.9 | 30.0 * | 31.0 | 30.4 | |
| XGB | 323.6 * | 454.0 | 443.2 | 17.7 * | 19.8 | 18.9 | |
| RF | 264.2 * | 424.0 | 350.9 | 15.9 * | 17.4 | 16.0 | |
| a2 | SVR | 116.1 | 139.6 | 111.3 * | 13.0 | 10.2 * | 11.8 |
| NNET | 140.6 * | 150.1 | 140.9 | 15.4 * | 16.2 | 15.5 | |
| XGB | 137.8 * | 164.7 | 160.7 | 12.3 | 12.0 | 12.0 * | |
| RF | 108.7 * | 150.2 | 133.4 | 10.7 | 10.6 | 10.5 * | |
| a3 | SVR | 50.6 | 55.7 | 43.1 * | 9.9 | 7.5 | 7.4 * |
| NNET | 50.1 | 51.2 | 48.4 * | 9.5 | 9.4 | 9.3 * | |
| XGB | 56.4 * | 83.9 | 73.2 | 7.3 * | 7.5 | 7.5 | |
| RF | 47.8 * | 75.7 | 63.0 | 7.1 | 7.0 | 6.6 * | |
| a4 | SVR | 21.6 * | 24.5 | 22.5 | 5.2 | 4.9 | 4.6 * |
| NNET | 20.8 | 21.2 | 17.8 * | 4.6 | 4.2 | 4.1 * | |
| XGB | 32.7 * | 37.9 | 37.9 | 4.5 | 4.4 | 4.3 | |
| RF | 21.2 * | 28.0 | 23.2 | 4.4 | 4.8 | 4.2 * | |
| a5 | SVR | 51.7 | 67.8 | 50.2 * | 8.6 | 8.2 | 8.1 * |
| NNET | 62.9 * | 70.5 | 63.0 | 10.3 | 10.7 | 10.2 * | |
| XGB | 55.9 * | 82.3 | 77.0 | 8.2 * | 8.9 | 8.6 | |
| RF | 51.2 * | 82.0 | 64.0 | 7.8 | 8.0 | 7.4 * | |
| a6 | SVR | 150.6 | 152.8 | 136.6 * | 16.8 | 16.2 | 15.2 * |
| NNET | 138.2 | 143.2 | 128.4 * | 16.5 | 16.6 | 15.8 * | |
| XGB | 147.7 * | 211.0 | 189.0 | 14.4 | 14.9 | 14.4 * | |
| RF | 132.3 * | 196.2 | 151.0 | 13.2 | 12.5 | 12.4 * | |
| a7 | SVR | 28.1 | 28.9 | 26.6 * | 8.2 | 7.8 | 7.7 * |
| NNET | 26.1 * | 35.9 | 27.5 | 7.4 | 7.2 | 7.1 * | |
| XGB | 34.4 * | 50.4 | 43.7 | 6.2 * | 7.2 | 6.4 | |
| RF | 25.9 * | 40.4 | 33.1 | 6.2 | 6.1 | 5.6 * | |
| abal | SVR | 4.9 | 5.3 | 4.8 * | 2.3 | 2.2 | 2.2 * |
| NNET | 5.2 * | 6.3 | 6.2 | 2.2 | 2.0 * | 2.3 | |
| XGB | 5.5 * | 6.2 | 5.8 | 2.2 | 2.1 * | 2.2 | |
| RF | 4.8 * | 5.7 | 4.8 | 2.1 | 2.0 * | 2.1 | |
| accel | SVR | 0.9 * | 1.3 | 0.9 | 0.8 | 0.9 | 0.8 * |
| NNET | 1.3 * | 3.4 | 1.7 | 1.0 * | 1.5 | 1.1 | |
| XGB | 0.6 * | 1.1 | 0.7 | 0.5 * | 0.8 | 0.6 | |
| RF | 0.8 * | 1.3 | 0.8 | 0.7 * | 0.9 | 0.7 | |
| avail | SVR | 194.8 | 1174.7 | 186.8 * | 11.0 * | 33.6 | 11.4 |
| NNET | 334.7 * | 1449.1 | 1459.6 | 16.4 * | 31.0 | 35.2 | |
| XGB | 22.4 * | 368.2 | 32.3 | 2.0 * | 13.5 | 2.6 | |
| RF | 55.8 * | 560.1 | 57.3 | 5.6 * | 20.1 | 5.6 | |
| bank | SVR | 0.05 * | 0.83 | 0.11 | 0.12 * | 0.58 | 0.13 |
| NNET | 0.05 * | 0.83 | 0.12 | 0.12 * | 0.57 | 0.14 | |
| XGB | 0.05 * | 0.83 | 0.12 | 0.08 * | 0.54 | 0.08 * | |
| RF | 0.06 * | 0.83 | 0.12 | 0.08 | 0.52 | 0.07 * | |
| bost | SVR | 17.3 * | 18.5 | 18.2 | 3.3 * | 3.4 | 3.4 |
| NNET | 127.5 * | 184.1 | 208.2 | 10.2 * | 12.0 | 13.0 | |
| XGB | 10.5 * | 16.0 | 12.3 | 2.7 * | 3.2 | 2.8 | |
| RF | 11.1 * | 15.2 | 12.1 | 2.8 * | 3.2 | 2.9 | |
| cpu | SVR | 65.9 * | 118.8 | 84.8 | 6.6 * | 7.5 | 7.5 |
| NNET | 1227.2 | 825.9 * | 2586.5 | 27.9 * | 28.7 | 40.6 | |
| XGB | 12.5 * | 14.3 | 14.5 | 2.7 * | 2.9 | 2.9 | |
| RF | 82.0 | 83.1 | 72.8 * | 3.0 | 3.1 | 3.8 * | |
| dAil | SVR | 0.32 * | 0.45 | 0.32 * | 1.55 | 1.91 | 1.47 * |
| NNET | 0.32 * | 0.45 | 0.33 | 1.43 | 1.78 | 1.35 * | |
| XGB | 0.36 | 0.48 | 0.35 * | 1.51 | 2.01 | 1.47 * | |
| RF | 0.31 * | 0.46 | 0.32 | 1.53 | 2.01 | 1.48 * | |
| dElev | SVR | 0.37 | 0.56 | 0.36 * | 1.16 | 1.40 | 1.15 * |
| NNET | 0.37 * | 0.55 | 0.38 | 1.19 | 1.44 | 1.10 * | |
| XGB | 0.45 * | 0.51 | 0.46 | 1.16 | 1.48 | 1.14 * | |
| RF | 0.38 * | 0.50 | 0.39 | 1.15 | 1.46 | 1.14 * | |
| fuel | SVR | 0.23 * | 0.29 | 0.25 | 0.35 * | 0.40 | 0.36 |
| NNET | 0.45 * | 0.78 | 0.48 | 0.45 * | 0.62 | 0.49 | |
| XGB | 0.19 * | 0.35 | 0.24 | 0.33 * | 0.46 | 0.36 | |
| RF | 0.28 * | 0.46 | 0.31 | 0.43 * | 0.57 | 0.45 | |
| heat | SVR | 165.9 | 144.2 * | 166.5 | 12.9 | 11.1 * | 12.7 |
| NNET | 183.0 * | 421.0 | 527.2 | 12.9 * | 17.6 | 23.4 | |
| XGB | 11.5 * | 39.0 | 17.9 | 3.1 * | 5.6 | 3.8 | |
| RF | 50.5 * | 78.4 | 53.9 | 7.0 * | 8.6 | 7.2 | |
| maxt | SVR | 283.9 * | 1784.8 | 369.0 | 14.2 * | 37.2 | 16.7 |
| NNET | 3518.2 * | 4958.3 | 7282.4 | 53.6 * | 64.3 | 90.0 | |
| XGB | 31.4 * | 759.0 | 45.8 | 2.2 * | 20.2 | 2.9 | |
| RF | 45.3 * | 1204.3 | 61.7 | 4.5 * | 29.4 | 5.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
In, D.D.; Kim, H. Distance-Based Relevance Function for Imbalanced Regression. Stats 2025, 8, 53. https://doi.org/10.3390/stats8030053
In DD, Kim H. Distance-Based Relevance Function for Imbalanced Regression. Stats. 2025; 8(3):53. https://doi.org/10.3390/stats8030053
Chicago/Turabian StyleIn, Daniel Daeyoung, and Hyunjoong Kim. 2025. "Distance-Based Relevance Function for Imbalanced Regression" Stats 8, no. 3: 53. https://doi.org/10.3390/stats8030053
APA StyleIn, D. D., & Kim, H. (2025). Distance-Based Relevance Function for Imbalanced Regression. Stats, 8(3), 53. https://doi.org/10.3390/stats8030053






