Levels of Confidence and Utility for Binary Classifiers
Abstract
1. Introduction
- An identically and independently distributed () sample of size n is taken,, where is a random element on according to some distribution and is, conditioning on , a Bernoulli random variable with . To construct a binary tree classifier is to find, based on the sample, a partition of , denoted , such that in each sub-group indexed by , , or more simply , is a Bernoulli random variable, conditioning on with and . Let . is a multinomial vector of size n with its realization . The first sample of size n, , may be thought of as a pair , where is a random element on with probability distribution , and is conditionally Bernoulli with given . Let and be the frequency and the relative frequency of the sample of size n in the j th sub-group. Another element, denoted , is to be taken.
- A tree classifier is defined as follows: given , (a) if , is projected to be 1 (a success); (b) if , is projected to be 0 (a failure); or (c) if , a fair coin is tossed to determine the classification of .
- Let the binary alphabet be denoted and associated with a probability distribution and .
- Let and , and assume .
- Let the letter, corresponding to probability , be denoted , that is,. Letter is also referred to as the true letter.
2. Main Results
2.1. Entropies and Entropic Objects
2.2. Entropic Binomial Distributions
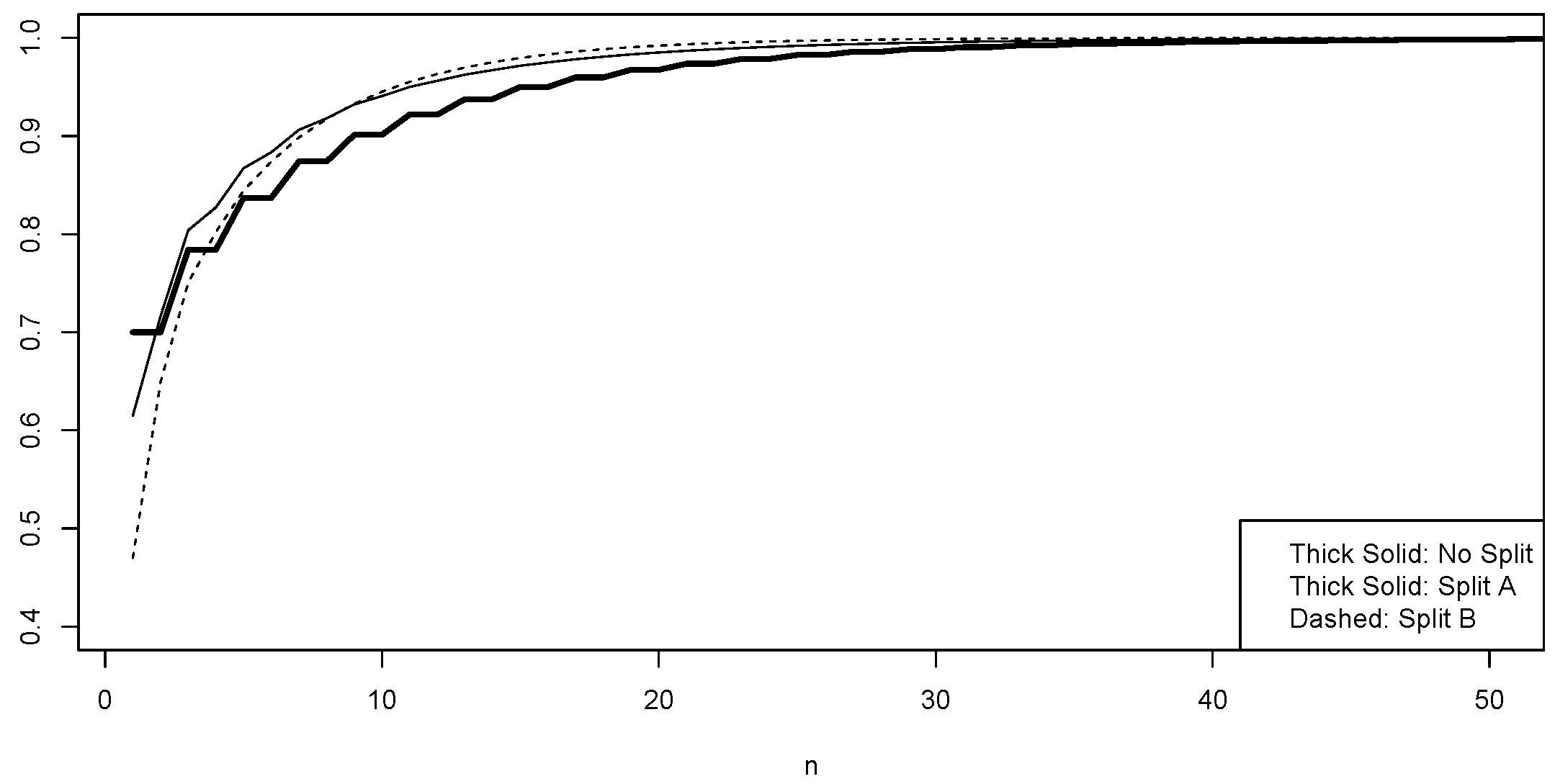
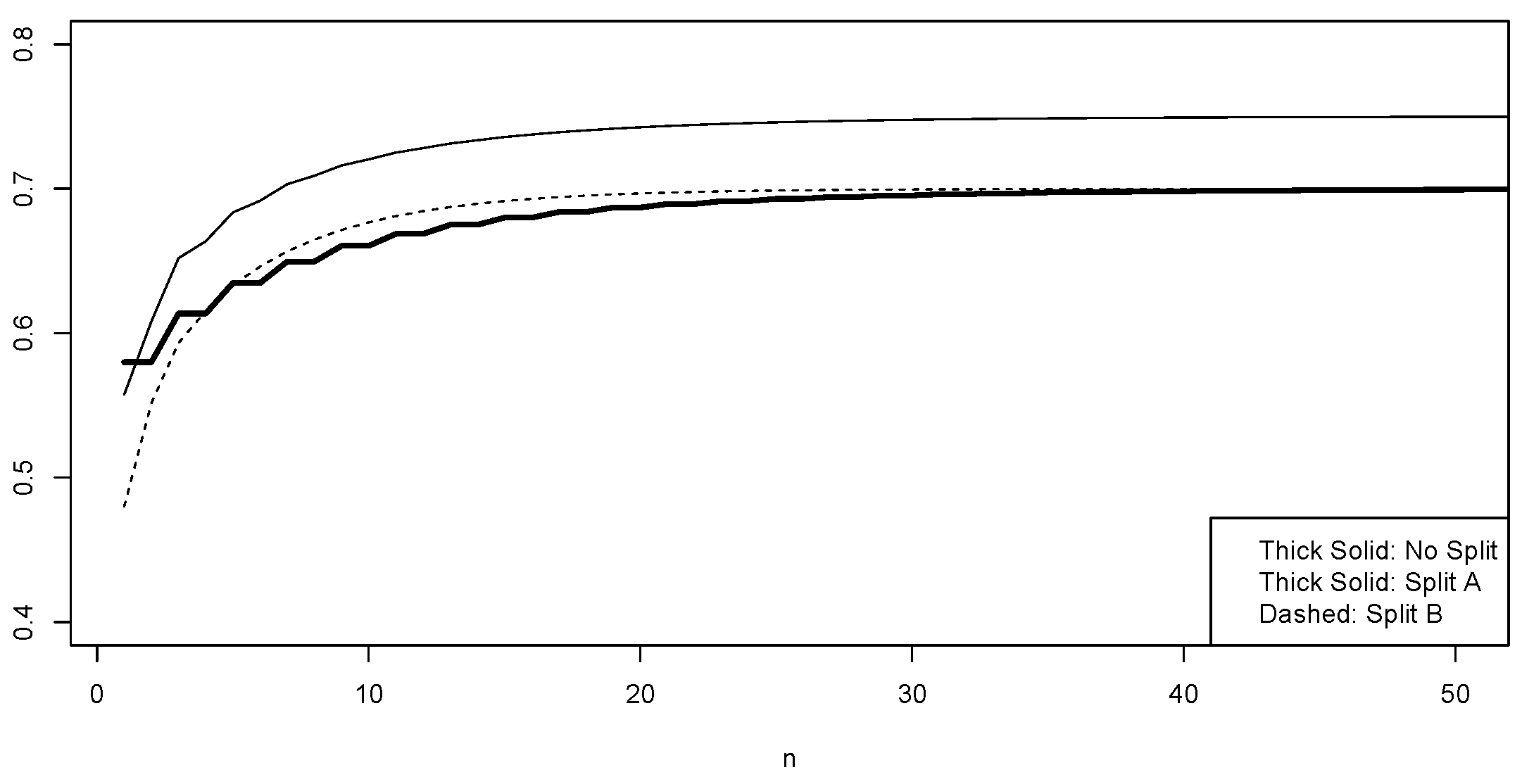
2.3. Levels of Confidence and Utility
- falls into a sub-population (or a tree node), say for some j, where the classifier correctly identifies the true letter based on the sample of size n,
- is correctly predicted based on the sample of size n,
- 1.
- Split A: , (hence );
- 2.
- Split B: , (hence );
- 3.
- No Split: and .
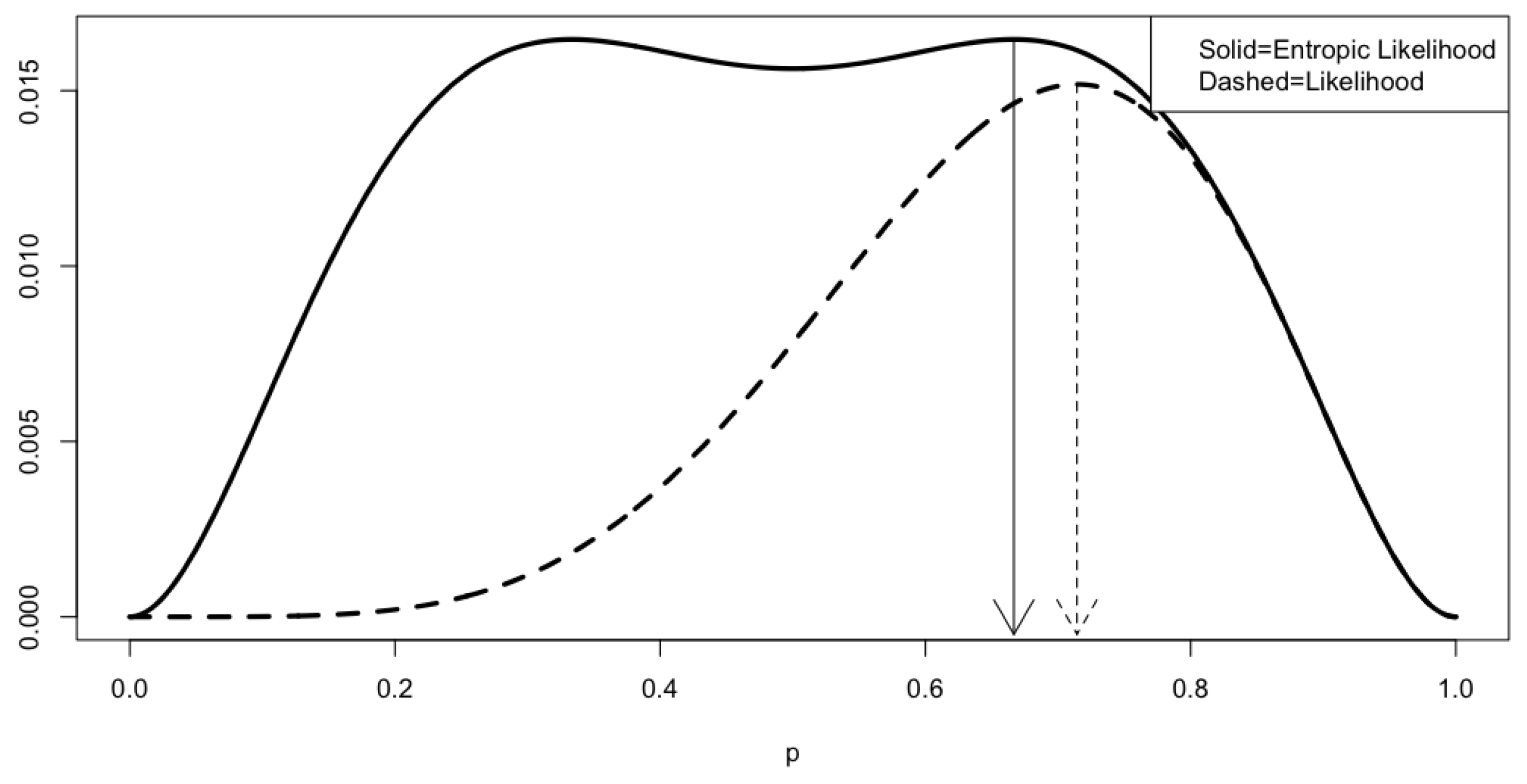
2.4. MLE and Entropic MLE
2.5. Several Numerical Studies
3. Summary
- Small sample size considerations are important because, in developing a tree classifier, the perpetual question is whether to go further into the next layer, regardless of the macro modeling logic one may use. At the end of splitting, the sample size races toward zero. No matter what macro logic is employed in construction, a tree always comes to nodes to be developed with samples of smaller sizes. One of the most important questions is whether the sample size is sufficiently large to be statistically meaningful. To answer this question, the best approach is to have a prior empirical judgment on the range for . If a range is judged as reasonable, say , where , then that may be used to determine the appropriate sample size via Formulas (5) and (6) at a given desired level, say for and another practically chosen level for , noting that has a ceiling, that is, , according to Fact 1.
- If no sufficient prior knowledge exists for , then a preliminary estimate for it is needed. The proposed estimator in (20), , is preferred to the usual , . The estimated is then used in Formulas (5) and (6) to produce estimated levels of confidence and utility, which in turn could give baseline information for further adjustments, such as pruning or further splitting. Of course, in such estimation, a reasonable sample size is needed. A recommended initial minimum sample size, according to Table 17 with a reasonable range , is if is used and if is used.
- For a given binary tree classifier with leaves or nodes, both the level of confidence and the level of utility after is estimated for each and every j, . The formulas of (10) and (11) may be used, with the of λ, , and the or the proposed estimator of and for each and every j, , to produce estimates of overall levels of confidence and utility. Noting that both (10) and (11) are λ-weighted averages, the overall level of confidence or the overall level of utility may be negatively affected if individual nodes have particularly low or for some j, . If individual nodes are found to be low in confidence or utility, some repair or adjustment may be called for.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Breiman, L. Statistical modeling: The two cultures (with discussion). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Kass, R.E. The Two Cultures: Statistics and Machine Learning in Science. Obs. Stud. 2021, 7, 135–144. [Google Scholar] [CrossRef]
- Tan, P.-N.; Seinbach, M.; Karpatne, A.; Kumar, V. Introduction to Data Mining, 2nd ed.; Pearson: London, UK, 2018. [Google Scholar]
- Zhang, Z. Entropy-Based Statistics and Their Applications. Entropy 2023, 25, 936. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Rényi, A. On measures of information and entropy. Berkeley Symp. Math. Stat. Probab. 1961, 4.1, 547–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Simpson, E.H. Measurement of diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, J. Re-parameterization of multinomial distribution and diversity indices. J. Stat. Plan. Inference 2010, 140, 1731–1738. [Google Scholar] [CrossRef]
| 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.57 | 0.65 | 0.72 | 0.78 | 0.84 | 0.90 | 0.94 | 0.97 | 0.99 | 1.00 | |
| 0.50 | 0.57 | 0.65 | 0.72 | 0.78 | 0.84 | 0.90 | 0.94 | 0.97 | 0.99 | 1.00 | |
| 0.50 | 0.59 | 0.68 | 0.76 | 0.84 | 0.90 | 0.94 | 0.97 | 0.99 | 1.00 | 1.00 | |
| 0.50 | 0.59 | 0.68 | 0.76 | 0.84 | 0.90 | 0.94 | 0.97 | 0.99 | 1.00 | 1.00 | |
| 0.50 | 0.61 | 0.71 | 0.80 | 0.87 | 0.93 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.61 | 0.71 | 0.80 | 0.87 | 0.93 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.62 | 0.73 | 0.83 | 0.90 | 0.95 | 0.98 | 0.99 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.62 | 0.73 | 0.83 | 0.90 | 0.95 | 0.98 | 0.99 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.65 | 0.79 | 0.89 | 0.95 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.67 | 0.81 | 0.91 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.69 | 0.85 | 0.94 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.71 | 0.86 | 0.95 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.72 | 0.89 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.74 | 0.90 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.75 | 0.91 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.76 | 0.92 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.78 | 0.94 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.80 | 0.95 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.81 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.83 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.84 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.92 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.50 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.50 | 0.51 | 0.52 | 0.55 | 0.58 | 0.63 | 0.68 | 0.75 | 0.82 | 0.91 | 1.00 | |
| 0.50 | 0.51 | 0.52 | 0.55 | 0.58 | 0.63 | 0.68 | 0.75 | 0.82 | 0.91 | 1.00 | |
| 0.50 | 0.51 | 0.53 | 0.57 | 0.61 | 0.67 | 0.74 | 0.81 | 0.88 | 0.94 | 1.00 | |
| 0.50 | 0.51 | 0.53 | 0.57 | 0.61 | 0.67 | 0.74 | 0.81 | 0.88 | 0.94 | 1.00 | |
| 0.50 | 0.51 | 0.54 | 0.58 | 0.63 | 0.70 | 0.77 | 0.83 | 0.89 | 0.95 | 1.00 | |
| 0.50 | 0.51 | 0.54 | 0.58 | 0.63 | 0.70 | 0.77 | 0.83 | 0.89 | 0.95 | 1.00 | |
| 0.50 | 0.51 | 0.54 | 0.59 | 0.65 | 0.71 | 0.78 | 0.84 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.51 | 0.54 | 0.59 | 0.65 | 0.71 | 0.78 | 0.84 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.51 | 0.54 | 0.60 | 0.66 | 0.73 | 0.79 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.51 | 0.54 | 0.60 | 0.66 | 0.73 | 0.79 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.52 | 0.56 | 0.62 | 0.68 | 0.74 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.52 | 0.56 | 0.62 | 0.69 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.52 | 0.56 | 0.63 | 0.69 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.52 | 0.57 | 0.64 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.52 | 0.58 | 0.64 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.52 | 0.58 | 0.64 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.53 | 0.58 | 0.64 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.53 | 0.58 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.53 | 0.59 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.53 | 0.59 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.53 | 0.59 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.53 | 0.59 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.53 | 0.59 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.54 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 | |
| 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 |
| () | (0.6, 0.6) | (0.6, 0.7) | (0.6, 0.8) | (0.6, 0.9) | (0.7, 0.7) | (0.8, 0.8) | (0.9, 0.9) |
|---|---|---|---|---|---|---|---|
| 0.5358 | 0.5752 | 0.6107 | 0.6419 | 0.6145 | 0.6855 | 0.7480 | |
| 0.6045 | 0.6577 | 0.7017 | 0.7360 | 0.7109 | 0.7989 | 0.8675 | |
| 0.6574 | 0.7252 | 0.7726 | 0.8017 | 0.7930 | 0.8879 | 0.9460 | |
| 0.6941 | 0.7691 | 0.8136 | 0.8351 | 0.8441 | 0.9331 | 0.9761 | |
| 0.7232 | 0.8015 | 0.8410 | 0.8561 | 0.8798 | 0.9588 | 0.9890 | |
| 0.7475 | 0.8268 | 0.8609 | 0.8712 | 0.9061 | 0.9742 | 0.9949 | |
| 0.8303 | 0.8999 | 0.9137 | 0.9151 | 0.9696 | 0.9971 | 0.9999 | |
| 0.9130 | 0.9546 | 0.9565 | 0.9565 | 0.9961 | 1.0000 | 1.0000 | |
| 0.9524 | 0.9759 | 0.9762 | 0.9762 | 0.9994 | 1.0000 | 1.0000 |
| () | (0.6, 0.6) | (0.6, 0.7) | (0.6, 0.8) | (0.6, 0.9) | (0.7, 0.7) | (0.8, 0.8) | (0.9, 0.9) |
|---|---|---|---|---|---|---|---|
| 0.5392 | 0.5500 | 0.5601 | 0.5694 | 0.6341 | 0.7159 | 0.7820 | |
| 0.6215 | 0.6384 | 0.6536 | 0.6670 | 0.7447 | 0.8347 | 0.8921 | |
| 0.6925 | 0.7159 | 0.7356 | 0.7515 | 0.8371 | 0.9159 | 0.9514 | |
| 0.7338 | 0.7614 | 0.7832 | 0.7993 | 0.8819 | 0.9448 | 0.9688 | |
| 0.7650 | 0.7956 | 0.8183 | 0.8337 | 0.9093 | 0.9596 | 0.9781 | |
| 0.7900 | 0.8230 | 0.8459 | 0.8602 | 0.9275 | 0.9686 | 0.8941 | |
| 0.8679 | 0.9062 | 0.9259 | 0.9339 | 0.9664 | 0.9882 | 0.9963 | |
| 0.9314 | 0.9686 | 0.9792 | 0.9811 | 0.9877 | 0.9978 | 0.9998 | |
| 0.9565 | 0.9884 | 0.9935 | 0.9939 | 0.9944 | 0.9996 | 1.0000 |
| () | (0.6, 0.6) | (0.6, 0.7) | (0.6, 0.8) | (0.6, 0.9) | (0.7, 0.7) | (0.8, 0.8) | (0.9, 0.9) |
|---|---|---|---|---|---|---|---|
| 0.5902 | 0.5917 | 0.5931 | 0.5944 | 0.7156 | 0.8140 | 0.8785 | |
| 0.6579 | 0.6611 | 0.6641 | 0.6669 | 0.8047 | 0.8906 | 0.9261 | |
| 0.7432 | 0.7487 | 0.7537 | 0.7581 | 0.8952 | 0.9466 | 0.9577 | |
| 0.7955 | 0.8024 | 0.8085 | 0.8138 | 0.9336 | 0.9633 | 0.9699 | |
| 0.8311 | 0.8391 | 0.8459 | 0.8517 | 0.9515 | 0.9702 | 0.9762 | |
| 0.8573 | 0.8660 | 0.8737 | 0.8795 | 0.9606 | 0.9740 | 0.9801 | |
| 0.9249 | 0.9365 | 0.9453 | 0.9514 | 0.9743 | 0.9833 | 0.9895 | |
| 0.9621 | 0.9764 | 0.9852 | 0.9898 | 0.9830 | 0.9917 | 0.9964 | |
| 0.9715 | 0.9868 | 0.9944 | 0.9974 | 0.9880 | 0.9956 | 0.9986 |
| () | (0.6, 0.6) | (0.6, 0.7) | (0.6, 0.8) | (0.6, 0.9) | (0.7, 0.7) | (0.8, 0.8) | (0.9, 0.9) |
|---|---|---|---|---|---|---|---|
| 0.5072 | 0.5265 | 0.5592 | 0.6028 | 0.5458 | 0.6113 | 0.6984 | |
| 0.5209 | 0.5526 | 0.6001 | 0.6574 | 0.5844 | 0.6794 | 0.7940 | |
| 0.5315 | 0.5743 | 0.6321 | 0.6942 | 0.6172 | 0.7328 | 0.8568 | |
| 0.5388 | 0.5882 | 0.6493 | 0.7099 | 0.6376 | 0.7600 | 0.8809 | |
| 0.5446 | 0.5983 | 0.6560 | 0.7179 | 0.6519 | 0.7753 | 0.8912 | |
| 0.5495 | 0.6060 | 0.6670 | 0.7227 | 0.6624 | 0.7845 | 0.8959 | |
| 0.5661 | 0.6269 | 0.6822 | 0.7330 | 0.6878 | 0.7983 | 0.9000 | |
| 0.5826 | 0.6405 | 0.6913 | 0.7413 | 0.6984 | 0.8000 | 0.9000 | |
| 0.5905 | 0.6451 | 0.6952 | 0.7452 | 0.6998 | 0.8000 | 0.9000 | |
| 0.6000 | 0.6500 | 0.7000 | 0.7500 | 0.7000 | 0.8000 | 0.9000 |
| () | (0.6, 0.6) | (0.6, 0.7) | (0.6, 0.8) | (0.6, 0.9) | (0.7, 0.7) | (0.8, 0.8) | (0.9, 0.9) |
|---|---|---|---|---|---|---|---|
| 0.5078 | 0.5037 | 0.5035 | 0.5067 | 0.5536 | 0.6296 | 0.7256 | |
| 0.5243 | 0.5311 | 0.5436 | 0.5608 | 0.5979 | 0.7008 | 0.8137 | |
| 0.5385 | 0.5522 | 0.5731 | 0.5988 | 0.6348 | 0.7495 | 0.8611 | |
| 0.5468 | 0.5636 | 0.5880 | 0.6166 | 0.6528 | 0.7669 | 0.8751 | |
| 0.5530 | 0.5721 | 0.5988 | 0.6287 | 0.6637 | 0.7757 | 0.8825 | |
| 0.5580 | 0.5790 | 0.6071 | 0.6375 | 0.6710 | 0.7811 | 0.8873 | |
| 0.5736 | 0.6000 | 0.6305 | 0.6560 | 0.6866 | 0.7929 | 0.8970 | |
| 0.5863 | 0.6162 | 0.6450 | 0.6711 | 0.6949 | 0.7987 | 0.8998 | |
| 0.5913 | 0.6216 | 0.6485 | 0.6738 | 0.6978 | 0.7997 | 0.9000 | |
| 0.6000 | 0.6250 | 0.6500 | 0.6750 | 0.7000 | 0.8000 | 0.9000 |
| () | (0.6, 0.6) | (0.6, 0.7) | (0.6, 0.8) | (0.6, 0.9) | (0.7, 0.7) | (0.8, 0.8) | (0.9, 0.9) |
|---|---|---|---|---|---|---|---|
| 0.5180 | 0.5106 | 0.5037 | 0.4973 | 0.5862 | 0.6884 | 0.8028 | |
| 0.5516 | 0.5277 | 0.5250 | 0.5233 | 0.6219 | 0.7343 | 0.8408 | |
| 0.5486 | 0.5495 | 0.5521 | 0.5564 | 0.6581 | 0.7680 | 0.8662 | |
| 0.5591 | 0.5622 | 0.5675 | 0.5747 | 0.6734 | 0.7780 | 0.8759 | |
| 0.5662 | 0.5705 | 0.5774 | 0.5861 | 0.6806 | 0.7821 | 0.8810 | |
| 0.5715 | 0.5765 | 0.5843 | 0.5940 | 0.6842 | 0.7844 | 0.8841 | |
| 0.5850 | 0.5922 | 0.6024 | 0.6140 | 0.6897 | 0.7900 | 0.8916 | |
| 0.5924 | 0.6019 | 0.6137 | 0.6258 | 0.6932 | 0.7950 | 0.8971 | |
| 0.5943 | 0.6050 | 0.6171 | 0.6287 | 0.6952 | 0.7974 | 0.8989 | |
| 0.6000 | 0.6100 | 0.6200 | 0.6300 | 0.7000 | 0.8000 | 0.9000 |
| Bias of | |||||||
|---|---|---|---|---|---|---|---|
| 0.51 | 0.51 | 0.51 | 0.51 | 0.51 | 0.51 | 0.51 | |
| 0.0307 | 0.0121 | 0.0220 | 0.1847 | 0.1242 | 0.0268 | 0.0207 | |
| 0.0192 | 0.0062 | 0.0130 | 0.1518 | 0.0915 | 0.0186 | 0.0141 | |
| 0.0142 | 0.0042 | 0.0094 | 0.1284 | 0.0711 | 0.0148 | 0.0113 | |
| 0.0112 | 0.0023 | 0.0069 | 0.1094 | 0.0502 | 0.0124 | 0.0092 | |
| 0.0093 | 0.0016 | 0.0056 | 0.0951 | 0.0375 | 0.0108 | 0.0080 | |
| 0.0080 | 0.0009 | 0.0046 | 0.0826 | 0.0257 | 0.0096 | 0.0071 | |
| 0.0069 | 0.0005 | 0.0038 | 0.0710 | 0.0146 | 0.0086 | 0.0063 | |
| 0.0061 | 0.0001 | 0.0032 | 0.0608 | 0.0049 | 0.0079 | 0.0057 |
| Outlook | Temp | Humidity | Windy | Play Golf |
|---|---|---|---|---|
| Rainy | Hot | High | False | No |
| Rainy | Hot | High | True | No |
| Overcast | Hot | High | False | Yes |
| Sunny | Mild | High | False | Yes |
| Sunny | Cool | Normal | False | Yes |
| Sunny | Cool | Normal | True | No |
| Overcast | Cool | Normal | True | Yes |
| Rainy | Mild | High | False | No |
| Rainy | Cool | Normal | False | Yes |
| Sunny | Mild | Normal | False | Yes |
| Rainy | Mild | Normal | True | Yes |
| Overcast | Mild | High | True | Yes |
| Overcast | Hot | Normal | False | Yes |
| Sunny | Mild | High | True | No |
| Outlook | Rainy | Overcast | Sunny |
|---|---|---|---|
| 5 | 4 | 5 | |
| 2 | 4 | 3 | |
| 5/14 | 4/14 | 5/14 | |
| 3/5 | 4/4 | 3/5 | |
| 0.8418 | 0.7397 | 0.8418 | |
| 0.5684 | 0.7397 | 0.5684 |
| Temp | Hot | Mild | Cool |
|---|---|---|---|
| 4 | 6 | 4 | |
| 2 | 4 | 3 | |
| 4/14 | 6/14 | 4/14 | |
| 2/4 | 4/6 | 3/4 | |
| 0.6426 | 0.9408 | 0.7268 | |
| 0.5000 | 0.6470 | 0.6134 |
| Humidity | High | Normal |
|---|---|---|
| 7 | 7 | |
| 3 | 6 | |
| 7/14 | 7/14 | |
| 4/7 | 6/7 | |
| 0.9246 | 0.9915 | |
| 0.5606 | 0.8511 |
| Windy | False | True |
|---|---|---|
| 8 | 6 | |
| 6 | 3 | |
| 8/14 | 6/14 | |
| 6/8 | 3/6 | |
| 0.9916 | 0.8547 | |
| 0.7458 | 0.5000 |
| Weather | Outlook | Temp | Humidity | Windy |
|---|---|---|---|---|
| 0.8126 | 0.7945 | 0.9581 | 0.9329 | |
| 0.6173 | 0.5954 | 0.7059 | 0.6405 | |
| 0.7143 | 0.7976 | 0.3673 | 0.4286 |
| Bias of | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | |
| 0.1021 | 0.0468 | 0.0158 | 0.0037 | 0.0468 | −0.0014 | −0.0141 | −0.0077 | 0.0781 | 0.0284 | 0.0048 | −0.0001 | |
| 0.0743 | 0.0278 | 0.0076 | 0.0025 | −0.0016 | −0.0370 | −0.0364 | −0.0136 | 0.0490 | 0.0063 | −0.0070 | −0.0028 | |
| 0.0740 | 0.0282 | 0.0073 | 0.0020 | 0.0231 | −0.0111 | −0.0160 | −0.0055 | 0.0544 | 0.0137 | −0.0008 | −0.0004 | |
| 0.0578 | 0.0183 | 0.0048 | 0.0013 | 0.0056 | −0.0212 | −0.0165 | −0.0036 | 0.0385 | 0.0038 | −0.0029 | −0.0004 | |
| 0.0578 | 0.0184 | 0.0040 | 0.0008 | −0.0202 | −0.0434 | −0.0301 | −0.0070 | 0.0292 | −0.0036 | −0.0078 | −0.0018 | |
| 0.0471 | 0.0125 | 0.0024 | 0.0008 | 0.0058 | −0.0161 | −0.0101 | −0.0013 | 0.0310 | 0.0016 | −0.0022 | 0.0000 | |
| 0.0212 | 0.0031 | 0.0010 | 0.0007 | −0.0138 | −0.0140 | −0.0019 | 0.0006 | 0.0067 | −0.0039 | −0.0002 | 0.0006 | |
| 0.0122 | 0.0015 | 0.0007 | 0.0005 | −0.0098 | −0.0052 | 0.0002 | 0.0027 | −0.0013 | 0.0005 | 0.0005 | 0.0005 | |
| 0.0078 | 0.0009 | 0.0008 | 0.0005 | −0.0125 | −0.0031 | 0.0007 | 0.0005 | −0.0011 | −0.0008 | 0.0007 | 0.0005 | |
| 0.0052 | 0.0007 | 0.0006 | 0.0004 | −0.0093 | −0.0009 | 0.0006 | 0.0004 | −0.0012 | 0.0000 | 0.0006 | 0.0004 | |
| MSE of | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | |
| 0.0250 | 0.0237 | 0.0232 | 0.0162 | 0.0320 | 0.0360 | 0.0358 | 0.0223 | 0.0282 | 0.0277 | 0.0276 | 0.0183 | |
| 0.0274 | 0.0237 | 0.0224 | 0.0144 | 0.0274 | 0.0386 | 0.0413 | 0.0244 | 0.0230 | 0.0263 | 0.0271 | 0.0171 | |
| 0.0193 | 0.0192 | 0.0189 | 0.0122 | 0.0209 | 0.0270 | 0.0271 | 0.0159 | 0.0197 | 0.0219 | 0.0217 | 0.0133 | |
| 0.0183 | 0.0191 | 0.0180 | 0.0109 | 0.0215 | 0.0292 | 0.0273 | 0.0138 | 0.0181 | 0.0218 | 0.0209 | 0.0118 | |
| 0.0150 | 0.1063 | 0.0157 | 0.0097 | 0.0200 | 0.0321 | 0.0146 | 0.0308 | 0.0147 | 0.0202 | 0.0198 | 0.0111 | |
| 0.0147 | 0.0161 | 0.0147 | 0.0088 | 0.0175 | 0.0233 | 0.0199 | 0.0100 | 0.0150 | 0.0184 | 0.0165 | 0.0093 | |
| 0.0076 | 0.0093 | 0.0078 | 0.0044 | 0.0114 | 0.0143 | 0.0092 | 0.0044 | 0.0086 | 0.0111 | 0.0083 | 0.0044 | |
| 0.0056 | 0.0067 | 0.0052 | 0.0029 | 0.0086 | 0.0054 | 0.0053 | 0.0029 | 0.0064 | 0.0074 | 0.0029 | 0.0029 | |
| 0.0045 | 0.0051 | 0.0039 | 0.0022 | 0.0071 | 0.0064 | 0.0040 | 0.0022 | 0.0054 | 0.0056 | 0.0040 | 0.0022 | |
| 0.0038 | 0.0041 | 0.0031 | 0.0018 | 0.0057 | 0.0046 | 0.0032 | 0.0018 | 0.0045 | 0.0043 | 0.0031 | 0.0018 | |
| Bias of | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | |
| −0.0004 | −0.0610 | −0.0213 | −0.0014 | −0.1192 | −0.1183 | −0.0311 | −0.0016 | −0.0479 | −0.0834 | −0.0251 | −0.0015 | |
| −0.0318 | −0.0460 | −0.0067 | −0.0001 | −0.1149 | −0.0712 | −0.0082 | −0.0001 | −0.0685 | −0.0562 | −0.0073 | −0.0001 | |
| −0.0479 | −0.0309 | −0.0020 | −0.0000 | −0.1423 | −0.0489 | −0.0023 | −0.0000 | −0.0872 | −0.0382 | −0.0022 | −0.0000 | |
| −0.0561 | −0.0199 | −0.0006 | 0.0000 | −0.1301 | −0.0279 | −0.0007 | 0.0000 | −0.0877 | −0.0232 | −0.0007 | 0.0000 | |
| −0.0594 | −0.0125 | −0.0002 | −0.0000 | −0.1258 | −0.0169 | −0.0002 | −0.0000 | −0.0878 | −0.0143 | −0.0002 | −0.0000 | |
| −0.0599 | −0.0079 | −0.0000 | −0.0000 | −0.1245 | −0.0104 | −0.0000 | −0.0000 | −0.0875 | −0.0089 | −0.0000 | −0.0000 | |
| -0.0595 | −0.0049 | −0.0000 | -0.0000 | −0.1116 | −0.0060 | −0.0000 | −0.0000 | −0.0820 | −0.0054 | −0.0000 | −0.0000 | |
| −0.0570 | −0.0031 | -0.0000 | −0.0000 | −0.1023 | −0.0036 | −0.0000 | −0.0000 | −0.0766 | −0.0033 | −0.0000 | −0.0000 | |
| −0.0531 | −0.0020 | -0.0000 | −0.0000 | -0.0993 | −0.0025 | −0.0000 | −0.0000 | −0.0729 | −0.0022 | −0.0000 | −0.0000 | |
| −0.0222 | −0.0000 | −0.0000 | 0.0000 | −0.0337 | −0.0000 | −0.0000 | 0.0000 | −0.0272 | −0.0000 | −0.0000 | 0.0000 | |
| −0.0074 | −0.0000 | −0.0000 | 0.0000 | −0.0096 | −0.0000 | −0.0000 | 0.0000 | −0.0084 | −0.0000 | −0.0000 | 0.0000 | |
| Bias of | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | |
| 0.0408 | 0.0024 | −0.0043 | 0.0000 | 0.0252 | −0.0065 | −0.0062 | 0.0000 | 0.0302 | −0.0033 | −0.0054 | 0.0000 | |
| 0.0250 | −0.0030 | −0.0011 | 0.0006 | 0.0129 | −0.0077 | −0.0015 | 0.0006 | 0.0180 | −0.0055 | −0.0013 | 0.0006 | |
| 0.0158 | −0.0033 | 0.0002 | 0.0005 | 0.0055 | −0.0058 | 0.0001 | 0.0005 | 0.0090 | −0.0048 | 0.0002 | 0.0005 | |
| 0.0098 | −0.0024 | 0.0004 | 0.0005 | 0.0017 | −0.0036 | 0.0004 | 0.0004 | 0.0048 | −0.0030 | 0.0004 | 0.0005 | |
| 0.0060 | −0.0014 | 0.0006 | 0.0004 | −0.0014 | −0.0021 | 0.0006 | 0.0004 | 0.0016 | −0.0018 | 0.0006 | 0.0004 | |
| 0.0033 | −0.0008 | 0.0005 | 0.0005 | −0.0028 | −0.0012 | 0.0005 | 0.0005 | −0.0006 | −0.0010 | 0.0005 | 0.0005 | |
| 0.0013 | −0.0004 | 0.0005 | 0.0004 | −0.0038 | −0.0006 | 0.0005 | 0.0004 | −0.0038 | −0.0005 | 0.0005 | 0.0004 | |
| −0.0001 | −0.0000 | 0.0005 | 0.0004 | −0.0046 | −0.0001 | 0.0005 | 0.0004 | −0.0028 | −0.0001 | 0.0005 | 0.0004 | |
| −0.0007 | −0.0002 | 0.0004 | 0.0004 | −0.0046 | −0.0003 | 0.0004 | 0.0004 | −0.0032 | −0.0003 | 0.0004 | 0.0004 | |
| −0.0021 | −0.0002 | 0.0002 | 0.0002 | −0.0030 | −0.0002 | 0.0002 | 0.0002 | −0.0027 | −0.0002 | 0.0002 | 0.0002 | |
| −0.0010 | −0.0003 | 0.0002 | 0.0002 | −0.0011 | −0.0003 | 0.0002 | 0.0002 | −0.0011 | −0.0003 | 0.0002 | 0.0002 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z. Levels of Confidence and Utility for Binary Classifiers. Stats 2024, 7, 1209-1225. https://doi.org/10.3390/stats7040071
Zhang Z. Levels of Confidence and Utility for Binary Classifiers. Stats. 2024; 7(4):1209-1225. https://doi.org/10.3390/stats7040071
Chicago/Turabian StyleZhang, Zhiyi. 2024. "Levels of Confidence and Utility for Binary Classifiers" Stats 7, no. 4: 1209-1225. https://doi.org/10.3390/stats7040071
APA StyleZhang, Z. (2024). Levels of Confidence and Utility for Binary Classifiers. Stats, 7(4), 1209-1225. https://doi.org/10.3390/stats7040071






