Abstract
We adapt the classical mixed Poisson process models for investigation of consumer behaviour in a situation where after a random time we can no longer identify a customer despite the customer remaining in the panel and continuing to perform buying actions. We derive explicit expressions for the distribution of the number of purchases by a random customer observed at a random subinterval for a given interval. For the estimation of parameters in the gamma–Poisson scheme, we use the estimator minimizing the Hellinger distance between the sampling and model distributions, and demonstrate that this method is almost as efficient as the maximum likelihood being much simpler. The results can be used for modelling internet user behaviour where cookies and other user identifiers naturally expire after a random time.
1. Introduction
In the classical mixed Poisson process (MPP) model for consumer behaviour [1,2], a population of distinct individuals is considered, where each individual generates purchase events through a Poisson process, characterized by a unique arrival rate reflecting the purchasing frequency of this individual. The frequencies of the individual Poisson processes are random and follow a certain mixture distribution. If this mixture distribution is the gamma distribution, then the resulting distribution for the number of events in a given time period is the negative binomial distribution (NBD) and the model is often called the NBD process model [3]. This NBD process model is the main MPP model for consumer behaviour, which is actively promoted by the Ehrenberg–Bass Institute for Marketing Science. In the present paper, we concentrate exclusively on an adaptation of this MPP model.
Digital marketing has emerged over the last two decades with the adoption of the internet and has offered new ways for brands to work with their customers [4]. Today, websites are able to capture the buying habits of their clients in a great amount of detail. Though the quantity of data has increased, the quality of the analysis has been limited by the mechanisms of tracking users [5,6]. Up until recently, third party cookies, a piece of text stored on user’s device, was one of key ways of identifying users online. During the last ten years, this method has become less and less reliable, as internet browsers started to delete cookies automatically as well as the ability for end users to opt out. As a result, the lifespan of cookies reduced to a couple of weeks and marketers are not able to distinguish between new customers and repeat customers. This problem of the market analysis has significant consequences for businesses. Many decisions in marketing are made based on calculating the customer lifetime value, which is the value of customers, which incorporates profits from all purchases they made [7,8]. Deleting cookies means that brands are only able to attribute a small amount of purchases to repeat buyers, thus undervaluing repeat buyers and overvaluing new buyers. In turn, the efficiency of new customer acquisition is overinflated and attracts more investment into marketing activities that are less efficient than stated.
The MPP model is known to be a good tool for describing repeat purchases and has widely been applied in so-called offline studies, where information was collected directly from customers. When applying the MPP model to online customers, we noticed that the predictive power of such a model deteriorated due to the reliance on cookies. Thus, we approach this issue by incorporating information about the cookie decay process into the repeat purchase behaviour model. In particular, it is clear that the use of the NBD for estimation of the parameters of the mixture distribution in the framework of the classical MPP model is poor in the case where dropout occurs. As shown in [9], dropout is observable in real-life user data. To resolve the estimation problem for the MPP model with dropout, we derive the novel distributions for the number of events (purchases, clicks, and visits) generated by users.
The present paper is organized as follows. In Section 2, we state the main problem, which is derivation of the distribution for the number of events that random consumers create in a given time interval when they make dropout. The fundamental theoretical result is the explicit expressions of the pmf, where dropout is assumed to have a constant density, a linear density, or an exponential density.
In Section 3, we describe several estimators and perform a large numerical study in which we argue that one of the most reliable methods of parameter estimation is the method based on the minimization of the Hellinger distance between the observed frequencies and the probability mass function (pmf), using the truncated NBD as an example.
In Section 3.4, we demonstrate that this method is significantly more accurate than the method based on the minimizing the total variation between the empirical and theoretical distributions and almost as efficient as the maximum likelihood method being much simpler (in terms of the geometrical interpretation) than the latter.
In Section 3.5, we apply the Hellinger distance and the explicit form of the pmf from Section 2 to estimate the mixture parameters of the MPP model with dropout. We demonstrate that the estimators are unbiased and have an admissible standard deviation, which is comparable to the case of the truncated NBD. Conclusions are given in Section 4.
2. Main Results
Suppose that we observe a consumer with a purchase rate at an interval . Assume that this consumer is observable from time 0 and further makes a dropout at time , where is a random variable with density . Then, the number of purchases for this consumer is a value of the Poisson process with rate at time .
Let be the number of purchases for a random consumer for the time interval . We note that has the marginal distribution of the MPP at time . Using the rule of conditional probability on a certain time of dropout, the pmf of can be written as
where and is the pmf of the MPP at time t, which is the pmf of the NBD with shape parameter k and the mean parameter . If T is large enough, such that , then the number of purchases for a random consumer has approximately the distribution with pmf
2.1. The Piecewise-Constant Density for Dropout
Assume that the time to dropout has a uniform distribution on the interval . For the time interval with , the number of purchases for a random consumer has the distribution with pmf
Using Maple [10] we derive
where is the hypergeometric function. Note that the mean of this distribution is
Assume that the time to dropout has the piecewise-constant distribution with density . For the time interval with , the number of purchases for a random consumer has the distribution with pmf
In Figure 1, we depict the theoretical pmf for various and mixture parameters. We can see that the pmf is moving right as becomes larger and shows the mean . The R code with the computation of the pmf is given in Appendix A.
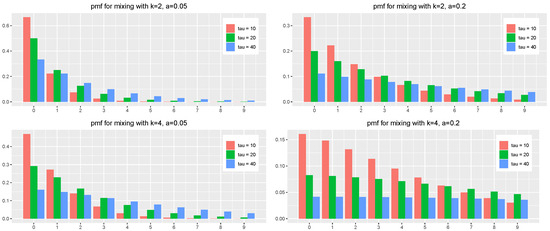
Figure 1.
The theoretical pmf of the number of purchases of a random consumer for the constant density of dropout with various and various mixture parameters k and a.
2.2. The Linear Density for Dropout
Assume that the time to dropout has a distribution with a linear density at an interval . For the time interval with , the number of purchases for a random consumer has the distribution with pmf
Using Maple [10] we obtain
where is the hypergeometric function. Note that the mean of this distribution is
In Figure 2, we depict the theoretical pmf for various and mixture parameters.
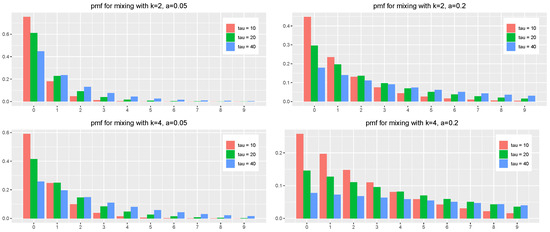
Figure 2.
The theoretical pmf of the number of purchases of a random consumer for the linear density of dropout with various and various mixture parameters k and a.
2.3. The Exponential Density for Dropout
Assume that the time to dropout has the exponential distribution with mean As argued in [9], this model for the time-life for the user identifiability, when used for modelling internet user behaviour, is the most natural when one restricts it to a particular type of browser.
For the time interval , the number of purchases for a random consumer has the distribution with pmf
where . If is very small, then , where
Using Maple [10] we obtain
where is the incomplete Gamma function.
Let the random variable X be the number of purchases for a random consumer on the interval . Then, the mean of X is
where is a random variable following the NBD with mean . Consequently, we obtain
Similarly, we derive
Therefore, we obtain
In Figure 3, we depict the theoretical pmf for various and mixture parameters.
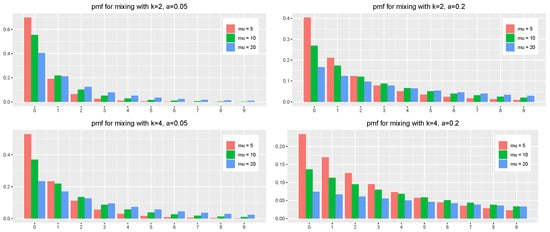
Figure 3.
The theoretical pmf of the number of purchases of a random consumer for the exponential density of dropout with various and various mixture parameters k and a.
3. Estimation
In the present section, we describe three estimators and perform a simulation study on the estimation of the mixture parameters of the MPP model. Specifically, we present the maximum likelihood estimator in Section 3.1, the minimum Hellinger distance estimator in Section 3.2, and the minimum total variance distance estimator in Section 3.3. We compare the accuracy of estimators for the case of the classical MPP model in Section 3.4 and apply the minimum Hellinger distance estimator for the case of the MPP model with dropout in Section 3.5.
3.1. The ML Estimator
Let be a sample from a distribution with parameter and pmf . The log-likelihood of the parameters for the sample is given by
We note that the expression of the log-likelihood is quite complex for distributions like , and their truncated versions. Even if a sample is taken from the NBD with parameters k and m, the log-likelihood of the parameters can be written as
The ML estimator for the parameter m is given by the sample mean
however, there is no explicit expression for the ML estimator of the parameter k, which should be numerically obtained as a solution of the equation
where is the observed frequency of within the sample. However, if a sample is taken from a truncated NBD, the ML estimator of both parameters should be computed numerically by maximizing the log-likelihood as a function of two variables.
The ML estimator for the parameter k in the negative binomial distribution is powerful, but it relies on access to the frequencies of how often each number of purchases occurs. In market research, obtaining this raw data can be challenging due to collection difficulties or data ownership restrictions. Usually, market research companies often have easier access to summary statistics associated with consumer purchases. This is where moment-based estimators become a valuable alternative. They can leverage these readily available statistics, making them a practical choice for estimating NBD parameters in such scenarios; see, for example, refs. [11,12,13].
The negative binomial distribution models the number of successes (e.g., consumer purchases) occurring in a sequence of independent trials before a fixed number of failures (e.g., stopping after a certain time). However, in practical applications, we might encounter situations where the data only reflects non-negative counts. This can happen if the observation process starts at a specific point, excluding observations with zero or fewer successes (left truncation) and/or the data collection terminates after a fixed number of successes, censoring observations with higher counts (right truncation).
3.2. The MHD Estimator
The Hellinger distance, denoted by , is a measure of similarity between two probability distributions, P and Q, defined on the same discrete space. It is given by
where and represent the probabilities of outcome x under distributions P and Q, respectively, and denotes the set of all possible outcomes. The Hellinger distance has the following properties: (i) non-negativity: for all probability distributions P and Q, (ii) symmetry: , (iii) triangle inequality: for any three probability distributions P, Q, and R.
The Hellinger distance is related to the Kullback–Leibler (KL) divergence, another measure of distributional discrepancy, through the inequality
Minimum Hellinger distance (MHD) estimators, introduced by [14], belong to a broader class of efficient estimators with desirable second-order properties, as shown in [15]. MHD estimators are particularly attractive due to their robustness. They demonstrate resilience to outliers and model misspecification [14,16]. In fact, Ref. [16] demonstrated a stronger result, showing that all minimum distance estimators are inherently robust to variations in the estimated quantity. This combination of efficiency and robustness makes MHD estimators a practical choice. Additionally, the appeal of the Hellinger distance lies in its unitless nature. For a comparison of MHD estimators with maximum likelihood estimators (MLEs) and a discussion on the trade-off between robustness and efficiency, refer to [15].
3.3. The MTVD Estimator
The total variation distance, denoted by , is a measure of similarity between two probability distributions, P and Q. For general distributions, it represents the maximum absolute difference between the cumulative distribution functions (CDFs) of P and Q. The total variation distance for discrete distributions is given by
where and represent the probabilities of outcome x under distributions P and Q, respectively, and denotes the set of all possible outcomes.
The total variation distance has the following properties: (i) non-negativity: for all probability distributions P and Q, (ii) symmetry: , (iii) metric property: the total variation distance satisfies the metric axioms, making it a formal measure of distance between probability distributions.
Note that for any two real numbers a and b, we have that . Therefore, there is a link between the total variation distance and the Hellinger distance
While Kullback–Leibler (KL) divergence is a stronger measure of the distributional difference than the Hellinger distance; the Hellinger distance offers advantages in statistical inference. Convergence in KL divergence implies convergence in the Hellinger distance, which further implies convergence in the total variation distance. However, unlike KL divergence, the Hellinger distance remains bounded (between 0 and 1), even for distributions with different supports, and shares a closer connection to the total variation distance, which is crucial for statistical inference, as KL divergence lacks a useful lower bound for it. These properties position the Hellinger distance as a valuable middle ground between KL divergence and the total variation distance. It captures meaningful relationships for inference while avoiding the limitations of unboundedness seen in KL divergence, especially for distributions defined on the real line.
3.4. Comparison of the Estimators
Let us consider samples of size 10,000 from the TNBD distribution, which is obtained from the NBD by left truncation at a value z.
Let us compare the MHD estimator and the MLE of the NBD parameters using data from the TNBD. We show scatterplots of MHD and MLE estimators for samples from the TNBD with and in Figure 4, with and in Figure 5 and the TNBD with and in Figure 6. We can see that the MHD estimator is very close to the MLE estimator and all estimators are almost unbiased. This behaviour of estimators was observed for other values of parameters, but we will not report more figures here for the sake of brevity. The computational costs for three estimators are similar to each other and take seconds. We note that the Hellinger distance and the total variance distance provide the intuitive values on a quality of the estimators for the pmf fitting to a given sample.
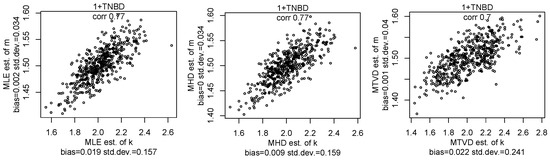
Figure 4.
The scatterplots of the MLE, MHD, and MTVD estimators of parameters k and m for samples with a size of 10,000 from the TNBD with and .
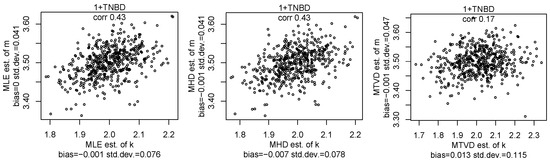
Figure 5.
The scatterplots of the MLE, MHD, and MTVD estimators of parameters k and m for samples with a size of 10,000 from the TNBD with and .
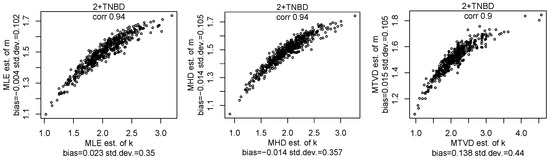
Figure 6.
The scatterplots of the MLE, MHD, and MTVD estimators of parameters k and m for samples of a size of 10,000 from the TNBD with and .
3.5. Estimation of Mixture Parameters for MPP with Dropout
Let us simulate the MPP model with the specified density of dropout on the time interval . Specifically, we consider 10,000 consumers and simulate purchases rates from the gamma density with parameters k and a. Note that is the average number of purchases per a random consumer without dropout on any time interval with a length of 1. Then, we simulate purchases times from the Poisson process with parameter for the l-th consumer. Then, we independently simulate dropout times for all consumers. Finally, we record the number of purchases made by each consumer who had at least one purchase. Therefore, the recorded sample of observations has the truncated distribution of (1), and the MHD estimator with the explicit form of the pmf (1) can be used for efficient estimation of mixture parameters. The R code with simulation of the MPP model with the exponential density of the cookie lifetime is given in Appendix A.
In Figure 7, Figure 8 and Figure 9, we show the MHD estimators of mixture parameters for various densities of dropout. We can see the mixture parameters can be well estimated in all cases where the classical NBD process is not observed. Indeed, the shape of the pmf for the number of purchases with dropout is similar to the pmf of the TNBD. We can see that the values of the bias of estimators for the case with dropout are very close to zero and similar to values of the bias of the estimators for the TNBD. We also observe that the values of the standard deviation of estimators for the case with dropout are comparable with the values of the standard deviation of estimators for TNBD.
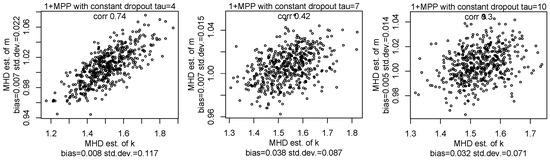
Figure 7.
The scatterplots of the MHD estimators of parameters k and m for samples with a size of 10,000 from the MPP with a constant dropout , , and for various .
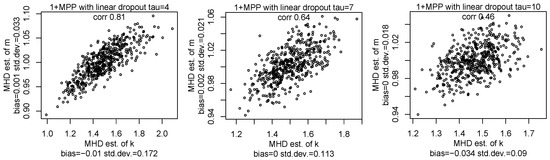
Figure 8.
The scatterplots of the MHD estimators of parameters k and m for samples with a size of 10,000 from the MPP with linear dropout , , and for various .
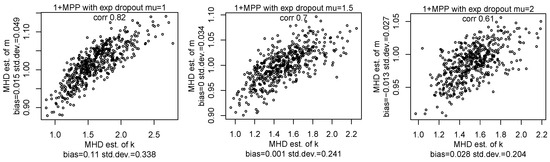
Figure 9.
The scatterplots of the MHD estimators of parameters k and m for samples with a size of 10,000 from the MPP with exponential dropout , , and for various .
4. Conclusions
In this paper, we adapted the classical mixed Poisson process model for modelling consumer buying behaviour to the situation where a customer loses identifiability after a random time, despite this customer continuing to perform buying actions. The results can be used for modelling internet user behaviour where cookies and other user identifiers naturally expire after a random time. One particular area of applications where modelling internet user behaviour may be of significant interest is the area of internet advertisement where assessing the propensity of a user for making purchase occasions is of the paramount importance, see [6].
Author Contributions
Conceptualization, A.P. and Y.S.; methodology, A.P.; software, A.P. and I.S.; validation, I.S.; writing—original draft preparation, A.P. and I.S.; writing—review and editing, I.S. and Y.S.; visualization, A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Simulated data were created and analyzed in this study. The program of simulation is contained within the article. Data sharing is not applicable to this article.
Conflicts of Interest
Authors Irina Scherbakova and Yuri Staroselskiy were employed by the company Crimtan. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MPP | mixed Poisson process |
| NBD | negative binomial distribution |
| MLE | maximum likelihood estimator |
| MHD | minimum Hellinger distance |
| MTVD | minimum total variance distance |
| pmf | probability mass function |
Appendix A
The R code with computing the pmf for the constant density of dropout is given below.
- getTruePdfCon = function (x, k, a, tau)
- {
- taua = tau ∗ a
- den = factorial (x) ∗ taua^ (k − 1) ∗ gamma (k)
- f = gamma (k + x)/den
- dd = (k − 1) ∗ taua
- res = (1 − Gauss2F1 (k − 1, x + k, k, −1/taua) ∗ f)/dd
- res[is.na (res)] = 0
- names (res) = x
- return (res)
- }
- x = c (0:9)
- qx = getTruePdfCon (x, k = 2, a = 0.1, tau = 10)
- plot (x, qx)
The R code with computing the pmf for the linear density of dropout is given below.
- Gauss2F1 <− function (a, b, c, x) {
- if (x> = −1 & x < 1) {
- hyperg_2F1 (a, b, c, x)
- } else {
- hyperg_2F1 (a, c − b, c, 1 − 1/ (1 − x))/ (1 − x)^a
- }
- }
- getTruePdfLin = function (x, k, a, tau) {
- taua = tau ∗ a
- den = factorial (x) ∗ taua^ (k) ∗ gamma (k)
- f = 2 ∗ gamma (k + x)/den
- dd = (k − 1) ∗ (k − 2) ∗ taua^2
- res = Gauss2F1 (k − 2, x + k, k − 1, −1/taua) ∗ f/ (k − 2) −
- Gauss2F1 (k − 1, x + k, k, −1/taua) ∗ f/ (k − 1) +
- 2 ∗ (taua ∗ (k − 2) − x − 1)/dd
- res[is.na (res)] = 0
- names (res) = x
- return (res)
- }
- x = c (0:9)
- qx = getTruePdfLin (x, k = 2, a = 0.1, tau = 10)
- plot (x, qx)
The R code with computing the pmf for the exponential density of dropout and small is given below.
- getTruePdfExp = function (x, k, a, mu) {
- mua = mu ∗ a
- res = rep (0,length (x))
- for (j in c (1:length (x))) {
- xj = x[j]
- den = factorial (xj) ∗ mua^ (k + xj) ∗ gamma (k)
- rx = 0:xj
- ss = gamma_inc (−k − xj + rx + 1,1/mua) ∗
- choose (xj,rx) ∗ mua^rx ∗ (−1)^ (xj − rx)
- res[j] = exp (1/mua) ∗ gamma (k+xj) ∗ sum (ss)/den
- }
- names (res) = x
- return (res)
- }
- x = c (0:9)
- qx = getTruePdfExp (x, k = 2, a = 0.1, mu = 5)
- plot (x, qx)
The R code with simulation of the MPP model with the exponential density of the cookie lifetime is given below.
- library (JuliaCall)
- julia <- julia_setup (JULIA_HOME=”C:/Programs/Julia-1.10.0/bin/”)
- julia_library (“Random”)
- julia_library (“Distributions”)
- #########################################
- # Generating MPP model with exponential-lifetime cookies
- #########################################
- # input:
- # N: number of customers
- # T: the duration of the time interval
- # k,a: parameters of the mixture distribution
- # mu: parameter of the exponential density of cookie lifetime
- # output:
- # first column: the id of a customer
- # second column: the time of a event
- # third column: the cookie id of a customer
- julia_command (“
- function get_MPP_data (N, T, k, a, mu)
- N = Int (N)
- id = zeros (0)
- event_time = zeros (0)
- cookie_id = zeros (0)
- for i in 1:N
- lam = 1 / rand (Gamma (k, a),1)[1]
- incr = rand (Exponential (lam),1)[1]
- t = zeros (0)
- nt = 0
- if (incr<T)
- append! (t, incr)
- nt = 1
- incr = rand (Exponential (lam),1)[1]
- while (t[nt]+incr<T)
- append! (t, t[nt]+incr)
- nt = nt + 1
- incr = rand (Exponential (lam),1)[1]
- end
- cid = zeros (nt)
- wt = rand (Exponential (mu),1)[1]
- currid = 1
- for j in 1:nt
- while t[j]>wt
- wt = wt+rand (Exponential (mu),1)[1]
- currid = currid+1
- end
- cid[j] = currid
- end
- append! (id, repeat ([i], nt))
- append! (event_time, t)
- append! (cookie_id, cid)
- end
- end
- Output=hcat (id, event_time, cookie_id)
- Output
- end”)
- N = 5000; T = 17; p = 0.95; k = 2; mu = 5; a = (1 − p)/p
- data = julia_call (“get_MPP_data”, N, T, k, a, mu)
References
- Ehrenberg, A. Repeat-Buying: Facts, Theory and Applications; Charles Griffin & Company Ltd.: London, UK; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Goodhardt, G.; Ehrenberg, A.; Chatfield, C. The Dirichlet: A comprehensive model of buying behaviour. J. R. Stat. Soc. Ser. A 1984, 147, 621–655. [Google Scholar] [CrossRef]
- Zhou, M.; Carin, L. Negative binomial process count and mixture modeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 37, 307–320. [Google Scholar] [CrossRef] [PubMed]
- Kannan, P. Digital marketing: A framework, review and research agenda. Int. J. Res. Mark. 2017, 34, 22–45. [Google Scholar] [CrossRef]
- Kagan, S.; Bekkerman, R. Predicting purchase behavior of website audiences. Int. J. Electron. Commer. 2018, 22, 510–539. [Google Scholar] [CrossRef]
- Pepelyshev, A.; Staroselskiy, Y.; Zhigljavsky, A. Adaptive targeting for online advertisement. In Proceedings of the Machine Learning, Optimization, and Big Data, Sicily, Italy, 21–23 July 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 240–251. [Google Scholar]
- Gupta, S.; Hanssens, D.; Hardie, B.; Kahn, W.; Kumar, V.; Lin, N.; Ravishanker, N.; Sriram, S. Modeling customer lifetime value. J. Serv. Res. 2006, 9, 139–155. [Google Scholar] [CrossRef]
- Kumar, V.; Rajan, B. Customer lifetime value: What, how, and why. In The Routledge Companion to Strategic Marketing; Routledge: London, UK, 2020; pp. 422–448. [Google Scholar]
- Scherbakova, I.; Pepelyshev, A.; Staroselskiy, Y.; Zhigljavsky, A.; Guchenko, R. Statistical Modelling for Improving Efficiency of Online Advertising. arXiv 2022, arXiv:2211.01017. [Google Scholar]
- Monagan, M.B.; Geddes, K.O.; Heal, K.M.; Labahn, G.; Vorkoetter, S.M.; Devitt, J.; Hansen, M.; Redfern, D.; Rickard, K. Maple V Programming Guide: For Release 5; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Anscombe, F.J. Sampling theory of the negative binomial and logarithmic series distributions. Biometrika 1950, 37, 358–382. [Google Scholar] [CrossRef] [PubMed]
- Savani, V.; Zhigljavsky, A. Efficient Estimation of Parameters of the Negative Binomial Distribution. Commun. Stat. Theory Methods 2006, 35, 767–783. [Google Scholar] [CrossRef]
- Savani, V.; Zhigljavsky, A. Efficient parameter estimation for independent and INAR (1) negative binomial samples. Metrika 2007, 65, 207–225. [Google Scholar] [CrossRef]
- Beran, R. Minimum Hellinger distance estimates for parametric models. Ann. Stat. 1977, 5, 445–463. [Google Scholar] [CrossRef]
- Lindsay, B.G. Efficiency versus robustness: The case for minimum Hellinger distance and related methods. Ann. Stat. 1994, 22, 1081–1114. [Google Scholar] [CrossRef]
- Donoho, D.L.; Liu, R.C. The “automatic” robustness of minimum distance functionals. Ann. Stat. 1988, 16, 552–586. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).