Abstract
The purpose of this paper is to discuss the problem of estimation and testing the equality of two autoregressive parameters of two first-order autoregressive processes , where for each process, the observations are made at different time points. The primary interest is to propose the testing procedures for the homogeneity of autocorrelation parameters and . Furthermore, we are interested in estimating under uncertain and weak prior information about the possible equality of and , though we may not have full confidence in the tenacity of this information. A large sample test for the homogeneity of the parameters is developed. Pooled “P” (or restricted estimator) and preliminary test “PT” estimators are proposed, and their properties are investigated and compared with the unrestricted estimator “UE” of .
Keywords:
autoregressive; homogeneity; pretest estimators; pooled estimator; asymptotic bias; asymptotic relative efficiency MSC:
62M10; 62F03; 62F12; 62F30
1. Introduction
The estimation of model parameters is a fundamental aspect of statistical analysis, particularly when data originate from distinct sources or experiments. Suppose that two research stations are conducting the same experiment independently, measuring the same characteristics at different time points. We have a sample of measurements corresponding to the time points for station 1 and a sample of measurements corresponding to the time points for station 2. It is assumed that there is an autoregression of order-1 in the population of both research stations. Let and be population autoregressive coefficients of two stations, respectively. The first-order stationary autoregressive model for research station 1 is given by
where are independently and identically distributed with mean zero and finite variance . Similarly, the first-order stationary autoregressive model for research station 2 is given by
where are independently and identically distributed with mean zero and finite variance . Suppose that for , we have samples for measurements corresponding to the time points for .
The ordinary least squares estimate (OLSE) or unrestricted estimator “UE” of based on observations is
In many practical scenarios, the choice between the pooled estimation and separate estimation of parameters can significantly impact the efficiency and reliability of the resulting estimators. The debate over pooling versus separate estimation has been extensively studied in the literature. Ahmed [1] investigated the conditions under which pooling discrete data yields more efficient estimators, laying the groundwork for subsequent research. Building on these foundational insights, Wang et al. [2] explored effective strategies for parameter estimation and forecasting in panel regressions, while Juodis et al. [3] examined the asymptotic properties of pooled factor-augmented regressions under more realistic conditions. Recent advancements, such as those by Aldeni et al. [4], who focused on pretest and shrinkage estimators for log-normal means, and Waqas et al. [5], who developed robust methodologies for optimizing shape parameters in Birnbaum–Saunders distributions, further contribute to the growing body of research in this area.
The concept of pretest estimators employs preliminary tests to decide whether to pool data or estimate parameters separately. This approach aims to balance the efficiency gains of pooled estimators (see [3]) with the robustness of separate estimation when there is uncertainty about parameter equality. Furthermore, Ahmed [1] explored penalty, shrinkage, and pretest strategies for variable selection and estimation, providing valuable methods for improving estimation efficiency. Recent works by Piladaeng et al. [6] introduced penalized, post-pretest, and post-shrinkage strategies in non-linear growth models and Stein-rule M-estimation in sparse partially linear models, respectively. In another contribution, Ahmed et al. [7] developed efficient estimators of reliability characteristics for a family of lifetime distributions under progressive censoring. These advancements expand the scope of pretest estimation methods and their practical applications. For a comprehensive review, Danilov [8] explored the effects of pretesting in econometrics, particularly in applications to finance, highlighting the comparative advantages of pretest estimators over unrestricted estimators.
In contrast to these approaches, our study focuses on estimating under the hypothesis that , emphasizing scenarios where combining data from two separate sources is crucial. Suppose we have two research stations conducting the same experiment independently, providing separate datasets. One dataset is known to be from the model of interest, while the second, acquired at a different time or location, is suspected to belong to the same model but is not definitively confirmed. The challenge is to estimate when prior information about the potential equality of and is uncertain. In this context, we propose a large sample test statistic to assess the homogeneity of autocorrelation parameters and introduce both pooled and preliminary estimators tailored to parallel sampling contexts. Our objective is to evaluate whether integrating information from these two datasets improves parameter estimation, given the uncertainty surrounding parameter equality. By combining information from the two sources, we aim to enhance the efficiency and accuracy of the estimators. Let the null or preliminary hypothesis be
The remainder of this article is structured as follows: In Section 2, we propose a large sample test statistic for assessing the homogeneity of autocorrelation parameters and introduce the pooled and preliminary estimators of . Section 3 investigates the properties of these estimators, providing a detailed analysis of their asymptotic bias and mean squared error. Section 4 compares the performance of the estimators using various tools such as dominance criteria. Section 5 presents a simulation study to evaluate both the asymptotic properties and the finite-sample performance of the estimators. Section 6 demonstrates two applications of the estimation method using real-world data from weather and economic studies. Finally, Section 7 summarizes the findings and discusses future research.
2. Improved Estimation
Let . Wei [9] showed that for the stochastic regression model,
where means convergence in distribution and , with being the autocovariance function of order h for the population. Note that for a stationary process, the autocovariance at lag is given by . In light of the above asymptotic distributional result, we propose a Pooled “P” or restricted estimator of under the null (preliminary) hypothesis (4) as
where , with and as consistent estimators of and , respectively, given by
This formulation is the most general case. If , we recover the scenario where the variances are equal, and thus the weights simplify. Additionally, if , the pooled estimator simplifies even further to a simple average. Therefore, our approach captures the most general situation, allowing for variations in both sample sizes and variances. Typically, the pooled estimator performs better than the unrestricted estimator under the null hypothesis (4). However, as the scale distance between and grows, becomes considerably biased and inefficient. The performance of remains unchanged over such departures. In an effort to improve the precision of estimators, its is reasonable to develop an estimator which is a combination of and by incorporating a preliminary test on the null hypothesis (4), following an approach which was discussed in [1]. As a result, when is rather suspicious, it is desirable to have a compromise estimator using a preliminary test on in (4) and then choose or based upon the outcome of the test.
First, we propose a large sample test statistic for :
The distribution of under the (4) tends to central chi-square distribution with 1 degree of freedom if . Consequently, under (4), the critical value of may be approximated by which denotes the upper critical value of . Finally, the preliminary test estimator “PT” is defined by
where is an indicator function of the set A. We notice that is a convex combination of and via a test statistic for testing , and this estimator may not be perfect in the whole parameter space. For some account of the parametric theory on the subject, we refer the reader to [1,10], among others. Two bibliographies in this area of research are provided by Piladaeng et al. [6], Chien-Pai Han and Ravichandran [11]. The asymptotic theory of preliminary test estimation for discrete models is discussed by Ahmed [1], among others.
We use the mean squared error (MSE) criterion to appraise the performance of the estimators under the following squared loss function:
where is a suitable estimator of . Then, the MSE of is given by ; further, is termed an inadmissible estimator of if there exists an alternative estimator such that
with strict inequality for some . If, instead of (8) holding for every n, we use the asymptotic MSE (AMSE), then we require that
with strict inequality for some . Then, is termed an asymptotically inadmissible estimator of .
3. Main Results
For large values of (6), the preliminary test estimator in (7) leads to the asymptotic equivalence with the usual maximum likelihood estimator. Also, when (4) does not hold and n is very large, by virtue of the consistency of the test-statistic, (6) will be large in probability, and the (7) will be asymptotically equivalent in probability, to the (3). Hence, in the asymptotic set-up, a fixed alternative will not make sense. A meaningful investigation is possible for local alternatives where is close to . Therefore, it is reasonable to restrict ourselves to local alternative , which contains the null hypothesis as a special case. Under an asymptotic set-up, we shall examine the performance of the estimators. We may also remark here that for parametric preliminary test estimation, unless the true parameters are close to each other, there is no substantial gain from the preliminary test estimation over classical methods. This closeness is precisely characterized in terms of local alternatives. Moreover, the asymptotic set-up enables us to obtain results which are quite comparable to the existing parametric preliminary test estimation theory. For given sample size , replacing by , we obtain
where is a fixed real number. Under the local alternatives in (10) and as , in such a way that and , the following lemmas are the consequences of the results of Wei [9].
Lemma 1.
.
Proof.
The detailed proof is provided in Appendix A. □
Lemma 2.
.
Proof.
See Appendix B for the detailed proof. □
Lemma 3.
.
Proof.
For a detailed proof, see Appendix C. □
Lemma 4.
As , the test statistics given in (6) has asymptotically a non-central chi-square distribution with 1 degree of freedom and a non-centrality parameter .
Proof.
See Appendix D. □
Now, we present the expressions for the asymptotic biases of the estimators as follows. By direct computation and using the results from [10], we arrive at the following bias expressions of the estimators:
where is the cumulative distribution function of a non-central chi-square distribution with m degrees of freedom and non-centrality parameter . First, note that . Thus, we conclude that is asymptotically unbiased (in the sense of ), but is not so. However, since the bias is a component of the asymptotic mean squared error (AMSE) and the control of the AMSE would control both bias and variance, we shall only compare the AMSE from this point onwards. Expressions for the AMSE of the estimators are presented in the following theorem, which follow from the results in [10].
Theorem 1.
Proof.
For a detailed proof, see Appendix E. □
4. Asymptotic Properties of the Estimators
We note that the AMSE of is a constant line, while the AMSE of is a straight line in terms of , which intersects the AMSE of at . Using the AMSE criterion to appraise performance, if the restriction is correct, then the AMSE of is less than the AMSE of . Furthermore, if . Hence, for , outperforms . However, beyond this interval, the AMSE of increases without bound. In an effort to identify some important characteristic of the PT estimators, first note that
for and . The left-hand side of (14) converges to 0 as approaches infinity. Now, we compare the AMSE of PT with that of the UE. We notice that dominates whenever
It is obvious from (15) that the AMSE of PT is less than the AMSE of UE when is equal to or near 0. Further, as , the level of the statistical significance, approaches one, the AMSE of PT tends to the AMSE of UE. Also, when increases and tends to infinity, the AMSE of approaches the AMSE of . Further, for larger values of , the value of the AMSE of increases, reaches its maximum after crossing the AMSE of , and then monotonically decreases and approaches the AMSE of . There are, therefore, points in the parameter space where has a larger AMSE than and a sufficient condition for this result to occur is that the following inequality holds:
Finally, under (4), the dominance picture of the estimators is as follows:
- None of the three estimators are inadmissible with respect to the other two.
- However, at , the estimators may be ordered according to the magnitude of their AMSE as follows: . Here, ≻ denotes domination.
5. Simulation Study
In this section, we employ simulated data to explore the relative efficiency of the estimators under consideration. The comparisons between the and estimators are conducted with respect to the unrestricted estimator “UE”, based on the simulated relative efficiency (SRE). The SRE of an estimator in comparison to the is defined as
here, represents the simulated risk of an estimator. The SR of an estimator is determined by the average risk over M replications, calculated by
It is evident that the SRE of the will always equal one, as it serves as the baseline for comparison. An SRE value greater than one indicates that the estimator outperforms , suggesting a higher efficiency relative to the . Conversely, an SRE value less than one implies that is less efficient than , indicating a certain degree of inferiority in its performance. This metric allows for a clear quantification of the relative merits of different estimators. We perform Monte Carlo simulations using various combinations of sample sizes and . Both small and large sample sizes are considered to assess their impact on the performance of the estimators, where . Two autoregressive models, (1) and (2), are generated with varying sizes and , and across a range of . The parameters are defined as follows: and . The scale parameter is selected to take small values, starting from 0 up to its maximum, ensuring the stationarity of our autoregressive models:
First, we compute the unrestricted estimators for using (3). Following this, the pooled or restricted estimator is determined using (5). Subsequently, we calculate the test statistic as described in (6), with the distribution of the test statistic being evaluated under the null hypothesis (4). Finally, the pretest estimators are derived using (7). This process allows us to systematically compare the performance of the different estimators under various conditions, ensuring a thorough assessment of their relative efficiencies. The SR for each estimator is computed by repeating the simulation times to ensure stable results. The SREs of the proposed estimators are evaluated across various combinations of , , and , with fixed at 0.05 and 0.10, and varying within the range . Table 1 and Table 2 present the values for the different estimators for both smaller and larger sample sizes, respectively, while the corresponding graphs are displayed in Figure 1. The figure illustrates the results when and at the top, and at the bottom.

Table 1.
SREs of estimators and when sample sizes and are small, for varying values.

Table 2.
SREs of estimators and when sample sizes and are larger, for varying values.
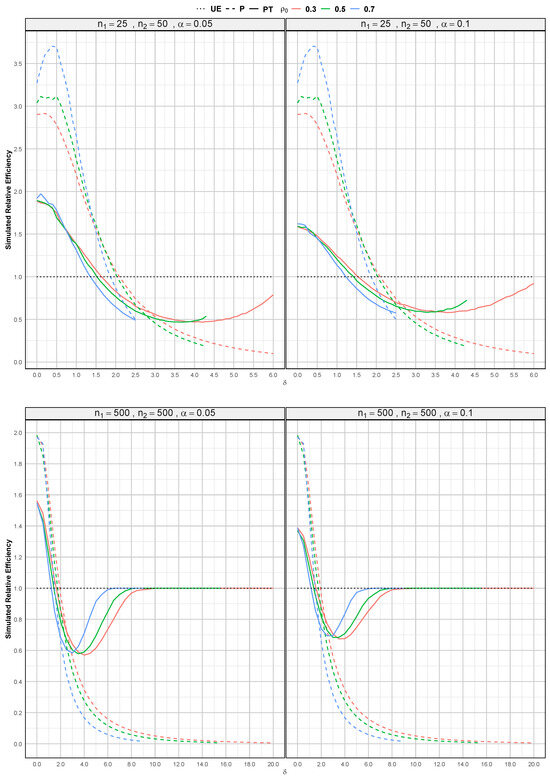
Figure 1.
SREs of the and estimators for , . (top) and , (bottom) .
From the simulation outcomes, the following observations can be made:
- Since the estimator achieves the highest SRE at , it outperforms all other estimators. This effectiveness further improves as the parameter of the autoregressive model increases. However, for the estimator, its efficiency declines as both the level of significance and the values of increase.
- When , none of the three estimators are superior to the others. This result is due to the SRE of decreasing continuously with increasing . However, beyond a certain point, as continues to rise, the efficiency gradually approaches one. Before reaching this point, experiences a sharp decline in efficiency, eventually being surpassed by . After this point, the SRE of the estimator becomes less significant compared to the estimator.
As we proceed in this study, our focus will shift towards a deeper investigation into the statistical properties and the performance of a test statistic given by (6). We derive the asymptotic distribution of under large sample conditions, which is a non-central chi-square distribution . Specifically, we prove the Lemma 4. To validate this result, we perform a series of simulations: we simulate times the statistic for different values of and a range of values (where satisfies the condition (16)). For each scenario, the degree of freedom and non-centrality parameters are estimated using the maximum likelihood method (MLE). Furthermore, we will compare the empirical findings with the theoretical expectations to ensure consistency across different scenarios. The simulation results confirm the theoretical findings derived in Lemma 4. The estimated values and coincide with the theoretically predicted values, demonstrating the accuracy of the asymptotic distribution for the test statistic . Additionally, we compile Table 3, which summarizes the descriptive statistics and the MLE for the asymptotic distribution of under different values of and , assuming . The table presents the mean, variance, median, skewness, and kurtosis of the simulated data, as well as the estimated degrees of freedom and non-centrality parameters for the corresponding distribution. This is further complemented by Figure 2, which provides a graphical representation of the fit, illustrating the consistency between the theoretical and simulated distributions.

Table 3.
Summary statistics and asymptotic distribution of for different values of and , when .
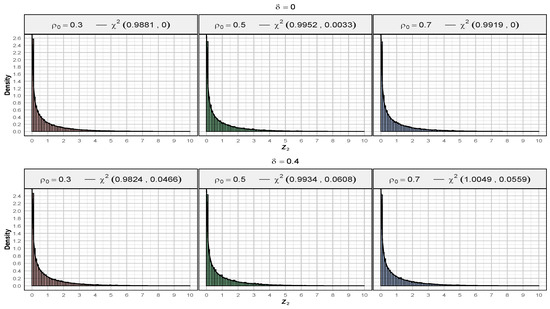
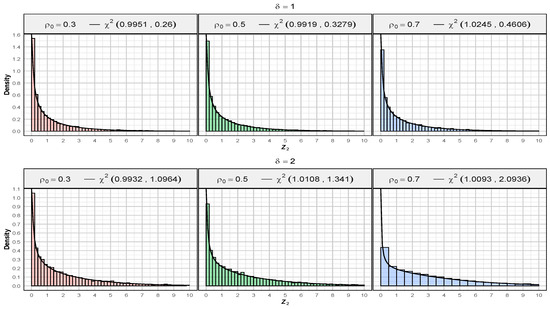
Figure 2.
Fitted distribution of for different values of and , with .
6. Real Data Applications
To demonstrate the usefulness of the suggested estimators from Section 2, we present two real-data applications (in weather and economy) in this section to validate their practical relevance and effectiveness.
6.1. Mean Annual Precipitation
Various precipitation metrics, including the daily totals, monthly accumulations, annual precipitation, extreme values, rainfall durations, and rain rates, have been modeled using a time series autoregressive model. As our initial application, we analyze two time series representing mean annual precipitation from two stations located in Washington State, USA. The first station “HOQUIAM BOWERMAN AP” provides the mean annual precipitation records from 1970 to 2024, covering a period of 54 years ( observations), and is denoted as . The second station “ABERDEEN” offers data spanning from 1950 to 2022, with a total of 72 years of precipitation records ( observations), and is denoted as . These datasets are publicly available on the National Weather Service website at https://www.weather.gov/wrh/Climate?wfo=sew (accessed on 25 August 2024). A summary of the statistical characteristics of the two time series and , along with the estimation of and for each series, is presented in Table 4, while their graphical representation is provided in Figure 3.

Table 4.
Summary of statistical characteristics and autocorrelation estimates for time series and .
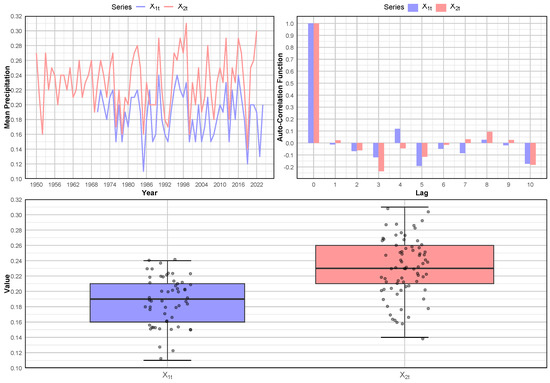
Figure 3.
Mean annual precipitation from the “HOQUIAM BOWERMAN AP” station () and the “ABERDEEN” station () over the periods 1970−2024 and 1950−2022, respectively. (Top Left): Time series; (Top Right): Autocorrelation function estimation (AFC); (Bottom): Box-plots.
The scientists wish to estimate from station 1, and they suspect that the parameter may be the same for both populations, i.e., . In such a case, it is advantageous to pool the two time series and to estimate . Hence, by (5),
The homogeneity of the two parameters, i.e., may be examined by means of (6), or numerically,
for , the upper 95% point of the non-central chi-squared distribution (asymptotically) which is the minimum value at (). The preliminary test estimator given by (7) is
The critical value of such a test statistic is with an upper tail probability value p-value = 0.9892. Thus, the result is not significant at the level, and the null hypothesis of homogeneity of the autocorrelation parameters cannot be rejected. Hence, is selected as an estimate of . We conclude that a scientist who wishes to find a good alternative to the and should be able to specify the minimum relative efficiency.
6.2. Annual Inflation Rates (AIRs)
Annual inflation rates represent the average change in the prices of goods and services within an economy over a one-year period. Inflation is a key indicator of economic health, reflecting the variation in the purchasing power of a currency. It is commonly measured by the Consumer Price Index (CPI), which tracks price changes in a representative basket of goods and services consumed by households. As a macroeconomic indicator, the annual inflation rate is crucial for understanding economic trends and inflationary pressures. To analyze the dynamic behavior of inflation over time, econometric models such as autoregressive models are often employed. These models are particularly useful in capturing the persistence of inflation, as they assume that the current inflation rate is dependent on the inflation rate from the previous period, along with a random shock. These models help policymakers and economists forecast future inflation and assess the potential impacts on monetary policy, wages, prices, and the purchasing power of consumers.
In this second application, we apply our estimation strategies to the annual inflation rates of two countries: Poland () and Algeria (). The datasets for cover the period from 1971 to 2023, comprising 53 observations, while the datasets for span from 1970 to 2023, with a total of 54 observations; we test the homogeneity of the autoregressive parameters by assessing whether the autocorrelation coefficients and for the two countries are statistically equal. The inflation data, which serve as the basis for this analysis, are publicly available through the World Bank’s World Development Indicators (WDI) database at https://databank.worldbank.org/ (accessed on 28 August 2024). For users of the R programming language [12], these data can also be directly accessed using the WDI package [13] available at https://CRAN.R-project.org/package=WDI (accessed on 28 August 2024). This datasets provide comprehensive time series data on various macroeconomic indicators, including the annual percentage change in the Consumer Price Index (CPI) for both countries. A summary of the statistical characteristics of the two countries, and , along with the estimates of and for each country, are provided in Table 5. A graphical representation of the inflation dynamics for both countries is shown in Figure 4, where the boxplot is presented on a logarithmic scale to enhance the visibility of the data, particularly in the presence of large data points.

Table 5.
Summary of statistical characteristics and autocorrelation estimates for annual inflation rates for Poland “” and Algeria “”.
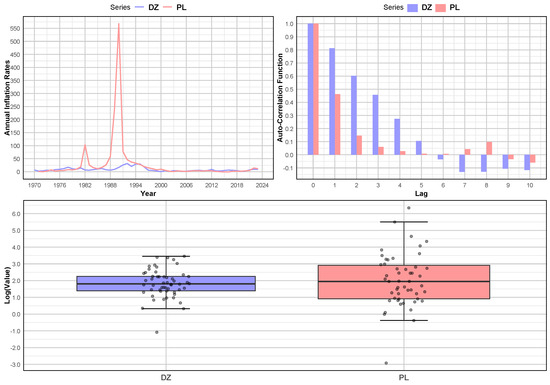
Figure 4.
Annual inflation rates for Poland “” and Algeria “” over the periods 1971−2023 and 1970−2023, respectively. (Top Left) Time series; (Top Right) Autocorrelation function estimation (AFC); (Bottom) Box-plots.
First, we obtain the pooled (or restricted) estimator . The test statistic is computed using and (unrestricted estimator). Under the null hypothesis, this test statistic follows a non-central chi-square distribution with one degree of freedom (asymptotically). For , the upper 95% critical value of the chi-square reference distribution is at () which yields . Thus, the result is significant at the 5% level, and the null hypothesis of homogeneity of the autocorrelation parameters is rejected. The pretest estimator is equal to the unrestricted estimator, i.e., . When the assumption of homogeneity of the autocorrelation parameters does not hold, the estimators based on the test statistic converge to the unrestricted estimator. This indicates that by rejecting the hypothesis of homogeneity, we conclude that the annual inflation dynamics in differ from those in . In other words, there are significant differences between the autocorrelation parameters of the inflation for these two countries. These findings are consistent with both the theoretical predictions and numerical results, especially for large values of .
To further analyze the impact of larger values of on the test of homogeneity of the autocorrelation parameters, we estimate non-centrality parameter by the formula (see Lemma 4)
where and . The results of the pretest estimator for different values of are presented in Table 6.

Table 6.
Results of pretest estimator for different values of .
7. Conclusions and Future Research
In this article, we develop and analyze preliminary test estimation methods for the homogeneity of autocorrelation parameters in parallel two-sample autoregressive models. Our findings demonstrate that the proposed pooled and preliminary estimators offer significant improvements in efficiency compared to traditional estimators, particularly when the assumption of parameter homogeneity does not hold. The large-sample properties of these estimators, including asymptotic bias and mean squared error, have been thoroughly investigated, showing that the proposed methods perform well in both asymptotic and finite-sample scenarios. Building on these theoretical results, the simulation study further underscores the robustness of the preliminary test estimator across various sample sizes, validating the theoretical properties derived earlier. Notably, the results reveal that when the homogeneity assumption is strongly challenged, the pooled estimator can introduce substantial bias, whereas the preliminary test estimator effectively adjusts by incorporating the test of homogeneity. This highlights the importance of pretesting in situations where parameter equality is uncertain. Despite these promising results, the performance of these estimators can still vary depending on specific data characteristics, such as the degree of autocorrelation and sample size. For example, in real-world applications like the inflation data for Poland and Algeria, the proposed method offers valuable insights into the differences in economic dynamics between countries, demonstrating its utility beyond purely theoretical settings.
Looking ahead, several avenues for future research can be explored. One potential direction is to extend the current methodology to more complex time series models, such as higher-order autoregressive models or models with mixed effects. Additionally, investigating the impact of non-stationarity and structural breaks on the performance of the preliminary test estimators could yield further insights. Another promising area for future work is the application of these methods to high-dimensional settings, where the number of parameters exceeds the number of observations, which is increasingly common in modern data analysis. Furthermore, exploring alternative testing methods, such as permutation, bootstrap, or other non-parametric techniques, in the context of our framework could offer additional flexibility. Finally, incorporating machine learning techniques for model selection and parameter estimation, particularly in cases where the data exhibit non-linear patterns, could further enhance the efficiency of the proposed estimators. These advancements could broaden the applicability of preliminary test estimation methods to a wider range of practical problems in statistics and econometrics.
Author Contributions
Methodology, S.E.A. and S.B.; Software, A.C.G.; Validation, A.C.G.; Formal analysis, S.B.; Investigation, S.E.A. and S.B.; Data curation, A.C.G.; Writing—original draft, S.E.A.; Writing—review & editing, S.E.A. and S.B.; Visualization, A.C.G.; Supervision, S.E.A. and S.B.; Project administration, S.E.A.; Funding acquisition, S.E.A.. All authors have read and agreed to the published version of the manuscript.
Funding
Prof. Ahmed S.E research is funded by the Natural Sciences and Engineering Research Council (NSERC), Canada.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The R code can be found on GitHub at: https://github.com/acguidoum/R-code-stats-2024 (accessed on 25 August 2024), so that readers can replicate the results. The data used in this study are publicly available from multiple sources. The mean annual precipitation data for the “HOQUIAM BOWERMAN AP” and “ABERDEEN” stations were obtained from the National Weather Service and can be accessed at https://www.weather.gov/wrh/Climate?wfo=sew (accessed on 28 August 2024). The inflation data for Poland and Algeria were sourced from the World Bank’s World Development Indicators (WDI) database, which can be accessed through the World Bank’s Databank at https://databank.worldbank.org/ (accessed on 28 August 2024).
Acknowledgments
The authors are thankful to the editor and the anonymous referees for their thorough review and highly appreciate the comments and suggestions which significantly contributed to increasing the quality of our paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proof of Lemma 1
From the asymptotic theory of estimation, it is known that . Let which is a linear function of so and
Appendix B. Proof of Lemma 2
As , where and , we have
under the assumption , we get and .
Appendix C. Proof of Lemma 3
Let
we obtain and .
Appendix D. Proof of Lemma 4
It is known that
which implies that
Under the null hypothesis (4), we have
Thus, the test statistic is given by (6), asymptotically, and the chi-square distribution with one degree of freedom becomes non-central, where the non-centrality parameter is given by
where
Hence, the non-centrality parameter is
Appendix E. Proof of Theorem 1
Lemma A1
(see [10]). Let y be a k-dimensional random vector that follows multivariate normal distribution with mean vector and covariance matrix . Then, for any measurable function ϕ, we have
where .
For (11), we have
and for (12), we can write
where
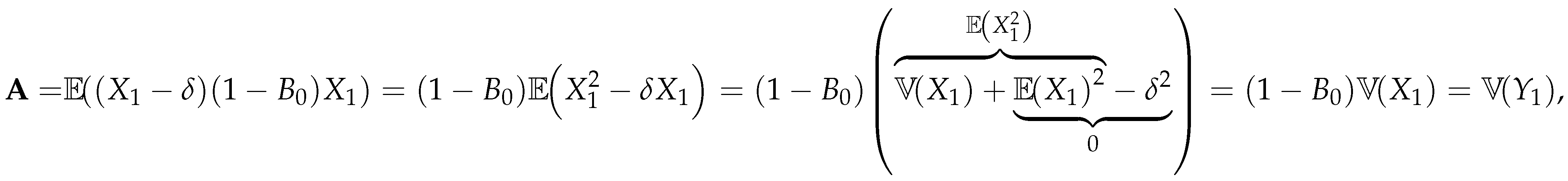 and therefore,
with . Finally, for (13), we have
by using (A1) and (A2), we have
and
substituting and in (A3), we obtain
and therefore,
with . Finally, for (13), we have
by using (A1) and (A2), we have
and
substituting and in (A3), we obtain
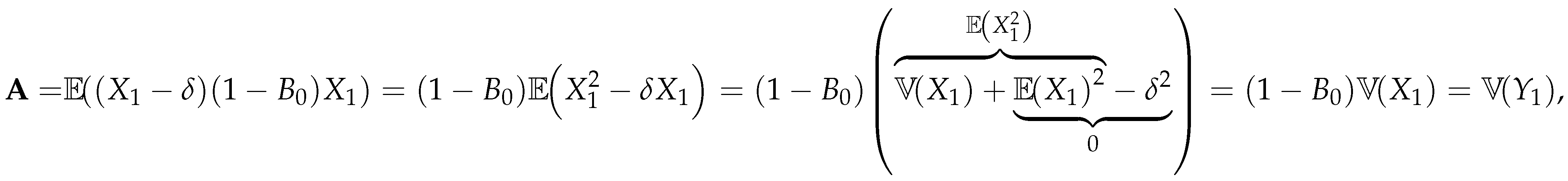
References
- Ahmed, S.E. Penalty, Shrinkage and Pretest Strategies: Variable Selection and Estimation, 1st ed.; SpringerBriefs in Statistics; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, X.; Paap, R. To pool or not to pool: What is a good strategy for parameter estimation and forecasting in panel regressions. J. Appl. Econ. 2019, 34, 579–596. [Google Scholar] [CrossRef]
- Juodis, A.; Karabiyik, H.; Westerlund, J. On the robustness of the pooled CCE estimator. J. Econ. 2021, 220, 325–348. [Google Scholar] [CrossRef]
- Aldeni, M.; Wagaman, J.; Amezziane, M.; Ahmed, S.E. Pretest and shrinkage estimators for log-normal means. Comput. Stat. 2023, 38, 1555–1578. [Google Scholar] [CrossRef]
- Waqas, M.; Muhammad, K.A.S.; Nighat, Z.; Ahmed, S.E. Optimizing robust shape parameter: Improved methodologies for Birnbaum–Saunders distribution. J. Stat. Theory Pract. 2024, 18, 1559–8616. [Google Scholar] [CrossRef]
- Piladaeng, J.; Ahmed, S.E.; Lisawadi, S. Penalised, post-pretest, and post-shrinkage strategies in nonlinear growth models. Aust. N. Z. J. Stat. 2022, 64, 381–405. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Belaghi, R.A.; Hussein, A.; Safariyan, A. New and Efficient Estimators of Reliability Characteristics for a Family of Lifetime Distributions under Progressive Censoring. Mathematics 2024, 12, 1599. [Google Scholar] [CrossRef]
- Danilov, D.L. The Effects of Pretesting in Econometrics with Applications in Finance; Tilburg University Research Paper; Tilburg University: Tilburg, The Netherlands, 2003. [Google Scholar]
- Wei, C.Z. Asymptotic properties of least-squares estimates in stochastic regression models. Ann. Stat. 1985, 13, 1498–1508. Available online: https://www.jstor.org/stable/2241368 (accessed on 2 September 2024). [CrossRef]
- Judge, G.G.; Bock, M.E. The Statistical Implications of Pre-Test and Stein-Rule Estimators in Econometrics, 2nd ed.; Studies in Mathematical and Managerial Economics; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1978. [Google Scholar] [CrossRef]
- Chien-Pai Han, C.R.; Ravichandran, J. Inference based on conditional speclfication. Commun. Stat.-Theory Methods 1988, 17, 1945–1964. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.r-project.org/.
- Arel-Bundock, V.; Bacher, E. WDI: World Development Indicators and Other World Bank Data, R package version 2.7.8; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).