Cross-Country Assessment of Socio-Ecological Drivers of COVID-19 Dynamics in Africa: A Spatial Modelling Approach

Abstract

Understanding how countries’ socio-economic, environmental, health status, and climate factors have influenced the dynamics of COVID-19 is essential for public health, particularly in Africa. This study explored the relationships between African countries’ COVID-19 cases and deaths and their socio-economic, environmental, health, clinical, and climate variables. It compared the performance of Ordinary Least Square (OLS) regression, the spatial lag model (SLM), the spatial error model (SEM), and the conditional autoregressive model (CAR) using statistics such as the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), Root Mean Square Error (RMSE), and coefficient of determination ($R^2$). Results showed that the SEM with the 10-nearest neighbours matrix weights performed better for the number of cases, while the SEM with the maximum distance matrix weights performed better for the number of deaths. For the cases, the number of tests followed by the adjusted savings, Gross Domestic Product (GDP) per capita, dependence ratio, and annual temperature were the strongest covariates. For deaths, the number of tests followed by malaria prevalence, prevalence of communicable diseases, adjusted savings, GDP, dependence ratio, Human Immunodeficiency Virus (HIV) prevalence, and moisture index of the moistest quarter play a critical role in explaining disparities across countries. This study illustrates the importance of accounting for spatial autocorrelation in modelling the dynamics of the disease while highlighting the role of countries’ specific factors in driving its dynamics.

1. Introduction

The coronavirus disease 2019 (COVID-19), caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and first reported in December 2019 in Wuhan, China, has become a global health concern [1,2]. Declared as a pandemic on 11 March 2020, the disease has severely hit the world [2]. For example, as of 2 August 2021, there had been 199,051,292 total cases, with 4,241,236 deaths (https://www.worldometers.info/coronavirus/, accessed on 8 August 2022). The incidence of the disease is, however, non-uniform across the globe. In Africa, the incidence of COVID-19 is relatively low, with 6,799,806 cases, including 171,445 deaths, as of 2 August 2021, i.e., 3.4% and 4.04% of total cases and deaths, respectively, yet the continent accounts for 17.2% of the world population. The reasons for such a contrast have interested scientists, especially considering the low-quality health care systems in African countries [1,3,4]. Furthermore, patterns of COVID-19 cases and deaths across African countries show high geographical disparities. For example, while about 180,000 cases per million people and about 800 deaths per million people were reported in Seychelles, fewer than 100 cases and 10 deaths per million people were noted in countries such as Benin, Angola, Guinea, etc. Why such spatial disparities, and which factors explain such patterns? Understanding the factors explaining the spatial heterogeneity in COVID-19 incidence in Africa is essential to inform public health policymakers who are aiming to better control the pandemic [2] and ensure effective preparedness for future epidemics.

There is evidence that environmental and socio-demographic factors may act in synergy or antagonistically with climate factors to exacerbate or lessen the severity of infectious disease transmission and fatality [5]. For example, migrants, either nationals or internationals, especially those involved in low-income jobs, are among the most vulnerable to death and infection by SARS-CoV-2 [6]. Population age structure was also suggested as a determinant in controlling COVID-19 deaths and spreading [7]; the high numbers of COVID-19 deaths and cases in Italy were linked with the demographic structure of the country (median age = 46 years) [6]. In Europe, more than 95 percent of people who died due to COVID-19 were 60+ years old (WHO, 2020), which has been suggested to explain the low number of cases and deaths due to COVID-19 in Africa, where the median age is 19 years. Income factors (e.g., median household income, median household income percent, Gini coefficient) were significantly associated with COVID-19 cases and deaths [6,7]. Similarly, the potential role of weather and climate in COVID-19 morbidity and mortality has been highlighted by several studies, some arguing for a negative correlation between ambient temperature and humidity and the number of COVID-19 cases/deaths and others the absence of any correlation or even a positive one [8].

Studies have been carried out to model and predict the dynamics of the pandemic [9]. Several sought to understand environmental (climate and pollution), socio-demographic, and socio-economic correlates of the spatial heterogeneity in COVID-19 incidences and deaths in Europe, the United States of America (USA), and Asia either on country, prefecture, or county scales [2,6,10,11]. In such studies, geography, which includes spatial locations and characteristics of the spatial determinants, was shown to play a crucial role in the early outbreak and transmission of the virus across scales [2,12]. For instance, the spatial variability and clustered patterns of COVID-19 cases and deaths in many countries showed a strong spatial dependency on confounding factors [13]. This indicates the need to understand spatial effects such as spatial autocorrelation, spatial stationarity, and heterogeneity in modelling COVID-19 morbidity and mortality and their correlates.

Comparatively, only a few studies have been carried out in Africa regarding these issues. The few attempts to obtain such insights in Africa (see [7,14]) have not explicitly considered spatial autocorrelation and spatial stationarity in the modelling and thus are potentially misleading. For example, Bouba et al. [7] used OLS regression on COVID-19 cases and deaths from 14 February 2020 to 4 February 2021 (first waves) to explore their relationship with 34 covariates (epidemiological, socio-demographic, climatic, environmental, and economic-financial) across 54 African countries. Similarly, Tamasiga et al. [15] used multivariate linear regression and a few predictors (seven demographic and income predictors) across 40 sub-Saharan countries to understand factors affecting COVID-19 cases and deaths based on the data from Janaury 2020 to March 2023. The authors obtained models with an ${\mathrm{R}}^2$ equal to 69% and 63%, indicating that substantial variations in COVID-19 cases and deaths are yet to be explained. Furthermore, Su et al. [14] conducted a global analysis (178 countries, including African countries) of the influence of socio-ecological factors on COVID-19 risk. The study considered 28 socio-ecological and demographic variables. All these studies used OLS regression or simple Generalised Poisson models. One of the shortcomings in using OLS or simple generalised models to model the incidence and deaths due to COVID-19 across countries is the ignorance of the spatial patterns that may exist in the incidence and deaths of COVID-19 [6,14]. For example, due to the proximity of some countries, they may show similar patterns, which may be confounded by other factors when this spatial relationship is not explicitly tested and considered [6,14]. Among the rare studies that used spatial regression is [16], where the authors used data from the first and second waves of COVID-19 (until May 2021) from 47 countries. The authors explored three linear spatial regression models, namely the spatial lag, spatial error, and spatial autoregressive condition (SAC) models and found that COVID-19 prevalence in an African country was highly dependent on that of neighbouring African countries as well as its economic wealth, transparency, and proportion of the population aged 65 or older. However, in this study, the authors ignored countries’ COVID-19 testing capacity and used only a few predictors (six), excluding, for example, climate and population migration, which are also important correlates of COVID-19 dynamics.

Our study aims to improve the assessment of the impact of socio-economic, environmental, and demographic parameters on the spread of COVID-19 cases and deaths across African countries by adopting spatial-regression-based approaches and using the most updated statistics on COVID-19 cases and deaths. The objective was to assess the socio-ecological patterns of the COVID-19 spatial dynamics in Africa. Specifically, the study sought to (i) map the spatial heterogeneity of the number of COVID-19 cases and deaths across African countries, (ii) test the existence of spatial autocorrelation and heterogeneity in the patterns of COVID-19 cases and deaths, and (iii) determine socio-ecological factors affecting the spatial heterogeneity of COVID-19 morbidity and mortality across African countries.

2. Materials and Methods

2.1. Study Area

The study considered all 54 African countries, including Madagascar. Based on the latest United Nations estimates, the population of Africa in 2023 was 1,460,481,772, i.e., about 18.2% of the world population (https://www.worldometers.info/world-population/#region, accessed on 5 January 2024). However, Africa carries 25% of the world’s disease burden, and its share of global health expenditures is less than 1%. Worse still, it manufactures less than 2% of the medicines consumed on the continent. A majority of Africans, mostly the poor and those in the middle-income bracket, rely on underfunded public health facilities, while a small minority have access to well-funded, quality private health care. The first three challenges identified were inadequate human resources, inadequate budgetary allocation to health, and poor leadership and management [17]. At the advent of COVID-19, and because most countries on the continent rank as poor on the United Nations Development Programme’s Human Development Index, experts predicted millions of COVID-19 deaths on the continent, which turned out to be wrong several years after the pandemic [1]. For example, as of 3 April 2024, only 1.82% and 3.69% of the total cases and deaths, respectively, were reported in Africa.

2.2. Data Acquisition

We sought to model the dynamics of the COVID-19 cases and deaths. As such, we compiled data on the cumulative cases and deaths of COVID-19 for each African country as of 8 August 2022. The numbers of cases and deaths were then divided per millions of people to make them comparable across countries. The number of cases detected highly depends on the number of tests carried out. Therefore, for modelling the number of cases, the total number of tests was added as a covariate to account for its effect on the number of reported cases and deaths. Data on the number of cases, deaths, tests, and population were obtained from the Worldometer database (https://www.worldometer.org/, accessed on 8 August 2022). In total, 43 explanatory variables grouped in 7 categories were considered as follows: demography (10 variables), migration (3 variables), economic (6 variables), health care systems (3), clinical or diseases (7), pollution (4), climate (8), and others (2). Demography variables included population density, annual change in population, fertility rate, median age, proportion of total population aged 65 and above, proportion of total population aged 15–64, dependence ratio as % of working-age population, dependence ratio for old people as % of total population, and median year of life expectancy at birth. Migration variables included the net migrants, number of airports in the country, and number of air transport passengers carried per capita. The economic variables included the adjusted savings, i.e., particulate emission damage (% of GNI), which is equal to net national savings plus education expenditure and minus energy depletion, mineral depletion, net forest depletion, carbon dioxide, and particulate emissions damage, the GDP per capita, the Human Development Index, and urbanisation rate. The health care systems variables included the number of nurses and midwives per 1000 population, number of physicians per 1000 population, and the Global Health Security Detection Index (weighted sum of all the Global Health Security (GHS) data normalised to a scale of 0 to 100, where 100 = best health security condition). The clinical variables included the prevalence of diabetes (% of population aged 20 to 79), the incidence rate of tuberculosis (TB) per 100,000 people, the Bacillus Calmette–Guérin (BCG) vaccination coverage in %, the prevalence of HIV (total % of population aged 15–49), the reported cases of malaria per 100,000 population, the raised total cholesterol (≥5.0 mmol/L) as an age-standardised estimate, and the burden of communicable diseases and maternal, prenatal, and nutrition conditions (including infectious and parasitic diseases, respiratory infections) per 100,000 people. Variables on pollution were PM2.5 air pollution (population exposed to levels exceeding the World Health Organization (WHO) guideline value (% of total)), the methane emissions in the energy sector (thousand metric tons of carbon dioxide (CO₂) equivalent), the nitrous oxide emissions (thousand metric tons of CO₂ equivalent), and the proportion of people practising open defection (% of population). Climate variables were annual mean temperature, temperature seasonality, annual precipitation, precipitation of driest quarter, moisture index, moisture index of the most arid quarter, moisture index of the moistest quarter, and potential evapotranspiration. The other variables were the total area land of the country and the proportion of the total land area that is covered by forests. Further details and sources of the data are provided in the Supplementary File, Table S1.

2.3. Data Analysis

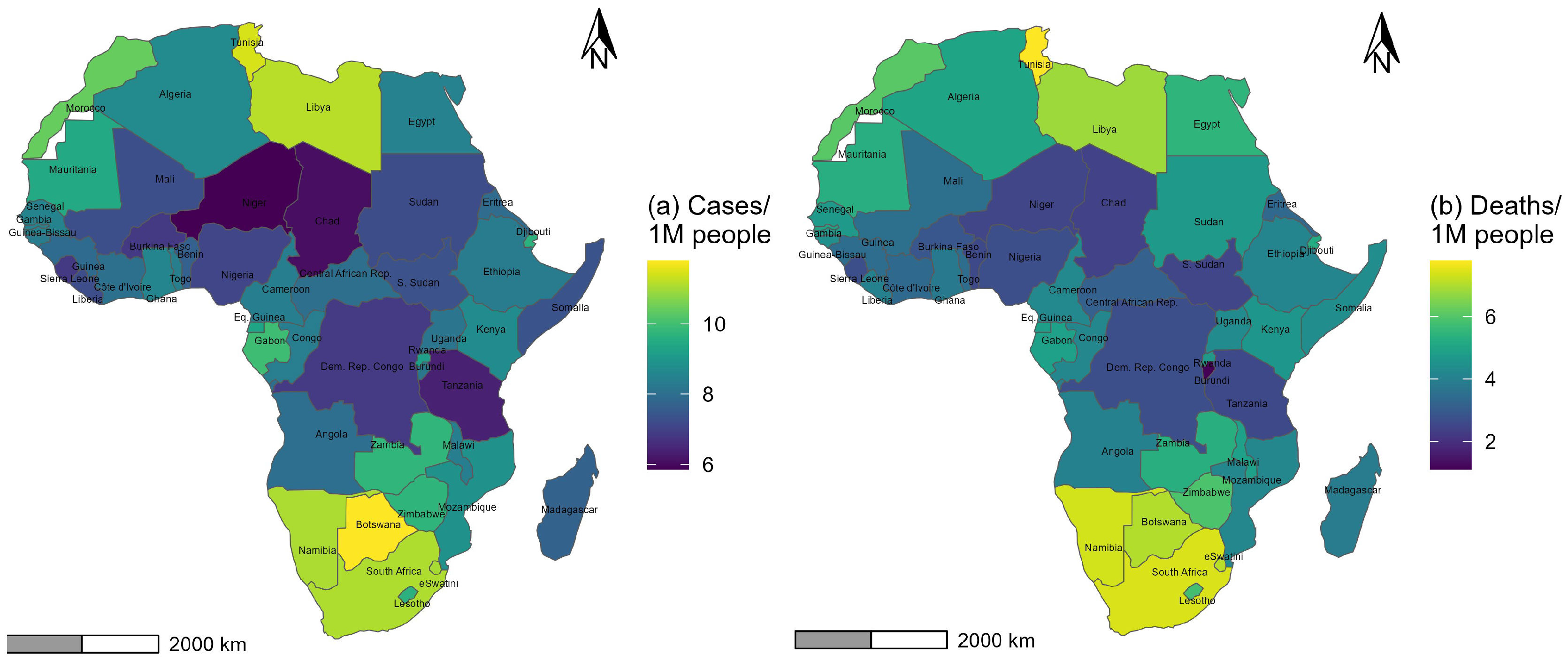
COVID-19 cases and deaths per million across African countries were considered response variables and plotted in a geographical information system to explore the spatial heterogeneity of the disease incidence and fatality across the continent. The correlation between both variables was moderate and positive (r = 0.672, p-value $<0.001$). The correlation between the total number of cases per million and the total number of tests per million was high and positive (r = 0.834, p-value $<0.001$). The correlation between the total number of deaths per million and the total number of tests per million was rather moderate and positive (r = 0.662, p-value $<0.001$).

Before diving into the statistical analyses, all explanatory variables were standardised using the min–max normalisation, which resulted in the values of all variables ranging from 0 to 1. The modelling of the relationship between explanatory variables and each of the two response variables involved three steps. As the number of explanatory variables was high, the first step dealt with collinearity analysis using the variance inflation factor (VIF). The process consisted of regressing each explanatory variable on the remaining explanatory variables and iteratively eliminating those with a variance inflation factor (VIF) greater or equal to 5, resulting in 23 variables selected out of the 43. The 18 variables selected included country’s total area, excluding area under inland water bodies, national claims to continental shelf, and exclusive economic zones (land_Area), methane emissions in the energy sector (thousand metric tons of CO₂ equivalent) in 2018 (Meth_em), nitrous oxide emissions (thousand metric tons of CO₂ equivalent) in 2018 (Nitro_oxide), number of airports in the country (Nb_Airport), dependence ratio for old people (% of total population) in 2020 (DepR_old), number of tests per 1 million people (Tests_1Mpop), urbanisation rate (Urban_Rate), the net migrants (Migrants), population density (Density_2020), precipitation of driest quarter (bio17), moisture index of the most moist quarter (mimq), adjusted savings in % of GNI (AdjSav), annual mean temperature (bio1), annual change in the population (Yearly_change), dependence ratio (% of working-age population) in 2020 (DepR), proportion of the total land area that is covered by forests (Forest_area), BCG vaccination coverage, in % (BCG.19), prevalence of HIV as total % of population aged 15–49 (HIV.19), raised total cholesterol (≥5.0 mmol/L) as an age-standardised estimate (Raised_Choleste_2018), GDP per capita (current US$) (GDP.19), reported cases of malaria per 100,000 population (Malaria.19), the burden of communicable diseases and maternal, prenatal, and nutrition conditions (including infectious and parasitic diseases, respiratory infections) per 100,000 people (Commun_DiseasePrevalence2019), and the Global Health Security Detection Index (weighted sum of all the GHS data normalised to a scale of 0 to 100, where 100 = best health security condition) (GHS.index.19).

Then, an OLS regression was performed on the response variables (total cases per 1 million population and total deaths per 1 million population), including the 23 pre-selected explanatory variables. The parsimonious model was identified after a backward selection on the initial regression model. Then, the Global Moran’s I was used to explore the spatial autocorrelation of COVID-19 cases and deaths across African countries. This index was calculated using the parsimonious OLS regression model, which was performed on each response variable using various weight matrices. Three row-standardised weight matrices were considered for testing the global spatial autocorrelation, including the maximum distance matrix, the 4-nearest neighbours matrix, and the 10-nearest neighbours matrix. The maximum distance was the maximum of the minimum distance, which allowed each country to have at least one neighbour. The average number of neighbours within this distance was 6.03. Based on this, the 4-nearest neighbours matrix and the 10-nearest neighbours matrix were considered in addition to the maximum distance matrix. This analysis allowed prior assessment of the relevance of spatial models.

Four global spatial models (GSMs) [2] were considered, including OLS regression (OLS), the spatial lag model (SLM), the spatial error model (SEM), and the conditional autoregressive model (CAR) [18]. The OLS model was used because it is one of the most used regression techniques, though it has some constraining assumptions which limit its applicability for data with special features like spatial data. It was used as a reference for comparison purposes. The SLM, SEM, and CAR were considered because (i) we were primary interested in global (not local) spatial modelling, and (ii) they are the most used global spatial regression techniques in epidemiological modelling [2,6,19].

The SLM and SEM are also known as Simultaneous Autoregressive Models (SARs). OLS regression assumes spatial stationarity across the scale and, therefore, hypothesises that a model conceptualised for a particular area can be applied effectively to other areas of interest [20]. According to Anselin and Arribas-Bel [21], the global OLS has fundamental assumptions; the observation in the feature space does not vary with space, and therefore should be independent, and the residual model errors should not be correlated [22]. The OLS is formulated as follows:

$$\mathrm{Y}=\mathrm{X}\beta +\epsilon ,$$

(1)

where Y is the vector of response variable, $\beta$ the vector of slopes associated with the predictors matrix X, and $\epsilon$ the error term.

The spatial lag model (SLM) assumes spatial dependence between the explanatory and response variables in feature space and conceptualises the global regression by incorporating spatial dependence attributes in the modelling process. The SLM also assumes that spatially lagged dependent variables are in the model estimation, which can be ensured by the spatial dependence test resulting from the OLS [2]. The effect of this spatial variable generated from a weighted contiguity matrix quantifies the level of interactions of an observation with its neighbour values in the feature space. Suppose that the determinant factors tested by Moran’s I (error), the Lagrange Multiplier (lag), and Robust LM (lag) exhibited statistically significant estimates at a defined probability level. In that case, one should reconsider the model selection process and opt for the SLM (i.e., the unrestricted model) as a replacement for the OLS (the restricted model without spatial term). The SLM is formulated as follows:

$$\mathrm{Y}=\rho \mathrm{W}\mathrm{Y}+\mathrm{X}\beta +\epsilon ,$$

(2)

where $\rho$ is the autoregression parameter, W is a matrix of weights, and the remaining parameters are defined as above.

The spatial error model (SEM) is an extension of global models that fundamentally stands on the assumption of spatial dependence in the residual error of the OLS [20]. The SEM posits that spatial autocorrelation among regression residuals is thus evident. Two standard spatial dependence tests, the Lagrange Multiplier (error) and Robust LM (error), were performed to ensure statistical significance in the spatial dependency in error terms. The SEM can be written as follows:

$$\mathrm{Y}=\mathrm{X}\beta +\lambda \mathrm{W}\zeta +\epsilon ,$$

(3)

where $\lambda$ is the autoregression parameter, $\zeta$ is the spatial error term, and the rest is as above.

The conditional autoregressive (CAR) model assumes a conditional spatial dependence between the response and the explanatory variables through a symmetric weights matrix. The model can be written as follows [18]:

$$\mathrm{Y}=\mathrm{X}\beta +\rho \mathrm{W}(\mathrm{Y}-\mathrm{X})+\epsilon ,$$

(4)

with $\epsilon =N(0,{\mathrm{V}}_{\mathrm{c}})$. If the error variance ${\sigma }^2$ is constant for all locations i, the covariance matrix is ${\mathrm{V}}_{\mathrm{c}}={\sigma }^2{(\mathrm{I}-\rho \mathrm{W})}^{-1}$, where W is a matrix of weights that must be symmetric. Though the CAR and SAR models are related, the terms $\rho \mathrm{W}$ used in both the CAR and SAR models are not identical because the matrix W does not need to be symmetric in the SAR models.

All statistical analyses were implemented in R software version 4.1.0 [23]. The spatial regression models were implemented in the package “spatialreg” [24] and the LM tests in the package spdep [25]. The best model was selected based on the AIC, BIC, $R^2$, Root Mean Squared Error (RMSE), and statistical difference from the spatial autocorrelation tests. The coefficient of determination ($R^2$) statistics denote the overall model strength and robustness. The AIC and BIC values measure the overall model accuracy and parsimonious character. The RMSE measures the precision of the model fitted to the observed data. The residuals of the models were plotted for further diagnostic purposes (see Figure S1 in the Supplementary File).

The relative importance of the selected explanatory variables for both response variables was assessed using the Random Forest model [26], which spots the key explanatory factors in the models [2]. This was implemented in the “randomForest” package in the R software [27]. Because the importance ranking can vary between runs due to the random selection of training data and variables to determine the split at each node [28], the model was run with 1000 trees [29], and the mean decrease in accuracy (%IncMSE) was used to measure predictor influence. %IncMSE is the average increase in the squared residuals of the test set when the variable is pruned, and it provides information on the variable’s contribution to the overall variance of the predicted variable. This measure was calculated for each tree in the forest and then averaged over all trees.

3. Results

3.1. Spatial Heterogeneity in COVID-19 Cases and Deaths across African Countries

The spatial distribution of COVID-19 cases and deaths is illustrated in Figure 1. The highest numbers of cases (>60,000 cases per million) were observed in Seychelles, Botswana, Cabo Verde, Tunisia, Libya, South Africa, Namibia, and Eswatini, while the lowest numbers of COVID-19 cases (<2000) were accounted for in Niger, Chad, Tanzania, Sierra Leone, Burkina Faso, the DRC, Nigeria, Sudan, Liberia, Mali, South Sudan, and Somalia. In the remaining countries, the levels of COVID-19 cases were relatively moderate (2000–30,000 cases) (Figure 1). Considering the COVID-19 deaths across Africa, the highest incidence (greater than 1000 deaths per million) was recorded in Tunisia, followed by Seychelles, South Africa, Namibia, Eswatini, and Botswana. In contrast, the lowest numbers of deaths (<20 deaths per million) were observed in Burundi, followed by Chad, Niger, South Sudan, Tanzania, Benin, Sierra Leone, the DRC, Nigeria, and Burkina Faso (Figure 1).

3.2. Association between Explanatory Factors and COVID-19 Cases and Deaths

The OLS regression model on the number of cases showed that variables such as Tests_1Mpop, Density_2020, Urban_Rate, DepR, DepR_old, bio1, bio17, HIV prevalence, raised total cholesterol, AdjSav, GDP, and number of airports in the country had significant relationships with the number of cases (

Table 1. Global regression estimates derived from OLS, SLM, and SEM for COVID-19 cases and deaths across African countries.

Number of Cases Per Million	OLS Regression				SEM with 10-Nearest Neighbour Weights Matrix
	Estimate	Std. Error	t Value	$Pr(>\mid t)$		Estimate	Std.Error	Statistic	p-Value
(Intercept)	7.838	0.489	16.031	<2 ×${10}^{-16}$		7.520	0.254	$2.96\times {10}^{01}$	$0.00\times {10}^{+00}$
Tests_1Mpop	1.875	0.440	3.959	0.0003		2.43	0.390	6.1	<0.001
Forest_area	−0.655	0.427	−1.532	0.134		0.098	0.272	$3.59\times {10}^{-01}$	$7.20\times {10}^{-01}$
Density_2020	1.195	0.498	2.40	0.022		1.527	0.361	$4.23\times {10}^{00}$	$2.31\times {10}^{-05}$
Urban_Rate	0.997	0.40	2.033	0.0490		1.07	0.28	3.8	0.0001
DepR	−1.896	0.590	−3.166	0.0030		−2.03	0.43	−4.7	$2.38\times {10}^{-06}$
DepR_old	1.245	0.602	2.070	0.0460		2.000	0.464	$4.31\times {10}^{00}$	$1.63\times {10}^{-05}$
Meth_em	−0.957	0.568	−1.686	0.1010		−0.944	0.487	$-1.94\times {10}^{00}$	$5.25\times {10}^{-02}$
biol	−1.735	0.570	−3.016	0.0045		−1.920	0.340	−5.50	$3.52\times {10}^{-08}$
bio17	−0.883	0.427	−2.066	0.0460		−1.496	0.264	$-5.67\times {10}^{00}$	$1.45\times {10}^{-08}$
BCG.19	0.673	0.444	1.516	0.1380		0.538	0.253	$2.13\times {10}^{00}$	$3.36\times {10}^{-02}$
HIV.19	1.488	0.548	2.717	0.0100		2.596	0.369	$7.03\times {10}^{00}$	$2.07\times {10}^{-12}$
Raised_Choleste_2018	1.494	0.602	2.483	0.0180		0.875	0.505	$1.73\times {10}^{+00}$	$8.31\times {10}^{-02}$
AdjSav	−2.305	0.476	−4.838	$2.46\times {10}^{-05}$		−2.031	0.337	$-6.03\times {10}^{00}$	$1.670\times {10}^{-09}$
GDP. 19	2.098	0.571	3.675	0.0008		2.312	0.550	$4.20\times {10}^{00}$	$2.63\times {10}^{-05}$
Nb Airport	−1.029	0.503	−2.047	0.0480		−0.839	0.396	−2.122	$3.38\times {10}^{-02}$
lambda						−3.034	0.336	−9.043	$0.00\times {10}^{00}$
Number of Death Per Million	OLS Regression					SEM with Maximum Distance Weights Matrix
(Intercept)	5.622	0.466	12.068	0.0000		5.880	0.315	$1.87\times {10}^{+01}$	$0.00\times {10}^{+00}$
Tests_1Mpop	1.502	0.63	2.381	0.0221		1.19	0.51	2.30	$2.09\times {10}^{-02}$
Density_2020	−2.056	0.73	−2.787	0.0081		−1.40	0.61	−2.29	$2.20\times {10}^{-02}$
Forest_area	−0.666	0.411	−1.621	0.1129		−0.521	0.265	$-1.97\times {10}^{00}$	$4.89\times {10}^{-02}$
DepR	−1.531	0.69	−2.219	0.0322		−1.81	0.57	−3.14	$1.67\times {10}^{-03}$
Meth_em	−1.980	0.562	−3.526	0.0010		−1.974	0.442	−4.464	$8.03\times {10}^{-06}$
bio17	−0.728	0.486	−1.499	0.1418		−1.148	0.363	−3.163	$1.56\times {10}^{-03}$
mimq	−1.808	0.67	−2.708	0.0099		−1.69	0.54	−3.08	$2.00\times {10}^{-03}$
HIV. 19	2.249	0.565	3.982	0.0002		2.375	0.371	6.406	$1.49\times {10}^{-10}$
Malaria. 19	−2.048	0.539	−3.8	0.0004		−1.900	0.367	$-5.18\times {10}^{00}$	$3.58\times {10}^{-07}$
Commun_DiseasePrevalence2019	−1.224	0.671	−1.823	0.0759		−1.613	0.454	−3.550	$3.85\times {10}^{-04}$
GHS.index.19	1.197	0.534	2.240	0.0308		0.977	0.383	2.550	$1.07\times {10}^{-02}$
AdjSav	−2.635	0.466	−5.659	$1.54\times {10}^{-6}$		−2.783	0.307	$-9.07\times {10}^{+00}$	$0.00\times {10}^{+00}$
GDP.19	1.319	0.576	2.29	0.0275		1.446	0.422	$3.43\times {10}^{+00}$	$6.1\times {10}^{-04}$
lambda						−0.835	0.194	−4.296	$1.74\times {10}^{-05}$

Tests_1Mpop = total number of tests per 1 million people; Forest_area = total land area that is covered by forests (ha); Density_2020 = number of people by land area in 2020, measured in square kilometers, most recent year available; Urban_Rate = population in urban agglomeration of more than 1 million, % of total population; DepR = dependence ratio (% of working-age population in 2020); DepR_old = dependence ratio for old people (% of total population in 2020); Meth_em = methane emissions in energy sector (thousand metric tons of CO₂ equivalent) in 2018; bio1 = annual mean temperature; bio17 = precipitation of driest quarter; BCG.19 = BCG vaccination coverage, in %; HIV.19 = prevalence of HIV; Raised_Choleste_2018 = raised total cholesterol (≥5.0 mmol/L); AdjSav = adjusted savings in % of GNI (AdjSav); GDP.19 = GDP per capita (current US dollars) in 2019; NbAirport = number of airports in the country; mimq = moisture index of the most moist quarter; Malaria.19 = reported cases of malaria per 100,000 population; Commun_DiseasePrevalence2019 = burden of communicable diseases and maternal, prenatal, and nutritional conditions per 100,000 population; GHS.index.19 = GHS index.

). Tests_1Mpop, Density_2020, Urban_Rate, DepR_old, HIV prevalence, raised total cholesterol, AdjSav, and GDP had positive relationships (estimate > 0), while the other variables (DepR, bio1, bio17, AdjSav, and Nb_Airport) had negative relationships (estimate < 0). For the number of deaths, Tests_1Mpop, population density (Density_2020), dependence ratio (DepR), methane emissions (Meth_em), moisture index of the moistest quarter (mimq), HIV prevalence, malaria prevalence, GHS index, AdjSav, and GDP turned out to have a significant (p-value < 0.05) relationship (Table 1). Tests_1Mpop, population density (Density_2020), HIV prevalence, GHS index, and GDP had positive relationships (estimate > 0), while the other variables (DepR, Meth_em, mimq, Malaria.19, and AdjSav) had negative relationships (estimate < 0) (Table 1).

Among the three weight matrices considered to test the global spatial autocorrelation (the maximum distance matrix, the 4-nearest neighbours matrix, and the 10-nearest neighbours matrix) (

Table 2. Summary of the global spatial autocorrelation test (Moran’s I).

Weights Matrix	Moran’s I Statistic	Expected Value	Variance	p-Value
Number of cases
Maximum distance	−0.0942	−0.0208	0.006	0.811
4-nearest neighbours	−0.0501	−0.0208	0.007	0.631
10-nearest neighbours	−0.0931	−0.0208	0.002	0.920
Number of deaths
Maximum distance	−0.0584	−0.0208	0.006	0.170
4-nearest neighbours	0.1304	−0.0208	0.007	0.044
10-nearest neighbours	0.0753	−0.0208	0.002	0.033

, Figure S2), significant spatial autocorrelation was observed for the number of deaths with the 4-nearest neighbours matrix and the 10-nearest neighbours weights matrix (Table 2).

Using the robust Lagrange Multiplier (LM) test and based on fit statistics such as the $R^2$, AIC, BIC, deviance, and RMSE, we were able to compare the performance of the SEM, SAR, and CAR models (

Table 3. Evaluation statistics for the models on the number of cases and death.

Weights	Models	${\mathbf{R}}^2$	AIC	BIC	Deviance	logLik	RMSE	Robust LM	p-Value
Log number of cases
Identity	OLS	0.888	93.53	120.01	10.93	−34.764	0.477
Max Dist	SEM	0.917	87.41	115.783	8.099	−28.703	0.411	6.762	0.0093
Max Dist	SLM	0.889	95.372	123.749	10.885	−32.686	0.476	3.149	0.0760
10-NN	SEM	0.949	78.186	106.563	4.975	24.093	0.322	7.000	0.0033
10-NN	SLM	0.889	95.398	123.775	10.894	−32.699	0.476	0.420	0.5167
4-NN	SEM	0.893	94.542	122.920	10.478	−32.271	0.467	2.938	0.0865
4-NN	SLM	0.893	93.668	122.045	10.442	31.834	0.466	4.066	0.0438
Max Dist	CAR	n.a.	95.479	123.857	n.a.	−32.740	0.476	n.a.	n.a.
10-NN	CAR	n.a.	95.254	123.901	n.a.	−32.762	0.477	n.a.	n.a.
Log number of deaths
Identity	OLS	0.860	103.595	124.404	15.167	−40.797	0.316
Max Dist	SEM	0.897	96.754	119.456	11.225	−36.377	0.484	9.175	0.0025
Max Dist	SLM	0.864	104.455	127.157	14.779	−40.227	0.555	5.952	0.0147
10-NN	SEM	0.888	100.431	123.133	12.182	−38.216	0.504	4.051	0.0442
10-NN	SLM	0.865	103.923	126.625	14.598	−39.962	0.551	4.376	0.0365
4-NN	SEM	0.873	103.379	126.081	13.801	−39.690	0.536	2.783	0.0953
4-NN	SLM	0.862	104.954	127.655	14.945	−40.477	0.558	2.718	0.0992
Max Dist	CAR	n.a.	105.28	127.986	n.a.	−40.642	0.557	n.a.	n.a.
10-NN	CAR	n.a.	105.28	128.285	n.a.	−40.642	0.562	n.a.	n.a.

Max Dist = maximum distance, 4-NN = 4-nearest neighbours, 10-NN = 10-nearest neighbours, n.a. = not applicable, SLM = spatial lag model, SEM = spatial error model, CAR = conditional autoregressive model. Values in bold represent statistics of models that significantly differed from the OLS.

). For the number of cases, the SEM with the 10-nearest neighbours matrix weight was the best performing and differed significantly from the OLS (LM = 7.000, p-value = 0.0033, Table 3). This model had the highest $R^2$ ($R^2$ = 0.949) and the lowest values for the other criteria (AIC, BIC, and RMSE). For the number of deaths, the SEM and SLM with the maximum distance matrix weight and the 10-nearest neighbours matrix weight significantly outperformed the OLS and the CAR models. Based on fit statistics, the SEM with the maximum distance matrix weight was the best. This model had the highest $R^2$ ($R^2$ = 0.897) and the lowest values for the other criteria (AIC, BIC, and RMSE) (Table 3).

The summary of the SEM for the number of cases showed that most variables (11 out of 12) that were significant in the OLS remained significant in the SEM, except the raised total cholesterol, which turned out to be non-significant. However, the effect of BCG coverage, which was not significant in the OLS, turned out to be significant in the SEM with a positive effect on the number of cases. The direction (sign of the estimate) of the effects of the variables did not change from the OLS to the SEM, but, for most of the variables (except AdjSav and the number of airports), the magnitude of their effects (absolute value of the estimate) increased from the OLS to the SEM and even doubled for some variables (e.g., bio17 and prevalence of HIV). These results indicate misleading conclusions if the autocorrelation is not considered in the modelling (Table 1). For the number of deaths, the summary of the SEM (Table 1) indicated that all variables that were significant in the OLS also had a significant relationship with the number of deaths per million. The directions (sign of the estimates) did not also change, but the magnitude of their effects changed slightly. Variables such as Forest_area, bio17, and Commun_DiseasePrevalence2019 that were not significant in the OLS turned out to be significant, all with a negative relationship with the number of deaths per 1 million population, indicating that countries with higher forest cover, higher precipitation in the driest quarter, and higher prevalence of communicable diseases had a lower number of deaths per million population (Table 1).

3.3. Variable Importance

Figure 2 summarises the relative importance of the selected variables (fifteen for COVID-19 cases and twelve for COVID-19 deaths) based on the Random Forest. For the COVID-19 cases, among the variables, the five with the highest relative importance were found to be the number of tests per 1 million people (Tests_1Mpop, 28%) followed by adjusted savings (AdjSav, 7%), GDP per capita (GDP.19, 6.5%), dependence ratio (DepR, 5%), and annual mean temperature (bio1, 4%) (Figure 2a). The contribution of the other variables was roughly null. For the COVID-19 deaths, the number of tests per 1 million people (Tests_1Mpop, 17%) had the highest relative importance, followed by the prevalence of malaria (Malaria.19, 14%), the prevalence of communicable diseases (Commun_DiseasePrevalence2019, 7%), AdjSav (6.8%), and GDP (6.5%) (Figure 2b). The contributions of the dependence ratio, prevalence of HIV (HIV.19), and moisture index of the most moist quarter (mimq) were very low and those of Forest_area, methane emissions (Meth_em), precipitation of driest quarter (bio17), and population density (Density_2020) were roughly null.

4. Discussion

Although the African continent has not been severely affected by the COVID-19 pandemic [1], a better understanding of how socio-economic and climate factors have shaped the pandemic dynamics is crucial for informing the policymakers at both country and continental levels. Among the several existing models, choosing the most appropriate ones is important to avoid misleading conclusions, especially when dealing with multi-location data where spatial autocorrelation matters. In this study, we showed that the distribution of COVID-19 cases and deaths was heterogeneous across the 54 African countries and sought to understand underlying socio-economic and climate factors. To do so, we compared the performance of OLS, SLM, SEM, and CAR models on the number of COVID-19 cases and deaths per million population.

Consistent with previous findings (e.g., [2,6]), we found that models incorporating spatial autocorrelation (SLM and SEM) outperformed the OLS for both the number of COVID-19 cases and deaths. This finding highlights the importance of exploring the potential effect of spatial autocorrelation in fitting models with multi-location data. We found an increase of 6% for the $R^2$ for the number of cases and 4.5% for the number of deaths. These are, respectively, larger than the 4% increase reported for the number of cases and lower than the 33% increase for the number of deaths found by Maiti et al. [2] in a study of socio-economic and ecological drivers of COVID-19 dynamics at the county level in the United States of America. This suggests that the magnitude of the model improvement when accounting for spatial autocorrelation likely depends on the context and the studied variables. Our models also have a better explanatory power than previously established models for Africa (e.g., Adj-$R^2$ = 70% for the number of cases and Adj-$R^2$ = 50% for the number of deaths in Bouba et al. [7]).

Population demography pattern and structure, migration, socio-economic conditions, health care systems, pollution, and climate have been shown to modulate the dynamics of COVID-19 and hence may be epidemiologically informative in several places [2,6,30]. For example, Su et al. [14] found that paying more attention to controlling migration, either national or international, restricted population flows, modernising the health care system by improving diagnosis and treatment capacity, and upgrading the public welfare system to make it fully functional for the crisis situation could be the points of interest to effectively fight against COVID-19. Our results showed that variables such as the number of tests per million population, age dependency ratio, old dependency ratio, urbanisation rate, bioclimatic variables, and pollution metrics are important drivers of COVID-19 incidence in Africa.

The low burden of COVID-19 in most African countries was suggested to be partly explained by the flaws in the detection and reporting system [31], which appeared to be supported by the positive and significant association with both the number of cases and deaths per million population that we found. Bouba et al. [7] also found similar results, suggesting that the statistics reported in African countries might be sufficiently underestimated, at least for the number of cases. This also indicates the relevance of accounting for the number of tests as a covariate for proper estimations of the effect of other variables. Indeed, bias, especially underreporting and reporting delays, is a major issue in African COVID-19 cases and deaths data, which some studies have shown to being largely underestimated by a factor of 8.5 on average due to the weakness of the health systems at country level [32,33,34]. To consider this potential bias, we have included the number of tests [33] as an explanatory variable, which turned out to be significant for both the number of cases and number of deaths. Nevertheless, this might not have entirely addressed the issue of underreporting as this is heterogeneous across countries [33], which introduces uncertainty in our modelling.

Children and the old-aged population are often more vulnerable to respiratory diseases [35,36], thus indicating the relevance of examining the potential role of the age dependency ratio (DpR) and old dependency ratio (DepR_old) in the morbidity and mortality of COVID-19. DpR is the sum of the young population (under the age of 15) and elderly population (aged 65 and over) relative to the working-age population (aged 15 to 64). DepR_old is the number of people (in the age group of 65 and older) per 100 people (aged 15 to 64). Our data and models indicate significant negative relationships between DpR and the number of cases and number of deaths and, marginally, a significant negative relationship between DepR_old and the number of deaths, consistent with the findings of Varkey et al. [35] for Asian countries. This result supports the fact that, although statistics of earlier waves indicate that older adults are more prone to COVID-19, the subsequent waves provide evidence that even young adults are also affected by the disease.

The urbanisation level was one of the first confirmed positive driving factors of COVID-19 transmission and subsequent deaths. This resulted in the first non-pharmaceutical interventions to curb the disease dynamics, such as forbidding people gathering, social distancing, airport closures, limited travel, sanitary cordons, etc. [37], which all aimed to reduce people gathering, and hence the propagation of the virus through, e.g., aerosols, droplets, and bioaerosols. Using data from 184 countries, Upadhyaya et al. [38] found a positive and statistically significant association between urbanisation level and COVID-19 mortality. Similarly, Fan et al. [39] reported a positive association between urbanisation with regional health vulnerability and the severity of the COVID-19 case rate and death rate.

In addition to the social, viral, and human dimensions regulating COVID-19 cases and death patterns, climate may also play a pivotal role as a co-factor in the disease dynamics [40]. For example, the duration of survival and transmission of SARS-CoV-2 through aerosols, droplets, and bioaerosols are negatively affected by temperature [41]. The negative relationship between annual mean temperature (Bio1) and COVID-19 cases that we found agreed with several previous findings, supporting the conclusion that temperature has a negative relationship with the incidence of COVID-19 [42,43]. In particular, a 1 °C rise in temperature was associated with a 1.92 decrease in cases per million. Our findings also indicated that the precipitation of the driest quarter (Bio17) was negatively associated with the number of cases, corroborating previous evidence that bioclimatic variables are important factors shaping the incidence distribution of COVID-19 [40]. In addition to temperature- and precipitation-related variables, moisture has also been suggested as a significant correlate of the number of COVID-19 cases and deaths [44]. There is evidence that moisture is an important risk factor for respiratory diseases, where infection is enhanced in low-humidity conditions [45], resulting in a negative relationship between humidity and the incidence of respiratory disease. In this regard, Ma et al. [44] reported a negative association between humidity and the daily death counts of COVID-19 in Wuban. Consistent with these findings, our results also indicate that the number of COVID-19 deaths decreases with the moisture index of the most moist quarter (Mimq), highlighting the importance of this factor, particularly for the number of deaths. This negative relationship might somehow explain the low number of deaths in the arid countries of Africa (e.g., Niger, Mali, and Burkina Faso), where the Mimq is often high. Contrary to Bouba et al. [7], who did not find any association between COVID-19 cases and deaths and climate variables, our findings provide evidence of the significant role of climate variables in the patterns of the disease in Africa. These differences could be linked either to the collinearity among predictors, diluting the effect of some variables, or the fact that we explicitly considered spatial autocorrelation in our models, which was not the case in [7].

Changes in levels of air pollution affect urban environmental health and are often associated with an increased likelihood of viral infection [46], which includes COVID-19. Our findings suggest that high methane emissions and many people practising open defection are negatively associated with the number of cases and deaths, respectively. These findings are counter-intuitive as increased pollution is expected to increase the likelihood of infections and mortality. These findings could hide an indirect effect of confounding factors that our model might not capture. It may also be linked to the fact that the data used for these two variables are too old (1 to 2 years before the pandemic’s start) to determine the current patterns of the disease. Unfortunately, these are the most recent data that we found, thus revealing a critical issue with public data in African countries.

Among the significant variables, the number of tests per 1 million people (Tests_1Mpop), adjusted savings (AdjSav), and GDP were identified as the most important for both the number of COVID-19 cases and the number of deaths, illustrating the importance of these variables in driving the overall pattern of COVID-19 on the continent. The number of tests per 1 million people varied from 5073 (Algeria) to 878,731 (Eswatini) with a coefficient of variation of 129.9%. The adjusted savings varied from 0.14 (Mauritius) to 3.64 (Chad) with a coefficient of variation of 59.3%, and the GDP varied from 217 (Burundi) to 16,850 (Seychelles) with a coefficient of variation of 121.3%. As illustrated by these figures, these variables varied greatly across countries. In addition to the above variables that were common to both number of cases and deaths, dependence ratio (DepR) and annual mean temperature (bio1) were identified as important variables for the number of cases, while prevalence of malaria (Malaria.19) and the prevalence of communicable diseases (Commun_DiseasePrevalence2019) were identified as important for the number of deaths. These variables have a coefficient of variation of 39.96%, 14.2%, 130%, and 20.62%, respectively. For the prevalence of malaria, which showed the greatest variation across countries, the negative effect we found was supported by previous findings. For example, Anyanwu [47] reported a reduced number of COVID-19 deaths in malaria-endemic countries, although they suggested further clinical trials. The prevalence of malaria in our dataset varied from 0 in countries such as Algeria, Cabo Verde, Egypt, Lesotho, Libya, Mauritius, Morocco, Seychelles, and Tunisia, where the numbers of cases and deaths were high, to more than 300 in countries such as Sierra Leone, Mozambique, the CAR, and Burundi, where the reported numbers of cases and deaths were relatively low. Concerning the prevalence of communicable disease, previous evidence also showed a strong association between the COVID-19 pandemic and the control and prevention programs, diagnosis capacity, and adherence to treatment of major infectious diseases (e.g., HIV, TB, and malaria), including neglected diseases and non-communicable diseases [48].

Other variables not considered in this study have been suggested to drive the patterns of COVID-19. For example, the Gini inequality index, the Global Health Security (GHS) index, and the mean body mass index (BMI) have been identified as significant correlates of the number of COVID-19 cases in Africa [7]. Similarly, the prevalence of diabetic patients, the number of nurses per 1000 population, and the GHS index were also identified as determinants of mortality due to COVID-19 in Africa [7]. These variables might be correlated with some of the variables included in our models. Nevertheless, this indicates that multi-dimensional perspectives should be considered to understand the drivers of COVID-19 better and consequently design appropriate actions and public health policies.

5. Conclusions

This study performed a cross-country assessment of the socio-ecological drivers of the COVID-19 dynamics in Africa using four global spatial regression models, namely Ordinary Least Square (OLS) regression, the spatial lag model (SLM), the spatial error model (SEM), and the conditional autoregressive model (CAR). The SEM outperformed the other models for both the number of cases and the number of deaths per million people. This study illustrates the importance of accounting for spatial autocorrelation in understanding the dynamics of epidemics while highlighting the important role of socio-economic conditions and climate in driving the dynamics of the epidemics. The study also shows the importance of testing different weight matrices in exploring the performance of the global spatial models. For COVID-19 cases, urbanisation rate, dependence ratio, methane emissions in the energy sector, adjusted savings, annual mean temperature, and precipitation of the driest quarter were the strongest covariates. For the COVID-19 deaths, population density, dependence ratio for old people, adjusted savings, and moisture index of the moist quarter were the strongest covariates. These identified variables explained 94.9% of the variation in the number of cases and 89.7% of the variation in the number of deaths, which is a very good performance. We conclude that improving socio-economic conditions and the environment can help lower the impacts of future epidemics. The study, however, considered only global spatial models, which assume spatial stationarity in the studied features. Further studies could explore local spatial models such as geographical weighted regression (GWR) or multiscale geographical weighted regression (MGWR) which instead assume non-stationarity and this could bring additional insights.