1. Introduction
In this paper, we consider a class of stochastic differential equations (SDE) with fraction Brownian motion with Hurst parameter
as
where the state variable
takes values from a convex open set in
, the initial condition
, and the diffusion coefficient
. We assume that
is an n-dimensional Brownian motion defined on a probability space
, and
be its natural filtration augmented with an independent
-algebra
, where
be the probability law. Our main objective in this paper is to estimate the Hurst parameter by using the maximum likelihood estimation (MLE) method. The SDE expressed in Equation (
1) is very useful in
sticky-price general equilibrium economic models under
Calvo-type settings (Calvo [
1], Alvarez et al. [
2]).
Brownian motion, also referred to as a Wiener process, is a crucial concept in probability theory and stochastic processes. This mathematical model depicts the random movement of particles in a fluid, a phenomenon first observed by botanist Robert Brown. Brownian motion has the following properties: (i) it has continuous trajectories over time, (ii) its increments over non-overlapping time intervals are independent, (iii) its increments over any given time interval depend solely on the duration of the interval, regardless of its specific position on the time axis, and (iv) its increments throughout length
t follow a normal distribution with a mean of 0 and a variance of
t. Mathematically the Brownian motion
for
is defined as
,
, and
has continuous paths with respect to time
s almost surely. Fractional stochastic differential equations extend classical SDEs by using fractional Brownian motion (fBm) rather than standard Brownian motion. Fractional Brownian motion is a broader concept of Brownian motion that accounts for memory and
long-range dependence characteristics, defined by the Hurst parameter
: if
, fBm reduces to a standard Brownian motion if
, fBm shows positive correlation or exhibits persistent behavior, and if
, fBm shows negative correlation or exhibits
anti-persistent behavior. Fractional Brownian motion has the following properties: it exhibits self-similarity property or, for any constant
,
, the increments
are stationary for every
, and the increments of fBm are correlated, reflecting the memory of the process (i.e., long-range dependence). A fractional stochastic differential equation has the integral form
where
is an unknown process,
is the drift coefficient,
is the diffusion coefficient, and
is the fractional Brownian motion with Hurst parameter
H. Since in this paper, we are considering driftless fractional stochastic differential equation, hence,
.
Fractional Brownian motion is a commonly used extension of the standard Brownian motion, incorporating long-range dependence while maintaining self-similarity and Gaussian properties. These characteristics render it a favored stochastic process for modeling a range of complex systems, including financial scenarios and surface growth dynamics (Gairing et al. [
3]). The demand for detecting and studying such systems has spurred the creation of several established statistical tools, such as wavelet analysis, R/S estimators, and generalized variations, among others, which are extensively covered in referenced monographs (Beran [
4], Embrechts [
5], Tudor [
6]). Fractional Brownian motion demonstrates spatial homogeneity. However, many physical systems encounter external forces that confine them to particular areas with high likelihood. In such instances, investigating SDEs as an extension of the fBm model may prove more appropriate. In this context, fBm serves as a stochastic driving force that substantially influences the dynamics of the system. Consequently, exploring and comprehending this random driving force emerge as pivotal pursuits.
Since the publication of Rogers [
7], there has been a sustained discourse surrounding the utilization of fBm in financial modeling. While much of the scholarly literature concentrates on mitigating arbitrage, some publications explore the market microstructure foundations associated with fBm (Rostek and Schöbel [
8]). The predictability mentioned earlier presents hurdles when using fBm to model stock prices. Rogers [
7] highlighted arbitrage possibilities within a fractional Bachelier-type model, which led him to conclude that fBm is not suitable for financial modeling. However, concerns about the broader applicability of Rogers’ findings emerged as they were limited to a linear scenario without drift (Rostek and Schöbel [
8]). The contribution of Shiryaev [
9] involved crafting a precise arbitrage strategy within the fractional market framework, igniting additional debate on the topic. Despite initial findings on financial market models using fBm being misleading, there was still hope for overcoming the shortcomings of the proposed market framework. The research enthusiasm in this area was reignited by fresh insights in stochastic analysis, primarily sparked by the contributions of Duncan et al. [
10]. They introduced a stochastic integration calculus concerning fBm, leveraging the Wick product. This integration framework enables drawing parallels to the established Itô calculus, revitalizing interest in the field (Rostek and Schöbel [
8]).
Even with the introduction of this novel stochastic integration concept, the overall situation faced little improvement. Debaen and Schachermayer [
11] had previously established a significant result applicable to continuous-time market models: regardless of the chosen integration theory, a type of weak arbitrage called
free lunch with vanishing risk can only be eliminated if the underlying stock price process S is a semimartingale. It is apparent that processes driven by fBm, due to their persistent behavior, do not fulfill the semimartingale criterion. Additionally, Cheridito [
12] successfully devised explicit arbitrage strategies in both the fractional Bachelier model and the fractional Black–Scholes market, regardless of whether pathwise or Wick-based calculus was utilized for integration.
In recent studies, attention has shifted towards establishing a market microstructure basis for fBm. Klüppelberg and Kühn [
13] propose a concept called a
shot noise process, aimed at modeling the arrival of new information at random intervals, which then diffuses into the market (Rostek and Schöbel [
8]). This implies that new information can exert a prolonged influence on the price process. Ultimately, Klüppelberg and Kühn [
13] model converges to fractional Brownian motion in the limit. Bayraktar et al. [
14] characterize the passive behavior of investors. This implies that following a trading activity, there exists a probability that an investor refrains from conducting any further transactions during the subsequent period. This is explicitly achieved by introducing a stochastic process. When this process remains at zero for all time intervals, the investor remains inactive. Orders from market participants arrive asynchronously, and trades are executed by a market maker who adjusts prices based on the demand-supply imbalance. In the limit, the price process converges to a geometric fBm. In the absence of this passive behavior exhibited by investors, a classical Brownian motion is observed. Consequently, a market model incorporating both passive investors and continuously active market participants leads to a mixed model akin to Cheridito [
15].
2. Long Memory as Hurst Parameter
The concept of memory effect holds significant importance within financial systems, prompting extensive research into understanding the persistence of patterns, commonly referred to as
long memory, within financial markets. Recently, fractional-order ordinary differential equations have emerged as a valuable tool for characterizing this memory effect within intricate systems (Li et al. [
16]). Consider a stochastic process denoted by
, where observations
are made at discrete intervals
, for all
. A time series exhibits long memory when the correlation between current and past observations decays slowly over time. This stochastic process
is considered stationary if the distributions of
and
remain the same for all integers
K, shifts
, and time indices
, with
T representing vector transposition. In the context of Gaussian processes, this is equivalent to the autocovariance function
being independent of
s, see (Chronopoulou and Viens [
17]). These notions are often termed as
strict stationarity and
second-order stationarity. Here,
represents the autocovariance function, and
stands as the autocorrelation function. If the sum of absolute autocovariances
diverges, the process
exhibits long memory. Conversely, if this sum is finite, the process demonstrates short memory, and if
for all
, the process lacks memory (Li et al. [
16]). Traditionally, the autocorrelation function has been used to quantify the stochastic memory process, but recently, the Hurst index has gained popularity as a practical alternative for identifying long or short-range dependence.
Definition 1. Consider a stationary process . When the sum of absolute autocovariances diverges, represented as , the process displays a long memory or long range dependence. One sufficient condition for this phenomenon is the presence of the Hurst parameter such that Remark 1. Typically, a long memory model satisfies the stronger condition , where H is the long range dependence parameter of [17]. Proof. Definition 1 implies that a typical long memory model satisfies
. Let there be an autocorrelation function
of the long memory process
such that for a positive finite constant
, following condition holds:
Equation (
2) implies,
Since
, we conclude
. Therefore, for typical long memory models where the autocorrelation function decays according to
the limit
is indeed positive. This implies that the Hurst parameter
H can be called the long memory parameter of
. □
An autocorrelation function that exhibits long memory demonstrates a gradual decay over time. This observation was first made by Hurst, who identified extended persistence in the annual minimum water levels of the Nile River ( Hurst [
18]). The Hurst parameter serves to quantify the smoothness of a time series by examining how it scales concerning the stochastic process. A crucial aspect of memory processes is self-similarity, a concept characterized by the Hurst parameter. In geometry, self-similarity refers to shapes that consist of repeating patterns across multiple scales, potentially extending infinitely. From a statistical perspective, self-similarity suggests that the distributional properties of the process paths remain consistent, regardless of the observation distance (Chronopoulou and Viens [
17]). The rigorous definition of the
self-similarity property is as follows:
Definition 2. A stochastic process is self-similar with self-similarity Hurst parameter H, for any positive constant α, To better understand the impact of the fraction of derivative,
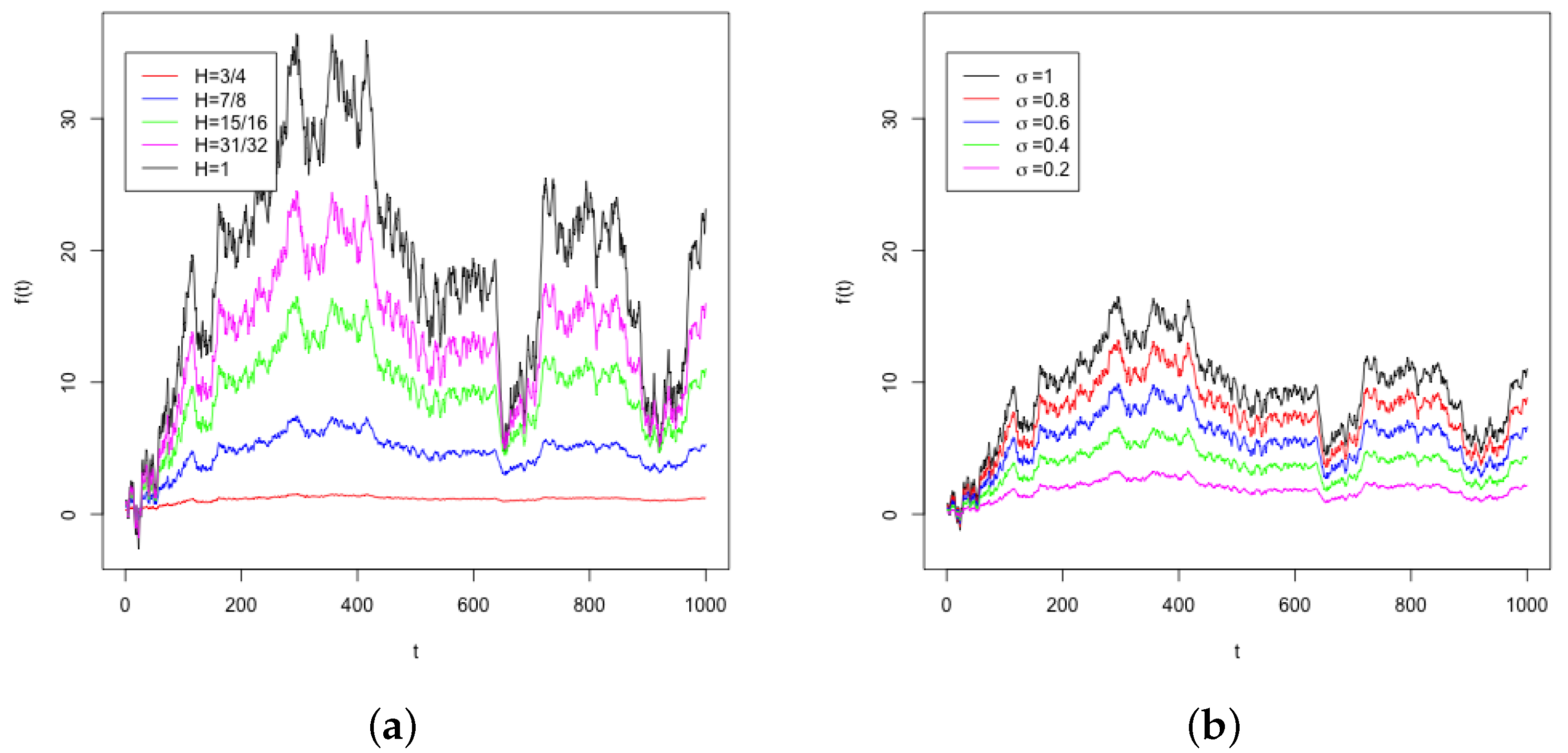
H, on the resulting stochastic process, Panel (a) in
Figure 1 shows the stochastic process for a set of realized deviates across different values of
H. The black line is for
which corresponds to no fraction of the derivative, which is for reference. Notice that the fraction of the derivative compresses the stochastic process and small changes in
H have a large impact on the resulting process. For example, compare
(black) to
(magenta) and notice at the peak near
, the value of the realized process for
is above 30 in contrast to the realized process for
which is under 30. Panel (b) shows the same set of deviates with
across
and
. Notice as the standard deviation decreases it is much more of a simple scaling of the process. The fraction of the derivative has more of an exponential effect on the process. For reference across the two panels, the green line in Panel (a) is the same as the black line in Panel (b). Hence,
H has a much different impact on the process than
, and care should be taken when estimating
H.
3. A Calvo-Type Construction
This section explores an issue concerning strategic complementarities and pricing, as originally discussed by Calvo [
1]. This particular scenario garners frequent attention in studies on sticky prices owing to its practical significance. The model offers a clear-cut framework for elucidating the core elements of the analysis and for scrutinizing crucial outcomes such as the existence, uniqueness, and non-monotonic characteristics of impulse response profiles, which also bear relevance to the state-dependent problem.
At time
s,
is the consumer price index (CPI),
is a consumer preference shock corresponding to the
ith variety and the price set by a firm on consumer good of
ith variety is
such that
(Kimball [
19]). Define
and
as percent deviation from a symmetric equilibrium of a firm’s own and the aggregate price (CPI), respectively (Alvarez et al. [
2]). The economy comprises a range of
atomistic individual firms, each operating independently. Each firm operates under the assumption of a consistent fluctuation in markup averages, denoted by
for all times
. The firm can adjust its pricing only at specific, randomly occurring times denoted by
, which follows a Poisson process characterized by a parameter
. These instances of adjustment are referred to as
adjustment opportunities, and the state of the firm’s pricing at these times is termed the
optimal reset value. Following a price adjustment at time s, the difference in markup,
, jumps according to a Brownian motion without a drift component but with a variance of
. Additionally, the markup experiences abrupt jumps immediately after a price adjustment at
, with each jump in markup denoted by
. Therefore, the markup gap evolves as
where
is an n-dimensional standard Brownian motion. Furthermore, in the absence of any markup jump the continuous version of Equation (
3) becomes,
Moreover, the fractional version of the above equation is Equation (
1), where the variance
is indeed a function of time and markups.
4. Hurst Index Estimators
In this section, we are going to discuss different types of estimators of the Hurst index. The most renowned estimator among these is known as the
R/S estimator, initially proposed by Hurst [
18] in the context of a hydrological issue related to Nile river water storage. Hurst divided the dataset into finite, equal-length blocks and computed the adjusted range (R/S), which is the ratio of the range (R) to the standard error (S) of the new dataset. To ascertain the Hurst index value, the natural logarithm of the adjusted range was first calculated, followed by constructing a regression model where the natural logarithms of the adjusted range and the total number of observations served as the response variable and regressor, respectively (Chronopoulou and Viens [
17]). The slope of this regression equation served as the estimator for
H. This method relies on graphical analysis, where it is up to the statistician to identify the portion of data exhibiting
nicely scattered behavior along a straight line. Particularly in smaller samples, the distribution of the
R/S statistic deviates significantly from normal, exacerbating the problem. Moreover, the estimator is biased and prone to a large standard error.
Gladyshev [
20] formulated a limit theorem concerning a statistic derived from the first-order quadratic variations of fBms. This theorem led to the development of an estimator for the Hurst parameter
H, which exhibited strong consistency but lacked asymptotic normality. Istas and Lang [
21] introduced another estimator tailored specifically for centered Gaussian processes with stationary increments. This estimator, which also utilized first-order quadratic variations, demonstrated asymptotic normality for values of
. Next, Benassi et al. [
22] investigated the second-order quadratic variations of a particular class of Gaussian processes that possessed local fractal properties similar to fractional Brownian motion. They derived an estimator for the Hurst index
H that showed asymptotic normality across all possible values of
H (Melichov [
23]). Coeurjolly [
24] devised a set of consistent estimators for
H based on the asymptotic behavior of the
kth absolute moment of discrete variations of sample paths over discrete intervals within the range of
. These estimators were accompanied by explicit convergence rates applicable throughout the entire range of
, and their asymptotic normality was established. Moreover, Begyn [
25] explored second-order quadratic variations across general subdivisions for processes with Gaussian increments. For a more comprehensive investigation into the asymptotic behavior of quadratic variations for Gaussian processes. Finally, Fhima et al. [
26] presented a technique for conducting change point analysis on the Hurst index concerning a piece-wise fBm, which is an extension of the conventional fBm. Their approach combines two methodologies: the filtered derivative with
p-value (FDpV) method for detecting changes in mean, variance, or regression parameter, and a modified version of the increment ratios (IR) statistic estimator initially introduced in Bardet and Surgailis [
27].
Based on Definition 1, we can derive the sample autocorrelation function
by dividing
by
. Using the
Correlogram approach, we can then plot this function against the total number of observations, denoted as
n. As a heuristic, it is common practice to draw two horizontal lines at
. Any observations falling outside these lines are deemed significantly correlated at the significance level of 0.05 (Chronopoulou and Viens [
17]). In cases where the process demonstrates long memory, the plot should exhibit a slow decay. However, the graphical nature of this method introduces limitations, as it cannot ensure precise results. Given that long memory is an asymptotic concept, it is essential to analyze the correlogram at high lags. Nonetheless, distinguishing long memory from short memory can be challenging, particularly when, for instance,
. To mitigate this challenge, a more appropriate plot involves plotting
against
(Chronopoulou and Viens [
17]). If the asymptotic decay follows a precise hyperbolic pattern, then for large lags, the points should cluster around a straight line with a negative slope equal to
, indicating long memory in the data. Conversely, if the plot diverges toward
with at least an exponential rate, it suggests short memory. Similar to a
Correlogram, a
Variogram can be graphed against the total number of observations, represented as
N. Assessing whether the data display short or long memory using the
Variogram approach poses similar challenges as with the
Correlogram. The primary benefit of these methods lies in their simplicity. Furthermore, because they are non-parametric, they can be applied to any long-memory process. However, these graphical techniques lack precision. Additionally, they often lead to erroneous conclusions, suggesting the presence of long memory even when it is absent. For instance, in scenarios where a process exhibits short memory alongside a rapidly decaying trend, both a
Correlogram and a
Variogram might erroneously indicate long memory.
Maximum likelihood estimation (MLE) stands out as the predominant method for parameter estimation within the realm of Statistics. However, its application within the class of Hermite processes is confined to fBm. This limitation arises from the absence of distribution function expressions for other processes. MLE estimation within this context typically occurs in the spectral domain, utilizing the spectral density of fBm in the following manner.
Let
be a vector of the fractional Gaussian noise (increments of fBm) with covariance matrix
Therefore, the log-likelihood has the following expression:
where
is the normal probability density function (pdf), matrix
is non-singular and
is the transposition of the vector
. To determine the MLE of
H (i.e.,
) we need to maximize the log-likelihood equation with respect to
H.
5. Fractional Brownian Motion
For a fixed t, an
n-dimensional Brownian motion on
, and Hurst parameter
the covariance function is
It is important to note that fractional Brownian motion becomes the usual Brownian motion when
which we are not considering here. Since
, fractional Brownian motion has a stationary increment (Hayashi and Nakagawa [
28]).
Lemma 1. (Kolmogorov–Chenstov continuity criterion) [
29])
. The random field with index set j is a dense of points s on open domain . For and there exists positive constants , and such that then the random field can be extended to a random field indexed by the closure of in such a way that, with probability one, the mapping is continuous, and so that for each , we have that , almost surely. Furthermore, if there exists another positive constant λ such that for each compact set , almost surely for all . For simplicity to prove Lemma 1, we consider a special case where be a unit cube. Let be the set of dyadic rationals in . Now we are going to state and prove the following Lemma 2 Then by using this Lemma 2, we can prove Lemma 1. The general statement of Lemma 1 can be proved by using a similar argument with some changes.
Lemma 2. Let be a real-valued function of random variable in . Consider a set of points with the coordinates such that . Suppose for some and finite the following condition holds:for all neighboring pairs in the same dyadic level . Then the real-valued function extends to a continuous function in , and the extension is Hölder of exponent λ, such thatfor some positive finite . Proof. To prove this Lemma we are utilizing the fact that every
can be attained by a sequence of points
. For every
there is a point
within distance
of
s, so that
. We choose such a point and label it as
. Hence,
as
. Furthermore, the distance between the consecutive points
and
is less than
. This leads to a shorter chain of neighboring pairs in level
connecting
and
. By Equation (
5),
As
is positive, the above expression is additive in
u. Thus, for every
, the sequence
is Cauchy. Since the sequence is convergent, define
. It is important to note that, if
, then the limit converges to the original value
. Moreover, since the chain from
is dominated by the terms of a geometric series with ratio
, then
where
is a positive finite constant.
We need to prove that indeed
is continuous and satisfies the Hölder condition (
6). Set two distinct points
such that for some
u the following condition holds:
The distance between
and
is less than
. This leads to a short chain of neighboring pairs in level
connecting
and
. There is a positive finite constant
such that,
As
for all
, by construction, inequality (
6) follows by triangle inequality. □
Proof of Lemma 1. Since
is an open unit cube, the cardinality of
grows like
. Two points
are subsequent if
is a unit vector times
. Since,
and
s are neighbors in
, imposing Markov inequality on Condition (
4) implies
Since we are using the fact that,
grows like a constant multiple of
,
such that
where
is a positive finite constant. Since
is positive, it is possible to choose
so that
. Therefore, probabilities expressed in Equation (
7) are additive in
u. Therefore, the Borel–Cantelli lemma guarantees the sum to be one and the events
appear finitely in
u. Finally, w.p. 1 there exists a random number
, so that
, for all
at the same dyadic level. The final result is followed by Lemma 2. This process is
-Hölder continuous. □
Lemma 3. The fractional Brownian motion with a Hurst index H has a version where the sample paths are λ-Hölder continuous if . However, if , the fractional Brownian motion is almost surely not λ-Hϊder continuous over any time interval.
Proof. We first prove the sufficiency condition
. Let us choose
such that
. Self-similarity and stationarity in the increment of
s in
imply,
where
is
th absolute moment of a standard normal variable. The Kolmogorov–Chentsov criterion implies this claim.
Now, we prove the necessity of the condition
. Due to the stationarity of increments, it suffices to examine the point
. Following [
30], the fractional Brownian motion adheres to the following law of the iterated logarithm,
Therefore,
fails to satisfy
-Hölder continuity at
for every
. □
From Lemma 3 we conclude that
has to be less than the Hurst index
H. Therefore, by Lemma 1 the bound of the absolute distance between two increments of fractional Brownian motion becomes,
where
. Therefore, the process described in Equation (
8) is
-Hölder continuous.
Remark 2. Lemma 1 and Equation (8) imply that, if the Hurst parameter takes larger values, the sample paths of the fractional Brownian motion have better regularity. For instance, see Figure 1 in [28]. Proof. Stationary increment of fractional Brownian motion implies the increments
have the same distribution as
for every
. On the other hand, The regularity of the sample paths of a stochastic process can be quantified using Hölder continuity. Lemma 3 implies that, for
the fractional Brownian motion
is
-Hölder continuous almost surely. Thus, the larger the Hurst parameter
H, the larger the exponent
that can be chosen. This leads to a better regularity. The variance of increments is
Equation (
9) implies that the expected magnitude of the increments decreases as
H increases. By Kolmogorov continuity theorem, if there exist positive finite constants
and
such that,
then
is
-Hölder continuous. Choose
sufficiently large. Combining Equations (
9) and (
10) implies
For inequalities (
10) and (
11), as
for
, the Kolmogorov continuity theorem is satisfied. Hence, if
H takes larger values, the sample paths of fractional Brownian motion have better regularity. □
For
, the fractional Brownian motion has the representation
where
is some Brownian motion on the probability space
. The kernel function
is defined as
with constant
where
is the Euler Beta function with the corresponding Euler Gamma function
(Buckdahn and Jing [
31]). For Kernel
, define
as the set of Borel measurable functions
f such that
for all
. Let
given by,
stays in the set of step functions
in
such that the function
is symmetric and positive semidefinite in the general sense. Since
we define
(Duncan and Hu [
10]). In Equation (
12),
represents the derivative of the covariance function of fBm with respect to time. This derivative is sometimes referred to as the
incremental variance or
incremental covariance and is crucial in understanding the behavior of fBm. Moreover, this expression provides an in-depth understanding of the local behavior of the covariance structure of fractional Brownian motion. It is valuable for analyzing the characteristics of fBm. It is applicable in fields like signal processing, finance, and other areas where fBM models phenomena with self-similarity and long-range dependence. Equation (
12) has been used to estimate the Hurst parameter
H.
6. Estimators for
In the cases presented here, it is assumed that the data are equally spaced can be scaled to a unit spacing, and have a homogeneous variance of one unit which can easily be obtained by simply standardizing the data. If the data
are observed, the first difference in the data:
This will produce a series with zero mean and variance
. As the data are generated by a fractional Brownian motion process the data will have a normal likelihood of:
Then using Equation (13) the following Maximum Likelihood Estimator (MLE) can be derived.
Furthermore, the variance can be approximated by considering the inverse of the Fisher Information matrix evaluated at the MLE. This results in:
With a quick examination of (
15) one can see that
is inconsistent as
,
, which is problematic as it typically desired that the variance converge to asymptotically to 0 with respect to
n. The issue of inconsistency will not be covered in this work.
It is very difficult to theoretically assess the Bias associated with the MLE due to the square root; however, numerical techniques can be used instead. A simulation study is conducted to determine the Bias of the estimator for
across the values of
H. At each
H value, 10,000 simulated datasets were created and the MLE,
was calculated. The mean
from the 10,000 samples was calculated for each value of
H and plotted against the true value of
H. This is shown in
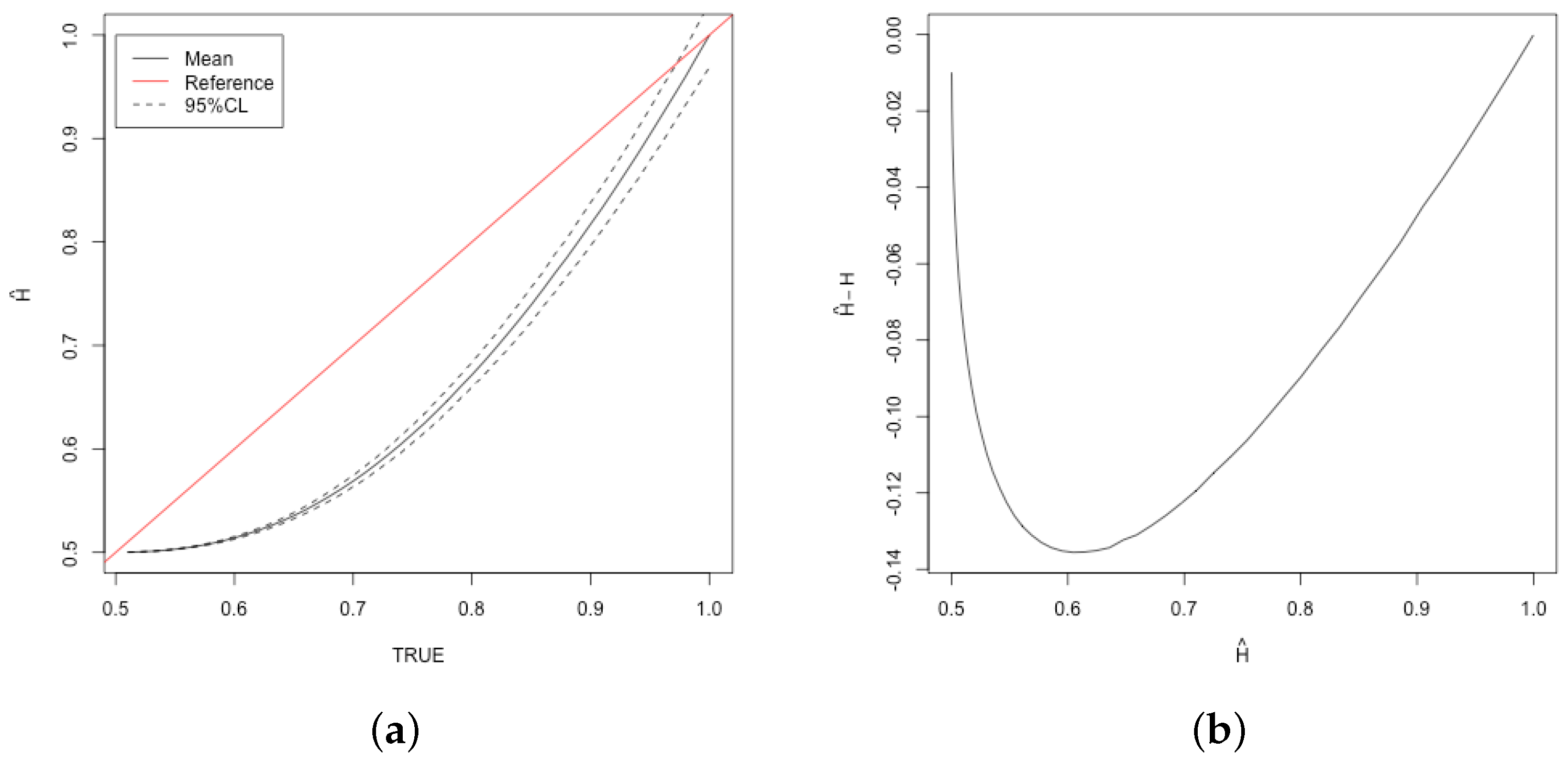
Figure 2 panel (a). Notice there is also a reference line where
in red. From the graph, it is apparent that the estimator tends to be biased on the high side as the mean line is above the red line. To further study the bias
is plotted against
in
Figure 2 panel (b) using the 1000 already obtained simulations. Notice that the shape of this curve allows one to see that the bias is worst for values around 0.61 and best at values around 0.5 and 1.0. The general shape of the curve also allows for the creation of a possible polynomial-based correction.
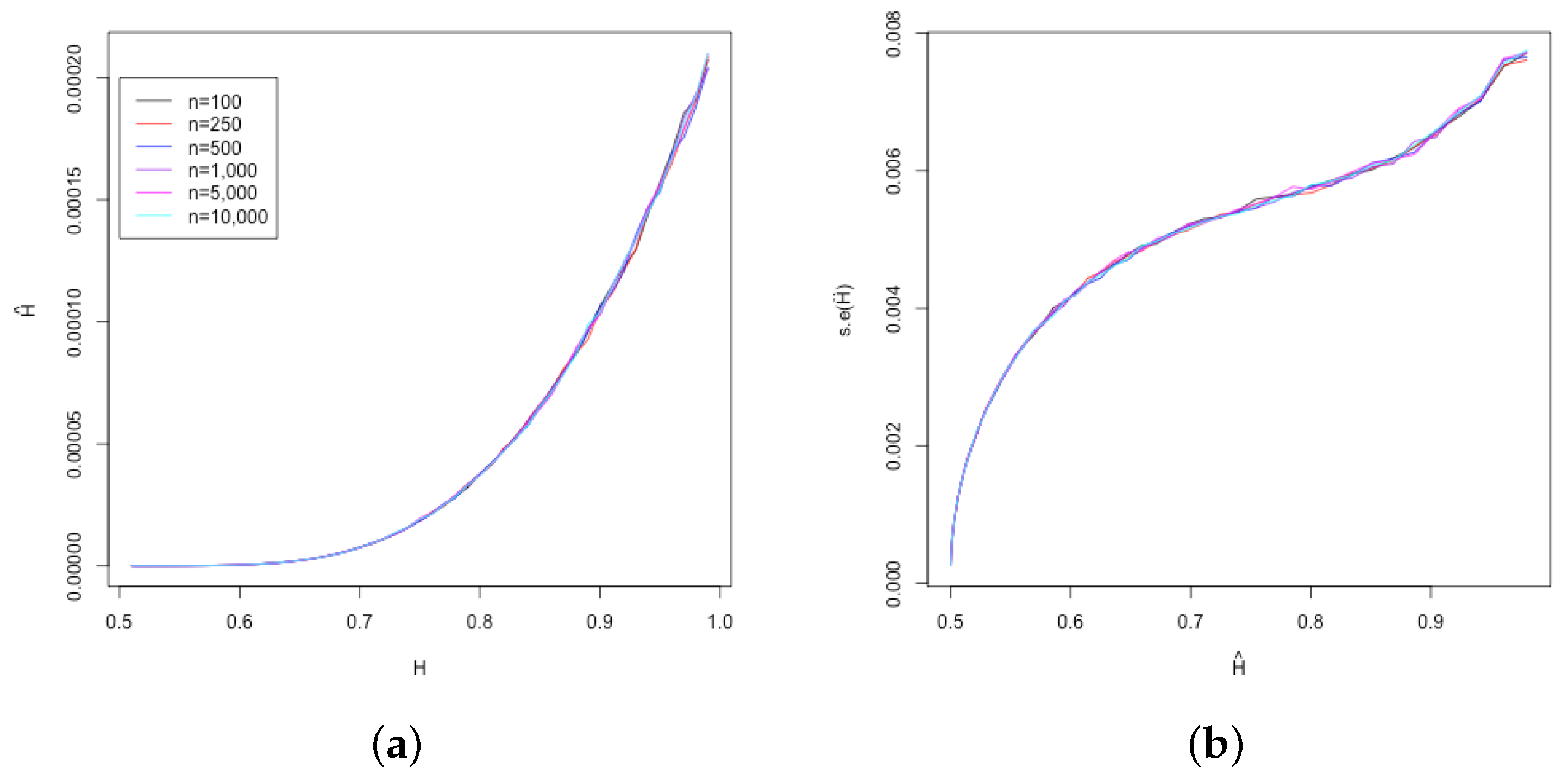
To study the nature of the bias as sample size increases, a simulation study was performed generating 10,000 datasets for each value of
H between
and
in
increments and estimating
for sample sizes of
n = 100, 250, 500, 1000, 5000 and 10,000.
Figure 3 shows the results of this study. Notice that the curve does not change much as the sample size increases. This implies that any correction method does not need to depend on the sample size.
Using the data from the simulation study and the fact that the bias correction function must be 0 at 0.5 and 0 at 1 the following functional form is proposed for the bias correction.
where
and
. Equation (16) is fit to the simulation data using nonlinear least squares to obtain the parameters
and
in order to create an
empirical bias correction function resulting in the following:
Combining Equation (17) with (14) produces the following
approximately unbiased estimator for
H:
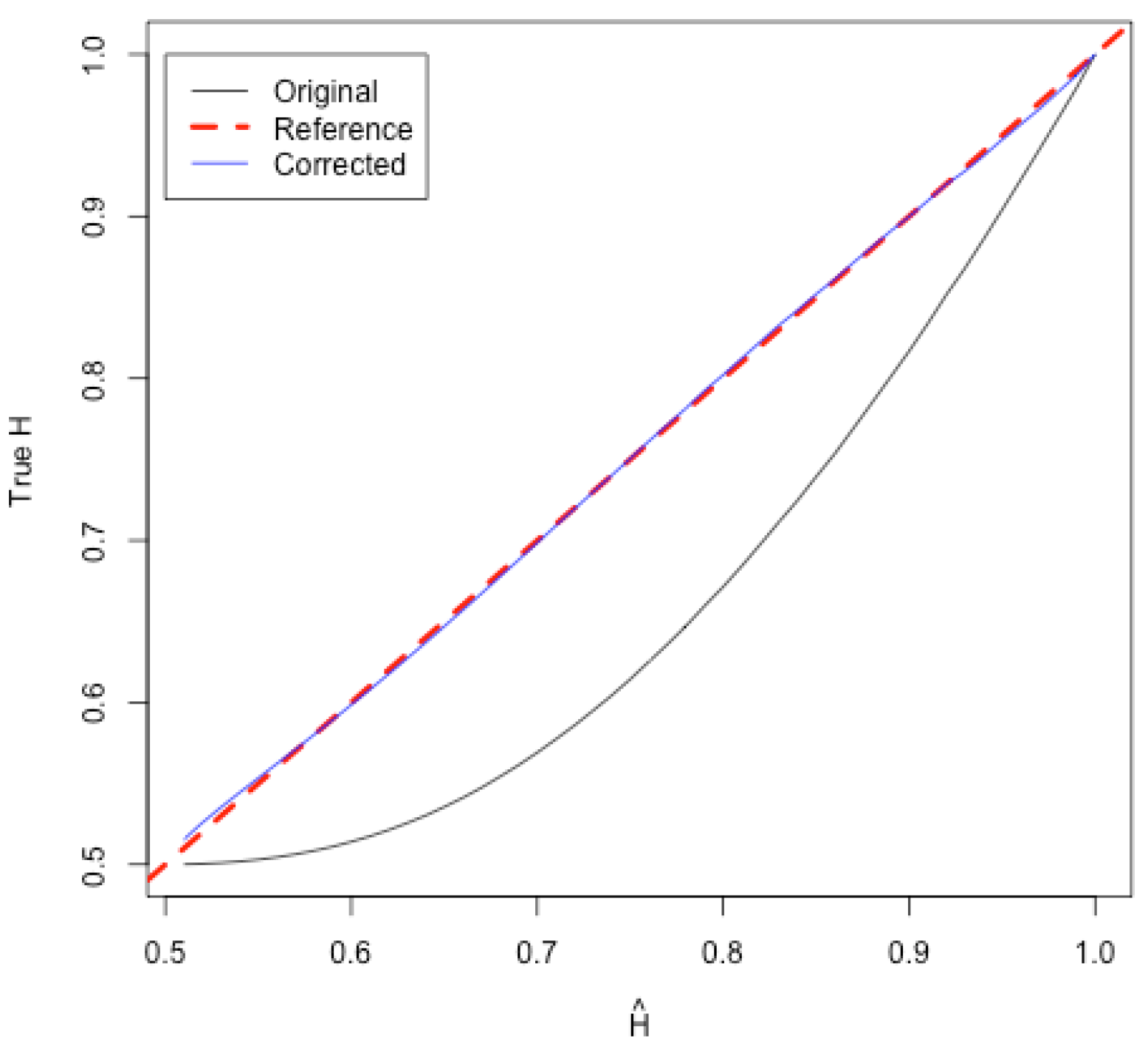
To examine the performance of the estimator given in (18) a simulation study was performed across true values of
H. For each
H, 10,000 datasets were generated and Equation (18) was calculated for each with the resulting mean of the simulations recorded.
Figure 4 shows the results of this simulation study, where the mean
(black) versus true
H and bias-corrected estimator
(blue) and reference line (red-dashed). Notice that the approximate bias-corrected estimate
is very close to the reference line indicating that most of the bias has been accounted for. While a small amount of bias does remain, the “corrected” estimator
is much better than the MLE alone.
Using the variance of the simulated means for
one can create a standard error for
by taking the square root of the variances. This is shown in
Figure 3 Panel (b). Using a least squares polynomial approximation to the simulation data one arrives at:
To be clear, this is an approximation to simulation results and hence there is both simulation and estimation error associated with this standard error. However, there is no clear analytical way to address this problem. Using the results from a dense simulation across the domain should provide us with a reasonable approximation. Here, due to the nonlinear nature of the simulation results, a higher-order polynomial is used.
Using the corrected mean value and the estimated standard error one can create a 95% confidence interval using:
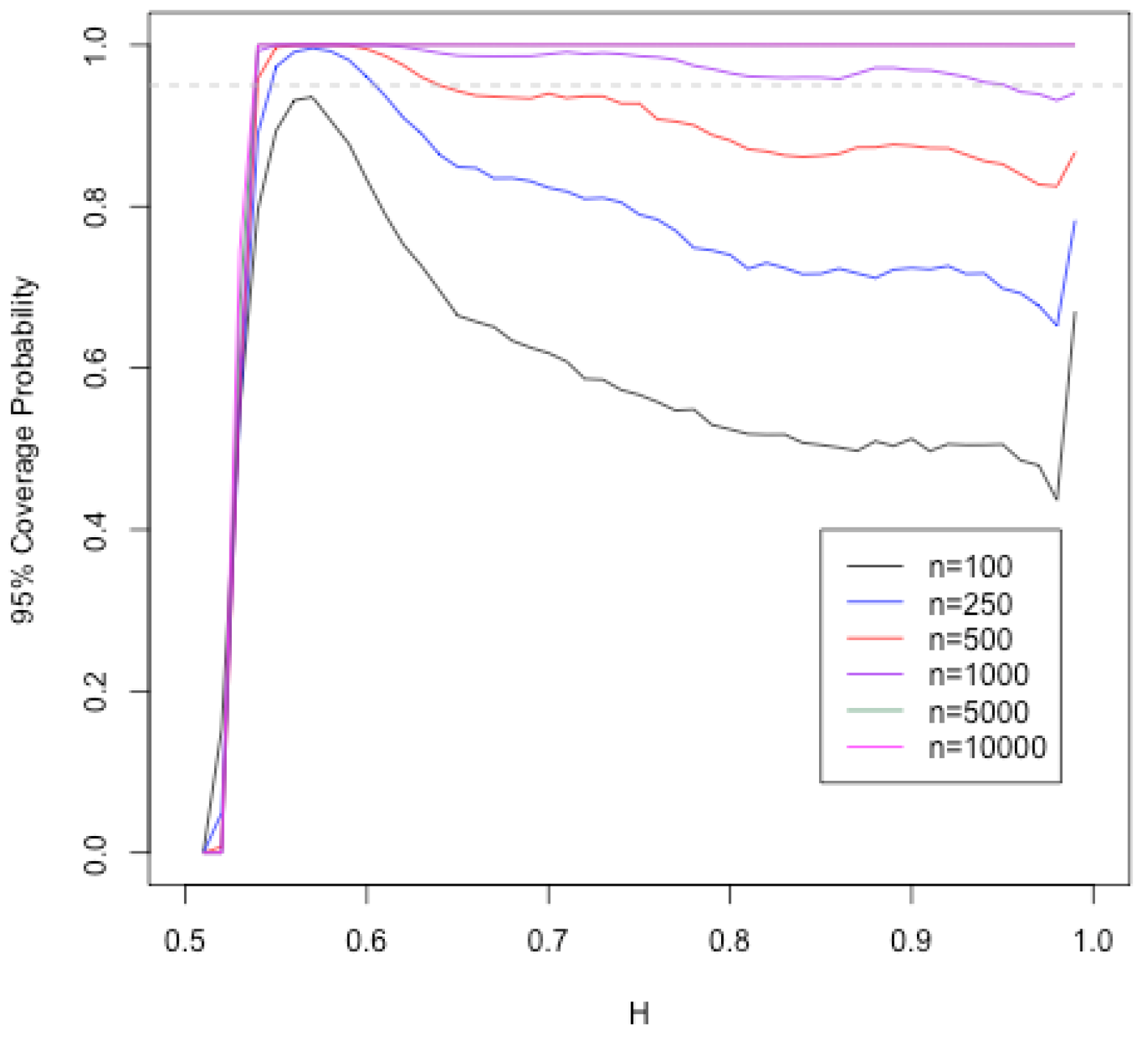
Figure 5 shows the coverage probabilities for 95% confidence intervals using Equation (
20) across the true values of
H for sample sizes
and 10,000. Each is evaluated on 10,000 simulated datasets at each level of
H. A grey dashed line is provided for reference to 95%. One particular item to notice is that no matter the sample size, confidence intervals when the true value of
H is near 0.5 have very poor coverage. As
H obtains larger from 0.5 the coverage probabilities increase dramatically for all sample sizes. Once
H is larger than 0.6, the coverage probabilities for sample sizes 100, 250 and 500 fall below the 95% benchmark with sample size 100 falling as low as 0.4. This suggests that the variance model is quite sensitive to low sample sizes. This result also shows that once the sample size is 1000 or greater the 95% coverage probabilities are maintained. Hence, if one wishes to estimate
H, a sample size of 1000 or more is a good guideline.
7. Example: S&P500 and VIX
To illustrate the method, the same financial datasets used in Beskos et al. [
32] are evaluated here. The S&P500 which is a broad measure of the economy and the Volatility Index (VIX) are each examined for the year prior to the Bear Sterns closure and the year after the Lehmans closure. These are interesting because they reflect how the 2008 financial crisis unfolded as both Bear Sterns and Lehman’s were trading houses that were casualties of the crisis. Specifically, prior to Bear Sterns’s closure the daily close data for 5 March 2007 to 5 March 2008 (labeled 2007 data) and for the year after Lehman’s closure, the daily close data from 15 September 2008 to 15 September 2009 (labeled 2008) were utilized. To employ the method presented here, all-time series were standardized by creating a
Z score for each observation.
Table 1 shows the MLE,
, the approximate corrected MLE,
, and the 95% confidence intervals for the Hurst parameter
H are given for each of the datasets. One particular item to notice is that the parameter for
H estimates does not seem to change that much in the before and after times for either the S&P500 or VIX. Another interesting note is that
is considerably higher here. When comparing with the Bayesian approach of Beskos et al. [
32], the estimated
H is considerably different. In their work, they consider when
and estimate
H to be 0.3 for S&P500 and 0.29 for VIX for 2007 and 0.36 for S&P500 and 0.38 for VIX for 2008. The formulation here allows only for
and hence is not directly applicable.
8. Discussion
This work shows how to estimate the Hurst parameter H in a Fractional Stochastic Differential Equation using both an MLE, and an approximately bias-corrected MLE . Simulations demonstrate that the MLE alone is a biased estimator. An approximately biased corrected MLE, , is constructed using a model based on simulation results which performs much better in terms of bias than the MLE. Furthermore, a simulation approach is used to obtain an approximate standard error for allowing for confidence intervals to be constructed. The coverage performance of these confidence intervals is studied via simulation which shows that as n increases the coverage probability increases, except for when the true value of H is near 0.5, in which the coverage probabilities are very low.
The definition of
indicates that when
,
equals
, effectively rendering the fBM akin to standard Brownian motion. A careful examination of
Table 1 yields several insights. Notably, when scrutinizing the
values for S&P500 and VIX, they cluster around 0.5, suggesting an absence of long-term memory in these indices. Conversely, post-bias correction, each
value exhibits long-memory characteristics, especially notable in the VIX data from 2007. This finding implies that during the 2007–2008 period, stock indices tended towards weak-form efficiency, as indicated by the lack of long-memory effect under
. However, upon utilizing
, the opposite trend emerges, hinting at increased long-term memory and persistence during the 2008 financial crisis, post-bias correction. This stark contrast could significantly erode investor confidence, potentially prompting major institutional investors to divest from stock markets, leading to diminished liquidity and market efficiency. Notably, investors can only observe
, neglecting the informative insights provided by
.
Balancing accuracy and efficiency in parameter estimation poses a perennial challenge. Consequently, determining the appropriate trade-off between the two factors remains a conundrum. While MLE is widely used for its accuracy in estimating the Hurst exponent, its computational demands have historically been considerable, rendering it unsuitable for rapid-response systems such as the case in the stock market. Chang et al. [
33] suggest that the combination of the
Levinson algorithm and
Cholesky decomposition offers a pathway to enhance computational efficiency, thus mitigating the aforementioned dilemma. However, their focus was solely on conducting efficiency tests. In this paper, our primary objective is to identify an unbiased estimator for the Hurst index, which we accomplish through the application of a least squares polynomial approximation method.