Doubly Robust Estimation and Semiparametric Efficiency in Generalized Partially Linear Models with Missing Outcomes
Abstract
1. Introduction
2. A Formalization of the Inferential Problem
3. The Estimation Procedure
3.1. The AIPW Kernel–Profile Estimating Equations
3.2. Doubly Robust, Locally Efficient Estimation
4. Semiparametric Efficiency Theory for Estimation of
5. Asymptotic Properties
5.1. Asymptotic Results of the AIPW Profile Estimator
5.2. Asymptotic Results of the IPW Profile Estimator
6. Simulations
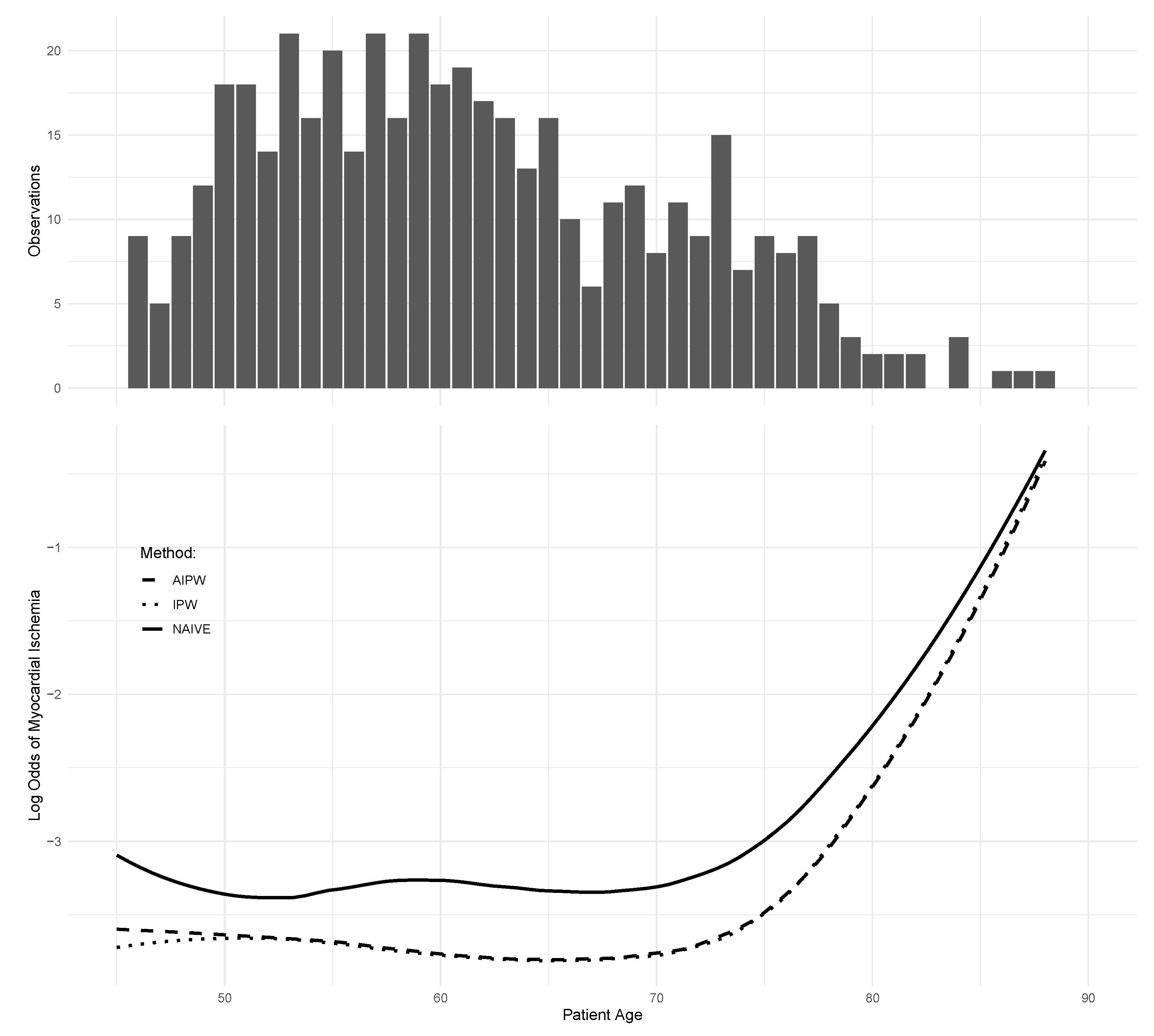
7. Application to the SPECT Data
8. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McCullagh, P.; Nelder, J. Generalized Linear Models; Chapman & Hall: London, UK, 1989. [Google Scholar]
- Severini, T.A.; Staniswalis, J.G. Quasi-Likelihood Estimation in Semiparametric Models. J. Am. Stat. Assoc. 1994, 89, 501–511. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman & Hall/CRC: Boca Raton, FL, USA, 1990. [Google Scholar]
- Fan, J.; Heckman, N.E.; Wand, M.P. Local Polynomial Kernel Regression for Generalized Linear Models and Quasi-Likelihood Functions. J. Am. Stat. Assoc. 1995, 90, 141–150. [Google Scholar] [CrossRef]
- Carroll, R.J.; Fan, J.; Gijbels, I.; Wand, M.P. Generalized Partially Linear Single-Index Models. J. Am. Stat. Assoc. 1997, 92, 477–489. [Google Scholar] [CrossRef]
- Lin, X.; Carroll, R.J. Semiparametric Regression for Clustered Data Using Generalized Estimating Equations. J. Am. Stat. Assoc. 2001, 96, 1045–1056. [Google Scholar] [CrossRef]
- Lin, X.; Carroll, R.J. Semiparametric Regression for Clustered Data. Biometrika 2001, 88, 1179–1185. [Google Scholar] [CrossRef]
- Muller, M. Estimation and Testing in Generalized Partial Linear Models: A comparative Study. Stat. Comput. 2001, 11, 299–309. [Google Scholar] [CrossRef]
- Hu, T.; Cui, H. Robust estimates in generalised varying-coefficient partially linear models. J. Nonparametr. Stat. 2010, 22, 737–754. [Google Scholar] [CrossRef]
- Rahman, J.; Luo, S.; Fan, Y.; Liu, X. Semiparametric efficient inferences for generalised partially linear models. J. Nonparametr. Stat. 2020, 32, 704–724. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 2nd ed.; John Wiley: New York, NY, USA, 2002. [Google Scholar]
- Chu, H.; Halloran, M.E. Estimating vaccine efficacy using auxiliary outcome data and a small validation sample. Stat. Med. 2004, 23, 2697–2711. [Google Scholar] [CrossRef]
- Braun, J.; Oldendorf, M.; Moshage, W.; Heidler, R.; Zeitler, E.; Luft, F.C. Electron beam computed tomography in the evaluation of cardiac calcifications in chronic dialysis patients. Am. J. Kidney Dis. 1996, 27, 394–401. [Google Scholar] [CrossRef]
- Little, R.J.A. Models for nonresponse in sample surveys. J. Am. Stat. Assoc. 1982, 77, 237–250. [Google Scholar] [CrossRef]
- Little, R.J.A. Modeling the Drop-Out Mechanism in Repeated-Measures Studies. J. Am. Stat. Assoc. 1995, 90, 1112–1121. [Google Scholar] [CrossRef]
- Robins, J.M.; Rotnitzky, A. Semiparametric Efficiency in Multivariate Regresion Models with Missing Data. J. Am. Stat. Assoc. 1995, 90, 122–129. [Google Scholar] [CrossRef]
- Robins, J.M.; Rotnitzky, A.; Zhao, L.P. Analysis of Semiparametric Regression Models for Repeated Outcomes in the Presence of Missing Data. J. Am. Stat. Assoc. 1995, 90, 106–121. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, S.; Gutierrez, R.G.; Carroll, R.J. Local Linear Regresion for Generalized Linear Models with Missing Data. Ann. Stat. 1998, 26, 1028. [Google Scholar]
- Chen, J.; Fan, J.; Li, K.H.; Zhou, H. Local quasi-likelihood estimation with data missing at random. Stat. Sin. 2006, 16, 1044–1070. [Google Scholar]
- Wang, L.; Rotnitzky, A.; Lin, X. Nonparametric Regression with Missing Outcomes Using Weighted Kernel Estimating Equations. J. Am. Stat. Assoc. 2010, 105, 1135–1146. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, E.H.; Ma, Z.; McHugh, M.D.; Small, D.S. Non-parametric methods for doubly robust estimation of continuous treatment effects. J. R. Stat. Soc. Ser. B Stat. Methodol. 2017, 79, 1229–1245. [Google Scholar] [CrossRef]
- Liang, H.; Wang, S.; Robins, J.M.; Carroll, R.J. Estimation in partially linear models with missing covariates. J. Am. Stat. Assoc. 2004, 99, 357–367. [Google Scholar] [CrossRef]
- Liang, H. Generalized partially linear models with missing covariates. J. Multivar. Anal. 2008, 99, 880–895. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, Q. Statistical estimation in partial linear models with covariate data missing at random. Ann. Inst. Stat. Math. 2009, 61, 47–84. [Google Scholar] [CrossRef]
- Wang, Q.; Linton, O.; Hardle, W. Semiparametric Regression Analysis With Missing Response at Random. J. Am. Stat. Assoc. 2004, 99, 334–345. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, Z. Estimation in partially linear models with missing responses at random. J. Multivar. Anal. 2007, 98, 1470–1493. [Google Scholar] [CrossRef]
- Liang, H.; Wang, S.; Carroll, R.J. Partially linear models with missing response variables and error-prone covariates. Biometrika 2007, 94, 185–198. [Google Scholar] [CrossRef]
- Chen, S.; Keilegom, I.V. Estimation in semiparatric models with missing data. Ann. Inst. Stat. Math. 2013, 65, 785–805. [Google Scholar] [CrossRef][Green Version]
- Robins, J.M.; Rotnitzky, A.; Zhao, L.P. Estimation of Regression Coefficients When Some Regressors Are Not Always Observed. J. Am. Stat. Assoc. 1994, 89, 846–866. [Google Scholar] [CrossRef]
- Rotnitzky, A.; Robins, J.M.; Scharfstein, D.O. Semiparametric Regression fro Repeated Outcomes with Nonignorable Nonresponse. J. Am. Stat. Assoc. 1998, 93, 1321–1339. [Google Scholar] [CrossRef]
- Bang, H.; Robins, J.M. Doubly Robust Estimation in Missing Data and Causal Inference Models. Biometrics 2005, 61, 962–972. [Google Scholar] [CrossRef]
- Pepe, M.S. Inference Using Surrogate Outcome Data and a Validation Sample. Biometrika 1992, 79, 355–365. [Google Scholar] [CrossRef]
- Reilly, M.; Pepe, M.S. A mean score method for missing and auxiliary covariate data in regression models. Biometrika 1995, 82, 299–314. [Google Scholar] [CrossRef]
- Wang, N.; Carroll, R.J.; Lin, X. Efficient Semiparametric Marginal Estimation for Longitudinal/Clustered Data. J. Am. Stat. Assoc. 2005, 100, 147–157. [Google Scholar] [CrossRef]
- Ruppert, D. Empirical-Bias Bandwidths for Local Polynomial Nonparametric Regression and Density Estimation. J. Am. Stat. Assoc. 1997, 92, 1049. [Google Scholar] [CrossRef]
- Begun, J.M.; Hal, W.J.; Huang, W.M.; Wellner, J.A. Information and Asymptototic Efficiency in Parametric-Nonparametric Models. Ann. Stat. 1983, 11, 432–452. [Google Scholar] [CrossRef]
- Newey, W.K. Semiparametric Efficiency Bounds. J. Appl. Econom. 1990, 5, 99–135. [Google Scholar] [CrossRef]
- Bickel, P.J.; Klaassen, C.A.; Bickel, P.J.; Ritov, Y.; Klaassen, J.; Wellner, J.A.; Ritov, Y. Efficient and Adaptive Estimation for Semiparametric Models; Springer: New York, NY, USA, 1998. [Google Scholar]
- Ibragimov, I.; Hasminskii, R. Statistical Estimation: Asymptotic Theory; Springer: New York, NY, USA, 1981. [Google Scholar]
- Robins, J.M.; Rotnitzky, A. Recovery of information and adjustment for dependent censoring using surrogate markers. In AIDS Epidemiology: Methodological Issues; Jewell, N., Dietz, K., Farewell, V., Eds.; Birkhäuser: Boston, MA, USA, 1992; pp. 297–331. [Google Scholar]
- Rotnitzky, A.; Holcroft, C.; Robins, J.M. Efficiency comparisons in multivariate multiple regression with missing outcomes. J. Multivar. Anal. 1997, 61, 102–128. [Google Scholar] [CrossRef][Green Version]
- van der Laan, M.; Robins, J.M. Unified Methods for Censored Longitudinal Data and Causality; Springer: New York, NY, USA, 2003. [Google Scholar]
- Tsiatis, A.A. Semiparametric Theory and Missing Data; Springer Series in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Robins, J.M.; Rotnitzky, A. Comment on the Bickel and Kwon article, Inference for semiparametric models: Some questions and an answer. Stat. Sin. 2001, 11, 920–936. [Google Scholar]
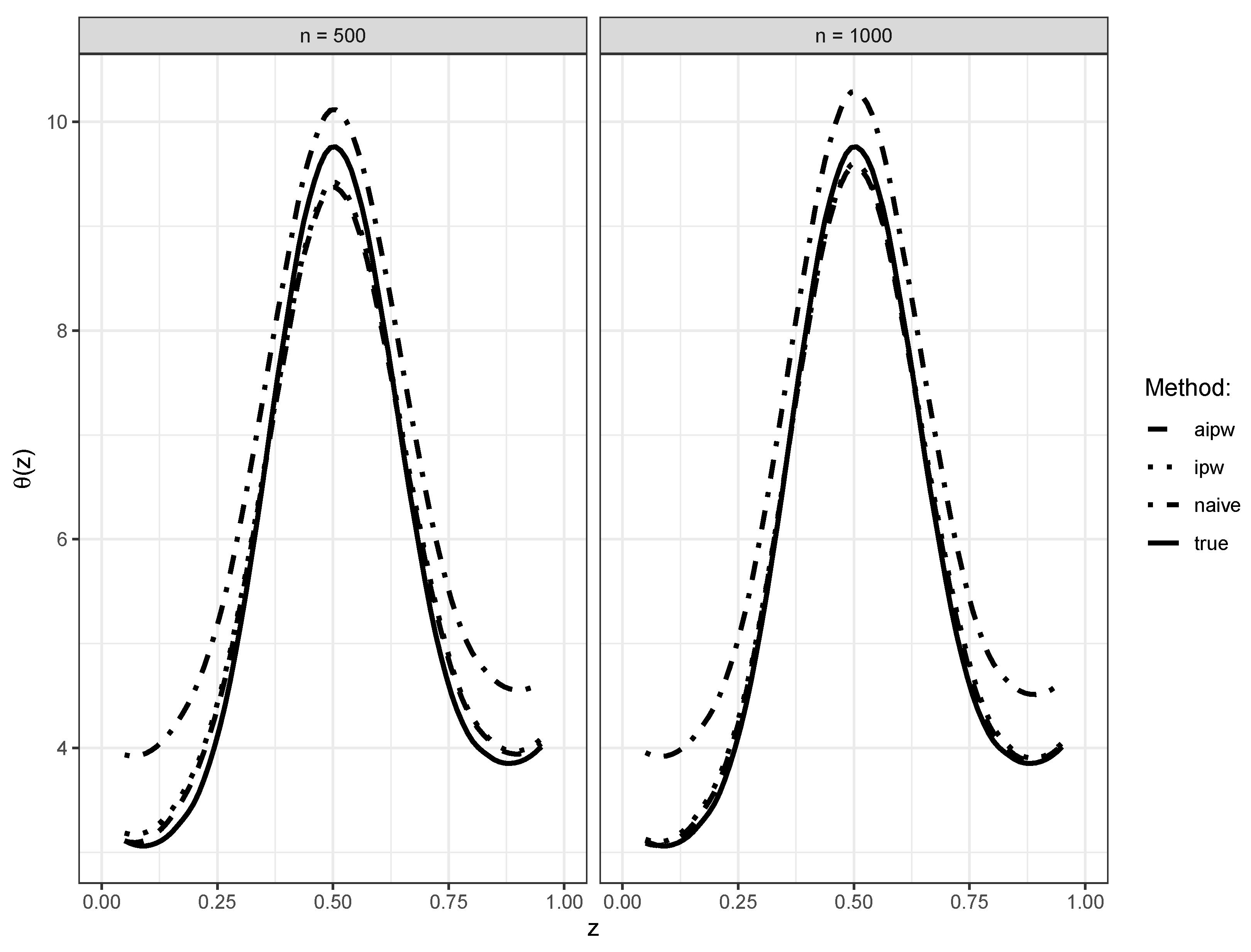
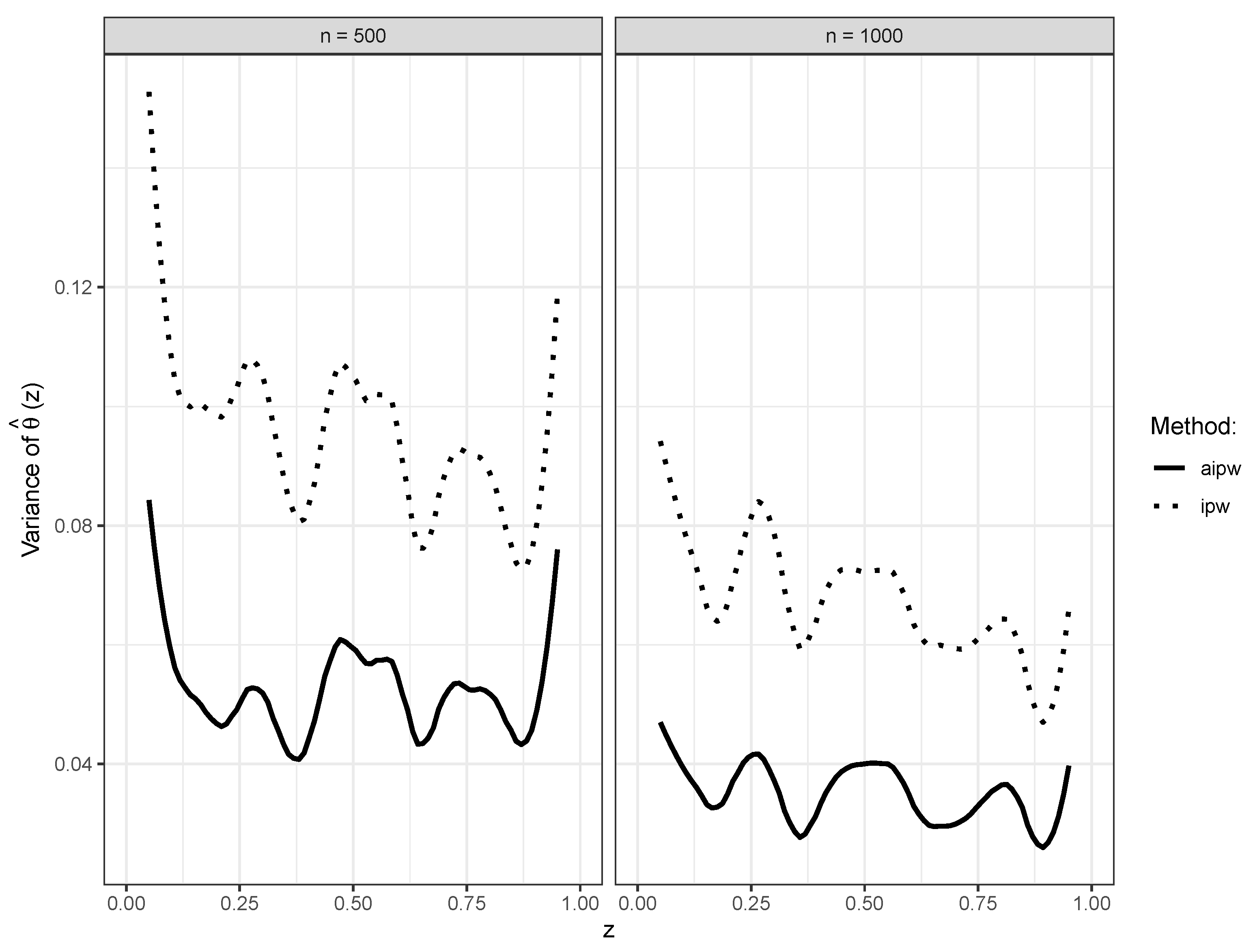
| Kernel Estimator | Profile Estimator | |||||||
|---|---|---|---|---|---|---|---|---|
| of | of | |||||||
| Relative | EMP | EST | EMP | Bias | EMP | EST | EMP | |
| Bias 1 | S.E. 2 | S.E. 3 | MISE 4 | of | S.E. | S.E. | MSE | |
| Naive Estimator | 0.166 | 0.231 | 0.226 | 0.672 | 0.120 | 0.108 | 0.102 | 0.070 |
| IPW Estimator | ||||||||
| True | 0.066 | 0.338 | 0.308 | 0.167 | 0.055 | 0.140 | 0.124 | 0.019 |
| Consistent | 0.064 | 0.329 | 0.311 | 0.158 | 0.051 | 0.130 | 0.125 | 0.017 |
| Wrong | 0.162 | 0.222 | 0.226 | 0.638 | 0.137 | 0.115 | 0.102 | 0.088 |
| AIPW Estimator | ||||||||
| True and 5 | 0.049 | 0.228 | 0.228 | 0.100 | 0.041 | 0.099 | 0.101 | 0.010 |
| Consistent and consistent | 0.047 | 0.231 | 0.233 | 0.092 | 0.040 | 0.099 | 0.100 | 0.010 |
| Wrong and consistent | 0.048 | 0.124 | 0.213 | 0.096 | 0.046 | 0.110 | 0.092 | 0.012 |
| Consistent and wrong | 0.077 | 0.399 | 0.404 | 0.218 | 0.067 | 0.169 | 0.153 | 0.029 |
| Both wrong | 0.162 | 0.279 | 0.286 | 0.653 | 0.109 | 0.125 | 0.114 | 0.060 |
| Naive | IPW | AIPW | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Risk Factors | SE | p -Value | SE | p -Value | SE | p -Value | |||
| female | −1.56 | 0.76 | 0.040 | −1.55 | 0.76 | 0.043 | −1.54 | 0.76 | 0.044 |
| smoking | 0.36 | 0.27 | 0.173 | 0.51 | 0.27 | 0.059 | 0.51 | 0.27 | 0.060 |
| chest pain | 0.32 | 0.49 | 0.514 | 0.39 | 0.49 | 0.430 | 0.39 | 0.49 | 0.433 |
| blood pressure med. | 1.14 | 0.34 | 0.001 | 1.28 | 0.35 | <0.001 | 1.28 | 0.35 | <0.001 |
| cholesterol med. | 1.13 | 0.84 | 0.177 | 1.21 | 0.84 | 0.152 | 1.22 | 0.84 | 0.148 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Ouyang, Z.; Lin, X. Doubly Robust Estimation and Semiparametric Efficiency in Generalized Partially Linear Models with Missing Outcomes. Stats 2024, 7, 924-943. https://doi.org/10.3390/stats7030056
Wang L, Ouyang Z, Lin X. Doubly Robust Estimation and Semiparametric Efficiency in Generalized Partially Linear Models with Missing Outcomes. Stats. 2024; 7(3):924-943. https://doi.org/10.3390/stats7030056
Chicago/Turabian StyleWang, Lu, Zhongzhe Ouyang, and Xihong Lin. 2024. "Doubly Robust Estimation and Semiparametric Efficiency in Generalized Partially Linear Models with Missing Outcomes" Stats 7, no. 3: 924-943. https://doi.org/10.3390/stats7030056
APA StyleWang, L., Ouyang, Z., & Lin, X. (2024). Doubly Robust Estimation and Semiparametric Efficiency in Generalized Partially Linear Models with Missing Outcomes. Stats, 7(3), 924-943. https://doi.org/10.3390/stats7030056




