1. Introduction
People who inject drugs (PWID) are a population with a high risk for HIV infection via sexual and injection risk behaviors. PWID often have limited access to harm reduction resources, and engagement in harm reduction is further compounded by stigma associated with HIV and drug use, incarceration, unstable housing, and socioeconomic factors [
1,
2,
3,
4]. Currently, there are three medications approved by the Food and Drug Administration for the treatment of opioid use disorder (buprenorphine, methadone, and naltrexone) [
5]. Unfortunately, large treatment gaps remain for opioid use disorder (OUD), and less than 20% of people with OUD received medication for opioid use disorder (MOUD) in the US in 2022 [
6,
7]. Individuals treated for OUD are less likely to engage in injection risk behavior [
8,
9,
10,
11,
12,
13]. Furthermore, MOUD may benefit individuals beyond those treated and impact other individuals in close physical or social proximity who may not be able or willing to receive the treatment themselves [
14,
15,
16,
17]. Few studies have assessed the effect of MOUD on reducing HIV injection risk behavior among PWID and their risk contacts in a network study [
18]. This is broadly known as spillover, meaning that the treatment (intervention or exposure) of one individual could possibly affect the outcome of another individual. Importantly, PWID are often part of social, drug use, or sexual networks, where individuals are connected by social interaction, sexual, non-injection drug use, or injection drug use behaviors [
19]. Patients receiving MOUD may share these medications with their network contacts who experience withdrawal and related symptoms, and subsequently also reduce those individuals’ drug use and injection risk behaviors, such as sharing syringes [
20,
21,
22,
23,
24]. MOUD recipients may also receive information on harm reduction, which, in turn, can also benefit their contacts if this information is disseminated. Due to such possible spillover, increasing MOUD uptake in a PWID network may have a protective effect against HIV injection risk behaviors beyond treated individuals. MOUD is known to reduce injection risk behaviors among those who are treated and may also protect treated individuals’ network contacts and possibly their contacts’ contacts from HIV injection risk behaviors. This may protect against HIV acquisition among individuals who are HIV seronegative or onward HIV transmission if they are HIV-positive. By estimating spillover, we can gain a more complete understanding of its potential benefits in reducing HIV injection risk behaviors among not only PWID who are treated with MOUD themselves but also their contacts.
The causal inference methods used in this study to assess spillover rely on a partial interference assumption [
25,
26], where non-overlapping communities or clusters can be identified in the study data, and spillover is assumed to possibly occur between individuals within communities (or “interference sets”) but not between individuals in different communities. We define communities as groups of individuals who are connected through sexual partnerships, drug use partnerships, or frequenting the same venues for drug use, with only sparse connections to individuals in other groups.
In the setting of HIV risk networks, these separate and independent groups are often challenging to identify, and methods for assessing spillover in networks where interference sets are not known a priori are not well established in the causal inference literature [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34]. Other studies of spillover defined interference sets based on an agglomerative spatial clustering method when group membership was not predefined [
32,
33,
34]. However, these studies did not consider the impact of different community detection methods on the analysis results. Therefore, new approaches are needed to evaluate whether communities identified using community detection methods represent a meaningful structure relevant for spillover in network studies among PWID. In this paper, we consider the significance of the community structure to be the degree to which a true underlying community structure actually exists in the network, where communities are distinct from one another with many connections within them and few between them. In a network with a non-significant community structure, the network can be thought of as one large community without truly separate or distinct groupings within it.
This study focuses on the Transmission Reduction Intervention Project (TRIP), which was a sociometric study of PWID and their contacts conducted in Athens, Greece, from 2013 to 2015 [
35]. We first identified communities in the PWID network using a modularity-based community detection method [
27,
28]. We then employed an inverse probability weighted approach with community-level propensity scores to adjust for measured time-invariant confounding. To account for uncertainty in the community structures ascertained using two community detection methods, the cluster-fast-greedy method and the leading-eigenvector method, we conducted a sensitivity analysis to compare the causal effect estimates for each community detection method. In this work, we highlight the importance of analyzing the community structure when conducting causal analysis in the presence of spillover in network studies.
The rest of the paper is organized as follows. In
Section 2, we provide details about TRIP (
Section 2.1), a brief overview of causal inference methodology in the presence of spillover and the community detection methods (
Section 2.2), the notation for the statistical methods (
Section 2.3), and a detailed explanation of the parameters of interest and their corresponding estimators (
Section 2.4). We explain our assessment of the significance of the community structure (
Section 2.5), and the application of this approach to the TRIP data (
Section 2.6).
Section 3 provides the results of the evaluation of spillover and the analysis of the community structure. In
Section 4 we discuss our findings, conclusions, and directions for further research.
3. Results
Baseline characteristics of the study population, including demographics, substance use, study recruitment type, and other health-related characteristics, are shown in
Table 1. All participants were adults between the ages of 18 and 71. Most participants were male (78%), had a high school education or more (69%), were unemployed or unable to work (70%), were not married (85%), or were of Greek nationality (88%). Seventy-four (27%) participants reported homelessness. In the 6 months prior to the baseline visit, 90% reported having injected drugs. Daily use of cocaine and daily use of alcohol were reported among 20% and 5% of participants, respectively. Of the participants, 14% reported the use of crack, and 22% reported the use of methamphetamines. The majority of participants (70%) reported heroin use. Fifty-one percent of participants reported being unable to get medical care when they needed it, and fifty-two percent had a positive HIV status as ascertained by TRIP. Seventy-five percent of participants reported HIV injection risk behaviors in the 6 months prior to baseline.
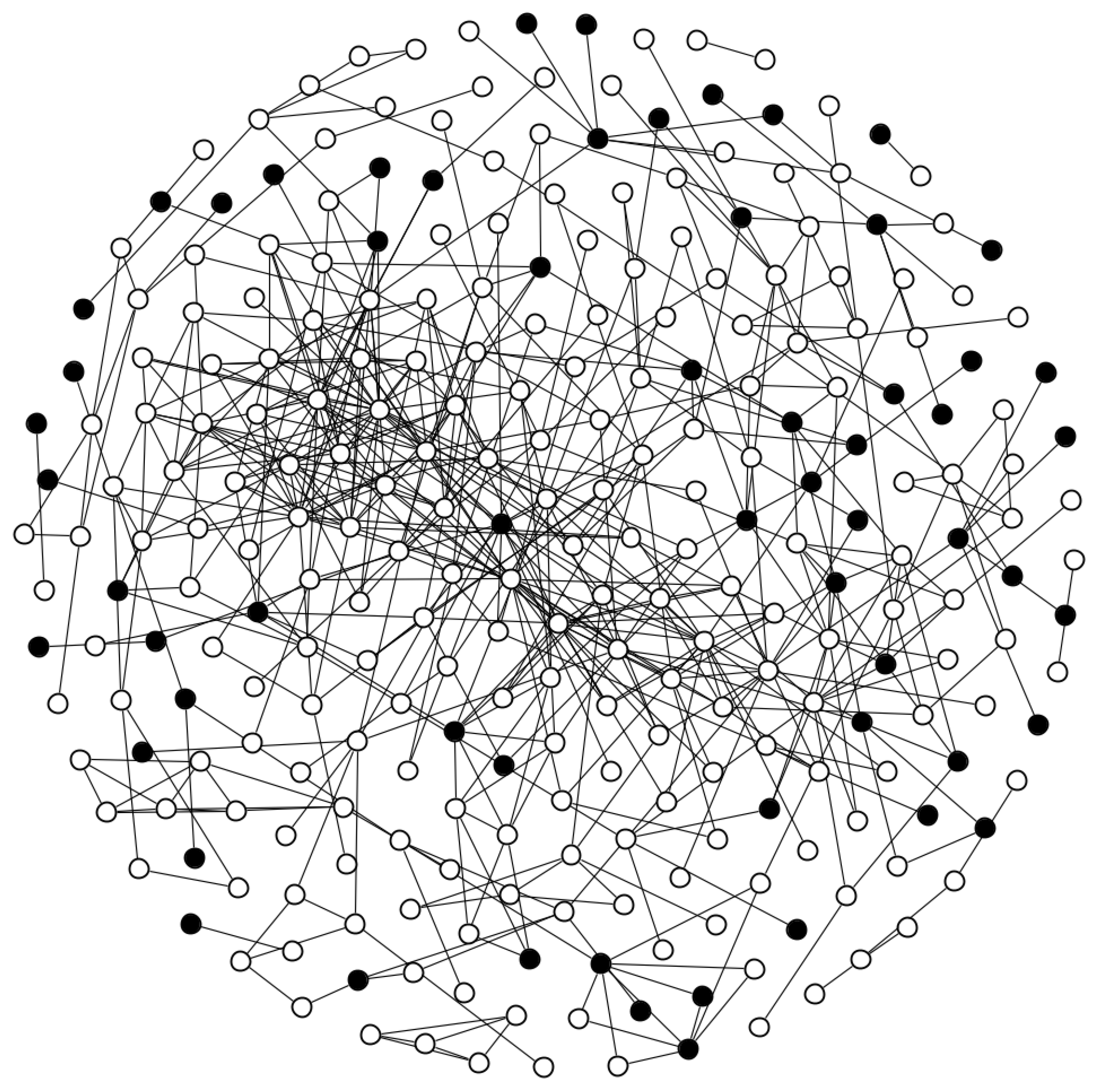
The observed TRIP network includes 356 participants with 829 dyadic connections. After removing duplicate edges and 79 (22%) participants who did not share edges with anyone else in the study, the network includes 277 nodes and 542 dyadic connections. Among the 277 participants, there are 7 (2.5%) participants with missing data imputed for covariates and 56 (20%) participants with missing data imputed for the outcome. One participant enrolled in the TRIP study twice and, therefore, had two baseline records and two follow-up records. We include the baseline and follow-up records that are closest to being 6 months apart (the follow-up period for the TRIP study). All edge information from both of these baseline records for this participant is included in the analysis.
Figure 1 illustrates the network using unshaded nodes to represent participants who were not treated with MOUD at baseline and shaded nodes to represent participants who were treated with MOUD at baseline. Black lines connecting the nodes represent participants who were drug use or sexual partners, i.e., if they injected drugs together or had sex; injected or had sex in each other’s presence; or injected, used drugs or had sex with the same people; or were reported to have frequented the same venues to use drugs, have sex, or meet new sex partners. Participants sharing edges indicate the possibility of spillover, where participants who received MOUD treatment (i.e., the shaded nodes) may affect the HIV injection risk behaviors of other untreated participants (i.e., the unshaded nodes). As illustrated in
Figure 1, the TRIP network is highly connected with many edges connecting treated and untreated participants.
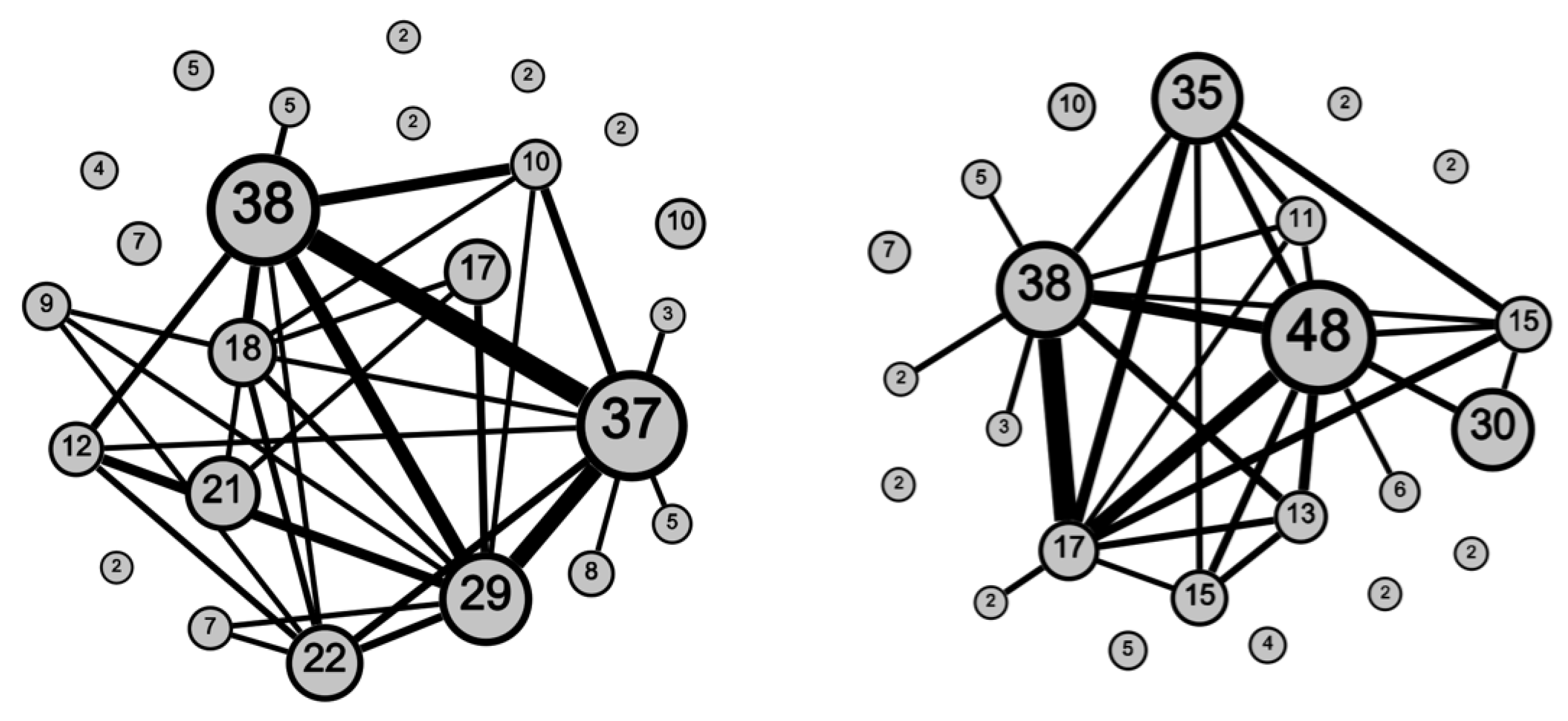
We used community detection to determine non-overlapping groupings of nodes (i.e., subnetworks) in the network.
Figure 2 illustrates the identified community structure for both the CFG and LE methods. The labels indicate the number of nodes (participants) in the community, and the width of the edges is scaled to express the number of edges (i.e., connections) between communities. As illustrated in
Figure 2, under both the CFG (left) and LE (right) methods, there are eight communities detected that had no participants sharing edges with participants in other communities. The remaining communities had varying levels of connectivity between them, with greater connectivity between the largest communities using either community detection method. The CFG method resulted in 24 communities and a community structure with 451 edges within communities and 91 edges between them. The LE method also resulted in 24 communities. One of the communities from the LE method had only one participant, and therefore spillover was not possible in this community. As a result, this participant’s records were not included in any of the models with communities identified from the LE method. The LE method resulted in a community structure with 424 edges within communities and 117 edges between them. The Tchetgen Tchetgen and Coull diagnostic test showed that the normal distribution was a reasonable fit for the random effects (
for communities identified by the CFG method,
for the LE method) [
46].
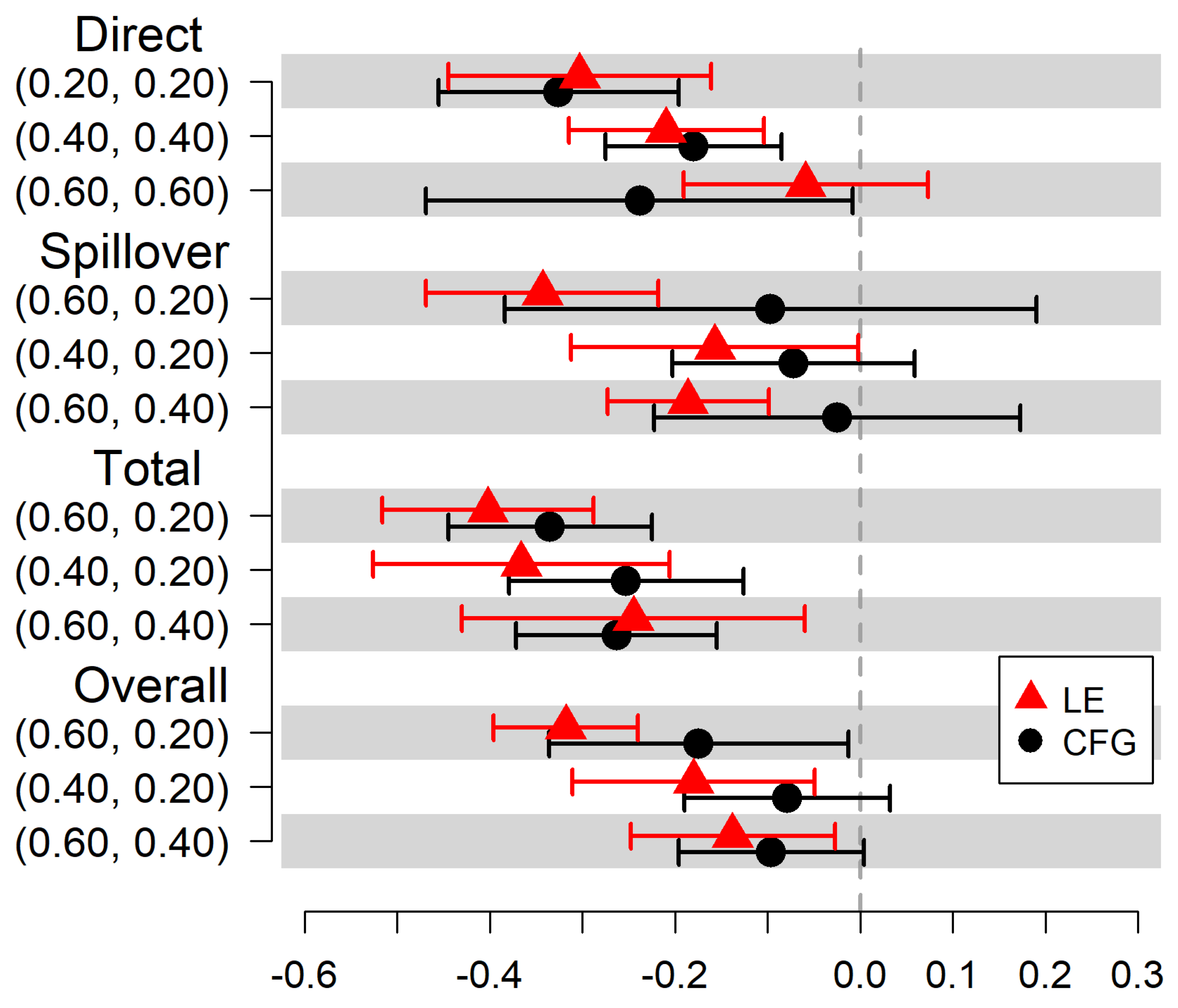
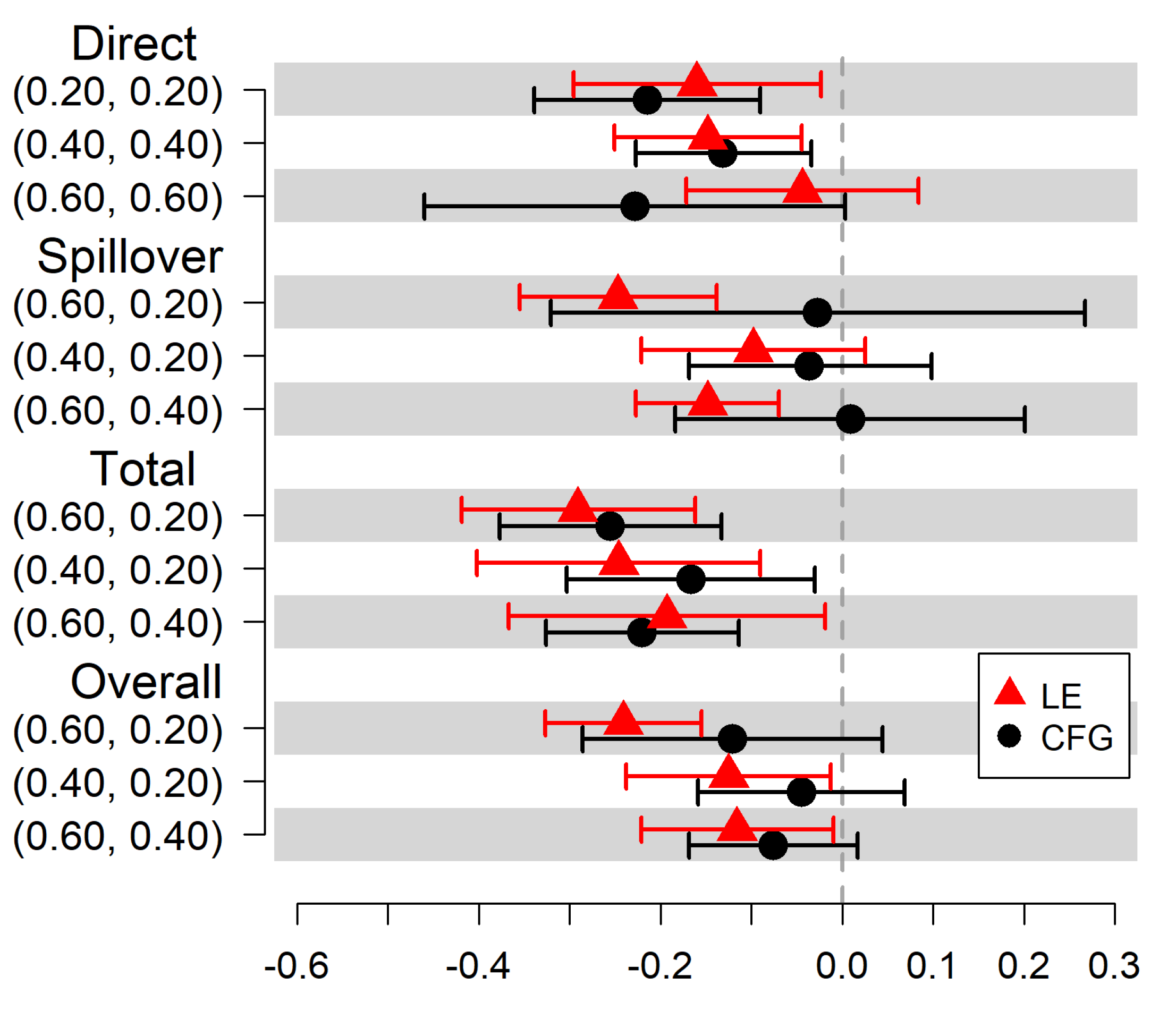
We estimate the direct, spillover, total, and overall effects of MOUD treatment on self-reported HIV injection risk behavior at 6 months after baseline. The estimated causal effects on the risk difference scale under both community detection methods are displayed in
Table 2, and shown graphically in
Figure 3. When communities are identified using the CFG method, we expect 21 fewer reports of HIV injection risk behaviors per 100 persons (95% Confidence Interval (CI) = −0.34, −0.09) at the 6-month visit among treated participants compared to untreated participants with 20% of participants treated in the community. When communities are identified using the LE method, the estimated direct risk reduction is attenuated to 16 per 100 persons (95% CI = −0.30, −0.02). When communities are identified using the CFG method, we expect 3 fewer reports of HIV injection risk behaviors per 100 persons (95% CI = −0.32, 0.27) at the 6-month visit in untreated participants if community coverage is 60% compared to 20%. When communities are identified using the LE method, the estimated spillover risk reduction is 25 per 100 persons (95% CI = −0.35, −0.14). When communities are identified using the CFG method, we expect 26 fewer reports per 100 persons (95% CI = −0.38, −0.13) at the 6-month visit under treatment in communities with 60% coverage compared to under no treatment in communities with 20% coverage. The estimated total risk reduction is 29 per 100 persons (95% CI = −0.42, −0.16) when communities are identified using the LE method. For the estimated overall effect, 12 fewer reports per 100 persons at the 6-month visit would be expected if 60% of participants in the community are treated compared to if only 20% are treated when communities are identified using the CFG method (95% CI = −0.29, 0.04). The estimated overall risk reduction is 24 per 100 persons (95% CI = −0.33, −0.16) when communities are identified using the LE method.
There are differences in the magnitudes of estimated risk differences based on the community detection method used; however, few changes in direction of the effects are observed. Causal estimates under the LE method are significant more times than under the CFG method. The sensitivity analysis shows that the CFG method and the LE method result in estimated risk differences that differ at most by 22% (see
Table 2: Spillover (0.60, 0.20)).
The
curves (or VOI curves) in
Figure 4 illustrate the significance of the network community structure in TRIP, i.e., the robustness of the community structure to random edge reassignment. Each point represents the average VOI, or
, of 30 perturbed graphs. The upper and lower bounds of the bands around the points represent
and
, of the 30 perturbed graphs, respectively. We include the maximum and minimum to illustrate the variation of
. A VOI band for a null network, which is defined to have no community structure, is included as a reference for comparison against the TRIP network. The light gray VOI band represents the null network, and the dark gray VOI band represents the TRIP network. Also included are horizontal lines corresponding to the value of VOI if
and
(lower and upper lines, respectively) of nodes were randomly reassigned to other communities.
For both the CFG and the LE methods, we observe a possibly meaningful departure of the TRIP network from the null network, indicating a possible presence of community structure in the TRIP network. However, if we consider the value of at which for TRIP crosses the horizontal lines, the community structure is still highly sensitive to small perturbations. The value of at which the VOI curve crosses the lower line (or upper line) represents the proportion of edges that would have to be reassigned in the network for (or ) of the nodes to be assigned to different communities, respectively. For both community detection methods, less than (or less than ) of the edges must be perturbed before (or ) of nodes are reassigned to different communities, respectively. This indicates a potentially non-significant community structure and a possible explanation for the sensitivity of point estimates of the direct, spillover, total, and overall effects to the choice of the community detection method.
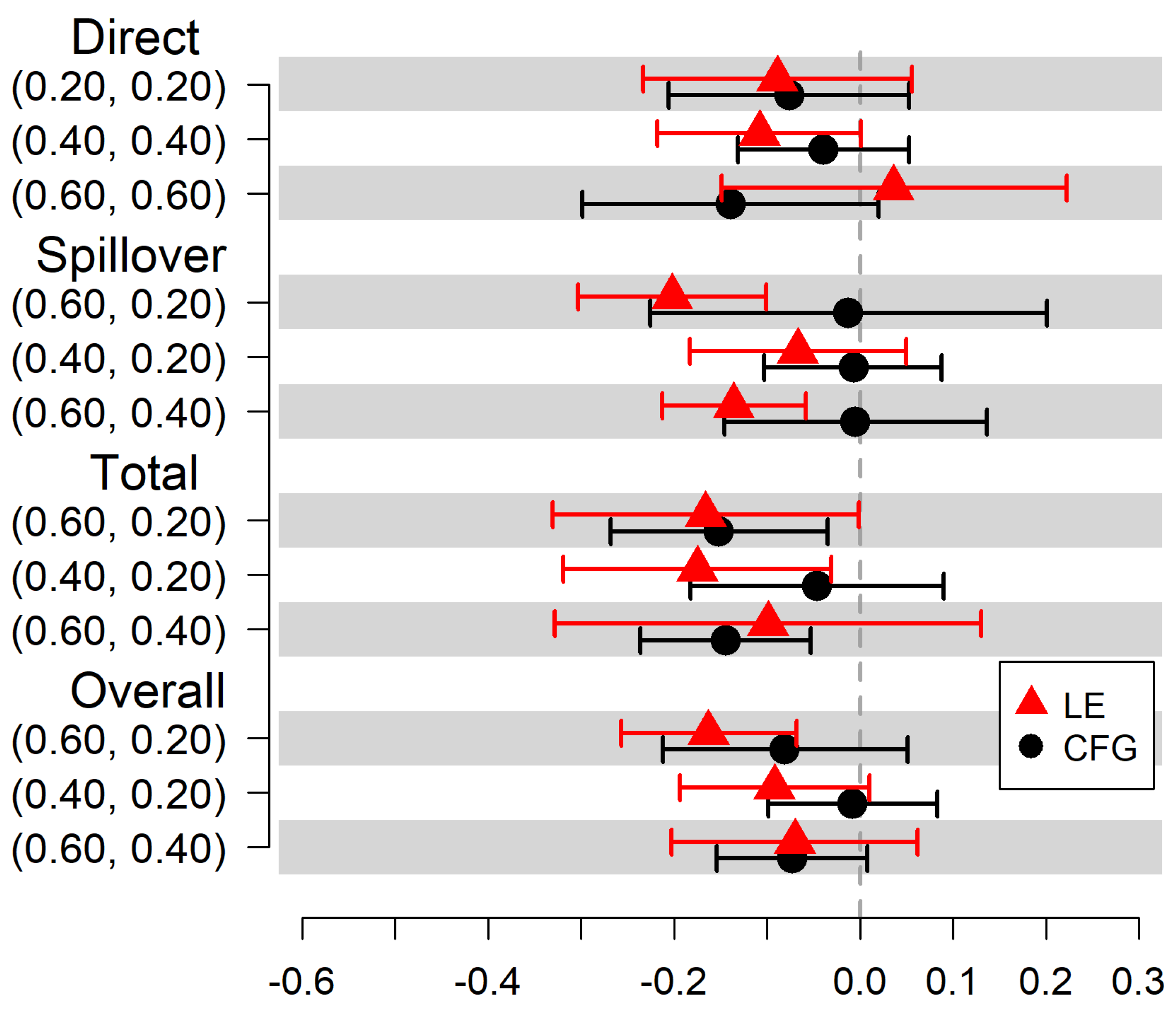
A sensitivity analysis using a best/worst-case scenario approach demonstrated that the estimated effects were, at times, sensitive to the missing outcome imputation. However, the estimated causal effects showed a benefit of MOUD for reducing HIV injection risk behaviors. Further details are presented in the
Appendix B.1. Under the best-case scenario, we expect 34 fewer reports of HIV injection risk behaviors per 100 persons (95% CI = −0.47, −0.22) at the 6-month visit in untreated participants if community coverage is 60% compared to 20% when communities are identified using the LE method. This estimate is attenuated to 20 fewer reports of HIV injection risk behaviors per 100 persons (95% CI = −0.30, −0.10) at the 6-month visit under the worst-case scenario (shown in
Table A2 and
Table A3, and graphically in
Figure A1 and
Figure A2). As expected, the best-case scenario shows a greater reduction in HIV injection risk behaviors, and the worst-case scenario shows a smaller reduction than in the main analysis, where we estimate 24 fewer reports of HIV injection risk behaviors if community coverage is 60% compared to 20% under the LE method.
An additional sensitivity analysis shows that when the imputed outcomes are identical for both community structures (i.e., no fixed or random effect for the community is included in the missing outcome imputation model), the causal effect estimates are sensitive to the community detection method. Under the CFG method, we expect 9 fewer reports of HIV injection risk behaviors per 100 persons (95% CI = −0.30, 0.12) at the 6-month visit in untreated participants if community coverage is 60% compared to 20%. This estimate is 26 fewer reports of HIV injection risk behaviors per 100 persons (95% CI = −0.37, −0.16) at the 6-month visit under the LE method. Results and discussion of this sensitivity analysis can be found in the
Appendix B.2.
In a third sensitivity analysis, we estimate the same causal effects as in the main analysis but with communities removed which have extreme IPWs. Four of the community-level IPWs are close to zero (i.e., <0.001) under the CFG method and three are close to zero under the LE method. None of the IPWs are especially large (all <8, see
Figure A4 and
Figure A5). Under the CFG method, after removing the four communities with IPWs close to zero, we expect 15 fewer reports of HIV injection risk behaviors per 100 persons (95% CI = −0.37, 0.08) at the 6-month visit in untreated participants if community coverage is 60% compared to 20%. This estimate is 25 fewer reports of HIV injection risk behaviors per 100 persons (95% CI = −0.34, −0.16) at the 6-month visit after removing the three communities with IPWs close to zero under the LE method (see
Table A5 and
Figure A6). The estimated reduction in reports of HIV injection risk behaviors is greater than in the main analysis under the CFG method (where we estimate 3 fewer reports of HIV injection risk behaviors per 100 persons) but similar to the main analysis under the LE method. Further details are presented in the
Appendix C.
4. Discussion
By employing causal inference methods for observational studies with spillover in a network setting, we estimate both direct and spillover effects of MOUD on HIV injection risk behaviors among PWID. The estimated causal effects of MOUD treatment using either community detection method are protective for participants who received or were prescribed MOUD, which is consistent with the current literature. Previous studies have shown that individuals treated for OUD are less likely to engage in injection risk behavior [
8,
9,
10,
11,
12,
13]. We also find that the receipt or prescription of MOUD may reduce the risk of self-reported HIV injection risk behavior at the 6-month follow-up visit for the drug use and sexual contacts of treated individuals. Notably, in this work, we perform multiple sensitivity analyses to the community structure, and the results are fairly robust. However, the magnitudes of the estimated risk differences are sensitive at times to the community detection method used, namely, for the spillover effects, where estimates under the CFG method are smaller in magnitude and have wider confidence intervals. Variation between the two methods is due to the largest connected component, as the communities outside of the largest connected component are the same for both methods. A large number of edges between communities may imply a violation of the partial interference assumption depending on the number, and type of connections between communities. We also find evidence of a possible non-significant community structure (i.e., where the network can be thought of as one large community without truly separate or distinct groupings within it) in the TRIP network, potentially explaining differences in the magnitudes of causal effect estimates between the two community detection methods.
This paper makes two important contributions to the analysis of PWID networks. First, an analysis of community structure should precede and guide any causal analysis in the presence of spillover in a network study. Based on such an analysis, a decision should then be made as to the most valid method for defining interference sets. If a network has a significant community structure, then community detection may be a valid choice. If a network has a non-significant community structure, then a sensitivity analysis to the community detection methods should be employed, or an alternative approach could be considered. Second, although the magnitudes of the estimated causal effects are sensitive to the community detection method, the results consistently support that MOUD has a protective effect against HIV injection risk behavior for treated individuals and possibly for their contacts in the network. This implies that the protective effect of increasing the prescribing and availability of MOUD may extend beyond the treated individual to other individuals in the PWID network, and the delivery of MOUD may have a further impact by considering the social and risk networks.
A potential limitation of this analysis is bias due to social desirability [
56,
57,
58,
59]. Further research on social desirability in network settings may lead to insights into how social norms diffuse and sustain through networks, allowing researchers to better account for social desirability when outcomes are self-reported and spillover may be present. An additional limitation is the absence of data on adherence to MOUD, limiting our analysis to a treatment defined by receipt or prescription. One possible spillover mechanism occurs when treated participants do not adhere to their MOUD regimen and instead share some portion with their network contacts (known as “diversion”) [
21,
22,
23]. Due to lack of data on adherence, we are unable to disentangle the specific spillover mechanisms in this analysis (e.g., diversion, spread of knowledge about injection risk reduction, and behavior modification).
An additional limitation of this analysis is the limited theoretical basis for using community detection to define the interference sets [
25,
26,
29,
30,
31,
32,
33,
34]. Although spillover was assessed in settings where interference sets were not known a priori, methods for defining interference sets in this setting are not well established, and further research is needed to develop a theoretical basis to support this approach, including an evaluation of finite-sample performance. More appropriate estimands may be obtained by defining interference sets in a way that better reflects spillover mechanisms, such as using
nearest neighbors rather than non-overlapping communities that maximize modularity as the interference sets [
60,
61]. In this approach, spillover only occurs between individuals who share edges (i.e., partnerships), rather than between all individuals in the same community [
61]. An additional approach for analyzing the TRIP network could be a chain graph approach that uses
auto-g-computation for estimation, which allows for arbitrary forms of interference [
62]. An area for future research could compare the performance of community detection against other methods such as nearest neighbors and chain graphs in networks with varying characteristics (e.g., significance of community structure, community sizes, and number of communities). Future research may also consider community detection methods that also account for the characteristics of both nodes and edges [
63,
64,
65].