A Spatial Gaussian-Process Boosting Analysis of Socioeconomic Disparities in Wait-Listing of End-Stage Kidney Disease Patients across the United States

Abstract

In this study, we employed a novel approach of combining Gaussian processes (GPs) with boosting techniques to model the spatial variability inherent in End-Stage Kidney Disease (ESKD) data. Our use of the Gaussian processes boosting, or GPBoost, methodology underscores the efficacy of this hybrid method in capturing intricate spatial dynamics and enhancing predictive accuracy. Specifically, our analysis demonstrates a notable improvement in out-of-sample prediction accuracy regarding the percentage of the population remaining on the wait list within geographic regions. Furthermore, our investigation unveils race and gender-based factors that significantly influence patient wait-listing. By leveraging the GPBoost approach, we identify these pertinent factors, shedding light on the complex interplay between demographic variables and access to kidney transplantation services. Our findings underscore the imperative for a multifaceted strategy aimed at reducing spatial disparities in kidney transplant wait-listing. Key components of such an approach include mitigating gender disparities, bolstering access to healthcare services, fostering greater awareness of transplantation options, and dismantling structural barriers to care. By addressing these multifactorial challenges, we can strive towards a more equitable and inclusive landscape in kidney transplantation.

1. Introduction

Renal transplantation is the foremost treatment for End-Stage Kidney Disease (ESKD), providing notably better survival rates and quality of life when contrasted with dialysis [1]. There are disparities in both ESKD prevalence and wait-listing for transplantation due to demographic factors across states and counties, healthcare resource availability, and the social determinants of health [2].

Efforts to reduce spatial disparities in kidney transplant wait-listing require a multifaceted approach that addresses the underlying determinants of healthcare access and delivery [3]. This includes expanding access to healthcare services in underserved areas, improving outreach and education about transplantation options, increasing awareness about living donation, and addressing structural barriers to care [4].

Furthermore, healthcare policies and interventions should prioritize equity and fairness in access to transplantation, ensuring that all individuals have equal opportunities for evaluation and listing for transplantation regardless of their geographic location or socioeconomic status. This may involve implementing policies such as the regionalization of transplant services, improving reimbursement for transplantation-related services, and promoting diversity and inclusion in transplant programs. Spatial analysis has the potential to improve care for patients with ESKD for several reasons, as shown below.

Identifying Geographic Disparities: Spatial analysis helps to identify geographic regions or areas where there are disparities in the burden of kidney disease and wait-listing for transplantation [5]. By examining the distribution of kidney disease and wait-listing across different geographic regions, researchers and policymakers can pinpoint areas with low donation rates or limited access to transplantation services.

Understanding Socioeconomic Factors: Spatial analysis allows for the exploration of the relationship between ESKD prevalence and socioeconomic factors such as income, education level, and access to healthcare [6,7]. By analyzing spatial patterns, researchers can uncover disparities that may be influenced by socioeconomic factors, thereby highlighting areas where interventions are needed to improve access to transplantation services.

Optimizing Organ Allocation: Spatial analysis can inform organ allocation policies by identifying regions with high demand for kidney transplants and low donation rates [8]. By understanding the spatial patterns of organ supply and demand, policymakers can develop more efficient allocation strategies to ensure that organs are distributed equitably and reach those in need.

Targeting Interventions: Spatial analysis enables policymakers and healthcare providers to target interventions to specific geographical areas where they are needed the most. By identifying regions with high burden of disease, low wait-listing or rates, or disparities in access to transplantation services, interventions such as community outreach programs, education campaigns, and healthcare infrastructure improvements can be implemented to increase donation rates and improve access to transplantation services.

Improving Health Equity: The spatial analysis of kidney donation in ESKD is essential for promoting health equity [3,8]. By identifying and addressing geographic disparities in kidney disease, policymakers and healthcare providers can work towards ensuring that all individuals with ESKD have equal access to transplantation services, regardless of their geographic location or socioeconomic status.

This paper aims to make inferences on the spatial variability in wait-listed ESKD patients based on Gaussian processes (GPs), a popular method used in spatial aspects, with an effort to add the essence of predictive modeling via a well-known technique called Boosting.

Gaussian processes are powerful tools for modeling spatio-temporal data due to their flexibility and ability to capture complex patterns. They offer a non-parametric approach to modeling spatial dependencies, allowing for incorporating uncertainty and providing probabilistic predictions. Boosting techniques, on the other hand, aim to improve the predictive performance of models by sequentially combining weak learners into strong learners. When applied to spatial data modeling, boosting algorithms enhance a GP’s ability to capture intricate spatial dynamics, thereby improving predictive accuracy [9,10]. Recent research has shown the effectiveness of combining Gaussian processes with boosting for spatial data modeling tasks [10]. This hybrid approach harnesses the strengths of both Gaussian processes and boosting algorithms, enabling more robust and accurate modeling of complex spatio-temporal phenomena. In this study, we modeled End-Stage Kidney Disease (ESKD) data using the Gaussian process boosting model (GPBoost) [10]. In our analysis, we modeled the percentage of ESKD patients whitelisted by the end of the observation date (ESKD-LIST-status-PCT) as the response variable with relevant demographic and socioeconomic variables as predictors in conjunction with spatial information to account for spatial variability.

A concise literature review on Gaussian processes: Gaussian processes, as introduced by [11], are highly adaptable non-parametric function models renowned for their exceptional predictive accuracy and ability to provide probabilistic forecasts, as highlighted by [12]. They find application across diverse domains, including the non-parametric regression and modeling of time series, spatial, and spatio-temporal data as noted by [13,14,15]. Moreover, Gaussian processes are instrumental in emulating large computer experiments, optimizing costly black-box functions, and facilitating parameter tuning in machine learning models, as evidenced by [16,17,18], respectively. Additionally, mixed effects models, pioneered by [19] and developed by [20], incorporate grouped or clustered random effects and are widely employed across various scientific disciplines. These models are particularly valuable for analyzing data with a grouping structure, such as panel and longitudinal data, providing a robust framework for understanding complex relationships within datasets.

The remainder of this paper is structured as follows: in Section 2, we describe the significance of ESKD in the United States (US) and highlight the importance of the problem. In Section 3, we provide a general description of the GPBoost model used in this study. In Section 4, we present our detailed analysis of the US ESKD data with the GPBoost model, taking into account the spatial variability in the data. Finally, in Section 5, we delve into related issues and potential extensions for future research endeavors.

2. Significance of Eskd in the Current US Society/Spatial Disparities of Kidney Transplant Wait-Listing across the US

ESKD is a critical health issue with significant implications for individuals, families, and the society at large. In this section, we aim to explore the significance of ESKD within the context of the United States, focusing particularly on the spatial disparities in kidney transplant wait-listing across the nation.

ESKD represents the final stage of chronic kidney disease (CKD), where the kidneys are no longer able to function effectively to sustain life. In the US, ESKD affects a considerable portion of the population, with thousands of individuals diagnosed each year [2,6]. The prevalence of ESKD has been steadily rising due to factors such as aging populations, increasing rates of diabetes and hypertension, and disparities in healthcare access [21].

The impact of ESKD extends beyond individual health, affecting families, communities, and the healthcare system as a whole. Individuals with ESKD often require costly and time-consuming treatments such as dialysis or kidney transplantation to survive. The financial burden of ESKD is significant, with healthcare costs associated with ESKD accounting for a substantial portion of Medicare spending. Furthermore, ESKD can significantly impair an individual’s quality of life, leading to physical symptoms, emotional distress, and limitations in daily activities [22]. The psychological impact of living with ESKD, coupled with the challenges of managing complex treatment regimens, can take a toll on patients and their families [23].

One of the critical aspects of managing ESKD is access to kidney transplantation, which offers better outcomes and quality of life compared to dialysis [24]. However, access to kidney transplantation is not uniform across the US, leading to spatial disparities in kidney transplant wait-listing. Several factors contribute to these disparities, including geographic location, socioeconomic status, racial and ethnic disparities, and healthcare infrastructure. Studies have shown that individuals living in rural or underserved areas face barriers to accessing transplantation, including limited access to transplant centers, transportation challenges, and a lack of awareness about transplantation options [25].

Racial and ethnic disparities also play a significant role in kidney transplant wait-listing, with African American and Hispanic individuals being less likely to be wait-listed compared to their White counterparts [26,27]. These disparities are multifactorial and influenced by factors such as cultural beliefs, mistrust of the healthcare system, and unequal access to healthcare services.

Overall, the spatial analysis of kidney donation in ESKD is vital for understanding geographic disparities [28], optimizing organ allocation [29], targeting interventions [30], and promoting health equity [31]. By leveraging spatial analysis techniques, policymakers and healthcare providers can work towards improving access to transplantation services and ultimately enhancing outcomes for individuals with ESKD.

3. A Boosting-Based Spatial Model to Capture the Spatial Variability in Wait-Listed Eskd Patients

In this section, we present a predictive model for End-Stage Kidney Disease (ESKD), focusing on the response variable “percentage of wait-listed patients” while adjusting for covariate effects and spatial dependency. When dealing with spatial data, it is crucial to consider the underlying spatial effects, as articulated by Tobler’s 1st Law of Geography [32], which states that “near things are more related than distant things”. To accurately capture these spatial effects, they need to be incorporated alongside the fixed effects of non-spatial predictors in our model. To achieve this, we adopt a semi-parametric spatial model that utilizes boosting to capture the intricate relationship between covariates and the response variable. Additionally, we address spatial dependency through a Gaussian process framework. The model we adopt here is known as Gaussian Process Boosting or GPBoost [10]. Below, we provide a short description of the GPBoost method. Full details of GPBoost can be obtained from [10].

Let us consider that we have ESKD data where the outcome variable is denoted by $y_i$, the predictors/covariates/fixed effects are denoted by ${\mathbf{x}}_i$, and $s_i$ denotes the spatial locations/coordinates of the i-th location (county codes or FIPS codes), $i=1,\dots ,n$. Treating the outcome/response variable as continuous, the boosting with Gaussian Process model (GPBoost) can be written as

$$y_i=f\left(x_i\right)+b\left(s_i\right)+e_i,$$

(1)

where $f\left(x_i\right)$ is the non-linear predictor function for the covariates explained in Section 4.2.1, $\overrightarrow{b}=(b\left(s_1\right),b\left(s_2\right),\dots ,b\left(s_n\right))$ represents the spatial random effects, ($i=1,\dots ,n$) that accounts for the spatial dependence of the locations, and $e_i$ is the independent Gaussian error term with $e_i\sim N(0,{\sigma }_e^2)$.

In the GPBoost model, the predictor function $f\left(\right)$ is estimated using a tree-based boosting method [33], which provides a high degree of model flexibility and generalizations. The tree-boosting model can accommodate non-linearity, discontinuities, and intricate high-order interactions among predictor variables. Additionally, it is robust to outliers in the data and multicollinearity among predictors, and it can automatically manage missing values within the predictor variables.

The spatial random effects $\overrightarrow{b}=(b\left(s_1\right),b\left(s_2\right),\dots ,b\left(s_n\right))$ are modeled through Gaussian Processes as follows:

$$\overrightarrow{b}=\left[\begin{array}{c}b\left(s_1\right)\\ b\left(s_2\right)\\ ⋮\\ b\left(s_n\right)\end{array}\right]\sim N(0,\Sigma ),$$

(2)

where $\Sigma$ is the covariance function of the Gaussian Process which captures the spatial dependence pattern among the counties (FIPS Code). In this paper, we employ a Gaussian Process with covariance function $\Sigma$ to capture the spatial dependence among counties identified by their FIPS codes. Specifically, we adopt an exponential covariance function $c(s_i,s_j)={\sigma }^{2}exp(-d(s_i,s_j)/\rho )$, where $d(s_i,s_j)$ represents the Euclidean distance between locations $s_i$ and $s_j$. Therefore, an exponential covariance function represents a decay in correlation as the distance between locations increases [11]. Here, $\theta =[{\sigma }^2,\rho ]$ denotes the parameters of the covariance function. The parameter $\rho$ serves as the lengthscale, dictating the smoothness of the function. A smaller $\rho$ indicates rapid fluctuations, while larger values signify gradual changes. Moreover, $\rho$ determines the extent of reliable extrapolation from training data. Conversely, ${\sigma }^2$ represents the variance parameter, determining the deviation of a function’s values from their mean. Smaller ${\sigma }^2$ values denote functions closely aligned with their mean, whereas larger values allow for greater variability. Excessive variance permits the modeled function to be influenced by outliers. Overall, the exponential covariance function provides a versatile and effective tool for modeling spatial dependence in Gaussian processes, offering a balance between simplicity, interpretability, and computational efficiency.

In the GPBoost model, the primary concept involves optimizing the model at each boosting step. This optimization entails identifying the predictors/covariates/fixed effects response, along with the Gaussian process covariance matrix, to minimize the negative log-likelihood loss function. This process iterates until the algorithm concludes after a specified number of iterations. The model exhibiting the lowest test error is ultimately chosen. These iterative steps are outlined in Algorithm 1 below.

Algorithm 1: GPBoost with Out-Of-Sample covariance parameter estimation. Note that this is a summarized version of the framework and two algorithms presented in [10,34].

Input: Initial values ${\theta }_0\in \Theta$, learning rate $\nu >0$, number of boosting iterations $M\in \mathbb{N}$. BoostType = “gradient”, sequence ${\mu }_m\in (0,1]$ Output: Prediction function $\widehat{f}(·)$ and covariance parameters $\widehat{\theta }$ 1. Partition data into training and validation sets 2. Initialize $f_0(·)=argmi{n}_{c\in \mathbb{R}}L(y,f_{m-1},{\theta }_0)$ 3. Find ${\theta }_m=argmi{n}_{\theta \in \Theta }L(y,f_{m-1},\theta )$, where $f_{m-1}$ is initialized with ${\theta }_{m-1}$ 4. Find $f_m(·)=argmi{n}_{f(·)\in S}{∥{\Psi }_m^{-1}(f_{m-1}-y)-f∥}^2$ (Step Gradient Algorithm), where $f\sim {[f\left(x_1\right),f\left(x_2\right),\dots f\left(x_n\right)]}^T$. 5. Update $f_m(·)=f_{m-1}(·)+\nu f_m(·)$ 6. Generate predictions for the predictor function on the validation data ${\widehat{f}}_{val}$ 7. Find $\widehat{\theta }=argmi{n}_{\theta \in \Theta }L(y_{val},{\widehat{f}}_{val},\theta )$ 8. Run 4 and 5 on the full data while holding covariance parameters $\theta$ fixed at $\widehat{\theta }$ 9. Repeat (3–8) for M iterations

4. Application of Gpboost in Modeling End-Stage Kidney Disease in the US

In this section, we describe the application of the previously mentioned GPBoost model for modeling End-Stage Kidney Disease (ESKD) in the US. Firstly, in this data set, as we have observations over the spatial domain, it is essential to model the spatial dependence structure. Secondly, there is no clear understanding about how several social and health factors can influence the percentage of ESKD wait-listed patients; hence, the covariates are modeled non-parametrically using the boosting mechanism. Our adopted GPBoost model can handle these two special characteristics of our ESKD data set. Details of the data are available at https://www.niddk.nih.gov/-/media/Files/USRDS/For-Researchers/Merged-Data-Requests/Manuscript_Approval_Checklist_final-2023.pdf (accessed on 2 June 2024).

This study utilized data from the United States Renal Data System (USRDS) on end-stage kidney disease. To understand the social and economic contexts at the county level, we incorporated data from the Agency for Healthcare Research and Quality’s (AHRQ) Social Determinants of Health (SDOH) data file and the Area Deprivation Index (ADI) [35].

4.1. Study Cohort

Our analysis included adult patients (18 years or older) in the United States who initiated chronic dialysis for the first time between 2013 and 2018 (n = 652,350). We excluded patients who received transplants before starting dialysis (n = 0) and those wait-listed for a transplant before dialysis initiation (n = 30,861). This resulted in a final analytic cohort of 621,489 patients.

Next, we created county-level data using patient information linked to county codes (FIPS codes). County codes or FIPS (Federal Information Processing Standards) codes are numerical codes used to uniquely identify counties and county equivalents in the United States. FIPS codes consist of a two-digit state code followed by a three-digit county code, creating a five-digit unique identifier for each county. These codes are commonly used in data management, particularly in government agencies, research, and geographic information systems (GIS), to accurately reference and analyze data at the county level. The USRDS county-level data included demographics like race and body mass index (BMI). We then merged additional county-level data from other sources to provide a comprehensive picture. This included factors like median household income, income inequality (Gini index), Medicare coverage, and the Area Deprivation Index (ADI). In our analysis, we had data from 2435 counties covering the contiguous USA (48 adjoining states of US excluding Alaska and Hawaii). All covariate and outcome variables were obtained by calculating the average of those variables for each of the above-mentioned 2435 counties.

4.2. Variable Definitions

4.2.1. Covariates

The percentages of female patients, White race patients, Black race patients, and patients of other races were calculated by counting the total number of patients in each group and dividing it by the total number of chronic dialysis patients, respectively, for each county using USRDS data. County-level median Body Mass Index (BMI) was determined by ranking the BMIs for all patients in a county and selecting the median BMI value from USRDS data. Median household income, Gini index of income inequality, and percentage of the population with Medicare only were obtained from the AHRQ SDOH 2018 county-level file. An estimate of county-level ADI was derived by calculating the average State-specific decile of the block group ADI score for all census blocks within each county. In addition to that, we also had demographic variables such as percentage of females, percentage of Blacks, percentage of Whites, and percentages of other racial group per county collected from ACS data. In total, we had 9 covariates.

4.2.2. Outcome Variable

The percentage of wait-listed patients was calculated by dividing the total number of chronic dialysis patients wait-listed during the study period by the total number of chronic dialysis patients in each county separately.

4.2.3. Gpboost Model Setting

In our analysis, we fitted (a) Gaussian Process model with linear predictor (GPLinear) and (b) Gaussian Process model with Boosting predictor (GPBoost). The GPLinear is restricted in only capturing the linear relationship; on the other hand, the GPBoost model can capture linear and all non-linear relationships between the outcome variable and the covariates taking into account the spatial dependencies. To model spatial dependency through Gaussian Process, we used the exponential covariance function for both GPLinear and GPBoost as spatial dependency decreased with increased distance. The GPBoost model parameters were selected by performing a 5-fold cross-validation-based grid search on the model parameters. The grid for the grid search was set as follows: $learning\_rate$ = (10, 5, 1, 0.1, 0.01), $min\_data\_in\_leaf$ = (1, 10, 100, 1000), $max\_depth=(1,2,3,5,10)$. The final GPBoost model was based on the 5-fold cross-validation-based optimal boosting parameters $learning\_rate$ = 1, $max\_depth$ = 3, $min\_data\_in\_leaf$ = 100.

4.3. Gpboost Model Output and Result Discussion

In

Table 1. Gaussian Process Linear Regression Coefficients (fixed effects) for ESKD Data.

Variables	Parameter Estimate	SD	z-Value	p-Value
Intercept	17.8220	6.0247	2.9582	0.0031
Median BMI	−0.2416	0.0800	−3.0204	0.0025
Percentage of Females	0.1280	0.0152	8.4187	0.0001
Median House Hold Income	0.0001	0.0088	6.1759	0.0001
Gini Index of Income Inequality	−2.8126	4.9221	−0.5714	0.5677
Percentage of Population with Only Medicare	0.2314	0.0908	2.5475	0.0108
Area Deprivation Index (ADI)	0.1491	0.1258	1.1852	0.2359
Percentage of White	−0.1209	0.0442	−2.7361	0.0062
Percentage of Black	−0.1157	0.0467	−2.4757	0.0133
Percentage of Other Races	−0.1936	0.0489	−3.9598	0.0001

, we report the GPLinear fixed effects coefficients. From the GPLinear model, we note that race factors and the sex are both very important in explaining the percentage of wait-listed ESKD patients. In addition to that, health factors like BMI are also significant. In addition to that, socioeconomic factors like income and medicare accessibility also strongly impact the percentage of wait-listed ESKD patients.

On the other hand, the GPBoost model is based on the non-parametric function estimation of the covariates using the boosting procedure. Therefore, direct effect sizes or p-value for each individual covariates are not possible to calculate. However, in this respect, for the GPBoost model, we can calculate the “Variable Importance” score for each of the covariates. The variable importance plot, as reported in Figure 1, implies how useful or valuable, overall, each covariate is in the construction of the boosted decision trees within the model. Figure 1 clearly points out to the fact that sex plays the biggest role in explaining the percentage of wait-listed ESKD patients. After that, the next most important factor is BMI. This sharply points towards a gender-based disparity among the ESKD patients waiting to receive kidney transplants.

In Figure 2, we plot the interaction between all covariates as captured through Friedman’s H-statistic [36]. Friedman’s H-statistic is designed to capture any linear or on-linear interaction effects, and in this way, it provides much better insights into the interaction effect of any two predictors. In our study, we used 0.5 as a cut-off indicative of high interaction. In our case, Figure 2 points out that BMI and the percentage of White have a very strong interaction effect (Friedman’s H = 0.99), which means looking at the percentage white only may not be important for being in the ESKD wait list. However, if we focus on the percentage of White with a high BMI have, it has a different ESKD wait-list status than people with a lower BMI. This very interestingly points towards the fact that there is a disparity in the ESKD wait list status among Whites with a higher BMI and Whites with a lower or normal BMI. In addition to that, Figure 2 also indicates a very strong interaction effect (Friedman’s H = 0.95) for the percentage of White vs the percentage of other races in the county population. This means that different levels of the presence of other minority races have different effects on the wait-listing status of a White person with ESKD needing kidney donation.

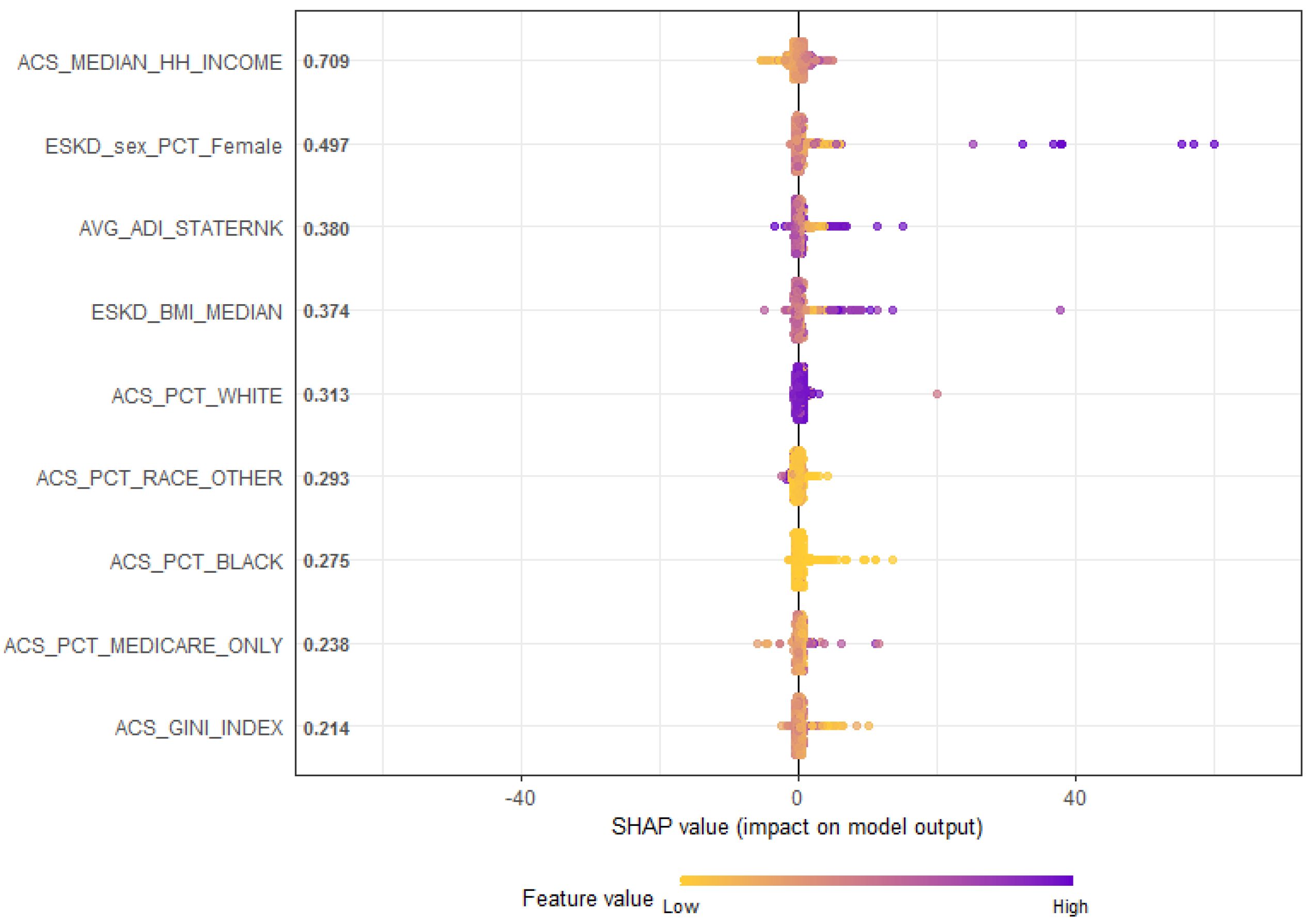
In Figure 3, we provide the SHAP values (SHapley Additive exPlanations) [37]. SHAP is a method based on cooperative game theory, and it is used to increase the transparency and interpretability of machine learning models like Gaussian Process Boosting. SHAP provides the individual contribution of each covariate or feature to the output of the Gaussian Process Boosting model for each observation. In our SHAP plot in Figure 3, variables are shown in the order of global feature importance (on left axis), the first one being the most important and the last being the least important. To interpret a SHAP plot, we need to look into the magnitude and “sign” (positive or negative) contribution of the prediction to the outcome variable. Effectively, SHAP in Figure 3 shows us both the global contribution by using the feature importance and the local feature contribution for the individual observation instance of the problem by the scattering of the beeswarm plot. High values of the percentage of females have a high positive contribution, and high values of BMI have a moderate positive contribution on the prediction of ESKD. Race features as a main effect and has very little contribution to the prediction. However, we notice from the interaction plots Figure 2 that race plays a significant role in several interaction effects.

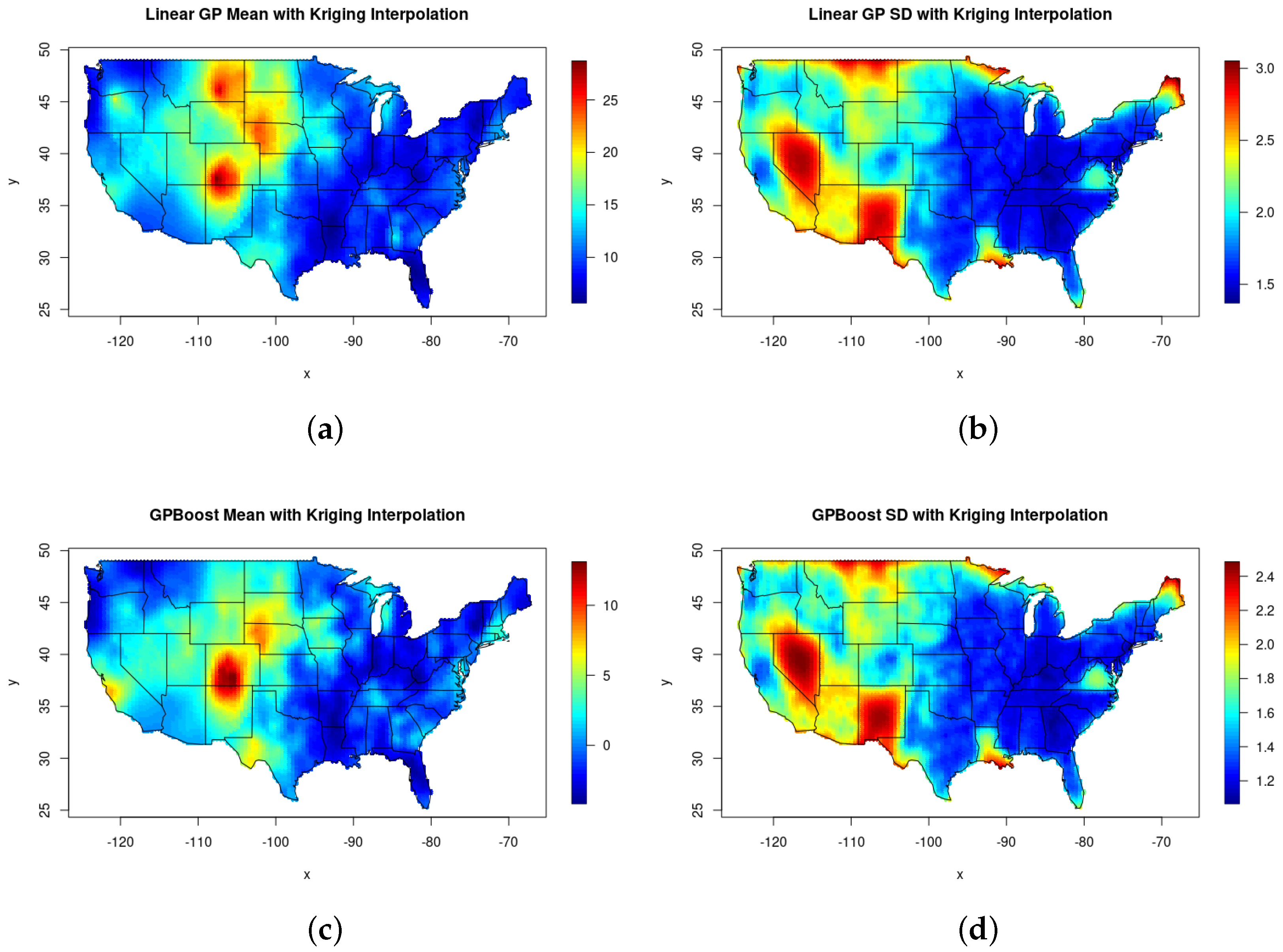
Figure 4 maps the county-specific estimated mean and across the reported 2435 counties in the US. The upper panels show the estimated means and variances of the county-specific spatial random effect using the Gaussian Process Linear model, while the lower panels map the estimated means and variances of the spatial random effect using the Gaussian Process boosting model. From the maps in Figure 4, it is clear that both the Gaussian Process Linear and Gaussian Process boosting models capture similar spatial variability in the data. Comparing Figure 4a,c, we can see that the Gaussian Process Boosting model provides a more distinct spatial band/cluster in Arkansas, Missouri, Illinois, Indiana, Ohio, and a portion of West Virginia than the Gaussian Process Linear model. From (a) and (c) of Figure 4, we also notice that some nonlinear effects are better captured by the Gaussian Process Boosting model in the state of Colorado, which was missed by the Gaussian Process Linear model. In terms of the variability of the spatial random effects when comparing (b) and (d) from Figure 4, we see that both models are in clear agreement.

4.4. Out of Sample Prediction

To study the predictive power of the Gaussian Process Linear and Gaussian Process Boosting models, we split our data set randomly 50 times into training sets and test sets. Each time, the training set was created with $90\%$ of the original data and the remaining $10\%$ was kept as the out of the sample test set. From the average out of the sample predictive mean square error (PMSE) in

Table 2. Average Out of Sample Predictive Accuracy (Predictive Mean Square Error or PMSE) of Gaussian Process Linear and Gaussian Process Boosting Models for ESKD Data.

Models	Average PMSE	SD of PMSE
Gaussian Process Linear Model	28.04	2.02
Gaussian Process Boosting Model	20.86	1.89

, we note that the nonlinear Gaussian Process Boosting model improves the prediction accuracy by $30\%$, which is significant.

In the given data set, several county data were either missing or not reported. In Figure 4, the missing counties are represented as empty or white spots. For all the missing or unreported data, we used the Krigging method with Gaussian Process Linear and Gaussian Process Boosting to perform interpolation and created a complete predictive map (Figure 5) of the mean and the standard deviation of the spatial random effect for the entire US. In the predictive map, we notice that the Gaussian Process Boosting does a superior job in interpolation and also has a lower standard deviation.

5. Discussion and Conclusions

In this paper, we describe a novel application of boosting with Gaussian Process (GPBoost) and Gaussian Process Linear models to map the percentage of wait-listed ESKD patients incorporating spatial dependencies and several demographic and socioeconomic confounding variables. The Gaussian process and boosting provide a flexible non-parametric way to model the effect of the demographic and socioeconomic factors. As we see in Section 4, the boosting architecture provides a significantly better output of sample prediction than a simple linear model framework. In addition to that, our Gaussian Process Boosting-based analysis points out the clear presence of disparity in the percentage of patients wait-listed based on the gender variable. We also discovered that though race as main effect, it does not always play a significant role, but in the presence of other minority race types, it has a significant interaction effect towards the percentage of wait-listed ESKD patients. Our findings are consistent with previous clinical studies [3,4,6,8].

As a future work, we wish to extend our analysis from only the spatial domain to the full spatio-temporal framework. Under the full spatio-temporal framework, we would be able analyze how, over time, the spatial variability of wait-listed patients is changing. The temporal effect will also be valuable in understanding over a period of time how several kidney donation and recipient regulations and policies are affecting the overall wait-listed patients [2,4].

In conclusion, ESKD represents a significant public health challenge in the US, with profound implications for individuals, families, and society [3,7]. Spatial disparities in kidney transplant wait-listing further exacerbate the inequities in access to transplantation, perpetuating disparities in health outcomes. Addressing these disparities requires concerted efforts from policymakers, healthcare providers, and community stakeholders to ensure equitable access to transplantation for all individuals with ESKD, regardless of their geographic location or socioeconomic status. By prioritizing equity and fairness in access to transplantation, we can work towards improving outcomes and quality of life for individuals living with ESKD across the US.