A New Predictive Algorithm for Time Series Forecasting Based on Machine Learning Techniques: Evidence for Decision Making in Agriculture and Tourism Sectors

Abstract

Accurate time series prediction techniques are becoming fundamental to modern decision support systems. As massive data processing develops in its practicality, machine learning (ML) techniques applied to time series can automate and improve prediction models. The radical novelty of this paper is the development of a hybrid model that combines a new approach to the classical Kalman filter with machine learning techniques, i.e., support vector regression (SVR) and nonlinear autoregressive (NAR) neural networks, to improve the performance of existing predictive models. The proposed hybrid model uses, on the one hand, an improved Kalman filter method that eliminates the convergence problems of time series data with large error variance and, on the other hand, an ML algorithm as a correction factor to predict the model error. The results reveal that our hybrid models obtain accurate predictions, substantially reducing the root mean square and absolute mean errors compared to the classical and alternative Kalman filter models and achieving a goodness of fit greater than 0.95. Furthermore, the generalization of this algorithm was confirmed by its validation in two different scenarios.

1. Introduction

At both supply and demand levels, accurate time series prediction techniques are becoming crucial for modern decision support systems. Linear models, such as the autoregressive integrated moving average (ARIMA), are typically employed in many areas of study [1,2,3,4,5,6]. Specifically, seasonal ARIMA (SARIMA) [7] models are being used for forecasting in retail trade [8], tourism demand [9,10], financial sectors [11] or coronavirus disease predictions (COVID-19) [12], in which the seasonal component is manifest.

The state-space model Kalman filter technique has also often been applied for forecasting purposes in different economic fields, such as oil price [13], stock markets [14], COVID-19 [15], fisheries [16] and road traffic [17].

In addition to linear models, several nonlinear algorithms, such as machine learning (ML) techniques, have been developed recently to predict data from time series [18]. Thus, a nonlinear autoregressive (NAR) neural network is a generalization of the ARIMA model with a more complex structure, and therefore it is more robust than linear regressions. We find several applications for this algorithm, including in: the pricing of minerals [19], quantification of waste [20] or water levels [21], displacements in foundation pits [22], COVID-19 [23] and others [24,25,26]. In addition, numerous studies have used support vector regression (SVR) to make time series predictions [27] in different domains, including: energy consumption [28,29], the financial sector [30,31,32], weather [33,34], water [35,36,37,38,39], COVID-19 [40] and education [41].

Finally, recent research has used hybrid models to predict much more diverse situations, such as the demand for flights in the aviation industry [42], electrical energy consumption [43], weather prediction [44] and financial trends [45].

The literature reveals certain limitations due to the inability to adequately detect trend variations. Linear models such as ARIMA and time series forecasting models based on previous data often continue data trends without taking into account potential changes in the future values of the observed variable. For this reason, when a time series presents peaks and changes in trend, those models usually reveal a very characteristic deviation to the right [46,47,48,49,50], and the fit of the prediction curve for the observed variable is less than what is desired [51,52,53,54]. Furthermore, the use of the Kalman filter could lead to a refinement of our prediction, but the implementation of this algorithm requires the simulation of an error term that might cause convergence problems. Although some research analyzes similar issues [55,56,57], this study tries to solve this problem using a new model that modifies the Kalman filter [58] and hybridizes it with ML techniques. The resolution of these problems could be very useful for any time series with few data, without the possibility of capturing information from exogenous variables and convergence problems, as is the case for the agricultural and tourism time series.

Recent agricultural forecasting research has employed ARIMA models [59,60,61], the Kalman filter method [62], NAR [46,63], SVR [64,65,66,67] and hybridized models [68,69,70,71]. This research does not provide conclusive results, except that ML-based models are widely used when large datasets and numerous variables are available, such as those that capture remote sensing data [72,73,74].

On the other hand, time series models are also widely applied in tourism demand forecasting [75,76], typically using ARIMA and SARIMA models [77,78,79,80,81,82], the Kalman filter econometric-based methodology [83,84] and artificial intelligence-based methods [85,86] as [87] pointed out. To date, hybrid methods in tourism forecasting are not universally preferred [88].

The main purpose of this research is to use the same idea described in the hybrid models built over ARIMA processes but with a double correction: first, a correction of the prediction on the observed variable using a Kalman filter [58] and its modified version [89] to solve the converge problems, and second, a correction of the system error with a nonlinear component. Therefore, this study tries to correct the deviation to the right by applying a hybridization with ML techniques, thus developing an efficient prediction system through a simple process using only previously gathered data without exogenous variables or complex models.

To verify the advantages of our hybrid model, it is applied to berry production and tourism demand time series. These are two economic activities with a noticeable seasonal character. Although little is known about berry yield forecasting from a variable perspective over time, the berry sector also presents seasonal productions that have not been well-studied in the literature even though they are important in the raw material markets [62]. Additionally, when reviewing the literature on tourism and passenger transportation demand forecasting from 2007 to 2017, it was noticed that seasonality and contingencies are the main obstacles to achieving more accurate forecasts [75].

Finally, we compared the root mean square error (RMSE), mean absolute error (MAE), mean absolute scaled error (MASE) and goodness-of-fit R² between hybridized and non-hybridized models.

2. Material and Methods

To demonstrate the full functionality of the new hybrid model developed, it is fitted using four datasets.

2.1. Data

Spain represents the highest proportion (40.1%) of land dedicated to fruit production in the European Union (EU-28) [90]. A daily berry yield dataset of strawberry and raspberry fruits was extracted from three large coops that operate in Huelva, situated in the southwestern part of Spain, corresponding to three periods, i.e., (2017–2018), (2018–2019) and (2019–2020). To ensure that the seasonal periods were equal, September 1 was chosen as the start date and July 15 of the following year as the end date for each agricultural season. The first two seasons were used as training datasets and the last as the test dataset to evaluate the results.

The dataset corresponding to the tourism sector of Huelva, extracted from the Hotel Occupancy Survey [91], comprises the number of travelers and monthly overnight stays, our predictor variables, for the period between 1999 and 2019 and contains 252 observations. Unfortunately, the year 2020 was not considered due to the exceptionality caused by the COVID-19 pandemic, with figures that are non-reflective of the normal evolution of the sector.

ARIMA models are especially useful for managing time series that exhibit seasonal patterns. Seasonality is a typical feature of both the agriculture and tourism industry and is quite pronounced in the case of Huelva. The berry yield time series datasets have a seasonal component with a lag of 317 days. With tourism highly marked by the sun and beach segment, the summer months are the ones in which tourist activity is most concentrated. Moreover, volumes of travelers and overnight stays in hotels are variables that are usually employed to quantify such seasonality and evolution. Taking the year 2019 as a reference, the seasonal ratio, or the quotient between the highest and the lowest number of overnight stays monthly reached in August and January, respectively [92], was 12.424. Again, the seasonality rate, the quotient between the sum of the overnight stays in the three months with the highest influx and the total number of overnight stays for the year, was 0.479, i.e., 47.9% of the overnight stays in hotels, ranked from July to September.

2.2. The ARIMA and Kalman Filter Linear Models

Firstly, an autoregressive integrated moving average (ARIMA) model was used as a base research model. Let Y_t be a stationary stochastic process with a mean of zero and differentiated d ϵ N times. The ARIMA (p,d,q) process is defined as

$$Y_t={\sum }_{i=1}^p{\varphi }_i{Y}_{t-i}+{\sum }_{j=1}^q{\theta }_j{ϵ}_{t-j}+{ϵ}_t,$$

(1)

where ${ϵ}_t$~ N (0, σ²) is a white noise process associated with the system, p, q ϵ N are the lags chosen for the model, and the parameters of the systems are ϕ_i, θ_j ϵ R.

To choose the appropriate values of p and q, we considered the ARIMA process, which minimizes the value of both the Akaike criterion (AIC) and the Bayesian criterion (BIC), automating the process with the R software. On the other hand, to determine the coefficients of the ARIMA process, we applied the Hannan–Rissanen algorithm [93].

Secondly, we used the Kalman filter [58], a recursive algorithm widely used in the fields of economics and econometrics based on a state-space system defined by the system state (2) and the output equation of the system (3):

$${\mathrm{y}}_{\mathrm{t}}={ \mathrm{Ay}}_{\left\{\mathrm{t}-1\right\}}+{ \mathrm{B}\mathsf{\omega }}_{\mathrm{t}},$$

(2)

$${\mathrm{z}}_{\mathrm{t}}={ \mathrm{H} \mathrm{y}}_{\mathrm{t}}+{ \mathsf{\nu }}_{\mathrm{t}},$$

(3)

where ${\mathrm{y}}_{\mathrm{t}}\in R^n$ ϵ is the state vector, ${\mathrm{z}}_{\mathrm{t}}\in R^n$ the value of the exit and ${\mathsf{\omega }}_{\mathrm{t}}$ ~ N^s (0, Q) and ${\mathsf{\nu }}_{\mathrm{t} }$~ N^m (0, R) the white noise processes. Finally, A ϵ R^nxn, B ϵ R^nxs and H ϵ R^mxn are the parameters of the state systems.

2.3. Nonlinear Autoregressive (NAR) Neural Networks and Support Vector Regression (SVR)

The main idea behind a nonlinear autoregressive neural network (NAR) is to eliminate the existing linearity constraint in the ARIMA model looking for an approximation of the form (4)

$$X_t=f (X_{t-i},... X_{t-\mathrm{p}})+{ϵ}_t,$$

(4)

where f is an unknown nonlinear function, X_t is the time series data, p ϵ N is the number of lags used in the estimation, and ${ϵ}_t$ ~ N (0, σ²) is a white noise process.

As NAR neural networks are a type of multilayer perceptron (MLP) with a single output value, and consequently there is no specific method to determine their architecture, we selected a hidden layer [94], by defining our algorithm as the following expression:

$${\widehat{X}}_{\mathrm{t}}={\phi }_2\left(\sum _{j=1}^M{\omega }_{jo}{\phi }_1\sum _{i=1}^p{\omega }_{ij}+{\beta }_j\right)+{\beta }_0,$$

(5)

where $p,M\in Z$ are the number of selected lags and the number of nodes in the hidden layer, respectively, which have been calculated using a node growth technique seeking to minimize the RMSE. We used the sigmoid function and the hyperbolic tangent function in the hidden layer and the identity function in the output layer as respective activation functions determined by ${\phi }_1$, ${\phi }_2$ [20,22,23,45,95]. Finally, w_ij, w_j0 are the selected weights from input i to hidden unit j and from hidden unit j to output o, respectively, and ${\beta }_j,{\beta }_0.\in R$ are the respective biases units.

We chose the backpropagation algorithm to train our NAR neural network and to fix the weights.

Support vector regression (SVR) is a ML model based on finding a nonlinear regression between N pairs of elements $\left(x_t,y_t\right),$ where $x_t\in R^n$ are the input vectors and $y_t\in R$ are their corresponding outputs, like the one described in Equation (6):

$${\widehat{y}}_i=w^{\prime }\Psi \left(x_i\right)+b,$$

(6)

where $\Psi$ is an unknown nonlinear function, $w\in R^n$ are the weights of the model and $b\in R$ is its respective bias. To find the values of $w$, we trained our model using the following loss function:

$$\underset{\mathrm{w}}{\min } \frac{1}{2} {\left|\left|\mathrm{w}\right|\right|}^2+\mathrm{C}\sum _{i=1}^N{\left|\left|{ \widehat{y}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}}\right|\right|}_{\epsilon }$$

(7)

with $ϵ, \mathrm{C}>0$. This definition means that we consider the error to be zero for all estimated values with a distance from their true value of less than ϵ. Therefore, by including slack variables in the loss function and applying the Lagrange multipliers method, we obtain a new equation to minimize, described in Equation (8).

$$\underset{\mathsf{\alpha },{\mathsf{\alpha }}^{*}}{\min }\frac{1}{2}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\sum }_{\mathrm{j}=1}^{\mathrm{N}}\left({\mathsf{\alpha }}_{\mathrm{i}}-{\mathsf{\alpha }}_{\mathrm{i}}^{*}\right)\left({\mathsf{\alpha }}_{\mathrm{j}}-{\mathsf{\alpha }}_{\mathrm{j}}^{*}\right)\mathrm{k}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)+{\sum }_{\mathrm{i}=1}^{\mathrm{N}} \left({\mathsf{\alpha }}_{\mathrm{i}}-{\mathsf{\alpha }}_{\mathrm{i}}^{*}\right){\mathrm{y}}_{\mathrm{i}}+{\sum }_{\mathrm{i}=1}^{\mathrm{N}}\left({\mathsf{\alpha }}_{\mathrm{i}}-{\mathsf{\alpha }}_{\mathrm{i}}^{*}\right)\mathsf{\epsilon },$$

(8)

subject to

$$\left\{\begin{array}{c}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}} \left({\mathsf{\alpha }}_{\mathrm{i}}-{\mathsf{\alpha }}_{\mathrm{i}}^{*}\right)\\ 0\le {\mathsf{\alpha }}_{\mathrm{i}},{\mathsf{\alpha }}_{\mathrm{i}}^{*}\le C\end{array}\right.$$

(9)

The values $\left({\mathsf{\alpha }}_{\mathrm{i}}-{\mathsf{\alpha }}_{\mathrm{i}}^{*}\right)$ are known as support vectors, ${\mathsf{\alpha }}_{\mathrm{i}},{\mathsf{\alpha }}_{\mathrm{i}}^{*}$ are the Lagrange multipliers, and $\mathrm{k}$ functions as the kernel function. Finally, if we use the results obtained in (8) and (9) in Equation (6), our final approximation is represented by Equation (10):

$${\widehat{y}}_i={\sum }_{\mathrm{j}=1}^{\mathrm{N}} \left({\mathsf{\alpha }}_{\mathrm{j}}-{\mathsf{\alpha }}_{\mathrm{j}}^{*}\right)\mathrm{k}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)+b,$$

(10)

In our research, we used the Gaussian function as the kernel function

$$k\left(x_i,x_j\right)=e^{{\gamma \left|\left|x_i-x_j\right|\right|}^2},$$

(11)

and we calculated the value of parameters γ, C, ε ϵ R using the package e1071 of R programming language [96].

Lastly, to determine the dimension of the input vector, we applied a growth technique like the one used in the NAR model, which involves increasing the number of input dimensions by one unit at each step and calculating the RMSE value until finding the input dimension that minimizes the RMSE value.

2.4. The Hybrid Models

In general, the introduction of an ARIMA process in the state space implies convergence problems when the variance of the associated white noise process is large. For this reason, in our study, we compared the classical method of introduction in the state-space [97,98], (KF), with the new inclusion method described in [89], named alternative Kalman filter (AFK), where converge problems are fixed, and hybridized it with ML techniques.

The main idea was to use the NAR and SVR models as correction factors to predict the error of the AKF model. So, let Y_t be a time series and ${ϵ}_t$~N (0, σ²) its white noise process associated with the AKF model; the hybrid system is described by Equation (12):

$${\widehat{Y}}_{t+1}={\widehat{L}}_{t+1}+{\widehat{ϵ}}_{t+1},$$

(12)

where $\widehat{L}$_t+1 is the linear value associated with the AKF prediction and ${\widehat{ϵ}}_{t+1}$ is an error estimation calculated by the NAR or the SVR model.

3. Results

In this section, weekly results from the two berry crops and the two tourism demand datasets are examined and analyzed, establishing a comparison among the (1) KF, (2) AKF, (3) AKF-SVR and (4) AKF-NAR hybrid models. The parameters on which each model depends are described in Section 2.

The criteria used for the comparisons were the RMSE, MAE, MASE and goodness-of-fit R² as there was a particular interest in error minimization and a higher number of parameters was not penalized, which is a requirement of a nonlinear process.

Finally, all our experiments were programmed using a CPU with a 2.6GHz i-7 processor and 16 GB of ram memory. On the other hand, as mentioned in Section 2, all the algorithms were programmed in R software using mainly the e1071, forecast and tseries packages.

3.1. Results for Berry Datasets

The weekly strawberry season forecast was built on an ARIMA (3,1,1). For the AKF-SVR model, the Gaussian kernel function with γ = 0.1, C = 1 and ε = 0.1 was used. Moreover, eight inputs were considered. For the AKF-NAR model, the hyperbolic tangent activation function was employed in the hidden layer, η = 0.01, p = 4 and M = 1.

Table 1. Results for strawberry time series: 2019–2020 (weekly).

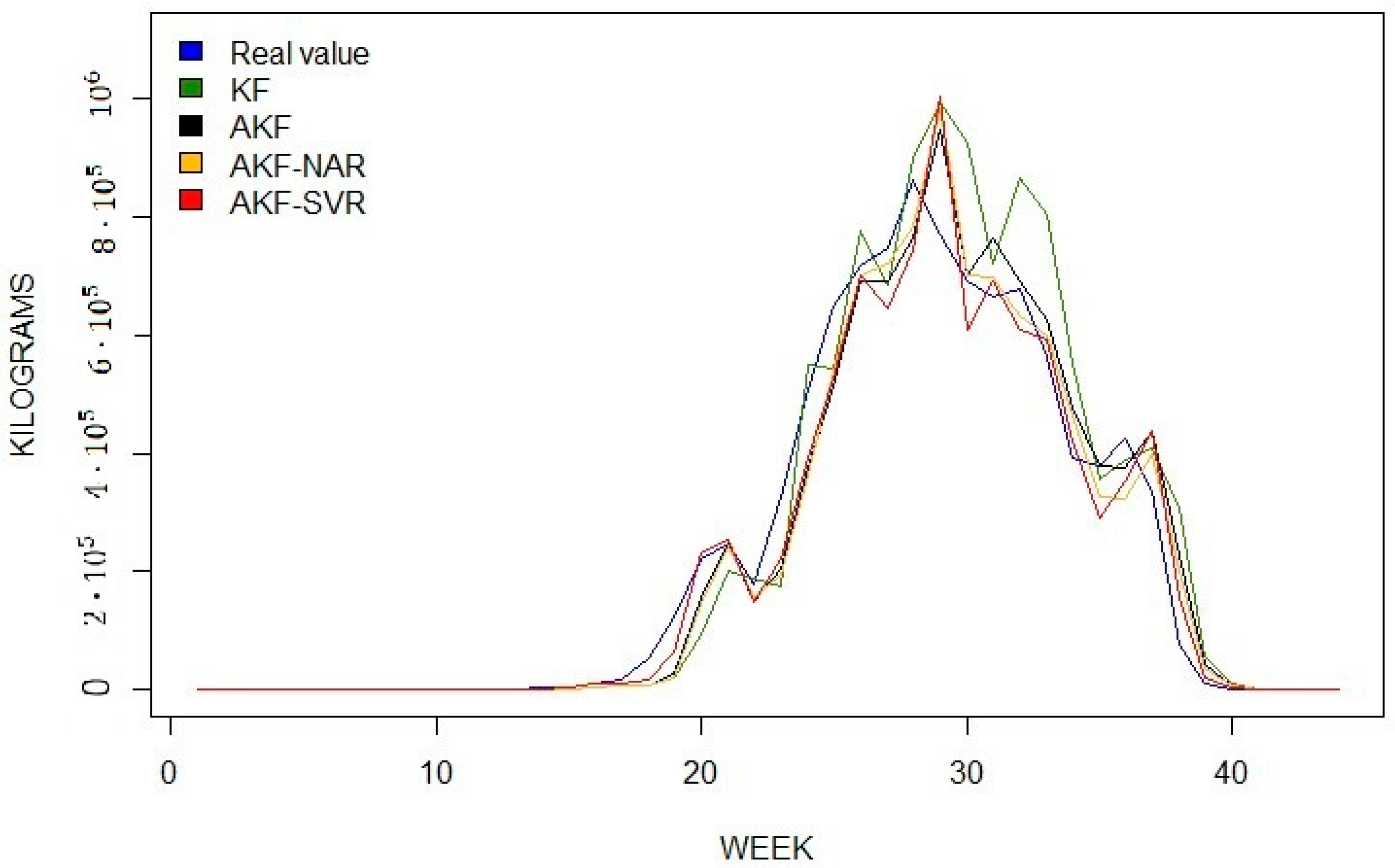
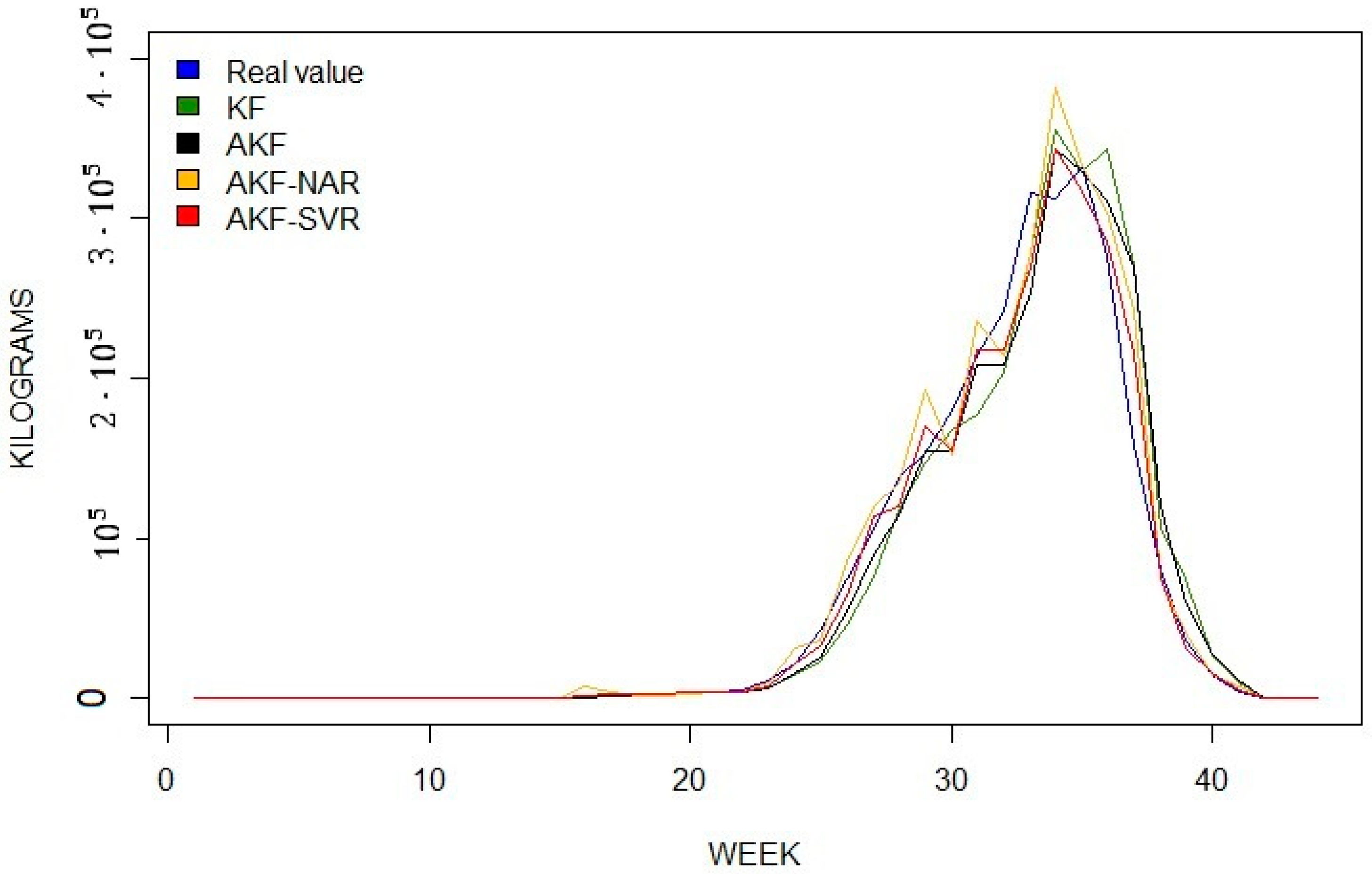
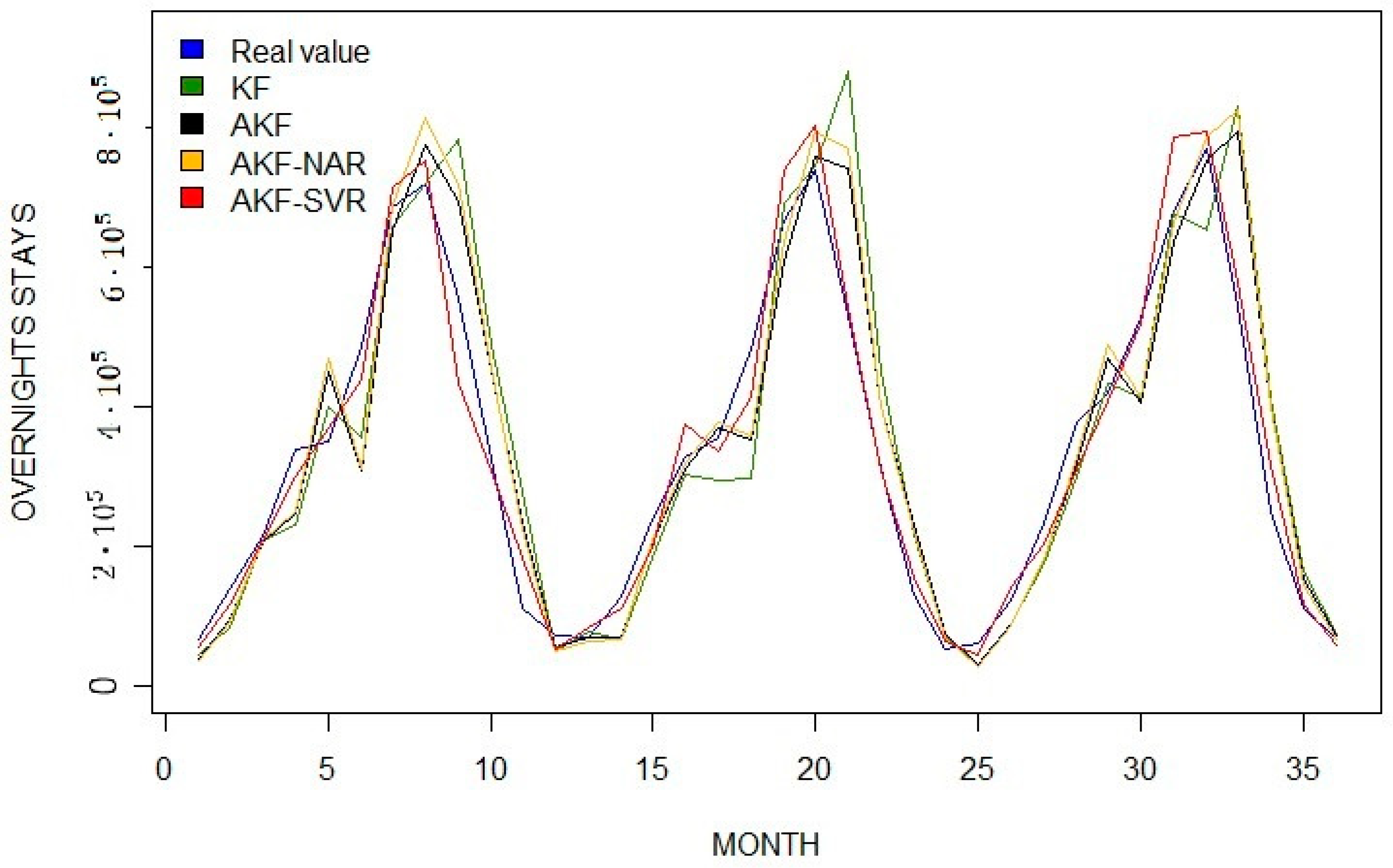
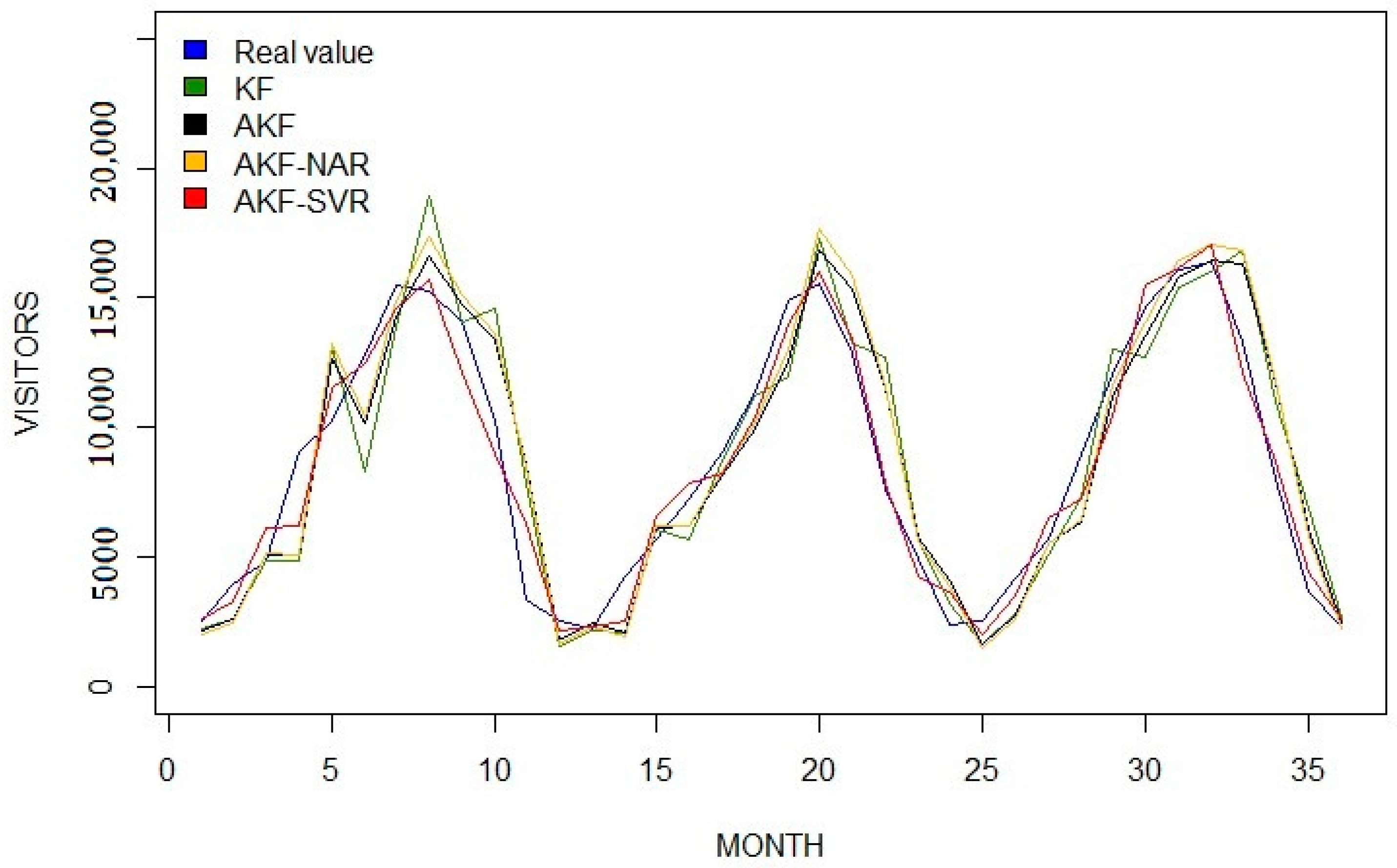
Model	RMSE	MAE	MASE	R2
KF	90,847.01	52,906.00	1.147	0.899
AKF	62,269.74	36,901.74	0.800	0.953
AKF-NAR	61,311.99	35,640.53	0.773	0.954
AKF-SVR	61,339.73	35,147.71	0.770	0.954

summarizes the results obtained for the 2019–2020 season. It was noticed that the models that best approximated the real values of the strawberry season were the hybrid AKF-SVR and AKF-NAR.

Similarly,

Table 2. Results for raspberry time series: 2019–2020 (weekly).

Model	RMSE	MAE	MASE	R2
KF	25,323.00	12,576.67	0.802	0.938
AKF	23,419,50	11,037.77	0.704	0.947
AKF-NAR	20,425.92	9324.95	0.595	0.960
AKF-SVR	14,248.64	6772.14	0.432	0.980

summarizes the results for the raspberry time series data. This predictive system was built on an ARIMA (1,1,1) using the Gaussian kernel function with γ = 0.071, C = 1, ε = 0.1 and 14 inputs for the AKF-SVR model. However, for the AKF-NAR model, the hyperbolic tangent function as an activation function was used in the hidden layer, η = 0.1, p = 16 and M = 1. Following the same criteria, the best predictive system was the hybrids.

Figure 1 and Figure 2 demonstrate a comparison of the four predictive models with respect to the observed real variable for each crop.

3.2. Results for Tourism Datasets

To predict the number of nights spent in Huelva Province hotels (2017–2019), an ARIMA (1,1,1) was used. The Gaussian kernel function with γ = 0.1, C = 1 and ε = 0.1 with 10 inputs was employed for the AKF-SVR model. The sigmoid function served as the activation function in the hidden layer. η = 0.1, p = 10 and M = 1 for the AKF-NAR model.

The best model was still the hybrid AKF-SVR (

Table 3. Results for total overnight visitors in Huelva: 2017–2019 (monthly).

Model	RMSE	MAE	MASE	R2
KF	116,602.9	82,500.06	0.708	0.739
AKF	93,020.33	70,959.72	0.609	0.834
AKF-NAR	98,669.07	72,939.55	0.626	0.813
AKF-SVR	44,416.79	34,270.45	0.294	0.962

and Figure 3). Identical results were obtained for visitors (

Table 4. Results for total visitors in Huelva: 2017–2019 (monthly).

Model	RMSE	MAE	MASE	R2
KF	23,131.54	17,501.85	0.759	0.775
AKF	20,542.48	16,267.91	0.706	0.822
AKF-NAR	21,328.9	16,844.93	0.731	0.808
AKF-SVR	11,433.17	9350.8	0.406	0.945

and Figure 4).

In conclusion, for all the datasets analyzed, the hybrid models developed improved the results over the linear ones, with the AKF-SVR algorithm showing the best performance.

4. Discussion

Different forecasting systems were analyzed by combining an ARIMA model with more sophisticated algorithms, such as a new approach to the classical Kalman filter combined with ML processes.

The results reveal that hybrid systems combining the AKF with error correction through a NAR neural network or an SVR model achieved higher accuracy than classical forecasting models. These results are better in the four time series analyzed for the two economic sectors. This is a simple model not seen in the literature in which the classical Kalman filter algorithm is modified, and the model error is estimated by a machine learning algorithm.

Three interesting outcomes were identified when the model results were compared with similar research that used different prediction models over the time series, such as ARIMA, Kalman filter, SVR or NAR.

First, our algorithm showed a better fit to the real data than those used in other studies [4,20,46,52,69,99,100,101,102], as we can confirm by the values of R².

Second, we can see that in Kalman-filter-based models and in other studies based on linear predictive models, prediction plots exhibit a deviation to the right since these predictive models do not quickly capture trend variation [1,16,20,28,49,50,71,103]. However, our hybrid models corrected for this standard deviation by capturing trend changes (Figure 1, Figure 2, Figure 3 and Figure 4).

Finally, after analyzing the time series data, it was evident that they had a relevant seasonal component. Consequently, a SARIMA model may be an excellent model to apply in time series with that peculiarity. However, when considering recent research in which that model has been used [8,9,10,11,12,104], it is seen that monthly or daily data with the short seasonal component are used; i.e., the seasonal component is not far from the data to be predicted. In the berry dataset, the seasonal component has a lag of approximately 317 days, making its use computationally unfeasible since the computation time outstrips the advantage of its usage.

5. Conclusions, Limitations and Future Research

In this study, different predictive methods used to obtain a weekly yield forecast of strawberries and raspberries during an agricultural season and monthly tourism forecasts for both visitors and overnight stays have been developed and compared.

An alternative method for introducing the ARIMA model in a state-space system that eliminates randomness in the algorithm and uses only the previous data and the error produced by the system was developed. In addition, ML techniques such as NAR and SVR were introduced in the model to correct the system error and improve performance.

First, based on the acquired results, it can be concluded that these new hybrid models that combine both techniques are the best for predicting weekly berry production and tourism demand, substantially reducing the RMSE, MAE and MASE and achieving a goodness of fit greater than 0.95 in all cases.

Secondly, predictive models applied on time series that, as in the case of the agriculture and tourism sectors analyzed in this research, have a seasonal component and convergence problems, show little reliability at the points of trend variation. Therefore, the time series forecasting method developed is also considered useful for time series data with a significant standard deviation in the white noise.

Finally, an increased computing capacity and automated data accessibility make it possible to implement machine-learning-based techniques to support decision making. However, for these algorithms to work properly they need a lot of data, and the advantage of the algorithm we present is that it does not need a lot of data or complex models with many variables, which makes it easy for practitioners to implement and use.

The models developed still have some weaknesses, such as poor forecasting of the maximum, minimum and turning points, which could be an idea for further research. Secondly, we only analyzed four time series from two sectors. We propose this predictive algorithm be tested with other time series data [105]. Thirdly, it could be interesting to add exogenous variables to the ARIMA model [106,107,108] or use a nonlinear autoregressive exogenous model (NARX) [109,110,111,112,113,114,115]. Finally, this approach could be compared with other research that uses different ML models than those presented here, such as extreme learning machines (ELMs), convolutional neural networks (CNNs), long short-term memory (LSTM) or singular-spectrum analysis (SSA), among others [116,117,118,119,120,121,122,123].