Selected Payback Statistical Contributions to Matrix/Linear Algebra: Some Counterflowing Conceptualizations

Abstract

Matrix/linear algebra continues bestowing benefits on theoretical and applied statistics, a practice it began decades ago (re Fisher used the word matrix in a 1941 publication), through a myriad of contributions, from recognition of a suite of matrix properties relevant to statistical concepts, to matrix specifications of linear and nonlinear techniques. Consequently, focused parts of matrix algebra are topics of several statistics books and journal articles. Contributions mostly have been unidirectional, from matrix/linear algebra to statistics. Nevertheless, statistics offers great potential for making this interface a bidirectional exchange point, the theme of this review paper. Not surprisingly, regression, the workhorse of statistics, provides one tool for such historically based recompence. Another prominent one is the mathematical matrix theory eigenfunction abstraction. A third is special matrix operations, such as Kronecker sums and products. A fourth is multivariable calculus linkages, especially arcane matrix/vector operators as well as the Jacobian term associated with variable transformations. A fifth, and the final idea this paper treats, is random matrices/vectors within the context of simulation, particularly for correlated data. These are the five prospectively reviewed discipline of statistics subjects capable of informing, inspiring, or otherwise furnishing insight to the far more general world of linear algebra.

1. Introduction

The unfolding of the statistics field over recent centuries discloses a transformation of the role of matrix algebra from a mostly notational tool for conveniently expressing statistical problems, to an essential component in the conceptualization, derivation, comprehension, and utilization of more mature, complex, and complicated analytical devices characterizing the modern-day statistical sciences. Matrix/linear algebra benefits began accruing in the theoretical and applied statistics literature in the early 1940 s, when Fisher, and then Wilks, used the word matrix for the first time in their publications [1]. Today, it is an indispensable part of the discipline’s subject matter. This one-way flow of contributions has bolstered the mathematization of statistics, with statisticians increasingly recognizing that it has become a necessary prerequisite in many parts of their discipline [2], especially for linear statistical models [3] and multivariate statistics [4] research and coursework. The primary purpose of this paper is to review at least some of the ideas shared between these two cognate subdisciplines, converting them into bilateral interactions by describing their converse issue, namely, the emerging and potential roles of statistics in the conceptualization, derivation, comprehension, and utilization of analytical mechanisms characterizing parts of matrix/linear algebra.

Many academic books and articles address matrix/linear algebra and its sundry relationships with statistics [4,5,6,7,8]. Perhaps foremost among the more targeted of such tomes/pieces is the set treating regression [3], long deemed the workhorse of traditional statistics, in either its linear or its iteratively linear (i.e., nonlinear) forms. Virtually all statisticians, whereas apparently relatively few matrix and linear algebraists and other specialized mathematicians, seem to be very familiar with and well versed in this rather customary data analytic technique, perhaps because it flourished in astronomy and geodesy during the age of discovery rather than in pure mathematics. In its simplest version, it specifies a response variable to be a linear combination of p ≥ 1 covariates, all individually organizing data in vector form. This notion provides a neat solution to the enduring matrix algebra problem of determining which, if any, of its rows and/or columns are collinear. Conceivably, the next ranking mutual opportunity focuses on eigenfunctions―dating back to 18th century mathematics but acquiring their contemporary name from Hilbert in 1940―which occupy a prominent place in matrix algebra theory and applications. Usually, a quantitative scholar first encounters this concept in statistics when studying multivariate principal components and/or factor analysis [4], or, frequently almost in passing, multiple regression multicollinearity complications [3]. It also is an important ingredient in correlated data analyses. Matrix algebra theory accompanying eigenvalues and their paired eigenvectors encompasses the establishment of upper and lower bounds upon the eigenvalues, an effort whose ultimate research goal is to shrink these bounds to exactly match their corresponding eigenvalues, with the well-known Perron-Frobenius theorem [9] historically initializing such an interval definition for the principal eigenvalue of a statistical (e.g., covariance) matrix. Statistics supplies estimation theory extendable to an approximation of eigenvalues, point-estimate quantities whose calculations should be intellectually appealing to matrix algebraists. The method of moments estimator is of particular relevance here, given that a matrix readily supplies the mean and variance of its set of eigenvalues.

A third common interest is special matrix operations, such as Kronecker sums and products, and Hadamard products [9]. Spatial statistics, for example, furnishes some informative insights into these categories of operators. Meanwhile, a fourth salient theme spanning these two disciplines is multivariable calculus, expressly the Jacobian term associated with variable transformations [10]. Again, spatial statistics provides correlated data auto-normal model specifications that highlight not only calculus-based, but also eigenvalue-based, illuminations directed from statistics to matrix/linear algebra. Finally, random matrices/vectors within the context of simulation, chiefly in terms of linkage variation for correlated data, promote accumulating sampling distribution understanding about a wide range of matrices, paralleling the body of knowledge already generated through Erdős-Rényi random matrix synergies; Wishart [11] first introduced such random matrix theory within the environment of multivariate statistics [12]. In summary, these are the five subjects prospectively reviewed in this paper.

Interestingly, matroids―combinatorial structures simultaneously but separately discovered by Whitney [13] and Nakasawa [14] in 1935, with Oxley [15] providing a grand survey of its theory, that have a habit of being ideal for describing a wide range of objects by abstracting and generalizing the notion of linear independence in vector spaces―appearing in algebraic statistics, which come in various forms, span this range of topics, illustrating other gestational possibilities as well as offering an identifiable potential avenue for backflow from statistics to linear algebra.

2. A Linear Regression Contribution to Matrix Algebra

A matrix/linear algebra problem seeking an uncomplicated solution concerns determining all of the distinct linear combination subsets of matrix rows/columns resulting in zero eigenvalues for a given matrix. Overlapping linear combinations constitute a complication whose astute management and treatment remain both elusive and a fruitful subject of future research. This section addresses the determination of the same number of subsets as zero eigenvalues, recognizing this preceding repetition situation possibility.

Multiple linear regression coupled with a sweep―a reader should not confuse this operation, whose name was coined in 1979, with the RProject basic function (see https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/sweep (last accessed on 4 October 2022)), named as such in 1988, which differs from it―algorithm [16] applied to a n-by-m matrix M give an elegant solution to this problem. Designating an arbitrary row/column as a regression response vector Y, and then treating the remaining rows/columns like the regression covariate matrix X—which does not include a vector 1 for the intercept term in this circumstance—enables a statistical package regression routine to invoke its aforementioned sweep operation. This procedure always begins by sweeping the first row/column in matrix X, followed by the next row/column in this matrix if the pivot―a matrix cell element selected to do certain computations that needs to be not only distinct, but also distant, from zero, used to determine row/column permutation swappings―is less than a near-zero value whose default threshold magnitude often is roughly 1.0$\times$10⁻⁹ (i.e., if that row/column is not a linear function of the preceding row/column), then continuing sequentially to each of the next rows/columns if their respective pivots are not less than this threshold amount, until it passes through all of the rows/columns of matrix X. If rows are evaluated first, then the transpose of matrix M allows an analysis of columns. In other words, postulating this setting, the aforementioned sweep algorithm can uncover linearly dependent subsets of matrix rows/columns by specifying its first row/column, C₁, as a dependent variable, and its (n − 1) remaining rows/columns, C₂-C_n, as covariates. Standard computer software package output from this specification usually includes an enumeration of the existing linearly dependent row/column subsets. A second no-intercept regression that is stepwise in its nature and execution can check whether or not C₁ itself is part of a linear combination subset. Simplicity dissipates here when n becomes too large, with prevailing numerical precision resulting in some linear combinations embracing numerous superfluous columns with computed near- or almost-identically zero regression coefficients (e.g., 1.0 × 10⁻¹¹). This rounding error corruption frequently emerges only after n or m is in the thousands.

The two matrices presented in

Table 1. Specimen illustrative example matrices.

Simple 5-by-5 Matrix	Simple 5-by-8 Matrix
$\left[\begin{array}{ccccc}0& \mathbf{1}& \mathbf{1}& 0& 1\\ \mathbf{1}& \mathbf{0}& \mathbf{0}& \mathbf{1}& \mathbf{0}\\ \mathbf{1}& \mathbf{0}& \mathbf{0}& \mathbf{1}& \mathbf{0}\\ 0& \mathbf{1}& \mathbf{1}& 0& 0\\ 1& \mathbf{0}& \mathbf{0}& 0& 0\end{array}\right]$	$\left[\begin{array}{cccccccc}\mathbf{3}& 0& \mathbf{3}& 9& 1& 2& 7& 6\\ \mathbf{1}& \mathbf{1}& \mathbf{1}& \mathbf{2}& \mathbf{2}& \mathbf{3}& \mathbf{4}& \mathbf{4}\\ \mathbf{2}& \mathbf{2}& \mathbf{2}& \mathbf{4}& \mathbf{4}& \mathbf{6}& \mathbf{8}& \mathbf{8}\\ \mathbf{4}& 7& \mathbf{4}& 8& 1& 9& 3& 6\\ \mathbf{5}& 9& \mathbf{5}& 7& 8& 2& 3& 5\end{array}\right]$
eigenvalues: 2.14, 0.66, 0, −0.66, −2.14	linear combinations: 1 row pair & 1 column pair

NOTE: bold font denotes linearly dependent rows/columns; matrices retrieved from the web site https://www.mathworks.com/matlabcentral/answers/574543-algorithm-to-extract-linearly-dependent-columns-in-a-matrix (accessed on 8 November 2022).

supply illustrative examples of this approach. One is a square symmetric matrix, meaning that an examination needs to be of only its rows or columns, not both. The second is a non-square asymmetric matrix.

Table 2. Regression sweep algorithm results for specimen matrices.

Software Package	Screen Printed Message	Matrix Column(s)/Row(s)
Minitab 17 & Table 1; 5-by-5 matrix	the following terms cannot be estimated and were removed	C3
SAS 9.4 & Table 1; 5-by-8 matrix	the following parameters have been set to 0, since the variables are a linear combination of other variables as shown	R3 = 2 * R2
		C6 = 222 * intercept − 3 * c3 − 4 * C4 − 4 * C5
		R5 = 111 * intercept − R2 − 2 * R3 − 2 * R4
SAS 9.4 & n = 10 complete undirected star graph adjacency matrix		C3 = C2 C4 = C2 C5 = C2 C6 = C2 C7 = C2 C8 = C2 C9 = C2 C10 = C2

NOTE: prefix C denotes matrix column, prefix R denotes matrix row, and suffix number denotes the horizontal/vertical rank order location of the column/row.

enumerates the specimen zero-eigenvalue problems, displaying screenshots of the proprietary output facing users of selected statistical software packages, using matrix column symbolism for convenience. Analyzing columns in the 5-by-5 Table 1 matrix, Minitab 17 reports (Table 2) removal of the third column from a no-intercept multiple linear regression analysis in which the first column is specified as Y (Table 2). Subsequently converting this arrangement to a stepwise linear regression returns no perfect linear combinations matching the first column. Meanwhile, handling the first of the eight columns in the 5-by-8 Table 1 matrix as Y, executing a no-intercept stepwise linear regression procedure identifies the third column as a perfect match to it. For the 8-by-5 transpose of this second matrix, SAS generates Table 2 output, uncovering the latent linear combination. A matrix publicly available on the internet yields Table 2 reports: although neither the first column nor first row produces an exact match, a complicated linear combination of each subset is an exact match to this designated row/column. Because of its ease of construction, accompanied by its n−1 zero eigenvalues, the final example is the adjacency matrix for a complete undirected star graph, which is symmetric, for n = 10. Casting the first column as Y, the SAS regression sweep algorithm uncovers eight linear combination pairs, followed by a stepwise regression revealing the ninth linear combination. Although the possible non-disjoint linear combination pairings numbers 45, the only feature of interest here is finding one combination for each zero eigenvalue.

Consequently, matrix and linear algebra pedagogy, if not research, could benefit from an operational awareness of standard linear regression implementations, one allowing the treatment of a given matrix as a regression problem. Accordingly, the task of identifying sets of linear combinations of a matrix’s rows/columns that produces zero eigenvalues becomes quite easy and straightforward.

3. Eigenfunctions, Statistics, and Matrix/Linear Algebra

The multivariate normal (MVN) probability density function (PDF) can draw attention to the eigenfunctions―Abdi [17] furnishes a reader-friendly exposition describing these mathematical entities, which, in brief, reduce any square n-by-n matrix to its constituent parts, and appear throughout, for example, multivariate statistics―subject area of a concomitant functional interest. Its classical PDF may be written as follows:

$$\mathrm{f} (\mathbf{X}, \mathbf{\mu }, \mathsf{\Sigma })=\frac{1}{{\left(\det \left|\Sigma \right|\right)}^{1/2} {\left(2\mathsf{\pi }\right)}^{\mathrm{p}/2}}{\mathrm{e}}^{-{\left(\mathbf{X}-\mathbf{\mu }\right)}^{\mathrm{T}}{\Sigma }^{-1}\left(\mathbf{X}-\mathbf{\mu }\right)/2},$$

(1)

where bold denotes matrix/vector, det|•| and superscript T, respectively denote the matrix determinant and transpose operators, X is a p-dimensional MVN random variable, µ is its p-by-1 vector of means, and Σ is its p-by-p covariance matrix. Adapting Equation (1) to a specific dependent observations problem that is a cornerstone of spatial statistics, one shared theme by matrix/linear algebra and statistics concerns the computation of det|Σ|. Equation (1) translates into the following univariate correlated data [18] expression:

$$\mathrm{f}(\mathbf{X}, \mathrm{\mu }, \mathbf{V}{\mathsf{\sigma }}^2)=\frac{1}{{\left(\det \left|V\right|\right)}^{1/2} {\left(2\mathsf{\pi }\right)}^{n/2}{ \mathsf{\sigma }}^{\mathrm{n}}}{\mathrm{e}}^{-{\left(X-\mathsf{\mu }\mathbf{1}\right)}^{\mathrm{T}}{V}^{-1}\left(X-\mathsf{\mu }\mathbf{1}\right)/\left(2{\mathsf{\sigma }}^2\right)},$$

(2)

where µ and σ², respectively are the common mean and variance for n-dimensional univariate random variable X, n is the sample size, 1 is an n-by-1 vector of ones, and V is an n-by-n covariance structure matrix (with positive real diagonal entries that tend to fluctuate around one). The common focal point here is det|V|, which may be rewritten as the product of its matrix V eigenvalues (a well-known eigenfunction property); because it is symmetric, all of them are real numbers. Griffith [18] notes that: (1) conventional matched/paired observations have a very simple block-diagonal eigenvalue structure; (2) time series observations have a simple known eigenvalue structure [19]; and, (3) spatial and network observation dependency structure computational intensities become daunting for massively large n.

Matrix/linear algebra provides the necessary square matrix eigenfunction theory employing graph theoretic articulations of observation dependency structures. Statistics provides accurate matrix determinant approximations through its method of moments estimation technique. By definition, following standard covariance matrix decomposition (e.g., Cholesky, spectral), all diagonal entries of an input n-by-n adjacency-based matrix A (i.e., a function of 0/1 adjacency matrix C, where c_ij = 1 if row areal unit i and column areal unit j are adjacent, and c_ij = 0 otherwise), for which A^TA = V, are zero, causing the eigenvalues to sum to zero (eigenvalues summing to their matrix trace is a well-known eigenfunction property); one of its most popular spatial statistics specifications (i.e., the simultaneous autoregressive model) is given by, for row-standardized (i.e., stochastic) adjacency matrix W = D⁻¹ C, where D denotes a diagonal matrix whose d_ii entries are the sum of elements in row i of matrix C, the spatial linear operator matrix A = (I − ρW), where I denotes the identity matrix, and ρ denotes the observation dependence parameter. This specification is reminiscent of that used in time series analyses. Meanwhile, the sum of squared eigenvalues is a quantity that is directly calculable from the entries in matrix V; for its row-standardized version, W, the specimen for this section, this sum of squares is given by

1^TD⁻¹CD⁻¹1 = (18PQ + 11P + 11Q + 12)/72

for a regular square tessellation overlaying a P-by-Q (i.e., P rows and Q columns of pixels/squares in the given grid) complete rectangular region; this total, whose formula’s proof is by mathematical induction, delivers the second moment of an eigenvalue set. Furthermore, Griffith [19] outlines an algorithm for quickly and precisely calculating the extreme eigenvalues of matrix V.

Griffith [20] exploits two additional properties: (1) the rank ordering of an eigenvalue set, which is applicable to any matrix; and, (2) a line graph analytical eigenvalue solution—namely $2\mathrm{COS} \left[\mathrm{i}\mathsf{\pi }/\left(\mathrm{n}-1\right)\right]$, i = 1, 2, …, n—foundation for calculating rook adjacency regular square tessellation case approximations. His approximation results match benchmark eigenvalue sets almost exactly, rendering extremely accurate known third and fourth moments for unknown eigenvalue sets as a portion of their quality assessment. For a more general eigenvalue situation, with ascending ranked values denoted by λ_r (r = 1, 2, …, n), the positive values organize into a near linear trend through eigenvalue zero with a power version of their relative rankings—i.e., λ_r = [1 − (r − 1)/n_p]^δ, where n_p denotes the number of positive eigenvalues, and δ > 0 denotes an inflating positive exponent. Their matrix inertia count of zero eigenvalues is n₀. Finally, a veritable description of their n_n values less than zero is λ_minLN [1 + αr/n_n]/LN [2 + α − (r/n_n)^β], where λ_min denotes the extreme smallest eigenvalue, and bestows the sign on these negative values. These formulae signify that determining the inertia of a matrix is necessary; Griffith [21] reports that most large planar graph eigenvalue sets have n_p/n ≈ 0.4, n₀ ≈ 0, and hence n_n ≈ 0.6. Ensuing Table 4 raises the question asking whether or not this percentage is a small sample property of planar matrices. The Syracuse (n = 7249) empirical example having 44.7% positive eigenvalues―this specimen is part of composite datasets for a number of papers, with more details about it, itself, appearing in Griffith and Luhanga [22]―is somewhat consistent with this conundrum.

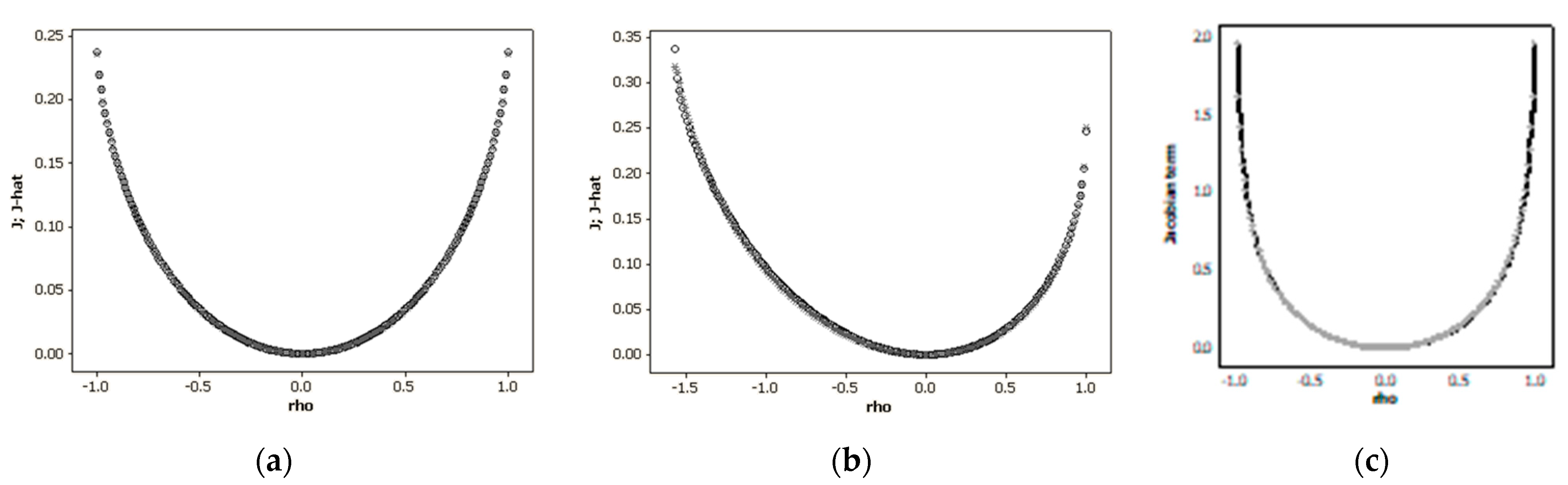
Figure 1 portrays a number of specimen scatterplots for a suite of larger planar graphs spanning a wide range of n and relating to convenient publicly available spatial statistics geographic weights adjacency matrices, corroborating the contention that these preceding formulae furnish excellent approximations. Envisaging that each matrix’s set of eigenvalues constitutes a population, the method of moments can calculate the three coefficient (i.e., α, β, and δ) calibrations for these formulae. Given that an adjacency matrix divulges its first and second moment quantities, a remaining task is to estimate the third and/or fourth moments from the characteristics (e.g., row sums, extreme eigenvalues) of that matrix. Here, the third moment was calibrated as a function of: n, maximum row sum, second moment, and minimum eigenvalue (i.e., λ_min). Most of the polygons were demarcated by the United States (US) Census Bureau census tracts or blocks; Canada’s polygons are Statistics Canada enumeration areas, and England’s polygons are NUTS-3 areal units.

Figure 1 overlays attest to a very good description by the simple moments-matched calibration, but with several conspicuous discrepancies (e.g., Figure 1a,e) indicating a need for further refinement research. Regardless,

Table 3. Summary statistics for a specimen set of empirical geographic adjacency matrix eigenvalue calibrations for administrate polygon surface partitionings.

Planar Graph	Eigenvalue (λ)	n	$\overline{\mathit{\lambda }}$	σλ	Skewness	Excess Kurtosis	–LN [det|V|1/2] ρ = 0.5
England	actual	893	0	0.45977	0.32159	−0.74953	0.02969
	calibrated		0	0.45965	0.41221	−0.79758	0.03007
Chicago	actual	2067	0	0.44276	0.52311	−0.70361	0.02824
	calibrated		0	0.44276	0.55394	−0.68962	0.02837
Edmonton	actual	2098	0	0.43532	0.58034	−0.70531	0.02743
	calibrated		0	0.43532	0.61421	−0.68708	0.02758
North Carolina	actual	2195	0	0.42308	0.71073	−0.59824	0.02630
	calibrated		0	0.42308	0.68182	−0.54499	0.02622
US hospital service areas	actual	3408	0	0.42659	0.65378	−0.62225	0.02657
	calibrated		0	0.42659	0.52563	−0.42271	0.02620
Texas	actual	5265	0	0.44578	0.43170	−0.75537	0.02825
	calibrated		0	0.44578	0.50926	−0.73931	0.02859

authenticates the closeness of these simple approximations, particularly regarding their matrix determinants. Some of these outcomes suggest an asymptotic mechanism may be at work here, yet another topic warranting subsequent research.

In conclusion, dating back to Perron [23] and Frobenius [24], if not before, matrix/linear algebra has been, and seemingly continues to be, preoccupied with establishing progressively tighter upper and lower bounds on individual, and particularly extreme, matrix eigenvalues [25,26]. Statistics supports realistic approximations/calibrations/estimations that may well be superior to a buffering of a rank-ordered eigenvalue set with close upper and lower bounds. The matrix determinant pairs listed in Table 3 are almost identical element couplings for the most common case of moderate positive spatial autocorrelation encountered in real-world geospatial socio-economic/demographic data. Extending these results to massively large georeferenced datasets (e.g., [20]), for example, enables the implementation of spatial statistics for any size GIScience problem. In addition, this numerical solution initiates a protocol capable of going beyond non-adjacency matrices, presumably to any real matrix. This setting portends a potential meaningful contribution to matrix/linear algebra by statistics.

4. Kronecker, Hadamard, and Other Nonstandard Operators: From the Spatial Statistical to the Matrix/Linear Algebra Domain

Kronecker matrix algebra―a generalization of outer product linear algebra operations from vectors to matrices that creates a block tensor product linear map matrix form with respect to a standard basis choice, differing from their usual direct product/sum linear algebra counterparts, which are entirely different operations―first appeared in the early to-mid 1800 s [27], followed by a rather controversial discovery credit history. The Kronecker product (denoted by symbol $\otimes$) promotes a narrow range of applications in matrix calculus and theory of equations, system theory and identification, signal processing, and other special engineering and computer science fields [28], such as the computation of search directions for semi-definite programming primal–dual interior–point algorithms. In contrast, Graham [29] advocates a more diverse set of applications by presenting this operation within the statistical problems of general least squares (§7.4), multivariate maximum likelihood estimation (§7.5), and Jacobians of transformations (§7.6), a somewhat scant assemblage, nonetheless. Neudecker [30] discusses its introduction into econometrics, where it has proved extremely useful in time series analyses, yet another cornucopia of consequential application examples. It also is becoming a popular addition to spatial statistics toolboxes [31], likewise enhancing its pool of prospective relatable illustrations. The Kronecker sum (denoted by symbol $\oplus$; e.g., Pease [32]) is a more obscure operator that is a version of the Kronecker product. Together, these two operations facilitated the work of spatial statisticians in solving the spatial autocorrelation problem plaguing spatial interaction flows data [33], embedding an n-by-n origin and destination surface partitioning adjacency matrix, C, into existing model specifications with the terms

$$\mathbf{C}\otimes \mathbf{I}, \mathbf{I}\otimes \mathbf{C}, \mathbf{C}\otimes \mathbf{C}, \mathrm{and} \mathbf{C}\oplus \mathbf{C} = \mathbf{C}\otimes \mathbf{I} + \mathbf{I}\otimes \mathbf{C},$$

which also can join the arsenal of application contributions from statistics to matrix/linear algebra. The dormant contribution here, which represents a host of empirical applications involving geographic flows spanning journey-to-work, -to-shop, and to-recreate, as well as migration/mobility and international trade, is bolstered by the Blieberger and Schöbel [34] railroad study employing Kronecker algebra. This collection constitutes a wealth of problem exemplars for next-generation matrix/linear algebra textbooks.

Graham [29] begins showing matrix/linear algebra application contributions from statistics that can enrich the breadth of Kronecker product textbook examples, although, as already noted, his repertoire is rather sparse, similar to the expansion of subject matter oriented statistics and calculus classroom texts during the last half of the twentieth century, following the debate in mathematics about whether or not mathematics-ladened topics of that time could be taught without being framed in a rigorous systematic theorem-proof context. Unfortunately, the incorporation of such feedback from statistics is atypical, as Bernstein [35] demonstrates; his book includes examples about signal processing, scientific algorithmic computing, matrix calculus, and tensor (i.e., the higher dimensional analogue of matrices) analysis, but not statistics. This paper certainly argues that his book would benefit greatly by adapting additional applications from statistics.

This lack of two-directional cross-fertilization transcends Kronecker algebra, also pertaining to other esoteric matrix/linear algebra themes, such as Hadamard algebra [36]―synonymously known as the element-wise, entry-wise, and Schur matrix product, it is a binary operation on two matrices of identical dimensions that produces a third matrix in which each cell (i, j) is the product of the corresponding (i, j) elements of the original two matrices. This matrix operation differs from its usual direct product linear algebra counterpart, which is an entirely different operation. During the last half of the last century, Styan [37] recognized this specific idea as both a neglected matrix theory concept, and an approach already finding scarce and scattered application in statistics. Meanwhile, Neudecker et al. [38] helped import it into econometrics practice. Later, Griffith [39] helped usher it into quantitative geography and spatial statistics usage. Again, statistics offers a fertile opportunity for reciprocal contributions, opening another reservoir of application possibilities to what could become a more inclusive matrix/linear algebra.

In conclusion, subsections of matrix/linear algebra presentations, such as those for Kronecker and Hadamard algebra, could gain immensely by more comprehensively diversifying their content through recognizing and formally staging and explicating their more recent novel statistical applications. Not only could their textbooks and research reference volumes be more appealing to a wider audience, but such publications also could spawn synergies fostering new research. This essentially is the story told by applied calculus and applied statistics endeavors. For example, although such topics as trigonometry, an integral ingredient in theoretical calculus courses, may not be treated in an applied calculus course, avoiding all of the material devoted to trigonometric substitutions or integrations/differentiation of trigonometric functions, frequently extra material from differential equations (e.g., growth through time), linear algebra (e.g., Markov chains), operations research (e.g., optimizing industry/manufacturing production functions), and/or statistics (e.g., parameter estimation) may be studied that students of mathematics, engineering, physics, and a few other disciplines, would not be exposed to until after, if at all, they completed their regular sequence of theoretical calculus courses. Similarly, applied statistics students rarely study proving theorems about estimators, hypothesis tests, and other inferential methods, often focusing on implementation and interpretation of data analysis outcomes, whereas mathematical statistics students tend to engage real world data less, and even more seldom large amounts of it, including its collection, authentication, and cleaning and quality control. In both cases, the two opposites perpetually advocate for discovery, with efforts in new undertakings like baseball analytics via applied calculus, and new data analytic tool formulations in statistics.

5. The Auto-Normal Model Jacobian Term and Spatial Autocorrelation: More Spatial Statistical Musings for Matrix/Linear Algebra

Auto-models (i.e., the response variable Y is on both sides of an equation equal sign), particularly the widely adopted auto-normal specification [e.g., Equation (2)], team multivariable calculus, especially the Jacobian term associated with variable transformations, with spatial statistics and other correlated data in a manner allowing payback through not only calculus-based, but also eigenfunction-based, illuminations directed from statistics to matrix/linear algebra. Graph theory is a backbone to contributions here, being glamorized by what at the beginning of this millennium became known as the new science of networks [40], in part sparked by a social networks revolution. The informative instrument at this juncture is scientific visualization, which serves, for example, many demystifying purposes. The formal teaching of auto-normal model parameter estimation together with fantasizing about paintings like those displayed in Figure 2 helped inspired this pursuit [41,42,43,44].

5.1. Jacobian Term Plots: Smiley Face Emojis in Science

The bivariate version of Equation (1) furnishes the simplest Jacobian term [i.e., det|Σ| in Equation (1), and det|V| in Equation (2)] plot demonstration (Figure 3c) for statistics. Figure 3a,b portray those drawings for usual spatial statistical auto-normal estimation problems. The surprise here is a visualization that resembles a smiley face emoji (e.g., https://depositphotos.com/308817798/stock-illustration-7cute-yellow-round-emoticon-smiling.html and https://www.pinterest.com/pin/300826450087576163/ (accessed on 4 October 2022)), an unexpected image that students of matrix/linear algebra most likely would find memorable. The ability to graph matrix determinants in such a parsimonious and unforgettable way seems remarkable, completely unexpected, and eye-opening to numerous quantitative scholars.

5.2. Eigenfunction Visualizations

Although graphics portraying matrix determinants may be extraordinary, a truly astonishing visualization embraces eigenfunctions themselves; until recently, the only public example seems to be that appearing in Figure 2a (https://sites.math.washington.edu/~burdzy/hot_spots.php (accessed on 4 October 2022)). This outcome is beyond the long-standing pairwise eigenvector-based abstract plots well-known to data analytic researchers for multivariate statistical techniques such as principal components and factor analysis, ones that eventually evolved into critical search engine input. Rosmarin’s paintings (e.g., Figure 2b,c) prompted this more current awareness [36,37]. Griffith [19] derives the analytical eigenfunctions for regular square tessellations forming complete rectangular regions; these are the planar graphs whose eigenvectors convert to somewhat impressionistic choropleth maps (e.g., Figure 4a) in which distinct two-dimensional visual patterns materialize.

The stunning similarities between selected theoretical eigenvector portrayals and Rosmarin’s paintings was a serendipitous first glimpse into simple eigenvector visualization [36,37] augmenting Kelly’s lone art specimen (Figure 2a) to that date. Quantitative scholars and students alike express amazement when confronted with such juxtapositions, mostly unaware that such extremely abstract entities as n-tuple matrix components can manifest themselves as optical paintings. This truly is an exploitable chance for matrix/linear algebra to better appeal to the masses, following in the footsteps of, for example, fractal digital art effectively invented by Benoit Mandelbrot [45].

Even more thought-provoking is that the eigenvalues accompanying these eigenvectors index the nature and degree of the spatial correlation—the correlation of nearby red-green-blue (RGB) spectral values on a canvas—latent in their respective eigenvector portrayals. The two eigenvectors depicted in Figure 4c, respectively account for 33% of the red and 19% of the green canvas-wide geographic variation in Figure 4b red-green painting [36]; their corresponding correlation measures are 0.998 and −0.906, revealing a modestly strong similarity, with a trace of contrasting, neighboring painting pixel RGB color values.

5.3. Network Dependencies in Pictures

Eigenfunction visualization does not culminate with planar graphs typifying spatial statistics situations. It also relates to the denser graph theoretic adjacency matrices coincident with contemporary social networks (e.g., Figure 5). Once more, the ability to scientifically visualize intangible n-tuples here is astounding, although not unprecedented in general [46], and certainly is reminiscent of how Rubik’s Cube aids in making mathematical group theory palpable [47]. Although the preceding maps may afford a more concrete exemplification of matrix/linear algebra ideas, social network realizations like those portrayed in Figure 5 also should join the repayment assets that should flow from correlated data statistics [18] to matrix/linear algebra.

6. Sampling Distributions for Customary Planar Graph Indices

An Atlas of Graphs [48] inventories and catalogues most, if not all, possible graphs involving relatively small numbers of nodes (e.g., ≤7). This is an invaluable resource for graph theorists and researchers in related fields. The internet avails other such sources (e.g., https://zenodo.org/record/4010122#.Yy0rLUzMKUk, https://houseofgraphs.org/ (accessed on 7 November 2022)). The undirected planar graph algorithm outlined in Griffith [21] created the database for this section, a tool capable of generating much larger graphs, ones with hundreds or thousands of nodes, although not exhaustively enumerating them because of their substantial numbers. These are distinct from the fashionable Erdős-Rényi random matrices. The goal of this section is to simulate selected sampling distributions for categories of adjacency matrices that can enlighten matrix/linear algebra, extending what already is known about them theoretically, such as, for example, the statistical distribution of the principal component (i.e., largest) eigenvalue of a correlation matrix [49], a rather limited knowledge base. One previously established outcome is that planar graphs tend to have a 40–60% split of positive-negative eigenvalues [21]. Other useful properties for non-negative matrices include: the number of complete bipartite K₄ subgraphs (i.e., the graph structure responsible for the maximum number of negative eigenvalues reaching 75%; [50]); the adjacency matrix row sums (i.e., vertex degrees) variance; and, the statistical distribution of the minimum eigenvalue. No doubt other matrix traits [e.g., spectral and eigenvalue gaps, supplementing K₄ subgraph counting with K₃ subgraph (K₅ and beyond are non-planar; Kuratowski’s Theorem) counting] are worthy of monitoring, as the literature echoes [51]. These are contributions from statistics to matrix/linear algebra that can be transformative in a descriptive attribute tabulating way, one that inputs accumulated facts into innovative classification scheme refinements.

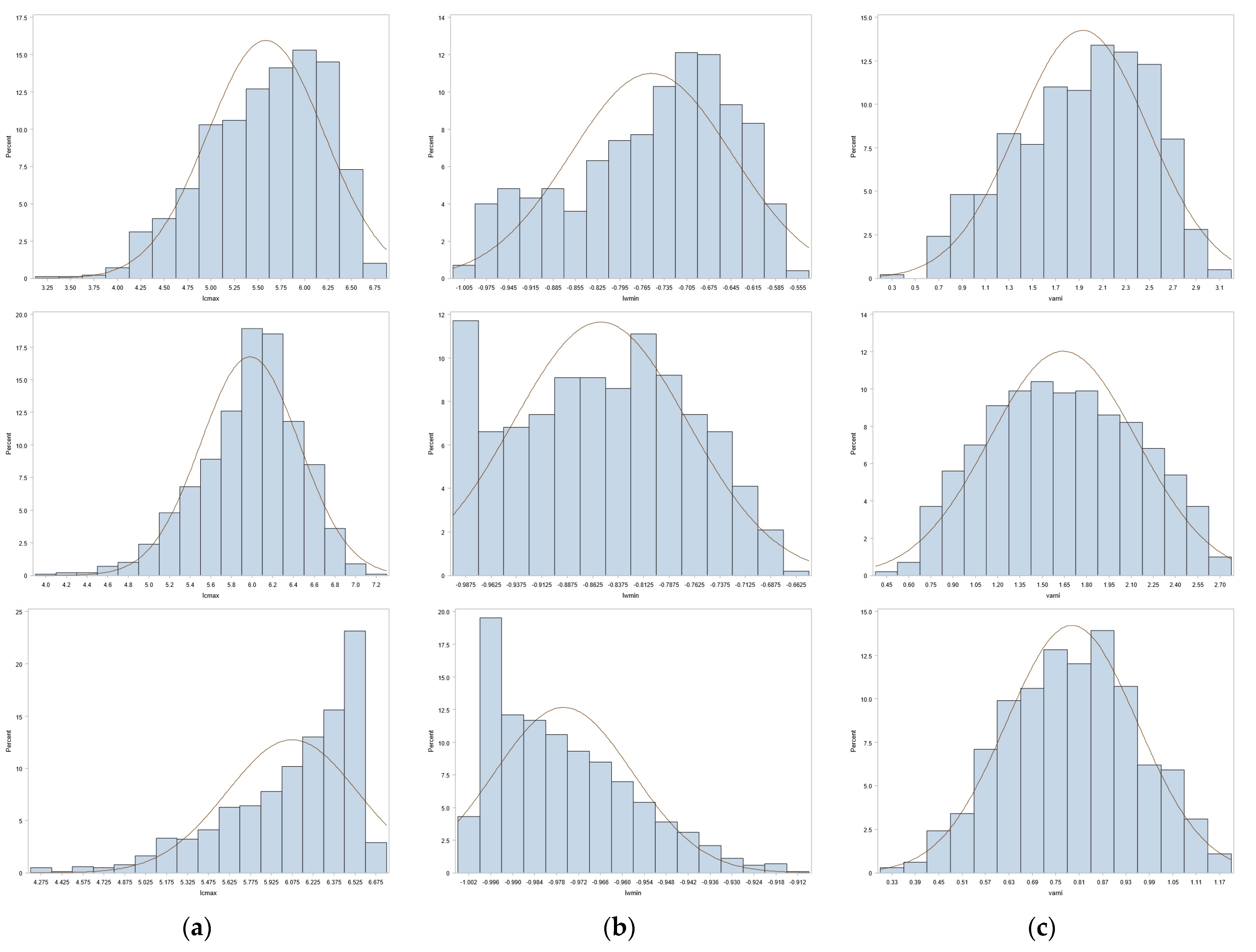
Salient noteworthy adjacency matrix facets include its principal eigenvalue, primarily because this quantity in its general role receives so much attention in the literature. Unlike conventional pairwise variate correlation matrices,

Table 4. Attribute arithmetic means for 1000 random planar graph adjacency matrices.

Number of Vertices	Raw Matrix		Stochastic Matrix λmin	ni Standard Deviation	% 1s| Planar	% λ > 0	K4,4 Sub-Graphs
	λmax	λmin
100	5.587 (0.625)	−3.533 (0.152)	−0.752 (0.109)	1.929 (0.560)	77.670 (6.807)	44.742 (2.045)	2.925 (3.299; 33.4 †)
500	5.979 (0.476)	−4.095 (0.251)	−0.855 (0.086)	1.640 (0.498)	76.190 (6.122)	46.087 (1.846)	4.996 (6.124; 53.9)
1000	6.122 (0.432)	−4.342 (0.322)	−0.912 (0.059)	1.290 (0.348)	72.896 (4.562)	47.134 (1.510)	4.335 (6.247; 52.9)
1500	6.120 (0.463)	−4.375 (0.341)	−0.948 (0.038)	1.031 (0.250)	70.422 (3.141)	47.956 (1.168)	3.679 (4.785; 52.0)
2000	6.075 (0.470)	−4.328 (0.301)	−0.976 (0.019)	0.792 (0.169)	68.086 (1.694)	48.845 (0.729)	5.225 (6.983; 51.1)

† percentage of simulated planar graphs with at least one K4,4 subgraph. NOTE: standard deviations in parentheses.

and Figure 6a imply that this matrix quantity fails to converge upon a bell-shaped normal distribution for complete undirected random planar graph adjacency matrices (i.e., Cs). One conspicuous tendency disclosed by Table 4 is that dispersion for various quantitative matrix indices tends to decrease with increasing n.

Two interesting aspects about the smallest row-standardized adjacency matrix (i.e., W) eigenvalue is that it displays a propensity to be nearer to −1 than −0.5 with increasing n, perhaps beckoning a trade-off tension between square and hexagonal tessellation proclivities in irregular surface partitionings. Accompanying this possible trend is a matrix inertia (see §3) inclination toward an equal number of positive and negative eigenvalues, rather than its expected 40–60% division, which merely may resonate nothing more than the aforementioned hexagonal partitioning predilection of administrative polygons. In addition, the standard deviation of individual complete undirected planar graph adjacency matrix vertex degrees (i.e., elements of vector C1) appears to converge upon a bell-shaped curve. This is counter to the expectation promoted by most administrative polygon surface partitions that some mixture of four and of six degrees often dominate an empirical adjacency matrix.

The K_4,4 subgraph statistics are captivating because of their already noted relationship to the adjacency matrix number of negative eigenvalues upper limit (i.e., 75%; also see [52]). Roughly half of the simulated matrices have no K_4,4 subgraphs, with this set tending to traverse the entire range of negative eigenvalue percentages, while rendering little evidence of a meaningful trendline describing the remaining percentages, regardless of n. Regardless, a graph embracing only a single K₄ subgraph requires the maximum number of colors required by the four-color theorem for graph/edge/vertex/face coloring.

These and other descriptive statistics computed for simulated complete undirected planar graph adjacency matrices underscore a host of informative matrix characteristics the discipline of statistics can tabulate for and transmit to the subdiscipline of matrix/linear algebra.

7. Conclusions and Implications

Statistics has a tradition of borrowing and importing conceptualizations from kindred disciplines and subdisciplines, particularly ones in mathematics. Matrix/linear algebra is a case in point. However, this flow of intellectual property does not have to be one-way. The literature review encapsulated in this paper argues and epitomizes a few ways in which statistics can compensate matrix/linear algebra for its numerous contributions that helped statistics to flourish as a more rigorous mathematical sciences discipline. In doing so, proper adaptions could aid parts of matrix/linear algebra to become more understandable to a wider audience of scholars. This paper reviews the following five potential candidate topics, all of which build upon key strengths of statistics that clearly inhabit its interface with matrix/linear algebra: uncovering all sources of a matrix’s zero eigenvalues; approximating eigenvalues for massively large matrices; special matrix operations, such as Kronecker and Hadamard products; the calculus-based Jacobian term associated with variable transformations, a topic covered in virtually all introductory mathematical statistics courses; and, properties of planar graph grounded random matrices/vectors detectable with simulation experiments.

Of course, these are not the only interchange junctures; others, some to which the previous narrative alludes, remain implicit or unidentified here. Among others, the subfield of multilinear (vector) algebra, with many adoptions of it in multivariate statistics, constitutes an emerging potential common ground rife with payback possibilities. For example, matrix decomposition is both a fundamental and widely studied topic, although its extension to the tensor case still encounters some difficulties [53,54]. Furthermore, reminiscent of the preceding eigenvector discussion, Loperfido [55,56] highlights connections between tensor eigenvectors and skewness maximization, within the framework of projection pursuits. Expanding upon this eigenfunction theme, the fully real eigenpairs (i.e., values and their corresponding vectors) problem is well-known for matrices, while still remaining open for tensor eigenvectors [57]. All in all, future contributions from especially algebraic statistics to multilinear algebra should come to fruition.

The discipline of statistics should, and most likely will be compelled to, produce more reviews of this type as it begins engaging the emerging subject that is being labeled data science [58].