1. Introduction
Process capability analysis has been widely used to identify how well the outputs from an in-control process meet the requirements, specifications and expectations of customers. In practice, process capability analysis methods aim to continuously monitor the process quality via utilizing capability indices to assure if the quality of products is capable of meeting the specifications and supply information based on the product design and process quality improvement. The results of process capability analysis can be the basis of cost reduction, which is attributable to the decrease in product failures; see Pan and Wu [
1]. Kane [
2] presented the relations of the process capability indices,
,
,
and
, which are, respectively, defined as
and
where
is the population mean,
is the population standard deviation,
L is the lower specification limit and
U is the upper specification limit. Kane [
2] also indicated that these indices can be a complementary system of measures for evaluating the process performance. Kocherlakota [
3] and Kotz and Johnson [
4] studied the statistical theories for various process capability indices. Comprehensive discussions about using process capability analysis methods for quality control can be found in the works of Rodriguez [
5], Palmer and Tsui [
6] and Montgomery [
7].
The process performance index is one of the widely used process capability indices for evaluating the quality of lifetime data. Let
X denote the product lifetime random variable and
L denote a specified threshold of a lower bound. The conforming rate can be defined as
. The process performance index can have a close connection with the conforming rate of
. The statistical properties regarding using the process capability indices of
,
,
and
under the normality assumption have been thoroughly studied in the literature. Hong et al. [
8] presented analytical procedures for the ML estimation and hypothesis testing to evaluate the process performance index when the lifetimes of products follow the Pareto distribution. Ahmadi et al. [
9] used generalized order statistics to conduct inferential procedures for the process performance index under an exponential distribution. Lee et al. [
10] proposed optimal inferential procedures to evaluate the process performance index based on progressively type-II censored samples that were taken from the Burr type XII distribution. Lee et al. [
11] proposed an inferential procedure by using uniformly minimum variance unbiased estimation and a hypothesis-testing method to evaluate the process performance index based on type-II censored samples that were taken from the two-parameter exponential distribution. Lee et al. [
12] proposed Bayesian inference procedures to assess the process performance index based on progressively type-II censored samples under the Rayleigh distribution. Ahmadi et al. [
13] proposed ML estimation methods to estimate the process performance index based on progressively first-failure censored samples when the lifetime data follow a Weibull distribution. Wu and Chiu [
14] obtained fourteen different estimates of the process performance index for the two-parameter exponential distribution under a multiple type-II censoring scheme. After a simulation study of a performance comparison, three estimates among them are recommended by Wu and Chiu [
14] to develop hypothesis-testing procedures for the process performance index. Wu and Lin [
15] proposed a statistical inference for the process performance index based on type-II exponentially distributed samples. Montgomery [
7] recommended using the process performance index to evaluate the quality of products. Zhu et al. [
16] proposed an inferential procedure by using the ML estimation method to evaluate the process performance index based on power-normal distribution samples. They also discussed the drawbacks of using the exact Fisher information matrix with a delta method under the power-normal distribution to obtain an approximate confidence interval (ACI) of the model parameters. All aforementioned works on process performance index are summarized in
Table 1 for easy reference.
Among widely used lifetime distributions, the inverse Gaussian (IG) distribution, also known as the Wald distribution, has been renowned as a versatile lifetime model with sound physical interpretation. The ML and Bayesian estimation methods were commonly used to estimate the IG distribution parameters. Banerjee and Bhattacharyya [
17] investigated the Bayesian inferential approach for estimating the IG distribution parameters for the application of equipment failure data. Amry [
18] studied the Bayesian inference of the IG parameters using Jeffrey’s prior under a quadratic loss function. More information about using the IG distribution for engineering applications can also be found in the books by Chhikara and Folks [
19] and Johnson et al. [
20]. Sun and Ye [
21] discussed the frequentist validity of posterior quantiles for a two-parameter exponential family that includes the IG distribution as a member. Rostamian and Nematollahi [
22] studied the stress–strength reliability using the ML estimation method via using an expectation-maximization algorithm and the Bayesian estimation method based on progressively type-II censored IG distribution samples. A survival analysis of the IG distribution based on using Bayesian and Fiducial approaches has been studied by Jayalath and Chhikara [
23]. Bera and Jana [
24] developed a bootstrap interval of stress–strength reliability assuming that the stress and strength variables are IG distributed.
Sundaraiyer [
25] proposed inferential procedures to obtain the ML estimator and bootstrap ACI of the process capability index proposed by Clements [
26] when the quality variable follows the IG distribution. We use the term of MLE to denote the ML estimator and ML estimate here and after. Investigating how to reduce the estimation bias for the process performance index based on IG distributed samples and obtain a reliable ACI for the process performance index is helpful for the applications of quality control. Balay [
27] used BCMLEs of the generalized inverse Lindley distribution parameters to compute the generalized process capability index
. The
was firstly proposed and studied by Maiti et al. [
28]. In addition, Balay [
27] obtained a bootstrap ACI of
. Considering the merit of IG distribution being a versatile lifetime model with sound physical interpretation, the IG distribution can be an alternative to the generalized inverse Lindley distribution for reliability analysis applications. The purposes of this article can be twofold. Firstly, we would like to propose analytical procedures to obtain the BCMLEs, whose bias is
based on the bias correction method proposed by Cordeiro and Klein [
29], B-BCMLEs and Bayes estimators via using the Jeffery’s prior distribution for the IG distribution parameters and the investigated process performance index. Secondly, we would like to establish the procedures taken to obtain an ACI and the highest posterior density interval (HPDI) for the one-sided version of
. The HPDI is the interval with the shortest length on the posterior density at the given confidence level. We use the term BE to denote the Bayes estimator and Bayes estimate here and after. Because the posterior distribution in the Bayesian estimation procedure is complicated, the Markov chain Monte Carlo (MCMC) approach is used to overcome the computational difficulty when generating random samples from the posterior distribution. To our knowledge, these two aforementioned purposes have not yet been studied in the literature.
The rest of this paper is organized as follows. We address the process capability indices and define the process performance index based on the one-sided version of
in
Section 2. In
Section 3, we derive the inferential procedures to obtain the CK-BCMLE and B-BCMLE of the model parameters through using the bias correction method proposed by Cordeiro and Klein [
29] and the bootstrap method, respectively. A bootstrap algorithm is suggested to obtain the B-BCMLEs of the model parameters and the bootstrap ACI of the process performance index. Moreover, the Bayesian estimation procedure is developed via using the Jeffery’s prior distribution, and an MCMC hybrid algorithm of Gibbs sampling and the Metropolis–Hastings algorithm is provided to obtain the BEs of the IG distribution parameters and process performance index. Monte Carlo simulations are conducted in
Section 4 to evaluate the performance of the proposed estimation methods. A real data set with 46 active repair times (in hours) for an airborne communication transceiver is given in
Section 5 for illustration. Concluding remarks are given in
Section 6.
2. The Generalized Process Performance Index
Based on
and
, two generalized process capability indices can be defined as follows:
and
where
and
T is the process target. When the quality measurements of products follow a normal distribution,
,
,
and
have been the four most widely used process capability indices in practical applications. However, non-normally distributed quality measurements, which have a skewed distribution, can be found in many works by Clements [
26], Gunter [
30], Constable and Hobbs [
31], Mukherjee and Singh [
32], Tang et al. [
33] and Chen et al. [
34]. Among the aforementioned studies, Clements [
26] proposed two generalized versions of process capability indices that are defined by
and
where
is the
th quantile of the quality characteristic measure,
X. When
X follows a normal distribution,
and
reduce to
and
, respectively.
and
are the two most popular process capability indices used to determine the quality of products if the distribution of the quality variable is not normal. Maiti et al. [
28] proposed a new generalized version of the process capability index,
where
is the cumulative distribution function (CDF).
and
are the specified lower and upper tailed probabilities of
F, respectively. For lifetime products, we are more concerned with if the lifetime is higher than the lower specification limit. Hence, the one-sided version of
was used in this study for the process performance index. We denote the one-sided version of
by
in this study for simplification. The
is defined by
4. Monte Carlo Simulations
In this section, Monte Carlo simulations were conducted to evaluate the performance of the estimation methods of the typical ML, CK-BCML, B-BCML and Bayesian. Random samples with a size of and 50 were generated from and , respectively, to obtain the MLEs, CK-BCMLEs, B-BCMLEs and BEs of and . The MLE, CK-BCMLE, B-BCMLE and BE of the process performance index were also obtained based on the plug-in method for and 1. When and , the true value of the process performance index can be obtained by and 0.9173 for and 1, respectively, and the corresponding parts per million are 2876, 7130, 22,625 and 45,939. When and , the true value of the process performance index can be obtained by and 0.9898 for and 1, respectively, and the corresponding parts per million are 138, 568, 3389 and 10,068.
Bootstrap repetition, , was used to implement the parametric bootstrap bias-correction method. For Bayesian estimation, firstly, we generated 51,000 Markov iterations to implement the MCMC method, and the leading 1000 Markov iterations were removed for the burn-in operation. Secondly, a spacing operation by selecting one of every ten iterations was used to reduce the autocorrelation in each Markov chain. Finally, 5000 Markov chains were used to obtain the BEs of the parameters , and PPI, respectively.
The measures of relative bias (rbias) and relative root mean squared error (rRMSE) were evaluated using 10,000 iteration runs. Assume that the target parameter is
and the obtained estimates are
,
10,000; the rbias and rsMSE are defined by
and
The rbias and rRMSE are scale-free measures. All simulation results for estimating model parameters are reported in
Table 2 and
Table 3.
From
Table 2 and
Table 3, we can find that the estimation quality of the MLE of
is good. The derivation processes in
Section 3.2 show that the CK-BCMLE of
is the same as the typical MLE; that is,
. Hence, the values of rbias and rRMSE of
are also close to that of the B-BCMLE
. However, we can find that the BCMLEs
and
outperform the MLE
, with a smaller rbias and rRMSE when the sample size is small. Because the proposed Bayes estimation method is developed with the parameter-free non-informative prior distribution of Jeffery, the performance of BE can be compared with its competitor of MLE. In
Table 2 and
Table 3, we also find that the rbias of
is small but larger than the the bias of
. The rRMSE of
is larger but close to the rRMSE of
. Based on the findings in this study, using gradient methods for optimization makes the ML estimation method less reliable for estimating the process performance index. The obtained ACI of the process performance index via using the MLEs with the delta method and exact Fisher information matrix is conservative. We will study the CPs of the ACI and HPDI of the process performance index to show the good performance of the proposed Bayesian estimation method.
To verify the performance of the delta and Bayesian estimation methods for the interval inference of PPI under small sample size cases, we established the 95% ACI and HPDI for the PPI at the lower specification limit
and 1. Moreover, the mean lower bounds and mean upper bounds of the 95% ACI and HPDI of the PPI and their CPs were evaluated based on 10,000 iterations. We use the terms of mLB and mUB to denote the mean lower bounds and mean upper bounds, respectively. All simulation results are summarized in
Table 4 and
Table 5.
In view of
Table 4 and
Table 5, we find that the condition of a small sample has an impact on the quality of the interval inference for the PPI. When
, the CP of the 95% ACI of
is below its nominal value. In particular, for the case of small
L and
, the CP of the 95% ACI of
seriously underestimates the nominal value 0.95 for the delta method with the ML, CK-BCML and B-BCML methods. The delta method with the ML method performs worst among all competitors. When the sample size increases, the estimation performance of the delta method with the ML, CK-BCML and B-BCML methods can be significantly improved. The proposed Bayesian estimation method outperforms all of the competitors based on the delta method in terms of the CP when obtaining a HDPI for the process performance index; even the sample size and
L are small. In summary, we recommend using the proposed Bayesian estimation method to obtain the HPDI of the process performance index for IG distribution.
5. An Example
A maintenance data set concerning the active repair times for an airborne communication transceiver is used to illustrate the applications of the proposed estimation methods. This data set contains 46 repair times in hours as follows: 0.2, 0.3, 0.5, 0.5, 0.5, 0.5, 0.6, 0.6, 0.7, 0.7, 0.7, 0.8, 0.8, 1.0, 1.0, 1.0, 1.0, 1.1, 1.3, 1.5, 1.5, 1.5, 1.5, 2.0, 2.0, 2.2, 2.5, 2.7, 3.0, 3.0, 3.3, 3.3, 4.0, 4.0, 4.5, 4.7, 5.0, 5.4, 5.4, 7.0, 7.5, 8.8, 9.0, 10.3, 22.0, 24.5. This data set of active repair times was initially investigated by Chhikara and Folks [
36]. They obtained the MLEs
and
and used the Kolmogorov–Smirnor test to show that the IG distribution can characterize this data set well. The data set was also analyzed based on Bayesian estimation methods by many studies after Chhikara and Folks [
36]; for example, Sinha [
37], Betrò and Rotondi [
38] and Jayalath and Chhikara [
23].
Using the proposed methods in
Section 3 for the data set of active repair times with
, we can obtain the MLEs, CK-BCMLEs, B-BCMLEs and BEs of
,
and
. The proposed Bayesian estimation method was implemented with
50,000 and the first
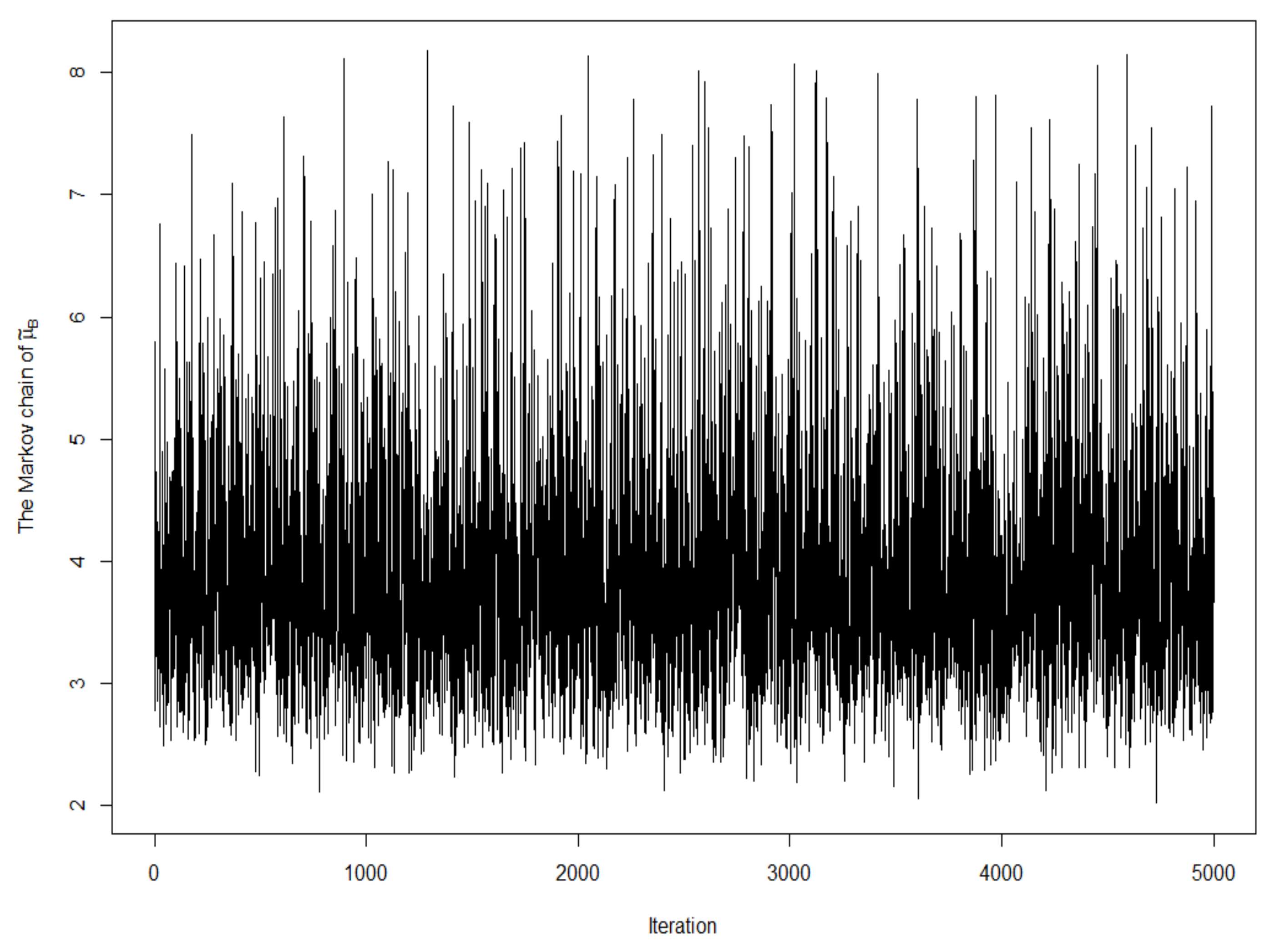
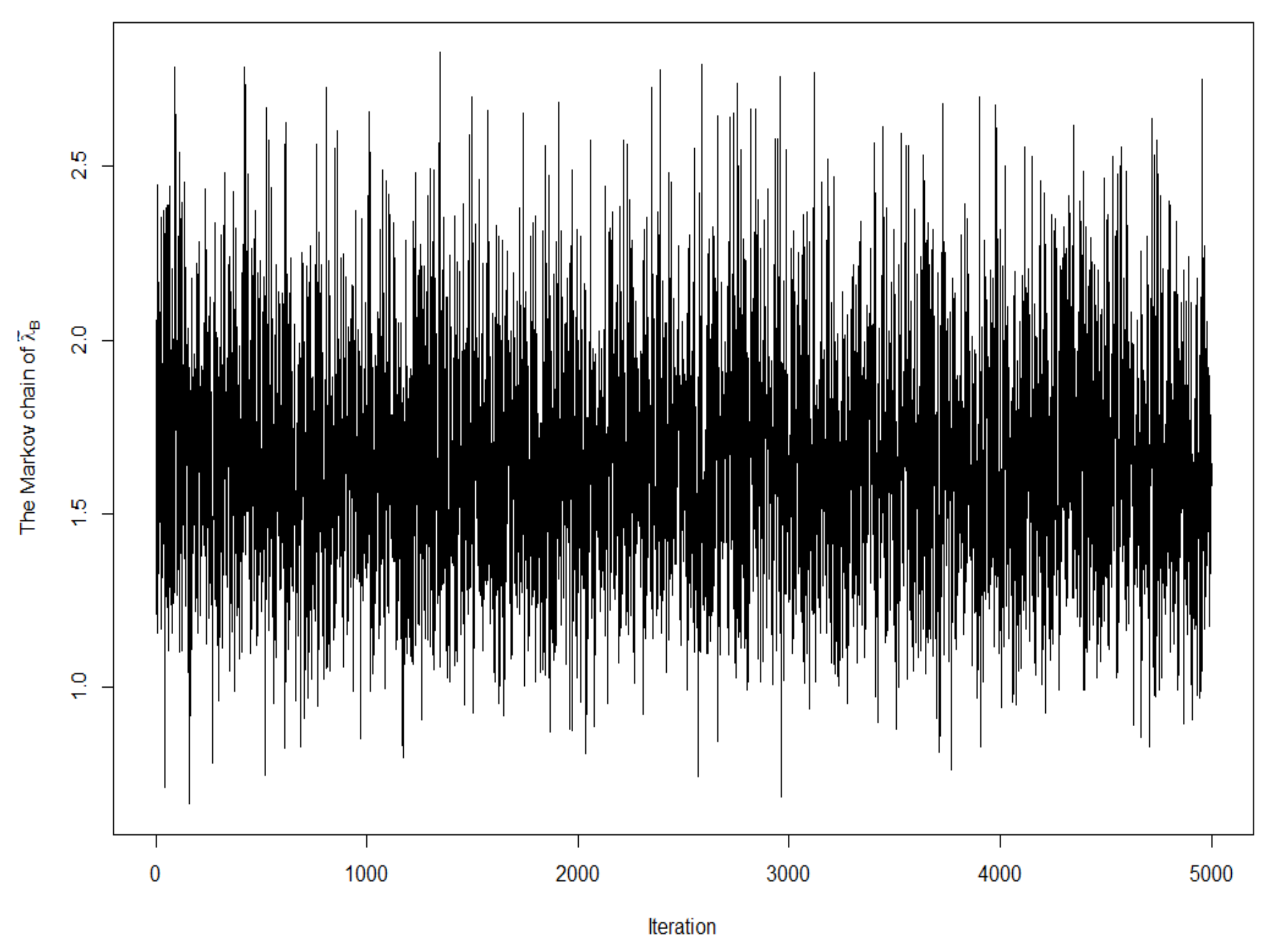
1000 generated estimates were removed for teh burn-in operation. The spacing operation, which selects one of every ten generated estimates, was used for cutting the Markov chain to reduce the first-order autocorrelation in every Markov chain. To check the quality of the MCMC method, the Markov chain plots based on 5000 generated estimates of
and
are given in
Figure A1 and
Figure A2, respectively. The first-order autocorrelation coefficients based on the 5000 generated estimates of
and
are 0.046 and 0.06, respectively. We note that two first-order autocorrelation coefficients are close to 0. These findings indicate that the generated Markov chains are almost independent chains. All of the obtained estimates are reported in
Table 6.
From
Table 6, we can find that the B-BCMLE and BE of
are slightly larger than the MLE and CK-BCMLE of
. The MLE and BE of
are larger than two BCMLEs of
. The BE of
is the smallest one among the four obtained estimates. The parts per million based on the MLE, CK-BCMLE, B-BCMLE and BE of
are 6232, 8160, 7813 and 6071, respectively.
Table 7 reports the 95% ACI and HPDI of
via using the delta method and Bayesian estimation method, respectively. Two proposed BCML methods generate close ACIs. We also find that the lower limit of the ACI based on the ML method is slightly larger than the lower limits of the ACIs based on the two proposed BCML methods and the lower limits of HPDI based on the proposed Bayesian method.
6. Concluding Remarks
Considering the restriction of the sample resource when evaluating the quality of lifetime products, we used the bias correction estimation method proposed by Cordeiro and Klein [
29] and the bootstrap bias correction method to improve the estimation quality of the typical ML estimation method for estimating the process performance index under the IG distribution. We derived the exact forms of CK-BCMLEs and provided an algorithm used to obtain the B-BCMLEs for the IG model parameters and process performance index. The delta method was used to obtain an ACI for the process performance index. Moreover, a Bayesian estimation procedure was proposed to obtain the BEs of the IG model parameters and the process performance index. The HPDI of the process performance index was obtained via using the proposed MCMC hybrid algorithm of the Gibbs sampling and Metropolis–Hastings algorithm.
An intensive simulation study was conducted to compare the performance of the proposed CK-BCML, B-BCML and Bayesian estimation methods with the typical ML estimation method. Simulation results show that the ACIs based on the delta method with the MLEs, CK-BCMLEs and B-BCMLEs performed less satisfactory, with a seriously underestimated CP when the sample size and lower specification limit were small. The proposed Bayesian estimation method can be an alternative method, other than the delta method, used to obtain a reliable HPDI for the process performance index when the sample size is small. Because the Jeffrey’s prior distribution is a parameter-free prior, the proposed Bayesian estimation method is less subjective and easy to be implemented. A data set composed of 46 active repair times for an airborne communication transceiver was used to illustrate the applications of the proposed methods.
For saving the testing time and cost, censoring schemes are often adopted in engineering applications to collect censored lifetime data. Extending two proposed BCML estimation methods and the Bayesian estimation procedures for the IG distribution with different censoring schemes is interesting and can be studied in the future.