Abstract
Due to the wide availability of functional data from multiple disciplines, the studies of functional data analysis have become popular in the recent literature. However, the related development in censored survival data has been relatively sparse. In this work, we consider the problem of analyzing time-to-event data in the presence of functional predictors. We develop a conditional generalized Kaplan–Meier (KM) estimator that incorporates functional predictors using kernel weights and rigorously establishes its asymptotic properties. In addition, we propose to select the optimal bandwidth based on a time-dependent Brier score. We then carry out extensive numerical studies to examine the finite sample performance of the proposed functional KM estimator and bandwidth selector. We also illustrated the practical usage of our proposed method by using a data set from Alzheimer’s Disease Neuroimaging Initiative data.
1. Introduction
Technology development has greatly improved the ability to record and store complex data. In many scientific fields such as biomedical, economic, and environmental studies, sampled data are functions of certain index variables, such as time, location, and temperature over a continuum. For example, in optical spectrometric data collected to analyze different compounds in food samples, the intensity of light is a function of continuous wavelength (e.g., [1]); in speech recognition, human voices pronouncing certain words were digitized and recorded as a function of time (e.g., [2]). In [3], the NOx level in the air is measured over a day near an industrial area. For more examples of function data, we refer readers to [4].
Let denote a functional variable, where s is some index variable on a continuum . However, in practice, due to limitations of measurement and storage, is usually collected only on a grid over . Therefore, the measured data are often in the form of discretized vectors . When the grid is fine, the covariate vector closely resembles a smooth curve of .
Although function data are commonly represented by vectors, they are inherently different from ordinary multivariate vectors due to the temporal/spatial intercorrelation between consecutive entries. As a result, direct use of traditional multivariate statistical methods inevitably faces the difficulty of multicollinearity and, therefore, may not produce reliable results (see, e.g., [4]). Motivated by this, enormous efforts have been devoted to developing statistical tools for functional data analysis. For instance, Ref. [5] considered the generalized functional linear models with functional covariates; Ref. [6] developed functional principal component analysis (FPCA); refs. [7,8,9,10] investigated functional B-splines regression methods; refs. [11,12] studied nonparametric kernel methods.
In biomedical applications, there is also a plethora of available functional data, such as the cornea images in ophthalmology [13], the magnetic resonance imaging in the studies of Alzheimer’s Disease [14], the electroencephalography in psychiatry [15], and the electrocardiograms in cardiology [16]. In many of those studies, the response variable of primary interest is the time-to-event measurement in the presence of censoring. For example, ref. [17] investigated multiple myeloma patients’ disease-free survival against absolute lymphocyte cell counts, which were measured as a function of time. Ref. [18] examined the association between the post-hospital mortality of patients who suffer from acute lung injury/respiratory distress syndrome and the sequential organ failure assessment score as a function of ICU time.
However, the related development for the time-to-event measurement subject to censoring has been relatively sparse in functional data analysis. Ref. [6] proposed a functional censored regression model coupled with an EM algorithm introduced by [19] to assess the expected survival time. Ref. [20] incorporated functional covariates as longitudinal covariates and developed time varying functional principal component scores for predicting age-at-death distributions. However, their method does not account for censoring. Ref. [18] developed a penalized signal regression for mixed effect proportional hazard models. Ref. [14] utilized FPCA and introduced a functional linear cox regression Model (FLCRM).
Kaplan–Meier (KM) estimator proposed by [21] has been a popular method in time-to-event data (see, e.g., [22,23,24]), as it is a nonparametric approach without stringent model assumptions and describes the survival probabilities directly. KM estimator has also been used in functional data. For example, Ref. [25] employed it to estimate the extreme quantiles. However, to the best of our knowledge, the asymptotic properties of the functional KM estimator have not been thoroughly investigated, and thus the procedures built upon it lack theoretical guarantees. In this paper, we attempt to meet this challenge by developing a generalized conditional KM estimator with desirable asymptotic properties for functional data. We also develop a bandwidth selection approach based on time-dependent Brier scores [26,27] so that users can confidently apply our proposed estimator to study functional time-to-event data.
The remainder of this paper is organized as follows. Section 2 discusses the model setup and develops the functional KM estimator. We provide theoretical properties, including consistency and asymptotic normality of the proposed estimator in Section 3. In Section 4, we conduct extensive numerical studies to examine the finite sample performance of the proposed method. Section 5 illustrates the practical use of our proposed approach through a case study on Alzheimer’s Disease Neuroimaging Initiative Data. Section 6 provides a discussion and some concluding remarks. All proofs are relegated to the Appendix A.
2. Model Setup and Estimation Method
We begin with introducing some notations to present our proposed procedure. For generic variables U and V, let and denote the cumulative distribution function and the survival function of U, respectively. Additionally, and denote the conditional cumulative distribution and survival functions, respectively, of U given V. Moreover, the conditional hazard and cumulative hazard functions of U given V are denoted by and , respectively. We denote the norm of a functional covaraite x by and denote the cardinality of a set A by . Given two sequences and , we use the notation to denote and .
2.1. The Proposed Method
In this section, we describe the proposed procedure for estimating , where T is the time-to-event of interest, subject to the right censoring by C and is a p-dimensional vector of functional covariates corresponding to the patient. Without loss of generality, we assume that . Here, any scalar covariate Z can also be represented as a constant function . For the simplicity of presentation, we only consider as a 1-dimensional functional covariate in this work. However, the proposed method can be readily applied to scenarios with , as demonstrated in our numerical analysis. Throughout the rest of this paper, we may write the functional covariate as X for simplicity in notation when there is no confusion. We also denote the functional space of by .
Let and be the observed outcome variable and the censoring indicator, respectively, where is an indicator function. The observed data consists of n i.i.d. replicates of , denoted by . Under the conditional independence between T and C given X, the conditional survival function of Y given X is . By simple algebra,
where is the sub-distribution of Y in the absence of censoring. As and in Equation (1) involve only the observed variables, we can estimate them by kernel-type methods (see, e.g., [28,29,30,31]).
A common approach to dealing with functional covariates is utilizing the Karhunen-Loève expansion (see, e.g., [14,32]). Namely, we first find L orthogonal basis functions defined on and represent each by scores obtained from projecting onto the space generated by L basis functions. However, as L is required to increase with the sample size n [33], the typical kernel estimation based on ’s would inevitably suffer from the curse of dimensionality and lead to inefficient estimation.
To overcome this challenge, we follow [12] and employ the functional kernel estimator directly. Let be some kernel function and be a sequence of positive real numbers. We may suppress the subscript of when there is no confusion. We obtain Nadaraya-Watson type weights as
Subsequently, the kernel type estimators of and can be constructed as and for . Given that the argument inside the kernel function K above is positive, K is typically an asymmetric probability density function. Following Dabrowska [34], Dabrowska [35], we acquire a natural estimator of
where the second equality follows from the fact that and are piece-wise constant functions that only jump at ’s. Then by Equation (1), a generalized conditional KM estimator of can be immediately obtained as
Remark 1.
Our proposed method can also be applied to settings where multiple functional or regular covariates are present. Let Z denote an additional covariate. We can construct multi-dimensional Nadaraya-Watson type weights as
where is an asymmetric kernel, and is either an asymmetric kernel (can be ) in case Z is a functional covariate or a symmetric kernel in case Z is a scalar covariate. Here, and are the bandwidths associated, respectively. We can then obtain by replacing with in Equation (3). It should be noted that convergence rates are negatively impacted when we have a product weight such as the above.
2.2. Bandwidth Selection
It is well-known that bandwidth selection is crucial to the performance of kernel-type estimators (see, e.g., [12,36]). One appealing approach is to study the asymptotic properties of and derive the optimal bandwidth by minimizing the mean integrated squared errors [37]. However, it is very challenging to obtain a closed form of the asymptotic variance of a generalized KM estimator (see, e.g., [24]). We thus propose to select the optimal bandwidth by a data-driven m-fold cross validation as follows:
- 1.
- Randomly split the index set into m equal-size blocks: . Let be the collection of indices that are not contained in .
- 2.
- Given a bandwidth h, for each ,
- (a)
- obtain , the survival probability estimates, using the observations .
- (b)
- obtain the fitness score for the estimates in 2(a) following certain model fitness metric E, based on the observations .
- 3.
- Summarize the overall fitness as .
- 4.
- Choose as the selected bandwidth.
For survival data, many fitness metrics often used for model selection may not be suitable, as they fail to account for censoring. The concordance index [38] and time-dependent Brier scores [26,27] are commonly used to evaluate the fitness of survival models [39]. In this study, we chose to use the Brier score, which takes into account both discrimination and calibration to assess the model fitness. In contrast, the concordance index reflects only discrimination [40]. The estimated Brier scores of observations with indices in at time t can be obtained as follows:
where is the inverse probability censoring weight (IPCW) of subject i at time t, given by,
in (5) is the estimated survival probability of C given X, which can be obtained by modifying (3). We further adopted a more general version of the IPCW Brier score [41] with in (4) replaced by . Now we can calculate the evaluation score in step (2.b) by integrating the Brier scores over a range of . Then following steps 3 and 4, we can select the optimal bandwidth.
3. Theoretical Properties
In this section, we establish the theoretical properties of the proposed conditional KM estimator. We begin with imposing the following technical conditions, which facilitate our theoretical derivations.
- (C1)
- Let for some constant . Given , let be a ball being centered at x and of radius [11]. There exists some , such that,
- (C2)
- The kernel function is Lipschitz-continuous over its support , satisfying and .
- (C3)
- Let denote the probability that the functional variable X is in . There exists a function and constants such that , and .
- (C4)
- Let , where is the minimal number of ’s to cover . This is called the Kolmogorov’s -entropy of [42]. For n large enough, and for some ,
The Lipschitz continuous condition (C1) has been widely adopted in the literature (see, e.g., [11,36]) to ensure the smoothness of functional operators. The conditions on kernel function in (C2) have been adopted in the functional nonparametric estimation literature [12,43]. is chosen to be an asymmetric kernel because is always positive. The bounded support of and that is bounded away from 0 are technical conditions to simplify the theoretical derivations. In the numerical studies, we chose the asymmetric Gaussian kernel and the results showed that it works quite well.
Conditions (C3) and (C4) follow from Ferraty and Vieu [11] and Ferraty et al. [42]. They are needed to establish the uniform consistency of the proposed conditional KM estimator over . in Condition (C3) controls the concentration of the probability measure of the functional variable X, which is related to all the asymptotic results in nonparametric statistics for functional variables. In Proposition 1, it can be seen that the more concentrated the random variable X, (the higher small ball probability function ), the more efficient will be the estimator. We refer the readers to Section 13.2 of Ferraty and Vieu [11] for some commonly considered infinite dimensional examples. in condition (C4) is a measure of the complexity of . A larger means that is a more complex function space. Condition (C4) essentially requires to have some suitable complexity so that local smoothing can be applied and the curse of dimensionality problem can be overcame [42]. The Kolmogorov’s -entropy is often used in dimensionality reduction problems (see, e.g., [44,45]). Condition (C4) is also often satisfied in practice. We refer the readers to Section 2 in Ferraty et al. [42] for some common examples where these two conditions are met.
We first establish the estimation consistency results for and .
Proposition 1.
Under Conditions (C1)–(C4), if and , then
If is a compact set in instead of a functional space and the density of X is bounded below and above, then and . Thus, Proposition 1 reduces to the results for the ordinary conditional KM estimator (see, e.g., [24,35]).
Next, we derive an almost sure representation for the cumulative hazard function , in terms of a sum of independent random variables as follows.
Theorem 1.
Under the same conditions as in Theorem 1,
where
There are two remainder terms in Proposition 1, One of them, , is the bias term, and the other, , is a dispersion component. Since they increase and decrease, respectively, as the bandwidth increases, we need to choose a suitable bandwidth to balance this trade-off. Noting that , we can obtain the following corollary.
Corollary 1.
Under the same assumptions as in Theorem 1,
Moreover, if and , ,
for some variance function .
The form of is quite complicated and the estimation of is beyond the scope of this work.
4. Numerical Studies
In this section, we conduct extensive simulation studies to examine the finite sample performance of our proposed procedure. We consider the following four different scenarios.
- Scenario 1: , where , Unif, Unif, and distribution.
- Scenario 2: )/5}, where and are generated in the same way as in scenario 1, and Z follows a standard normal distribution.
- Scenario 3: ., where and generated in the same way as in scenario 1.
- Scenario 4: , where , with , , and for .
Scenario 1 follows from [12], where the survival time depends on the functional covariates. In Scenario 2, we considered an accelerated failure time model with an extra covariate additional to functional covariates to elaborate what we discussed in Remark 1. Scenario 3 is considered to examine the performance of the proposed method when the survival time is independent of the covariates. Scenario 4 is a functional Cox regression model and was considered in [14]. It is worth mentioning that Scenarios 1 and 3 are still valid for survival data, since the time of event is extremely rarely negative.
The censoring time in each scenario was generated independently from a uniform distribution Unif, where is chosen to achieve the desired censoring rates of 15% and 25%, representing low and mild censoring, respectively. In addition, we consider two sample sizes and 400, simulating the small and moderate sample sizes, respectively. Additional simulations with an even smaller sample size are considered and discussed in the Appendix A. For each combination of scenario, censoring rate, and sample size, we generate 100 replications.
In each replication, we standardize functional covariates by first centering them according to their means and then scaling them by the standard deviation of their norms. The standardization of the covariates is critical for us to specify a uniform grid for bandwidth selection. We chose the kernel function to be the asymmetrical Gaussian kernel. To speed up locating the optimal bandwidth associated with the kernel function, we carried out a 2-fold search. We first considered a coarse grid of bandwidths, and selected a pilot bandwidth , according to the procedure described in Section 2.2. Then we constructed a refined grid of size 20 to select the optimal bandwidth.
In Scenario 2, we consider an additional grid of bandwidths for the Gaussian kernel function associated with the scalar covariate, Z. According to the Silverman’s rule of thumb [46], the optimal choice is approximately . We thus consider a grid of bandwidths . We conduct the cross validation method in Section 2.2 to obtain a pair of optimal bandwidths for the two kernel functions simultaneously. In scenario 3, we only conducted the search on the coarse grid as we expect the bandwidth to be large.
To evaluate the performance of our proposed bandwidth selection procedure, we compare the selected bandwidth to a hypothetical one obtained by using the mean squared error (MSE)
as the fitness metric E in our proposed cross validation procedure in Section 2.2. This can be done since is known in the simulations.
Figure 1 plots the average Brier score over 100 replications at different bandwidths against the bandwidth under four scenarios. The vertical lines in Figure 1 indicate the average optimal bandwidths selected from using Brier score (dotted) and MSE (dashed).
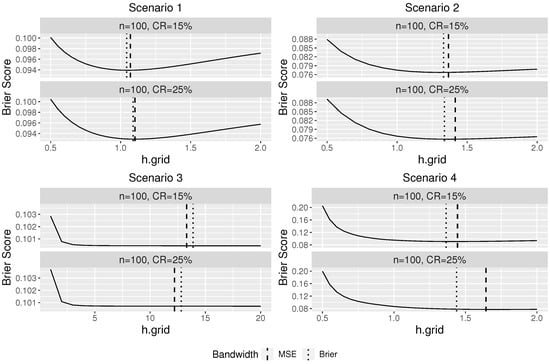
Figure 1.
The average Brier score over 100 replications plotted against the grid of bandwidth for different scenarios. The vertical lines indicate the optimal bandwidth based on Brier scores and MSE.
Figure 1 indicates a good performance of our proposed bandwidth selector. For scenarios 1, 2, and 4, it can be seen that the optimal bandwidth selected using the Brier score is close to the “oracle” optimal bandwidth selected based on the MSE, which assumes that the true conditional survival probabilities are known in advance. As the censorship rate decreases, the difference between the two selected bandwidths becomes smaller. In Scenario 3, since the survival time is independent of the covariates, the regular KM estimator should be used and the theoretical optimal bandwidth for our proposed conditional KM estimator is infinite so that all observations would be used to estimate the survival probability. Large bandwidths were selected by our proposed bandwidth selector as expected, and thus the resulting estimator would be similar to a regular Kaplan–Meier estimator.
We compare the proposed method to two benchmark methods: the regular KM estimator and the functional Cox method, FLCRM [14]. We considered the regular KM estimator for all scenarios and FLCRM for Scenario 4. The functional Cox regression model was implemented using the R codes provided by Kong et al. [14]. We assess the predictive performance of the three methods as follows: in each replication, we generate additional testing data set of sample size 100. For the proposed method, we compute for each in the testing data, based on (3) using the training data and the selected optimal bandwidth from the training data set. Then we calculated the mean squared prediction error (MSPE) of the estimates as . For the benchmark methods, we also obtained their corresponding predicted survival probabilities and MSPE. The summaries of the results are presented in Figure 2 and Table 1.
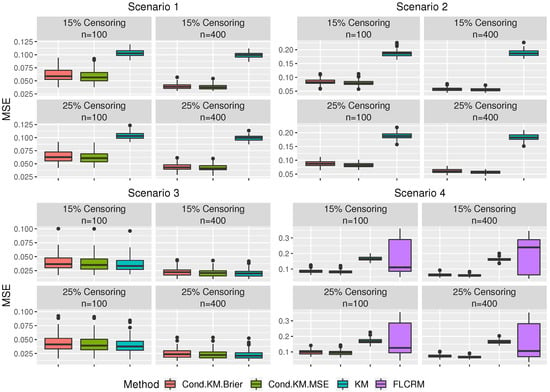
Figure 2.
The boxplots represent the sampling distribution of the MSPE based on the 100 simulation testing sets. Cond.KM.Brier = Conditional Kaplan–Meier (Bandwidth selection based on Brier scores), Cond.KM.MSE = Conditional Kaplan–Meier (Bandwidth selection based on MSE), KM = Kaplan–Meier and FLCRM = Functional Linear Cox Regression Model.

Table 1.
The MSPEs of the survival probability in the test data using conditional functional KM, regular KM, and FLCRM under different scenarios.
Figure 2 shows that for Scenarios 1, 2, and 4, the proposed method has comparatively lower MSPEs than the other methods. Furthermore, we can observe that the performance of the proposed estimator based on the bandwidth selected using the Brier score and “oracle” MSE (7) is comparable, confirming a good performance of our proposed bandwidth selector. Moreover, we note that as the sample size increases, the performance of our proposed conditional functional KM estimator enhances with lower MSPEs in all scenarios. On the contrary, the MSPE from the regular KM estimator does not necessarily get lower as the sample size increases. Table 1 shows that the MSPE of our conditional functional KM estimator decreases at a lower censoring rate, as expected. When the survival time is independent of covariates (Scenario 3), the regular KM estimator is expected to achieve the best performance. However, the proposed estimator performs on par with the regular KM estimator because our bandwidth selector chose a large bandwidth and the conditional KM estimator converges to KM estimator as the bandwidth increases. Therefore, regardless of the various scenarios considered in this study, we can claim that the proposed estimator performs the same or better than the comparison methods.
5. Application
In this section, we illustrate the practical use of our proposed method by analyzing Alzheimer’s Disease Neuroimaging Initiative (ADNI) data [14]. Alzheimer’s Disease (AD) is one of the most common causes of memory loss and dementia, affecting more than five million Americans. It is the 6th leading cause of death in the USA. It is a progressive disease. In earlier stages of the disease, the symptoms are mild, and the treatment is more likely to be beneficial as the symptoms gradually worsen over time. Therefore an earlier and more accurate diagnosis is one of the most critical goals in this area of research. The phase of mild cognitive impairment (MCI) is considered the initial stage of dementia, and the time that takes an individual to convert from MCI to AD is of primary interest in various studies (see, e.g., [47,48,49,50]).
The hippocampus is an area in the brain that is important for learning and memory. It is also vulnerable to affect at the early stage of AD. Multiple studies [51,52,53] have proposed to use hippocampal radial distances for studying the changes in the hippocampus of AD patients, as hippocampal radial distances are the distances between the medial core of the hippocampus and the corresponding vertex, and can reflect the hippocampal shape and size. This study uses the hippocampal radial distances of 30,000 surface points on the left and right hippocampal surfaces at baseline as functional covariates. We also consider the Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog) score as it was identified to be one of the most significant scalar covariates in predicting the time of conversion from MCI to AD in Kong et al. [14]. The data consist of 373 MCI patients, where 161 of them had developed AD before study completion.
The functional covariate (hippocampal radial distances) and the scalar covariate (ADAS-Cog score) were both scaled prior to the estimation. We split the data into a training and testing set. The training set contains 273 randomly chosen observations and was used to calculate the optimal bandwidth. The testing set is of sample size 100, to which we apply the proposed method and compare the performance of other methods considered in this work. To select the optimal bandwidths for the functional covariate and scalar covariate, we employed the same approach in Scenario 2 of our simulation studies and used the same grids of bandwidths for the functional and scalar covariates. The optimal bandwidths for the functional and scalar covariates were found to be 1.1 and 0.6, respectively. Then we computed the predicted survival probability for the testing data and subsequently obtained the Brier scores. To compare the performance of the proposed method, we also used FLCRM and regular KM methods to estimate the survival probabilities of the testing data and calculate their corresponding Brier scores. Noting that a smaller value of the Brier score indicates a more accurate estimation of survival probability, Figure 3 demonstrates that the performance of the proposed method is superior to the other two methods at most of the time points in the range of T. Furthermore, we estimated the area under the brier score curve (AUC) for each method. The proposed conditional functional KM has a significantly lower AUC (219.5) than FLCRM (326.7) and the regular KM method (418.7).
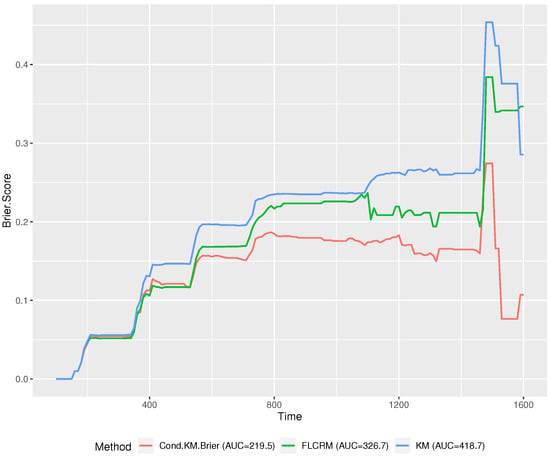
Figure 3.
Brier scores on the ADNI data for different methods: Cond.KM.Brier = Conditional Kaplan–Meier (Bandwidth selection based on Brier scores), KM = Kaplan–Meier and FLCRM = Functional Linear Cox Regression Model.
6. Discussion
Recent technological advancement has made functional data widely available in multiple disciplines, especially biomedical studies, where the response variable is often the time-to-event time in the presence of censoring. Therefore, it would be practically appealing to develop a conditional KM estimator that takes the functional covariates into account. In this paper, we rise to this challenge and propose a kernel-based conditional generalized KM estimator to analyze time-to-event data in the presence of functional covariates. We rigorously establish the proposed estimator’s asymptotic properties and develop a Brier scores-based bandwidth selector. The numerical studies in this paper evince the satisfactory performance of our proposed estimator when the functional covariate is present.
In this paper, we only considered the estimation of the survival probability using a conditional Kaplan–Meier estimator with functional covariates. It is also of interest to carry out inferences on the proposed estimator. We shall pursue this research direction by constructing the confidence intervals/bands, conducting a hypothesis test, and examining the empirical performance in our future research.
Moreover, Wang and Wang [54] and Leng and Tong [55] studied the weighted quantile regression for censored survival data with weights constructed from the conditional KM estimator. The quantile regression can accommodate and investigate the heterogeneous effects of covariates on survival time. It is possible to develop a quantile regression for functional covariates and examine their varying effects, which often entail significant practical implications (see, e.g., [56,57]). The detailed development is beyond the scope of this paper and will be studied in our forthcoming work.
Author Contributions
Conceptualization, Q.Z., K.B.K.; Formal analysis, S.T.; Methodology, S.T., Q.Z. and K.B.K.; Project administration, Q.Z.; Software, S.T.; Supervision, Q.Z.; Writing—original draft, S.T., Q.Z. and K.B.K.; Writing—review & editing, Q.Z. and K.B.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work was partially supported by grants from NIH 1R03AG067611, 1R21AG070659 and NSF DMS1952486.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Let and .
Proof of Proposition 1.
Since the proofs of the consistency of and are similar, we only deal with . The proof follows from the standard arguments used in [35].
Since Y is completely observed, we can utilize the consistency of nonparametric functional estimator in Ferraty et al. [42]. According to Lemma 12 of [42], under (C1) and (C4), we have
Moreover, following Lemma 13 of [42], under (C1)–(C4), we can obtain,
Combining the above two results together completes the proof of Proposition 1. □
Proof of Theorem 1.
By simple algebra, we obtain the following decomposition:
By Proposition 1 and the fact that , we can write I as follows
We now decompose into , where
First, we deal with .
where the last equality follows from Proposition 1. Noting that , we have
Next, we evaluate . Let denote a partition for the interval , where . By integration by parts and Proposition 1,
According to Condition (C1), there exists a constant such that . Now, divide each into sub-intervals . Then we have, . By Proposition 1, we get
These two results and the monotonicity of over t together yield that
almost surely, where is some constant. Then we have,
As deduced in [24], we have
Combining the results of and together completes the proof of Theorem 1. □
Proof of Corollary 1.
By Taylor’s expansion of the function around , there exists a between and such that
Noting that
by Proposition 1, we have,
Therefore,
By Theorem 1, we obtain
If and ,
Therefore, and have the same asymptotic distribution.
Since satisfies and , for and it is easy to see that , we have
by Central Limit Theorem, for some variance function . □
Additional Simulations: Per the suggestion of one of the referees, we extended the simulation study to examine the performance of the proposed method when the sample size is very small. We consider the sample size 50 for Scenarios 1 and 3 with censoring rates and . The results are presented in Figure A1 and Table A1.
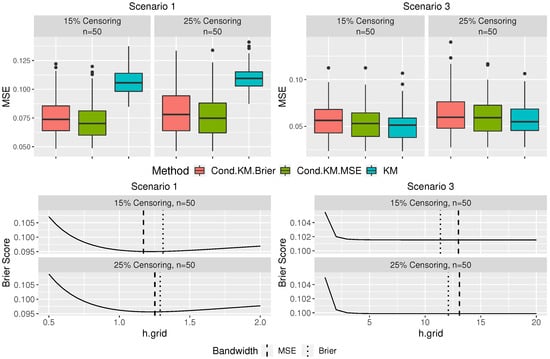
Figure A1.
The boxplots of the MSPE and the average Brier score over 100 replications plotted against the grid of bandwidth for scenario 1 and scenario 3 with sample size 50.
We first examine the performance of the proposed Brier score-based bandwidth selector. By comparing Figure 1 and Figure A1, it is clear that the differences between the bandwidths selected by the proposed method and the “optimal” one using the hypothetical MSE increase as the sample size decreases, which suggests a performance degradation of our proposed bandwidth selector, in both scenarios. Moreover, the accuracy of the proposed method in estimating the conditional survival probability also decreases, as sample sizes decrease (see Table 1 and Table A1). However, we note that in Scenario 1 where the survival probability depends on the functional covariate, the proposed estimator is still superior to the KM estimator. More importantly, the performance of the proposed method is still comparable to the KM estimator in Scenario 3, where the functional covariate does not affect the survival probability, indicating that the reliability of the proposed estimator for a small sample is on the same level as the traditional KM estimator.

Table A1.
The MSPEs of the survival probability in the test data using conditional functional KM, regular KM, and FLCRM for scenario 1 with sample size 50.
Table A1.
The MSPEs of the survival probability in the test data using conditional functional KM, regular KM, and FLCRM for scenario 1 with sample size 50.
| 15% Censoring | 25% Censoring | |||||
|---|---|---|---|---|---|---|
| n | Method | Mean | SD | Mean | SD | |
| Scenario 1 | 50 | Cond.KM.MSE | 0.0156 | 0.0178 | ||
| Cond.KM.Brier | 0.0759 | 0.0163 | 0.0806 | 0.0191 | ||
| KM | 0.1065 | 0.0108 | 0.1103 | 0.0106 | ||
| Scenario 3 | 50 | Cond.KM.MSE | 0.0533 | 0.0176 | 0.0607 | 0.0197 |
| Cond.KM.Brier | 0.0566 | 0.0184 | 0.0636 | 0.0214 | ||
| KM | 0.0165 | 0.0176 | ||||
Cond.KM.Brier = Conditional Kaplan–Meier (Bandwidth selection based on Brier scores), Cond.KM.MSE =Conditional Kaplan–Meier (Bandwidth selection based on MSE), KM = Kaplan–Meier and FLCRM = FunctionalLinear Cox Regression Model. □ indicates the best MSE.
References
- Borggaard, C.; Thodberg, H.H. Optimal minimal neural interpretation of spectra. Anal. Chem. 1992, 64, 545–551. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Curves discrimination: A nonparametric functional approach. Comput. Stat. Data Anal. 2003, 44, 161–173. [Google Scholar] [CrossRef]
- Febrero, M.; Galeano, P.; González-Manteiga, W. Outlier detection in functional data by depth measures, with application to identify abnormal NOx levels. Environmetrics Off. J. Int. Environmetrics Soc. 2008, 19, 331–345. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Applied Functional Data Analysis: Methods and Case Studies; Springer: Berlin/Heidelberg, Germany, 2002; Volume 77. [Google Scholar]
- Müller, H.G.; Stadtmüller, U. Generalized functional linear models. Ann. Stat. 2005, 33, 774–805. [Google Scholar] [CrossRef]
- James, G.M. Generalized linear models with functional predictors. J. R. Stat. Soc. Ser. B Stat. Methodol. 2002, 64, 411–432. [Google Scholar] [CrossRef]
- Marx, B.D.; Eilers, P.H. Generalized linear regression on sampled signals and curves: A P-spline approach. Technometrics 1999, 41, 1–13. [Google Scholar] [CrossRef]
- Cardot, H.; Ferraty, F.; Sarda, P. Functional linear model. Stat. Probab. Lett. 1999, 45, 11–22. [Google Scholar] [CrossRef]
- Cardot, H.; Ferraty, F.; Sarda, P. Spline estimators for the functional linear model. Stat. Sin. 2003, 13, 571–591. [Google Scholar]
- Cardot, H.; Sarda, P. Estimation in generalized linear models for functional data via penalized likelihood. J. Multivar. Anal. 2005, 92, 24–41. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis: Theory and Practice; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ferraty, F.; Mas, A.; Vieu, P. Nonparametric regression on functional data: Inference and practical aspects. Aust. N. Z. J. Stat. 2007, 49, 267–286. [Google Scholar] [CrossRef]
- Locantore, N.; Marron, J.; Simpson, D.; Tripoli, N.; Zhang, J.; Cohen, K.; Boente, G.; Fraiman, R.; Brumback, B.; Croux, C.; et al. Robust principal component analysis for functional data. Test 1999, 8, 1–73. [Google Scholar] [CrossRef]
- Kong, D.; Ibrahim, J.G.; Lee, E.; Zhu, H. FLCRM: Functional linear cox regression model. Biometrics 2018, 74, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Hasenstab, K.; Scheffler, A.; Telesca, D.; Sugar, C.A.; Jeste, S.; DiStefano, C.; Şentürk, D. A multi-dimensional functional principal components analysis of EEG data. Biometrics 2017, 73, 999–1009. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Sedransk, N. Functional data analytic approach of modeling ECG T-wave shape to measure cardiovascular behavior. Ann. Appl. Stat. 2009, 3, 1382–1402. [Google Scholar] [CrossRef]
- Fang, H.B.; Wu, T.T.; Rapoport, A.P.; Tan, M. Survival analysis with functional covariates for partial follow-up studies. Stat. Methods Med. Res. 2016, 25, 2405–2419. [Google Scholar] [CrossRef]
- Gellar, J.E.; Colantuoni, E.; Needham, D.M.; Crainiceanu, C.M. Cox regression models with functional covariates for survival data. Stat. Model. 2015, 15, 256–278. [Google Scholar] [CrossRef]
- Schmee, J.; Hahn, G.J. A simple method for regression analysis with censored data. Technometrics 1979, 21, 417–432. [Google Scholar] [CrossRef]
- Müller, H.G.; Zhang, Y. Time-varying functional regression for predicting remaining lifetime distributions from longitudinal trajectories. Biometrics 2005, 61, 1064–1075. [Google Scholar] [CrossRef]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Beran, R. Nonparametric Regression with Randomly Censored Survival Data; Technical Report; University of California: Berkeley, CA, USA, 1981. [Google Scholar]
- Gentleman, R.; Crowley, J. Graphical methods for censored data. J. Am. Stat. Assoc. 1991, 86, 678–683. [Google Scholar] [CrossRef]
- Gonzalez-Manteiga, W.; Cadarso-Suarez, C. Asymptotic properties of a generalized Kaplan–Meier estimator with some applications. Commun. Stat.-Theory Methods 1994, 4, 65–78. [Google Scholar] [CrossRef]
- Rutikanga, J.U.; Diop, A. Functional Kernel Estimation of the Conditional Extreme Quantile under Random Right Censoring. Open J. Stat. 2021, 11, 162. [Google Scholar] [CrossRef]
- Graf, E.; Schmoor, C.; Sauerbrei, W.; Schumacher, M. Assessment and comparison of prognostic classification schemes for survival data. Stat. Med. 1999, 18, 2529–2545. [Google Scholar] [CrossRef]
- Gerds, T.A.; Schumacher, M. Consistent estimation of the expected Brier score in general survival models with right-censored event times. Biom. J. 2006, 48, 1029–1040. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Nadaraya, E.A. On estimating regression. Theory Probab. Its Appl. 1964, 9, 141–142. [Google Scholar] [CrossRef]
- Watson, G.S. Smooth regression analysis. Sankhyā Indian J. Stat. Ser. A 1964, 26, 359–372. [Google Scholar]
- Gasser, T.; Müller, H.G. Kernel estimation of regression functions. In Smoothing Techniques for Curve Estimation; Springer: Berlin/Heidelberg, Germany, 1979; pp. 23–68. [Google Scholar]
- Ma, S. Estimation and inference in functional single-index models. Ann. Inst. Stat. Math. 2016, 68, 181–208. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Applied Mathematical Sciences Volume 27; Springer: New York, NY, USA, 2001. [Google Scholar]
- Dabrowska, D.M. Non-parametric regression with censored survival time data. Scand. J. Stat. 1987, 14, 181–197. [Google Scholar]
- Dabrowska, D.M. Uniform consistency of the kernel conditional Kaplan–Meier estimate. Ann. Stat. 1989, 17, 1157–1167. [Google Scholar] [CrossRef]
- Kara-Zaitri, L.; Laksaci, A.; Rachdi, M.; Vieu, P. Uniform in bandwidth consistency for various kernel estimators involving functional data. J. Nonparametr. Stat. 2017, 29, 85–107. [Google Scholar] [CrossRef]
- Berg, A.; Suaray, K. Bootstrap bandwidth selection for a smooth survival function estimator from censored data. J. Stat. Res. 2010, 44, 207. [Google Scholar]
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis; Springer: Berlin/Heidelberg, Germany, 2015; Volume 3. [Google Scholar]
- Kattan, M.W.; Gerds, T.A. The index of prediction accuracy: An intuitive measure useful for evaluating risk prediction models. Diagn. Progn. Res. 2018, 2, 7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Cortese, G.; Combescure, C.; Marshall, R.; Lee, M.; Lim, H.J.; Haller, B. Overview of model validation for survival regression model with competing risks using melanoma study data. Ann. Transl. Med. 2018, 6, 325. [Google Scholar] [CrossRef] [PubMed]
- Kvamme, H.; Borgan, Ø. The brier score under administrative censoring: Problems and solutions. arXiv 2019, arXiv:1912.08581. [Google Scholar]
- Ferraty, F.; Laksaci, A.; Tadj, A.; Vieu, P. Rate of uniform consistency for nonparametric estimates with functional variables. J. Stat. Plan. Inference 2010, 140, 335–352. [Google Scholar] [CrossRef]
- Bouzebda, S.; Nemouchi, B. Uniform consistency and uniform in bandwidth consistency for nonparametric regression estimates and conditional U-statistics involving functional data. J. Nonparametr. Stat. 2020, 32, 452–509. [Google Scholar] [CrossRef]
- Kuelbs, J.; Li, W.V. Metric entropy and the small ball problem for Gaussian measures. J. Funct. Anal. 1993, 116, 133–157. [Google Scholar] [CrossRef]
- Nicoleris, T.; Yatracos, Y.G. Rates of convergence of estimates, Kolmogorov’s entropy and the dimensionality reduction principle in regression. Ann. Stat. 1997, 25, 2493–2511. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018. [Google Scholar]
- Jack, C.R.; Petersen, R.C.; Xu, Y.C.; O’Brien, P.C.; Smith, G.E.; Ivnik, R.J.; Boeve, B.F.; Waring, S.C.; Tangalos, E.G.; Kokmen, E. Prediction of AD with MRI-based hippocampal volume in mild cognitive impairment. Neurology 1999, 52, 1397. [Google Scholar] [CrossRef]
- Fjell, A.M.; Walhovd, K.B.; Fennema-Notestine, C.; McEvoy, L.K.; Hagler, D.J.; Holland, D.; Brewer, J.B.; Dale, A.M.; Initiative, A.D.N. CSF biomarkers in prediction of cerebral and clinical change in mild cognitive impairment and Alzheimer’s disease. J. Neurosci. 2010, 30, 2088–2101. [Google Scholar] [CrossRef]
- Barnes, D.E.; Cenzer, I.S.; Yaffe, K.; Ritchie, C.S.; Lee, S.J.; Alzheimer’s Disease Neuroimaging Initiative. A point-based tool to predict conversion from mild cognitive impairment to probable Alzheimer’s disease. Alzheimer’s Dement. 2014, 10, 646–655. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Chan, W.; Doody, R.S.; Quinn, J.; Luo, S.; Alzheimer’s Disease Neuroimaging Initiative. Prediction of conversion to Alzheimer’s disease with longitudinal measures and time-to-event data. J. Alzheimer’s Dis. 2017, 58, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.M.; Hayashi, K.M.; De Zubicaray, G.I.; Janke, A.L.; Rose, S.E.; Semple, J.; Hong, M.S.; Herman, D.H.; Gravano, D.; Doddrell, D.M.; et al. Mapping hippocampal and ventricular change in Alzheimer disease. Neuroimage 2004, 22, 1754–1766. [Google Scholar] [CrossRef] [PubMed]
- Apostolova, L.G.; Dinov, I.D.; Dutton, R.A.; Hayashi, K.M.; Toga, A.W.; Cummings, J.L.; Thompson, P.M. 3D comparison of hippocampal atrophy in amnestic mild cognitive impairment and Alzheimer’s disease. Brain 2006, 129, 2867–2873. [Google Scholar] [CrossRef]
- Blanken, A.E.; Hurtz, S.; Zarow, C.; Biado, K.; Honarpisheh, H.; Somme, J.; Brook, J.; Tung, S.; Kraft, E.; Lo, D.; et al. Associations between hippocampal morphometry and neuropathologic markers of Alzheimer’s disease using 7 T MRI. NeuroImage Clin. 2017, 15, 56–61. [Google Scholar] [CrossRef]
- Wang, H.J.; Wang, L. Locally weighted censored quantile regression. J. Am. Stat. Assoc. 2009, 104, 1117–1128. [Google Scholar] [CrossRef]
- Leng, C.; Tong, X. A quantile regression estimator for censored data. Bernoulli 2013, 19, 344–361. [Google Scholar] [CrossRef]
- Peng, L.; Huang, Y. Survival analysis with quantile regression models. J. Am. Stat. Assoc. 2008, 103, 637–649. [Google Scholar] [CrossRef]
- Zheng, Q.; Peng, L.; He, X. High dimensional censored quantile regression. Ann. Stat. 2018, 46, 308. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).