Abstract
It is now widely recognized that small area estimation (SAE) needs to be model-based. Global-local (GL) shrinkage priors for random effects are important in sparse situations where many areas’ level effects do not have a significant impact on the response beyond what is offered by covariates. We propose in this paper a hierarchical multivariate model with GL priors. We prove the propriety of the posterior density when the regression coefficient matrix has an improper uniform prior. Some concentration inequalities are derived for the tail probabilities of the shrinkage estimators. The proposed method is illustrated via both data analysis and simulations.
1. Introduction
Small area estimation (SAE) has been gaining increasing popularity in recent years. Its need is felt both in the public and private sectors. By now, it is well recognized that SAE must be model-based due to the lack of sufficient samples in individual local areas. The most well-known area-level SAE model is due to Fay and Herriot [1], which essentially is a random effect model, each area level effect being treated as a random effect.
While the Fay–Herriot model has enjoyed wide popularity for nearly four decades, questions have been raised recently regarding the need to include random effects for all areas. Datta et al. [2] were the first to address this problem. They suggested a preliminary test-based approach where the null hypothesis was that the common random effect variance was zero. The test was based on a discrepancy statistic measuring the lack of fit of the fixed effect model. Their proposal was to use a fixed or a random effect model based on the acceptance or rejection of the null hypothesis. Further results in this direction are due to Molina et al. [3] and Morales et al. [4].
The method performs well when the number of small areas is moderately large, but, as often happens in practice, the number of small areas is very large, for example, when one considers all counties in the United States. In such situations, even if the regression estimates can describe the small area means very well in most of the small areas, the null hypothesis of no random effects is still very likely to be rejected. This phenomenon appears because, for a few areas, the direct estimates deviate from the regression estimates significantly, even after taking into account the large sampling errors. This problem was first realized by Datta and Mandal [5]. They proposed to model random effects through a mixture of a point mass at zero and a zero-mean normal distribution. Such priors belong to the general class of spike-and-slab priors. The point mass part is suitable for areas where fixed effect models are adequate, while the normal distribution part models random effects when this is not the case.
In contrast to the spike-and-slab priors of Datta and Mandal [5], Tang et al. [6] used global-local shrinkage priors for random effects in small area estimation, which captured wide area-level variation when the number of small areas was very large. These global-local priors employ two levels of parameters, global and local parameters, to express variances of area-specific random effects so that both small and large random effects can be captured properly. The global parameter causes shrinkage on all random effects to capture the small random effects, while the local parameters try to avoid over-shrinkage for areas that need large random effects. The degree of this neutralizing effect is closely related to the tails of the priors for the local parameters. If the prior is appropriately heavy-tailed, then both small and large random effects can be well captured. Moreover, one of the virtues of global-local priors is that they enable one to assess the individual area-level effects, rather than the blanket dichotomization of zero or non-zero effects.
The objective of this paper is to generalize the arguments of Tang et al. [6] to a multidimensional SAE model. There are many instances when one needs multivariate SAE models. A classic example is the simultaneous estimation of the median income of three-, four- and five-person families initiated in Fay [7], and followed up later by Ghosh et al. [8]. A second example is the estimation of unemployment rates, as considered in Datta et al. [9]. A third example is the adjustment of census undercounts considered in Datta et al. [10]. Unlike this paper, the above articles model the area-level effects with only one global variance matrix. In many cases, there is built-in dependence among the direct estimates for different components, which demands the multivariate model.
Returning to the present paper, a hierarchical prior is introduced in Section 2, where we have proven the propriety of the resulting posterior under some conditions. Section 3 discusses the implementation of the proposed method via Markov chain Monte Carlo, and several priors for local parameters are listed in Section 3.2. Concentration inequalities related to the tail behavior of the posterior are given in Section 4. A real data example is considered in Section 5, while Section 6 provides some simulation results. Final remarks are made in Section 7.
The global-local shrinkage priors were introduced in a series of articles by Carvalho et al. [11], Polson and Scott [12], Polson and Scott [13], Polson and Scott [14], Polson and Scott [15] and Scott [16]. They have been extended into a richer class. Some recent inventions are the three-parameter beta normal (TPBN) priors by Armagan et al. [17] and the generalized double Pareto (GDP) priors by Armagan et al. [18]. TPBN itself is a large class and includes the now famous horseshoe (HS) prior Carvalho et al. [11], the normal-exponential-gamma (NEG) priors Griffin and Brown [19] and the Strawderman–Berger (SB) priors (Strawderman [20], Berger [21]). These priors have been used successfully in multiple testing by Datta and Ghosh [22], Ghosh et al. [23], and also in other contexts. GL priors can be further classified into polynomial-tailed priors and exponential-tailed priors according to the tail behavior of the local parameters.
2. The Hierarchical Model
We begin with a multivariate analog of the model proposed in Tang et al. [6].
where the direct survey estimators , the corresponding means , the random effects and the error term are all k-dimensional vectors for the i-th area; is a matrix of regression coefficients; and m is the number of small areas. The variance matrices s are assumed to be known to avoid nonidentifiability. are local parameters and is a matrix for the global parameter. All error terms and random effects are independent random variables. It is assumed that all the are positive definite. Moreover, the smallest eigenvalues of all the are bounded below by , while the corresponding largest eigenvalues are bounded above by , where .
We introduce the notations , , , and . In matrix notations, .
Thus, , where . We assume rank . Moreover, we will write . Hence, . Since an improper prior density has been used for , we need to find conditions under which the posterior density is proper. To this end, we first define a matrix normal distribution.
Definition 1.
A random matrix is said to have the matrix-normal density if has the density function (on the space
where , and and are positive definite matrices of dimension and , respectively. We write . Thus, the random effect matrix .
We establish the propriety of the posterior under arbitrary proper priors for the local parameters and the global parameter in the following theorem, whose proof is given in Appendix A.1. In Section 3, we will have particular choices of priors for the and for actual implementation.
Theorem 1.
The posterior distribution corresponding to the (1) is proper if both , and are proper.
In the next section, we will consider several choices of priors for the local parameters . Throughout, for actual implementation, we will consider the inverse Wishart prior
which we symbolically denote as .
3. Computation and Local Prior Selection
3.1. Computation
In this section, we have derived the full conditionals for Gibbs sampling. It is convenient to compute all the conditionals in terms of the rather than the . Since , which is a one–one linear transformation from , and the Jacobian matrix is constant and depends only on , we can rewrite the joint density of our model in (1) as
To compute the conditional distribution for , we need to simplify the following expression:
where and .
Using (2) and (4), one can obtain the Gibbs sampler designed to sample from the posterior density. Full conditional distributions are given below.
To complete the computation, in the next section, we introduce several widely used local priors, and then discuss some specifics regarding their implementation.
3.2. Local Prior Selection
We have provided a short list of widely used priors for the local parameters in Table 1. The priors are derived after marginalizing out the local parameters .

Table 1.
Global-local shrinkage prior for .
To facilitate the discussion of computation, we further group the priors in Table 1 into generalized inverse Gaussian priors and normal beta prime priors.
- Generalized Inverse Gaussian (GIG): if . Thus, . Using this, we can see that if is exponential, viz. , then . The Laplace prior is a special case of GIG priors with , and .
- Normal Beta Prime (NBP):One obtains NBP prior by introducing a latent variable and . Therefore, and . By setting different values for a and b, we will obtain Strawderman–Berger (SB), horseshoe (HS) and negative exponential gamma (NEG) as special cases. For NEG, we choose b = 0.75 in our Data Analysis section.
We will study Laplace and normal beta prime priors in Section 4 to illustrate our theoretical results. For the simulation study and real data analysis, we will use Laplace (LA), Strawderman–Berger (SB), horseshoe (HS) and negative exponential gamma (NEG, ) as local priors in our multivariate models.
4. Shrinkage Factor
Despite their distinct forms, these multivariate GL shrinkage priors possess a common feature—the ability to assign nontrivial probability mass both near zero and in the tail—which enables our multivariate GL model to capture both small and large random effects based on data. To see this, first note that, given the local and global parameters, the conditional posterior mean of the small area mean shrinks the direct estimate toward the synthetic regression estimate as
where is called a shrinkage factor. A larger (smaller) shrinkage factor causes more (less) shrinkage and produces an estimate closer to the synthetic estimate (direct estimate). Here, denotes the Frobenius norm of a matrix in this section.
Theorem 2.
Suppose is a proper pdf with support . Then, for ,
where and an arbitrary positive constant.
The proof of the theorem is provided in Appendix A.2. This theorem leads immediately to the result as . We now illustrate this result with some of the global-local priors.
Example 1.
Consider the Laplace prior . Then,
which converges to zero at an exponential rate when .
Example 2.
Consider the NEG prior . Then, for and by variable transformation , we obtain
which again converges to zero as . For ,
Theorem 3.
Suppose that the prior has support Then, for , , where , is a positive constant and , where and are the smallest and largest eigenvalues of Σ, respectively.
The proof of the theorem is provided in Appendix A.3.
Remark 1.
It is only by proper choice that we obtain as in the examples to consider. Moreover, we need to assume that or, alternatively, we can rewrite this assumption as .
We now apply Theorem 3 for Examples 1 and 2.
Example 3.
This example is the continuation of Example 1. The ratio simplifies to , which converges to zero for as , where .
Example 4.
This example is the continuation of Example 2. , say, where . For ,
Now, for ,
Hence, , where . For any arbitrarily small δ, choose such that . Therefore, as .
Theorem 4.
Suppose is a proper prior with support on ; then,
, where and d are some positive finite constants.
The proof of Theorem 4 is given in Appendix A.4 and this theorem immediately gives us as .
5. Data Analysis
We consider the problem of estimating median income. The Census Bureau releases estimates of median household income for many different demographic and geographic subgroups. A model-based approach is needed to obtain finer breakdowns (by demographics and/or geography) while still maintaining adequate precision. We applied our method to estimate a four-dimensional response, which is the median income of the homeowner, renter, married and unmarried populations. These groups are determined by the head of the household, and some of these groups overlap each other, e.g., a homeowner could be both married and an owner. The dataset was compiled using the one-year public-use microsample from the 2015 American Community Survey (data available at https://data.census.gov, accessed on 1 May 2019). The direct estimates are obtained at state level, including the District of Columbia. Thus, the number of small areas m is 51. The descriptive statistics are presented in Table 2. Besides the intercept, per-capita income is included as the covariate (data available at https://bea.gov, accessed on 1 May 2019). Moreover, we have scaled down the values of the data by dividing both the direct estimates and the covariate by 1000. The error variance–covariance matrices, , are also rescaled accordingly.

Table 2.
Descriptive statistics for sample sizes and median household income across the 51 states/districts.
In our data analysis, we consider model (1) with five different choices of the priors on the variance–covariance matrix of . In the first model, we assume for . Thus, the random effects share a common variance–covariance matrix across different small areas. It is essentially a multivariate Fay–Herriot model. The remaining four models vary in the prior of the local parameters . We consider the LA, HS, SB, and NEG priors, which are stated in Table 1. Among the four choices, HS, SB, and NEG are special cases of the normal beta prime family and have polynomial tails. In all five models, we used an inverse-Wishart prior for with degrees of freedom and . For each of these models, we run the Gibbs sampler described in Section 3 for 20,000 iterations. The first half is discarded as the burn-in period. The samples from the remaining 10,000 iterations are used for inference. The small area means and the random effects are estimated by the corresponding posterior sample means.
We first examine the estimated random effects from different models. Figure 1 presents the posterior means of random effects . Since the results from the three models with polynomial-tailed local priors are similar, we only present the results for HS as a representative. For most of the states, the estimated random effects from different models do not differ much. However, significant differences are seen in the District of Columbia, especially for the married and the renter groups. There is also a visible difference in Connecticut for the renter and the unmarried groups. When there is a difference, the estimated random effects from the LA model are usually smaller than those from the HS model and larger than those from the FH model. This observation demonstrates that polynomial-tailed priors lead to less shrinkage towards zero when compared with exponential-tailed priors.
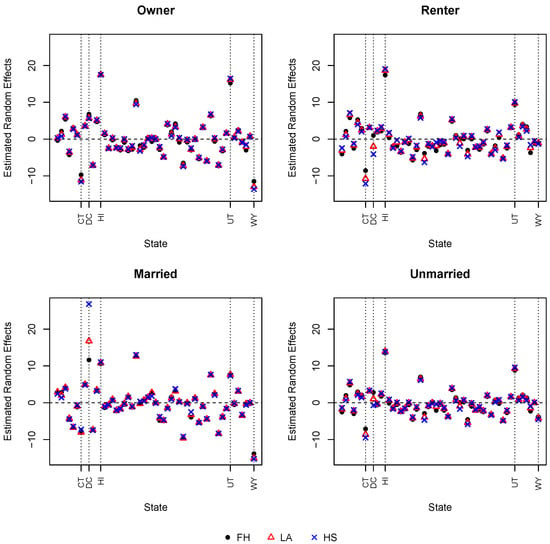
Figure 1.
Estimated random effects from FH, LA, and HS models for four subgroups in all states.
Figure 2 presents the estimated from two GL models (LA and HS) against those from the FH model. For most of the states, the estimates agree for all four subgroups. For the District of Columbia, the estimates for the married group from the GL models, especially the HS model, are higher than those from the FH model. It is the only state or district where the estimated from the HS model differs from that from the FH model by more than 5%. It is not surprising that DC differs from the rest of the states since this area is more similar to large urban counties than other states, but it is typically included in state-level small area models for completeness of the entire U.S. population. The flexibility in our GL model is able to account for the difference through a larger random effect.
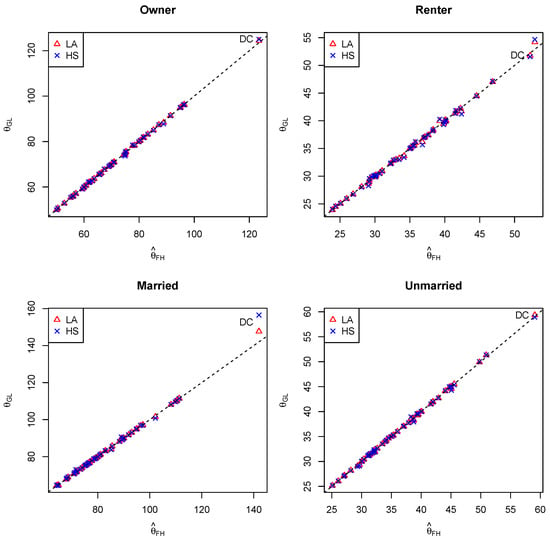
Figure 2.
Estimated small area means from FH, LA, and HS models for four subgroups in all states.
To select an appropriate model for the dataset, we use the deviation information criterion (DIC) proposed by Spiegelhalter et al. [24]. The simulation study in Section 6 shows that the model selected by DIC and the model producing the lowest deviation measurements often give comparable estimates of small area means. For the real median income dataset, the DICs for the FH, LA, HS, SB, and NEG models are 1018.30, 967.79, 957.10, 957.46, and 959.48, respectively. The HS model has the smallest DIC and is thus selected. Table 3 gives the estimated median income from the HS model for the four subgroups in each state.

Table 3.
Median income estimates from the HS model.
6. Simulation Study
In this section, we investigate the performance of different priors for estimating the small area means on simulated datasets. In the simulation study, data are generated according to , where and for . We first consider a data generation setting similar to the real dataset in Section 5. We set and . The per-capita income (pci) from the real dataset is used as the covariate. The matrix consists of centered pci and a column of ones, so . The coefficient matrix is set at the least square estimate computed from the real data. The error variance matrices are also borrowed from the real dataset. Three models are considered for generating :
- common variance: with the element in the j-th row and l-th column of being ;
- two-component: , where is 0.01 or 10 with equal probability and is the same as in the common variance model;
- multi-variance: , where are equally spaced values from 0.01 to 10 and is the same as in the common variance model.
To investigate the performance when the number of small areas is large, we consider two additional choices of m, 500 and 1000. For both choices, k, p, and are the same as in the previous setting. The matrix contains a column of ones and a column of values generated from , where is the sample variance of pci in the real dataset. For each small area, is randomly sampled from the error variance matrices in the real dataset. The three models for generating in the setting are also used in the settings of and 1000.
We generate 100 datasets for each combination of m and the model for . For each dataset, the five models considered in Section 5 are fitted. For each model, the Gibbs sampler is run for 20,000 iterations. The samples from the first 10,000 iterations are discarded. Then, is estimated by the posterior sample mean computed from the remaining 10,000 samples. The estimation accuracy is evaluated using four deviance measures, average absolute deviation (AAD), average squared deviation (ASD), average absolute relative deviation (ARB), and average squared relative deviation (ASRB), which are defined as follows:
The averages of each deviation measure across 100 datasets are presented in Figure 3. Under the common variance setting, the FH model produces the smallest estimation errors in terms of all four measures. This is expected because the fitted model is the same as the data generation model. Although the GL models do not match the data generation model, their performance is similar to the FH model.

Figure 3.
Average deviation measures for different models under different data generation settings in the simulation study.
Under the other two settings for , the GL models often have the best performance. Especially under the two-component setting, the FH model produces much higher deviation measures compared to GL models. Although the results from different GL models do not vary much under the two settings, the HS, SB, and NEG models have better performance than the LA model under the two-component setting, while the reverse is true under the multi-variance setting. The difference in the performance is caused by the tail of the prior on the local parameters. Polynomial-tailed priors often shrink the signals less than the exponential-tailed priors, so the models with polynomial-tailed priors (HS, SB, NEG) tend to perform better in the two-component case, where the signals (large random effects) and the noises (small random effects) are well separated.
We also investigate the performance of the model selected according to DIC. The results are also plotted in Figure 3. As the figure shows, the deviation measurements produced by the model selected by DIC are often close to the lowest among all models in each setting. This observation indicates that DIC usually selects a reasonable model for a given dataset.
7. Final Remarks
In this paper, we have addressed the situation of multivariate sparsity in random effects. We are able to estimate the random effects in income for different correlated groups and the correlation structure is used in the estimation process. We are able to derive concentration inequalities of the tail behavior of shrinkage factors. Our simulation study shows that the proposed multivariate GL estimators are very close to the truth. The data analysis shows that our multivariate GL model can identify the states/districts that have significantly large random effects.
Our simulation study shows that the prior that works best varies across data generation settings. Overall, priors with polynomial tails perform better when the small and large random effects are well separated, while the priors with exponential tails perform better when there are many intermediate random effects. We demonstrate that DIC can be used to select a suitable prior for a dataset.
There is potential for generalizing these results. In particular, in the proposed model, the same local parameter is assumed for different components of a small area. To account for heterogeneous dependence among components across areas, one can assume the area-level variance matrix for area i to be instead of . Moreover, one can address the same problem for unit-level models with global-local priors involving two variance components for area-level effects.
Moreover, independent random effects are considered in the proposed model. Recently, random effects with spatial or spatio-temporal dependence have been considered in small area estimation when suitable covariates for accounting for dependence in the geographic or time domain are not available (cf. Chung and Datta [25], Bradley et al. [26]). Combining the global-local shrinkage prior with spatial or spatio-temporal priors is also a potential future direction.
Author Contributions
Conceptualization, T.G. and M.G.; methodology, T.G. and M.G.;writing—original draft preparation, T.G. and M.G.; writing—review and editing, X.T. and M.G.; data curation, J.J.M.; supervision, M.G.; Software, T.G. and X.T.; validation, J.J.M. and M.G.; formal analysis; T.G., M.G. and X.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets are based on a one-year public-use microsample from the 2015 American Community Survey available at https://data.census.gov, accessed on 1 May 2019. The per-capita income dataset is available at https://bea.gov, accessed on 1 May 2019.
Acknowledgments
The authors are grateful to the editor and anonymous reviewer(s) for their constructive comments and suggestions, which greatly improved an earlier version of this article. Author Tamal Ghosh wants to dedicate his part of the work to his late father Chittaranjan Ghosh.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Proof of Theorem 1
Proof.
The joint posterior pdf is given by
Writing , ,
Next, use the identity , where . The cross-product term vanishes since . Hence, the left-hand side of (A2) is bounded below by Using (A1), we obtain
Equation (A3) is integrable with respect to since it is the pdf of a matrix normal distribution with and . After integrating out , we obtain
Note that K is some generic constant.
Now, Equation (A4) is integrable with respect to each since it has a normal density kernel. Thus,
Hence, if the priors for and are proper, then the posterior density is proper. □
Appendix A.2. Proof of Theorem 2
Proof.
Using the properties and of the Frobenius norm, one obtains
where .
where we define N and D as the numerator and denominator of (A7). Now,
and for any , we have
It is easy to see that Theorem 2 follows from (A7)–(A9). □
Appendix A.3. Proof of Theorem 3
Proof.
We begin with the following inequality:
Hence, , where . Thus,
where the and are defined as the numerator and denominator of (A10). Since and are, respectively, the smallest and largest eigenvalues of , Now, writing , we have the inequality
Now, for some arbitrary , we have
Thus, which proves the theorem. □
Appendix A.4. Proof of Theorem 4
Proof.
We begin with the inequality
Hence, , where . Thus,
where and are defined as the numerator and the denominator of (A11).
Recall that and are the smallest and largest eigenvalues of , and and are the smallest and largest eigenvalues of , respectively. Therefore, the upper bound for is
For some , we have
where does not depend on . Now, we choose large such that . Hence, using (A12) and (A13), we have
where is some positive finite constant. Therefore, if , then . □
References
- Fay, R.E.; Herriot, R.A. Estimates of Income for Small Places: An Application of James-Stein Procedures to Census Data. J. Am. Stat. Assoc. 1979, 74, 269–277. [Google Scholar] [CrossRef]
- Datta, G.S.; Hall, P.; Mandal, A. Model selection by testing for the presence of small-area effects, and application to area-level data. J. Am. Stat. Assoc. 2011, 106, 362–374. [Google Scholar] [CrossRef]
- Molina, I.; Nandram, B.; Rao, J.N.K. Small area estimation of general parameters with application to poverty indicators: A hierarchical Bayes approach. Ann. Appl. Stat. 2014, 8, 852–885. [Google Scholar] [CrossRef]
- Morales, D.; Pagliarella, M.C.; Salvatore, R. Small area estimation of poverty indicators under partitioned area-level time models. SORT Stat. Oper. Res. Trans. 2015, 39, 19–34. [Google Scholar]
- Datta, G.S.; Mandal, A. Small Area Estimation With Uncertain Random Effects. J. Am. Stat. Assoc. 2015, 110, 1735–1744. [Google Scholar] [CrossRef]
- Tang, X.; Ghosh, M.; Ha, N.S.; Sedransk, J. Modeling Random Effects Using Global–Local Shrinkage Priors in Small Area Estimation. J. Am. Stat. Assoc. 2018, 113, 1476–1489. [Google Scholar] [CrossRef]
- Fay, R.E. Application of of multivariate regression to small domain estimation. In Small Area Statistics; Platek, R., Rao, J.N.K., Sarndal, C.E., Singh, M.P., Eds.; Wiley: Hoboken, NJ, USA, 1987; pp. 91–102. [Google Scholar]
- Ghosh, M.; Nangia, N.; Kim, D.H. Estimation of median income of four-person families: A Bayesian time series approach. J. Am. Stat. Assoc. 1996, 91, 1423–1431. [Google Scholar] [CrossRef]
- Datta, G.S.; Lahiri, P.; Maiti, T.; Lu, K.L. Hierarchical Bayes estimation of unemployment rates for the states of the US. J. Am. Stat. Assoc. 1999, 94, 1074–1082. [Google Scholar] [CrossRef]
- Datta, G.S.; Fay, R.E.; Ghosh, M. Hierarchical and Empirical Multivariate Bayes Analysis in Small Area Estimation. In Proceedings of the Bureau of Census Annual Research Conference, Arlington, VA, USA, 17ߝ20 March 1991; US Department of Commerce, Bureau of the Census: Washington, DC, USA, 1991; pp. 63–79. [Google Scholar]
- Carvalho, C.M.; Polson, N.G.; Scott, J.G. The horseshoe estimator for sparse signals. Biometrika 2010, 97, 465–480. [Google Scholar] [CrossRef]
- Polson, N.G.; Scott, J.G. Alternative Global–Local Shrinkage Rules Using Hypergeometric–Beta Mixtures; Technical Report 14; Duke University, Department of Statistical Science: Durham, NC, USA, 2009. [Google Scholar]
- Polson, N.G.; Scott, J.G. Shrink Globally, Act Locally: Sparse Bayesian Regularization and Prediction. Bayesian Stat. 2010, 105, 501–538. [Google Scholar]
- Polson, N.G.; Scott, J.G. Local shrinkage rules, Lévy processes and regularized regression. J. R. Stat. Soc. Ser. B Stat. Methodol. 2012, 74, 287–311. [Google Scholar] [CrossRef]
- Polson, N.G.; Scott, J.G. On the half-Cauchy prior for a global scale parameter. Bayesian Anal. 2012, 7, 887–902. [Google Scholar] [CrossRef]
- Scott, J.G. Bayesian estimation of intensity surfaces on the sphere via needlet shrinkage and selection. Bayesian Anal. 2011, 6, 307–327. [Google Scholar] [CrossRef]
- Armagan, A.; Clyde, M.; Dunson, D.B. Generalized Beta Mixtures of Gaussians. In Advances in Neural Information Processing Systems 24; Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2011; pp. 523–531. [Google Scholar]
- Armagan, A.; Dunson, D.B.; Lee, J. Generalized Double Pareto Shrinkage. Stat. Sin. 2013, 23, 119–143. [Google Scholar] [CrossRef] [PubMed]
- Griffin, J.; Brown, P. Alternative Prior Distributions for Variable Selection with Very Many More Variables than Observations; Technical Report; University of Warwick: Coventry, UK, 2005. [Google Scholar]
- Strawderman, W.E. Proper Bayes Minimax Estimators of the Multivariate Normal Mean. Ann. Math. Stat. 1971, 42, 385–388. [Google Scholar] [CrossRef]
- Berger, J. A Robust Generalized Bayes Estimator and Confidence Region for a Multivariate Normal Mean. Ann. Statist. 1980, 8, 716–761. [Google Scholar] [CrossRef]
- Datta, J.; Ghosh, J.K. Asymptotic properties of bayes risk for the horseshoe prior. Bayesian Anal. 2013, 8, 111–132. [Google Scholar] [CrossRef]
- Ghosh, P.; Tang, X.; Ghosh, M.; Chakrabarti, A. Asymptotic Properties of Bayes Risk of a General Class of Shrinkage Priors in Multiple Hypothesis Testing Under Sparsity. Bayesian Anal. 2016, 11, 753–796. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B Stat. Methodol. 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Chung, H.C.; Datta, G.S. Bayesian Hierarchical Spatial Models for Small Area Estimation; Research Report Series; Census Bureau: Washington, DC, USA, 2020. [Google Scholar]
- Bradley, J.R.; Holan, S.H.; Wikle, C.K. Multivariate spatio-temporal models for high-dimensional areal data with application to longitudinal employer-household dynamics. Ann. Appl. Stat. 2015, 9, 1761–1791. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).