Abstract
Clustered count data are commonly modeled using Poisson regression with random effects to account for the correlation induced by clustering. The Poisson mixed model allows for overdispersion via the nature of the within-cluster correlation, however, departures from equi-dispersion may also exist due to the underlying count process mechanism. We study the cross-sectional COM-Poisson regression model—a generalized regression model for count data in light of data dispersion—together with random effects for analysis of clustered count data. We demonstrate model flexibility of the COM-Poisson random intercept model, including choice of the random effect distribution, via simulated and real data examples. We find that COM-Poisson mixed models provide comparable model fit to well-known mixed models for associated special cases of clustered discrete data, and result in improved model fit for data with intermediate levels of over- or underdispersion in the count mechanism. Accordingly, the proposed models are useful for capturing dispersion not consistent with commonly used statistical models, and also serve as a practical diagnostic tool.
1. Introduction
The most commonly used distribution for count data is the Poisson model. Poisson regression models consider the relationship between count response and explanatory data under the strict assumption of equi-dispersion. Count data often arise in clusters where multiple outcome occasions observed for a cluster are naturally related. Positive correlation inherent to clustered data is a frequent cause of over-dispersion [1]. Poisson random effects regression models are regularly used for clustered count data because they account for additional variability induced by correlation of measurements within a cluster and thus address over-dispersion. Specifically, the Poisson random intercept model allows the intercept to vary by cluster, inducing a compound symmetric correlation structure [2]. This model combines the standard Poisson count model with a cluster-specific term that reflects cluster-level heterogeneity [3,4]:
for and , where is a scalar count outcome for cluster i at occurrence j, is a p-dimensional vector of explanatory variables, and is the density of the random effect characterized by parameters . That is, the count outcome for cluster i at occurrence j follows a Poisson distribution conditional on a cluster-specific random effect, a set of covariates and a vector of regression parameters that are common to all subjects. If an intercept parameter is included in the vector of regression parameters, then the mean of the random effect is assumed to be zero. Models of this type assume that data are independent over clusters and that correlation within cluster is adequately controlled for through the cluster-specific effects. Responses within a cluster are assumed independent conditional on the random effect: . Introducing additional variability due to the random intercept allows the cluster-specific rates to vary in a way that cannot be accounted for by observables. Allowing this additional randomness naturally relaxes the strict equi-dispersion assumption of the Poisson distribution as the marginal mean and variance depend on the variance of . The assumed distribution for yields two typical Poisson mixed models: the Poisson-lognormal model [5,6,7] and the Poisson-gamma model [8,9].
The underlying count outcome may exhibit under-dispersion or additional over-dispersion that is not adequately modeled by the cluster correlation structure alone. Such data requires a more flexible count model to account for underlying count dispersion as well as clustering. Booth et al. [10] recognized the practical need for combining clustering with additional dispersion allowance via a negative binomial mixed model. The negative binomial distribution is a commonly used distribution for addressing over-dispersion and mixing with a random effect naturally addresses dependence. Molenberghs et al. [11], Molenberghs et al. [12] and Rizzato et al. [13] discuss a Poisson hierarchical model using two separate sets of random effects to accommodate both over-dispersion with respect to variability inconsistent with the strict mean-variance relation of the Poisson distribution and over-dispersion due to repeated outcomes. These models—extensions of the negative binomial and Poisson regression models—were illustrated to be useful for addressing over-dispersion.
The Conway–Maxwell–Poisson (COM-Poisson or CMP) distribution is a flexible model for count data that relaxes the equi-dispersion assumption to capture any degree of data dispersion. The COM-Poisson model was shown to be useful for modeling over-dispersed (see, for example, [14,15]) and under-dispersed (see, for example, [16,17]) count data. Regression modeling based on the COM-Poisson distribution was originally proposed by Sellers and Shmueli [18]. Sellers and Shmueli [18] and Chatla and Shmueli [19] describe maximum likelihood estimation of a COM-Poisson regression model with a log link for the rate parameter , whereas Huang [20] and Ribeiro Jr. et al. [21] study maximum likelihood estimation of a mean-reparameterized form of the model. Guikema and Coffelt [22] and Huang and Kim [23] propose Bayesian estimation of a form of the COM-Poisson regression model based on a mean approximation and a mean reparametrization, respectively.
The COM-Poisson regression model was further extended to allow overdispersion with respect to clustering in addition to dispersion due to the nature of the underlying count process. Marginal COM-Poisson models [24,25] and COM-Poisson mixed models using frequentist [26,27,28] and Bayesian [29] estimation techniques were proposed to jointly account for within-cluster association and dispersion. Using the mixed model framework, we continue study of maximum likelihood estimation of a COM-Poisson mixed model based on the Sellers and Shmueli [18] COM-Poisson regression model. We further compare assumptions of the random effects distribution, introducing the use of the COM-Poisson conditional conjugate [30], to assess sensitivity to such assumptions. We find that the flexibility in both the data distribution and the random effects distribution can lead to better model fit. Even though using the COM-Poisson conditional conjugate density does not yield computational simplicity (i.e., a closed form marginal likelihood), we find that it yields greater flexibility in some data scenarios.
The rest of this paper proceeds as follows. Section 2 reviews the COM-Poisson distribution and the COM-Poisson regression model. Section 3 describes the random intercept COM-Poisson mixed model and presents its formulation under normal-distributed random effects (COM-Poisson-lognormal) and conjugate-distributed random effects (COM-Poisson-conjugate). Section 4 demonstrates the flexibility of the COM-Poisson mixed model and its sensitivity to the choice of random effects distribution via data simulated from a variety of count distributions. Section 5 presents a comparison of random intercept count models fit on real data. Section 6 concludes and discusses possible extensions of this work.
2. COM-Poisson Distribution and Regression Model
The COM-Poisson distribution is a flexible distribution for count data that allows for over- or under-dispersion [15,31,32]. The COM-Poisson probability mass function for a single observation takes the form
for a random variable Y, where is a normalizing constant. In this setting, , where is the dispersion parameter such that denotes equi-dispersion and signifies under- (over-)dispersion. The moments of the COM-Poisson distribution are not of closed form, however, Shmueli et al. (2005) note that assuming an asymptotic approximation for leads to a close approximation for the mean:
The COM-Poisson distribution includes three well-known distributions as special cases: Poisson with rate parameter (); geometric with success probability (); and Bernoulli with success probability ().
Sellers and Shmueli [18] extend the COM-Poisson distribution to the regression context allowing varying for each observation i. This regression formulation relates to explanatory variables using the link
thus specifying an indirect link between the mean and the linear predictor. This formulation links the logarithm of the raw moment of to the linear predictor. The associated log-likelihood is
Given this construct, the COM-Poisson regression model has two notable special cases: Poisson regression with , and logistic regression with . The dispersion parameter may be modeled, however, we assume a constant in the development of the COM-Poisson mixed model for clustered data.
3. COM-Poisson Regression Mixed Model
We further study the extension of the Sellers and Shmueli [18] COM-Poisson regression model to include a random intercept for modeling clustered data. Throughout this paper we use the term clustered data in a general sense to include specific types of correlated data such as longitudinal, repeated measures, as well as spatial and family data [5].
3.1. Model Formulation
The COM-Poisson regression random intercept model is defined as
where notation is defined as in Section 1. In this formulation, the additive intercept shift of can be reparameterized in terms of a multiplicative effect with . This mixed model assumes that the association between the explanatory and response variables are the same across all clusters, while allowing for variability in the intercept value associated with different clusters. The associated conditional probability mass function for observation j of cluster i is
Assuming conditional independence, the marginal likelihood for cluster i can be written as
where is the set of and is a vector of the clustered response outcomes (). The random effect parameter captures all the dependence between multiple outcomes within a cluster, including the association of outcomes measured on different observation units. Under certain assumptions, this likelihood reduces to familiar models that can be easily estimated with maximum likelihood. For example, for the special case of Poisson (), is sometimes chosen to be the conjugate gamma distribution such that reduces to a tractable form.
3.2. COM-Poisson-Lognormal Model
It is a common assumption in the mixed model literature to let the random effects be normal-distributed: or equivalently . For the COM-Poisson mixed model—as well as the standard Poisson mixed model—this assumption does not result in a closed form marginal loglikelihood and requires computational techniques. The marginal likelihood for the COM-Poisson-lognormal (CMP-LN) model for cluster i as per Equation (8) is
As described in Morris and Sellers [27], maximum likelihood estimates can be obtained in R using (1) numerical integration (e.g., the integrate function) to obtain an approximation of the marginal loglikelihood:
and (2) optimization (e.g., the nlminb function) to maximize the approximate marginal loglikelihood. The integrate function in the base stats package in R implements a variant of Gaussian quadrature based on QUADPACK routines [33]. A variety of alternatives for numerical integration exist, but this standard function suffices for this work. We use the default settings in nlminb to implement unconstrained optimization using PORT routines where positivity constraints for and are incorporated into the objective function by exponential transformations. Maximum likelihood estimates for the CMP-LN model can similarly be obtained in SAS via a user-defined loglikelihood function in the NLMIXED procedure [26]. Approximate standard errors are obtained from the square root of the diagonal entries of the inverse observed Fisher information associated with the numerically-derived loglikelihood using the hessian function in the numDeriv package in R. The Z function is approximated with a finite summation using a truncation point at which successive terms are small; a truncation point of 100 sufficed for analysis in this paper. The loglikelihood is programmed using Rcpp in R [34] which greatly decreases the computing time.
3.3. COM-Poisson-Conjugate Model
Kadane et al. [30] established the probability density function that serves as the joint conjugate prior for a COM-Poisson distribution,
for and , where is the integration constant. This joint conjugate density is a proper density for finite which occurs for . This distribution is conjugate for the COM-Poisson distribution in the Bayesian sense: the posterior distribution has the same form as Equation (11). The associated conditional distribution of derived from this “extended bivariate gamma distribution” is
where is the integration constant. This conditional conjugate density is a proper density for finite . Figure 1 depicts the conditional conjugate distribution for select values of a, c and . The interested reader can further explore behavior of the conditional conjugate distribution via an R Shiny app developed by Morris [35]. For the Poisson, geometric, and Bernoulli special cases of the COM-Poisson distribution, the conditional conjugate distribution reduces to well-known distributions, respectively: gamma for ; beta for ; and F with or equivalently beta for [30]. These are the familiar conjugate relationships between the Poisson-gamma, geometric-beta, and Bernoulli-beta distributions.
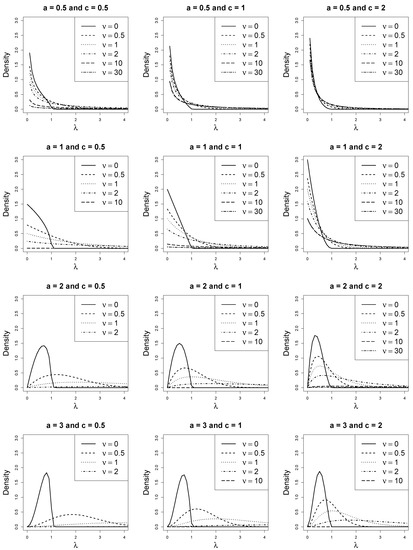
Figure 1.
Plots of the conditional conjugate probability density function at select values of a, c and .
Kadane et al. [30] determine precise parameter constraints to induce a proper joint conjugate density. We find empirically that the corresponding conditional conjugate density is not proper when and is large. Specifically,
is divergent when and is not small enough to compensate for the large numerator . Figure 2 presents combinations for which numerical integration evaluates respectively with and without error. This empirical assessment indicates a complex boundary that depends on the relative size of the a and c parameters compared with the size of the dispersion parameter .
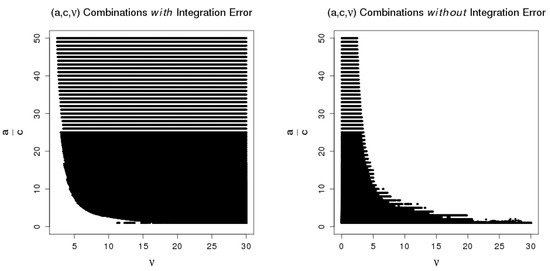
Figure 2.
Empirical illustration of parameter constraints for conditional conjugate density . is evaluated over by 0.1 and by 0.05 for .
As an alternative to the CMP-LN model, we propose a model that assumes the random effects follow the conditional conjugate distribution so that
This assumption leads to the marginal likelihood for the COM-Poisson-conjugate (CMP-C) model for cluster i as per Equation (8):
It is assumed that the same shapes the data distribution and the random effects distribution. This assumption yields the familiar special case of the Poisson-gamma random intercept model (CMP-C with ); however, a model with one to define the data distribution and another to define the random effects distribution would allow further flexibility.
The marginal likelihood for the CMP-C model is not generally of closed form and thus maximum likelihood estimation requires computational techniques. This is true despite the fact that the distribution of Equation (13) is the conditional conjugate for the COM-Poisson distribution because the model violates the notion of “strong conjugacy” [12]. Under the stated distributional assumptions, the posterior distribution of the random effects is of the form
which differs from the form of the random effects distribution in Equation (13), and therefore violates the Bayesian notion of conjugacy. For the random effects distribution, the Z function depends on alone, whereas the Z function from the data distribution depends on . For the commonly used Poisson-gamma random intercept model, the form of the Z function allows all Z functions to reduce together. This is true because for gamma distributed random effects, one can write so that the random effect multiplied by a fixed term results in the same random effect distribution with a scaled set of parameters [12]. This property of the random effect distribution defines strong conjugacy [12]. The CMP conditional conjugate, however, does not allow for this multiplicative invariance, and thus the CMP-C model generally does not have closed form. This holds true also for the geometric-beta and Bernoulli-beta special cases because multiplicative invariance is not a property of the beta distribution.
The flexibility of the CMP-C model is achieved through the modeling of over- and under-dispersion with the CMP conditional distribution, together with the variety of random effect distributional forms allowed through the extended gamma conjugate distribution. Despite not leading to a closed form marginal likelihood, the flexibility of the conjugate distribution offers a potential advantage over the CMP-LN model, as well as an opportunity to assess sensitivity to the assumed random effect distribution. If a similarly flexible conditional count distribution is found to have an associated conjugate distribution with multiplicative invariance, then the existence of such a combination would certainly be more computationally efficient. Study of the formulation and properties of conjugate distributions for alternative over- and underdispersion count distributions is a topic of future research.
Assuming clusters are independent, the full loglikelihood of the CMP-C model is
We obtain maximum likelihood estimates in R using (1) numerical integration (e.g., the integrate function) to obtain an approximation of this marginal loglikelihood and (2) optimization (e.g., the nlminb function) to maximize the approximate marginal loglikelihood. The standard error calculations, Z function approximation and use of Rcpp is as described in Section 3.2.
4. Analysis: Simulated Data
To illustrate the flexibility and utility of these COM-Poisson mixed models, we present analysis of simulated clustered count data under a variety of data generation specifications. For each specification, count responses are generated for clusters observed times for a total of 500 observations in each of 50 replications. The simulation study is designed as
where in Scenario I and in Scenario II. The parameters of the gamma distribution in Scenario II are defined to correspond to the same mean and variance as the lognormal distribution in Scenario I. Five conditional response distributions are assessed: Poisson, Bernoulli, geometric, CMP, and CMP. These distributions correspond to the three special cases of the COM-Poisson distribution and two cases with intermediate levels of under- or over-dispersion in the underlying count mechanism. Simulated data from the special cases are generated using the rpois, rbinom and rgeom functions in R, while the intermediate cases are generated using the rcmp function in the COMPoissonReg package [36].
Four candidate random intercept models are fit to the simulated data: Poisson-lognormal (Poi-LN), negative binomial-lognormal (NB-LN), COM-Poisson-lognormal (CMP-LN), and COM-Poisson-conjugate (CMP-C). These four models capture variations in distributional assumptions of the data and the random effects. The Poi-LN and NB-LN models are chosen for comparison because they are the most widely used and easily accessible models. They are fit using the default settings in glmer and glmer.nb from the lme4 function in R [37]. Logistic random intercept models with normal-distributed random effects (L-LN) are also fit using glmer for the Bernoulli special case simulated data. We measure model fit through two measures: the proportion that result in the largest loglikelihood, and the proportion of the 50 replications that result in the smallest AIC within 2. The tolerance for AIC comparisons follows from Burnham and Anderson [38] assessing that models with an AIC value no more than 2 greater than the lowest AIC have favorable evidence comparable to that of the lowest AIC model.
Embedded in this simulation study are two types of misspecification. First, the link between the mean and the linear predictor is misspecified in CMP-LN and CMP-C models for geometric simulated data, and in the Poi-LN and NB-LN models for the CMP simulated data. For the three special case simulated data, the link to the linear predictor is assumed through the mean. In the Poisson and Bernoulli special cases, that coincides with the specification of the CMP-LN and CMP-C models linked through . That is, the additive random effect on the linear predictor has the same interpretation. For geometric data, however, a specified mean of a geometric random variable is not equivalent to the mean of a COM-Poisson random variable with . That is, the additive random effect on the linear predictor relates directly to the mean in the geometric case, but relates to an indirect function of the mean in the COM-Poisson case, making the CMP-LN and CMP-C models misspecified with respect to the link to the linear predictor. Conversely, for the COM-Poisson simulated data, the Poi-LN and NB-LN models are misspecified with respect to the link to the linear predictor. This misspecification affects interpretation of and . Second, the random effect distribution is misspecified for the CMP-C model in Scenario I, and for all models in Scenario II except for the CMP-C model fit to the Poisson simulated data.
4.1. Simulated Data Scenario I: Normal-Distributed Random Effects
Table 1 presents results from fitting the four models on Scenario I simulated data. We find that one or both of the CMP models have better or comparable model fit for all simulated data settings except for the geometric special case. For the Poisson special case, the Poi-LN and CMP-LN models achieve the smallest AIC for 96% of the 50 simulated datasets. The CMP-LN model, however, yields the largest loglikelihood in 76% of the Poisson simulated datasets as compared to 0% for the Poi-LN model. For the Bernoulli special case, the L-LN, CMP-LN and CMP-C models achieve the smallest AIC for 100% of the 50 simulated datasets. The CMP-LN model, however, yields the largest loglikelihood in 55% of the Bernoulli simulated datasets as compared to 0% for the L-LN model. The dominant loglikelihood of the CMP-LN over the special case models is mitigated with respect to AIC because the CMP-LN model has an additional dispersion parameter. For the geometric simulated data, the NB-LN model outperforms both of the CMP models. We expect the NB-LN model counting to one success (i.e., a geometric-LN model) to perform similar to the CMP models because it is a special case. The simulation result, however, shows that the additional flexibility of the unrestricted NB-LN provides better fit for a majority of the extreme overdispersed simulated datasets. For both cases of the CMP simulated data, one or both of the CMP models greatly outperform the Poi-LN and NB-LN models.

Table 1.
Average of dispersion and variance estimates, and model fit measures for simulated data in Scenario I. Model fit measures: min AIC is the proportion of 50 replications where AIC ≤ min(AIC) + 2, and max is the proportion of 50 replications where is largest. Bold values indicate the model with the largest proportion of min AIC or max .
The CMP-LN model fits better or similarly to the CMP-C model in all cases. The CMP-LN greatly outperforms the CMP-C model in the equi-dispersion and intermediate over-dispersion cases; while the CMP-LN and CMP-C models result in similar model fit for the under-dispersed and extreme over-dispersed data even though the random effect distribution of the CMP-C model is misspecified in this Scenario I.
The CMP models recognize true dispersion levels in all cases: for Poisson, is large for Bernoulli, for geometric, for COM-Poisson (under-dispersion), and for COM-Poisson (over-dispersion). The dispersion parameter for the NB-LN model is appropriately for the equi- and underdispersed simulated data and for the extreme overdispersed data. For the case of intermediate over-dispersion, however, all of the overdispersion is attributed by NB-LN to the clustering rather than overdispersion in the underlying count process .
The estimated random effect variance indicates the magnitude of the cluster effect, on average, for each model that assumes lognormal-distributed random effects. Because the conjugate distribution does not have closed form moments, we plot in Figure 3 the estimated random effect distribution for each of the simulated datasets based on the CMP-C model parameter estimates. For comparison we also include the density associated with the CMP-LN model and the true distribution. The plot legend includes the mean and standard deviation for the estimated distribution. These quantities are calculated by theoretical moments and moment definitions for the lognormal and conjugate density, respectively. An appropriate level of cluster variability is captured by all models for equi-dispersed data: and see Figure 3a. For the under-dispersed simulated data, however, the Poi-LN and NB-LN are inadequate for jointly capturing cluster variability when the data have underlying underdispersion: for Bernoulli and CMP with intermediate under-dispersion simulated data. For the overdispersed simulated data, the cluster variability is slightly over-estimated with the Poi-LN and NB-LN models, however, in the intermediate overdispersed CMP simulated data, this is likely due to misspecification in the linear predictor. For all simulated data, except for the geometric special case, Figure 3 depicts cluster variability close to the true magnitude for the CMP-LN and CMP-C models. In the geometric special case, the estimated random effect distributions are observed close to the true distribution when the true distribution is adjusted to reflect the differences in the link between the mean and the linear predictor.
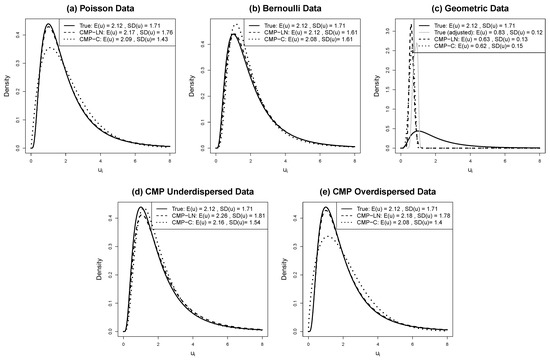
Figure 3.
Lognormal and conjugate densities evaluated at estimated in CMP-LN and CMP-C models for Scenario I simulated data. Mean and standard deviation for estimated density are calculated from moment expressions for lognormal distribution and empirically from moment definitions for conjugate distribution.
4.2. Simulated Data Scenario II: Gamma-Distributed Random Effects
Table 2 presents results from fitting the four models on Scenario II simulated data. Similar to the Scenario I findings, we find that one or both of the CMP models have better or comparable model fit for all simulated data settings except for the geometric special case. Interestingly, we find in this Scenario II that the CMP-C greatly outperforms even the Poi-LN model for the Poisson simulated data, indicating sensitivity of the Poi-LN model to random effect misspecification. Contrary to Scenario I findings, we find that the CMP-C model fits better or similarly to the CMP-LN model in all cases. The CMP-C greatly outperforms the CMP-LN model for the equi- and overdispersed data; while the CMP-LN and CMP-C models result in similar model fit for the underdispersed data.

Table 2.
Average of dispersion and variance estimates, and model fit measures for simulated data in Scenario II. Model fit measures: min AIC is proportion of 50 replications where AIC ≤ min(AIC) + 2, and max is proportion of 50 replications where is largest. Bold values indicate model with largest proportion of min AIC or max .
Similar to Scenario I, the CMP models recognize true dispersion levels in all cases. The NB-LN jointly captures the two sources of overdispersion for the extreme overdispersion case (i.e., geometric), but not the intermediate over-dispersed CMP case. Both the Poi-LN and NB-LN models over-estimate clustering variability for equi- and overdispersed data, while they cannot capture any clustering variability when the data have underlying underdispersion. Figure 4 depicts cluster variability for the CMP-LN and CMP-C models. Just as in Scenario I, the estimated random effect distributions are observed close to the true distribution except for the geometric special case on the original log link scale. Figure 4 shows that the estimated densities from Scenario II are further from the true distribution than in Scenario I, likely because all models (except CMP-C for the Poisson case) are misspecified with respect to the random effect distribution.
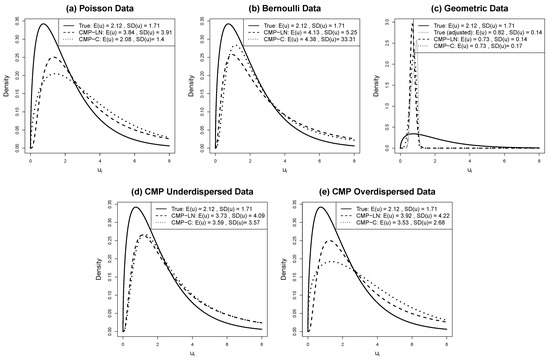
Figure 4.
Lognormal and conjugate densities evaluated at estimated in CMP-LN and CMP-C models for Scenario II simulated data. Mean and standard deviation for estimated density are calculated from moment expressions for the lognormal distribution and empirically from moment definitions for conjugate distribution.
5. Analysis: Epilepsy Data
To illustrate the practical flexibility of the COM-Poisson mixed models, we study the epilepsy dataset originally analyzed by Thall and Vail [39], subsequently discussed in Diggle et al. [40], and generally often used as an example for longitudinal data analysis of discrete outcomes (e.g., [6,10,11]). This dataset concerns the number of seizures measured for 59 epileptic patients in an initial 8-week baseline period, followed by 4 consecutive 2-week treatment periods. The outcome variable of interest is the number of seizures for subject i in time period j for . We assume the following form of the linear predictor:
where is the length of time period j in weeks, indicates the receipt of an anti-epileptic drug Progabide as opposed to a placebo, is an indicator of a period after baseline (weeks 8–16), and is the random intercept. This differs from the specification in Diggle et al. [40] in that we include as a covariate rather than an offset. This specification change is because an offset in a linear predictor linked indirectly to the mean (e.g., for the COM-Poisson regression model) can no longer be interpreted as a rate as in Poisson and negative binomial regression. Furthermore, all are the same value except for the baseline measurement making it colinear with , so we exclude as a main effect.
Table 3 presents the parameter estimates for the Poi-LN, NB-LN, CMP-LN and CMP-C models. All four of the models indicate a cluster/longitudinal effect. This is evident through the variance parameter estimate of the normal random effect distribution in the Poi-LN, NB-LN and CMP-LN, where , respectively. Recall from discussion of the analysis of simulated data, that the random effect variance estimated in the CMP-LN is not comparable to the Poi-LN and NB-LN models because the random effect is linked indirectly to the mean. For the CMP-C model, the empirical mean and variance associated with the conditional conjugate distribution at the estimated parameter values are and , respectively. Likelihood ratio tests for all models indicate that the longitudinal effect is statistically significant, recognizing that the test is conservative due to testing on the boundary of the parameter space [41]. Figure 5 shows that the lognormal and conjugate random effects distribution at the estimated parameter values are similar, with both indicating a nonzero variance.

Table 3.
Epilepsy data parameter estimates (standard errors), AIC, loglikelihood, and Pearson statistic . Expected counts use empirical Bayes estimates for random intercept in all models, and mean approximation in Equation (3) for CMP models. AIC and are displayed for models fit with and without Subject 207. Likelihood ratio test p-values for hypothesis testing of , and are displayed in brackets next to associated estimate.
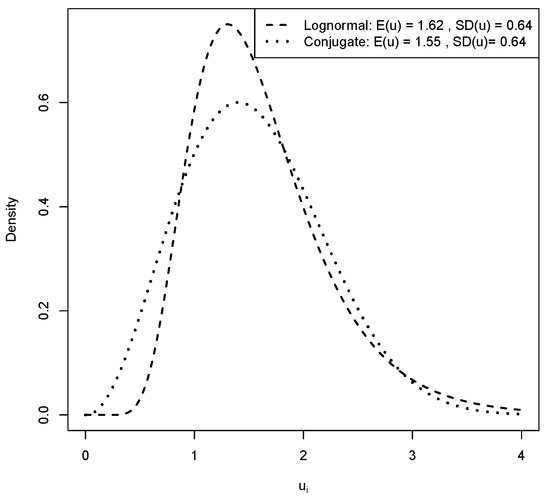
Figure 5.
Lognormal and conjugate densities evaluated at from epilepsy data.
The NB-LN and both CMP models can account for variability beyond the longitudinal effect. We find that overdispersion is evident in the negative binomial model () and both of the COM-Poisson models (). These effects are statistically significant based on the likelihood ratio test comparing NB-LN, CMP-LN and CMP-C to the Poi-LN model: see Table 3. These findings of longitudinal effects and over-dispersion are consistent with previous analyses of this dataset, but further illustrate the utility of a more flexible mixed model for clustered count data.
The two COM-Poisson models offer better model fit over the negative binomial model, with the CMP-LN model outperforming the CMP-C model according to AIC. Model fit based on the Pearson statistic of squared Pearson residuals show that the Poi-LN model outperforms the NB-LN and both CMP models: see Table 3. Consistent with the outlier analysis in Diggle et al. [40], we find that the set of observations from Subject 207 contribute greatly to the magnitude of the overall Pearson statistic, particularly for the CMP models. The analysis excluding this set of observations shows a smaller Pearson statistic—substantially smaller for the CMP models—and a smaller AIC for all models except CMP-LN. We find that excluding the observations for results in the NB-LN model outperforming the CMP models according to both AIC and the Pearson statistic. This suggests an interesting interpretation and influence of outliers defined with respect to the simpler Poi-LN model. The main advantage of the NB-LN and CMP models is how they account for dispersion in the underlying count process that is inconsistent with the assumption of the Poi-LN model. The estimation of a dispersion parameter incorporates information about all observations, even those deemed outliers via the Poi-LN model. In this sense, an outlier with respect to the Poi-LN model is likely to influence the model fit and the expected counts in the NB-LN and CMP models by design. In this data example, the effect of the influential observations is more pronounced in the Pearson statistic for the CMP models than for the NB-LN model, but less pronounced in the AIC. This highlights the importance of data quality and exploratory investigation into unusual data points. If unusual data points are deemed accurate, then the NB-LN and CMP models can naturally incorporate their influence through the flexibility of a dispersion parameter. In contrast, if the unusual data points are deemed inaccurate, then they may inappropriately influence the model fitting in the NB-LN and CMP models.
6. Conclusions and Discussion
The COM-Poisson mixed model is a flexible model for count data in light of data dispersion due to clustering and the underlying count process. Analysis of a variety of simulated clustered count datasets with varying degrees of underlying dispersion illustrates the flexibility of the COM-Poisson mixed model to provide a good model fit for special cases of well-known count distributions, as well as cases with intermediate levels of over- or underdispersion. In addition to the flexibility that the COM-Poisson data distribution allows, we illustrate further flexibility through the choice of normal- and conjugate-distributed random effects. Even though conjugacy does not allow generally for computational simplification, we find that it can be useful to assume the nonstandard random effects distribution to achieve better fit and to assess robustness of fixed parameter estimates. In the analysis of the classic epilepsy data, we find that the COM-Poisson mixed models indicate multiple sources of dispersion due the longitudinal nature and the underlying overdispersion in seizure counts. In this example of overdispersed data, the negative binomial mixed model provides similar insight, however the COM-Poisson mixed models would provide unique insight in the case of underdispersed data. The ability of the COM-Poisson mixed models to jointly capture clustering and underlying data under- or over dispersion makes them a practical diagnostic tool. Through comparison to simpler (nested) models, e.g., via likelihood ratio tests, COM-Poisson mixed models allow one to assess if accounting for data dispersion and/or clustering is necessary.
These models could be extended in a straightforward way to allow to vary with covariates; for simplicity we have considered only a constant . Allowing fixed effects for dispersion parameter modeling is conceptually simple, but potentially leads to identifiability complications because assuming a “common dispersion parameter across the entire data” allows estimable dispersion effects separate from clustering effects [28]. In some data scenarios, it may make sense to consider to also be a function of its own random effects. This introduces additional computational complexity due to multiple integrals in the marginal loglikelihood, and in the case of assuming the COM-Poisson conjugate distribution, the violation of strong conjugacy with respect to remains. Incorporating random slopes in the and/or formulation is similarly conceptually straightforward, but adds computational complexity.
Computational challenges and efficiency issues are not unfamiliar in the formulation and fitting of random effects models for discrete outcomes. The random intercept CMP-LN and CMP-C model fit to the 295 observations in the epilepsy dataset required only 2–3 min of computation time. As the number of clusters/observations per cluster/fixed effects/random effects increase, the estimation procedure may become computationally prohibitive. For the simulation and data analysis in this paper, general purpose numerical integration and optimization procedures sufficed. Computational efficiency may be improved by tailoring the numerical integration and optimization procedures to the specific nuances of the CMP-LN and CMP-C model functional form.
Author Contributions
Conceptualization, D.S.M. and K.F.S.; methodology, D.S.M. and K.F.S.; software, D.S.M.; analysis, D.S.M. and K.F.S.; writing, D.S.M.; editing, D.S.M. and K.F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The epilepsy dataset used in Section 5 is freely available as the object epil in the MASS package in R; see https://stat.ethz.ch/R-manual/R-devel/library/MASS/html/epil.html for details. Last accessed on 5 January 2022.
Acknowledgments
The authors would like to thank Andrew Raim, Austin Menger, and Yves Thibaudeau for comments and discussion. This paper is intended to inform interested parties of research and to encourage discussion. Any views expressed on statistical, methodological, or technical issues are those of the authors and not necessarily those of the U.S. Census Bureau.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| COM-Poisson | Conway-Maxwell-Poisson |
| CMP | Conway-Maxwell-Poisson |
| CMP-LN | COM-Poisson-lognormal |
| CMP-C | COM-Poisson-conjugate |
| Poi-LN | Poisson-lognormal |
| NB-LN | negative binomial-lognormal |
| L-LN | logistic-lognormal |
| AIC | Akaike information criterion |
References
- Hilbe, J.M. Negative Binomial Regression; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Aerts, M.; Geys, H.; Molenberghs, G.; Ryan, L.M. Topics in Modelling of Clustered Data; Monographs on Statistics and Applied Probability; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Cameron, A.C.; Trivedi, P.K. Regression Analysis of Count Data; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Winkelmann, R. Econometric Analysis of Count Data; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Agresti, A. Categorical Data Analysis, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Breslow, N. Extra-Poisson variation in log-linear models. Appl. Stat. Sci. 1984, 33, 38–44. [Google Scholar] [CrossRef]
- Hinde, J. Compound Poisson regression models. In GLIM 82: Proceedings of the International Conference on Generalised Linear Models; Gilchrist, R., Ed.; Springer: New York, NY, USA, 1982; pp. 109–121. [Google Scholar]
- Hausman, J.; Hall, B.H.; Griliches, Z. Econometric Models for Count data with an application to the patents-R&D relationship. Econometrica 1984, 52, 909–938. [Google Scholar]
- Greene, W.H. Fixed and Random Effects Models for Count Data. SSRN eLibrary. 2007. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=990012 (accessed on 5 January 2022).
- Booth, J.; Casella, G.; Friedl, H.; Hobart, J. Negative binomial loglinear mixed models. Stat. Model. 2003, 3, 179–191. [Google Scholar] [CrossRef]
- Molenberghs, G.; Verbeke, G.; Demétrio, C.G.B. An extended random-effects approach to modeling repeated, overdispersed count data. Lifetime Data Anal. 2007, 13, 513–531. [Google Scholar] [CrossRef]
- Molenberghs, G.; Verbeke, G.; Demétrio, C.G.B.; Afranio, M.C. A family of generalized linear models for repeated measures with normal and conjugate random effects. Stat. Sci. 2010, 25, 325–347. [Google Scholar] [CrossRef]
- Rizzato, F.B.; Leandro, R.A.; Demertrio, C.G.; Molenberghs, G. A Bayesian approach to analyse overdispersed longitudinal data. J. Appl. Stat. 2016, 43, 2085–2109. [Google Scholar] [CrossRef]
- Lord, D.; Guikema, S.D.; Geedipally, S.R. Application of the Conway-Maxwell-Poisson Generalized Linear Model for Analyzing Motor Vehicle Crashes. Accid. Anal. Prev. 2008, 40, 1123–1134. [Google Scholar] [CrossRef]
- Shmueli, G.; Minka, T.P.; Kadane, J.B.; Borle, S.; Boatwright, P. A useful distribution for fitting discrete data: Revival of the Conway-Maxwell-Poisson distribution. Appl. Stat. 2005, 54, 127–142. [Google Scholar] [CrossRef]
- Lord, D.; Guikema, S.D.; Geedipally, S.R. Extension of the application of Conway-Maxwell-Poisson models: Analyzing traffic crash data exhibiting underdispersion. Risk Anal. 2010, 30, 1268–1276. [Google Scholar] [CrossRef] [Green Version]
- Sellers, K.F.; Morris, D.S. Underdispersion models: Models that are “under the radar”. Commun. Stat.-Theory Methods 2017, 46, 12075–12086. [Google Scholar] [CrossRef]
- Sellers, K.F.; Shmueli, G. A Flexible Regression Model for Count Data. Ann. Appl. Stat. 2010, 4, 943–961. [Google Scholar] [CrossRef] [Green Version]
- Chatla, S.B.; Shmueli, G. Efficient estimation of COM-Poisson regression and a generalized additive model. Comput. Stat. Data Anal. 2018, 121, 71–88. [Google Scholar] [CrossRef]
- Huang, A. Mean-parameterized Conway-Maxwell-Poisson Regression Models for Dispersed Counts. Stat. Model. 2017, 17, 359–380. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, E.E., Jr.; Zeviani, W.M.; Bonat, W.H.; Demétrio, C.G.B.; Hinde, J. Reparameterization of COM-Poisson Regression Models with Applications in the Analysis of Experimental Data. Stat. Model. 2020, 20, 443–466. [Google Scholar] [CrossRef]
- Guikema, S.D.; Coffelt, J.P. A Flexible Count Data Regression Model for Risk Analysis. Risk Anal. 2008, 28, 213–223. [Google Scholar] [CrossRef]
- Huang, A.; Kim, A.S.I. Bayesian Conway-Maxwell-Poisson regression models for ovedispersed and underdispersed counts. Commun. Stat.-Theory Methods 2021, 50, 3094–3105. [Google Scholar] [CrossRef] [Green Version]
- Khan, N.M.; Jowaheer, V. Comparing joint GQL estimation and GMM adaptive estimation in COM-Poisson longitudinal regression model. Commun. Stat.-Simulations Comput. 2013, 42, 755–770. [Google Scholar] [CrossRef]
- Choo-Wosoba, H.; Levy, S.M.; Datta, S. Marginal regression models for clustered count data based on zero-inflated Conway-Maxwell-Poisson distribution with applications. Biometrics 2016, 72, 606–618. [Google Scholar] [CrossRef] [Green Version]
- Morris, D.S.; Sellers, K.F.; Menger, A. Fitting a Flexible Model for Longitudinal Count Data Using the NLMIXED Procedure. In SAS Global Forum Proceedings; SAS Institute: Cary, NC, USA, 2017. [Google Scholar]
- Morris, D.S.; Sellers, K.F. A COM-Poisson Mixed Model with Normal Random Effects for Clustered Count Data. In Proceedings of the 61st World Statistics Congress of the International Statistical Institute, Marrakech, Morocco, 16–21 July 2017; ISI: The Hague, The Netherlands, 2017. [Google Scholar]
- Choo-Wosoba, H.; Datta, S. Analyzing clustered count data with a cluster-specific random effect zero-inflated Conway-Maxwell-Poisson distribution. J. Appl. Stat. 2018, 45, 799–814. [Google Scholar] [CrossRef]
- Choo-Wosoba, H.; Gaskins, J.; Levy, S.M.; Datta, S. A Bayesian approach for analyzing zero-inflated clustered count data with dispersion. Stat. Med. 2018, 37, 801–812. [Google Scholar] [CrossRef]
- Kadane, J.B.; Shmueli, G.; Minka, T.P.; Borle, S.; Boatwright, P. Conjugate Analysis of the Conway-Maxwell-Poisson Distribution. Bayesian Anal. 2018, 1, 363–374, Erratum in Bayesian Anal. 2018, 13, 1005. [Google Scholar]
- Conway, R.W.; Maxwell, W.L. A queuing model with state dependent service rates. J. Ind. Eng. 1962, 12, 132–136. [Google Scholar]
- Sellers, K.F.; Borle, S.; Shmueli, G. The COM-Poisson model for count data: A survey of methods and applications. Appl. Stoch. Model. Bus. Ind. 2012, 28, 104–116. [Google Scholar] [CrossRef]
- Piessens, R.; de Doncker Kapenga, E.; Uberhuber, C.; Kahaner, D. Quadpack: A Subroutine Package for Automatic Integration; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Eddelbuettel, D.; François, R. Rcpp: Seamless R and C++ Integration. J. Stat. Softw. 2011, 40, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Morris, D.S. COM-Poisson Conditional Conjugate. Available online: https://dsteeg.shinyapps.io/CMPMMshinyapp (accessed on 5 January 2022).
- Sellers, K.F.; Lotze, T.; Raim, A. COMPoissonReg: Conway-Maxwell-Poisson Regression. Version 0.4.1. 2017. Available online: https://cran.r-project.org/web/packages/COMPoissonReg/index.html (accessed on 5 January 2022).
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodal Inference; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Thall, P.F.; Vail, S.C. Some covariance models for longitudinal count data with overdispersion. Biometrics 1990, 46, 657–671. [Google Scholar] [CrossRef] [Green Version]
- Diggle, P.; Heagerty, P.J.; Liang, K.Y.; Zeger, S.L. Analysis of Longitudinal Data; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Self, S.G.; Liang, K.Y. Asymptotic Properties of Maximum Likelihood Estimators and Likelihood Ratio Tests under Nonstandard Conditions. J. Am. Stat. Assoc. 1987, 82, 605–610. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).