Optimal Neighborhood Selection for AR-ARCH Random Fields with Application to Mortality
Abstract
:1. Introduction
2. Random Fields Memory Models for Mortality Improvement Rates
2.1. Classic Mortality Models
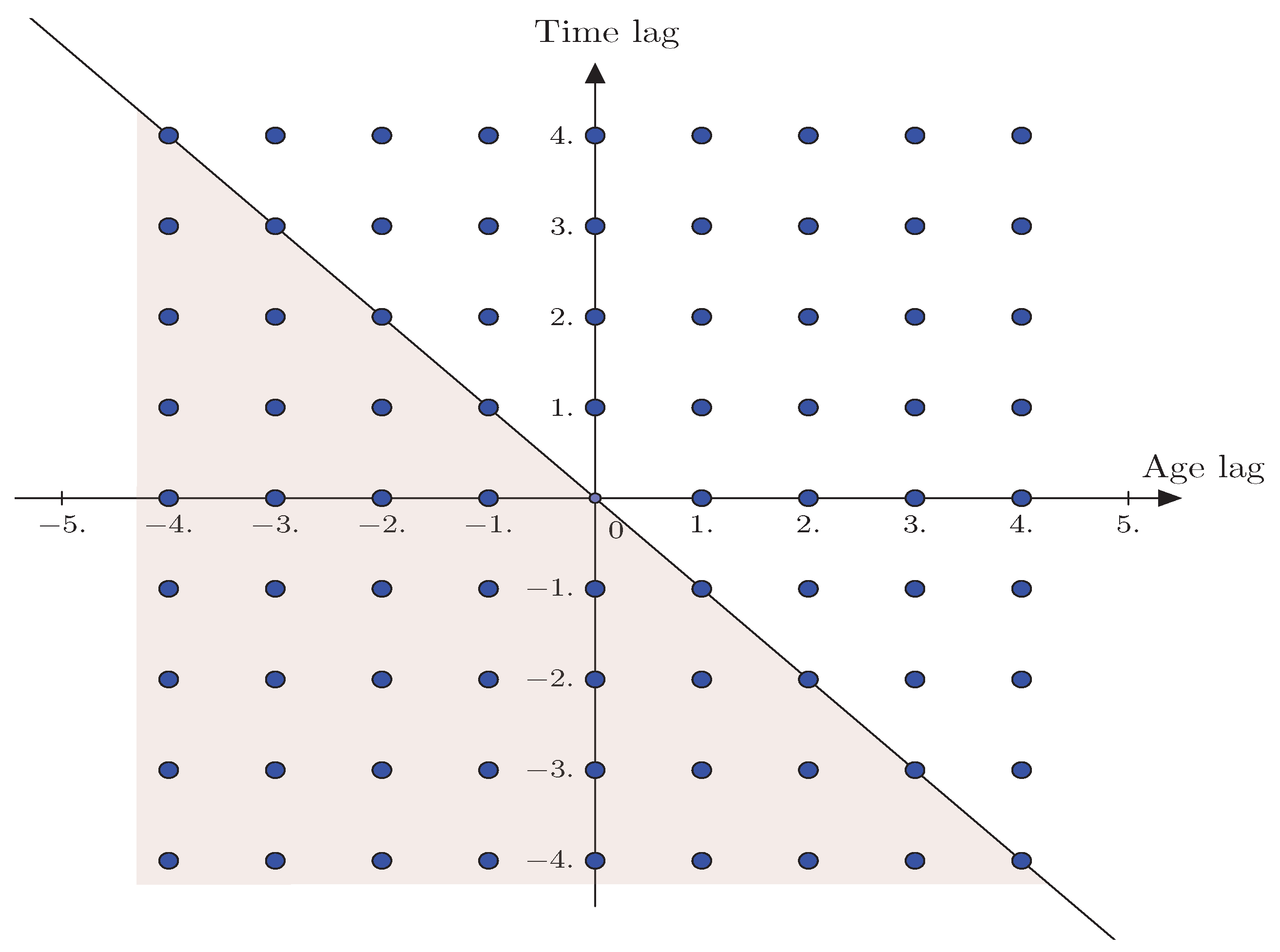
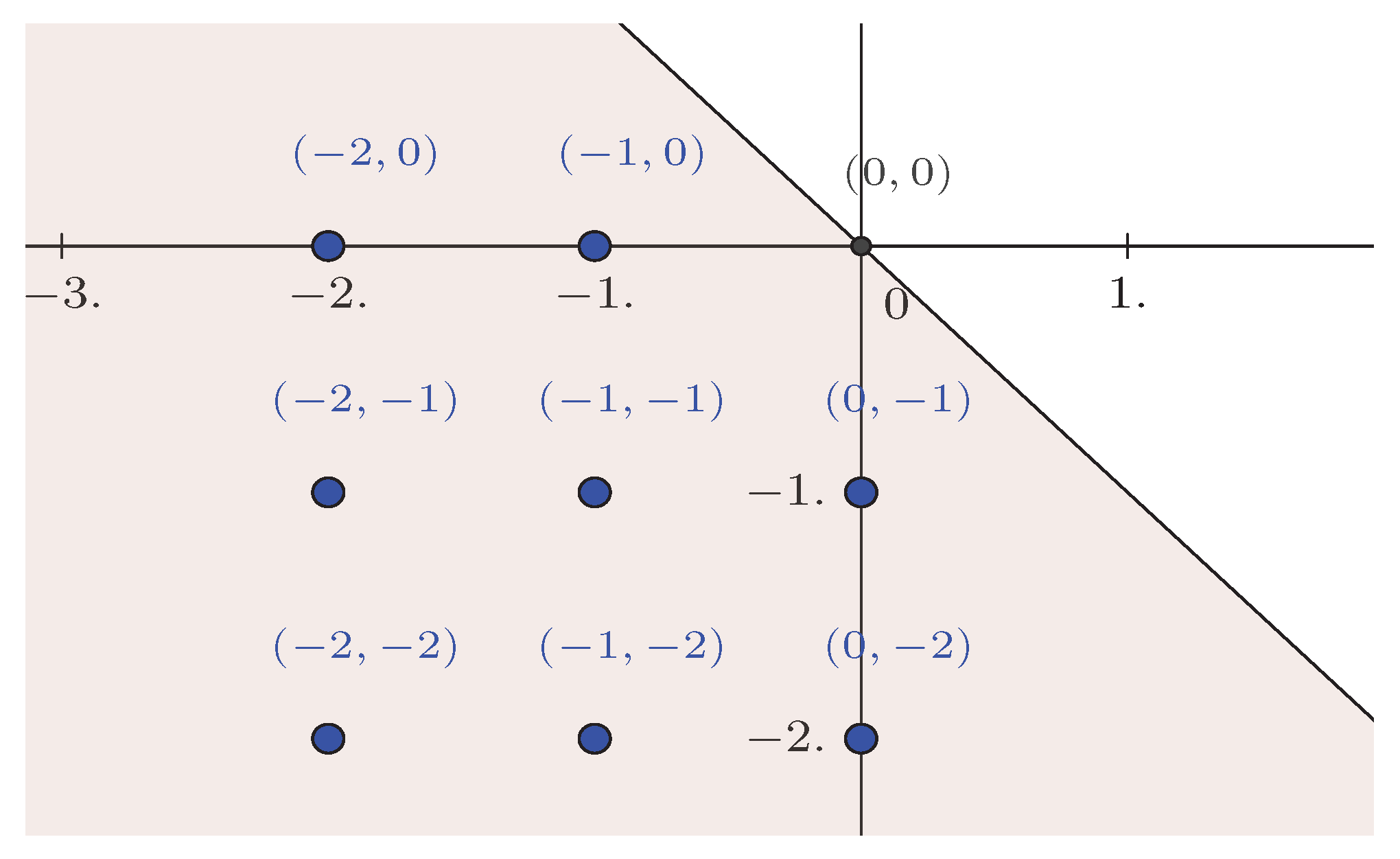
2.2. Through a Random Field Framework
- (i)
- Mortality Surface
- (ii)
- Random Field Memory Models
- A-1
- for some ,
- A-2
- for all , where the coefficients are such that .
2.3. AR-ARCH-Type Random Fields
3. Estimation, Asymptotic Inference, and Model Selection
3.1. Quasi-Maximum Likelihood Estimator (QMLE)
- (i)
- Consistency. If the assumptions H1, H2, and H3 hold, then the QMLE estimator in Equation (11) is consistent in the sense that for each , and , we have
- (ii)
- Asymptotic normality. Under assumptions H1, H2, H3, and H4,
3.2. Optimal Model Selection
- (i)
- Likelihood ratio test statistic (LRTS)
- (ii)
- Penalized QMLE
- I-1
- , (maximal possible neighborhoods) are a finite set and , .
- I-2
- is increasing, goes to infinity as T tends to go to infinity as soon as , and tends to 0 as T tends to go to infinity for any .
- (iii)
- Bayesian Information Criterion
- (iv)
- Search Algorithm
- (v)
- Spatial Autocorrelation Function
4. Numerical and Empirical Analyses
4.1. Simulation Study
4.2. Real-World Data Application
- (i)
- Model Selection
- (ii)
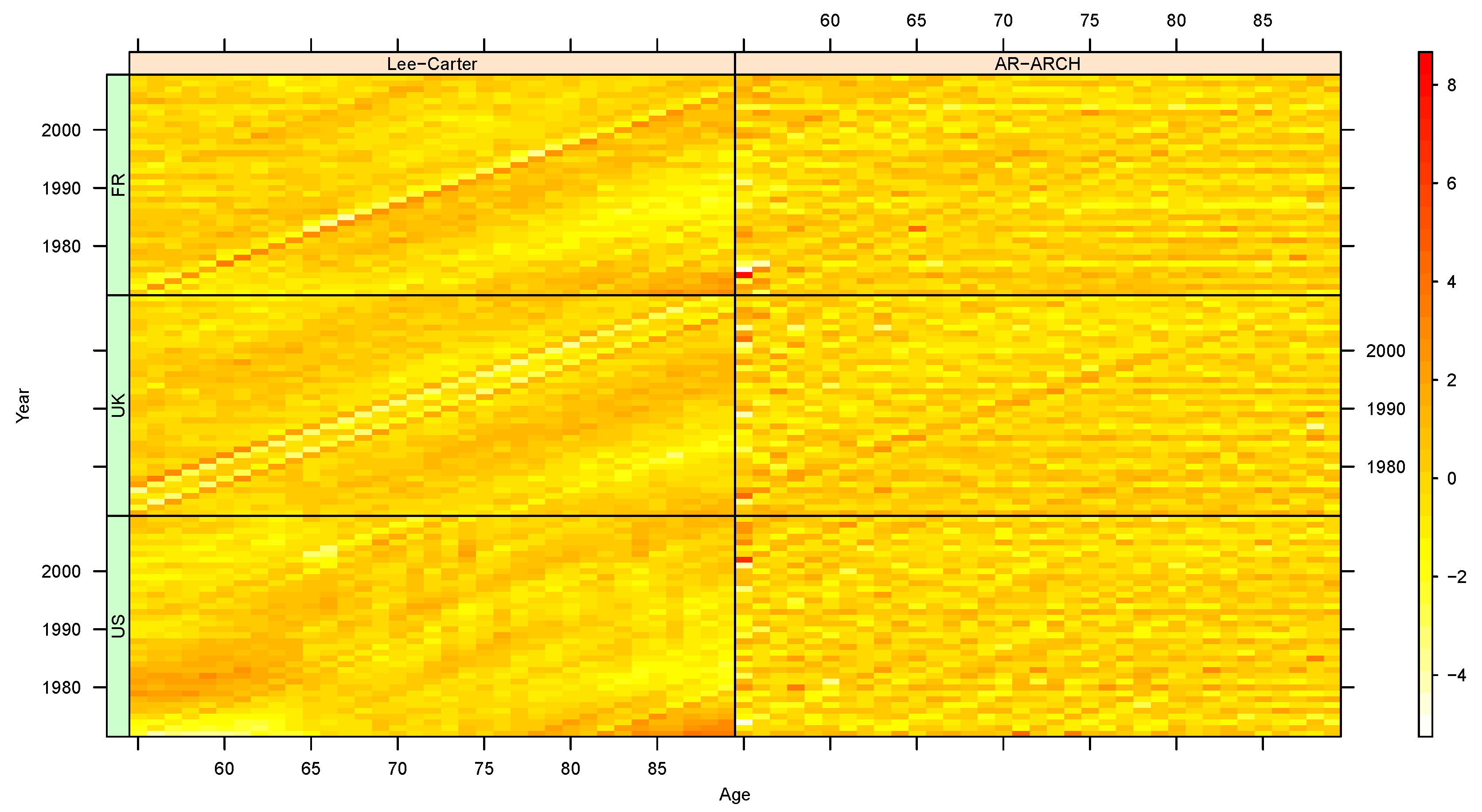
- Diagnostic Checks
- (iii)
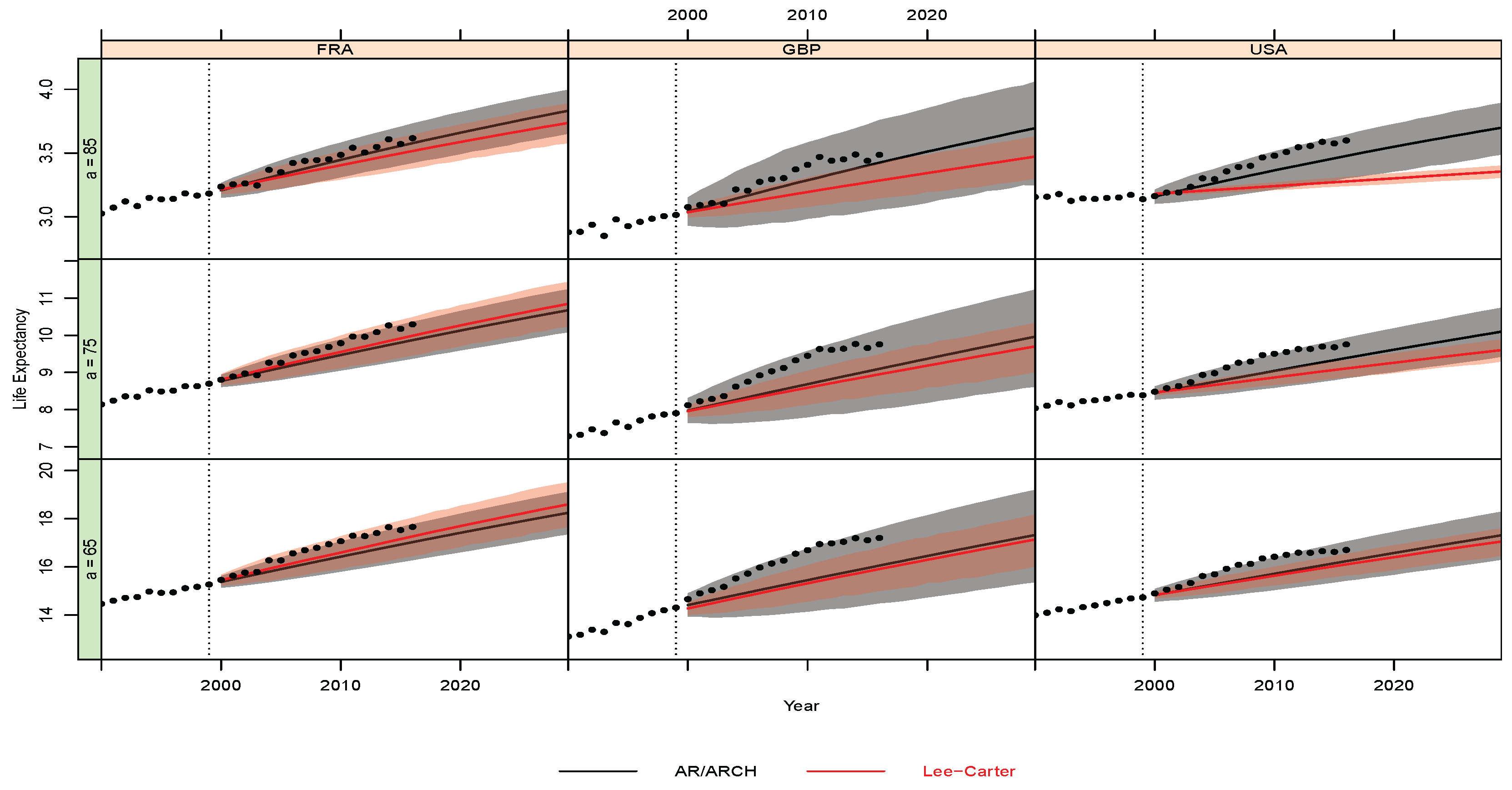
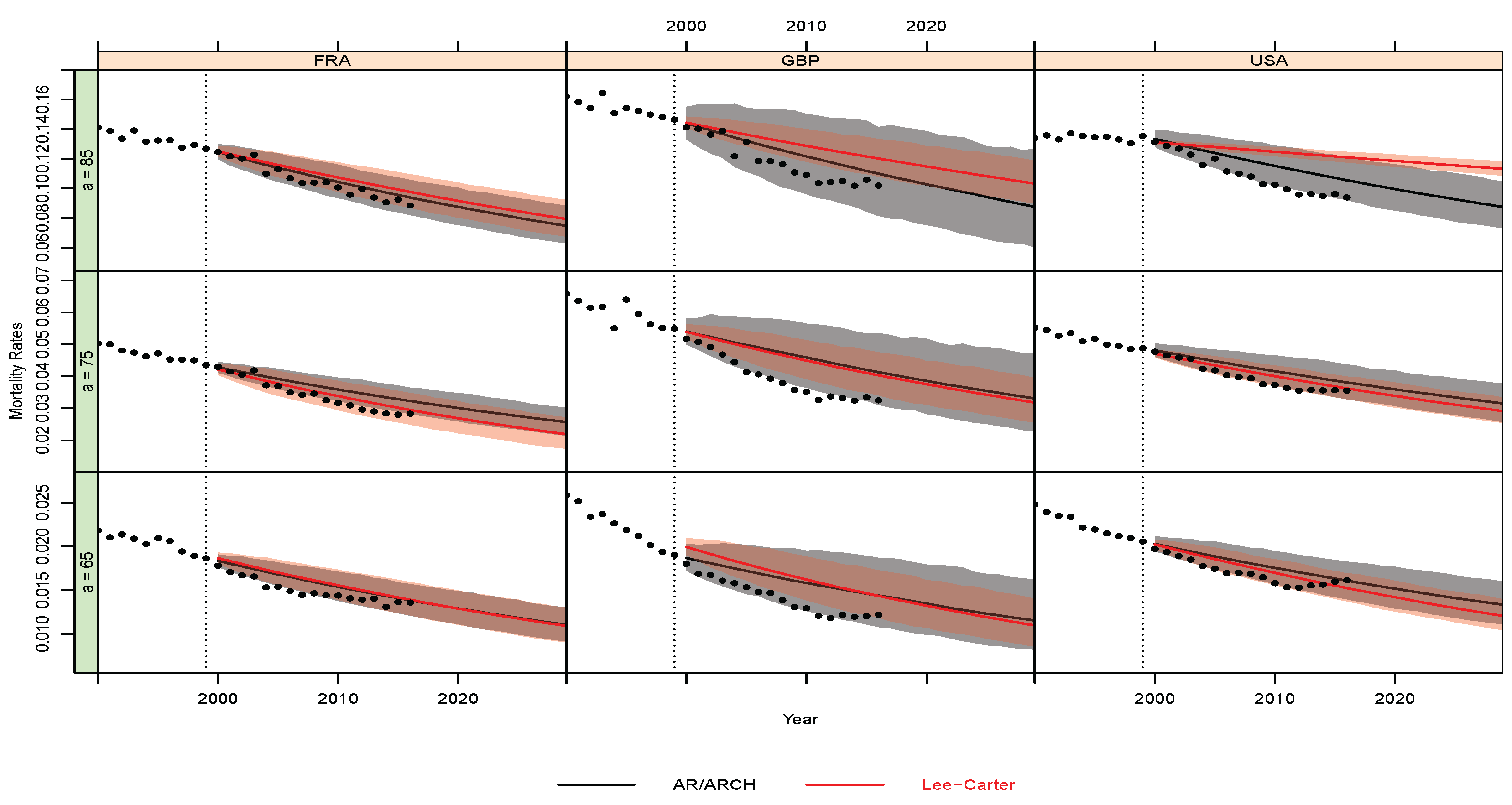
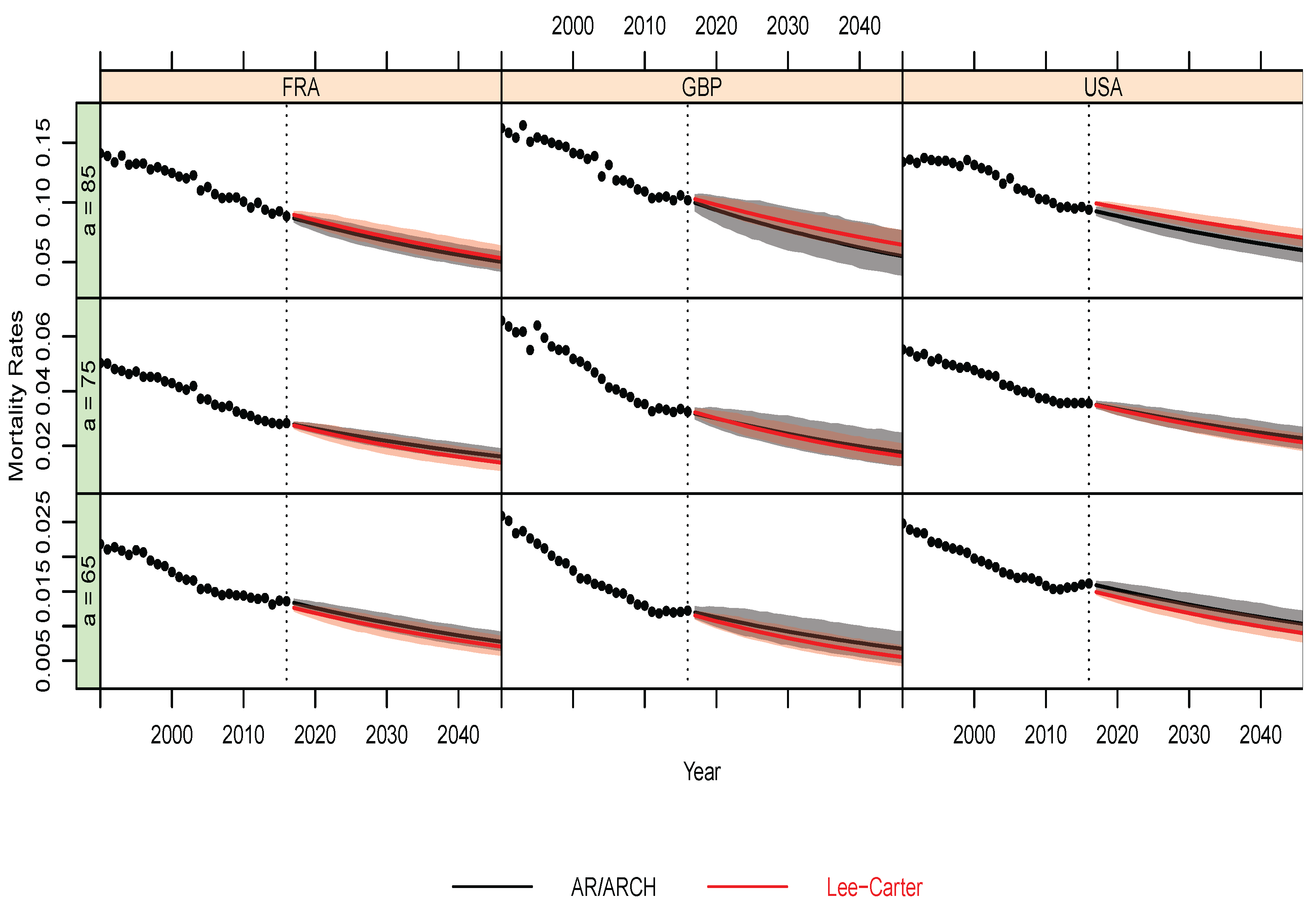
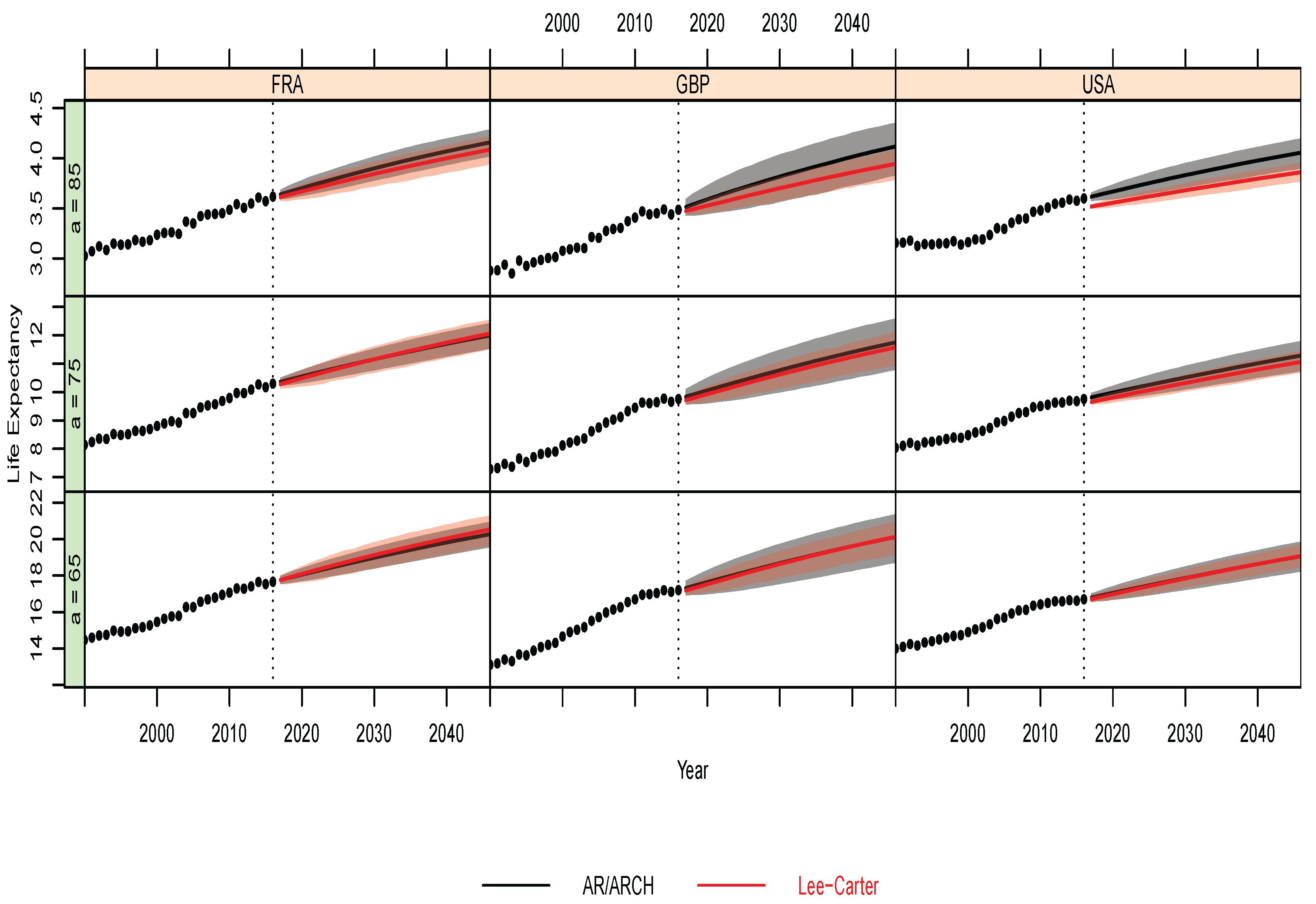
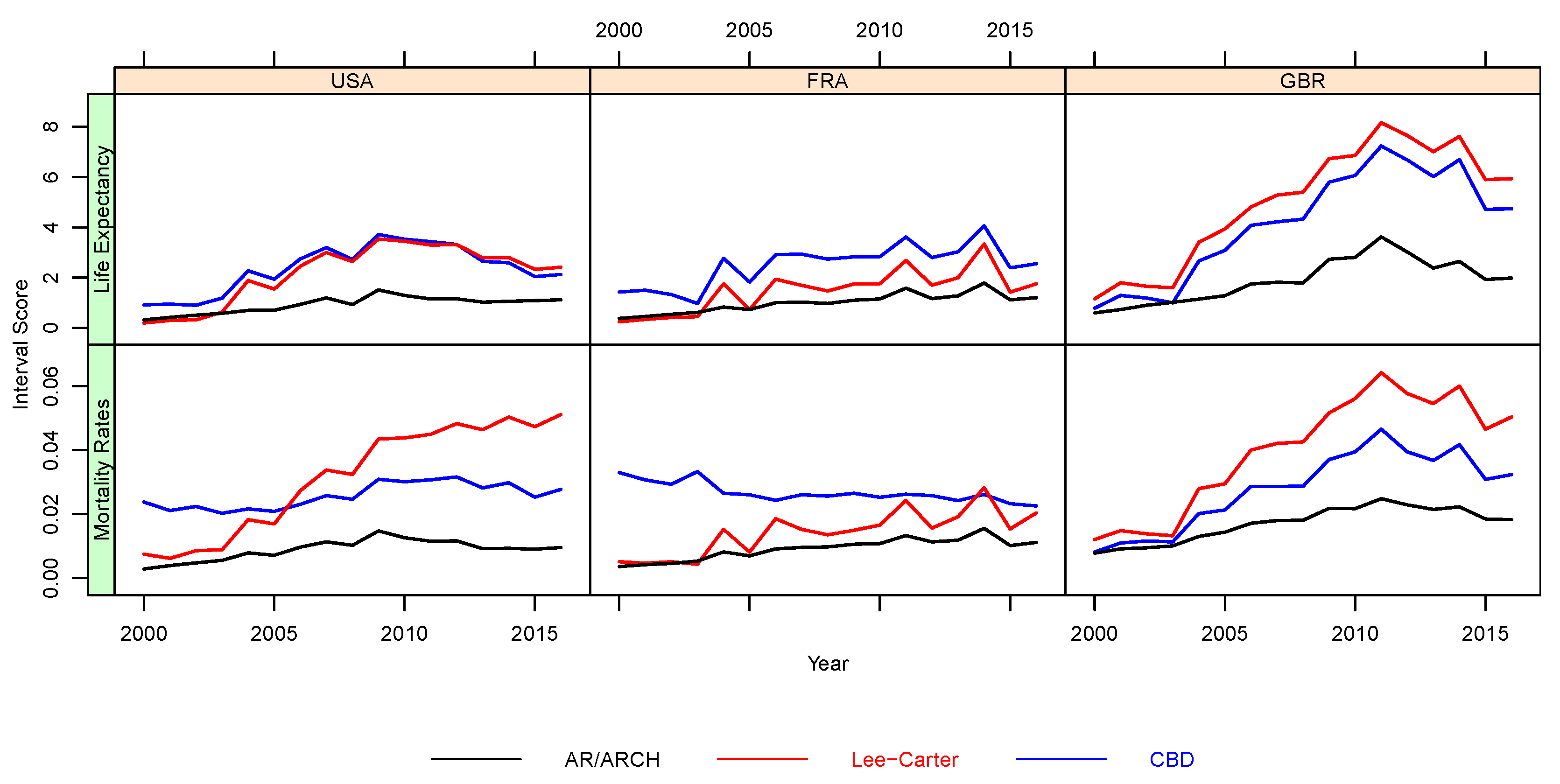
- Predictive Performance
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Appendix The Gradient and the Hessian of the Quasi-Likelihood Function
Appendix B. Additional Figures
Appendix B.1. Diagnostic Checks of Models’ Residuals
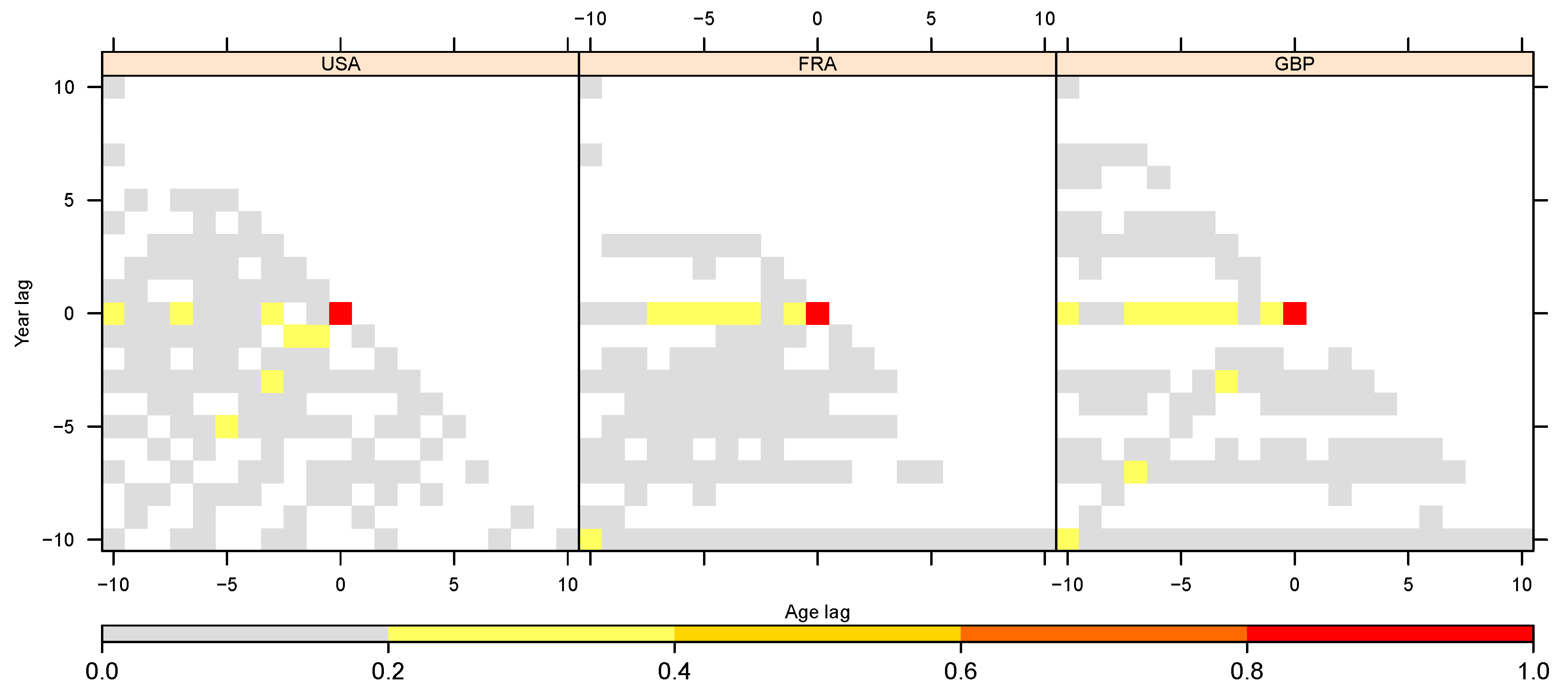
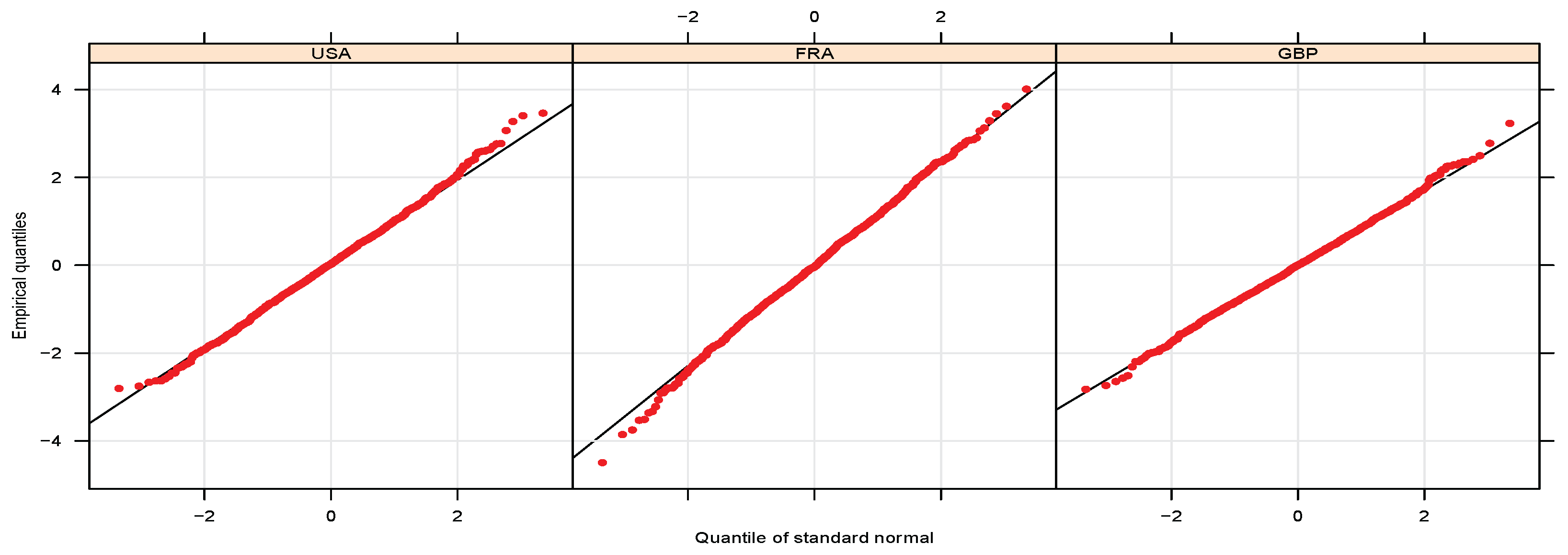

Appendix B.2. Out-of-Sample Analysis and Predictive Performance
References
- Barrieu, P.; Bensusan, H.; El Karoui, N.; Hillairet, C.; Loisel, S.; Ravanelli, C.; Salhi, Y. Understanding, modelling and managing longevity risk: Key issues and main challenges. Scand. Actuar. J. 2012, 2012, 203–231. [Google Scholar] [CrossRef] [Green Version]
- Lee, R.D.; Carter, L.R. Modeling and forecasting US mortality. J. Am. Stat. Assoc. 1992, 87, 659–671. [Google Scholar]
- Hunt, A.; Villegas, A.M. Robustness and convergence in the Lee–Carter model with cohort effects. Insur. Math. Econ. 2015, 64, 186–202. [Google Scholar] [CrossRef]
- Doukhan, P.; Pommeret, D.; Rynkiewicz, J.; Salhi, Y. A Class of Random Field Memory Models for Mortality Forecasting. Insur. Math. Econ. 2017, 77, 97–110. [Google Scholar] [CrossRef] [Green Version]
- Doukhan, P.; Truquet, L. A fixed point approach to model random fields. ALEA: Lat. Am. J. Probab. Math. Stat. 2007, 3, 111–132. [Google Scholar]
- Cairns, A.J.G.; Blake, D.; Dowd, K. A Two-Factor Model for Stochastic Mortality with Parameter Uncertainty: Theory and Calibration. J. Risk Insur. 2006, 73, 687–718. [Google Scholar] [CrossRef]
- Renshaw, A.E.; Haberman, S. A cohort-based extension to the Lee–Carter model for mortality reduction factors. Insur. Math. Econ. 2006, 38, 556–570. [Google Scholar] [CrossRef]
- Cairns, A.J.G.; Blake, D.; Dowd, K.; Coughlan, G.D.; Epstein, D.; Ong, A.; Balevich, I. A quantitative comparison of stochastic mortality models using data from England and Wales and the United States. N. Am. Actuar. J. 2009, 13, 1–35. [Google Scholar] [CrossRef]
- Dowd, K.; Cairns, A.J.G.; Blake, D.; Coughlan, G.D.; Epstein, D.; Khalaf-Allah, M. Evaluating the goodness of fit of stochastic mortality models. Insur. Math. Econ. 2010, 47, 255–265. [Google Scholar] [CrossRef]
- Mavros, G.; Cairns, A.J.G.; Kleinow, T.; Streftaris, G. Stochastic Mortality Modelling: Key Drivers and Dependent Residuals. N. Am. Actuar. J. 2016, 21, 343–368. [Google Scholar] [CrossRef]
- Giacometti, R.; Bertocchi, M.; Rachev, S.T.; Fabozzi, F.J. A comparison of the Lee–Carter model and AR–ARCH model for forecasting mortality rates. Insur. Math. Econ. 2012, 50, 85–93. [Google Scholar] [CrossRef]
- Chai, C.M.H.; Siu, T.K.; Zhou, X. A double-exponential GARCH model for stochastic mortality. Eur. Actuar. J. 2013, 3, 385–406. [Google Scholar] [CrossRef]
- Lee, R.; Miller, T. Evaluating the performance of the Lee-Carter method for forecasting mortality. Demography 2001, 38, 537–549. [Google Scholar] [CrossRef]
- Gao, Q.; Hu, C. Dynamic mortality factor model with conditional heteroskedasticity. Insur. Math. Econ. 2009, 45, 410–423. [Google Scholar] [CrossRef]
- Brouhns, N.; Denuit, M.; Vermunt, J.K. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insur. Math. Econ. 2002, 31, 373–393. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Pitt, D.; Li, H. Dispersion modelling of mortality for both sexes with Tweedie distributions. Scand. Actuar. J. 2021, 1–19. [Google Scholar] [CrossRef]
- Willets, R.C. The cohort effect: Insights and explanations. Br. Actuar. J. 2004, 10, 833–877. [Google Scholar] [CrossRef]
- Hitaj, A.; Mercuri, L.; Rroji, E. Lévy CARMA models for shocks in mortality. Decis. Econ. Financ. 2019, 42, 205–227. [Google Scholar] [CrossRef]
- Loisel, S.; Serant, D. In the Core of Longevity Risk: Hidden Dependence in Stochastic Mortality Models and Cut-Offs in Prices of Longevity Swaps. 2007. Available online: https://hal.archives-ouvertes.fr/hal-00201393/ (accessed on 18 December 2016).
- Jevtić, P.; Luciano, E.; Vigna, E. Mortality surface by means of continuous time cohort models. Insur. Math. Econ. 2013, 53, 122–133. [Google Scholar] [CrossRef]
- Lazar, D.; Denuit, M.M. A multivariate time series approach to projected life tables. Appl. Stoch. Model. Bus. Ind. 2009, 25, 806–823. [Google Scholar] [CrossRef]
- Li, H.; Lu, Y. Coherent Forecasting of Mortality Rates: A Sparse AutoRegression Approach. ASTIN Bull. 2017, 47, 1–24. [Google Scholar] [CrossRef]
- Gaille, S.; Sherris, M. Modelling mortality with common stochastic long-run trends. Geneva Pap. Risk Insur. Issues Pract. 2011, 36, 595–621. [Google Scholar] [CrossRef] [Green Version]
- Salhi, Y.; Loisel, S. Basis risk modelling: A co-integration based approach. Statistics 2017, 51, 205–221. [Google Scholar] [CrossRef] [Green Version]
- Millossovich, P.; Biffis, E. A bidimensional approach to mortality risk. Decis. Econ. Financ. 2006, 29, 71–94. [Google Scholar]
- Olivieri, A.; Pitacco, E. Life tables in actuarial models: From the deterministic setting to a Bayesian approach. Adv. Stat. Anal. 2012, 2012, 127–153. [Google Scholar] [CrossRef]
- Loubaton, P. Champs Stationnaires au Sens Large sur Z2: Propriétés Structurelles et Modèles Paramétriques; Ecole Nationale Supérieure des Télécommunications: Paris, France, 1989. [Google Scholar]
- Guyon, X. Random Fields on a Network: Modeling, Statistics, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Chen, H.; MacMinn, R.; Sun, T. Multi-population mortality models: A factor copula approach. Insur. Math. Econ. 2015, 63, 135–146. [Google Scholar] [CrossRef]
- Van der Vaart, A. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Vuong, Q.H. Likelihood ratio Tests for model selection and non-nested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar] [CrossRef] [Green Version]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Cairns, A.; Blake, D.; Dowd, K.; Kessler, A. Phantoms never die: Living with unreliable population data. J. R. Stat. Soc. Ser. A 2016, 179, 975–1005. [Google Scholar] [CrossRef] [Green Version]
- Lee, R. The Lee-Carter method for forecasting mortality, with various extensions and applications. N. Am. Actuar. J. 2000, 4, 80–91. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.H. The Locally Linear Cairns–Blake–Dowd Model: A Note On Delta–Nuga Hedging of Longevity Risk. ASTIN Bull. 2017, 47, 79–151. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Shang, H.L. Point and interval forecasts of age-specific life expectancies: A model averaging approach. Demogr. Res. 2012, 27, 593–644. [Google Scholar] [CrossRef] [Green Version]
- Doukhan, P. Mathematics and Applications; Stochastic Models for Time Series; Springer: Berlin/Heidelberg, Germany, 2018; Volume 80. [Google Scholar]
- Ferland, R.; Latour, A.; Oraichi, D. Integer-valued GARCH processes. J. Time Ser. Anal. 2006, 27, 923–942. [Google Scholar] [CrossRef]


| (1,1) | (2,2) | (0,1) | (1,0) | (1,1) | (2,2) | (0,1) | (1,0) | |||
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 64.8% | |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 11.1% | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 7.2% | |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 6.1% | |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 42.30% | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 12.00% | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 8.1% | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 8.1% | |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 6.4% | |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 5.4% | |
| SW | AD | CVM | PC | SF | |
|---|---|---|---|---|---|
| USA | 0.3428 | 0.7048 | 0.7991 | 0.8523 | 0.3947 |
| FRA | 0.6171 | 0.5212 | 0.5438 | 0.6279 | 0.4322 |
| GBP | 0.6114 | 0.7626 | 0.8548 | 0.9309 | 0.4827 |
| AR-ARCH | LC | CBD | |||
|---|---|---|---|---|---|
| USA | Mortality rate | RMSFE | 1.51 | 5.30 | 3.68 |
| MAFE | 2.47 | 3.99 | 4.14 | ||
| Life expectancy | RMSFE | 1.13 | 1.69 | 2.72 | |
| MAFE | 2.75 | 3.42 | 4.34 | ||
| FRA | Mortality rate | RMSFE | 1.07 | 2.30 | 5.04 |
| MAFE | 2.19 | 2.84 | 4.49 | ||
| Life expectancy | RMSFE | 1.66 | 2.11 | 4.01 | |
| MAFE | 3.28 | 3.79 | 5.24 | ||
| GBR | Mortality rate | RMSFE | 4.11 | 8.34 | 8.01 |
| MAFE | 4.36 | 5.83 | 5.72 | ||
| Life expectancy | RMSFE | 7.29 | 8.64 | 8.70 | |
| MAFE | 7.03 | 7.87 | 7.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doukhan, P.; Rynkiewicz, J.; Salhi, Y. Optimal Neighborhood Selection for AR-ARCH Random Fields with Application to Mortality. Stats 2022, 5, 26-51. https://doi.org/10.3390/stats5010003
Doukhan P, Rynkiewicz J, Salhi Y. Optimal Neighborhood Selection for AR-ARCH Random Fields with Application to Mortality. Stats. 2022; 5(1):26-51. https://doi.org/10.3390/stats5010003
Chicago/Turabian StyleDoukhan, Paul, Joseph Rynkiewicz, and Yahia Salhi. 2022. "Optimal Neighborhood Selection for AR-ARCH Random Fields with Application to Mortality" Stats 5, no. 1: 26-51. https://doi.org/10.3390/stats5010003
APA StyleDoukhan, P., Rynkiewicz, J., & Salhi, Y. (2022). Optimal Neighborhood Selection for AR-ARCH Random Fields with Application to Mortality. Stats, 5(1), 26-51. https://doi.org/10.3390/stats5010003






