Optimal Investment and Consumption for Multidimensional Spread Financial Markets with Logarithmic Utility
Abstract
1. Introduction
2. Market Model
3. Hamilton–Jacobi–Bellman Equation
4. Main Results
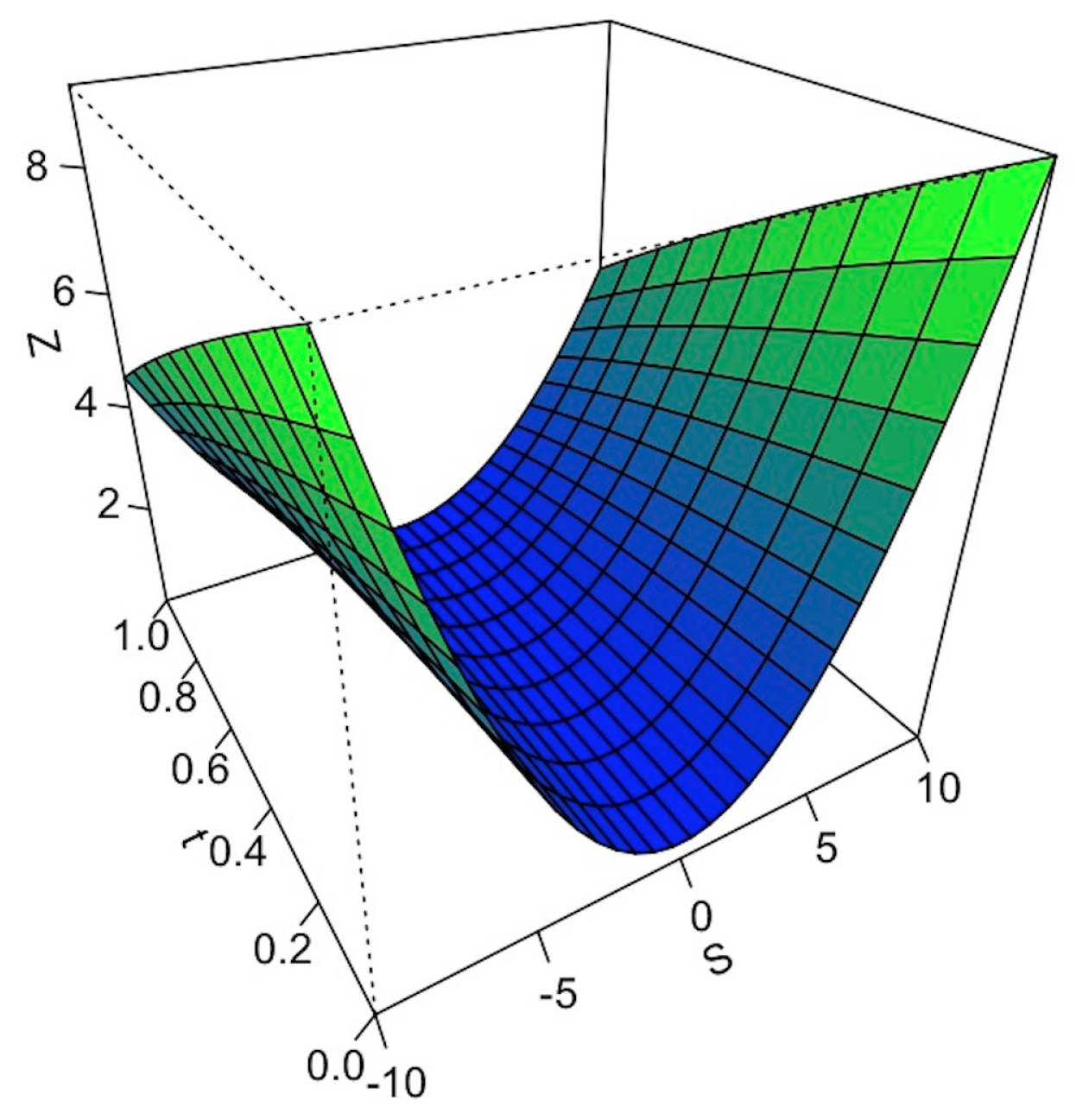
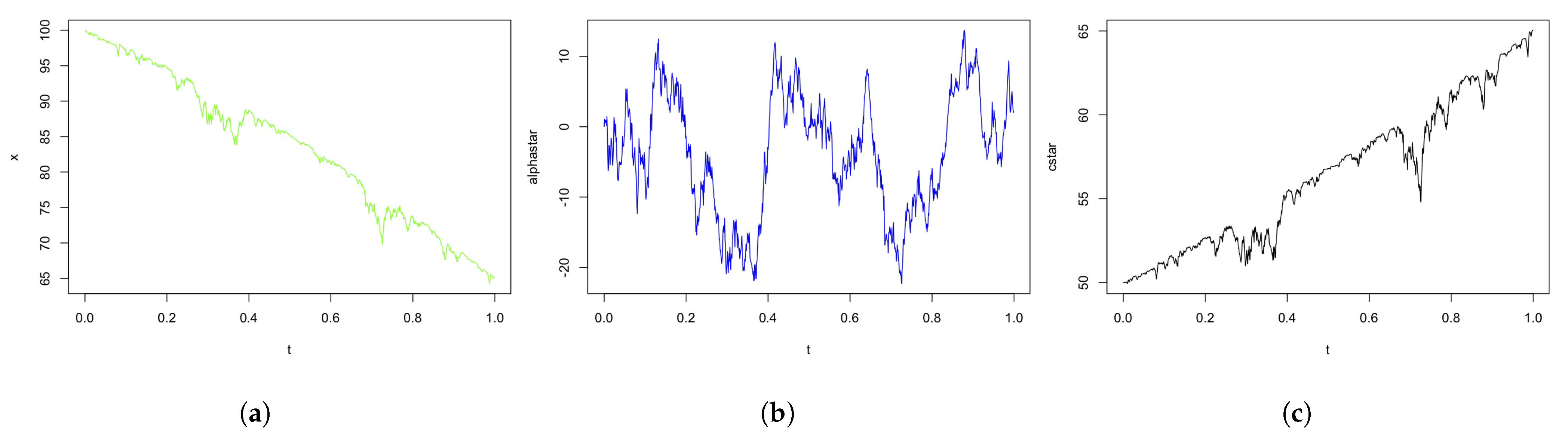
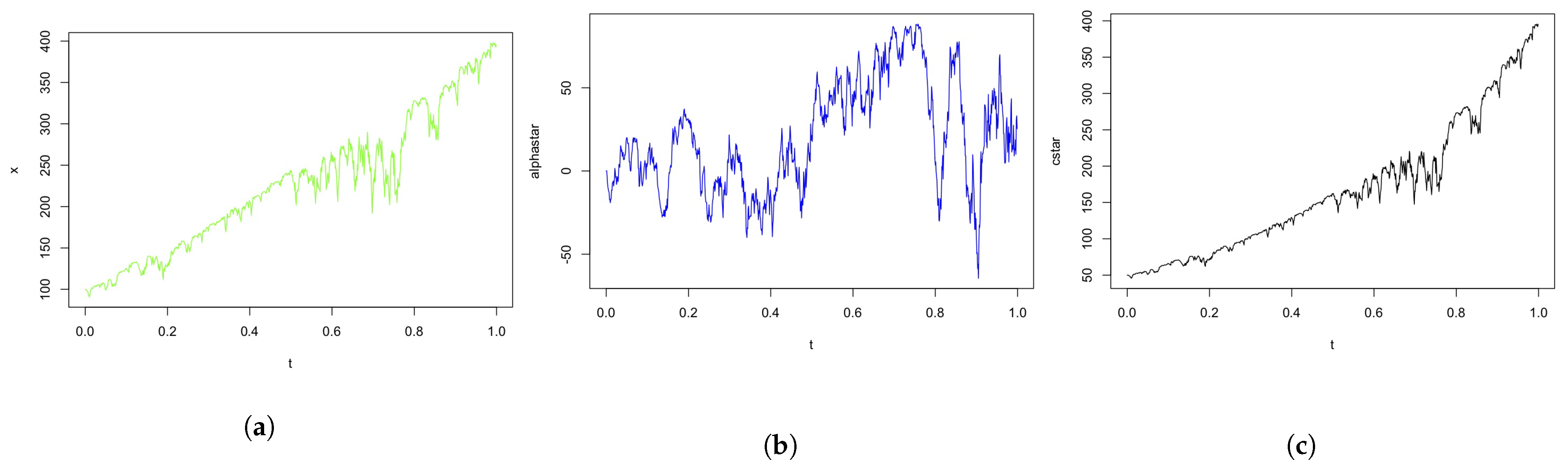
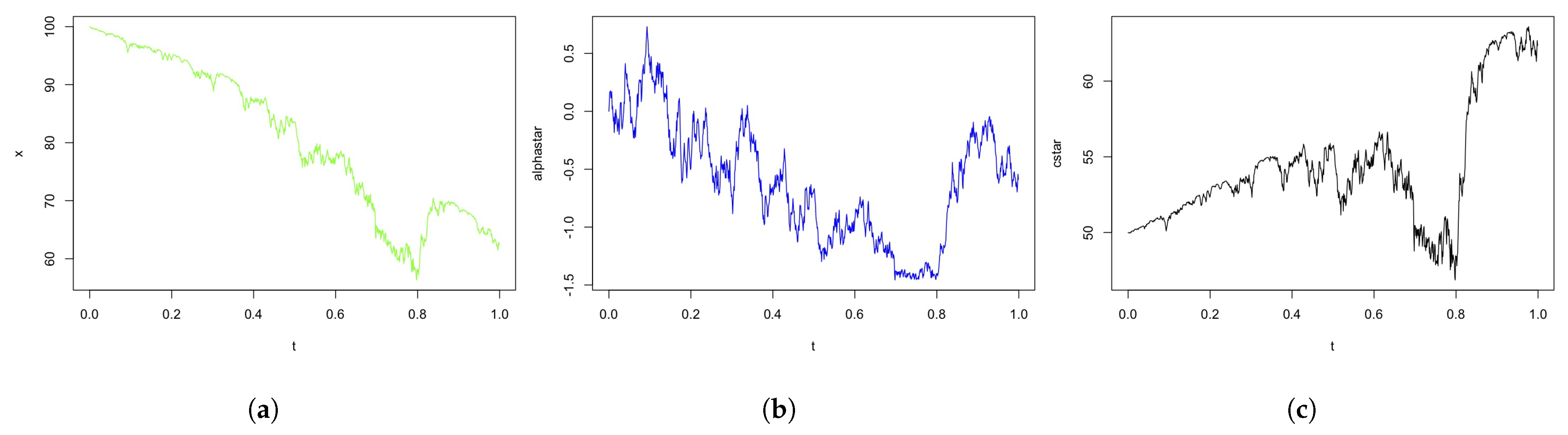
5. Numerical Simulation
6. Verification Theorem
- ()
- For all , the functions and are continuous on .
- ()
- For every deterministic vector , the stochastic differential Equation (17) has a unique strong non-negative solution with .
- ()
- There exists a function from which satisfies the HJB equation such that for any , any and ,
- ()
- There exists a measurable function , such that for all and ,
- ()
- There exists a unique strong solution to the Itô equationwhere and . Moreover, the optimal control process for belongs to , and
7. Proofs
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boguslavsky, M.; Boguslavskaya, E. Arbitrage under power. Risk 2004, 17, 69–73. [Google Scholar]
- Caldeira, J.; Moura, G. Selection of a Portfolio of Pairs Based on Cointegration: A Statistical Arbitrage Strategy. 2013. Available online: http://ssrn.com/abstract=2196391 (accessed on 5 January 2013).
- Arato, M. Linear Stochastic Systems with Constant Coefficients: A Statistical Approach; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1982. [Google Scholar]
- Kabanov, Y.M.; Pergamenshchikov, S.M. Two-Scale Stochastic Systems. Asymptotic Analysis and Control; Applications of Mathematics. Stochastic Modelling and Applied Probability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Elliott, R.J.; Der Hoek, J.V.; Malcolm, W.P. Pairs trading. Quant. Financ. 2005, 5, 271–276. [Google Scholar] [CrossRef]
- Liu, J.; Timmermann, A. Optimal convergence trade strategies. Rev. Financ. Stud. 2013, 26, 1048–1086. [Google Scholar] [CrossRef]
- Monroe, M.A.; Cohn, R.A. The relative efficiency of the gold and treasury bill futures markets. J. Fut. Mark 1986, 6, 477–493. [Google Scholar] [CrossRef]
- Girma, P.B.; Paulson, A.S. Risk arbitrage opportunities in petroleum futures spreads. J. Futur. Mark. 1999, 19, 931–955. [Google Scholar] [CrossRef]
- Reverre, S. The Complete Arbitrage Desk-Book; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- Zebedee, A.A.; Kasch-Haroutounian, M. A closer look at co-movements among stock returns. J. Econ. Bus. 2009, 61, 279–294. [Google Scholar] [CrossRef]
- Raghava, M.; Bharadwaj, S. Pairs Trading Using Cointegration in Pairs of Stocks; Saint Mary’s University: Halifax, NS, Canada, 2014. [Google Scholar]
- Karatzas, I.; Shreve, S.E. Methods of Mathematical Finance; Springer: Berlin, Germany, 1998. [Google Scholar]
- Klüpelberg, C.; Pergamenshchikov, S.M. Optimal Consumption and Investment with Bounded Downside Risk for Power Utility Functions; Optimality and Risk: Modern Trends in Mathematical Finance; Springer: Berlin/Heidelberg, Germany, 2009; pp. 133–150. [Google Scholar]
- Duffie, D.; Filipovic, D.; Schachermayer, W. Affine processes and applications in finance. Ann. Appl. Probab. 2003, 13, 984–1053. [Google Scholar] [CrossRef]
- Berdjane, B.; Pergamenshchikov, S.M. Optimal consumption and investment for markets with randoms coefficients. Financ. Stoch. 2013, 17, 419–446. [Google Scholar] [CrossRef][Green Version]
- Kraft, H.; Seiferling, T.; Seifried, F.T. Optimal consumption and investment with Epstein-Zin recursive utility. Financ. Stoch. 2017, 21, 187–226. [Google Scholar] [CrossRef]
- Krauss, C. Statistical arbitrage pairs trading strategies: Review and outlook. J. Econ. Surv. 2017, 31, 513–545. [Google Scholar] [CrossRef]
- Albosaily, S.; Pergamenshchikov, S.M. Optimal Investment and Consumption for Pairs Trading Financial Markets on Small Time Interval; Cornell University Library: Ithaca, NY, USA, 2018; Available online: https://arxiv.org/abs/1712.04333 (accessed on 21 September 2018).
- Bellman, R. Introduction to Matrix Analysis, 2nd ed.; Society for Industrial and Applied Mathematics: New York, NY, USA, 1987. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albosaily, S.; Pergamenchtchikov, S. Optimal Investment and Consumption for Multidimensional Spread Financial Markets with Logarithmic Utility. Stats 2021, 4, 1012-1026. https://doi.org/10.3390/stats4040058
Albosaily S, Pergamenchtchikov S. Optimal Investment and Consumption for Multidimensional Spread Financial Markets with Logarithmic Utility. Stats. 2021; 4(4):1012-1026. https://doi.org/10.3390/stats4040058
Chicago/Turabian StyleAlbosaily, Sahar, and Serguei Pergamenchtchikov. 2021. "Optimal Investment and Consumption for Multidimensional Spread Financial Markets with Logarithmic Utility" Stats 4, no. 4: 1012-1026. https://doi.org/10.3390/stats4040058
APA StyleAlbosaily, S., & Pergamenchtchikov, S. (2021). Optimal Investment and Consumption for Multidimensional Spread Financial Markets with Logarithmic Utility. Stats, 4(4), 1012-1026. https://doi.org/10.3390/stats4040058





