Estimating the RMSE of Small Area Estimates without the Tears

Hindmarsh, Diane; Steel, David

doi:10.3390/stats4040054

Open AccessArticle

Estimating the RMSE of Small Area Estimates without the Tears

by

Diane Hindmarsh

^*

and

David Steel

National Institute for Applied Statistics Research Australia, School of Mathematics and Applied Statistics, Faculty of Engineering and Information Sciences, University of Wollongong, Wollongong, NSW 2252, Australia

^*

Author to whom correspondence should be addressed.

Stats 2021, 4(4), 931-942; https://doi.org/10.3390/stats4040054

Submission received: 24 July 2021 / Revised: 9 November 2021 / Accepted: 11 November 2021 / Published: 17 November 2021

(This article belongs to the Special Issue Small Area Estimation: Theories, Methods and Applications)

Download

Browse Figures

Versions Notes

Abstract

:

Small area estimation (SAE) methods can provide information that conventional direct survey estimation methods cannot. The use of small area estimates based on linear and generalized linear mixed models is still very limited, possibly because of the perceived complexity of estimating the root mean square errors (RMSEs) of the estimates. This paper outlines a study used to determine the conditions under which the estimated RMSEs, produced as part of statistical output (‘plug-in’ estimates of RMSEs) could be considered appropriate for a practical application of SAE methods where one of the main requirements was to use SAS software. We first show that the estimated RMSEs created using an EBLUP model in SAS and those obtained using a parametric bootstrap are similar to the published estimated RMSEs for the corn data in the seminal paper by Battese, Harter and Fuller. We then compare plug-in estimates of RMSEs from SAS procedures used to create EBLUP and EBP estimators against estimates of RMSEs obtained from a parametric bootstrap. For this comparison we created estimates of current smoking in males for 153 local government areas (LGAs) using data from the NSW Population Health Survey in Australia. Demographic variables from the survey data were included as covariates, with LGA-level population proportions, obtained mainly from the Australian Census used for prediction. For the EBLUP, the estimated plug-in estimates of RMSEs can be used, provided the sample size for the small area is more than seven. For the EBP, the plug-in estimates of RMSEs are suitable for all in-sample areas; out-of-sample areas need to use estimated RMSEs that use the parametric bootstrap.

Keywords:

small area estimation; SAE; empirical best predictor; MSE; parametric bootstrap; model-based survey estimation; SAS procedures

1. Introduction

Local estimates of health risk factors are important for health promotion, service delivery, evaluation and planning purposes. The New South Wales Population Health Survey (NSWPHS) [1] is a large telephone survey that produces estimates of health risk factors on an annual basis for the Australian state of New South Wales (NSW) and for the broad health-administrative areas in NSW. Due to the small and sometimes non-existent sample sizes at the local government area (LGA) level, conventional direct survey estimates can only be used to create results with reasonable standard errors if data are aggregated over multiple years or to broader geographic regions. In order to create local estimates of health risk factors at the LGA level on an annual basis, small area estimation (SAE) methods are needed.

There are three major hurdles to implementing SAE methods as part of routine analysis of surveys such as the NSWPHS. One is determining the appropriate covariates to include in the model. The second hurdle is obtaining estimates of the reliability associated with the small area estimates, as measured by the root mean square error (RMSE). Finally, the SAE methods need to fit seamlessly into the processes used for the routine analysis, which, for this study, meant that analysis needed to use the statistical package SAS.

In a previous paper [2] we showed how to create LGA-level small area estimates for health risk factors from the NSWPHS. We considered how to determine the best set of covariates, and estimation of bias in the absence of a gold standard. The small area estimates were based on the empirical best linear unbiased predictor (EBLUP) for linear mixed models and the empirical best predictor (EBP) for generalized linear mixed models. As all routine analysis of data from the NSWPHS is run in SAS, the SAE processes also need to be run in SAS. The estimates of RMSEs presented in [2] were based on ‘plug-in’ estimators of RMSEs obtained from these SAS procedures. By plug-in, we mean the estimates of RMSE created by the SAS procedure itself. This current paper explains the reasoning behind using the plug-in estimates of RMSE in [2].

Providing estimates of RMSEs is important as they indicate the confidence users can have in the small area estimates. The Prasad-Rao estimator of the RSME of the EBLUP estimator consists of three components. The first component is the naïve estimator of variance, which ignores the variability in the random effects term and is of O(1). The second measures the variability due to estimating the fixed effects. Provided there are a large number of small areas, G, it is of order O(G⁻¹). The final component measures the variability created by estimating the random effect term. It is the smallest of the three components. See [3,4] for details. The estimation of the RMSE for a EBP is more complex, usually requiring either Monte Carlo methods or maximum penalized quasi-likelihood (MPQL) and REML methods [5]. Implementing these methods tends to require high-level understanding of the underlying processes.

Statistical software packages are increasingly including options that can be used for SAE, such as emdi [6] and sae [7] in R. The estimation of RMSEs is incorporated into the programming in these packages; however, at times the estimation of MSEs can be computationally complex, for instance, taking 38 min for a GLMM in [8].

If the estimates of the RMSEs obtained from plug-in estimated RMSEs—those created automatically when obtaining predicted values from the analytical procedure—were similar to those obtained by running the more computationally expensive methods, it would potentially increase the use of SAE methods in routine reporting. Rao [3] mentions that the SAS MIXED procedure can be used to estimate EBLUPs, but reports that the associated estimates of RMSE are missing the third component of the Prasad-Rao estimator of RMSE. The potential impact of missed components in the estimated RMSE will depend to some extent on the use made of the small area estimates. Annual LGA-level estimates of health risk factors from the NSWPHS would be used as one of many inputs in local evaluation and planning. In this case the plug-in estimator of RMSEs may be suitable.

Resampling methods can also be used to create estimated RMSEs for small area estimates [8,9,10,11,12,13]. The non-parametric bootstrap and Jackknife estimation of RMSEs involve resampling from the observed values of the sample. The parametric bootstrap creates estimates of the RMSEs of small area estimates by assessing the variability between the replicates created by re-sampling and re-fitting the model to a large number of replicate samples. The asymptotics of the various bootstrap methods have been extensively studied; for instance, see [7,8]. This paper provides a practical example of using two different estimation methods for RMSE to decide when the plug-in estimates of RMSE (those produced as part of the standard output by statistical packages) can be considered reasonable for the purpose for which the estimates are likely to be used. This was part of a practical assessment of the potential of using SAS to provide small area estimates and the associated estimates of RMSE.

We first fit an EBLUP model to the well-known corn data in Battese, Harter & Fuller (BHF) [14] in SAS using the MIXED procedure. The RMSEs presented in the paper, which are based on analytical approximations, are compared with the plug-in estimates of RMSEs from the MIXED procedure in SAS and the estimated RMSEs created using a parametric bootstrap. We then use data from the NSWPHS to create small area estimates for current smoking in males in 2006 at the LGA level together with plug-in estimates of RMSEs obtained from the MIXED procedure and estimates of RMSEs obtained using the parametric bootstrap. Because the response variable being assessed from the NSWPHS is binary, the EBP based on the generalized linear mixed model with logit link is more appropriate. In SAS, this requires use of the GLIMMIX procedure. Therefore, we then fit a GLMM to the data for current smoking in males in 2006 using the GLIMMIX procedure in SAS. The plug-in estimates of RMSE are then compared with those created using a parametric bootstrap.

The questions being asked are:

When applying the EBLUP estimator to the BHF corn data how well do the estimated RMSEs using the parametric bootstrap compare with the estimated RMSEs created by the MIXED procedure in SAS and the estimated RMSEs from Battese et al. [14]?
When applying the EBLUP estimator to the data from NSWPHS, how do the estimated RMSEs from a parametric bootstrap compare with the estimated RMSEs obtained from the MIXED procedure?
When fitting the more appropriate EBP to the data from the NSWPHS, how do estimated RMSEs from a parametric bootstrap compare with the RMSEs of predictions obtained using the SAS GLIMMIX procedure?
Does the parametric bootstrap for estimating RMSEs for the EBP provide sufficient improvement over using the estimated RMSEs created by the GLIMMIX procedure to require the additional time required to run the parametric bootstrap when presenting results?

The aim of this work is to show the situations in which plug-in estimates of RMSE associated with small area estimates of health risk factors at the LGA level can be considered sufficiently robust to be used for guidance, policy development and evaluation, instead of having to use more computationally extensive estimation methods.

Rao [3] provides a very good overview of other methods of RMSE estimation. Other papers provide details of specific methods; for example, [15] provides information on hierarchical Bayes methods. For resampling methods, see [8,9,10,11,12,13].

The rest of the paper is as follows. Section 2 outlines the methods used for producing EBLUPs and EBPs and their RMSEs in SAS, and the associated estimates of RMSEs created using the parametric bootstrap in SAS. It also provides background to the data used from the NSWPHS. Further detail is provided in [2]. Section 3 provides the results of the analyses comparing the different methods of estimating RMSEs, with discussion in Section 4.

2. Materials and Methods

2.1. Model and Parametric Bootstrap Estimation in SAS

In SAS, unit-level small area estimates are created using the MIXED procedure [16] with the Kenward-Roger version of covariance estimation, REML estimation and the asymptotic variance-covariance matrix of the estimators of the person and area level variance components,

σ_{e}^{2}

and

σ_{ν}^{2}

[17]. Categorical covariates are fitted as indicator values when fitting the model to sample data. The estimates and associated plug-in estimates of RMSE for each small area are obtained by appending population data for each area to the unit level dataset and requesting predictions by setting the option OUTP = name to the model statement.

The method used to create estimates of RMSEs using a parametric bootstrap requires the estimates of the area level variance component (

{\hat{σ}}_{ν}^{2}

), person level variance (

{\hat{σ}}_{e}^{2}

) and regression coefficients (

\hat{β}

) from the MIXED procedure. The process used to obtain the parametric bootstrap estimates of RMSEs is presented in Appendix A.

EBPs for small areas require the fitting of a generalized linear mixed model with a logit link. The SAS GLIMMIX procedure was used, setting a logit link and binary distribution in the model statement. The plug-in estimates of RMSEs created by the GLIMMIX procedure are based on linearization [16]. The parameter estimate convergence criterion was set to 1 × 10⁻⁵. As with the estimation process for the linear models, the predicted values and associated plug-in estimates of RMSEs were obtained by appending records for each of the LGAs to the unit record dataset. The indicator variables contained the LGA-specific population proportions for each of the covariates used to fit the model. As the outcome variable field remained empty, these rows are not used in the development of the model; however, predicted values are obtained for all records in the dataset, including these LGA-level summary rows. The EBPs and associated estimated plug-in RMSEs for each area were obtained by requesting PRED(BLUP ILINK) and STDERR(BLUP ILINK), respectively, in the output statement.

The bootstrap process was based on the estimated values of

{\hat{σ}}_{ν}^{2}

and

\hat{β}

output from the GLIMMIX procedure. See Appendix B for the parametric bootstrap process for estimating RMSEs for the EBPs.

2.2. Data Sources

Two data sources were used in this paper. The first source was the corn crop data in the seminal paper on the EBLUP model [14]. The original paper provides the full dataset used to fit a linear mixed model to estimate the total area of corn crop by county. The covariates in the model are the number of pixels for corn and soybeans in the sampled segments, with the dependent variable being the reported number of hectares of corn in those sampled segments.

The second data source arises from a project that investigated the feasibility of using SAS procedures to create LGA level estimates of health risk factors from the NSWPHS. The NSWPHS is a continuous CATI survey designed to provide reliable estimates of health risk factors at the level of the health administrative areas in NSW [1]. At the time this work was undertaken there were eight health administrative areas. The aim of the project was to obtain estimates of health risk factors, together with estimates of their precision, for each of the 153 LGAs from a single year of data. Details about the data source, analytical methods and assessment of bias when there is no gold standard were presented in a previous paper [2]. The unit record data for the project were supplied by the NSW Ministry of Health under a privacy and confidentiality agreement. Binary versions of health risk factors were used as the outcome variables; responses for demographic questions such as age group, sex, marital status, level of qualification, language spoken at home and private health cover were also available for use as covariates. Population proportions for these demographic variables were mainly obtained from the Australian Bureau of Statistics Census of Population and Housing [18], with information on private health cover obtained from the social health atlas of NSW [19].

2.3. Fitting the Models to the Data Sources

For the data from the BHF paper, we fitted the linear mixed model using the MIXED procedure in SAS, obtaining the plug-in estimates of RMSE for each area. The estimated variance components and regression coefficients from the model were then used to obtain the estimated RMSEs using the parametric bootstrap. Both sets of estimated RMSEs were then visually compared to the estimated RMSEs presented in the original paper.

The MIXED and GLIMMIX procedures were applied to the data from the NSWPHS to obtain the EBLUPs and EBPs for each of the 153 LGAs, and associated estimates of RMSEs. In both cases age group, marital status, level of qualification and private health cover were included in the model as indicator variables. The sampling fraction for the NSWPHS is negligible, so the impact of including the sample means for each LGA in the SAE method would be negligible.

The estimates

{\hat{σ}}_{ν}^{2}

,

{\hat{σ}}_{e}^{2}

and

\hat{β}

obtained from fitting the EBLUP were used in the parametric bootstrap process to estimate the RMSEs using the process outlined in Appendix A. The estimates of

{\hat{σ}}_{ν}^{2}

and

\hat{β}

obtained from fitting the EBP model were used to estimate the RMSEs based on the logistic version of the parametric bootstrap process, as outlined in Appendix B.

The linear model and parametric bootstrap estimation of RMSEs was repeated using a model where the only covariate group was the age group.

In each case, the estimated RMSEs from the bootstrap process were compared with the plug-in estimates of RMSEs produced by the SAS procedure. As the project was aimed at providing a practical example of using SAE methods with real data, we did not use a simulation.

3. Results

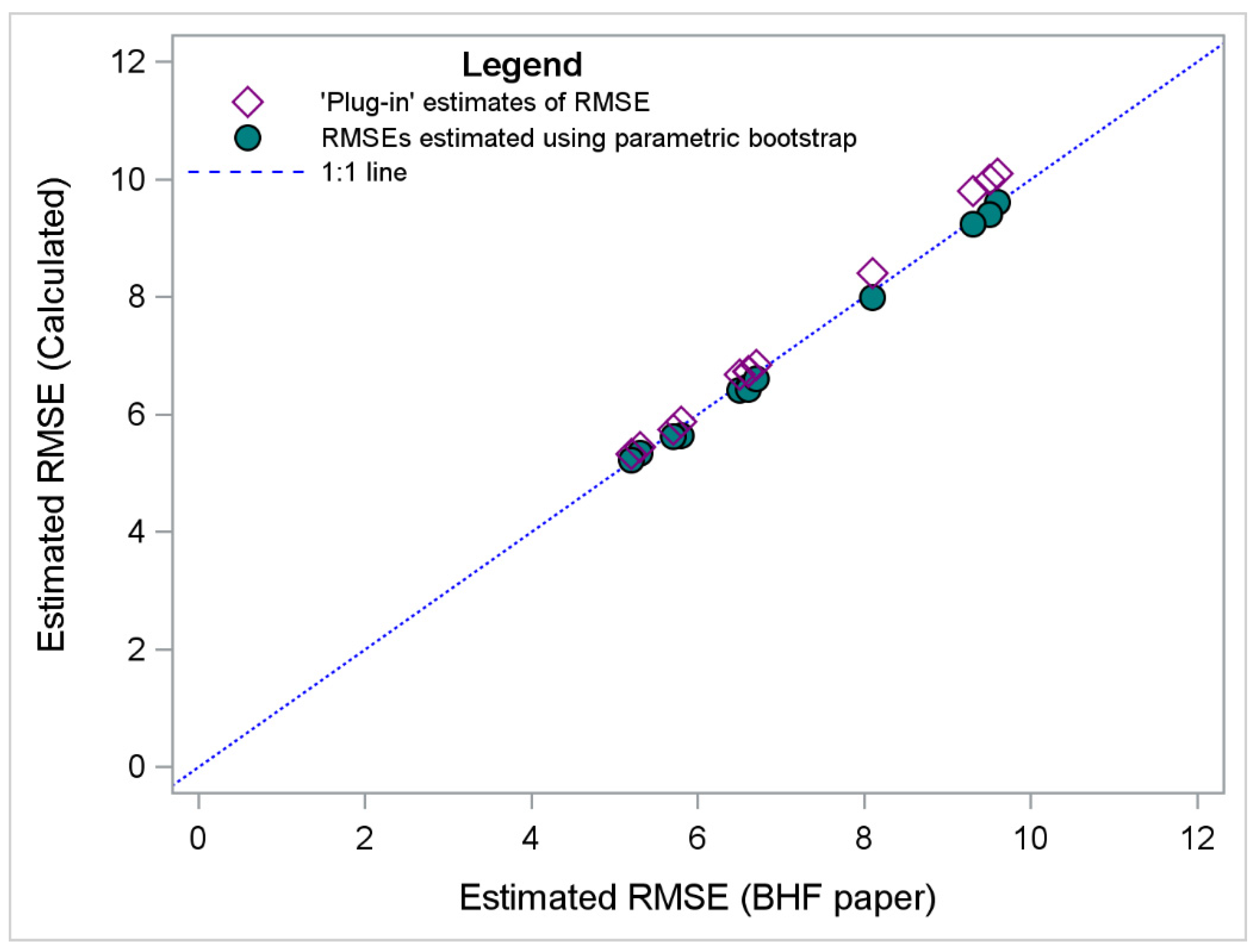
3.1. Validation Using BHF Data

For the BHF data the plug-in estimates of RMSEs created by the MIXED procedure were slightly higher than the estimated RMSEs presented in the original paper (Figure 1). In comparison, the bootstrap estimates of RMSEs were almost identical to the RMSEs presented in the original paper and slightly lower than the estimated RMSEs from the MIXED procedure. The estimated RMSEs were highly correlated (R² > 0.99).

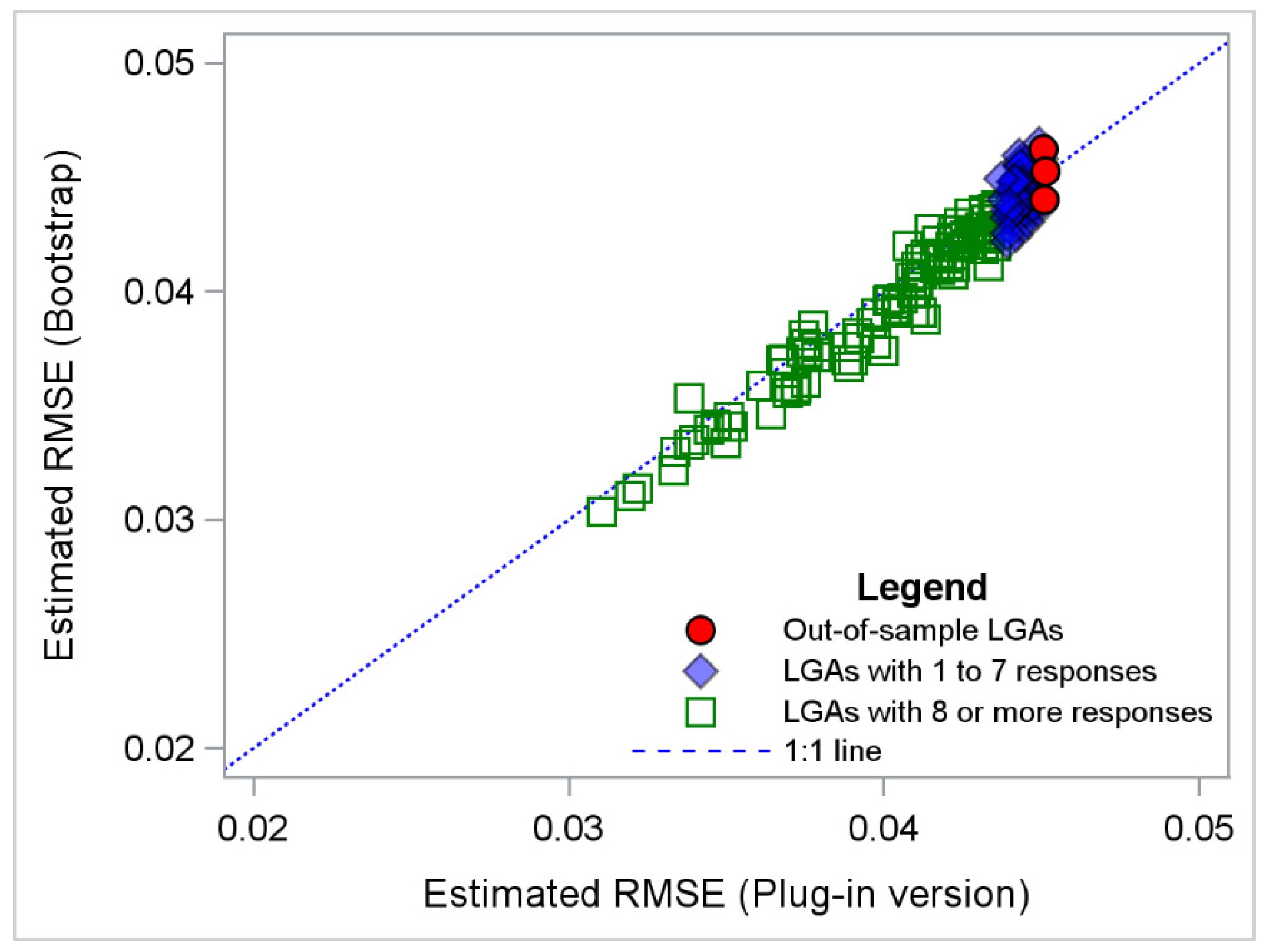
3.2. Estimated RMSE When Fitting EBLUP to Data from NSWPHS

Figure 2 shows the estimated RMSEs for the EBLUPs using the parametric bootstrap and the MIXED procedure for current smoking in males, 2006 (also see Figure S1 in the Supplementary Material Online). The bootstrap estimates of RMSE are, in general, slightly lower than, but in the same order of magnitude, as the plug-in estimates of RMSE. There is a cluster of areas where the plug-in estimates of RMSEs are around 0.032. All these areas have seven or fewer responses, and, contrary to theory, it suggests that the estimated RMSEs for areas with fewer than seven responses are lower than the estimated RMSEs for areas with larger sample sizes. The value of 0.032 is very close to the theoretical maximum RMSE based on the first term of the Prasad-Rao estimator of MSE ([3], p. 137) and [4]. This term is the dominant component of the RMSEs.

The issue does not occur for estimated RMSEs obtained from the bootstrap (the green squares in Figure 2), nor is it observed when a less complex model using only age group as a covariate is fitted (Figure 3), and Figure S2 in the Supplementary Material Online.

In the three situations presented for the linear model, the plug-in estimates of RMSE are almost always higher than those obtained from the parametric bootstrap (see Figure 1, Figure 2 and Figure 3). The level of agreement between the two sets of estimates of RMSEs is greater for the less complex model, however, as shown by comparing Figure 2 and Figure 3.

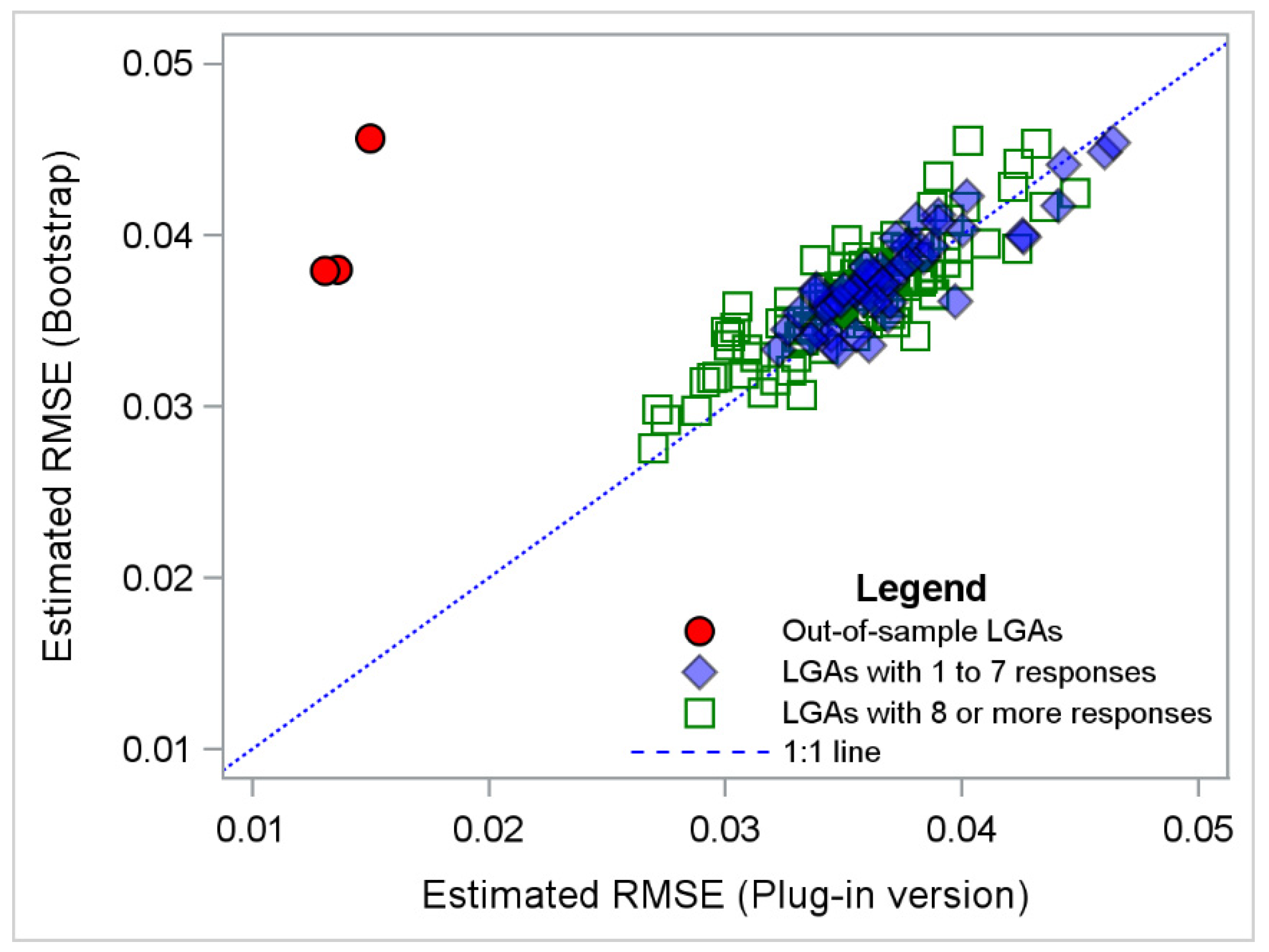
3.3. Estimated RMSE When Fitting EBP to Data from the NSWPHS

Apart from three points where the sample size for these is zero, the bootstrap and plug-in estimates of RMSEs for EBPs based on the GLIMMIX procedure are highly correlated (Figure 4 and Figure S3 in the Supplementary Material Online), and both sets of estimated RMSEs have similar median, mean and maximum values (Table 1).

The three outliers are for out-of-sample areas. For these, the minimum estimated RMSEs from the bootstrap method is 2.7%, compared with 1.3% for the plug-in version. It is well known that, because the random effect term in the estimates for out-of-sample areas is zero, the estimates of RMSEs produced by a GLMM for out-of-sample areas will revert to the RMSE of the associated synthetic estimate. In these cases the parametric bootstrap provides a much better estimate of the RMSE because it takes into account the variability in the random effects term, even for out-of-sample areas.

Graphs of the estimated RMSEs of the EBLUP and EBP model-based LGA estimates against the number of responses are provided in the supplementary material available online.

4. Discussion

At times there may be a need to use more complex methods for estimating RMSEs associated with small area estimates, however in the work being undertaken using the NSWPHS data, and in other applications involving routine production of small area estimates, it may be sufficient to base RMSEs on plug-in estimates, and at least in preliminary work, as this will reduce the length of time required for processing.

When compared with the estimated RMSEs for the corn data provided in the original BHF paper [14], the plug-in estimates of RMSE from the MIXED procedure were marginally higher than those reported in the paper. We expected that the plug-in estimates of RMSE would be slightly lower than the estimated RMSEs in the paper because of the potentially missed component of the Prasad-Rao estimator [3]. The same result was obtained by Mukhopadhyay and McDowell [17]. The plug-in estimates of RMSE could therefore be considered ‘conservative’.

Estimates of the RMSEs obtained from the parametric bootstrap were almost identical to those in the paper.

The bootstrap estimates of RMSEs for the EBLUP model tend to underestimate the true variance because, although they account for the variability created by the

{\hat{σ}}_{ν}^{2} and {\hat{σ}}_{e}^{2}

terms, they don’t consider the variance of the regression coefficients. The impact of this should be small, as the estimation of the regression coefficients is based on the entire data set.

One of the disadvantages of the parametric bootstrap process is that any model misspecification is ignored: underlying the entire parametric bootstrap process is the assumption that the model applies. Therefore, any potential misspecification of the model needs to be addressed based on model diagnostics applied to the original model, as in any statistical analysis.

An advantage of the parametric bootstrap is that it can be used to obtain an estimate of the precision of the estimated RMSEs by repeating the bootstrap process many times, much like what is possible through a hierarchical Bayes approach, but from a frequentist paradigm.

When applied to data from the NSWPHS, the plug-in and parametric bootstrap estimates of RMSEs under the linear mixed model gave very similar results for most areas.

There are three possible reasons for the anomalies in estimated plug-in RMSEs observed for areas with small sample size and complex models.

The linear model may be the issue here. The outcome variable is binary in nature, and this may provide evidence that the linear model is not appropriate when the sample size is very small.
It may indicate a breakdown of the SAS version of the Prasad-Rao estimate of RMSE. The Kenward-Roger method of variance estimation in SAS uses a Satterthwaite-type method to estimate the degrees of freedom. And the behavior of the Satterthwaite method of assessment has not been assessed fully when there are small sample sizes [16].
The Taylor series linearization approximation process used to estimate the Prasad-Rao estimator of RMSE in SAS may not be accurate with small sample sizes.

There is no such issue with the estimated RMSEs for the EBP estimates, however the plug-in estimates of RMSEs were too low for out-of-sample areas, as in these situations they reverted to the RMSEs of the synthetic estimates. Although the ideal approach to estimate RMSEs for these out-of-sample areas would involve either the parametric bootstrap or other methods of estimation; a quicker alternative could be to substitute the maximum estimated RMSE from in-sample areas for out-of-sample areas. Public reporting of the results for such out-of-sample areas should be accompanied by an appropriate note to indicate how the RMSEs have been estimated.

The results of this work were used to justify using the plug-in estimates of the RMSEs from the MIXED and GLIMMIX procedures in SAS in [2,20]. Out-of-sample areas were given the maximum RMSE for in-sample areas.

The ability to use plug-in estimates of the RMSEs when creating small area estimates may lead to more opportunities for SAE methods to be routinely used in health and social agencies. One such application would be in creating estimates of health risk factors for LGAs in NSW from the NSWPHS, although this survey was developed to provide estimates for the large health areas in the state. As with any estimates, small area estimates should be accompanied by details of the method of estimation of both the estimates themselves and the RMSEs.

We have used the BHF data and the NSWPHS data to compare plug-in estimates of RMSEs created by SAS procedures and parametric bootstrap procedures. For the practical purposes to which the small area estimates are expected to be put, these methods are considered effective. For binary outcome variables where the GLMM is the more appropriate model, the estimated RMSEs for out-of-sample areas should be obtained from the parametric bootstrap, or alternatively they can be given the maximum RMSE for in-sample areas, provided such a decision is documented clearly.

Other papers provide comparisons between parametric bootstrap estimates and other methods of estimation of RMSE, including the use of simulation studies. See, for instance, [8,9,21,22]. They generally find that the parametric bootstrap compares favorably with more computationally complex estimation methods.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/stats4040054/s1, Figure S1: Bootstrap and plug-in RMSEs for EBLUP model-based estimates of proportion of smoking against number of responses to the question by LGA, males, 2006. Model included age group, marital status, education level and private health status, Figure S2: Bootstrap and plug-in RMSEs for EBLUP model-based estimates of proportion of smoking against number of responses to the question by LGA, males, 2006. Model included age group only, Figure S3: Bootstrap and plug-in RMSEs for EBP model-based estimates of proportion of smoking against number of responses to the question by LGA, males, 2006. Model included age group, marital status, education level and private health status.

Author Contributions

Conceptualization, methodology, D.S. and D.H.; formal analysis, investigation, data curation, writing—original draft preparation D.H.; writing—review and editing, D.S. and D.H.; supervision, D.S.; funding acquisition, D.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Australian Research Council linkage grant, LP0776810ARC. The industry partners included Australian Bureau of Agriculture and Resource Economics, NSW Health, NZ Ministry of Health and Australian Bureau of Statistics.

Institutional Review Board Statement

Ethical review and approval were unnecessary for this study, due to the data being non-identifiable.

Informed Consent Statement

Written consent to publish this paper has been obtained from the data custodian for the NSW Population Health Survey program.

Data Availability Statement

Restrictions apply to the availability of these data. Data were obtained from NSW Population Health Survey program following submission of a formal data request and after permission was granted from NSW Health.

Acknowledgments

The authors wish to thank Professor Ray Chambers for valuable discussions regarding this work. The involvement of the linkage partners is acknowledged and sincerely appreciated as is the support of the NSW Health Chief Health Officer for providing access to the NSW Population Health Survey data through a data request. Thank you also to the reviewers for their constructive feedback.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Appendix A. Steps to Create Parametric Bootstrap Estimate of MSE of EBLUP Estimator

Fit the linear mixed model (Equation (A1)) to the data and save the values of ${\hat{σ}}_{ν}^{2}$ ${\hat{σ}}_{e}^{2}$ and $\hat{β}$ .

$y_{i g} = x_{i g}^{'} β + ν_{g} + e_{i g}$

(A1)

where $y_{i g}$ is the response of the $i^{t h}$ person in the $g^{t h}$ small area,
- $n_{g}$ is the sample size in the $g^{t h}$ small area, $i = 1 \dots n_{g}$ , $g = 1 \dots G$ ,
- $x_{i g}^{'}$ is the vector of covariate values from the survey,
- $β$ is the vector of regression coefficients,
- $ν_{g}$ is a random effect reflecting area level effects, $ν_{g}$ are independent N(0, $σ_{ν}^{2}$ ),
- $e_{i g}$ are the random errors independent N(0, $σ_{e}^{2}$ ).

For each simulation

(k = 1 \dots K)

, continue as follows:

2.: For each area ( $g$ ) generate a random area term ${ν_{g}}^{*}$ from the distribution ${ν_{g}}^{*} \sim N (0, {\hat{σ}}_{ν}^{2})$ .
3.: For each observation $i = 1 \dots n$ , generate a normal error term ${e_{i}}^{*}$ from the distribution ${e_{i}}^{*} \sim N (0, {\hat{σ}}_{e}^{2})$ .
4.: Use Equation (A1) to simulate $n$ values of $y_{i g}$ , $y_{i g}^{*}$ using $e_{i}^{*}$ and $ν_{g}^{*}$ generated in steps 2 and 3, together with the covariates and vector of regression coefficients, and with $n_{g}$ being the same as in the sample.
5.: Fit the linear mixed model to the simulated values and obtain the EBLUP estimates for each simulation ( ${\tilde{\bar{Y}}}_{g}^{*}$ ) for each area (Equation (A2)).

${\tilde{\bar{Y}}}_{g}^{*} = X_{i g}^{'} {\hat{β}}^{*} + {\hat{ν}}_{g}^{*}$

(A2)

where $X_{i g}^{'}$ is the vector of covariates associated with the $i^{t h}$ person in the $g^{t h}$ small area, obtained from census or other origin, and assumed known without error.
6.: Also, calculate the ‘true’ value of ${\tilde{\bar{Y}}}_{g}$ (Equation (A3)) associated with the $k^{t h}$ simulation.

${\hat{\bar{Y}}}_{g} = X_{i g}^{'} \hat{β} + ν_{g}^{*}$

(A3)
7.: Repeat steps 2 to 6, K times (at least 1000 is suggested).
8.: Calculate the bootstrap estimate of the MSE of the EBLUP estimator for the $g^{t h}$ area using Equation (A4).

$M S E_{b_{g}} = \frac{1}{K} \sum^{} {({\hat{\bar{Y}}}_{g} - {\tilde{\bar{Y}}}_{g}^{*})}^{2}$

(A4)

Appendix B. Steps to Create Parametric Bootstrap Estimate of MSE of EBP Estimator

Fit the non-linear mixed model (Equation (A5)) to the data using a logit link with the required covariates and save the values of ${\hat{σ}}_{ν}^{2}$ and $\hat{β}$ .

$logit (y_{i g}) = x_{i g}^{'} β + ν_{g}$

(A5)

where $y_{i g}$ is the response of the $i^{t h}$ person in the $g^{t h}$ small area, $g = 1 \dots G$ ,
- $n_{g}$ is the sample size in the $g^{t h}$ small area, $i = 1 \dots n_{g}$ ,
- $x_{i g}^{'}$ is the vector of covariate values from the survey,
- $β$ is the vector of regression coefficients
- $ν_{g}$ is a random effect reflecting area level effects, $ν_{g}$ are independent, $N (0, σ_{ν}^{2})$ ,

For each simulation

(k = 1 \dots K)

, continue as follows:

2.

For each area (

g

) generate a random area term

ν_{g}^{*}

from the distribution

ν_{g}^{*} \sim N (0, {\hat{σ}}_{ν}^{2})

.

3.

Generate

n

simulated values of

y_{i g,}, with n_{g} being the same as in the sample, y_{i g}^{*}

. This is a two-step process.

First, use Equation (A6) to calculate $E (p)$ substituting $ν_{g}^{*}$ generated in step 2, together with the observed value of covariates and vector of estimated regression coefficients from step 1.

$E (p) = \frac{\exp (x_{i g}^{'} \hat{β} + {\hat{ν}}_{g}^{*})}{1 + \exp (x_{i g}^{'} \hat{β} + {\hat{ν}}_{g}^{*})}$

(A6)
Create a random variable between 0 and 1, for the n observations. For each observation, if the random variable is less than $E (p)$ then $y_{i g}^{*} = 1$ for the $k^{t h}$ similation, otherwise $y_{i g}^{*} = 0$ .

4.

Fit the same model as in step 1 to this set of simulated values, obtaining the estimated EBP for each area

{\hat{P}}_{g}^{*}

(Equation (A7)) associated with the

k^{t h}

simulation.

{\hat{P}}_{g}^{*} = \frac{\exp ({\bar{X}}_{g}^{'} {\hat{β}}^{*} + {\hat{ν}}_{g}^{*})}{1 + \exp ({\bar{X}}_{g}^{'} {\hat{β}}^{*} + {\hat{ν}}_{g}^{*})}

(A7)

5.

For each replicate also calculate the ‘true’ value, given the simulated value of the random error variance term (Equation (A8)).

P_{g}^{*} = \frac{\exp ({\bar{X}}_{g}^{'} \hat{β} + {\hat{ν}}_{g}^{*})}{1 + \exp ({\bar{X}}_{g}^{'} \hat{β} + {\hat{ν}}_{g}^{*})}

(A8)

6.

Repeat steps 2 to 6, K times (at least 1000 is suggested).

7.

Calculate the bootstrap estimate of the MSE of the EBP estimator for the

g^{t h}

area using Equation (A9).

M S E_{b_{g}} = \frac{1}{K} \sum^{} {({\hat{P}}_{g}^{*} - P_{g}^{*})}^{2}

(A9)

References

Williamson, M.; Baker, D.; Jorm, L. The NSW Health Survey Program Overview and Methods, 1996–2000. N. S. W. Public Health Bull. Suppl. Ser. 2001, 12, 1–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Hindmarsh, D.M.; Steel, D. Creating local estimates from a population health survey: Practical application of small area estimation methods. AIMS Public Health 2020, 7, 403–424. [Google Scholar] [CrossRef] [PubMed]
Rao, J.N.K. Small Area Estimation (Methods and Applications), 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 2003; p. 137. [Google Scholar]
Prasad, N.G.N.; Rao, J.N.K. On robust small area estimation using a simple random effects model. Surv. Methodol. 1999, 25, 67–72. [Google Scholar]
Saei, A.; Chambers, R. Small Area Estimation under Linear and Generalized Linear Mixed Models with Time and Area Effects. S3RI Methodology Working Papers, M03/15 2001. Available online: https://eprints.soton.ac.uk/8165/1/8165-01.pdf (accessed on 28 June 2021).
Hall, P.; Maiti, T. On parametric bootstrap methods for small area prediction. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 221–238. [Google Scholar] [CrossRef]
Kreutzmann, A.-K.; Pannier, S.; Rojas-Perilla, N.; Schmid, T.; Templ, M.; Tzavidis, N. The R Package emdi for Estimating and Mapping Regionally Disaggregated Indicators. J. Stat. Softw. 2019, 91, 1–33. [Google Scholar] [CrossRef] [Green Version]
Molina, I.; Marhuenda, Y. Sae: An R Package for Small Area Estimation. R J. 2015, 7, 81–98. [Google Scholar] [CrossRef] [Green Version]
Molina, I.; Strzalkowska-Kominiak, E. Estimation of proportions in small areas: Application to the labour force using the Swiss Census Structural Survey. J. R. Stat. Soc. A 2020, 183 Pt 1, 281–310. [Google Scholar] [CrossRef] [Green Version]
González-Manteiga, W.; Lombardía, M.J.; Molina, I.; Morales, D.; Santamaría, L. Bootstrap mean squared error of a small-area EBLUP. J. Stat. Comput. Simul. 2008, 78, 443–462. [Google Scholar] [CrossRef]
Lahiri, S.N.; Maiti, T.; Katzoff, M.; Parsons, V. Resampling-based empirical prediction: An application to small area estimation. Biometrika 2007, 94, 469–485. [Google Scholar] [CrossRef] [Green Version]
Pereira, L.; Coelho, P. Assessing different uncertainty measures of EBLUP: A resampling-based approach. J. Stat. Comput. Simul. 2010, 80, 713–727. [Google Scholar] [CrossRef]
Herrador, M.; Morales, D.; Esteban, M.; Sanchez, A.; Santamaria, L.; Marhuenda, Y.; Perez, A. Sampling design variance estimation of small area estimators in the Spanish Labour Force Survey. SORT-Stat. Oper. Res. Trans. 2008, 32, 177–197. [Google Scholar]
Battese, G.E.; Harter, R.M.; Fuller, W.A. An error-components model for prediction of county crop areas using survey and satellite data. J. Am. Stat. Assoc. 1988, 83, 28–36. [Google Scholar] [CrossRef]
Gomez-Rubio, V.; Best, N.; Richardson, S.; Li, G.; Clarke, P. Bayesian Statistics for Small Area Estimation; Technical Report (Unpublished); Imperial College London: London, UK, 2010; Available online: http://eprints.ncrm.ac.uk/1686/1/BayesianSAE.pdf (accessed on 28 June 2021).
SAS Institute Inc. SAS/STAT 9.2 Users Guide, 2nd ed.; SAS Institute Inc.: Cary, NC, USA, 2009; Online Documentation. [Google Scholar]
Mukhopadhyay, P.K.; McDowell, A. Small Area Estimation for Survey Data Analysis Using SAS Software. SAS Global Forum 2011 Paper 336-2011. 2011. Available online: http://support.sas.com/resources/papers/proceedings11/336-2011.pdf (accessed on 28 June 2021).
Australian Bureau of Statistics. 2006 Census Community Profile Series: Basic Community Profile. Cat. No. 2001.0. 2007. Available online: https://www.abs.gov.au/websitedbs/censushome.nsf/home/communityprofiles?opendocument&navpos=230 (accessed on 28 June 2021).
Glover, J.; Tennant, S. Social Health Atlas of New South Wales (incl. ACT) Local Government Areas. 2010. Electronic Report. Available online: https://phidu.torrens.edu.au/social-health-atlases/data-archive/data-archive-social-health-atlases-of-australia#social-health-atlas-of-australia-data-released-august-november-december-2011-by-statistical-local-area-local-government-area-based-on-the-asgc-2006-and-medicare-local (accessed on 28 June 2021).
Hindmarsh, D.M. Small Area Estimation for Health Surveys. Doctoral Thesis, University of Wollongong: School of Mathematics and Applied Statistics, Wollongong, NSW, Australia, March 2013. Available online: https://ro.uow.edu.au/theses/3746 (accessed on 3 November 2021).
Wu, P.; Jiang, J. Robust estimation of mean squared prediction error in small-area estimation. Can. J. Stat. 2021, 49, 362–396. Available online: https://doi-org.ezproxy.uow.edu.au/10.1002/cjs.11567 (accessed on 3 November 2021). [CrossRef]
González-Manteiga, W.; Lombardía, M.J.; Molina, I.; Morales, D.; Santamaría, L. Estimation of the mean squared error of predictors of small area linear parameters under a logistic mixed model. Comput. Stat. Data Anal. 2007, 51, 2720–2733. [Google Scholar] [CrossRef]

Figure 1. Estimated RMSEs of predicted area of corn from parametric bootstrap and SAS MIXED procedure against estimated RMSE presented in [14]. 1:1 line included for reference purposes.

Figure 2. Bootstrap versus plug-in RMSEs for LGA-level EBLUP model-based estimates of proportion of smoking in males, 2006, using a linear mixed model. The model included age group, marital status, education level and private health status.

Figure 3. Bootstrap versus plug-in RMSEs for LGA-level EBLUP model-based estimates of proportion of smoking in males, 2006, using linear mixed model. Model included age group only.

Figure 4. Bootstrap versus plug-in RMSEs for LGA-level EBP model-based estimates of proportion of smoking in males, 2006, using a generalised linear mixed model with logit link. The model included age group, marital status, education level and private health status.

Table 1. Summary statistics for estimated RMSE using output from the GLIMMIX procedure, parametric bootstrap.

Source of Estimates of RMSE	Minimum	Median	Mean	Maximum
Plug-in (from procedure)	1.3%	3.5%	3.5%	4.6%
Parametric Bootstrap	2.7%	3.6%	3.6%	4.5%

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Hindmarsh, D.; Steel, D. Estimating the RMSE of Small Area Estimates without the Tears. Stats 2021, 4, 931-942. https://doi.org/10.3390/stats4040054

AMA Style

Hindmarsh D, Steel D. Estimating the RMSE of Small Area Estimates without the Tears. Stats. 2021; 4(4):931-942. https://doi.org/10.3390/stats4040054

Chicago/Turabian Style

Hindmarsh, Diane, and David Steel. 2021. "Estimating the RMSE of Small Area Estimates without the Tears" Stats 4, no. 4: 931-942. https://doi.org/10.3390/stats4040054

APA Style

Hindmarsh, D., & Steel, D. (2021). Estimating the RMSE of Small Area Estimates without the Tears. Stats, 4(4), 931-942. https://doi.org/10.3390/stats4040054

Article Menu

Estimating the RMSE of Small Area Estimates without the Tears

Abstract

1. Introduction

2. Materials and Methods

2.1. Model and Parametric Bootstrap Estimation in SAS

2.2. Data Sources

2.3. Fitting the Models to the Data Sources

3. Results

3.1. Validation Using BHF Data

3.2. Estimated RMSE When Fitting EBLUP to Data from NSWPHS

3.3. Estimated RMSE When Fitting EBP to Data from the NSWPHS

4. Discussion

Supplementary Materials

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A. Steps to Create Parametric Bootstrap Estimate of MSE of EBLUP Estimator

Appendix B. Steps to Create Parametric Bootstrap Estimate of MSE of EBP Estimator

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI