Learning Time Acceleration in Support Vector Regression: A Case Study in Educational Data Mining
Abstract
1. Introduction
2. Background
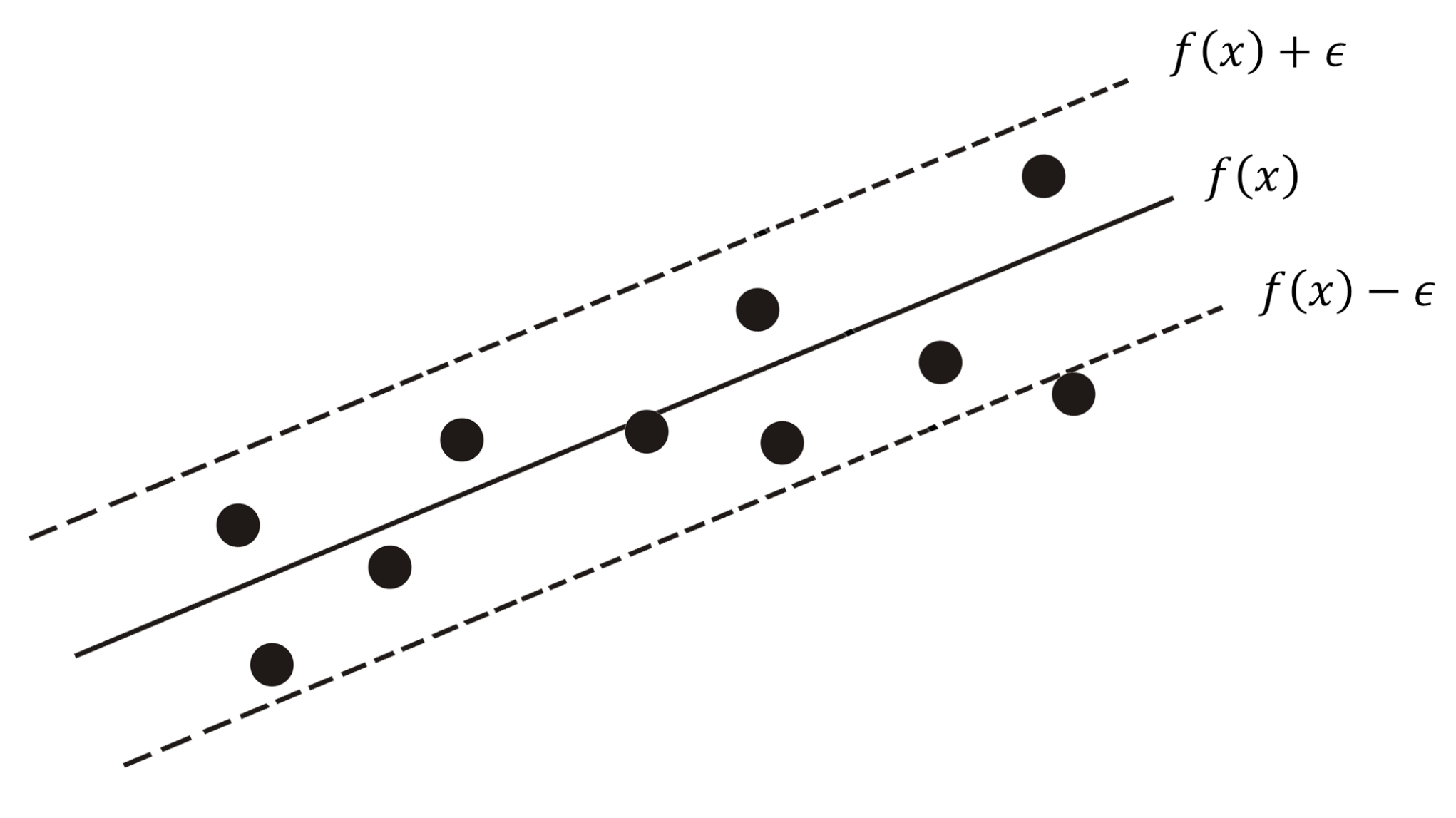
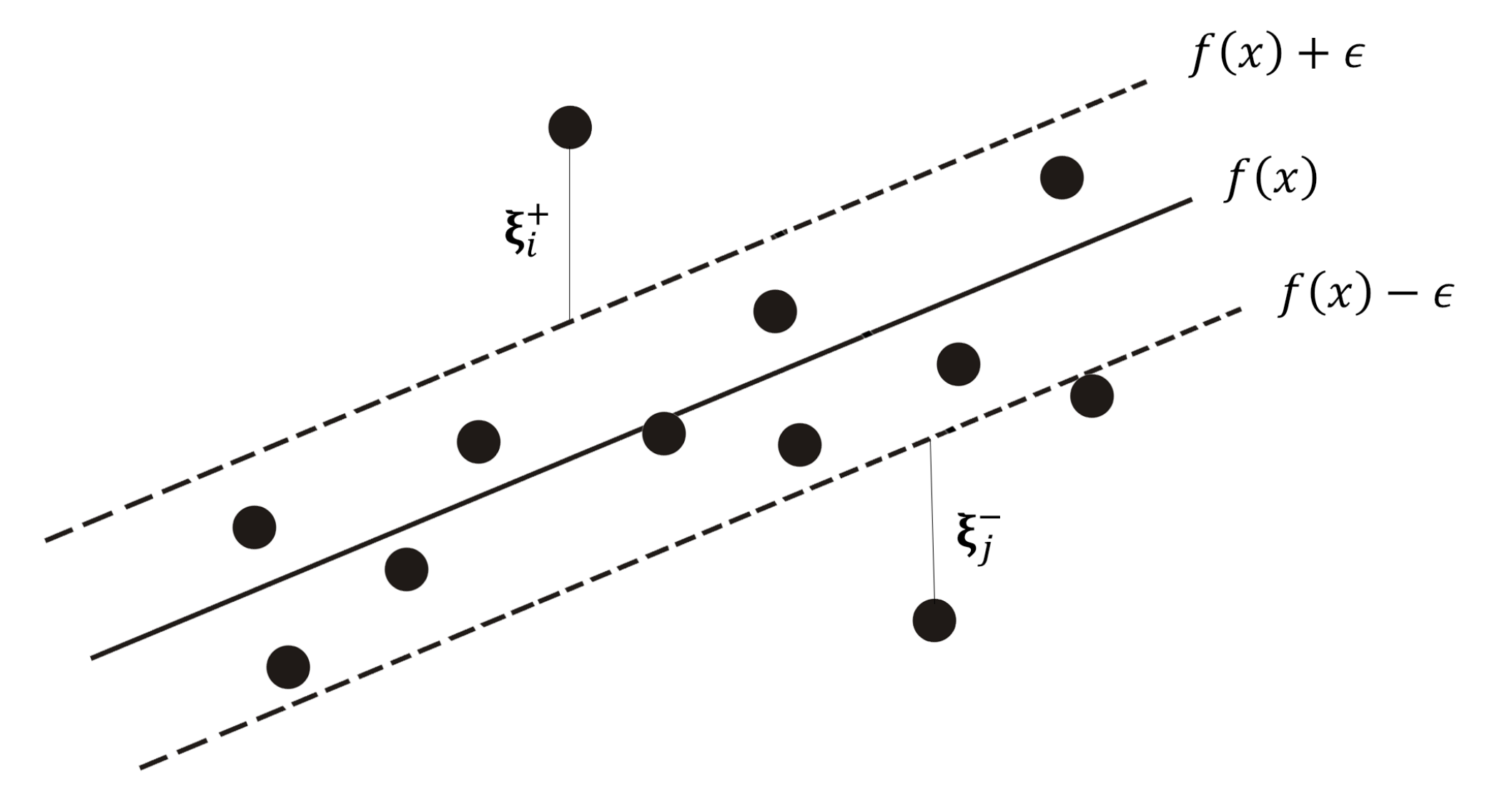
2.1. Support Vector Regression
2.2. SVM Applied to Large Databases
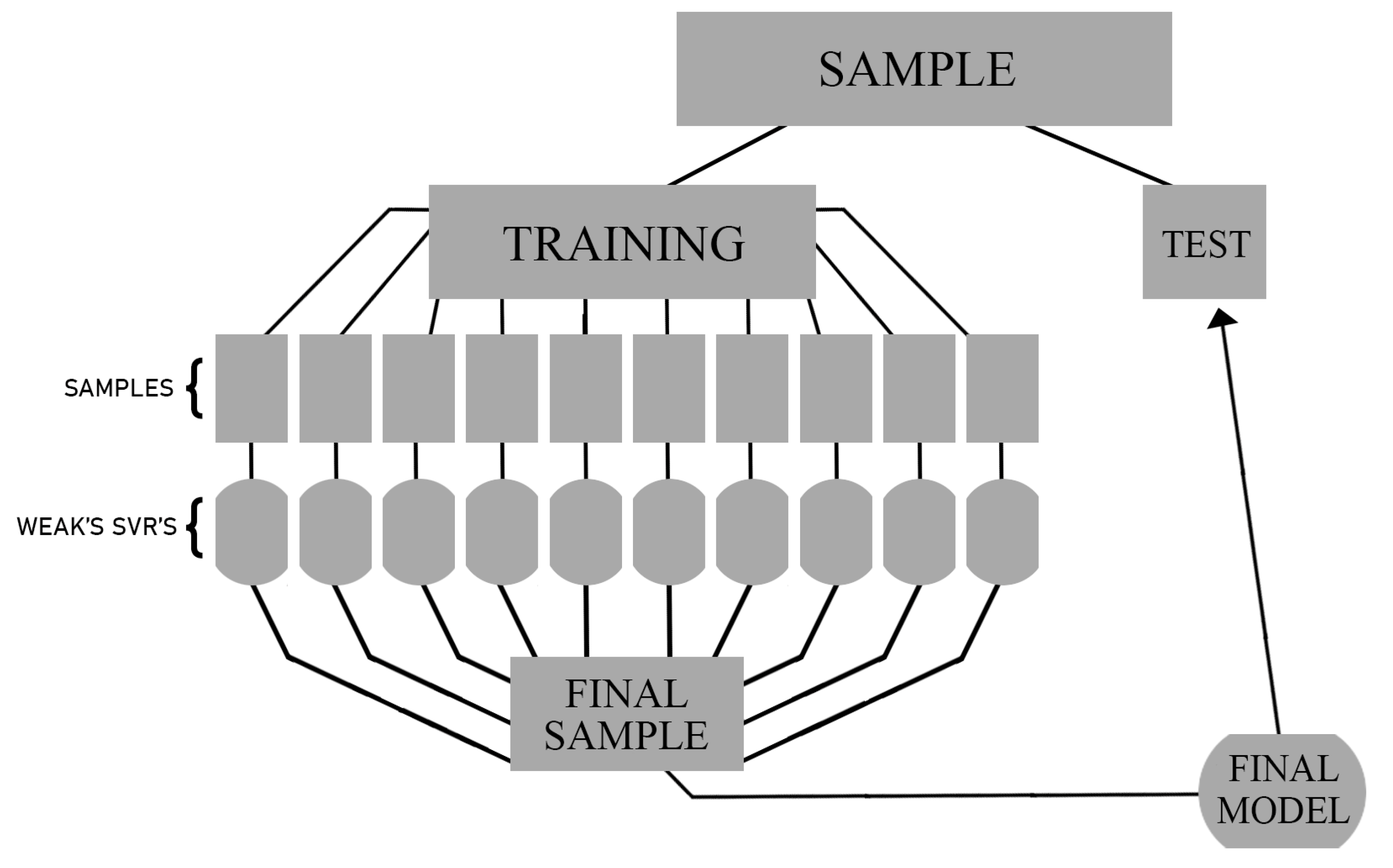
3. Reducing Learning Time Using Weak SVMs
3.1. Initial Sampling
3.2. Adjustment and Prediction of Weak SVRs
3.3. Selection of the Final Sample
| Algorithm 1: Speed Up SVR. |
|
4. ENEM as an Educational Selection Procedure
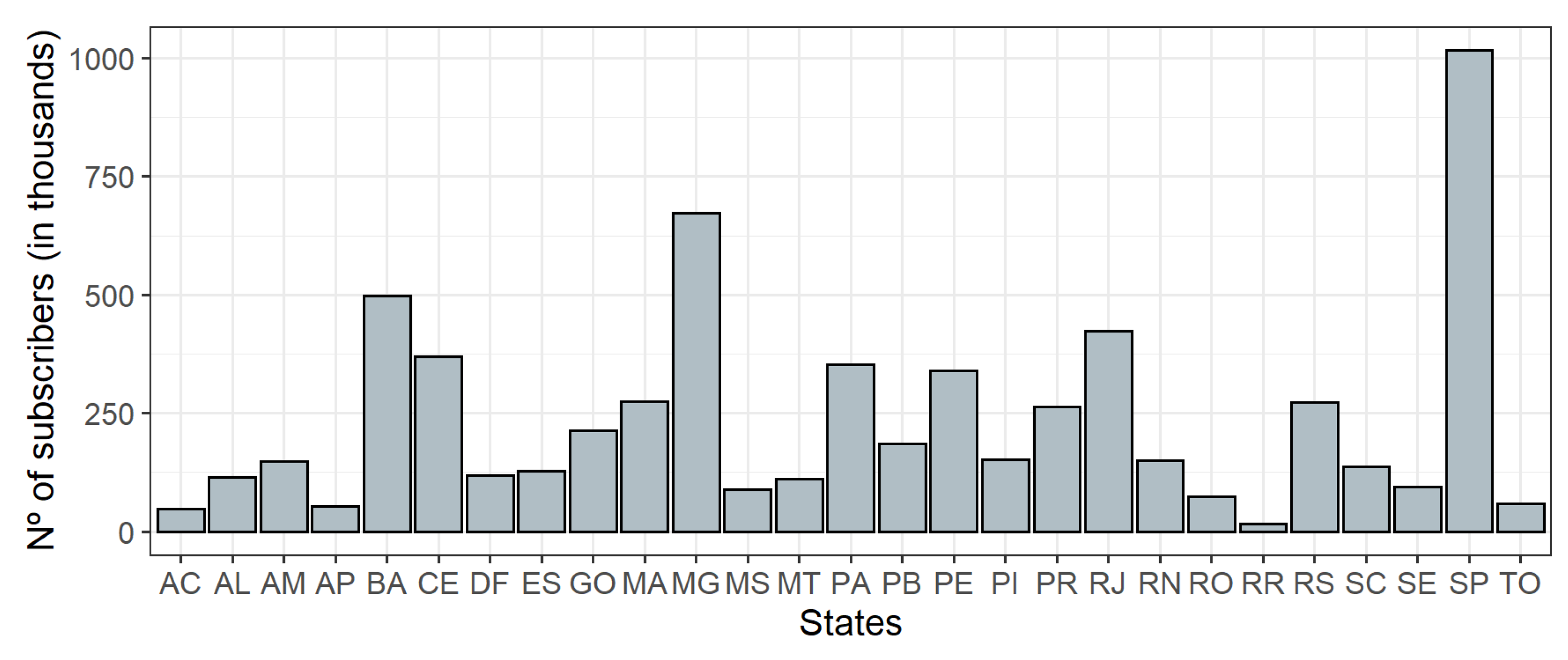
Data
5. Applications and Results
5.1. Modeling
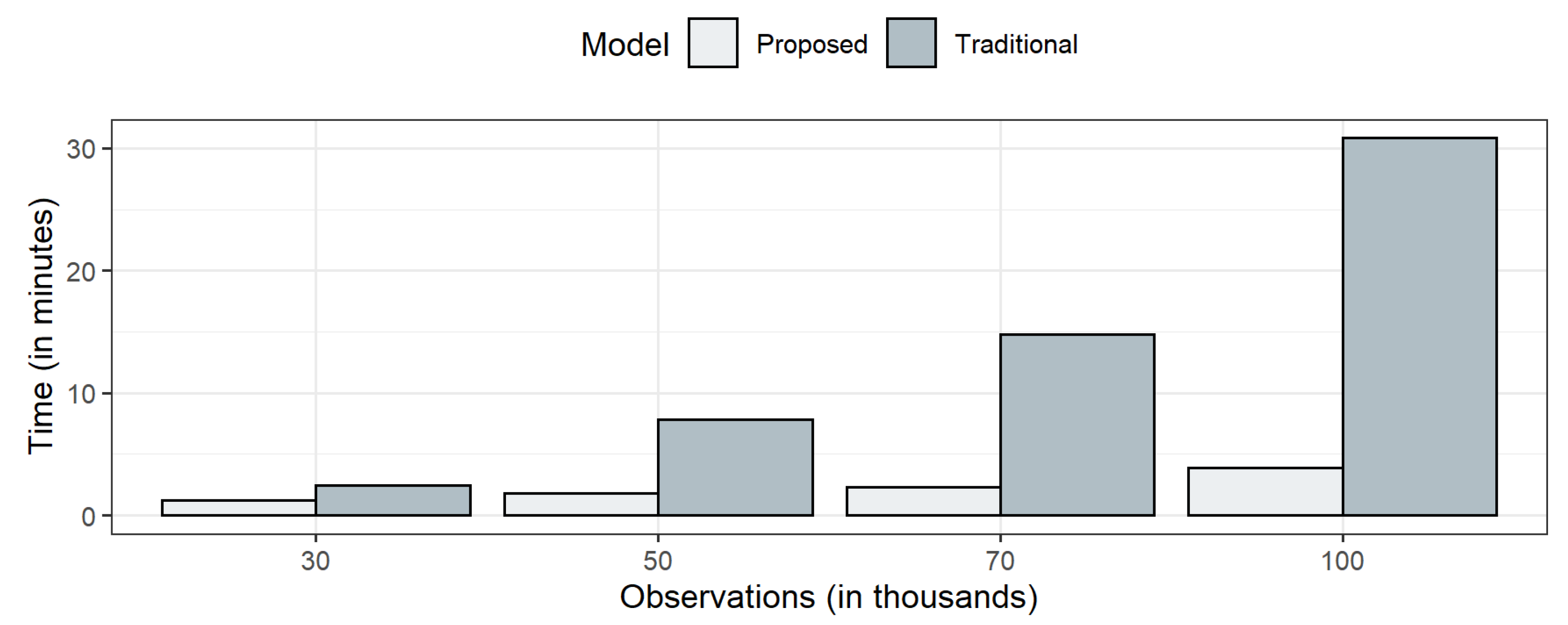
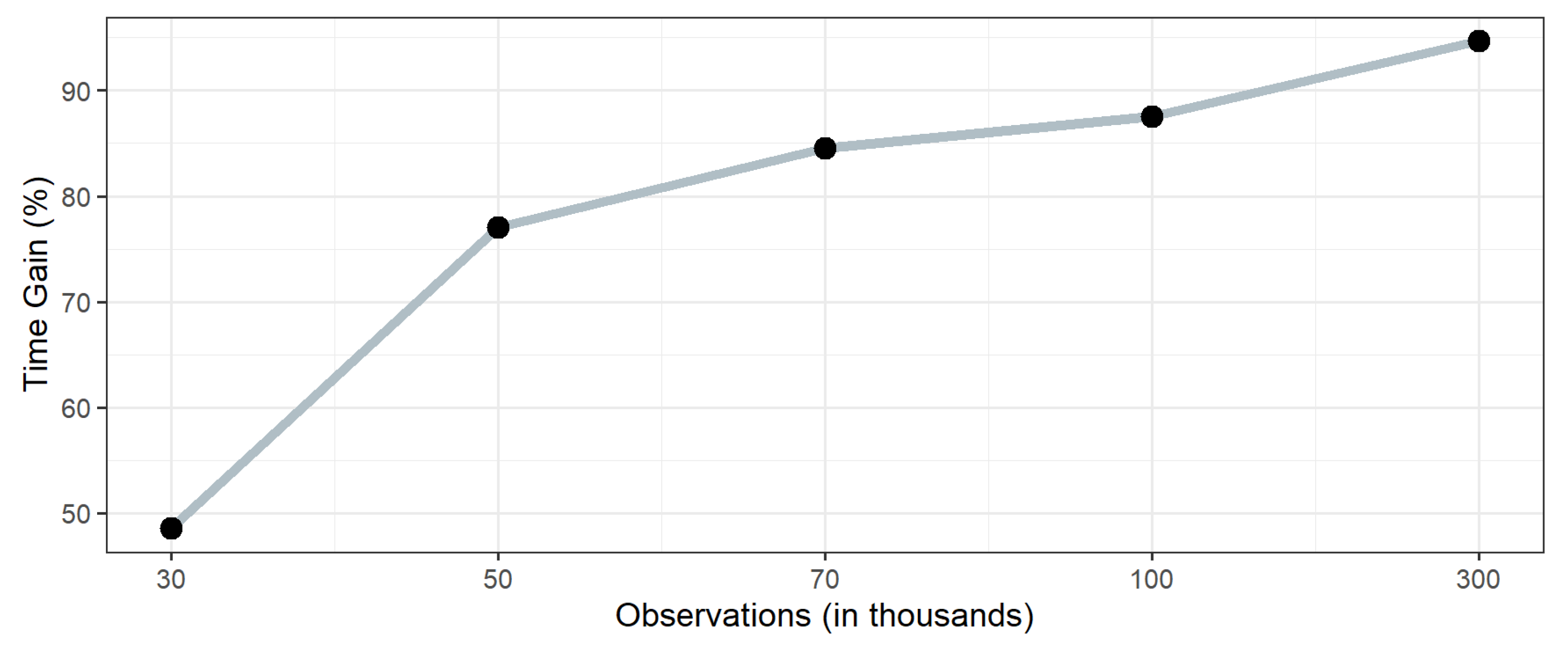
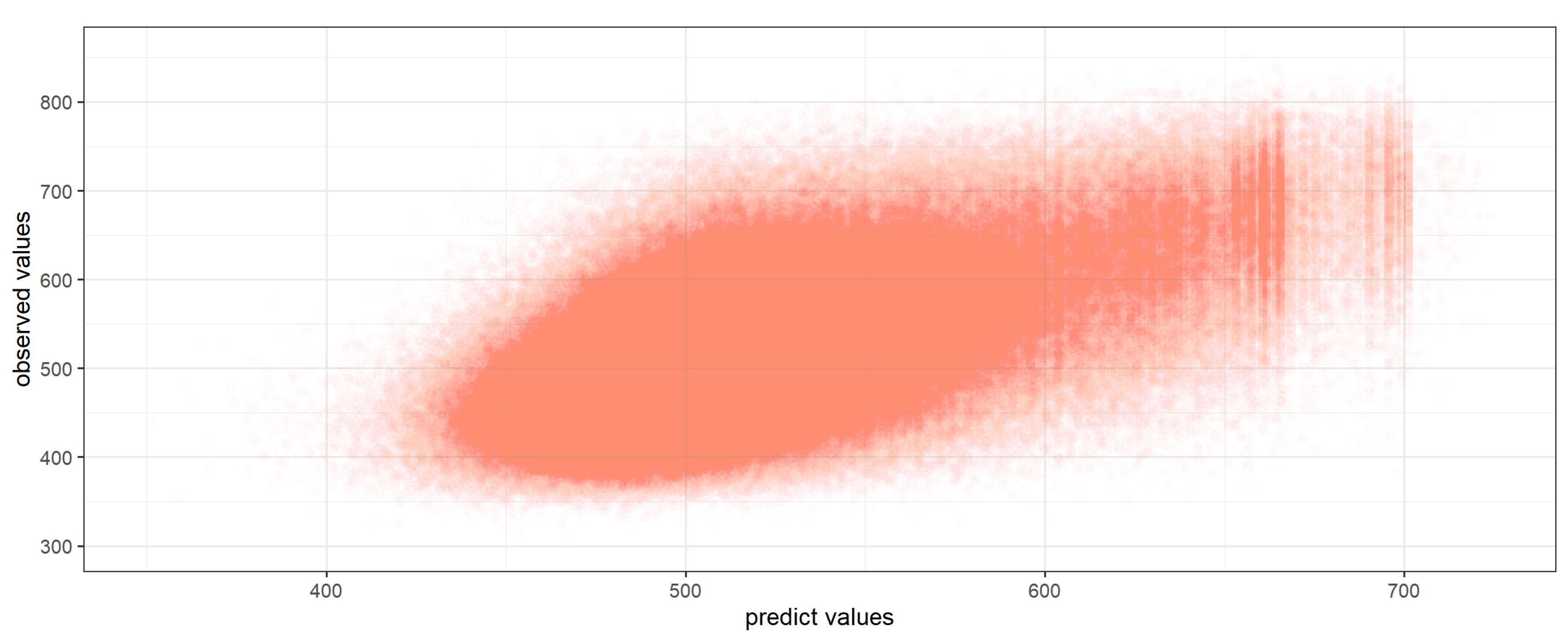
5.2. Comparative Analysis of the Predicted Grades
6. Final Considerations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Jaccoud, L.D.B.; Beghin, N. Desigualdades Raciais no Brasil: Um Balanço da Intervenção Governamental. Technical Report IPEA, 2002. Available online: http://repositorio.ipea.gov.br/handle/11058/9164 (accessed on 25 April 2020).
- Walker, J.; Pearce, C.; Boe, K.; Lawson, M. The Power of Education to Fight Inequality: How Increasing Educational Equality and Quality Is Crucial to Fighting Economic and Gender Inequality. 2019. Available online: https://oxfamilibrary.openrepository.com/handle/10546/620863 (accessed on 1 July 2021).
- Hamel, L.H. Knowledge Discovery with Support Vector Machines; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; Volume 3. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Shivaswamy, P.K.; Chu, W.; Jansche, M. A support vector approach to censored targets. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; pp. 655–660. [Google Scholar]
- Liang, J.; Yang, J.; Wu, Y.; Li, C.; Zheng, L. Big data application in education: Dropout prediction in edx MOOCs. In Proceedings of the 2016 IEEE Second International Conference on Multimedia Big Data (BigMM), Taipei, Taiwan, 20–22 April 2016; pp. 440–443. [Google Scholar]
- Mite-Baidal, K.; Delgado-Vera, C.; Solís-Avilés, E.; Espinoza, A.H.; Ortiz-Zambrano, J.; Varela-Tapia, E. Sentiment analysis in education domain: A systematic literature review. In International Conference on Technologies and Innovation; Springer: Cham, Switzerland, 2018; pp. 285–297. [Google Scholar]
- Pujianto, U.; Zaeni, I.A.E.; Irawan, N.O. SVM Method for Classification of Primary School Teacher Education Journal Articles. In Proceedings of the 2019 International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Denpasar, Indonesia, 3–4 October 2019; Volume 6, pp. 324–329. [Google Scholar]
- Ranjeeth, S.; Latchoumi, T.; Sivaram, M.; Jayanthiladevi, A.; Kumar, T.S. Predicting Student Performance with ANNQ3H: A Case Study in Secondary Education. In Proceedings of the 2019 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), Dubai, United Arab Emirates, 11–12 December 2019; pp. 603–607. [Google Scholar]
- López-Martín, C.; Ulloa-Cazarez, R.L.; García-Floriano, A. Support vector regression for predicting the productivity of higher education graduate students from individually developed software projects. IET Softw. 2017, 11, 265–270. [Google Scholar] [CrossRef]
- Fefilatyev, S.; Smarodzinava, V.; Hall, L.O.; Goldgof, D.B. Horizon detection using machine learning techniques. In Proceedings of the 2006 5th International Conference on Machine Learning and Applications (ICMLA’06), Orlando, FL, USA, 14–16 December 2006; pp. 17–21. [Google Scholar]
- Ahmad, I.; Basheri, M.; Iqbal, M.J.; Rahim, A. Performance comparison of support vector machine, random forest, and extreme learning machine for intrusion detection. IEEE Access 2018, 6, 33789–33795. [Google Scholar] [CrossRef]
- Libbrecht, M.W.; Noble, W.S. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 2015, 16, 321–332. [Google Scholar] [CrossRef]
- Shi, P.; Ray, S.; Zhu, Q.; Kon, M.A. Top scoring pairs for feature selection in machine learning and applications to cancer outcome prediction. BMC Bioinform. 2011, 12, 1–15. [Google Scholar] [CrossRef]
- Huang, S.; Cai, N.; Pacheco, P.P.; Narrandes, S.; Wang, Y.; Xu, W. Applications of support vector machine (SVM) learning in cancer genomics. Cancer Genom. Proteom. 2018, 15, 41–51. [Google Scholar]
- Bartlett, M.S.; Littlewort, G.; Frank, M.; Lainscsek, C.; Fasel, I.; Movellan, J. Recognizing facial expression: Machine learning and application to spontaneous behavior. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 568–573. [Google Scholar]
- Zendehboudi, A.; Baseer, M.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Amorim, M.J.; Barone, D.; Mansur, A.U. Técnicas de Aprendizado de Máquina Aplicadas na Previsao de Evasão Acadêmica. In Brazilian Symposium on Computers in Education (Simpósio Brasileiro de Informática na Educação-SBIE); 2008; Volume 1, pp. 666–674. Available online: https://www.semanticscholar.org/paper/T%C3%A9cnicas-de-Aprendizado-de-M%C3%A1quina-Aplicadas-na-de-Amorim-Barone/7b547c1ccb2b24cc16e5da6dcf2ea0922bb32bf9 (accessed on 1 July 2021).
- Romero, C.; Ventura, S. Educational data mining and learning analytics: An updated survey. Wiley Interdiscip. Rev. 2020, 10, e1355. [Google Scholar] [CrossRef]
- Campbell, C.; Levin, B. Using data to support educational improvement. Educ. Assess. Eval. Account. 2009, 21, 47. [Google Scholar] [CrossRef]
- Chiquetto, M.J.; Krapas, S. Livros didáticos baseados em apostilas: Como surgiram e por que foram amplamente adotados. Revista Brasileira de Pesquisa em Educação em Ciências 2012, 12, 173–191. [Google Scholar]
- Motz, B.A.; Carvalho, P.F.; de Leeuw, J.R.; Goldstone, R.L. Embedding experiments: Staking causal inference in authentic educational contexts. J. Learn. Anal. 2018, 5, 47–59. [Google Scholar] [CrossRef]
- Wu, P.; Dietterich, T.G. Improving SVM accuracy by training on auxiliary data sources. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 110. [Google Scholar]
- Huang, J.; Saleh, S.; Liu, Y. A Review on Artificial Intelligence in Education. Acad. J. Interdiscip. Stud. 2021, 10, 206. [Google Scholar] [CrossRef]
- Mahareek, E.A.; Desuky, A.S.; El-Zhni, H.A. Simulated annealing for SVM parameters optimization in student’s performance prediction. Bull. Electr. Eng. Inform. 2021, 10, 1211–1219. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Liu, C.; Zhang, X.; Zhang, H. Training data reduction to speed up SVM training. Appl. Intell. 2014, 41, 405–420. [Google Scholar] [CrossRef]
- Campbell, C.; Ying, Y. Learning with support vector machines. Synth. Lect. Artif. Intell. Mach. Learn. 2011, 5, 1–95. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July, 1992; pp. 144–152. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, NY, 1995. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Batalha, C. Modelos de Vetores de Suporte em séries Temporais: Uma Aplicaçãopara Criptomoedas. Master’s Thesis, Universidade Federal da Bahia, Salvador, Bahia, Brasil, 2019. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Yaohao, P. Support Vector Regression Aplicado à Previsão de taxas de Câmbio. 2016. Available online: https://repositorio.unb.br/bitstream/10482/23270/1/2016_PengYaohao.pdf (accessed on 15 October 2020).
- Lin, P.T.; Su, S.F.; Lee, T.T. Support vector regression performance analysis and systematic parameter selection. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 2, pp. 877–882. [Google Scholar]
- Platt, J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report MSR-TR-98-14; Microsoft Research: 1998. Available online: https://www.microsoft.com/en-us/research/publication/sequential-minimal-optimization-a-fast-algorithm-for-training-support-vector-machines/ (accessed on 1 July 2021).
- Fan, R.E.; Chen, P.H.; Lin, C.J.; Joachims, T. Working set selection using second order information for training support vector machines. J. Mach. Learn. Res. 2005, 6, 889–1918. [Google Scholar]
- Tsang, I.W.; Kwok, J.T.; Cheung, P.M.; Cristianini, N. Core vector machines: Fast SVM training on very large data sets. J. Mach. Learn. Res. 2005, 6, 363–392. [Google Scholar]
- Sarmento, P.L. Avaliação de Métodos de Seleção de Amostras Para redução do Tempo de Treinamento do Classificador SVM. Master’s Thesis, INPE, Sao Jose dos Campos, São Paulo, Brazil, 2014. [Google Scholar]
- Lee, Y. Handwritten digit recognition using k nearest-neighbor, radial-basis function, and backpropagation neural networks. Neural Comput. 1991, 3, 440–449. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Networks 1997, 8, 98–113. [Google Scholar] [CrossRef]
- Torres-Barrán, A.; Alaíz, C.M.; Dorronsoro, J.R. Faster SVM training via conjugate SMO. Pattern Recognit. 2021, 111, 107644. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Srebro, N. SVM optimization: Inverse dependence on training set size. In Proceedings of the 25th International Conference on Machine Learning, New York, NY, USA, 5–9 July, 2008; pp. 928–935. [Google Scholar]
- Shalev-Shwartz, S.; Singer, Y.; Srebro, N.; Cotter, A. Pegasos: Primal estimated sub-gradient solver for svm. Math. Program. 2011, 127, 3–30. [Google Scholar] [CrossRef]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A library for large linear classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Lee, Y.J.; Mangasarian, O.L. RSVM: Reduced support vector machines. In Proceedings of the 2001 SIAM International Conference on Data Mining, SIAM, Chicago, IL, USA, 5–7 April 2001; pp. 1–17. [Google Scholar]
- Ebrey, P.B.; Ebrey, P.B.; Ebrey, P.B.; Ebrey, P.B. The Cambridge Illustrated History of China; Cambridge University Press: Cambridge, UK, 1996; Volume 1. [Google Scholar]
- Viggiano, E.; Mattos, C. O desempenho de estudantes no Enem 2010 em diferentes regiões brasileiras. Revista Brasileira de Estudos Pedagógicos 2013, 94, 417–438. [Google Scholar] [CrossRef][Green Version]
- Bastos, C. Inscrições no Enem Crescem 20 Vezes Desde 1998. Portal do MEC. 2006. Available online: http://portal.mec.gov.br/ultimas-noticias/201-266094987/6881-sp-1649249425 (accessed on 10 May 2020).
- IBGE. Censo Brasileiro de 2010. Ibge-Instituto Brasileiro de Geografia e EstatíStica. Rio de Janeiro. 2012. Available online: https://censo2010.ibge.gov.br/ (accessed on 1 July 2021).
- IBGE. Technical Research: Pesquisa Nacional por Amostra de Domicílios. 2005. Available online: https://www.ibge.gov.br/estatisticas/sociais/populacao/9127-pesquisa-nacional-por-amostra-de-domicilios.html?=&t=o-que-e (accessed on 1 July 2021).
- R Core Team. R: A Language and Environment for Statistical Computing. 2013. Available online: r.meteo.uni.wroc.pl/web/packages/dplR/vignettes/intro-dplR.pdf (accessed on 1 July 2021).
- Stearns, B.; Rangel, F.M.; Rangel, F.; de Faria, F.F.; Oliveira, J.; Ramos, A.A.d.S. Scholar Performance Prediction Using Boosted Regression Trees Techniques; ESANN: Bruges, Belgium, 2017. [Google Scholar]
- Cortes, C.; Jackel, L.D.; Chiang, W.P. Limits on learning machine accuracy imposed by data quality. KDD 1995, 95, 57–62. [Google Scholar]
- Aziz, O.; Klenk, J.; Schwickert, L.; Chiari, L.; Becker, C.; Park, E.J.; Mori, G.; Robinovitch, S.N. Validation of accuracy of SVM-based fall detection system using real-world fall and non-fall datasets. PLoS ONE 2017, 12, e0180318. [Google Scholar] [CrossRef] [PubMed]
- Reiss, M. The use of AI in education: Practicalities and ethical considerations. Lond. Rev. Educ. 2021, 19, 1–14. [Google Scholar]
- Tuomi, I. The Impact of Artificial Intelligence on Learning, Teaching, and Education; Publications Office of the European Union: Luxembourg, 2018. [Google Scholar]
- Guo, B.; Zhang, R.; Xu, G.; Shi, C.; Yang, L. Predicting students performance in educational data mining. In Proceedings of the 2015 International Symposium on Educational Technology (ISET), Wuhan, China, 27–29 July 2015; pp. 125–128. [Google Scholar]
- Huang, A.Y.; Lu, O.H.; Huang, J.C.; Yin, C.; Yang, S.J. Predicting students’ academic performance by using educational big data and learning analytics: Evaluation of classification methods and learning logs. Interact. Learn. Environ. 2020, 28, 206–230. [Google Scholar] [CrossRef]


| Kernel Type | Parameters | |
|---|---|---|
| Linear | ||
| Polynomial | ||
| Gaussian |
| Description | Variable | Scale | Labels |
|---|---|---|---|
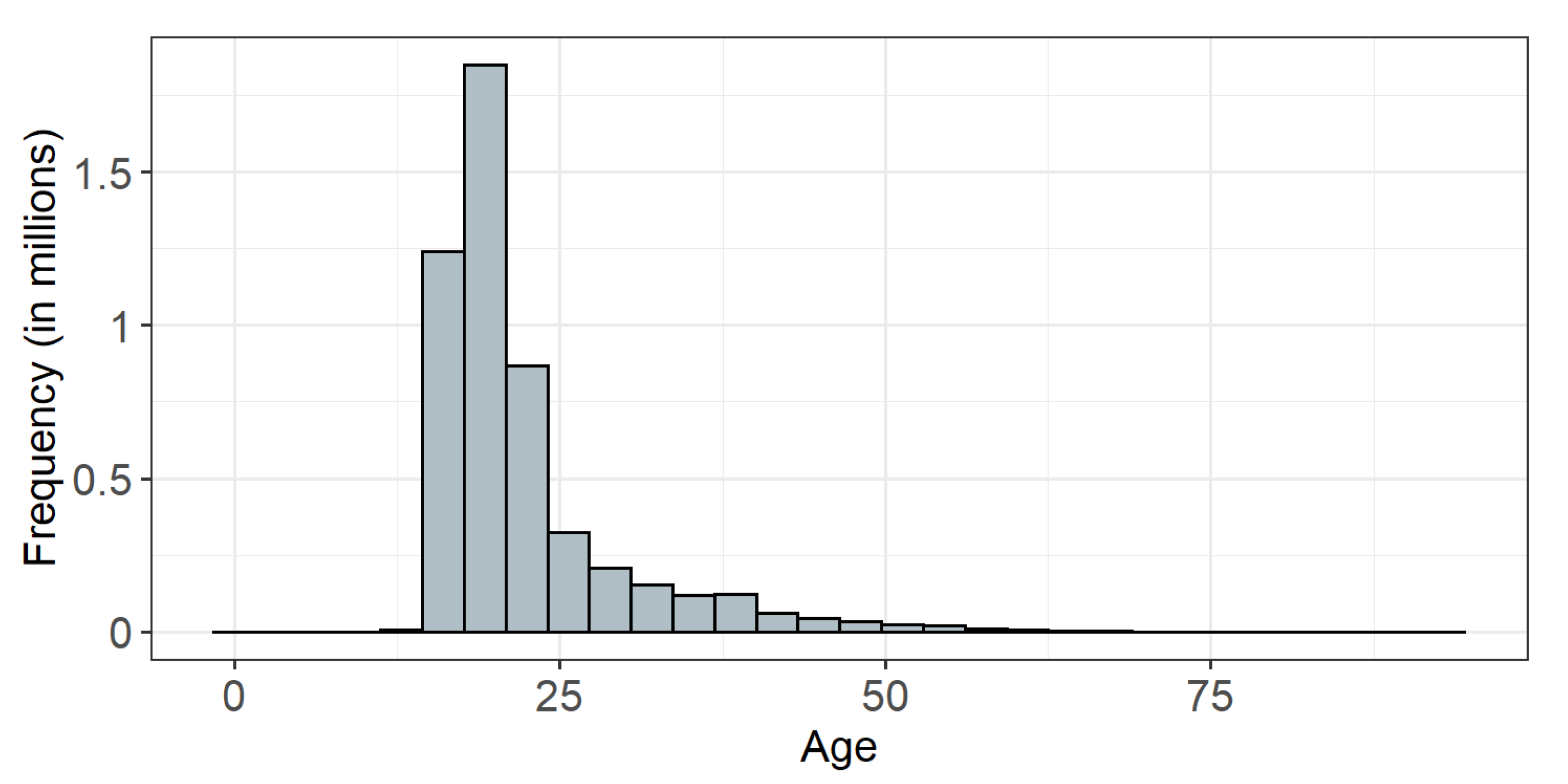
| Age | NU_IDADE | Numeric | 10, …, 90 |
| Gender | TP_SEXO | Categorical | M = Male, F = Female |
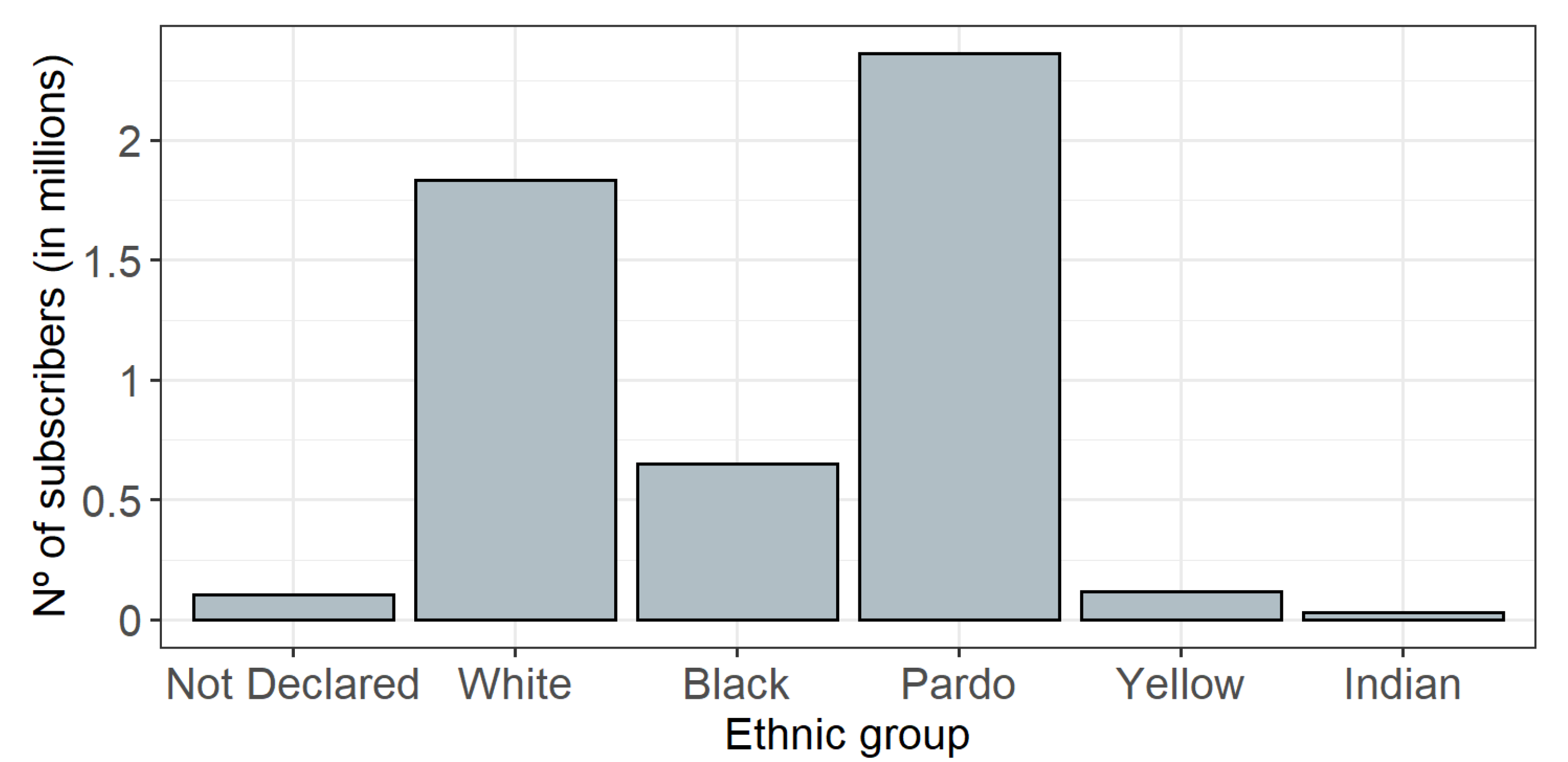
| Ethnic group | TP_COR_RACA | Categorical | Not Declared, White, Brown, Black, Yellow, Indigenous |
| Marital Status | TP_ESTADO_CIVIL | Categorical | Not Informed, Single, Married, Divorced, Widowed |
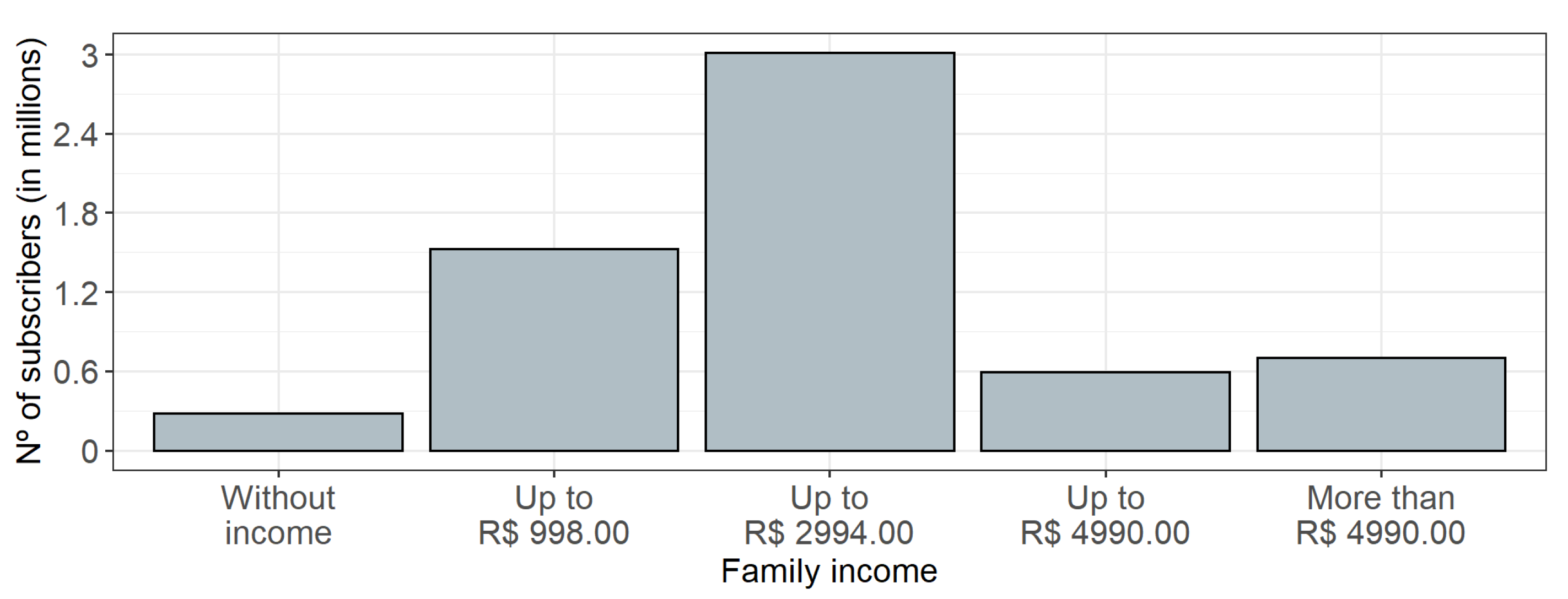
| Family income | Q006 | Categorical | Without Income, <998, 998–2994, 2994–4990, 4990+ |
| High School Completion Status | TP_ST_CONCLUSAO | Categorical | Complete High School, Completion in 2019, Incomplete High School |
| Conclusion year | TP_ANO_CONCLUIU | Categorical | Not Informed, 2016–2018, <2016 |
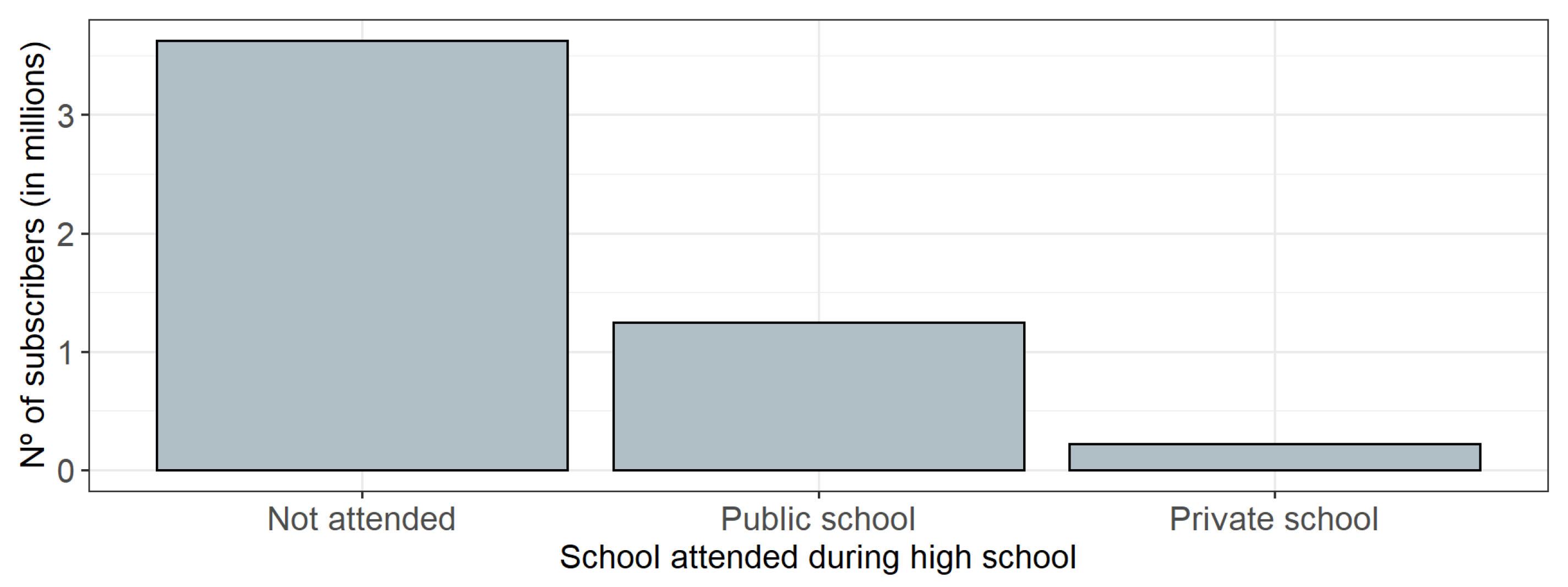
| High School Type | TP_ESCOLA | Categorical | Public, Private, Not attended |
| Foreign Language | TP_LINGUA | Categorical | English, Spanish |
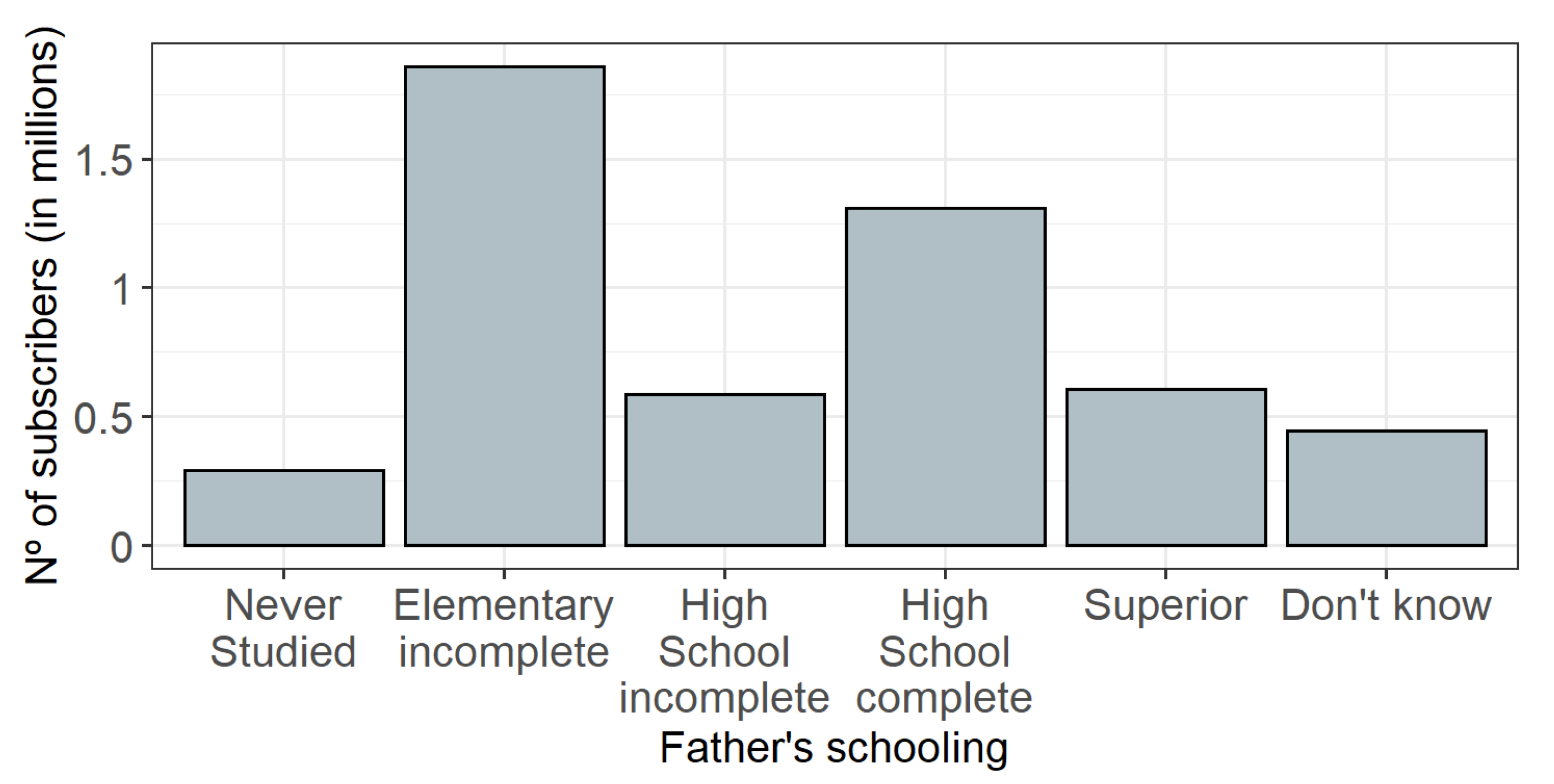
| Father’s Education | Q001 | Categorical | Never studied, Elementary incomplete, High school incomplete, High school complete, Superior, Don’t know |
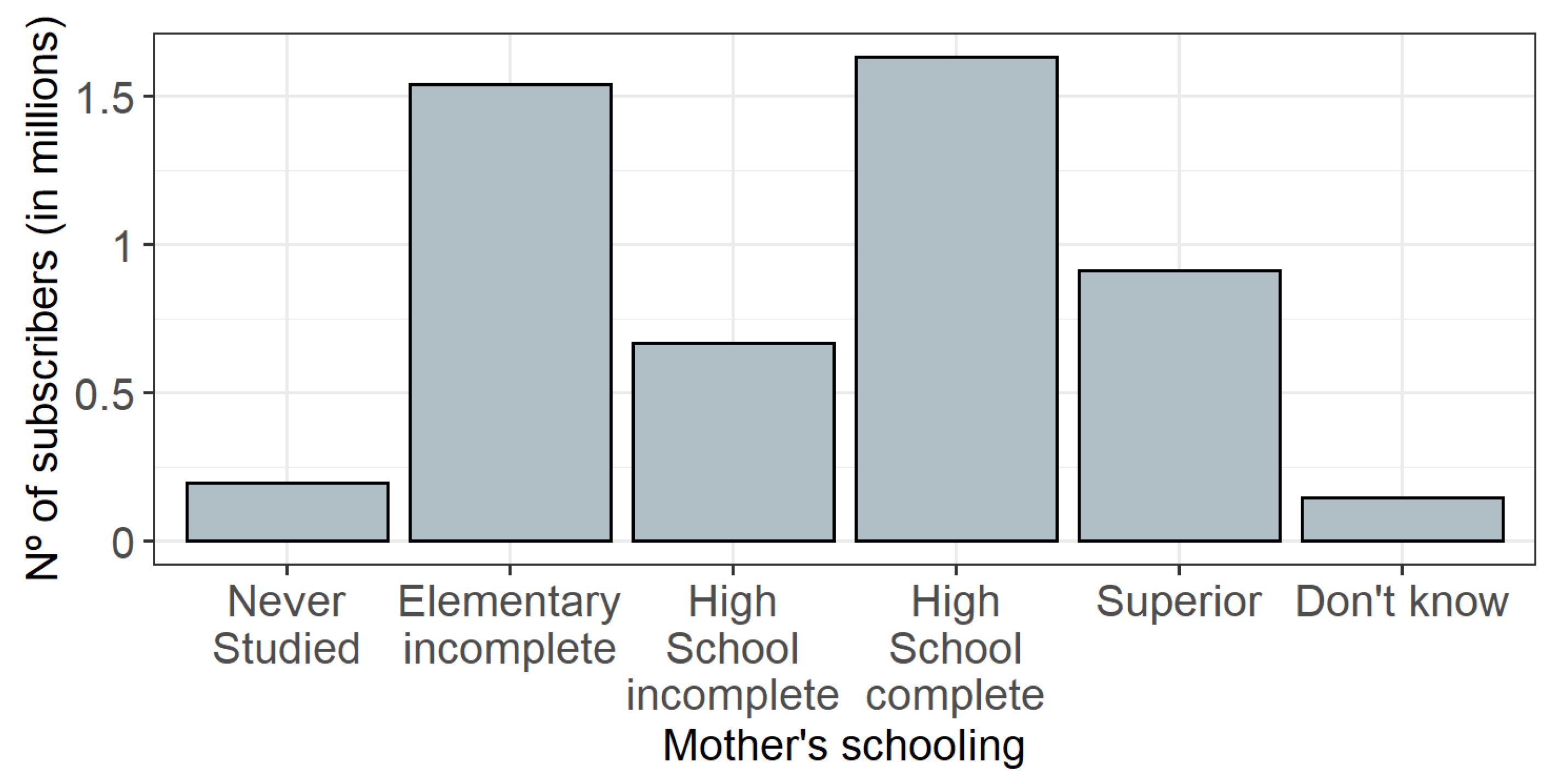
| Mother’s Education | Q002 | Categorical | Never studied, Elementary incomplete, High school incomplete, High school complete, Superior, Don’t know |
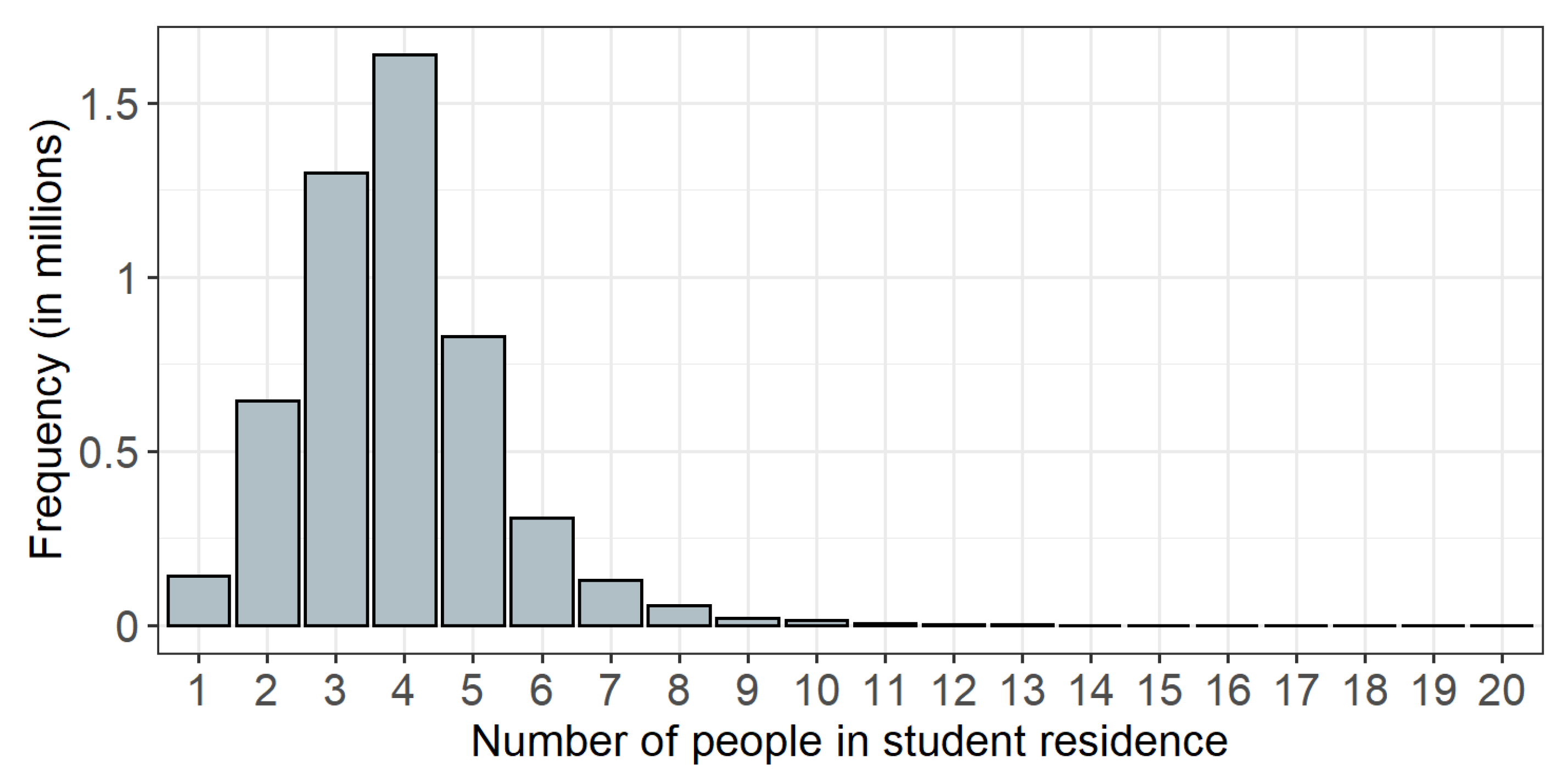
| Number of people in student residence | Q005 | Numeric | 1, …, 20 |
| Complete High School | Completion in 2019 | Completion after 2019 | Incomplete High School |
|---|---|---|---|
| 59% | 28% | 12% | 1% |
| English | Spanish |
|---|---|
| 2.4 million | 2.6 million |
| Humanities | Nature Sciences | Languages | Mathematics | Writing | |
|---|---|---|---|---|---|
| Absent | 22.9% | 27.1% | 22.9% | 27.1% | 23% |
| Present | 77% | 72.8% | 77% | 72.8% | 74.2% |
| Eliminated | 0.1% | 0.1% | 0.1% | 0.1% | 2.8% |
| Sample | RMSE | MAE | MAPE (%) | |
|---|---|---|---|---|
| 30 k observations | ||||
| Traditional Method | 21,000 | 72.83 | 57.23 | 57.27 |
| Proposed Method | 5250 | 74.64 | 58.93 | 57.58 |
| 50 k observations | ||||
| Traditional Method | 35,000 | 72.18 | 56.49 | 11.13 |
| Proposed Method | 8732 | 72.78 | 56.96 | 11.18 |
| 70 k observations | ||||
| Traditional Method | 49,000 | 71.94 | 56.63 | 11.14 |
| Proposed Method | 12,249 | 72.74 | 57.43 | 11.31 |
| 100 k observations | ||||
| Traditional Method | 70,000 | 72.22 | 56.78 | 11.18 |
| Proposed Method | 17,500 | 72.68 | 57.28 | 11.27 |
| 300 k observations | ||||
| Traditional Method | 210,000 | 72.23 | 56.75 | 16.70 |
| Proposed Method | 52,055 | 73.47 | 57.83 | 17.13 |
| Variables | 10% Worse Grades | 10% Better Grades |
|---|---|---|
| Age: Average; SD; [Min, Max] | 26.74; 10.29; [13, 86] | 19.57; 4.29; [2, 68] |
| Gender: Male (%)/Female (%) | 24/76 | 49/51 |
| Ethnic group: EG1 (%)/EG2 (%)/EG3 (%)/EG4 (%)/EG5 (%)/EG6 (%) | 2/11/20/62/2.5/2.5 | 3/71/3/20/2.5/0.5 |
| Marital Status: Not Informed (%)/Single (%)/Married (%)/Divorced (%)/Widowed (%) | 5/80/12/2/1 | 2.5/95/2/0.4/0.1 |
| High School Type: Not attended (%)/Public (%)/Private (%) | 61/38/1 | 56/3/41 |
| High School Completion Status: HSS1 (%)/HSS2 (%)/HSS3 (%) | 60/39/1 | 55/44/1 |
| Conclusion year: Not Informed (%)/2016-2018 (%)/<2016 (%) | 45/26/29 | 44/37/19 |
| Foreign Language: English (%)/Spanish (%) | 16/84 | 90/10 |
| Father’s Education: FE1 (%)/FE2 (%)/FE3 (%)/FE4 (%)/FE5 (%)/FE6 (%) | 23/49/5/4.5/0.5/17 | 0.5/4/4.5/28/62/1 |
| Mother’s Education: ME1 (%)/ME2 (%)/ME3 (%)/ME4 (%)/ME5 (%)/ME6 (%) | 19/49/9/10/1/12 | 0.1/1/2/25/71/0.9 |
| Number of people in student residence: Average; SD; [Min, Max] | 4.5; 1.92; [1, 20] | 3.6; 1.06; [1, 11] |
| Family income: FI1 (%)/FI2 (%)/FI3 (%)/FI4 (%)/FI5 (%) | 20/53/26/0.5/0.5 | 0.5/0.5/7/20/72 |
| Average Grade Predicted: Average; SD; [Min, Max] | 455.07; 13.15; [347.55, 469.85] | 643.14; 24.56; [606.85, 734.26] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pimentel, J.S.; Ospina, R.; Ara, A. Learning Time Acceleration in Support Vector Regression: A Case Study in Educational Data Mining. Stats 2021, 4, 682-700. https://doi.org/10.3390/stats4030041
Pimentel JS, Ospina R, Ara A. Learning Time Acceleration in Support Vector Regression: A Case Study in Educational Data Mining. Stats. 2021; 4(3):682-700. https://doi.org/10.3390/stats4030041
Chicago/Turabian StylePimentel, Jonatha Sousa, Raydonal Ospina, and Anderson Ara. 2021. "Learning Time Acceleration in Support Vector Regression: A Case Study in Educational Data Mining" Stats 4, no. 3: 682-700. https://doi.org/10.3390/stats4030041
APA StylePimentel, J. S., Ospina, R., & Ara, A. (2021). Learning Time Acceleration in Support Vector Regression: A Case Study in Educational Data Mining. Stats, 4(3), 682-700. https://doi.org/10.3390/stats4030041







