Inverted Weibull Regression Models and Their Applications

Abstract

In this paper, we propose the classical and Bayesian regression models for use in conjunction with the inverted Weibull (IW) distribution; there are the inverted Weibull Regression model (IW-Reg) and inverted Weibull Bayesian regression model (IW-BReg). In the proposed models, we suggest the logarithm and identity link functions, while in the Bayesian approach, we use a gamma prior and two loss functions, namely zero-one and modified general entropy (MGE) loss functions. To deal with the outliers in the proposed models, we apply Huber and Tukey’s bisquare (biweight) functions. In addition, we use the iteratively reweighted least squares (IRLS) algorithm to estimate Bayesian regression coefficients. Further, we compare IW-Reg and IW-BReg using some performance criteria, such as Akaike’s information criterion (AIC), deviance (D), and mean squared error (MSE). Finally, we apply the some real datasets collected from Saudi Arabia with the corresponding explanatory variables to the theoretical findings. The Bayesian approach shows better performance compare to the classical approach in terms of the considered performance criteria.

1. Introduction

McCullagh and Nelder [1] published a book on the generalized linear models (GLMs) that led to their widespread use and appreciation. They extended the scoring method to maximum likelihood estimation (MLE) in exponential families. Nelder and Pregibon [2] described methods of jointly estimating the parameters of both the link and variance functions. The iteratively reweighted least squares (IRLS) algorithm is amenable to some statistics and measures that are common to all the GLMs. Nelder and Wedderburn [3] used the Newton-Raphson process for regression coefficients estimates. They reported that the Newton-Raphson process with expected second derivatives is equivalent to the Fisher’s scoring technique. Additionally, De Jong and Heller [4] reported that the Newton-Raphson iteration equation leads to a sequence that often rapidly converges. These include the D statistic, along with some specific residuals and influence measures. Yuan and Bentler [5] reported that the convergence properties of the Fisher-scoring algorithm are affected by many factors. One of them is multicollinearity among the observed variables. If the sample or model implied covariance matrix is close to being singular, the Fisher-scoring algorithm may have difficulty reaching a set of converged solutions. Liao [6] introduced a systematic way of interpreting commonly used probability models: logit, probit, and the other GLMs.

The inverse Weibull (IW) model that was derived by Keller and Kamath [7] based on physical considerations on some mechanical components’ failures subject to degradation phenomena, assuming that the strength of a component decreases with time with a power law. Calabria and Pulcini [8] proposed the IW distribution as a suitable model to describe mechanical degradation phenomena. They investigated a statistical property of the maximum likelihood estimator of the IW reliability. Jiang et al. [9] derived the Weibull (W) and IW mixture models with a common shape parameter for a system’s components. They also used an example to illustrate that the proposed mixture model can be used to approximate the reliability behaviors of the consecutive-k-out-of-n systems. Mahmoud et al. [10] considered the order statistics arising from IW distribution. They also derived an exact expression for the single moments of order statistics. Pasari and Dikshit [11] investigated the suitability of W distribution in the probabilistic assessment of earthquake hazards. The performance is also compared with two other popular models from the same W family, namely the two-parameter W model and the IW model. Jazi et al. [12] proposed a discrete IW distribution, a discrete version of the continuous IW variable of fitting discrete-time reliability and survival data sets. Kundu and Howlader [13] considered the Bayesian inference and prediction problems of the IW distribution based on Type-II censored data. Qingtian et al. [14] discussed the definition of environmental factors and restricting conditions of constant failure mechanism Based on generally accepted basic hypotheses. They estimated the IW distribution environment factor using the MLE and Bayes estimation methods. Musleh and Helu [15] considered two types of inference procedures: the classical (MLE, Approximate MLE and the least square method (LSE)) and the Bayesians (the squared error loss function (SQR), Linex loss function (LIN), General entropy loss function (GE), the Precautionary loss function (PRE)) to estimate the unknown parameters of the IW distribution when data under consideration are progressively type-II censoring. Akgul et al. [16] used IW distribution for modeling the seasonal wind speed using the modified maximum likelihood (MML) estimators of the parameters. The MML estimators’ efficiencies are compared with the well-known maximum likelihood (ML) and the least-squares (LS) estimators via the Monte-Carlo simulation study. Nassar and Abo-Kasem [17] discussed the estimation problem of the unknown parameters of the IW distribution based on adaptive type-II progressively hybrid censored data. They used classical and Bayesian estimation methods to estimate the unknown parameters.

The Bayesian approach to modelling provides an alternative to the standard GLMs. The posterior mode estimation is an alternative to full posterior analysis or posterior mean estimation, which avoids numerical integrations or simulation methods. It has been proposed by many authors; see References [18,19]. Dey et al. [20] described how to conceptualize, perform, and critique the traditional GLMs from a Bayesian perspective and how to use modern computational methods to summarize inferences using simulation. Olsson [21] given an overview of the GLMs and has presented practical examples. The exponential family of distributions are discussed along with the maximum likelihood estimation and ways of assessing the fit of the model. Dobson and Barnett [22] presented a theoretical background of the GLMs. For the Bayesian estimation in this context, a useful asymmetric loss function, known as the LINEX loss function, was introduced by Varian (1975) and has been widely used by several authors. A suitable alternative to the modified LINEX loss is the general entropy (GE) loss function proposed by [23]. This loss function is a generalization of the entropy loss function used by several authors [23,24,25]. One highly used one is the zero-one loss function (for more details, see Reference [26]).

In order to reduce the influence of outliers on the estimate, some robust measures were proposed in the literature. The common robust estimation method can be divided into several categories: M, MM, median, L1, Msplit, R, S, least-trimmed squares, and sign-constraint robust least squares estimation. Among these, Huber’s M estimation has become one of the main robust estimation methods by virtue of its simple calculation and convenience to implement [27]. The key aspect is the involvement of a loss function that is applied to data errors that was selected to less rapidly increase than the square loss function that is used in least-squares or maximum-likelihood procedures. There exist several well-known families of loss functions, such as Huber, Hampel, and Tukey’s biweight (or bisquare) that can be used for the computation of M estimators [28]. The IW distribution is flexible distribution can be used as a competing to gamma and Weibull distributions to describe more widely real life data, failure characteristics, such as infant mortality, useful life and wear-out periods, applications in medicine and ecology, determining the cost-effectiveness, maintenance periods of reliability centered maintenance activities, and biological research (for more details, see References [7,9,13,29,30,31,32,33,34,35]).

This paper is structured as follows: In Section 2, we present an overview of the GLMs and propose the IW-Reg model under various link functions for estimating the model parameters. In Section 3, we estimate the IW-Bayesian regression (IW-BReg) model under a gamma prior, various link and two loss functions. In Section 4, we apply the theoretical results of both of IW-Reg and IW-BReg models to some real datasets collected from Saudi Arabia. Next, we investigate the performance of the proposed models in terms of some criteria, such as Akaike’s information criterion (AIC), mean squared error (MSE), and deviance (D). In addition, we propose Huber and Tukey’s bisquare (biweight) functions to improve IW-BReg models. In addition, we adopt the iteratively reweighted least squares (IRLS) algorithm to estimate the Bayesian regression coefficients. Finally, Section 5 draws a succinct conclusion to the findings.

2. Classical Approach

Nelder and Wedderburn [36] introduced the class of the GLMs, defined according to the assumption that $y_1,y_2,...y_n$ are observations of the response variable, with the density function of $y_i$ as follows:

$$\begin{array}{c}\hfill f(y_i;{\theta }_i)=e^{{\theta }_i{y}_i-\psi \left({\theta }_i\right)+c\left(y_i\right)},i=1,2,...,n,\end{array}$$

(1)

where $\psi (·)$, $c(·)$ are known functions, with ${\theta }_i$ being the canonical parameter. A link function, $g(.)$, relating to the regression coefficients, is given by

$$\begin{array}{c}\hfill g\left({\mu }_i\right)={\eta }_i=x_i^{\prime }\beta ,i=1,2,...,n,\end{array}$$

(2)

where $g\left({\mu }_i\right)={\theta }_i$, $\beta ={({\beta }_1,...,{\beta }_p)}^{\prime }$ is a vector of p unknown regression parameters, $x_i^{\prime }=(x_{i1},x_{i2},...,x_{ip})$ is a vector of explanatory variables, and ${\eta }_i$ is a linear predictor of the vectors $x_i^{\prime }$ and $\beta$. Here, the $g(.)$ is a link function, which is a monotonic differentiable invertible function. The model given by (1) and (2) is called the GLM. The GLM class includes, as special cases, linear regression and analysis of variance models, logit and probit models for quantal responses, log-linear models, and multinomial response models for counts; for more details, see Reference [36].

Consider that the probability density function of the IW distribution as follows [37]

$$\begin{array}{c}\hfill f(y;\alpha ,\gamma )=\alpha \gamma y^{-(\gamma +1)}{e}^{-\alpha y^{-\gamma }};y>0,\alpha ,\gamma >0;\end{array}$$

(3)

here, $\alpha >0$ and $\gamma >0$ are the shape and scale parameters, respectively. The mean value of the response variable is given by

$$\begin{array}{c}\hfill E\left(y\right)=\mu ={\alpha }^{\frac{1}{\gamma }}\Gamma \left(1-\frac{1}{\gamma }\right).\end{array}$$

(4)

The cumulative function of IW distribution is given by

$$\begin{array}{c}\hfill F(y;\alpha )=e^{-\alpha y^{-\gamma }};y>0.\end{array}$$

Let $y_i$ be a random sample from IW, and ${\alpha }_i={\left(\frac{{\mu }_i}{\Gamma \left(1-\frac{1}{\gamma }\right)}\right)}^{\gamma }$, the log-likelihood function based on $y_i$, is given by

$$\begin{array}{c}\hfill l_i=l\left({\mu }_i\right|y_i)=log{\left[\frac{{\mu }_i}{\Gamma \left(1-\frac{1}{\gamma }\right)}\right]}^{\gamma }+log\left(\gamma \right)-(\gamma +1)log\left(y_i\right)-{\left[\frac{{\mu }_i}{\Gamma \left(1-\frac{1}{\gamma }\right)}\right]}^{\gamma }{y}_i^{-\gamma }.\end{array}$$

(5)

The regression coefficients are estimated using the Fisher’s scoring technique [3,36]. In order to develop the GLMs for our models, the IW-Reg are similar to GLMs, except that the distribution of the response variable is not a member of the exponential family [38]. We also suggest some convenient link functions of $g(.)$, in view of (2), as in the following lemmas.

Lemma 1 (The IW-Reg model with a log link function).

Let the response variable Y have an IW distribution, $i=1,2,...,n$, and let the link function of the form be

$$\begin{array}{c}\hfill g\left({\mu }_i\right)=log\left({\mu }_i\right)={\eta }_i=x_i^{\prime }\beta ,i=1,2,...,n.\end{array}$$

(6)

Thus, the estimated coefficients ${\widehat{\beta }}^{\prime }=({\widehat{\beta }}_0,{\widehat{\beta }}_1,\cdots ,{\widehat{\beta }}_p)$ using Fisher’s scoring technique at the $s^{th}$ iteration is given by

$$\begin{array}{c}\hfill {\widehat{\beta }}^{\left(s\right)}={\left(X^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)X\right)}^{-1}{X}^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)Z,s=1,2,3,...,\end{array}$$

(7)

where X is a covariates matrix, ${\widehat{\beta }}_j^{\left(0\right)}$ is an initial vector, $W=diag(w_1,w_2,\cdots ,w_n)$,

$$\begin{array}{c}\hfill w_i={\left[\gamma \right]}^2,\end{array}$$

(8)

and $Z^{\prime }=(z_1,z_2,\cdots ,z_n)$, and

$$\begin{array}{c}\hfill z_i=\sum _{j=1}^p{x}_{ij}{\widehat{\beta }}_j^{(s-1)}+w_i^{-1}\gamma \left(1-\frac{{\left[{\mu }_i^{(s-1)}\right]}^{\gamma }}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)y_i\right]}^{\gamma }}\right).\end{array}$$

(9)

The procedure in (7) can be repeated until $|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}|\le \epsilon$. The IW-Reg model in this case is given by

$$\begin{array}{c}\hfill {\widehat{\mu }}_i^{\left(s\right)}=e^{\left({\widehat{\beta }}_0^{\left(s\right)}+{\widehat{\beta }}_1^{\left(s\right)}{x}_{i1}+....+{\widehat{\beta }}_p^{\left(s\right)}{x}_{ip}\right)}.\end{array}$$

(10)

Proof. 

Suppose that, in $y_i\sim f(y_i;\alpha ,\gamma )$, as in (3), the parameter $\gamma$ is assumed to be known. The log-likelihood function based on $y_i,i=1,2,...,n$ is given as in (5). The link function connecting the ${\mu }_i$ with the linear model $x_i^{\prime }\beta$, in this case, is given as in (6). $U_r$ for the log-likelihood is written from one observation as

$$\begin{array}{c}\hfill U_r\left(\beta \right)=\frac{\partial l\left(\beta \right)}{\partial {\beta }_r}=\sum _{i=1}^n\frac{\partial l_i}{\partial {\mu }_i}\frac{\partial {\mu }_i}{\partial {\eta }_i}\frac{\partial {\eta }_i}{\partial {\beta }_r},r=1,2,...,p.\end{array}$$

(11)

From (5) and (6), we have

$$\begin{array}{c}\hfill U_r\left(\beta \right)=\sum _i^n\gamma \left(\frac{1}{{\mu }_i}-\frac{{\mu }_i^{\gamma -1}}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)y_i\right]}^{\gamma }}\right){\mu }_i{x}_{ir},\end{array}$$

(12)

which can be written in the matrix notation as

$$\begin{array}{c}\hfill U\left(\widehat{\beta }\right)=X^{t}Q\left(y,\mu \left(\widehat{\beta }\right)\right).\end{array}$$

(13)

Taking the second derivatives of $l\left(\beta \right)$, we have

$$\begin{array}{c}\hfill \frac{\partial U_r\left(\beta \right)}{\partial {\beta }_j}=\frac{{\partial }^{2}l\left(\beta \right)}{\partial {\beta }_j\partial {\beta }_r}=\sum _i^n\gamma \left(\frac{-1}{{\mu }_i^2}-\frac{(\gamma -1){\mu }_i^{\gamma -2}}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)y_i\right]}^{\gamma }}\right){\mu }_i^2{x}_{ij}{x}_{ir},j=1,2,...,p;\end{array}$$

hence,

$$\begin{array}{c}\hfill -E\left(\frac{\partial U_r\left(\beta \right)}{\partial {\beta }_j}\right)=\sum _{i=1}^n\gamma \left(\frac{1}{{\mu }_i^2}+\frac{(\gamma -1){\mu }_i^{\gamma -2}E\left(y_i^{-\gamma }\right)}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)\right]}^{\gamma }}\right){\mu }_i^2{x}_{ir}{x}_{ij}.\end{array}$$

Since $E\left(y_i^{-\gamma }\right)={\left[\frac{{\mu }_i}{\Gamma \left(1-\frac{1}{\gamma }\right)}\right]}^{-\gamma }$ and $\frac{\partial {\mu }_i}{\partial {\beta }_j}={\mu }_i{x}_{ij}$, then $I_{rj}=-E\left(\frac{\partial U_r\left(\beta \right)}{\partial {\beta }_j}\right)={\sum }_i^n{\gamma }^2{x}_{ij}{x}_{ir},$ and

$$\begin{array}{c}\hfill I\left(\widehat{\beta }\right)=X^{\prime }W\left(\widehat{\beta }\right)X,\end{array}$$

(14)

where $W\left(\widehat{\beta }\right)$ is the diagonal matrix of weights, and $w_i$ is as it is in (8). Then,

$$\begin{array}{c}\hfill I\left({\widehat{\beta }}^{(s-1)}\right){\widehat{\beta }}^{\left(s\right)}=I\left({\widehat{\beta }}^{(s-1)}\right){\widehat{\beta }}^{(s-1)}+U\left({\widehat{\beta }}^{(s-1)}\right),s=1,2,3,....\end{array}$$

From (13) and (14), we have

$$\begin{array}{c}\hfill \left(X^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)X\right){\widehat{\beta }}^{\left(s\right)}=\left(X^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)X\right){\widehat{\beta }}^{(s-1)}+X^{\prime }Q\left(y,\mu \left({\widehat{\beta }}^{(s-1)}\right)\right).\end{array}$$

(15)

Finally, the estimated coefficients $\widehat{\beta }$ is given by

$$\begin{array}{c}\hfill {\widehat{\beta }}^{\left(s\right)}={\left(X^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)X\right)}^{-1}{X}^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)\left[X{\widehat{\beta }}^{(s-1)}+W^{-1}\left({\widehat{\beta }}^{(s-1)}\right)Q\left(y,\mu \left({\widehat{\beta }}^{(s-1)}\right)\right)\right],\end{array}$$

and

$$\begin{array}{c}\hfill {\widehat{\beta }}^{\left(s\right)}={\left(X^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)X\right)}^{-1}{X}^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)Z,\end{array}$$

as given in (7).

To derive the MLS of $\beta$, the IRLS is used. Under certain regularity conditions on the likelihood function, the MLE ${\widehat{\beta }}^{\left(s\right)}$ are asymptotically normal, unbiased, and efficient, with covariance matrix equal to the inverse of Fisher’s information matrix [39]. Thus, $\widehat{\beta }$ has asymptotically normal distribution,

$$\begin{array}{c}\hfill \widehat{\beta }\equiv N\left[\beta ,{\left(X^{\prime }WX\right)}^{-1}\right],\end{array}$$

where ${\left(X^{\prime }WX\right)}^{-1}$ is the inverse of Fisher’s information matrix. □

Lemma 2 (The IW-Reg model with identity link function).

Let the response variable Y have an IW distribution, $i=1,2,...,n$, and let the link function of the form be

$$\begin{array}{c}\hfill g\left({\mu }_i\right)={\mu }_i={\eta }_i=x_i^{\prime }\beta ,i=1,2,...,n.\end{array}$$

(16)

Thus, the estimated coefficients ${\widehat{\beta }}^{\prime }=({\widehat{\beta }}_0,{\widehat{\beta }}_1,\cdots ,{\widehat{\beta }}_p)$ using Fisher’s scoring technique at the $s^{th}$ iteration is given by

$$\begin{array}{c}\hfill {\widehat{\beta }}^{\left(s\right)}={\left(X^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)X\right)}^{-1}{X}^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)Z,s=1,2,3,...,\end{array}$$

(17)

where X is a covariates matrix, ${\widehat{\beta }}_j^{\left(0\right)}$ is an initial vector, $W=diag(w_1,w_2,\cdots ,w_n)$,

$$\begin{array}{c}\hfill w_i={\left[\frac{\gamma }{{\mu }_i^{(s-1)}}\right]}^2,\end{array}$$

(18)

and $Z^{\prime }=(z_1,z_2,\cdots ,z_n)$, and

$$\begin{array}{c}\hfill z_i=\sum _{j=1}^p{x}_{ij}{\widehat{\beta }}_j^{(s-1)}+w_i^{-1}\gamma \left(\frac{1}{{\mu }_i^{(s-1)}}-\frac{{\left[{\mu }_i^{(s-1)}\right]}^{\gamma -1}}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)y_i\right]}^{\gamma }}\right).\end{array}$$

(19)

The procedure in (17) can be repeated until $|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}|\le \epsilon$. The IW-Reg model in this case is given by

$$\begin{array}{c}\hfill {\widehat{\mu }}_i^{\left(s\right)}={\widehat{\beta }}_0^{\left(s\right)}+{\widehat{\beta }}_1^{\left(s\right)}{x}_{i1}+....+{\widehat{\beta }}_p^{\left(s\right)}{x}_{ip}.\end{array}$$

(20)

Proof. 

Suppose that, in $y_i\sim f(y_i;\alpha ,\gamma )$, as in (3), the parameter $\gamma$ is assumed to be known. The log-likelihood function based on $y_i,i=1,2,...,n$ is given as in (5). The link function connecting the ${\mu }_i$ with the linear model $x_i^{\prime }\beta$, in this case, is given in (16). From (5), (11), and (16), we have

$$\begin{array}{c}\hfill U_r\left(\beta \right)=\sum _{i=1}^n\gamma \left(\frac{1}{{\mu }_i}-\frac{{\mu }_i^{\gamma -1}}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)y_i\right]}^{\gamma }}\right)x_{ir},\end{array}$$

which can be written in the matrix notation as in (13). Taking the second derivatives of $l\left(\beta \right)$, we have

$$\begin{array}{c}\hfill \frac{{\partial }^{2}l\left(\beta \right)}{\partial {\beta }_j\partial {\beta }_r}=\sum _i^n\gamma \left(\frac{-1}{{\mu }_i^2}-\frac{(\gamma -1){\mu }_i^{\gamma -2}}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)y_i\right]}^{\gamma }}\right)x_{ir}{x}_{ir};\end{array}$$

hence,

$$\begin{array}{c}\hfill -E\left(\frac{\partial U_r\left(\beta \right)}{\partial {\beta }_j}\right)=-E\left(\frac{{\partial }^{2}l\left(\beta \right)}{\partial {\beta }_j\partial {\beta }_r}\right)=\sum _i^n\gamma \left(\frac{1}{{\mu }_i^2}+\frac{(\gamma -1){\mu }_i^{\gamma -2}E\left(y_i^{-\gamma }\right)}{{\left[\Gamma \left(1-\frac{1}{\gamma }\right)\right]}^{\gamma }}\right)x_{ij}{x}_{ir},\end{array}$$

since $E\left(y_i^{-\gamma }\right)={\left[\frac{{\mu }_i}{\Gamma \left(1-\frac{1}{\gamma }\right)}\right]}^{-\gamma }$ and $\frac{\partial {\mu }_i}{\partial {\beta }_j}=x_{ij}$, then $I_{rj}=-E\left(\frac{\partial U_r\left(\beta \right)}{\partial {\beta }_j}\right)={\sum }_i^n{x}_{ij}{\left[\frac{\gamma }{{\mu }_i^{(s-1)}}\right]}^2{x}_{ir}$ and $I\left(\widehat{\beta }\right)$ is given as in (14), where $W\left(\widehat{\beta }\right)$ is the diagonal matrix of weights, and $w_i$ is as it is in (18). Using (15), we have ${\widehat{\beta }}^{\left(s\right)}$ as in (17). □

Lemma 3 (Convergence estimates in the Fisher’s scoring process).

Let the response variable Y have an IW distribution, and let the link function of the form be $g\left({\mu }_i\right)={\eta }_i=x_i^{\prime }\beta$ i = 1,2,...,n, the estimated coefficients ${\widehat{\beta }}^{\prime }=({\widehat{\beta }}_0,{\widehat{\beta }}_1,\cdots ,{\widehat{\beta }}_p)$ using Fisher’s scoring technique at the $s^{th}$ iteration is given by

$$\begin{array}{c}\hfill {\widehat{\beta }}^{\left(s\right)}={\left(X^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)X\right)}^{-1}{X}^{\prime }W\left({\widehat{\beta }}^{(s-1)}\right)Z,s=1,2,3,...,\end{array}$$

Then, $p\left(|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}|\le \epsilon \right)=1$, where X is a covariate matrix, W is the diagonal matrix of weights, and Z is a vector of the response variable.

Proof. 

Suppose that, in $y_i\sim f(y_i;\alpha ,\gamma )$, as in (3), the parameter $\gamma$ is assumed to be known. The log-likelihood function based on $y_i,i=1,2,...,n$ is given as in (5). Furthermore, suppose that the link function $g\left({\mu }_i\right)$ connecting the ${\mu }_i$ with the linear model $x_i^{\prime }\beta$ is given as in (2). The Fisher’s scoring process to obtain the MLEs estimates $\widehat{\beta }$ is given by computing the iterations:

$$\begin{array}{c}\hfill {\widehat{\beta }}^{\left(s\right)}={\widehat{\beta }}^{(s-1)}+{\left[I\left({\widehat{\beta }}^{(s-1)}\right)\right]}^{-1}U\left({\widehat{\beta }}^{(s-1)}\right),s=1,2,3,....,\end{array}$$

(21)

where $U\left({\widehat{\beta }}^{(s-1)}\right)$ is the score vector for the log-likelihood (5), and $I\left({\widehat{\beta }}^{(s-1)}\right)$ is the Fisher’s information matrix. Taking the expectation of the Equation (21), we have

$$\begin{array}{c}\hfill E\left[{\widehat{\beta }}^{(s-1)}\right]=E\left[{\widehat{\beta }}^{(s-1)}\right]=\xi ,\end{array}$$

(22)

since the estimates ${\widehat{\beta }}^{(s-1)}$ are the MLEs, and $E\left[{\left[I\left({\widehat{\beta }}^{(s-1)}\right)\right]}^{-1}U\left({\widehat{\beta }}^{(s-1)}\right)\right]=0$. Hence, we get $E\left[{\widehat{\beta }}_j^{\left(s\right)}\right]=E\left[{\widehat{\beta }}_j^{(s-1)}\right]={\xi }_i$ for all $j=1,2,...,p$ where $\xi$ is a vector of expectations. From (21), we have

$$\begin{array}{c}\hfill \left|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right|=\left|{\left[I\left({\widehat{\beta }}^{(s-1)}\right)\right]}^{-1}U\left({\widehat{\beta }}^{(s-1)}\right)\right|.\end{array}$$

(23)

Using the Chebyshev inequality, for every $\omega >0$, we find

$$\begin{array}{c}\hfill p\left(\left|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right|\le \omega \right)\ge 1-\frac{E\left(\left|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right|\right)}{\omega }.\end{array}$$

(24)

Now, by the Jensen inequality,

$$\begin{array}{c}\hfill p\left(\left|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right|\le \omega \right)\ge 1-\frac{\left|E\left({\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right)\right|}{\omega }.\end{array}$$

(25)

Let $\omega =\epsilon$ and, using (25), we then obtain

$$\begin{array}{c}\hfill p\left(\left|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right|\le \epsilon \right)=1,\end{array}$$

(26)

since $E\left({\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right)=0$. On the other hand, by choosing $\omega =\frac{\epsilon }{n}$ into the Equation (26), this becomes $p\left(\left|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}\right|\le 0\right)=1$ as $n\to \infty$. □

3. Bayesian Approach

Diaconis and Ylvisker [40] introduced a conjugate prior distribution for the exponential family, which, as in (1), can be shown as

$$\begin{array}{c}\hfill \pi \left({\theta }_i\right)=k_1{e}^{m{\mu }_0{\theta }_i-m\psi \left({\theta }_i\right)},i=1,2,...,n\end{array}$$

(27)

where $k_1$ is a normalization constant, and $m,{\mu }_0$ are natural parameters. The ${\theta }_i$ values are connected to the regression coefficients by the link function ${\eta }_i=x_i^{\prime }\beta$ as

$$\begin{array}{c}\hfill g^{*}\left({\eta }_i\right)={\theta }_i.\end{array}$$

(28)

The posterior distribution of ${\theta }_i$ is given by

$$\begin{array}{c}\hfill \pi \left({\theta }_i\right|y_i)=k_2{e}^{(y_i+m{\mu }_0){\theta }_i-(1+m)\psi \left({\theta }_i\right)}.\end{array}$$

(29)

Das and Dey [41] suggested a Jacobian transformation and rewrote (29) with the term ${\eta }_i$, as

$$\begin{array}{c}\hfill \pi \left({\eta }_i\right|y_i)=K_2{e}^{(y_i+m{\mu }_0)g^{*}\left({\eta }_i\right)-(1+m)\psi \left(g^{*}\left({\eta }_i\right)\right)}\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i},\end{array}$$

(30)

where $k_2$ is a normalization constant, and $\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}\ne 0$. They used a zero-one loss function to attain the posterior mode of (30) as $\widehat{{\eta }_i}=h\left(y_i\right)$; hence, the estimated coefficients ${\widehat{\beta }}^{*}={({\widehat{\beta }}_0^{*},{\widehat{\beta }}_1^{*},...,{\widehat{\beta }}_p^{*})}^{\prime }$ are given by

$$\begin{array}{c}\hfill {\widehat{\beta }}^{*}={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }\widehat{\eta },\end{array}$$

(31)

where ${\widehat{\beta }}^{*}$ is the least square estimates, and ${\widehat{\eta }}^{\prime }=({\widehat{\eta }}_1,{\widehat{\eta }}_2,...,{\widehat{\eta }}_n)$ [40,41]. Under regularity conditions, the estimator ${\widehat{\beta }}^{*}$ has a asymptotically normal distribution $\widehat{\beta }\equiv N\left[\beta ,F^{-1}\right]$, where $F^{-1}$ is the inverse of Bayesian Fisher’s information (BIF). Note that the BFI is given by

$$\begin{array}{c}\hfill F={\left[\frac{\partial }{\partial \eta }log\pi \left(\eta \right|y)\right]}^2,\end{array}$$

where $\pi \left(\eta \right|y)$ is the posterior pdf of $\eta$ [39,42,43].

In order to develop the Bayesian approach, we propose a modified loss function of the general entropy (MGE) loss function to be appropriate for the Bayesian estimates. The MGE loss function is introduced in the following lemma.

Lemma 4 (The MGE loss function).

Consider that the posterior distribution of the ${\eta }_i$ is $\pi \left({\eta }_i\right|y_i)$, ${\widehat{\eta }}_i$ is an estimate of ${\eta }_i$, and $y_i$, $i=1,2,...,n$ are independent observations. A suitable alternative loss function to the GE loss is the MGE loss function, given as

$$\begin{array}{c}\hfill l\left(g^{*}({\widehat{\eta }}_i\right);g^{*}\left({\eta }_i\right))\propto {\left(\frac{g^{*}\left({\widehat{\eta }}_i\right)}{g^{*}\left({\eta }_i\right)}\right)}^{\kappa }-\kappa log\left(\frac{g^{*}\left({\widehat{\eta }}_i\right)}{g^{*}\left({\eta }_i\right)}\right)-1,\kappa \ne 0.\end{array}$$

(32)

Thus, the posterior Bayes estimates of ${\eta }_i$ is given by solving the equation

$$\begin{array}{c}\hfill E\left({\left[g^{*}\left({\eta }_i\right)\right]}^{-\kappa }|y_i\right)={\left[g^{*}\left({\widehat{\eta }}_i\right)\right]}^{-\kappa }\frac{\partial g^{*}\left({\widehat{\eta }}_i\right)}{\partial {\widehat{\eta }}_i}.\end{array}$$

(33)

Proof. 

Consider the MGE loss function is given as in (32). The posterior expectation of the loss function with respect to the posterior $\pi \left({\eta }_i\right|y_i)$ is given as

$$\begin{array}{c}\hfill E\left[l(g^{*}\left({\widehat{\eta }}_i\right);g^{*}\left({\eta }_i\right)|y_i)\right]={\int }_{\infty }^{-\infty }\left[{\left(\frac{g^{*}\left({\widehat{\eta }}_i\right)}{g^{*}\left({\eta }_i\right)}\right)}^{\kappa }-\kappa log\left(\frac{g^{*}\left({\widehat{\eta }}_i\right)}{g^{*}\left({\eta }_i\right)}\right)-1\right]\pi \left({\eta }_i\right|y_i)d{\eta }_i,\end{array}$$

$$\begin{array}{c}\hfill ={\left[g^{*}\left({\widehat{\eta }}_i\right)\right]}^{\kappa }{\int }_{\infty }^{-\infty }\left[{\left(\frac{1}{g^{*}\left({\eta }_i\right)}\right)}^{\kappa }\right]\pi \left({\eta }_i\right|y_i)d{\eta }_i-\kappa {\int }_{\infty }^{-\infty }\left[log{g}^{*}\left({\widehat{\eta }}_i\right)-log{g}^{*}\left({\eta }_i\right)\right]\pi \left({\eta }_i\right|y_i)d{\eta }_i-1.\end{array}$$

The value of ${\widehat{\eta }}_i$ that minimizes the posterior expectation of the MGE loss function is obtained by solving the equation

$$\begin{array}{c}\hfill \frac{\partial E\left[l(g^{*}\left({\widehat{\eta }}_i\right);g^{*}\left({\eta }_i\right)|y_i)\right]}{\partial {\widehat{\eta }}_i}=\kappa {\left[g^{*}\left({\widehat{\eta }}_i\right)\right]}^{\kappa -1}E\left({\left[g^{*}\left({\eta }_i\right)\right]}^{-\kappa }|y_i\right)-\kappa \frac{1}{g^{*}\left({\widehat{\eta }}_i\right)}\frac{\partial g^{*}\left({\widehat{\eta }}_i\right)}{\partial {\widehat{\eta }}_i}=0;\end{array}$$

hence,

$$\begin{array}{c}\hfill {\left[g^{*}\left({\widehat{\eta }}_i\right)\right]}^{\kappa -1}E\left({\left[g^{*}\left({\eta }_i\right)\right]}^{-\kappa }|y_i\right)=\frac{1}{g^{*}\left({\widehat{\eta }}_i\right)}\frac{\partial g^{*}\left({\widehat{\eta }}_i\right)}{\partial {\widehat{\eta }}_i},\end{array}$$

and

$$\begin{array}{c}\hfill E\left({\left[g^{*}\left({\eta }_i\right)\right]}^{-\kappa }|y_i\right)={\left[g^{*}\left({\widehat{\eta }}_i\right)\right]}^{-\kappa }\frac{\partial g^{*}\left({\widehat{\eta }}_i\right)}{\partial {\widehat{\eta }}_i},\end{array}$$

as given in (33). □

In order to develop a Bayesian approach, we suggest inverted Weibull Bayesian generalized linear models (IW-BReg) that are similar to the approach in Section 3, except that the distribution of the response variable is not a member of the exponential family. We use the general form of the posterior in (30), and since $g(·)$ is a monotonic differentiable function, then we attain the posterior Bayes estimates. Moreover, we use the a log and identity link functions with different loss functions. The IW-BReg estimates correspond to the link functions using different loss functions, as in the following lemmas.

Lemma 5 (The IW-BReg model based on zero-one loss function).

Let the response variable Y have an IW distribution and let the link function of the form be as in (2). Consider that α has a gamma prior $G\left(\nu ,\lambda \right)$ with the following density function:

$$\begin{array}{c}\hfill \pi \left(\alpha \right)=\frac{{\lambda }^{\nu }}{\Gamma \left(\nu \right)}{e}^{-\lambda \alpha }{\alpha }^{\nu -1},\alpha >0,\lambda ,\nu >0.\end{array}$$

(34)

Thus, the posterior mode of ${\eta }_i$ by using a zero-one loss function can be derived by solving the following equation:

$$\begin{array}{c}\hfill \frac{\nu }{g^{*}\left({\eta }_i\right)}-(y_i^{\gamma }+\lambda )+\frac{1}{{\left[\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}\right]}^2}\frac{{\partial }^2{g}^{*}\left({\eta }_i\right)}{\partial {\eta }_i^2}=0,i=1,2,...,n,\end{array}$$

(35)

where $g^{*}\left({\eta }_i\right)={\mu }_i$, ${\eta }_i$ is defined as in (6) and (16). The estimated coefficients ${\widehat{\beta }}^{*}$ are given as in (31). The IW-BReg model in this case is given by

$$\begin{array}{c}\hfill {\widehat{\mu }}_i^{*}=g^{-1}\left(x_i^{\prime }\beta \right),i=1,2,...,n.\end{array}$$

(36)

Proof. 

Suppose that $y_i\sim f(y_i;\alpha ,\gamma )$ is as it is in (3), the parameter $\gamma$ is assumed to be known, and the density function of $y_i$ is given by

$$\begin{array}{c}\hfill f(y_i;\alpha ,\gamma )=\alpha \gamma y_i^{-(\gamma +1)}{e}^{-\alpha y_i^{-\gamma }}.\end{array}$$

(37)

Consider a gamma prior for ${\alpha }_i$, which can be written as in (34). The posterior distribution of ${\alpha }_i$ is given by

$$\begin{array}{c}\hfill \pi \left({\alpha }_i\right|y_i)=\frac{{\alpha }_i^{\nu }\gamma {\lambda }^{\nu }}{\Gamma \left(\nu \right)}{y}_i^{-(\gamma +1)}{e}^{-{\alpha }_i(y_i^{-\gamma }+\lambda )}.\end{array}$$

Using Jacobian transformation from ${\alpha }_i$ to ${\eta }_i$, we have

$$\begin{array}{c}\hfill \pi \left({\eta }_i\right|y_i)\propto {\left[g^{*}\left({\eta }_i\right)\right]}^{\nu }{e}^{-g^{*}\left({\eta }_i\right)\left(y_i^{-\gamma }+\lambda \right)}\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}.\end{array}$$

(38)

Taking the derivative of the log posterior, we have

$$\begin{array}{c}\hfill \frac{\partial log\left(\pi \left({\eta }_i\right|y_i)\right)}{\partial {\eta }_i}\propto \frac{\nu }{g^{*}\left({\eta }_i\right)}\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}-(y_i^{-\gamma }+\lambda )\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}+\frac{1}{\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}}\frac{{\partial }^2{g}^{*}\left({\eta }_i\right)}{\partial {\eta }_i^2}=0;\end{array}$$

hence, we get the equation as in (35), and the posterior mode of ${\eta }_i$ is given by solving it. □

Lemma 6 (The IW-BReg model based on MGE loss function).

Let the response variable Y have an IW distribution, and let the link function of the form be as given in (2). Consider that ${\alpha }_i$ has a gamma prior with a density function as given in (34). Thus, the posterior Bayes estimates of ${\eta }_i$, by using an MGE loss function, can be derived by solving the equation

$$\begin{array}{c}\hfill \frac{-\gamma {\lambda }^{\nu }{y}_i^{-(\gamma +1)}}{\Gamma \left(\nu \right)\left(y_i^{-\gamma }+\lambda \right)}\underset{t\to \infty }{lim}{e}^{-g^{*}\left(t\right)\left(y_i^{-\gamma }+\lambda \right)}{|}_0^t-{\left[g^{*}\left({\eta }_i\right)\right]}^{-\nu }\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}=0.\end{array}$$

(39)

where $g^{*}\left({\eta }_i\right)={\mu }_i$, ${\eta }_i$ is defined as in (6) and (16). The estimated coefficients ${\widehat{\beta }}^{*}$ are given as in (31). The IW-BReg model in this case is given by

$$\begin{array}{c}\hfill {\widehat{\mu }}_i^{*}=g^{-1}\left(x_i^{\prime }\beta \right),i=1,2,...,n.\end{array}$$

(40)

Proof. 

Suppose that $y_i\sim f(y_i;\alpha ,\gamma )$ is as it is in (3). The parameter $\gamma$ is assumed to be known, and the density function of $y_i$ is given as in (37). Consider the gamma prior for ${\alpha }_i$, which can be written as given in (34). Using the posterior distribution of ${\eta }_i$ that is given in (38), we have

$$\begin{array}{c}\hfill E\left({\left[g^{*}\left({\eta }_i\right)\right]}^{-\nu }|y_i\right)={\int }_0^{\infty }{\left[g^{*}\left({\eta }_i\right)\right]}^{-\nu }\pi \left({\eta }_i\right|y_i)d{\eta }_i,\end{array}$$

$$\begin{array}{c}\hfill E\left({\left[g^{*}\left({\eta }_i\right)\right]}^{-\nu }|y_i\right)=\frac{-\gamma {\lambda }^{\nu }{y}_i^{-(\gamma +1)}}{\Gamma \left(\nu \right)\left(y_i^{-\gamma }+\lambda \right)}{\int }_0^{\infty }-\left(y_i^{-\gamma }+\lambda \right)e^{-g^{*}\left({\eta }_i\right)\left(y_i^{-\gamma }+\lambda \right)}\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}d{\eta }_i;\end{array}$$

hence,

$$\begin{array}{c}\hfill E\left({\left[g^{*}\left({\eta }_i\right)\right]}^{-\nu }|y_i\right)=\frac{-\gamma {\lambda }^{\nu }{y}_i^{-(\gamma +1)}}{\Gamma \left(\nu \right)\left(y_i^{-\gamma }+\lambda \right)}\underset{t\to \infty }{lim}{e}^{-g^{*}\left(t\right)\left(y_i^{-\gamma }+\lambda \right)}{|}_0^t.\end{array}$$

Using Lemma (4), we have

$$\begin{array}{c}\hfill \frac{-\gamma {\lambda }^{\nu }{y}_i^{-(\gamma +1)}}{\Gamma \left(\nu \right)\left(y_i^{-\gamma }+\lambda \right)}\underset{t\to \infty }{lim}{e}^{-g^{*}\left(t\right)\left(y_i^{-\gamma }+\lambda \right)}{|}_0^t={\left[g^{*}\left({\eta }_i\right)\right]}^{-\nu }\frac{\partial g^{*}\left({\eta }_i\right)}{\partial {\eta }_i}.\end{array}$$

Thus, the posterior Bayes estimates of ${\eta }_i$ by using the MGE loss function can be derived by solving the Equation (39). □

4. Data Analysis

In this section, we show the usefulness and performance of the IW-Reg and IW-BReg models by applying the theoretical findings in Section 2 and Section 3 to some real datasets. For simplicity, we use the following notations for the proposed models used throughout the applications.

Model	Description
Model I	IW-Reg model based on identity link function
Model II	IW-Reg model based on log link function
Model III	IW-BReg model based on identity link and zero-one loss function
Model IV	IW-BReg model based on log link and zero-one loss
Model V	IW-BReg model based on identity link and MGE loss
Model VI	IW-BReg model based on log link and MGE loss

4.1. Application 1: (The Minimum Temperatures)

Dataset in this application was collected from the meteorology station at King Khalid International Airport, Saudi Arabia during (2014–2018). This data contains 54 observations (monthly data), in which the response variable Y be the minimum of dry bulb temperatures in Celsius. The explanatory variables are; $X_1$; mean of relative humidity, $X_2$; mean of vapor pressure (mm), $X_3$; mean of sky cover oktes, $X_4$; maximum of station-level pressure (mm).

In order to aid in distributional assessment of the response variable Y, the empirical cumulative distribution function (ECDF) plot was proposed. Kolmogorov–Smirnov goodness of fit test (K–S) was calculated based on IW, Gaussian, and gamma distributions. The IW-Reg and IW-BReg models based on log and identity link, and loss functions were fitted using the proved Lemmas in Section 2 and Section 3. Bayes coefficients were obtained using a gamma prior $G\left(\nu ,\lambda \right)$ with some known values of the hyperparameters $\nu$ and $\lambda$. In addition, Huber’s function was suggested to avoid such distortions due to an outlier in $X_2$; see Appendix A. In this case, under regularity conditions, estimator ${\widehat{\beta }}^{*}$ has asymptotically normal distribution ${\widehat{\beta }}^{*}\equiv N\left[{\beta }^{*},{\left(X^{\prime }WX\right)}^{-1}\right]$ [39,42]. The performance of all these models were compared. Modeling performance is measured in terms of some criteria, such as AIC, D, D/df, and MSE [4]. We also used Thiel’s inequality coefficient $TIC=\frac{\sqrt{{\sum }_{}^{}{(y_i-{\widehat{y}}_i)}^2}}{\sqrt{{\sum }_{}^{}{y}_i^2}+\sqrt{{\sum }_{}^{}{\widehat{y}}_i^2}}$ to compare the prediction accuracy of the selected models [44,45]. The backward-selection method was used in the IW-BReg model to select the best fit in view of the covariates.

To check the adequacy for the selected models, we consider Pearson residuals [36,40]. R software was used to carry out calculations. In order to compare with known distributions, the glm() function in “stats” was used to fit the GLMs [46]. Functions qqPlot(), ecdf(), boxplot, and ks.test() in R package “stats” were used for the assessment distributions [47]. To solves n roots of n nonlinear equations in Section 3, the function multiroot() in R package “rootSolve” was used [48]. The fitting results and the relative errors (RE) of the selected model, and other numerical results are shown in Table 1, Table 2 and Table 3.

Table 1. Efficiency Gamma, Gaussian, inverted Weibull Regression (IW-Reg), IW-Bayesian regression (IW-BReg) models.

Model	AIC	D	D/df	MSE	Person	K-S Test
					Statistics	p-Value
Model I	344.997	43.950	0.897	191.828	2.122
Model II	579.782	0.009	0.000	7.026
Model III	477.534	15.311	0.312	9.137
Model IV	484.655	24.183	0.494	20.282
Model V	294.264	0.459	0.009	1.774	4.040
Model VI	364.333	0.350	0.007	2.349	0.446	0.3149
Gaussian (log)	186.800	80.491	0.936	1.643		0.0000
Gamma (log)	215.040	0.437	0.005	2.412		0.0321

Table 2. Akaike’s information criterion (AIC), deviance (D), and mean squared error (MSE) of the Model VI (backward selection method).

Function	Variables	$\widehat{\mathit{\beta }}$	Standard Error	z	p-Value	AIC	D	MSE
			(SE)
Step 1
No weight	Intercept	26.6539	6.5930	4.0427	0.0001	364.3330	0.3500	2.3490
	$X_1$	−0.0268	0.0036	−7.4222	0.0000
	$X_2$	0.1471	0.0180	8.1613	0.0000
	$X_3$	−0.0178	0.0282	−0.6296	0.5290
	$X_4$	−0.0255	0.0070	−3.6408	0.0003
Step 2
No weight	Intercept	26.5295	6.6037	4.0174	0.0001	364.3539	0.3709	2.3463 *
	$X_1$	−0.0271	0.0036	−7.6350	0.0000
	$X_2$	0.1422	0.0160	8.8633	0.0000
	$X_4$	−0.0254	0.0070	−3.6132	0.0003
Huber	Intercept	26.7509	6.7973	3.9355	0.0001	363.2006	0.8045	2.3451 **
	$X_1$	−0.0269	0.0037	−7.3672	0.0000
	$X_2$	0.1420	0.0165	8.6036	0.0000
	$X_4$	−0.0256	0.0072	−3.5423	0.0004

* The Model VI that was shown in Equation (41); ** The Model VI based on Huber’s function that was shown in Equation (42).

Table 3. Fitting results ${\widehat{y}}_i$ of the Model VI based on Huber’s function (during fitting interval, 2014).

Months	${\mathit{y}}_{\mathit{i}}$	${\widehat{\mathit{y}}}_{\mathit{i}}$	$|{\mathit{y}}_{\mathit{i}}-{\widehat{\mathit{y}}}_{\mathit{i}}|$	RE	Months	${\mathit{y}}_{\mathit{i}}$	${\widehat{\mathit{y}}}_{\mathit{i}}$	$|{\mathit{y}}_{\mathit{i}}-{\widehat{\mathit{y}}}_{\mathit{i}}|$	RE
1	7.813	7.790	0.023	0.295	7	27.484	27.202	0.282	1.027
2	9.626	10.749	1.123	11.668	8	27.435	30.610	3.174	11.571
3	15.671	16.080	0.409	2.607	9	24.677	25.372	0.694	2.813
4	20.177	19.730	0.448	2.218	10	21.335	21.765	0.430	2.014
5	24.665	24.721	0.056	0.229	11	13.410	12.967	0.443	3.301
6	25.842	24.066	1.776	6.872	12	9.426	9.639	0.213	2.262
TIC		0.011

Based on the results obtained from K–S test, the p-value = 0.315 for the test indicates that the IW distribution fits the response variable in the given data quite well. Figure 1 provides the ECDF plot, and it is clear that the IW distribution fits these data well.

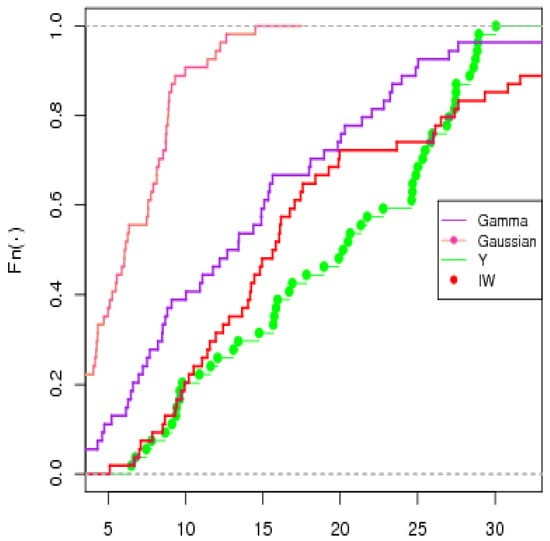
Figure 1. The empirical cumulative distribution function (ECDF) plot of the minimum temperatures $\left(Y\right)$ based on IW distribution and some other distributions.

To compare between the Bayesian fitting results, we observe that the results based on MGE loss function are better than zero-one loss function. Table 1 shows that the IW-BReg models based on MGE loss function (Model V and VI) are good in terms of MSE, AIC, and D statistics. Table 1 also shows that the $D/df$ of IW-Reg and IW-BReg models (I, II, III, IV, V, and VI) are less than 1, indicating that the fitting degree is very good. If the model is correct, the Pearson residuals $r_i=\frac{y_i-{\widehat{\mu }}_i}{\sqrt{V\left({\widehat{\mu }}_i\right)}}$ and Pearson statistics $Q={\sum }_{i=1}^{54}{r}_i^2$ have an approximately normal distribution with mean 0 and chi-square distribution ${\chi }_{n-k}^2$, respectively. For the IW-BReg model based on identity link and MGE loss function (Model V), the Pearson statistics is $Q=4.0396$, the p-value for Anderson-Darling is 0.0001, and the Cox Stuart test is 1, so the Pearson residuals are not normal but randomly scattered around zero at the level of significant $\alpha =0.05$. For the IW-BReg model based on log link and MGE loss function (Model VI), the Pearson statistics is $Q=0.4460$, the p-value for Anderson-Darling is 0.06379, and the Cox Stuart test is 1, so the Pearson residuals are normal and randomly scattered around zero.

Based on this analysis, we conclude that the Model VI is more appropriate for fitting these data, leading to the following equation

$$\begin{array}{c}\hfill \widehat{Y}=e^{26.6539-0.0268x_{i1}+0.1471x_{i2}-0.0178x_{i3}-0.0255x_{i4}},i=1,2,...,54.\end{array}$$

For the backward selection method results, Table 2, we can conclude that the predictive model is given as follows:

$$\begin{array}{c}\hfill \widehat{Y}=e^{26.5295-0.0271x_{i1}+0.1422x_{i2}-0.0254x_{i4}};i=1,2,...,54.\end{array}$$

(41)

We also can see that, this model has AIC = 364.3539 and a low MSE = 2.3463, and there was also a significant relationship among variables when using level of significance $\alpha =0.05$. For the residuals, the Pearson statistics is $Q=0.4520$, p-value for Anderson-Darling is 0.0443 and for the Cox Stuart test is 1.

Because of the presence of an outlier, we can conclude that the Model VI based on Huber’s function is the best for our data, and it is given as follows:

$$\begin{array}{c}\hfill \widehat{Y}=e^{26.7509-0.0269x_{i1}+0.1420x_{i2}-0.0256x_{i4}};i=1,2,...,54.\end{array}$$

(42)

From Table 2, we can see, this model has AIC = 363.2006 and a low MSE = 2.3451, and there was also a significant relationship among variables when using the level of significance $\alpha =0.05$. For the residuals, the Pearson statistics is $Q=0.4532$, the p-value for Anderson-Darling is 0.052, and the Cox Stuart test is 1. Hence, the Pearson residuals are normal randomly scattered around zero; see Figure 2. The fitting results for this model during the year 2014 are shown in Table 3. We can also see that the fitting accuracy is good because the TIC value is closer to 0 than 1.

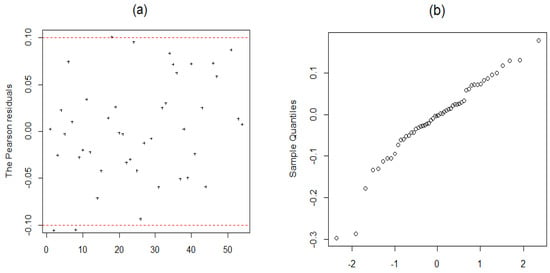
Figure 2. (a) Pearson residuals plot and (b) Normal Q-Q plot of the residuals using Model VI.

4.2. Application 2: (Wind Speed Data)

The dataset in this application was taken again from the meteorology station at King Khalid International Airport, Saudi Arabia, in 2016. This data contains 91 observations, during 7 June and 5 September, (summer season), in which the response variable Y be the mean wind speed (km/h). The explanatory variables are; $X_1$; maximum’s wind direction, $X_2$; maximum of station-level pressure (mm), $X_3$; mean of sea-level pressure (mm), $X_4$; mean of dry bulb temperatures of air (Celsius), $X_5$; mean of wet bulb temperatures (Celsius), $X_6$; mean of relative humidity, $X_7$; mean of vapor pressure (mm), $X_8$; mean of sky cover oktes, $X_9$; maximum of station-level pressure (mm), $X_{10}$; maximum of sea-level pressure (mm), $X_{11}$; maximum of dry bulb temperatures (Celsius), $X_{12}$; maximum of the wet bulb temperatures (Celsius), $X_{13}$; maximum of relative humidity, $X_{14}$; minimum of station-level pressure (mm), $X_{15}$; minimum of sea-level pressure (mm), $X_{16}$; minimum of dry bulb temperatures, $X_{17}$; minimum of the wet bulb temperatures, $X_{18}$; minimum of relative humidity, $X_{19}$; time of maximum daily wind (HH:MM).

Proceeding similarly, as in Application 1 to aid in the distributional assessment. In this dataset, we identify the outliers, different plots as the quantile-quantile (Q-Q) plot, ECDF, and box plot were proposed. Again, Lemmas in Section 2 and Section 3 were applied to these data to fit the IW-Reg based on log and identity link functions were used. Besides being an alternative analysis, the IW-BReg models were obtained using a log, identity link, and a gamma prior with known hyperparameters $\nu$ and $\lambda$ parameters. We also compare the performance of all these models. In addition, biweight function was suggested to avoid such distortions due to outliers; see Appendix A. In this case, under regularity conditions, estimator ${\widehat{\beta }}^{*}$ has asymptotically normal distribution ${\widehat{\beta }}^{*}\equiv N\left[{\beta }^{*},{\left(X^{\prime }WX\right)}^{-1}\right]$ [39,42]. The modeling performance was measured in terms of some criteria, such as AIC, D, D/df, and MSE [4]. We also used Theil’s Inequality coefficient (TIC) to measure the prediction accuracy of the selected models [44,45]. To compare the residual for all models, we consider Pearson residuals to check the adequacy of the regression model fitted to the data [36,40].

Furthermore, to detect the influential cases, we use the Cook’s distance measure using the formula $C_{\left(i\right)}=\frac{\left(\widehat{\beta }-{\widehat{\beta }}_{\left(i\right)}\right)\left(X^{\prime }X\right)\left(\widehat{\beta }-{\widehat{\beta }}_{\left(i\right)}\right)}{k{\widehat{\sigma }}^2}$ and ${\widehat{\sigma }}^2=\frac{{\widehat{\eta }}^{\prime }(I-X\left(X^{\prime }X\right)X^{\prime })\widehat{\eta }}{n-k}$ in the case of Bayesian analysis [40,49]. The backward selection method was used in the IW-Reg model to remove the input variable; see Table 4. R software was used to carry out the calculations. In order to compare with known distributions, the function glm in “stats” is used to fit the GLMs. The functions qqPlot, ecdf, boxplot, and ks.test in the R package “stats” are used for the assessment distributions [47]. To solves n roots of n nonlinear equations in Section 3, the function multiroot() in R package “rootSolve” was used [48]. The fitting, predictive results of these models and the other numerical results are shown on the Table 4, Table 5, Table 6, Table 7 and Table 8.

Table 4. The Model I (backward selection method).

Step	Variables	$\widehat{\mathit{\beta }}$	SE	z-Statistics	p-Value	AIC	D	MSE
Step 1	Intercept	385.557	129.470	2.978	0.0029	352.790	54.4782	3.549
	$X_1$	−0.013	0.014	−0.945	0.3446
	$X_2$	−0.883	0.851	−1.038	0.2993
	$X_3$	2.199	1.159	1.897	0.0579
	$X_4$	1.798	0.981	1.833	0.0668
	$X_5$	−4.039	2.254	−1.792	0.0732
	$X_6$	0.240	0.521	0.460	0.6456
	$X_7$	0.624	0.876	0.713	0.4760
	$X_8$	−0.537	0.188	−2.859	0.0042
	$X_9$	−0.741	0.882	−0.840	0.4010
	$X_{10}$	0.012	0.679	0.018	0.9855
	$X_{11}$	−0.555	0.225	−2.468	0.0136
	$X_{12}$	0.543	0.337	1.612	0.1070
	$X_{13}$	0.038	0.077	0.493	0.6218
	$X_{14}$	0.030	2.656	0.118	0.9065
	$X_{15}$	−1.110	0.690	−1.609	0.1075
	$X_{16}$	0.720	0.216	3.330	0.0009
	$X_{17}$	−0.124	0.386	−0.322	0.7475
	$X_{18}$	−0.055	0.271	−0.205	0.8376
	$X_{19}$	−0.048	0.062	−0.764	0.4447
Step 2	Intercept	385.734	128.470	3.003	0.0027	352.790	54.4785	3.735
	$X_1$	−0.014	0.014	−0.951	0.3414
	$X_2$	−0.884	0.847	−1.044	0.2964
	$X_3$	2.208	1.105	1.999	0.0456
	$X_4$	1.793	0.962	1.865	0.0622
	$X_5$	−4.034	2.248	−1.795	0.0727
	$X_6$	0.239	0.521	0.458	0.6466
	$X_7$	0.622	0.874	0.712	0.4765
	$X_8$	−0.537	0.188	−2.858	0.0043
	$X_9$	−0.731	0.590	−1.238	0.2155
	$X_{11}$	−0.555	0.225	−2.467	0.0136
	$X_{12}$	0.543	0.337	1.614	0.1065
	$X_{13}$	0.038	0.077	0.495	0.6205
	$X_{14}$	0.030	0.251	0.120	0.9048
	$X_{15}$	−1.116	0.647	−1.726	0.0844
	$X_{16}$	0.721	0.214	3.369	0.0008
	$X_{17}$	−0.126	0.368	−0.342	0.7324
	$X_{18}$	−0.055	0.270	−0.204	0.8385
	$X_{19}$	−0.048	0.062	−0.770	0.4415
.
.
.
Step 16	Intercept	355.1198	75.107	4.728	0.0000	369.9813	71.6697	3.192 *
	$X_2$	−0.3737	0.078	−4.798	0.0003
	$X_5$	−1.3347	0.227	−5.880	0.0000
	$X_8$	−0.6819	0.145	−4.711	0.0000
	$X_{16}$	0.7912	0.116	6.837	0.0000

* The Model I.

Table 5. Efficiency Gaussian, inverted Wiebull (IW-Reg), IW-Bayesian regression (IW-BReg) models.

Model	AIC	D	D/df	MSE	Person Statistics
Model I	369.981	71.670	0.833	3.192	57.937
Model II	818.882	0.232	0.003	3.008
Model III	372.847	26.195	0.305	3.275	19.807
Model IV	447.162	3.152	0.037	3.627	0.011
Model V	369.476	48.737	0.567	3.181	33.636
Model VI	446.981	3.312	0.039	3.093	0.103
Gaussian (ldentity)	369.357	270.422	3.144	3.144
Gaussian (log)	364.041	255.077	2.966	2.966

Table 6. AIC, BIC, D, and MSE of the Model VI based biweight function.

Function	Variables	Coefficient Estimate	SE	z-Statistics	p-Value	AIC	D	MSE
No weight	Intercept	42.8281	13.437	3.187	0.0014	446.9806	3.3117	3.093 *
	$X_2$	−0.0443	0.014	−3.161	0.0016
	$X_5$	−0.2023	0.042	−4.867	0.0000
	$X_8$	−0.0976	0.026	−3.702	0.0002
	$X_{16}$	0.1308	0.018	7.267	0.0000
Biweight	Intercept	47.259	13.956	3.386	0.0007	446.515	3.777	3.046 **
	$X_2$	−0.049	0.015	−3.385	0.0007
	$X_5$	−0.196	0.043	−4.571	0.0000
	$X_8$	−0.112	0.027	−4.070	0.0000
	$X_{16}$	0.136	0.019	7.326	0.0000

* The Model VI that was shown in Equation (43). ** The Model VI based on biweight function that was shown in Equation (44).

Table 7. Anderson-Darling and Cox Stuart test for Pearson residuals of the Model VI.

Function	Anderson-Darling		Cox Stuart
	Statistcs	p-Value	Statistcs	p-Value
No weight function	0.7483	0.0496	25, n = 45	0.5515
Biweight function	0.7117	0.0612	26, n = 45	0.3713

Table 8. Fitting and Predicted results ${\widehat{y}}_i$ for the Model VI based on biweight function.

Date	${\mathit{y}}_{\mathit{i}}$	${\widehat{\mathit{y}}}_{\mathit{i}}$	$|{\mathit{y}}_{\mathit{i}}-{\widehat{\mathit{y}}}_{\mathit{i}}|$	RE%	Date	${\mathit{y}}_{\mathit{i}}$	${\widehat{\mathit{y}}}_{\mathit{i}}$	$|{\mathit{y}}_{\mathit{i}}-{\widehat{\mathit{y}}}_{\mathit{i}}|$	RE%
Fitting results, 2016					Predicted results, 2017
7/21	5	5.685	0.685	13.708	8/21	8	10.553	2.553	31.915
7/22	7	5.867	1.133	16.190	8/22	8	7.211	0.789	9.862
7/23	11	8.784	2.217	20.150	8/23	6	6.974	0.974	16.238
7/24	6	6.859	0.859	14.322	8/24	4	3.657	0.343	8.571
7/25	5	4.880	0.120	2.393	8/25	5	4.510	0.491	9.811
7/26	4	5.067	1.067	26.686	8/26	7	7.082	0.082	1.165
7/27	5	5.672	0.672	13.433
TIC	0.087				0.088

Based on the results obtained from K–S test, the p-value = 0.139 for the test indicates that the IW distribution fits the response variable in the given data quite well. Figure 3 provides the Q-Q plot and ECDF, and it is clear that the IW distribution fits these data well. Figure 4 provides box plot corresponding to the mean wind speed variable Y, and this chart mapped one outlier (leverage point) that exceeds the values of $Q_3$.

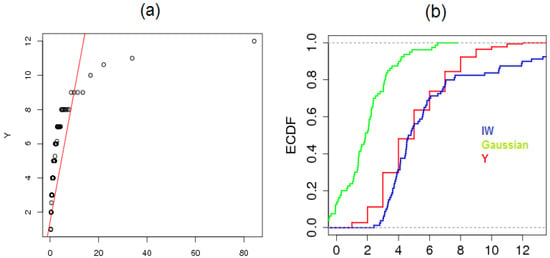
Figure 3. (a) Q-Q plots of the wind speed $\left(Y\right)$ based on IW distribution and (b) The ECDF plot of Y based on IW and some other distributions.

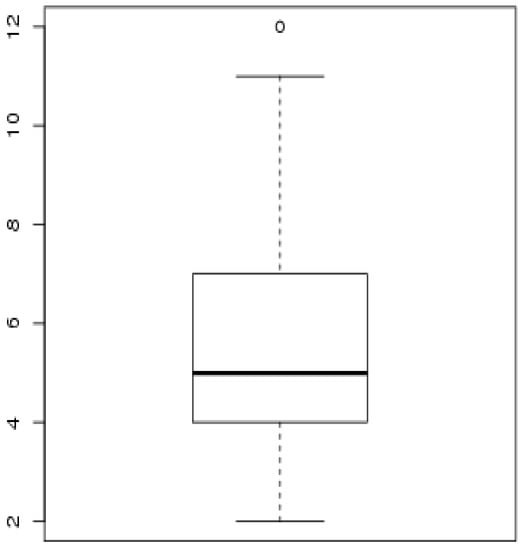
Figure 4. Box plot of the wind speed variable $\left(Y\right)$.

From Table 4, we can observe that the variables $X_2$, $X_5$, $X_8$, and $X_{16}$ are significant for the model, so there is a significant relationship among variables. In these models, ${\widehat{\beta }}^{\left(s\right)}$ is stabilizes when the Fisher’s scoring procedure is converged at $s=6$ and $s=15$, respectively, because of $|{\widehat{\beta }}^{\left(s\right)}-{\widehat{\beta }}^{(s-1)}|<\epsilon$. To compare the Bayesian fitting results we observe that the results based on MGE loss function (Model V and VI) better than zero-one loss function (Model III and IV); see Table 5. Table 5 also shows that the $D/df$ of the models I, II, III, IV, V, and VI are less than 1, indicating that the fitting degree is very good.

Based on this analysis, we also conclude that the Model VI is more appropriate for fitting these data, leading to the following equation

$$\begin{array}{c}\hfill \widehat{Y}=e^{42.8281-0.0443x_{i2}-0.2023x_{i5}-0.0976x_{i8}+0.1308x_{i16}},i=1,2,...,91.\end{array}$$

(43)

For the residuals, the Pearson statistics is $Q=0.1032$, p-value for Anderson-Darling is 0.0496, and for the Cox Stuart test is 1; see Table 5. This residuals have a large positive residual at the observation 91. However, for the model, this case is non-influential according to $C_{91}=0.1065<F_{(0.05,1,n-k)}$ where $F_{(0.05,1,n-k)}$ corresponding to upper $\alpha$-percentile from the F distribution [50].

Because of the presence of an outlier, we can conclude that the Model VI based on biweight function is the best for our data, and it is given as follows:

$$\begin{array}{c}\hfill \widehat{Y}=e^{47.259-0.049x_{i2}-0.196x_{i5}-0.112x_{i8}+0.136x_{i16}},i=1,2,...,91.\end{array}$$

(44)

From Table 6, we can see that this model has AIC = 446.515 and a low MSE = 3.046, and there was also a significant relationship among variables when using the level of significance $\alpha =0.05$. For the residuals, the Pearson statistics is $Q=0.1049$, the p-value for Anderson-Darling is 0.0612, and the Cox Stuart test is 1. Hence, the Pearson residuals are normal randomly scattered around zero at the level of significant $\alpha =0.05$; see Table 7 and Figure 5. This Figure shows no large positive residual. The fitting and predicted results for this model during 2016 and 2017 are shown in Table 8. We can also see that the prediction accuracy is good because the TIC value is closer to 0 than 1.

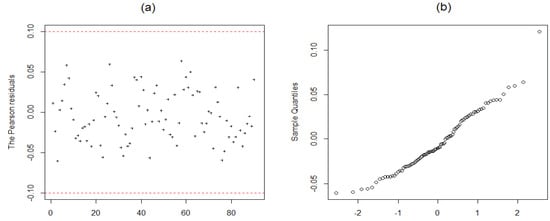
Figure 5. (a) Pearson residuals plot and (b) Normal Q-Q plot of the Pearson residuals for the Model VI based on biweight function as mentioned in Table 6.

5. Conclusions

In this paper, the regression models IW-Reg and IW-BReg for modeling Saudi datasets are considered. Zero-one and MGE loss functions were used to attain the Bayesian estimates based on a log and identity functions. In the classical approach, parameter estimation is done by the Fisher’s scoring technique, and closed-form expressions are provided for the score function, and for Fisher’s information matrix and its inverse. In the Bayesian approach, parameter estimation is performed using a gamma prior distribution, Jacobian transformation, and least-squares estimates. The IW-Reg and IW-BReg models were compared to find which model predicted better. To deal with outlier problems, IW-BReg based on Huber’s and biweight functions, and the adopted algorithm based on IRLS to find the estimates, were proposed. For distributional assessment, Q-Q, ECDF, box plots, and the K–S test were applied. Some criteria, namely AIC, D, D/df, and MSE, were also computed for all regression models.

According to the results of the Application (1), the IW-BReg model based on Huber’s and MGE loss with a log link function, performed the best in terms of the AIC, D, D/df, and MSE statistics, so it is recommended for these data. In contrast, the IW-Reg model showed poor results compared with those of the other models. Results indicated that the IW-BReg model based on Huber’s and MGE loss is highly capable of improving regression models’ performance to a greater extent in predicting the minimum of dry bulb temperatures (Celsius) in Saudi Arabia. It is found the following regressors are significant for the model: Explanatory variables are: $X_1$, the mean of relative humidity, $X_2$, the mean of vapor pressure (mm); and $X_4$, the maximum of station-level pressure (mm). Application (2), the IW-BReg model based on biweight function and MGE loss with a log link function, performed the best in terms of the AIC, D, D/df, and MSE statistics, so it is recommended for these data. In contrast, IW-Reg and IW-BReg based on zero-one loss function showed poor results than those of the other models. Finally, the results in this application indicated that the IW-BReg model based on biweight function and MGE loss with a log link function is highly capable of improving regression models’ performance to a greater extent in predicting the mean wind speed (km/h) in Saudi Arabia. It is found the following regressors are significant for the model: Explanatory variables are: $X_2$, the mean of station-level pressure (mm); $X_5$, the mean of wet–bulb temperatures (Celsius); $X_8$, the mean of sky cover oktes; and $X_{16}$, the minimum of dry bulb temperatures. From these discussions, we conclude that IW-BReg model based on log link and MGE loss has good performance for the response variables in the considered applications.