Abstract
Ecologists are interested in modeling the population growth of species in various ecosystems. Specifically, logistic growth arises as a common model for population growth. Studying such growth can assist environmental managers in making better decisions when collecting data. Traditionally, ecological data is recorded on a regular time frequency and is very well-documented. However, sampling can be an expensive process due to available resources, money and time. Limiting sampling makes it challenging to properly track the growth of a population. Thus, this design study proposes an approach to sampling based on the dynamics associated with logistic growth. The proposed method is demonstrated via a simulation study across various theoretical scenarios to evaluate its performance in identifying optimal designs that best estimate the curves. Markov Chain Monte Carlo sampling techniques are implemented to predict the probability of the model parameters using Bayesian inference. The intention of this study is to demonstrate a method that can minimize the amount of time ecologists spend in the field, while maximizing the information provided by the data.
1. Introduction
Population growth models are commonly used in ecology when studying plants, animals, and organisms as they grow over time and interact with the environment. In earlier research, Hsu et al. [1] evaluate seedling growth under laboratory and field conditions. According to Huang et al. [2], early life-cycle events play critical roles in determining the dynamics of plant populations and their interactions with the surrounding environment. Germination patterns modeled by growth help ecologists understand the diversity, variation, and climate change within a system. Gamito [3] further emphasize the importance of modeling growth and community dynamics using applications to fish populations. Population dynamics of fish are commonly studied to learn about water quality and the environment.
In riverine settings, the health of a waterway can be determined by the abundance of fish present. Kennard et al. [4] study species that are highly tolerant of human-induced disturbances and consider certain fish as good indicators of river health. Ecologists model the population growth of indicator species to preserve habitats as land is developed along the banks of rivers. Not only can population growth models help preserve the environment, but also ecologists model growth of crops to improve economies. In Vietnam, rice-shrimp farming highly impacts the economic security of the country as these are the two main crops in the region. Leigh et al. [5] study the environmental conditions of ponds used for harvesting and address the risks that affect the survival and yields of crops. In order to improve year-round farming, ecologists monitor the growth and abundance of shrimp and rice.
Whether researchers are interested in improving yields for farmers, preserving the health of rivers or studying germination of seedlings, collecting ecological data has always been a time consuming and expensive process. Ecologists fishing in rivers face strenuous terrain, varying water levels, and dangerous wildlife and prefer to limit their time collecting samples. Though farmers raise crops in controlled environments, limiting sampling costs can increase revenue. During germination studies, scientists prefer to optimize their time and resources required to grow samples. In all cases, researchers prefer to reduce costs when collecting data by decreasing their necessary sample size without compromising the ability to accurately track growth.
Rather than traditional sampling methods, this study proposes an approach that designs optimal sampling regimes based on the dynamics associated with a population. Though traditional methods are often convenient, statistically designing an experiment can optimize sampling procedures for ecologists without compromising the information obtained from the data. As seen in Pagendam and Pollett [6], experimental design is combined with Bayesian techniques to determine optimal designs for population growth models. Similarly, this paper investigates capturing the dynamics of various theoretical ecological growth models by designing optimal sampling regimes. Given the approach is intended to design experiments prior to data collection, simulations are conducted using a well-known ecological model with set parameters that can later be replicated with minimal error.
Using Bayesian inference, the probability of the model parameters are predicted based on simulated data by employing Markov Chain Monte Carlo (MCMC) sampling techniques demonstrated by Gilks et al. [7]. The intent of this study is to learn about dynamical systems in a sequential manner by using various criteria to optimize the system. The Bayesian model combined with design of experiment techniques can be used to determine the optimal sampling frequency that minimizes costs associated with data collection while obtaining the maximum amount of information from the data. The statistical methods in this paper are applied to various theoretical models and compared across optimality criteria to evaluate the performance. The goal of this research is to develop a new methodology that provides ecologists with optimal times to collect data that accurately captures the population growth dynamics of a system.
2. Logistic Growth Model
Logistic curves are used to model growth in various contexts. Originally developed by Verhulst [8], logistic curves were used to model population growth as an adaptation of exponential growth. Verhulst developed the logistic growth model by adding a multiplicative factor to exponential growth, which stabilizes the model at a particular population size due to competition for resources. The self-limiting growth of the population is referred to as the carrying capacity. The carrying capacity is the maximum population that terminates the growth rate, at which point the system enters a steady-state.
The logistic growth model has been implemented in numerous fields. Logistic growth has been used to estimate parameters and inform intervention strategies during a pandemic involving influenza as demonstrated by Hedge et al. [9]. Furthermore, coal production peaks and trends in China have been modeled with logistic growth by Lin and Liu [10]. Similarly, the logistic curve has taken the form of Hubbert’s model [11] to forecast the production of petroleum. In this paper, the proposed model represents ecological modeling of population growth.
The rediscovery of the logistic equation by Reed and Pearl [12] is often used in ecology to represent the population dynamic where the rate of reproduction is proportional to both the existing population and the amount of available resources. This model is popular in ecology due to the realistic dynamic of the carrying capacity and existence of the analytic solution. The equation is written in the mathematical form
with analytic solution
The variables N and t represent population size and time respectively. represents the population at time referred to as the initial population. Parameter r is the population growth rate, and parameter K is the carrying capacity.
The parameters of logistic growth can be difficult to estimate since the model does not always provide a good fit to true data. Thus, parameter estimation techniques are commonly studied in the literature. Oliver [13] demonstrates methods for estimating model parameters across a variety of logistic growth models. In more recent times, Bayesian inference has become more accessible to ecologists and used for parameter estimation. Heydari et al. [14] use Bayesian inference to determine fast estimation methods for logistic growth. In general, ecologists are shifting towards Bayesian modeling of population dynamics based on the increasing resources for ecological Bayesian models [15]. In this paper, logistic growth is specified probabilistically in the Bayesian framework in order to perform a new method for parameter estimation.
3. Methods
3.1. Statistical Model
Given that ecologists have expertise in modeling logistic growth, the Bayesian approach can be used to incorporate prior knowledge of the system. Thus, the model in Equation (1) can be specified probabilistically in the Bayesian framework. The Bayesian approach is implemented using Bayes’ Theorem [16]. The theorem combines prior beliefs with the likelihood of an experiment to determine a posterior belief. The prior belief of a parameter is noted by . The likelihood of the experiment is a conditional probability of the data x given the parameter noted by . The posterior belief is given by the continuous case of Bayes’ Theorem, also known as the posterior distribution. The posterior distribution defines the conditional probability of a parameter given the observance of data x, which is written mathematically as
Specifying Equation (1) as a Bayesian model requires the specification of the likelihood of the experiment and the prior distributions for each parameter. The nature of the logistic equation tracks the population of a species N across a fixed time t where the growth rate parameter r and carrying capacity K are independent fixed values. The population at a specified time is assumed to have a Poisson likelihood given that the observations are independent counts occurring at known times . The analytic solution to the logistic Equation (2) provides the expected value of the likelihood set as . This provides the conditional likelihood of the experiment
where depends on the parameters r and K. Thus, the prior distributions must be specified for the growth rate and carrying capacity parameters.
When modeling logistic growth, ecologists are aware that a population can only reach a maximum capacity by increasing at a positive rate. This implies that the growth rate r and carrying capacity K must be positive values. Though many distributions have positive supports, the log-normal distribution easily specifies numerical information by using the mean and variance. Less informative priors such as the gamma distribution can cause model instability, which defeats the purpose of incorporating prior beliefs. Thus, informative priors are specified as
where the expected growth rate is centered about one and the carrying capacity is assumed to reach a large quantity. These explicit priors are implemented to represent some form of prior knowledge of the system and will be used for all simulations in this paper. The Bayesian approach emphasizes combining informative prior beliefs with experimental knowledge to determine a posterior belief. Thus, the specified model will be used to predict the parameters of various theoretical population growth models that can be optimized by assessing various criteria.
3.2. Optimal Designs
Optimal designs are used to estimate statistical models while reducing experimental costs. The objective of optimal design is to eliminate uncertainty by minimizing the variability of the parameter estimates. Traditionally, optimal designs [17] minimize the variance of the parameter estimates while maximizing the information matrix. Specifically, the Fisher information matrix is defined as the negative expectation of the second derivative of the log-likelihood function with respect to the parameter
where the expectation is taken over the sample space of the observations x and parameter space of . Optimality criteria are applied to the Fisher information matrix and provide measures of fit to assist with model selection. The popular A and D optimal designs are commonly used in experimentation due to their ability to limit computational expenses. A optimality criterion minimizes the trace of the inverse of the Fisher information matrix, which equivalently minimizes the average variance of the parameter estimates of a model. Whereas, D optimal designs consist of maximizing the determinant of the Fisher information matrix, again minimizing the parameter estimates of the model.
Though these designs are commonly used in practice, can be difficult to calculate when the model parameters are unknown. Instead of estimating the Fisher information matrix using parameter estimates noted by , we consider the variance of the parameter estimates. The inverse of the estimated Fisher information matrix is an estimator of the asymptotic covariance matrix [18].
The covariance matrix is much easier to calculate than the Fisher information matrix for certain models. Thus, defining in terms of redefines the optimality criteria in terms of the estimated covariance matrix. I-optimal designs [19] known for minimizing the average prediction variance over the entire design region are also considered.
notes the average prediction variance of the model. Rather than minimizing the trace of the inverse of the Fisher information matrix, -optimal designs minimize the trace of the covariance matrix. -optimal designs minimize the determinant of the covariance matrix. While, I-optimal designs minimize the average prediction variance over the design space. Again, optimality criteria are measures of fit used to guide optimization processes. , and I optimality criteria are used in the proposed sequential optimality algorithm presented in the next section.
3.3. Sequential Optimality
In practice, design techniques are used prior to collecting data in order to optimize the amount of information obtained during experimentation. For instance, simulated annealing applied by Laarhoven and Aarts [20] is a commonly used probabilistic technique that searches the design region for an approximation of the global optimum of a given function. Though easy to implement, simulated annealing can be computationally expensive and does not learn about a system in a sequential manner. We compare simulated annealing to our proposed adaptation of the method that predicts the optimal future design point based on the current information of the system. We prefer this Bayesian approach to incorporate prior knowledge into the decision-making process. The proposed algorithm sequentially searches subsets of the design space to determine the best future time for ecologists to collect data. Sequential optimality is written below as Algorithm 1.
| Algorithm 1: Sequential Optimality. |
Begin Choose an initial design Set a design budget, b Set a design window, w Set criteria, C: (i). (ii). (iii). I = For : (a) Draw a sample (b) Accept the new state Repeat until End |
The algorithm begins by setting an initial design of size n typically set as the number of parameters in the model plus one. Then, a design point budget b is chosen according to the number of runs the experimenter can afford. Once the initial data is collected and a design budget is set, the design window w can be set. The design window can be established by dividing the planned time interval by the design point budget. The window of points following the current design D are explored as candidate samples. Each candidate is evaluated by running the Metropolis-Hastings (MH) algorithm [21] guided by specified optimality criterion, C. The optimal point within the window is added to the design, and the process repeats until the design point budget is exhausted. These steps are demonstrated and explained further through a worked example.
3.4. Worked Example
This worked example uses Algorithm 1 to find an optimal design for a normal 10% logistic growth model using A-optimality criterion. Each step is provided in detail as follows.
- Step 1:
- Choose an initial designLogistic growth has two parameters, growth rate and carrying capacity. Therefore, three initial design points, and , are selected as shown in Figure 1 representing samples collected on days 0, 5 and 10 of the season. The population size is calculated at these time points using the analytic solution from Equation (2) with random Poisson noise. In this example the coordinates are (0, 205), (5, 295) and (10, 453).
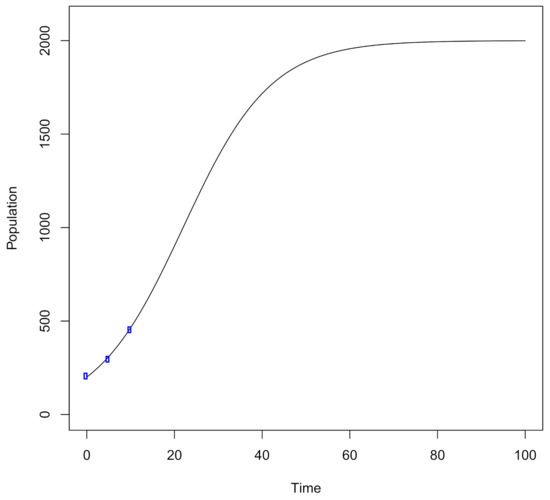 Figure 1. An initial design of three points is plotted in blue. The ground truth model of normal 10% growth is plotted as a black curve across one hundred time points with a carrying capacity of two thousand and initial population of two hundred.
Figure 1. An initial design of three points is plotted in blue. The ground truth model of normal 10% growth is plotted as a black curve across one hundred time points with a carrying capacity of two thousand and initial population of two hundred. - Step 2:
- Set a design budget, bThe design budget is chosen at the discretion of the expert based on available resources. In this example, we select a budget of ten, .
- Step 3:
- Set a design window, wThis study focuses on sampling across a one hundred day season with a design budget of size ten. A practical design window would be to search ten days into the future. Thus, we set .
- Step 4:
- Set criteria, CFor demonstration purposes, A-optimal criterion is selected as .
- Step 5:
- Draw a sampleThe initial design consists of three points. Therefore, represents a window of the ten consecutive points following the last point sampled from Day 11, …, Day 20.
- Step 6:
- Accept the new stateHere, we calculate the trace of the covariance matrix for each point in , which comes from the MH algorithm producing estimates for the carrying capacity and growth rate.Based on the calculations, the optimal point selected in the design window is Day 16, which leads to the selected design point (16, 661) calculated by the analytic solution with random Poisson noise. Figure 2 illustrates the candidate sample region in red and the selected point among the candidates.
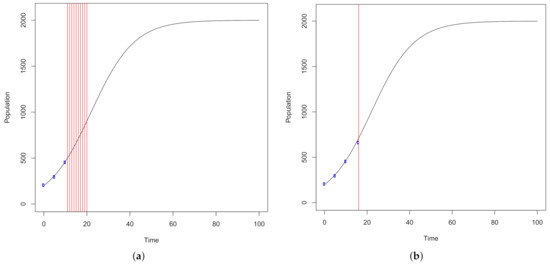 Figure 2. A window of ten candidate points are selected from the last point sampled illustrated by the red region in panel (a). Each point is evaluated using A optimality criterion and the argument with the minimum trace in the window is selected as shown in panel (b).
Figure 2. A window of ten candidate points are selected from the last point sampled illustrated by the red region in panel (a). Each point is evaluated using A optimality criterion and the argument with the minimum trace in the window is selected as shown in panel (b). - Step 7:
- Repeat untilSteps 5 and 6 are repeated until all ten points in the budget are exhausted. The parameter estimates are updated as each new design point is added as shown in Figure 3. The final design consists of ten points calculated by the analytic solution as follows: (0, 205), (5, 295), (10, 453), (16, 661), (26, 1202), (36, 1498), (46, 1885), (56, 1927), (64, 2019) and (68, 1961).
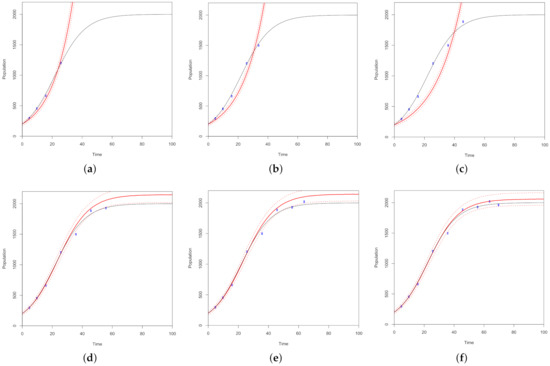 Figure 3. The fifth design point is selected in panel (a) found in a window following the design from Figure 2: panel (b). Panels (b–f) represent each additional design point added until the budget of ten points is exhausted. Each panel plots the ground truth model in black, the design points in blue and fits the design with a red curve based on the parameter estimates. The red dotted lines represent the 2.5% and 97.5% prediction quantiles.The sequential optimality algorithm is intended to search the design space of temporal models. The above example demonstrates the procedure learning about a temporal system in a sequential manner. The proposed method will be implemented later across various logistic growth models using all design criteria from Equation (9) to compare the technique in reference to simulated annealing. The purpose of this design study is to develop and demonstrate statistical methods that can optimize sampling procedures for ecologists.
Figure 3. The fifth design point is selected in panel (a) found in a window following the design from Figure 2: panel (b). Panels (b–f) represent each additional design point added until the budget of ten points is exhausted. Each panel plots the ground truth model in black, the design points in blue and fits the design with a red curve based on the parameter estimates. The red dotted lines represent the 2.5% and 97.5% prediction quantiles.The sequential optimality algorithm is intended to search the design space of temporal models. The above example demonstrates the procedure learning about a temporal system in a sequential manner. The proposed method will be implemented later across various logistic growth models using all design criteria from Equation (9) to compare the technique in reference to simulated annealing. The purpose of this design study is to develop and demonstrate statistical methods that can optimize sampling procedures for ecologists.
4. Simulation Results
This simulation study demonstrates methods that can be used to design sampling schedules for ecologists applied to three theoretical scenarios of logistic growth provided by Table 1. All simulations are programmed in R [22]. Data is simulated for normal, fast and slow logistic growth models across one hundred time points. The normal growth rate is set to 10%, the fast rate is set to 100%, and the slow rate is set to 5% growth. All models have a maximum carrying capacity of two thousand, and ten thousand MCMC samples are used to predict the probability of the model parameters. Based on the planned time interval of one hundred days, all optimal designs will consist of ten points that search windows of size ten. This allows the entire budget to be used should the farthest point in each window be selected. Simulated annealing is implemented first to demonstrate the global optimum for each scenario as a reference when comparing sequential optimality. Therefore, ten design points are also selected during simulated annealing for comparison purposes. Then, sequential optimality is demonstrated as a novel approach to designing optimal sampling regimes.

Table 1.
Logistic Growth Scenarios.
All ground truth models are generated using the logistic equation and analytic solution provided by Equation (1). Each simulation plots the ground truth model as a black curve tracking the population size across time. 10,000 MCMC samples are used for each simulation, and the optimal design points selected are plotted as blue open circles. The designs are fit by a red curve with the prediction interval plotted as red dotted lines calculated by the 2.5% and 97.5% quantiles of the predicted values. It will become clear by the results that there are many ways to successfully design experiments for logistic growth models.
4.1. Simulated Annealing
Simulated annealing is implemented as an adaptation of the MH algorithm to explore the design space for an optimal solution. Considering normal, fast and slow growth rates, the specified optimality criteria from Equation (9) are used to guide the algorithm and find global optimum solutions. As stated previously, the models simulate growth at 10%, 100%, and 5% rates. Each criterion guides the simulated annealing process to produce optimal designs for each model.
Simulated annealing successfully captures the dynamics of all growth models using each criterion. Figure 4 demonstrates the designs generated using optimality criterion. Figure 5 fits the -optimal designs. Figure 6 illustrates the fit of I—optimal designs. In the next section, simulation studies are conducted using sequential optimality to demonstrate a new method for prediction based optimization. Sequential optimality is an adaptation of simulated annealing that predicts optimal design points.
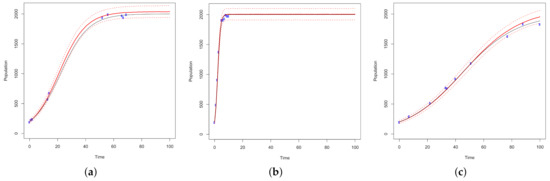
Figure 4.
10,000 MCMC samples are used to simulate —optimal designs for (a) normal, (b) fast and (c) slow growth models. All models are simulated across 100 time points with a carrying capacity of 2000. The ground truth models are plotted in black. The optimal design points are plotted in blue and fit by a solid red curve, where the 2.5% and 97.5% quantiles of the predicted values are plotted as red dotted lines.
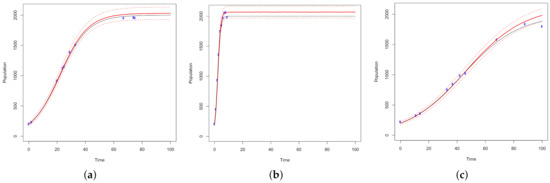
Figure 5.
10,000 MCMC samples are used to simulate —optimal designs for (a) normal, (b) fast and (c) slow growth models. All models are simulated across 100 time points with a carrying capacity of 2000. The ground truth models are plotted in black. The optimal design points are plotted in blue and fit by a solid red curve, where the 2.5% and 97.5% quantiles of the predicted values are plotted as red dotted lines.
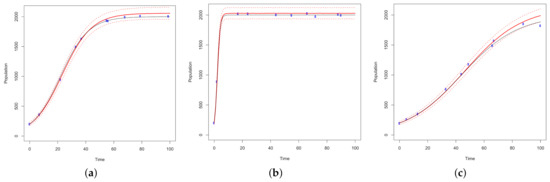
Figure 6.
10,000 MCMC samples are used to simulate I-optimal designs for (a) normal, (b) fast and (c) slow growth models. All models are simulated across 100 time points with a carrying capacity of 2000. The ground truth models are plotted in black. The optimal design points are plotted in blue and fit by a solid red curve, where the 2.5% and 97.5% quantiles of the predicted values are plotted as red dotted lines.
4.2. Sequential Design
Sequential optimality searches subsets of the design space to find the next best point. Normal, fast and slow growth at 10%, 100% and 5% rates respectively are simulated. All simulations use 10,000 MCMC samples plotted across one hundred time points. The carrying capacity is two thousand. The design point budget consists of ten points, and the algorithm uses the optimality criteria from Equation (9). As each criterion guides the sequential optimality process, the final optimal designs are compared for each model. Again, the ground truth model is plotted as a black curve. The optimal design points are plotted as blue points fit by a solid red curve with the 2.5% and 97.5% quantiles of the predicted values plotted as red dotted lines. As the system updates, our goal is to fit the ground truth model as accurately as possible with the final optimal design. I, , and optimal designs are compared across normal, fast, and slow growth rates.
The simulations begin with the I-optimality criterion to demonstrate prediction based designs. Figure 7 demonstrates sequential optimality using the prediction based I-optimality criterion to search a normal growth model. Given the model specification and priors from Equation (5), there is expert knowledge informing the growth rate parameter but limited knowledge regarding the carrying capacity. This simulation specifically demonstrates the ability of the algorithm to explore the uncertainty of the carrying capacity and capture the dynamic. An initial design is set of three points given the logistic equation has two parameters, carrying capacity and growth rate. One hundred day seasons are modeled with a design point budget of ten. The ten candidate points following the base design are evaluated using the I-optimality criterion to select the point with the minimum prediction variance. Once the optimal point is added to the design, the process repeats until all ten design points are sampled. Notice that the change from step 6 in panel (e) to step 7 in panel (f) of Figure 7 demonstrates the method searching uncertainty of the plateau level of the curve. As the process updates, the width of the decision boundary decreases showing more certainty around the steady state of the system. Based on the simulation, the prediction based I optimality criterion is successful in capturing the dynamics of a normal growth model. However, different combinations of criteria and growth models are simulated to test the robustness of the technique.
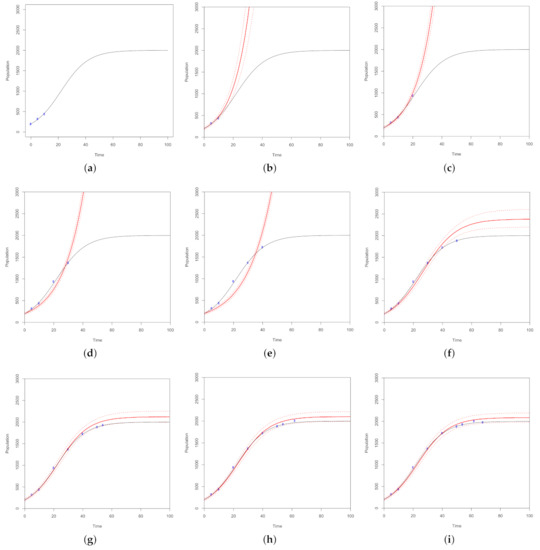
Figure 7.
10,000 MCMC samples are used to simulate the normal 10% growth curve across a 100 day period with a carrying capacity of 2000. The ground truth model is plotted as a black curve. I-optimality criterion guides the sequential optimality process. The optimal design points are plotted in blue and are fit by a solid red curve. The red dotted lines represent the 2.5% and 97.5% quantiles of the predicted values. Panel (a) plots the base design of three points, panel (b) plots the fit of the base design, and panels (c–i) plot the fourth through tenth optimal points in the design as they are fit.
The simulations of normal growth show varying results in Figure 8 across the optimality criteria. The I and optimal designs successfully capture the dynamics of the population with ten points. Whereas, the optimal design did not capture the dynamic of the carrying capacity. This indicates the need for a larger design point budget or smaller design window when using optimality criterion with a normal growth curve. On the other hand, all three optimality criteria capture the dynamics of the fast growth rate in Figure 9, which is expected given that the model plateaus rapidly. This implies that the design point budget could be decreased in this case. As for the slow growth rate model in Figure 10, no criteria could capture the population dynamics. This could indicate a need to increase the design point budget or decrease the design window for slow growth models. The size of the design point budget was set to ten points with a window of ten points to simply demonstrate this novel approach of sequential optimality.
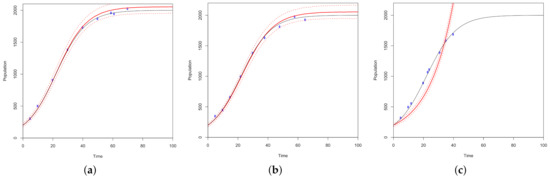
Figure 8.
10,000 MCMC samples are used in this simulation of a normal growth curve increasing at a 10% rate across 100 time points with a carrying capacity of 2000. Sequential optimality is used to find the ten best points for (a) I, (b) and (c) optimal designs. The optimal points are plotted in blue and fit with a solid red curve. The red dotted lines represent the 2.5% and 97.5% quantiles of the predicted values of the model. The black curve represents the ground truth model.
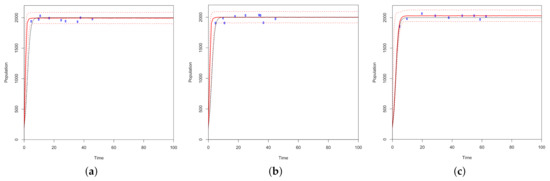
Figure 9.
10,000 MCMC samples are used in this simulation of a rapid growth curve increasing at a 100% rate across 100 time points with a carrying capacity of 2000. Sequential optimality is used to find the ten best points for (a) I, (b) and (c) optimal designs. The optimal points are plotted in blue and fit with a solid red curve. The red dotted lines represent the 2.5% and 97.5% quantiles of the predicted values of the model. The black curve represents the ground truth model.
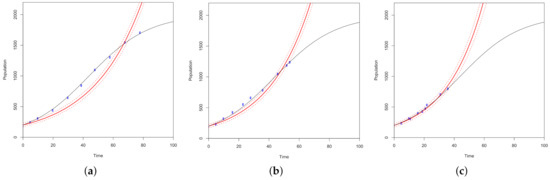
Figure 10.
10,000 MCMC samples are used in this simulation of a slow growth curve increasing at a 5% rate across 100 time points with a carrying capacity of 2000. Sequential optimality is used to find the ten best points for (a) I, (b) and (c) optimal designs. The optimal points are plotted in blue and fit with a solid red curve. The red dotted lines represent the 2.5% and 97.5% quantiles of the predicted values of the model. The black curve represents the ground truth model.
Bayesian optimal designs [23] are also examined for comparison purposes. Bayesian optimal designs can be written in the form of a utility function , where represents a design chosen from the design region . The design region is explored using Bayes I, D, and A optimal designs written mathematically as follows.
Bayesian I-Optimal
Bayesian D-Optimal
Bayesian A-Optimal
represents the predicted design points, while represents the current design. is the parameter space including parameters k and K from the model in Equation (1). Similar to the criteria from Equation (9), the Bayesian optimality criteria are minimizing the posterior predictive distribution across the parameter space and design space . The Bayesian I-Optimal designs minimizes the distance between the squared predictions. Bayesian D-optimal designs minimize the determinant of the covariance of the posterior predictive distribution. The Bayesian A-optimal designs minimize the trace of the posterior predictive distribution. Implementing the Bayesian criteria into our process of sequential optimality gives various results. The frequency tables illustrate the precision of each criteria based on the probabilities assigned to each candidate point.
The frequency plots in Figure 11 show the probability densities associated with the first set of candidate points evaluated in the sequential optimality algorithm. The Bayesian I-optimal design gives weight to specific candidate points, whereas the Bayesian A and D optimality criteria provide a wide range of optimal candidates. Based on the frequency charts, it is clear that the Bayesian I-optimal design can provide a precise optimal design point. Whereas, the Bayesian A and D optimal designs appear to lack precision. These results are further visualized by plotting the Bayesian sequential designs in Figure 12 for the normal growth model.
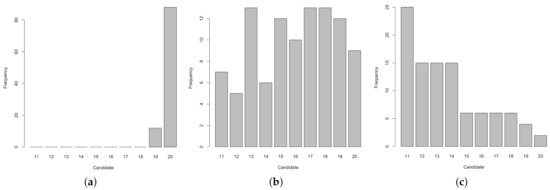
Figure 11.
Bayesian optimality criteria are used to guide the sequential optimality process. The frequency tables plot the probabilities assigned to the first ten candidate points following the initial base design for a normal growth model. Panel (a) represents candidate probabilities under the criterion. Panel (b) plots probabilities of the candidates for criterion. Panel (c) provides the frequencies associated with criterion.
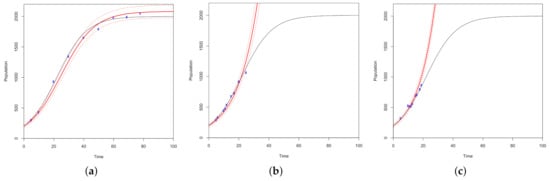
Figure 12.
10,000 MCMC samples simulate a normal growth curve increasing at a 10% rate across 100 time points with a carrying capacity of 2000. Sequential optimality is used with the Bayesian design criteria to find the ten best points for (a) , (b) and (c) optimal designs. The optimal points are plotted in blue and fit with a solid red curve. The red dotted lines represent the 2.5% and 97.5% quantiles of the predicted values of the model. The black curve represents the ground truth model.
Given all of the criteria and varying growth rates, the simulations using sequential optimality resulted in different designs. Some designs are able to capture the dynamics of the system while others require a larger design point budget. Ultimately, this indicates that there are several ways to design experiments for dynamic models. Using the simple example of population growth modeled by the logistic equation, the sequential optimality simulations demonstrate an adaptation of the commonly performed simulated annealing algorithm. Thus, sequential optimality can be recommended when limitations arise for sampling.
4.3. Potential Difficulties
As demonstrated previously, sequential optimality predicts optimal future design points in a sequential manner by learning about the dynamics of a system. Thus far, the simulations use the analytic solution to the logistic equation with Poisson noise to produce simulated data that closely resembles a specified model. This raises concern when evaluating the proposed method given that scenarios exist where logistic growth may not be appropriate. The following simulation details potential difficulties with the sequential optimality algorithm in a scenario that tests if the method can detect a model lack of fit. The simulated data is generated using a piecewise function where the population count suddenly decreases rather than reaching the carrying capacity.
This simulation is performed under the assumption that the logistic growth model is appropriate to fit the simulated data. Figure 13 illustrates sequential optimality being informed by data that does not follow the logistic growth trend. The prediction based I-optimality criterion is used for demonstration purposes. First, an initial design is set of three points given the logistic equation has two parameters, carrying capacity and growth rate. Then, the ten candidate samples following the initial design are evaluated using the I-optimality criterion to select the point with the minimum prediction variance. Once the optimal design point is added, the process repeats and updates three times. However on the fourth run, the logistic growth curve is poorly fit, and we see a decrease in the population size. By the fifth run and addition of the seventh design point, the I-optimality criterion creates a range that becomes extremely large, which signals an incorrect model. Though the budget is set for ten design points, the process fails to continue once the population reaches zero. This implies that the process can detect a lack of fit and abnormality in the system.
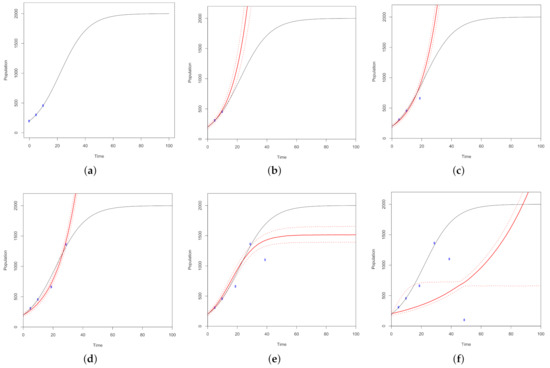
Figure 13.
10,000 MCMC samples are used to simulate normal 10% logistic growth across a 100 day period with a carrying capacity of 2000. The ground truth model is plotted as a black curve. I-optimality criterion guides the sequential optimality process. The optimal design points are plotted in blue and are fit by a solid red curve. The red dotted lines represent the 2.5% and 97.5% quantiles of the predicted values. Panel (a) plots the base design of three points, panel (b) plots the fit of the base design, and panels (c–f) plot the fourth through seventh optimal points in the design as they are fit. This simulation demonstrates a lack of fit scenario.
5. Discussion
In this study, the dynamics of various logistic growth models were investigated in order to design optimal sampling regimes for ecologists. Efforts were focused on a simple model with limited external factors to demonstrate the approach of sequential optimality. For the purpose of this study, the logistic equation provided a straightforward model used to compare sampling techniques. Simulated annealing was implemented to explore the design space using various optimality criteria. Despite the growth rate and criterion used, simulated annealing was able to capture the dynamics of the models by exploring the entire design region. However, sequential optimality found sampling regimes that capture the dynamics of a system in a sequential manner.
The proposed method of sequential optimality incorporates prior information into the design process. Rather than exploring the entire design space at once, the sampling method evaluates subsets of the region using parameter based criteria. Sequential optimality captured the dynamics of a normal growth rate using the I optimality criterion. However, implementing this method across criteria and growth rates led to different results. The normal growth rate model was captured by I and optimal designs but required more design points for the optimal design. Models with fast growth rates were always captured leading to the belief that a smaller design point budget could be explored. On the other hand, slow growth rates required a larger design point budget no matter the criteria used. The algorithm had a more difficult time distinguishing the dynamics of the slower growth rate.
Bayesian optimal designs were also considered as a method for comparison. The -optimality criterion had more precise candidate points than the or optimality criteria. This led to the results that only the Bayesian optimal design was able to capture the dynamics of the curve with a set of ten design points. The other two designs required more design points to capture the dynamics of the model. Comparing Bayesian sequential designs to the traditional criteria provided yet another technique available for determining the optimal design points in the region. Comparing these processes across criteria and models suggests that there are several ways to design experiments. Numerous approaches exist for Bayesian experimental design including studies by Müller et al. [24], Williamson and Goldstein [25] and Jones et al. [26]. Furthermore, research by Ford et al. [27] demonstrates advancements in experimental design for nonlinear systems. Though alternative methods are available to help ecologists allocate resources, our approach of sequential optimality is particularly beneficial when predicting the next step, or optimal time, to collect data.
6. Conclusions
In this paper, the ecological model known as the logistic equation was used based on the various applications and popularity of the model. The proposed design space tracked the change in population dynamics across time and was explored using the novel approach of sequential optimality. When using prediction based criteria for a normal growth model, the method captured the dynamics of the system and found an optimal design that translates to an optimal sampling regime for ecologists. Rather than sampling out of convenience or across an equal interval, the simulations demonstrate that the method can provide the next optimal time to sample given the current state of the environment. Real data cannot be incorporated at this time given that this paper introduces a new method for designing sampling regimes. However, the developed method does learn about theoretical processes in a sequential manner and has the potential to assist ecologists when planning sampling schedules.
Though the analysis is performed on a straightforward univariate model, we acknowledge that more complex dynamics exist and can represent more realistic environmental encounters. Incorporating external factors into the model could lead to substantial improvements to the method. Furthermore, there are many design problems that can be investigated by a Bayesian approach. Specifically related to sequential optimality, this study focuses on designs of a set size that explore a set window of time into the future. The method could be expanded by studying varying design sizes and design windows. Also, sampling techniques used by ecologists could be invasive and change the process. These changes could be taken into consideration as they may affect the model. In this paper, we focus on providing optimal designs based on temporal models. However, in the future spatial models could be explored along with a hierarchical network of temporal models. Given these additional conditions, there are many levels of uncertainty that could be incorporated to reflect the reality of an ecological system.
Author Contributions
Conceptualization, B.S.-K.; Methodology, R.E.A. and E.L.B.; Supervision, R.A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hsu, F.; Nelson, C.; Chow, W. A mathematical model to utilize the logistic function in germination and seedling growth. J. Exp. Bot. 1984, 35, 1629–1640. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, S.; Bradford, K.J.; Huxman, T.E.; Venable, D.L. The contribution of germination functional traits to population dynamics of a desert plant community. Ecology 2016, 97, 250–261. [Google Scholar] [CrossRef] [PubMed]
- Gamito, S. Growth models and their use in ecological modelling: An application to a fish population. Ecol. Model. 1998, 113, 83–94. [Google Scholar] [CrossRef]
- Kennard, M.; Arthington, A.; Pusey, B.; Harch, B. Are alien fish a reliable indicator of river health? Freshw. Biol. 2005, 50, 174–193. [Google Scholar] [CrossRef]
- Leigh, C.; Hiep, L.H.; Stewart-Koster, B.; Vien, D.M.; Condon, J.; Sang, N.V.; Sammut, J.; Burford, M.A. Concurrent rice-shrimp-crab farming systems in the Mekong Delta: Are conditions (sub) optimal for crop production and survival? Aquac. Res. 2017, 48, 5251–5262. [Google Scholar] [CrossRef]
- Pagendam, D.; Pollett, P. Optimal sampling and problematic likelihood functions in a simple population model. Environ. Model. Assess. 2009, 14, 759–767. [Google Scholar] [CrossRef]
- Gilks, W.R.; Richardson, S.; Spiegelhalter, D. Markov Chain Monte Carlo in Practice; Chapman and Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Verhulst, P.F. Notice sur la loi que la population suit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–126. [Google Scholar]
- Hedge, J.; Lycett, S.J.; Rambaut, A. Real-time characterization of the molecular epidemiology of an influenza pandemic. Biol. Lett. 2013, 9, 20130331. [Google Scholar] [CrossRef]
- Lin, B.Q.; Liu, J.H. Estimating coal production peak and trends of coal imports in China. Energy Policy 2010, 38, 512–519. [Google Scholar] [CrossRef]
- Hubbert, M.K. Nuclear energy and the fossil fuel. In Drilling and Production Practice; American Petroleum Institute: Washington, DC, USA, 1956. [Google Scholar]
- Reed, L.J.; Pearl, R. On the summation of logistic curves. J. R. Stat. Soc. 1927, 90, 729–746. [Google Scholar] [CrossRef]
- Oliver, F. Methods of estimating the logistic growth function. J. R. Stat. Soc. Ser. Appl. Stat. 1964, 13, 57–66. [Google Scholar] [CrossRef]
- Heydari, J.; Lawless, C.; Lydall, D.A.; Wilkinson, D.J. Fast Bayesian parameter estimation for stochastic logistic growth models. Biosystems 2014, 122, 55–72. [Google Scholar] [CrossRef]
- Hobbs, N.T.; Hooten, M.B. Bayesian Models: A Statistical Primer for Ecologists; Princeton University Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Bayes, T. An essay towards solving a problem in the doctrine of chances. Philos. Trans. R. Soc. Lond. 1763, 370–418. [Google Scholar] [CrossRef]
- Kiefer, J. Optimum experimental designs. J. R. Stat. Soc. Ser. B Methodol. 1959, 21, 272–304. [Google Scholar] [CrossRef]
- Abt, M.; Welch, W.J. Fisher information and maximum-likelihood estimation of covariance parameters in Gaussian stochastic processes. Can. J. Stat. 1998, 26, 127–137. [Google Scholar] [CrossRef]
- Atkinson, A.; Donev, A.; Tobias, R. Optimum Experimental Designs, with SAS; Oxford University Press: Oxford, UK, 2007; Volume 34. [Google Scholar]
- Laarhoven, P.J.; Aarts, E.H. Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: New York, NY, USA, 1987; pp. 7–15. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- R Core Team R. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Chaloner, K.; Verdinelli, I. Bayesian experimental design: A review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Müller, P.; Berry, D.A.; Grieve, A.P.; Smith, M.; Krams, M. Simulation-based sequential Bayesian design. J. Stat. Plan. Inference 2007, 137, 3140–3150. [Google Scholar] [CrossRef]
- Williamson, D.; Goldstein, M. Bayesian policy support for adaptive strategies using computer models for complex physical systems. J. Oper. Res. Soc. 2012, 63, 1021–1033. [Google Scholar] [CrossRef]
- Jones, M.; Goldstein, M.; Jonathan, P.; Randell, D. Bayes linear analysis of risks in sequential optimal design problems. Electron. J. Stat. 2018, 12, 4002–4031. [Google Scholar] [CrossRef]
- Ford, I.; Titterington, D.; Kitsos, C.P. Recent advances in nonlinear experimental design. Technometrics 1989, 31, 49–60. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).