Cumulative Median Estimation for Sufficient Dimension Reduction

Abstract

In this paper, we present the Cumulative Median Estimation (CUMed) algorithm for robust sufficient dimension reduction. Compared with non-robust competitors, this algorithm performs better when there are outliers present in the data and comparably when outliers are not present. This is demonstrated in simulated and real data experiments.

1. Introduction

Sufficient Dimension Reduction (SDR) is a framework of supervised dimension reduction algorithms that have been proposed mainly for regression and classification settings. The main objective is to reduce the dimension of the p-dimensional predictor vector $\mathit{X}$ without losing information on the conditional distribution of $Y|\mathit{X}$. In other words, we can state the objective as the effort to estimate a $p\times d$ matrix ꞵ, such that the following conditional independence model holds:

$$\begin{array}{c}\hfill Y╨\mathit{X}|{\mathit{ꞵ}}^{\mathsf{T}}\mathit{X},\end{array}$$

(1)

where $d<p$. The space spanned by the columns of ꞵ is called the Dimension Reduction Subspace (DRS). There are many ꞵ’s that satisfy the conditional independence model above, and therefore, there are many DRSs. The objective is to find the matrix ꞵ which achieves the minimum d. The space spanned by such ꞵ is called the Central Dimension Reduction Subspace (CDRS), or simply the Central Space (CS). CS does not always exist, but if it exists, it is unique. Conditions of existence of the CS are mild (see [1]) and we consider that these are met in the rest of this work. For a more comprehensive overview of the SDR literature, the interested reader is referred to [2].

The first approach to the SDR framework was Sliced Inverse Regression (SIR) introduced by [3] and which used inverse means to achieve efficient feature extraction. There are a number of other methods that used the idea of inverse moments like Sliced Average Variance Estimation (SAVE) by [4] which uses inverse variance, Directional Regression (DR) by [5] which uses both the inverse mean and variance, and Sliced Inverse Mean Difference (SIMD) by [6] which uses the inverse mean difference. A common aspect of these methods is the fact that one needs to define the number of slices as a tuning parameter. To avoid this, [7] proposed the Cumulative Mean Estimation (CUME), which uses the first moment and removes the necessity to tune the number of slices.

More recently, a number of methods were introduced for robust sufficient dimension reduction. [8] proposed Robust SIR by using the L1 median to achieve sufficient dimension reduction and [9] proposed the use of Tukey and Oja medians to robustify SIR. Similarly, ref. [10] proposed Sliced Inverse Median Difference (SIMeD), the robust version of SIMD using the L1 median. The main reason for using the L1 median is the fact that it is uniquely defined for $p>2$. On the other hand, Tukey and Oja medians may not be uniquely defined, but they are affine equivariant.

In this paper, we will investigate the use of the L1 median to robustify CUME. The new method is called Cumulative Median estimation (CUMed). As CUMed is the robust version of CUME, it has all the advantages CUME has with the additional advantage that it is robust to the presence of outliers. The rest of the paper is organised as follows. In Section 2 we discuss the previous methods in more detail, and we introduce the new method in Section 3. We present numerical studies in Section 4, and we close with a small discussion.

2. Literature Review

In this section, we discuss some of the existing methods in the SDR framework that mostly relate to our proposal. We discuss Sliced Inverse Regression (SIR), Cumulative Mean Estimation (CUME), and Sliced Inverse Median (SIME). We first introduce some standard notation. Let $\mathit{X}$ be the $p—$dimensional predictor vector, Y be the response variable (which we assume to be univariate without loss of generality), $\Sigma =\mathrm{var}\left(\mathit{X}\right)$ be the covariance matrix, and $\mathit{Z}={\Sigma }^{-1/2}(\mathit{X}-E\left(\mathit{X}\right))$ be the standardized predictors.

2.1. Sliced Inverse Regression (SIR)

SIR was introduced by [3] and it is considered the first method introduced in the SDR framework. SIR depends on the linearity assumption (or the linear conditional mean assumption), which states that for any ꞵ $\in {\mathbb{R}}^p$, the conditional expectation $E\left(\mathit{X}\right|{\mathit{ꞵ}}^{\mathsf{T}}\mathit{X})$ is a linear function of ${\mathit{ꞵ}}^{\mathsf{T}}\mathit{X}$. The author proposed to standardize the predictors and then use the inverse mean $E\left(\mathit{Z}\right|Y)$. By performing an eigenvalue decomposition of the variance-covariance matrix $\mathrm{var}\left(E\right(\mathit{Z}\left|Y\right))$, the authors find the directions which span the CS, ${\mathcal{S}}_{Y|\mathit{Z}}$. One can then use the invariance principle [11] to find the direction that spans ${\mathcal{S}}_{Y|\mathit{X}}$.

A key element in SIR is the use of inverse conditional means, that is, $E\left(\mathit{Z}\right|Y)$. To find these in a sample setting, one has to discretize Y, that is, to bin the observations into a number of intervals (denoted with $I_1,\dots ,I_H$, where H is the number of intervals). Therefore, the inverse mean $E\left(\mathit{Z}\right|Y)$ is, in practice, replaced by using $E\left(\mathit{Z}\right|Y\in I_i)$ for $i=1,\dots ,H$, and thus, it is the eigenvalue decomposition of $\mathrm{var}\left(E\left(\mathit{Z}\right|Y\in I_i)\right)$ which is used to find the directions which span the CS, ${\mathcal{S}}_{Y|\mathit{Z}}$.

2.2. Sliced Inverse Median (SIME)

A number of proposals exist in the literature to try to robustify SIR (see, for example, refs. [8,9]). We discuss here the work by [8] which uses the inverse L1 median instead of means to achieve this. The authors preferred the L1 median due to its uniqueness in cases where $p\ge 2$. In their work, they defined the inverse L1 median as:

Definition 1.

The inverse L1 median is given by $\tilde{m}=arg{min}_{\mathit{\mu }\in {\mathbb{R}}^p}E(\parallel \mathit{X}-\mathit{\mu }\parallel \left|Y\right)$, where $\parallel ·\parallel$ is the Euclidean norm.

Similarly, they denote with ${\tilde{m}}_{\mathit{Z}}=arg{min}_{\mathit{\mu }\in {\mathbb{R}}^p}E(\parallel \mathit{Z}-\mathit{\mu }\parallel \left|Y\right)$. To estimate the CS ${\mathcal{S}}_{Y|\mathit{Z}}$, they performed an eigenvalue decomposition of the covariance matrix $\mathrm{var}\left({\tilde{m}}_{\mathit{Z}}\right)$ in a similar manner that SIR works with the decomposition of the covariance matrix of the means.

2.3. Cumulative Mean Estimation (CUME)

As we described above, to use SIR one needs to define the number of slices. To avoid this, [7] proposed the use of the Cumulative Mean Estimation (CUME) algorithm, which removes the need of tuning for the number of slices by taking the cumulative mean idea. CUME uses the eigenvalue decomposition of the matrix $\mathrm{var}\left(E\right(\mathit{Z}I(Y\le y))$, where $I(·)$ is the indicator function, to find the directions which span the CS, ${\mathcal{S}}_{Y|\mathit{Z}}$. To achieve this, one needs to increase the value of y and recalculate the mean each time the value of y is large enough for a new observation to be included in the range $\{Y\le y\}$.

Like SIR, SIME needs to tune the number of slices as well. To our knowledge, there is not another proposal in the literature that removes the need to tune for the number of slices while simultaneously being robust to outliers. Therefore, in the next section, we will present our proposal to robustify CUME by using the Cumulative L1 median.

3. Cumulative Median Estimation

In this section, we introduce our new robust method. Like [8,10] we will use the L1 median as the basis for our proposed method due to the fact that it is unique in higher dimensions. To be more accurate, ref. [8] used the inverse L1 median as it was stated in Definition 1, and [10] used the inverse median difference. In this work, we will be using the cumulative L1 median, as it is defined below:

Definition 2.

The cumulative L1 median is given by $\tilde{m}\left(y\right)=arg{min}_{\mu \in {\mathbb{R}}^p}E(\parallel \mathit{X}-\mathit{\mu }\parallel I(Y\le y))$, where $\parallel ·\parallel$ is the Euclidean norm and $I(·)$ is the indicator function.

Before we prove the basic theorem of this work, let’s give some basic notation. Let $(Y_i,{\mathit{X}}_i)$, $i=1,\dots ,n$ the data pairs, where the response is considered univariate. Let also ${\mathit{Z}}_i$ denote the standardized value of ${\mathit{X}}_i$. It is standard in the SDR literature to work with the regression of $Y_i$ on ${\mathit{Z}}_i$, and then using the invariance principle (see [11]) to find the CS, ${\mathcal{S}}_Y|\mathit{X}$. In the following theorem, we demonstrate that one can use the cumulative L1 median to estimate the CS.

Theorem 1.

Let ${\widehat{\mathbb{K}}}_{CUMed}$ be the kernel matrix for our method, as defined in (4). Suppose $\mathit{Z}$ has an elliptical distribution with $p\ge 2$. Then, $span\left({\widehat{\mathbb{K}}}_{CUMed}\right)\subseteq S_{Y|\mathit{Z}}$.

Proof. 

First of all, note that

$$\begin{array}{c}\hfill E(\parallel \mathit{Z}-\mathit{\mu }\parallel I(Y\le y\left)\right)=E\left(E\right(\parallel \mathit{Z}-\mathit{\mu }\parallel I(Y\le y)\left|Y\right))=E(E(\parallel \mathit{Z}-\mathit{\mu }\parallel |Y\left)I\right(Y\le y\left)\right).\end{array}$$

(2)

Now suppose that $S_{Y|\mathit{Z}}$ has an orthonormal basis $A=\{{\mathit{\eta }}_1,\cdots ,{\mathit{\eta }}_d\}$. Let $\{{\mathit{\eta }}_{d+1},\cdots ,{\mathit{\eta }}_p\}$ be the orthonormal basis for $S_{Y|\mathit{Z}}^{\perp }$, the complement of $S_{Y|\mathit{Z}}$. Then,

$$I_p={\mathit{\eta }}_1{\mathit{\eta }}_1^T+\cdots +{\mathit{\eta }}_d{\mathit{\eta }}_d^T+{\mathit{\eta }}_{d+1}{\mathit{\eta }}_{d+1}^T+\cdots +{\mathit{\eta }}_p{\mathit{\eta }}_p^T.$$

For $t\in {\mathbb{R}}^p$$i=d+1,\cdots ,p$ consider the linear transformation ${\varphi }_i:{\mathbb{R}}^p\to {\mathbb{R}}^p$ such that

$${\varphi }_i\left(t\right)=\left({\mathit{\eta }}_1{\mathit{\eta }}_1^T+\cdots +{\mathit{\eta }}_d{\mathit{\eta }}_d^T+{\mathit{\eta }}_{d+1}{\mathit{\eta }}_{d+1}^T+\cdots -{\mathit{\eta }}_i{\mathit{\eta }}_i^T+\cdots +{\mathit{\eta }}_p{\mathit{\eta }}_p^T\right)t,$$

where $j=1,\cdots ,p,$${\mathit{\eta }}_j^T{\varphi }_i\left(t\right)={\mathit{\eta }}_j^{T}t$ for $j\ne i$ and ${\mathit{\eta }}_j^T{\varphi }_i\left(t\right)=-{\mathit{\eta }}_j^{T}t$ for $j=i$. Using this notation, Dong et al. (2015) showed that

$$\begin{array}{c}\hfill \mathbb{E}\left[\right||\mathit{Z}-\mathit{\mu }|\left|\right|Y]=\mathbb{E}[\left|\right|\mathit{Z}-\varphi \left(\mathit{\mu }\right)\left|\right|\left|Y\right].\end{array}$$

(3)

Using (2) and (3), one can then show that

$$E(\parallel \mathit{Z}-\mathit{\mu }\parallel I(Y\le y\left)\right)=E(\parallel \mathit{Z}-\varphi (\mathit{\mu })\parallel I(Y\le y\left)\right).$$

From this, $\varphi \left(\tilde{m}\left(y\right)\right)$ is the minimizer of $E(\parallel \mathit{Z}-\mathit{\mu }\parallel I(Y\le y\left)\right)$. By definition, $\tilde{m}\left(y\right)$ is also the minimizer of $E(\parallel \mathit{Z}-\mathit{\mu }\parallel I(Y\le y\left)\right)$. Therefore, $\tilde{m}\left(y\right)=\varphi \left(\tilde{m}\left(y\right)\right)$, and therefore, ${\mathit{\eta }}_i^{\mathsf{T}}\tilde{m}\left(y\right)=-{\mathit{\eta }}_i^{\mathsf{T}}\tilde{m}\left(y\right)$ which means ${\mathit{\eta }}_i^{\mathsf{T}}\tilde{m}\left(y\right)=0$ for $i=d+1,\dots ,p$. From the construction at the beginning of the proof $\tilde{m}\left(y\right)\in {\left({\mathcal{S}}_{Y|\mathit{Z}}^{\perp }\right)}^{\perp }={\mathcal{S}}_{Y|\mathit{Z}}$, and therefore $span\left({\widehat{\mathbb{K}}}_{CUMed}\right)\subseteq S_{Y|\mathit{Z}}$. □

Estimation Procedure

In this section we will present the algorithm to estimate the CS using the cumulative L1 median.

(1)

Standardise data to find $\widehat{\mathit{Z}}={\widehat{\Sigma }}^{-1/2}(\mathit{X}-\widehat{\mathit{\mu }})$, where $(\widehat{\mathit{\mu }})$ is the sample mean of ${\mathit{X}}_i$ and $(\widehat{\Sigma })$ is an estimate of the covariance matrix of ${\mathit{X}}_i$.

(2)

Sort Y and then for each value of y, find the cumulative L1 median

$$\widehat{\tilde{m}}\left(y\right)=arg\underset{\mu \in {\mathbb{R}}^p}{min}E(\parallel \mathit{Z}-\mathit{\mu }\parallel I(Y\le y)).$$

(3)

Using the $\widehat{\tilde{m}}\left(y\right)$’s from the previous step, estimate the candidate matrix by

$$\begin{array}{c}\hfill {\widehat{\mathbb{K}}}_{CUMed}=\sum _{y\in {\Omega }_Y}{\widehat{p}}_y\widehat{\tilde{m}}\left(y\right)\widehat{\tilde{m}}{\left(y\right)}^{\mathsf{T}},,\end{array}$$

(4)

where ${\Omega }_Y$ is the range of Y, ${\widehat{p}}_y$ the proportion of points used to find $\widehat{\tilde{m}}\left(y\right)$.

(4)

Calculate the eigenvectors ${\widehat{\beta }}_1,\cdots ,{\widehat{\beta }}_d$, which correspond to the largest eigenvalues of ${\widehat{\mathbb{K}}}_{CUMed}$, and estimate ${\mathcal{S}}_{Y|X}$ with $span({\widehat{\Sigma }}^{-1/2}{\widehat{\beta }}_1,\cdots ,{\widehat{\Sigma }}^{-1/2}{\widehat{\beta }}_d)$.

Note that the in the first step, it is more appropriate to use a robust estimator for Σ, and in this work we propose the use of the minimum covariance determinant (MCD) estimator, which is implemented in function covMcd in package robustbase in R (see [12]. Note that other alternative estimators, such as RFCH and RMVN [13,14] or the forward search estimator ([15]) could have been used. The same estimator is used in the last step as well to recover ${\mathcal{S}}_{Y|X}$.

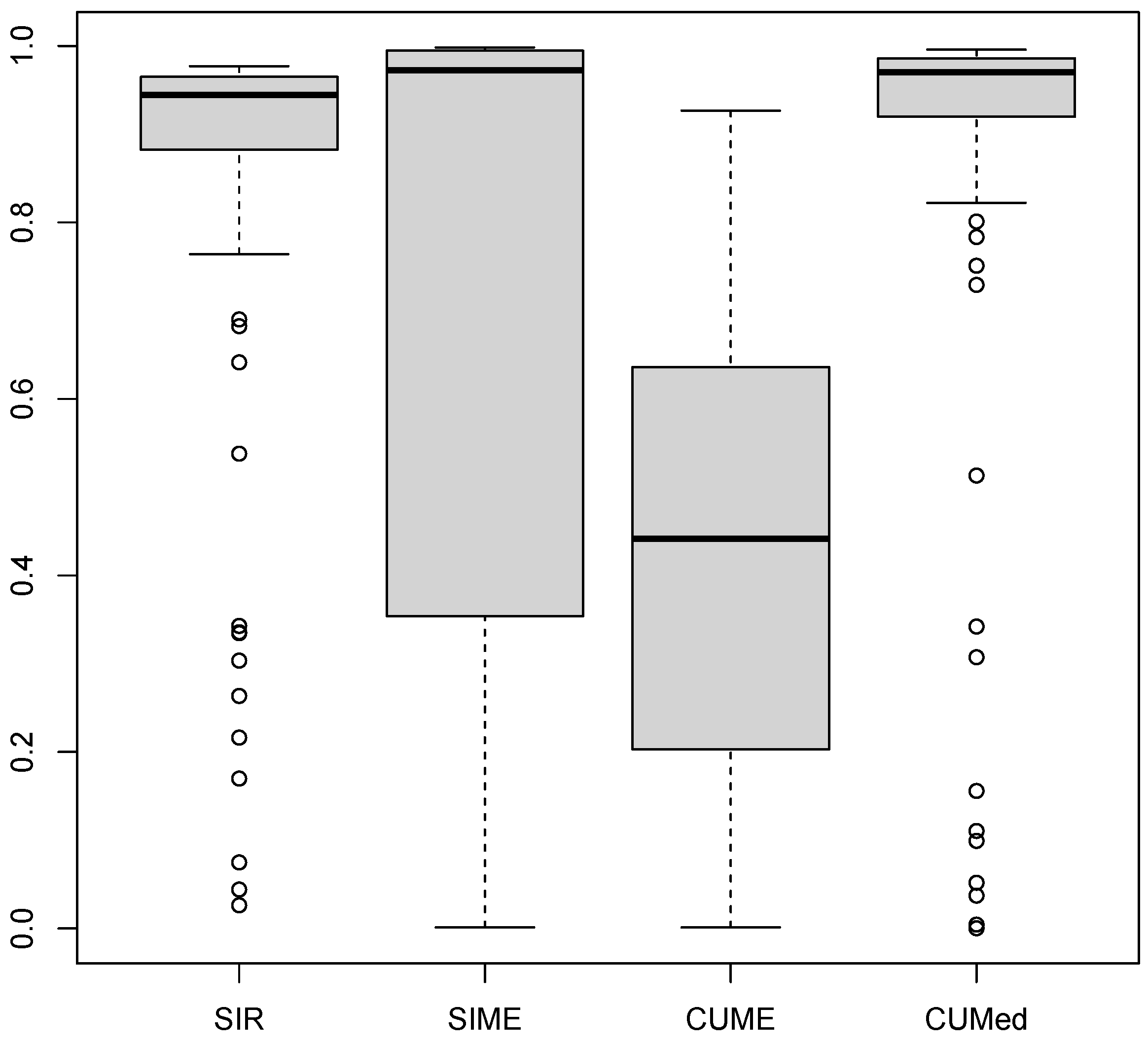
4. Numerical Results

In this section, we will discuss the numerical performance of the algorithm, both in a simulated as well as a real dataset setting.

4.1. Simulated Datasets

We compare the performance of our algorithms with algorithms based on means like SIR and CUME as well as SIME, which is the robust version of SIR proposed by [8] and, similarly to our case, it uses the L1 median. We ran a number of simulation experiments using the following models:

(1)

Model 1: $Y=X_1+X_2+\sigma ϵ$

(2)

Model 2: $Y=X_1/[0.5+{(X_2+1)}^2]+\sigma ϵ$

(3)

Model 3: $Y=(1+(\sigma /2)ϵ)X_1$

(4)

Model 4: $Y=exp(X_1+\sigma ϵ)$

(5)

Model 5: $Y=sin(X_1+\sigma ϵ)$

for $p=5,10$ or 20 and $ϵ\sim N(0,1)$. Note that $\sigma =0.2$. For SIR and SIME we used 10 slices. Note also that the predictors $\mathit{X}=(X_1,\cdots ,X_p)$ come either from multivariate standard normal, which produces no outliers, or from a multivariate standard Cauchy, which produces outliers. We denote them in the result Tables as follows:

• (Outl a): $\mathbf{X}$ is from multivariate standard normal.
• (Outl b): $\mathbf{X}$ is from multivariate standard Cauchy.

We ran 100 simulations and report the average trace correlation and its standard errors to compare performance. Trace correlation is calculated as follows:

$$\begin{array}{c}\hfill r=\frac{\mathrm{trace}\left\{{\mathit{P}}_{\mathit{B}}{\mathit{P}}_{\widehat{\mathit{B}}}\right\}}{d},\end{array}$$

(5)

where ${\mathit{P}}_{\mathit{B}}$ is the projection matrix on the true subspace and ${\mathit{P}}_{\widehat{\mathit{B}}}$ the projection matrix on the estimated subspace. It takes values between 0 and 1 and the closer to 1, the better the estimation.

The results in

Table 1. Mean and standard errors (in parentheses) of trace correlation (4) for 100 replications for all the models for different values of p. We use $n=200$ and the number of slices $H=10$ in SIR and SIME.

			Method
Model	p	outl	SIR	SIME	CUME	CUMed
		a	0.997 (0.002)	0.998 (0.002)	0.989 (0.010)	0.976 (0.018)
	5	b	0.647 (0.250)	0.436 (0.331)	0.479 (0.328)	0.600 (0.173)
1		a	0.993 (0.004)	0.996 (0.002)	0.978 (0.013)	0.949 (0.034)
	10	b	0.520 (0.227)	0.279 (0.356)	0.217 (0.247)	0.572 (0.185)
		a	0.985 (0.006)	0.992 (0.003)	0.943 (0.025)	0.891 (0.043)
	20	b	0.437 (0.249)	0.080 (0.152)	0.082 (0.146)	0.515 (0.203)
		a	0.962 (0.037)	0.981 (0.014)	0.961 (0.034)	0.803 (0.151)
	5	b	0.543 (0.204)	0.650 (0.183)	0.493 (0.247)	0.572 (0.139)
2		a	0.911 (0.039)	0.960 (0.020)	0.902 (0.043)	0.638 (0.130)
	10	b	0.329 (0.213)	0.555 (0.133)	0.283 (0.229)	0.483 (0.079)
		a	0.828 (0.045)	0.910 (0.034)	0.790 (0.063)	0.490 (0.056)
	20	b	0.282 (0.183)	0.456 (0.110)	0.124 (0.157)	0.399 (0.100)
		a	0.998 (0.002)	0.997 (0.002)	0.988 (0.009)	0.975 (0.019)
	5	b	0.603 (0.397)	0.478 (0.420)	0.405 (0.377)	0.957 (0.076)
3		a	0.994 (0.003)	0.996 (0.002)	0.975 (0.018)	0.951 (0.029)
	10	b	0.563 (0.375)	0.229 (0.361)	0.147 (0.251)	0.835 (0.241)
		a	0.986 (0.006)	0.993 (0.003)	0.946 (0.027)	0.886 (0.044)
	20	b	0.362 (0.354)	0.057 (0.162)	0.059 (0.141)	0.774 (0.211)
		a	0.906 (0.070)	0.949 (0.030)	0.888 (0.088)	0.855 (0.104)
	5	b	0.669 (0.342)	0.488 (0.436)	0.357 (0.349)	0.921 (0.174)
4		a	0.820 (0.090)	0.880 (0.054)	0.780 (0.098)	0.691 (0.135)
	10	b	0.539 (0.385)	0.181 (0.298)	0.158 (0.248)	0.824 (0.265)
		a	0.630 (0.133)	0.791 (0.085)	0.595 (0.127)	0.491 (0.158)
	20	b	0.417 (0.368)	0.031 (0.097)	0.052 (0.129)	0.751 (0.238)
		a	0.935 (0.048)	0.967 (0.019)	0.918 (0.059)	0.869 (0.095)
	5	b	0.176 (0.250)	0.166 (0.304)	0.259 (0.349)	0.318 (0.337)
5		a	0.871 (0.076)	0.929 (0.034)	0.844 (0.078)	0.741 (0.123)
	10	b	0.136 (0.238)	0.060 (0.151)	0.111 (0.236)	0.172 (0.240)
		a	0.743 (0.101)	0.871 (0.036)	0.700 (0.100)	0.542 (0.136)
	20	b	0.035 (0.074)	0.023 (0.064)	0.038 (0.117)	0.066 (0.155)

demonstrate the advantages of our algorithm. Our method CUMed performs well when there are no outliers (comparable performance with CUME) and it is better than CUME in the case where there are outliers. Comparing to SIME (the robust version of SIR), our method performs better with the exception of model 2, where SIME performs slightly better. We run a more extensive simulation and we have seen that when $d>1$, SIME tends to work better than CUMed.

On the second experiment, we describe the importance of using the L1 median by running a comparison of CUMed when the L1 median is used with CUMed when the Oja median is used. Here, we emphasize that the Oja median is not unique, and it is also computationally more expensive to be calculated. We run the experiment for $n=200$ and $p=10$ under both scenarios where there are outliers and where there are not outliers. As we can see from

Table 2. Mean and standard errors (in parentheses) of trace correlation (4) for 100 replications for the performance of CUMed using L1 and Oja medians for all five models with and without outliers. $n=200$ and $p=10$.

		Median
Model	outl	L1 Median	Oja
1	a	0.955 (0.023)	0.947 (0.044)
	b	0.598 (0.242)	0.133 (0.194)
2	a	0.636 (0.128)	0.586 (0.117)
	b	0.484 (0.063)	0.212 (0.208)
3	a	0.946 (0.024)	0.904 (0.099)
	b	0.835 (0.283)	0.190 (0.354)
4	a	0.684 (0.169)	0.507 (0.249)
	b	0.851 (0.199)	0.249 (0.107)
5	a	0.754 (0.128)	0.583 (0.285)
	b	0.122 (0.224)	0.108 (0.273)

, the L1 median behaves better for all models and both scenarios.

4.2. Real Data—Concrete Data

In this section, we compare the SIR, SIME, and CUME methods against our CUMed method on a real data set. We use the Concrete strength dataset (see [16]), which has eight predictors (Cement, Blast Furnace Slag, Fly Ash, Water, Superplasticizer, Coarse Aggregate, Fine Aggregate, Age) and a response variable (Concrete Strength). It has 1030 observations. To highlight our method’s ability to estimate the central subspace in the presence of outliers, we ran 100 experiments where we selected 30 data points randomly and multiplied them by 10 (therefore creating about $3\%$ outliers in the dataset). We then computed the trace correlation distance between the original projection matrix and the estimate projection matrix containing the outliers. As it is shown in Figure 1, if we compare the median trace correlations, both robust methods, SIME and CUMed, tend to have much less distance from the original projection (the one before introducing outliers) than SIR and CUME. CUMed is, overall, the best method, as it seems to have most distances above 0.8 and only in a few cases falls below that. On the other hand, for SIME, we can see from the boxplot that Q1 is at 0.35 (as opposed to CUMed, which has Q1 at 0.9).

5. Discussion

In this work, we discussed a robust SDR methodology which uses the L1 median to expand the scope of a previously proposed algorithm in the SDR literature, CUME, which uses the first moments. The new method utilizes all the advantages of CUME, by not having to tune for the number of slices as earlier SDR methods, like SIR, had to. In addition, it is robust to the presence of outliers, which CUME is not, as we demonstrated in our numerical experiments.

There have been a number of papers introduced recently in the SDR literature to robustify against outliers. We believe that this work adds to the existing literature and opens new roads to further discuss robustness within the SDR framework. In addition to the ones already discussed, which are based on inverse-moments, there is literature in the Support Vector Machine (SVM) based on SDR literature—see, for example, ref. [17], who used adaptively weighted schemes for SVM-based robust estimation, as well as the literature in iterative methods, like the ones proposed in [18,19].