A Consistent Estimator of Nontrivial Stationary Solutions of Dynamic Neural Fields
Abstract
1. Introduction
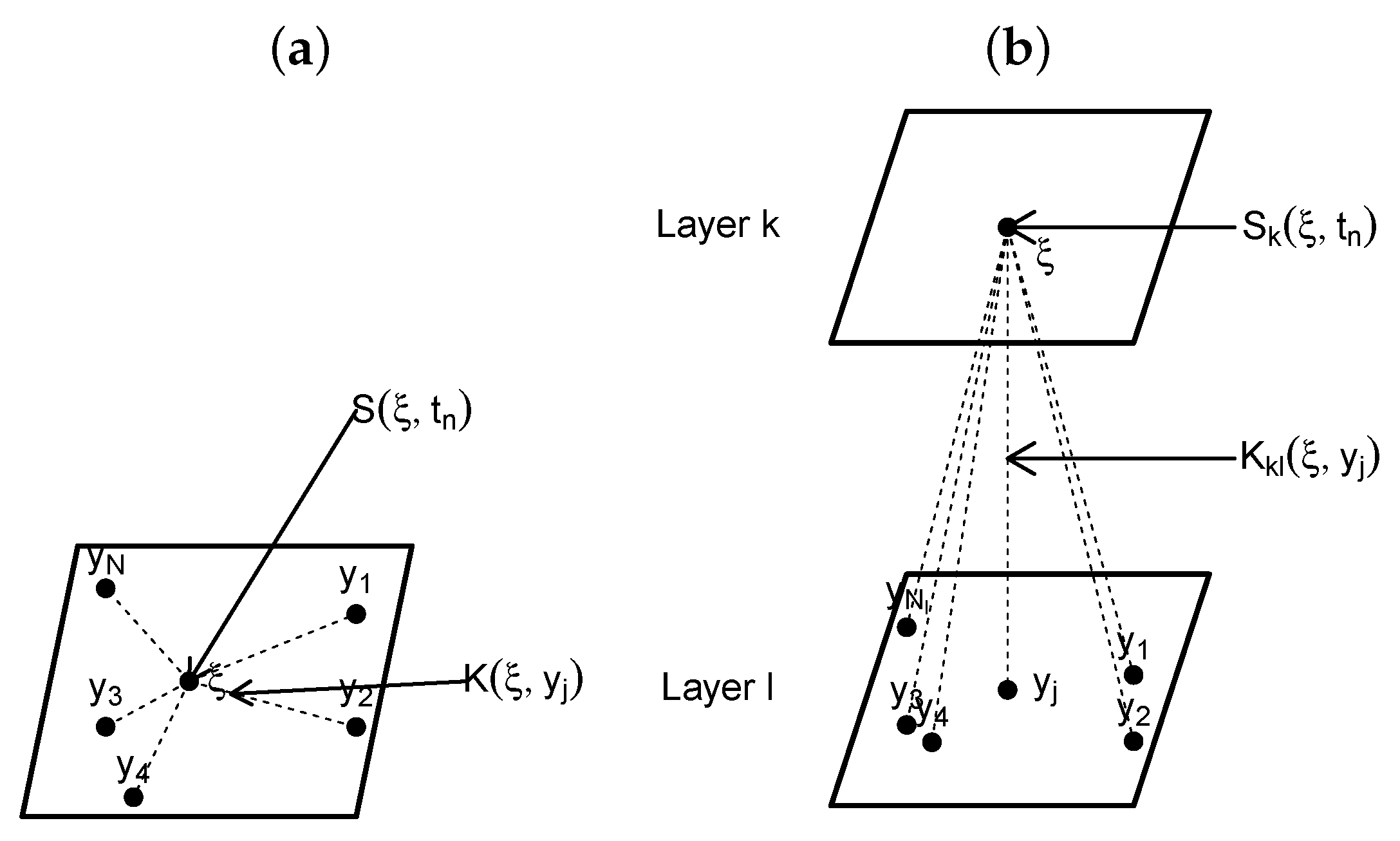
2. Main Results
3. Computational Algorithm
- Step 1: Select positive integers n and m.Here, the experimenter should choose the values of relative to how much computational capabilities ones has, knowing that very large values can lead to a significant slowdown of convergence.
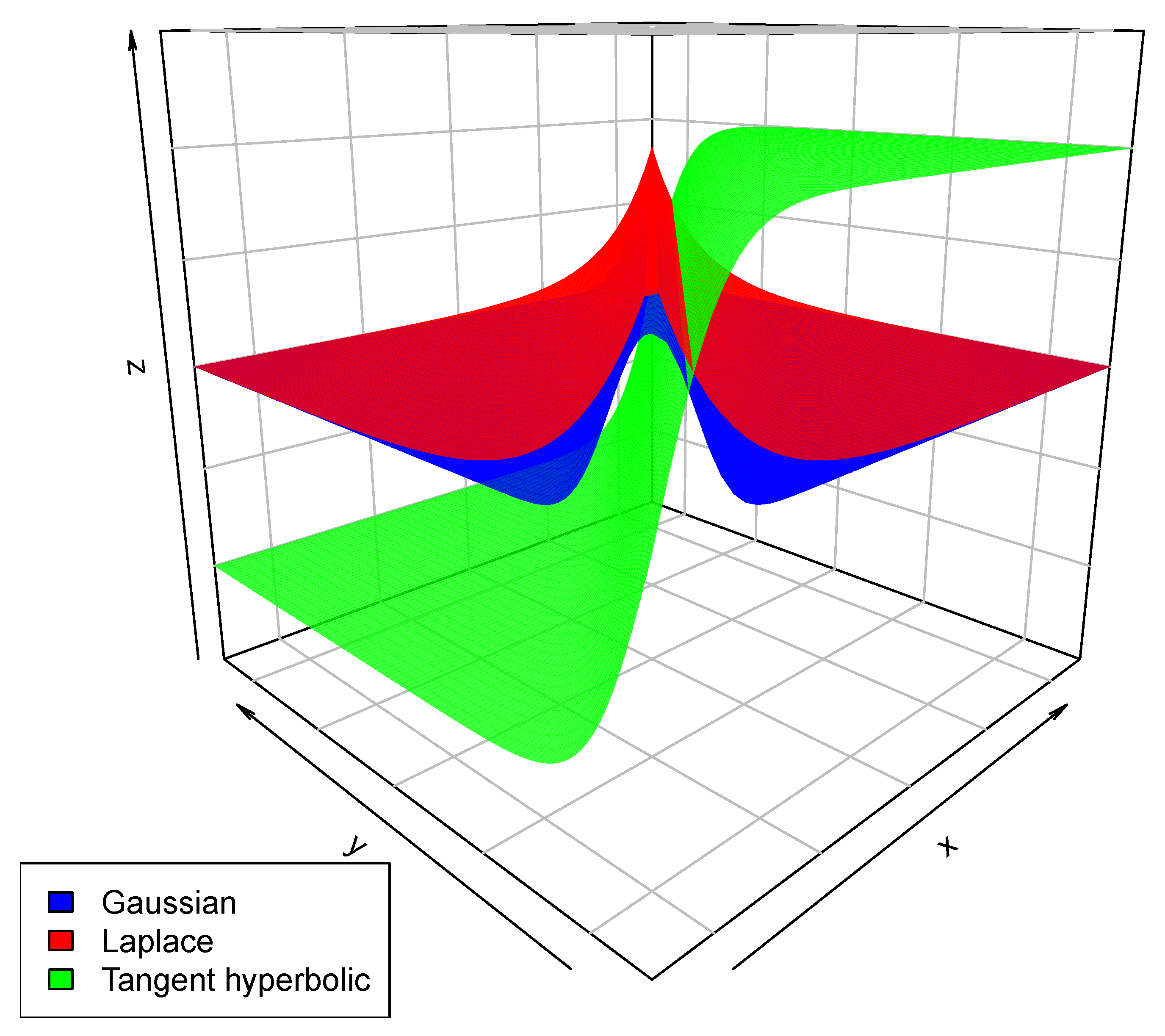
- Step 2: Select from the distribution .Knowing that is a known probability distribution (Gaussian, Laplace, or tangent hyperbolic, see the section below), this should be achievable with relative ease from any software.
- Step 3: Select from the distribution of of U associated with G.As in the previous step, sampling from a known probability distribution should be achievable. However, if G is not given as bounded function between 0, and 1, we can still truncate it adequately to obtain a probability distribution (see Section 4.1).
- Step 4: For , select from a uniform distribution .This step assumes that we have an external stimulus S arriving on the neuron at position given as a function of .
- Step 5: For given , evaluate .In this final step, one can choose different values of to plot the estimator in the space .
4. Technical Considerations
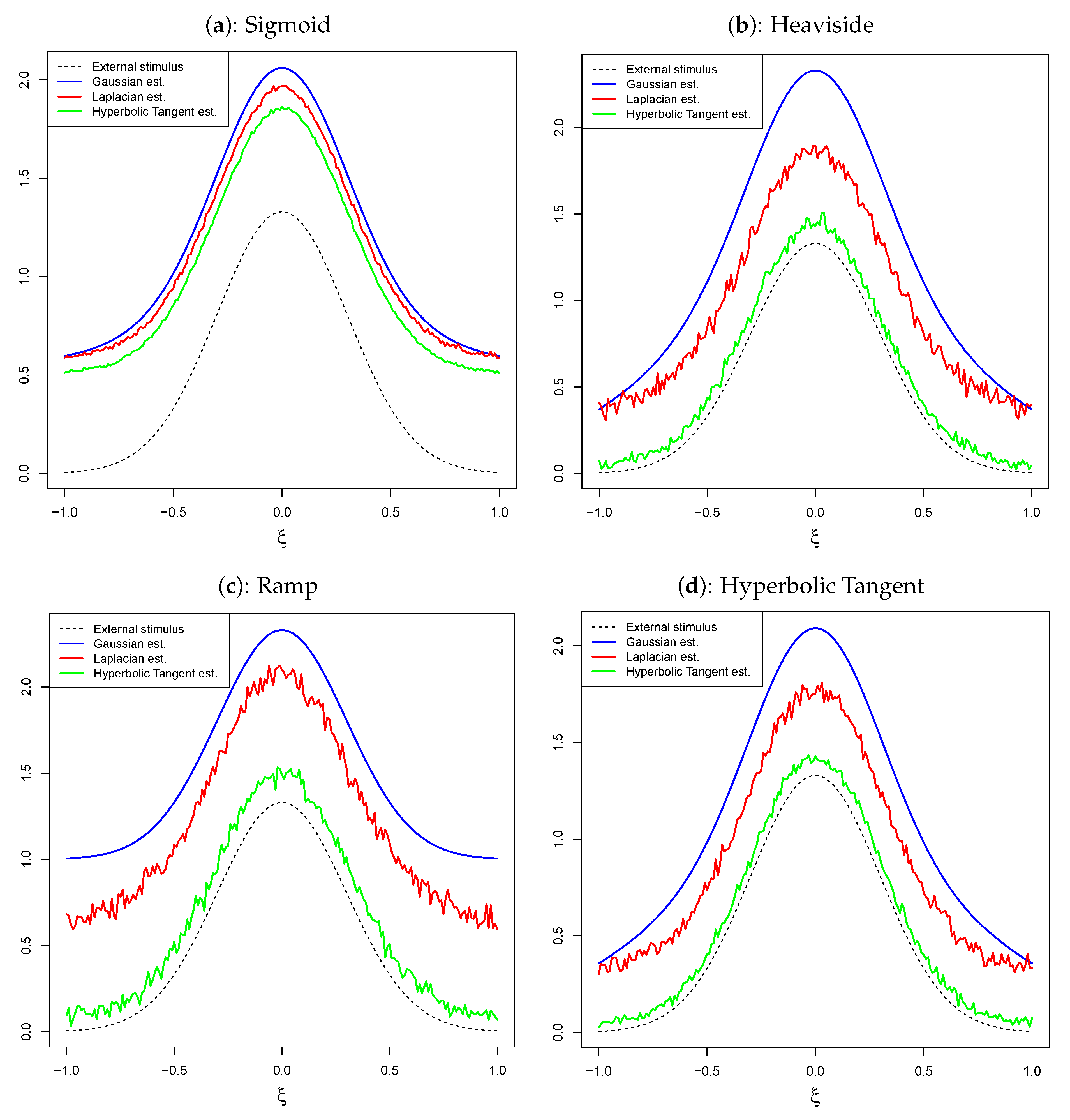
4.1. Pulse Emission Rate Function
- (1) We observe that the choice of the sigmoid activation function is widely preferred in the literature for its bounded nature, without condition.
- (2) Another reason is the fact that it is also suitable when thes are binary, that is, they may take the value 0 or 1, where 0 represents a non-active neuron at time n and 1 represents an active neuron at time n. In this case,would represent the probability that there is an activity on neuron at positionat time.
- (3) A third reason, which is important in our situation, is that it has an inverse that can be written in close form, unlike many other activation functions sometime used in the artificial neural networks (see, e.g., [21]) making it easy to generate random numbers from. The other functions would require the use of numerical inversion methods such as the bisection method, the secant method, or the Newton–Raphson method, all of which are computationally intensive (see, e.g., Chapter 4 in [22]).
4.2. Connection Intensity Function
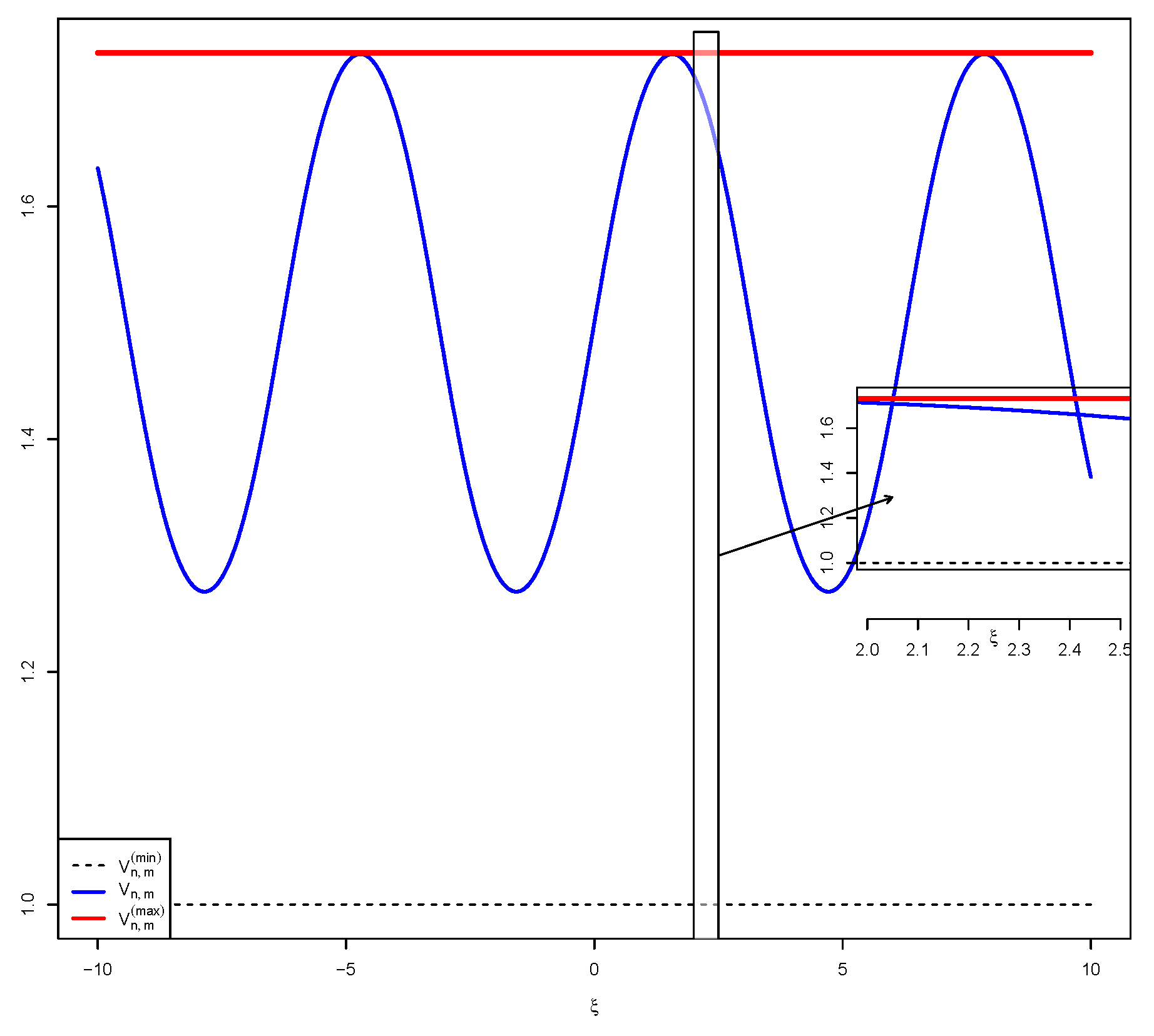
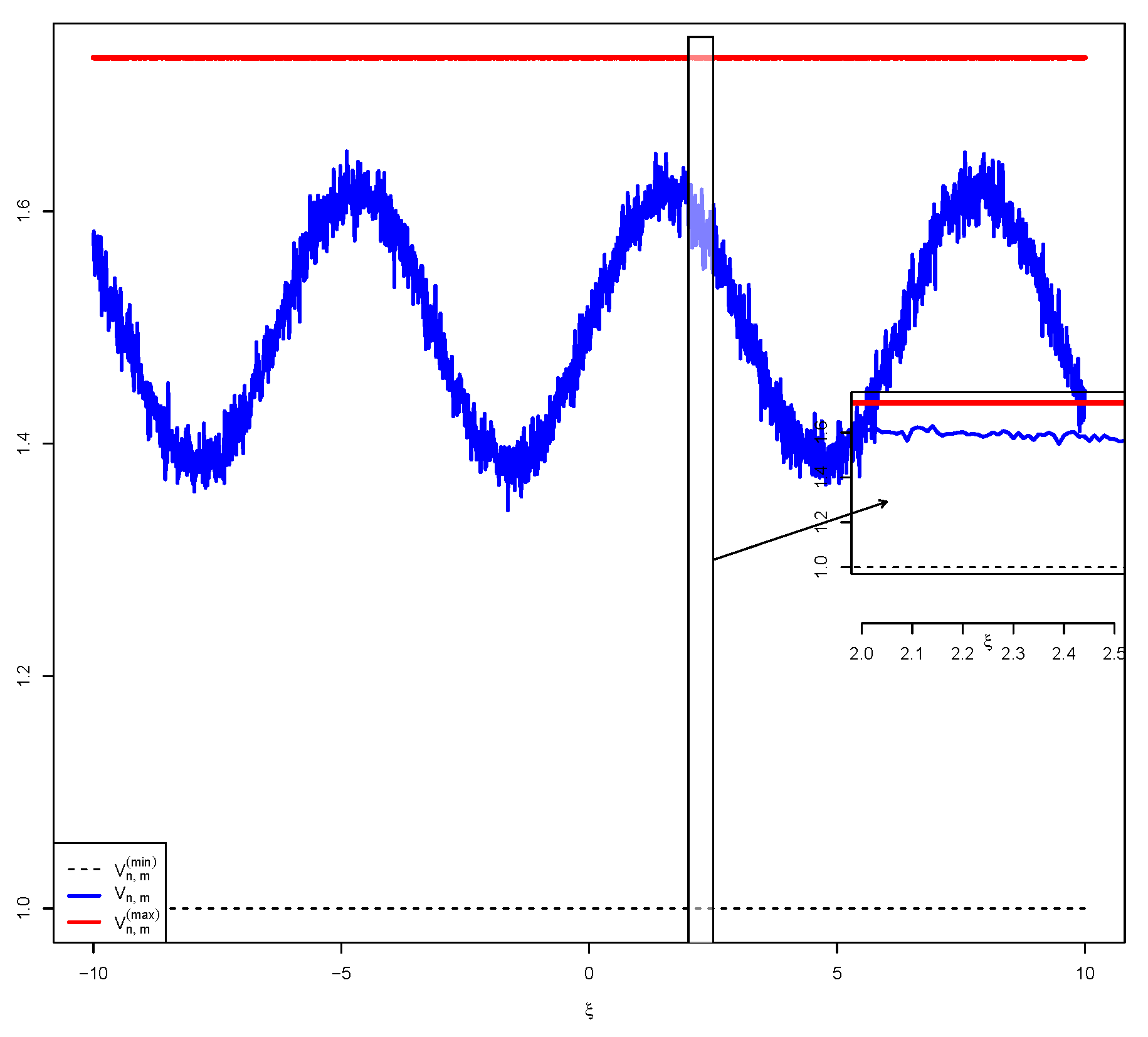
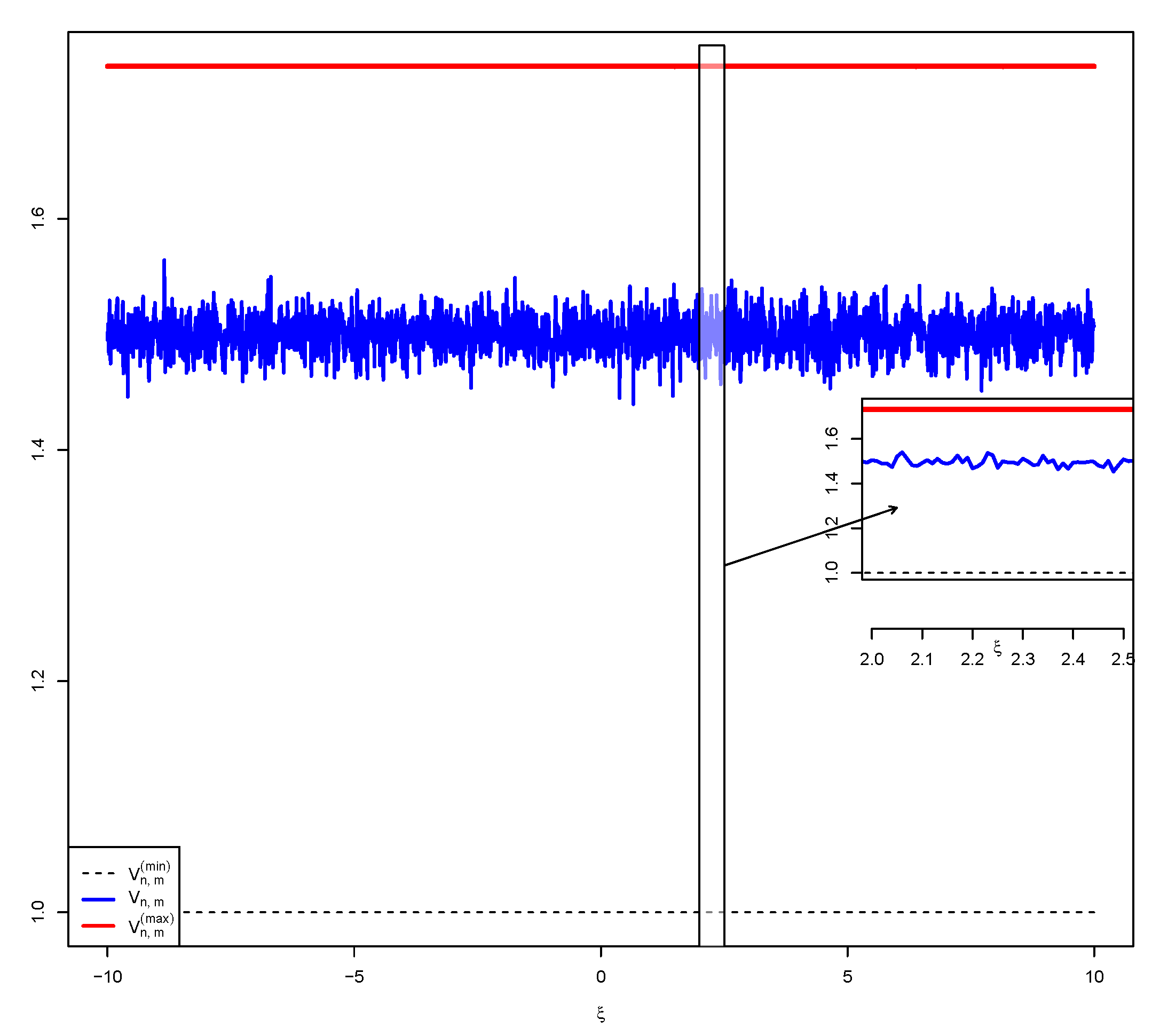
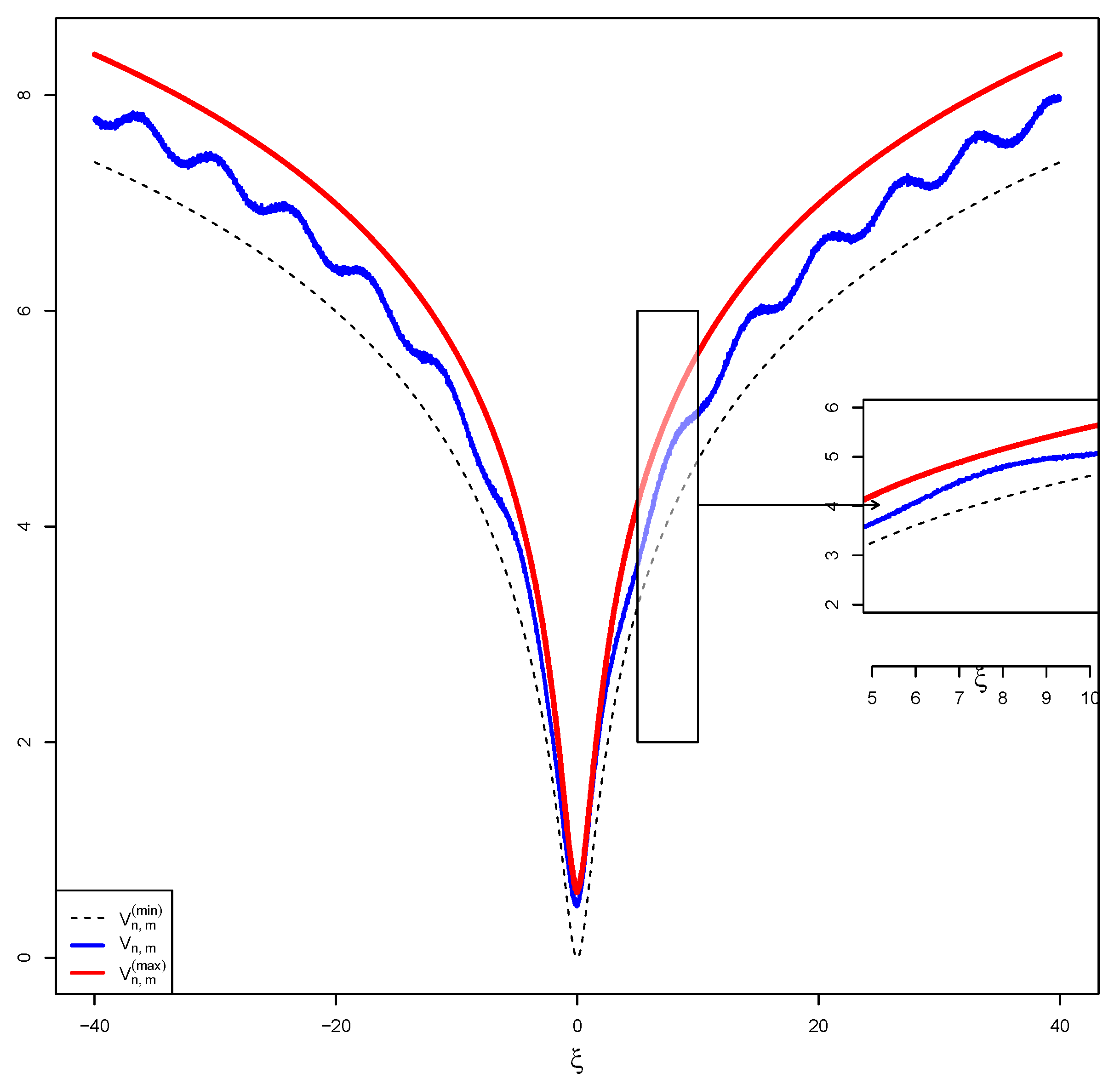
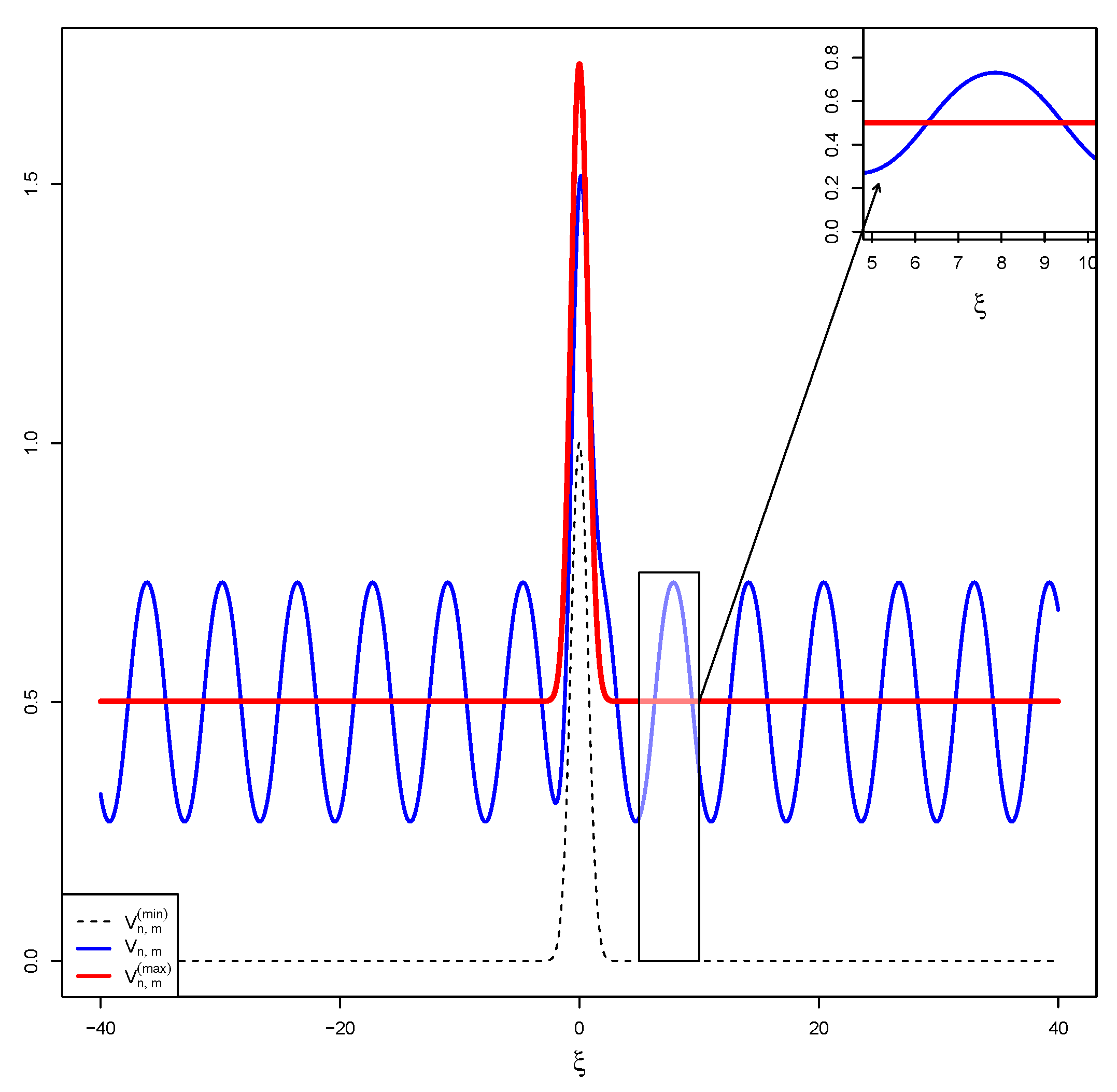
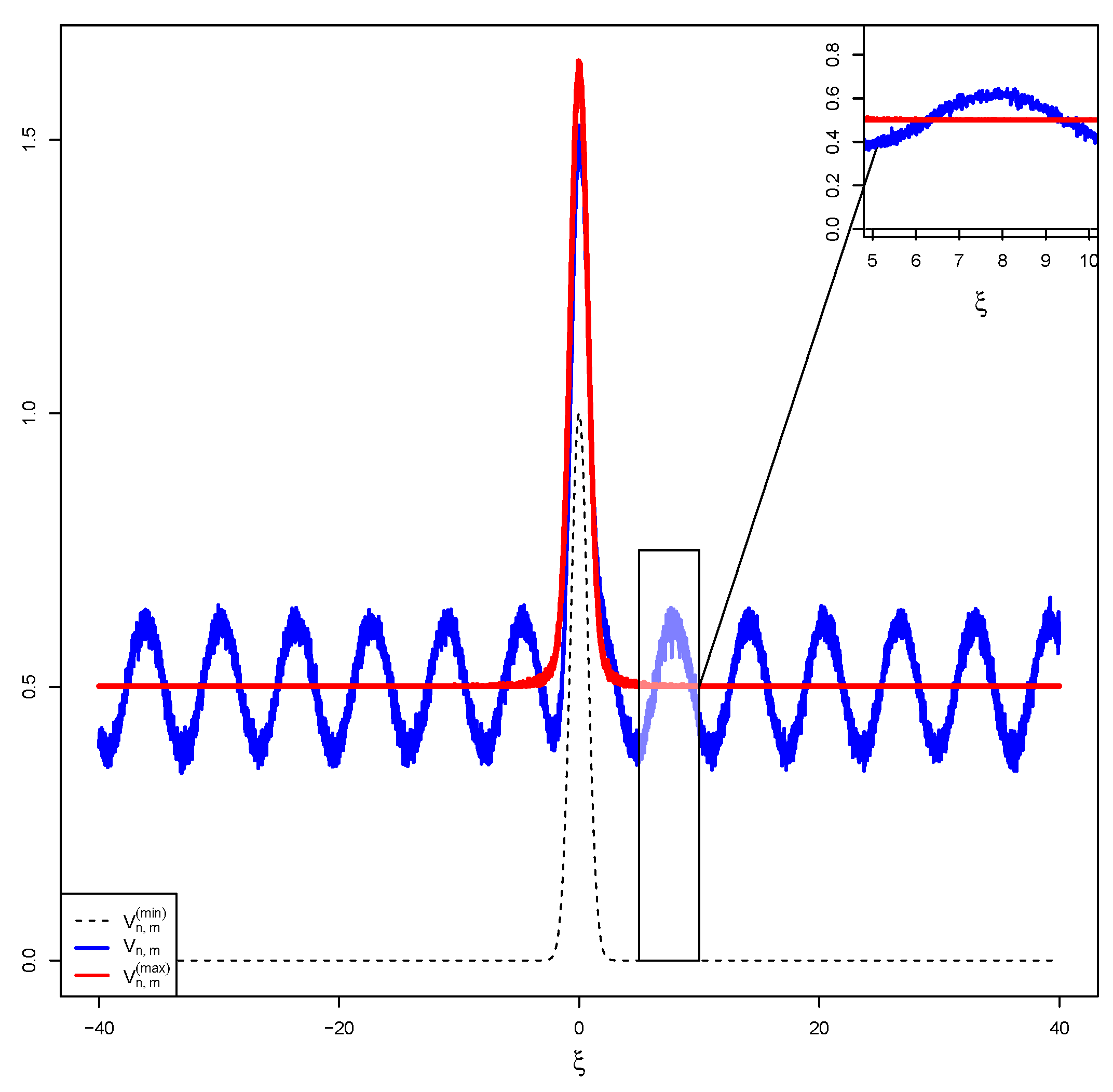
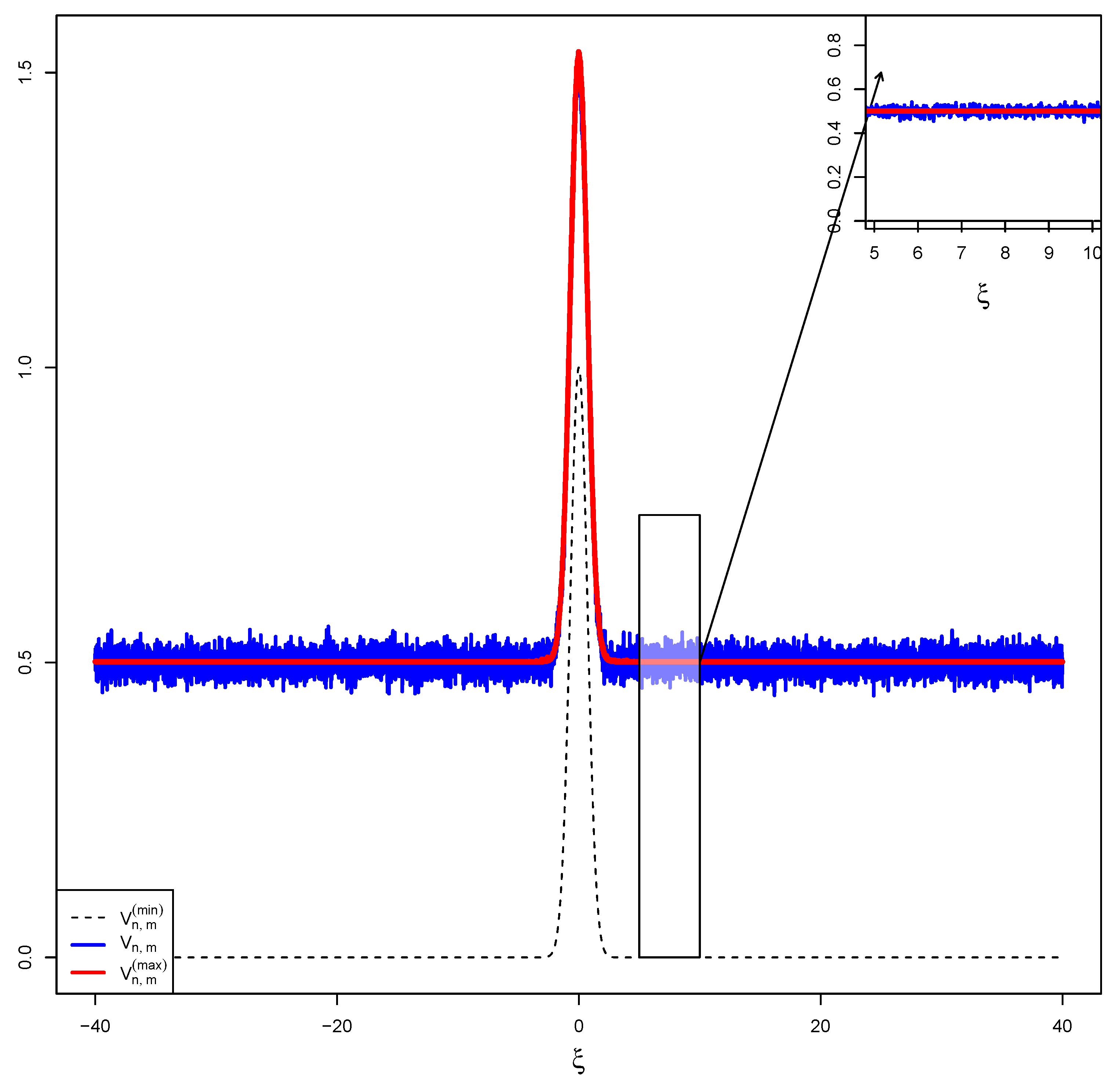
5. Simulations
5.1. Simulation 1: Constant External Stimulus
5.2. Simulation 2: Logarithm External Stimulus
5.3. Simulation 3: Exponentially Decaying External Stimulus
5.4. Simulation 4: Mexican Hat True Function
5.5. Discussion
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beurle, R.L. Properties of a mass of cells capable of regenerating pulses. Philos. Trans. R. Soc. Lond. B 1956, 240, 55–94. [Google Scholar]
- Wilson, H.R.; Cowan, J.D. Excitatory and inhibitory interactions in localized populations ofmodel neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef]
- Amari, S.I. Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 1977, 27, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Nunez, P.L.N.; Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG, 2nd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Camperi, M.; Wang, X.J. A model of visuospatial short-term memory in prefrontal cortex: Recurrent network and cellular bistability. J. Comp. Neurosci. 1998, 4, 383–405. [Google Scholar] [CrossRef] [PubMed]
- Ermentrout, G.B.; Cowan, J.D. A mathematical theory of visual hallucination patterns. Biol. Cybern. 1979, 34, 137–150. [Google Scholar] [CrossRef] [PubMed]
- Tass, P. Cortical pattern formation during visual hallucinations. J. Biol. Phys. 1995, 21, 177–210. [Google Scholar] [CrossRef]
- Bicho, E.; Mallet, P.; Schöner, G. Target representation on an autonomous vehicle with low-levelsensors. Int. J. Robot. Res. 2000, 19, 424–447. [Google Scholar] [CrossRef]
- Erlhangen, W.; Bicho, E. The dynamics neural field approach to cognitive robotics. J. Neural Eng. 2006, 3, R36–R54. [Google Scholar] [CrossRef] [PubMed]
- Erlhangen, W.; Schöner, G. Dynamic field theory of movement preparation. Psychol. Rev. 2001, 109, 545–572. [Google Scholar] [CrossRef] [PubMed]
- Bicho, E.; Louro, L.; Erlhangen, W. Integrating verbal and non-verbal communication in adynamic neural field for human-robot interaction. Front. Neurorobot. 2010, 4, 1–13. [Google Scholar]
- Beim, P.G.; Hutt, A. Attractor and saddle node dynamics in heterogeneous neural fields. EPJ Nonlinear Biomed. Phys. EDP Sci. 2014, 2. [Google Scholar] [CrossRef]
- Hammerstein, A. Nichtlineare Integralgleichungen nebst Anwendungen. Acta Math. 1930, 54, 117–176. [Google Scholar] [CrossRef]
- Djitte, N.; Sene, M. An Iterative Algorithm for Approximating Solutions of Hammerstein IntegralEquations. Numer. Funct. Anal. Optim. 2013, 34, 1299–1316. [Google Scholar] [CrossRef]
- Kwessi, E.; Elaydi, S.; Dennis, B.; Livadiotis, G. Nearly exact discretization of single species population models. Nat. Resour. Model. 2018. [Google Scholar] [CrossRef]
- Elman, J.L. Finding Structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Williams, R.J.; Zipser, D. A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1990, 1, 256–263. [Google Scholar] [CrossRef]
- Durstewitz, D. Advanced Data Analysis in Neuroscience; Bernstein Series in Computational Neuroscience; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Green, R.E.; Krantz, S.G. Function Theory of One Complex Variable; Pure and Applied Mathematics (New York); John Wiley & Sons, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Rudin, W. Real and Complex Analysis; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Kwessi, E.; Edwards, L. Artificial neural networks with a signed-rank objective function and applications. Commun. Stat. Simul. Comput. 2020. [Google Scholar] [CrossRef]
- Devroye, L. Complexity questions in non-uniform random variate generation. In Proceedings of COMPSTAT’2010; Physica-Verlag/Springer: Heidelberg, Germany, 2010; pp. 3–18. [Google Scholar]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise, 2nd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 1994; Volume 97. [Google Scholar]
- Rasmussen, C.E.; Ghahramani, Z. Bayesian Monte Carlo. In Proceedings of the 15th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 505–512. [Google Scholar]
- Deisenroth, M.P.; Huber, M.F.; Henebeck, U.D. Analytic Moment-based Gaussian Process Filtering. In Proceedings of the 26th International Conference on Machine Learning (ICML), Montreal, QC, Canada, 14–18 June 2009. [Google Scholar]
- Gerstner, T.; Griebel, M. Numerical integration using sparse grids. Numer. Algorithms 1998, 18, 209. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, Q. Gaussian Process Based Expected Information Gain Computation for Bayesian Optimal Design. Entropy 2020, 22, 258. [Google Scholar] [CrossRef] [PubMed]
- Movaghar, M.; Mohammadzadeh, S. Bayesian Monte Carlo approach for developing stochastic railway track degradation model using expert-based priors. Struct. Infrastruct. Eng. 2020, 1–22. [Google Scholar] [CrossRef]
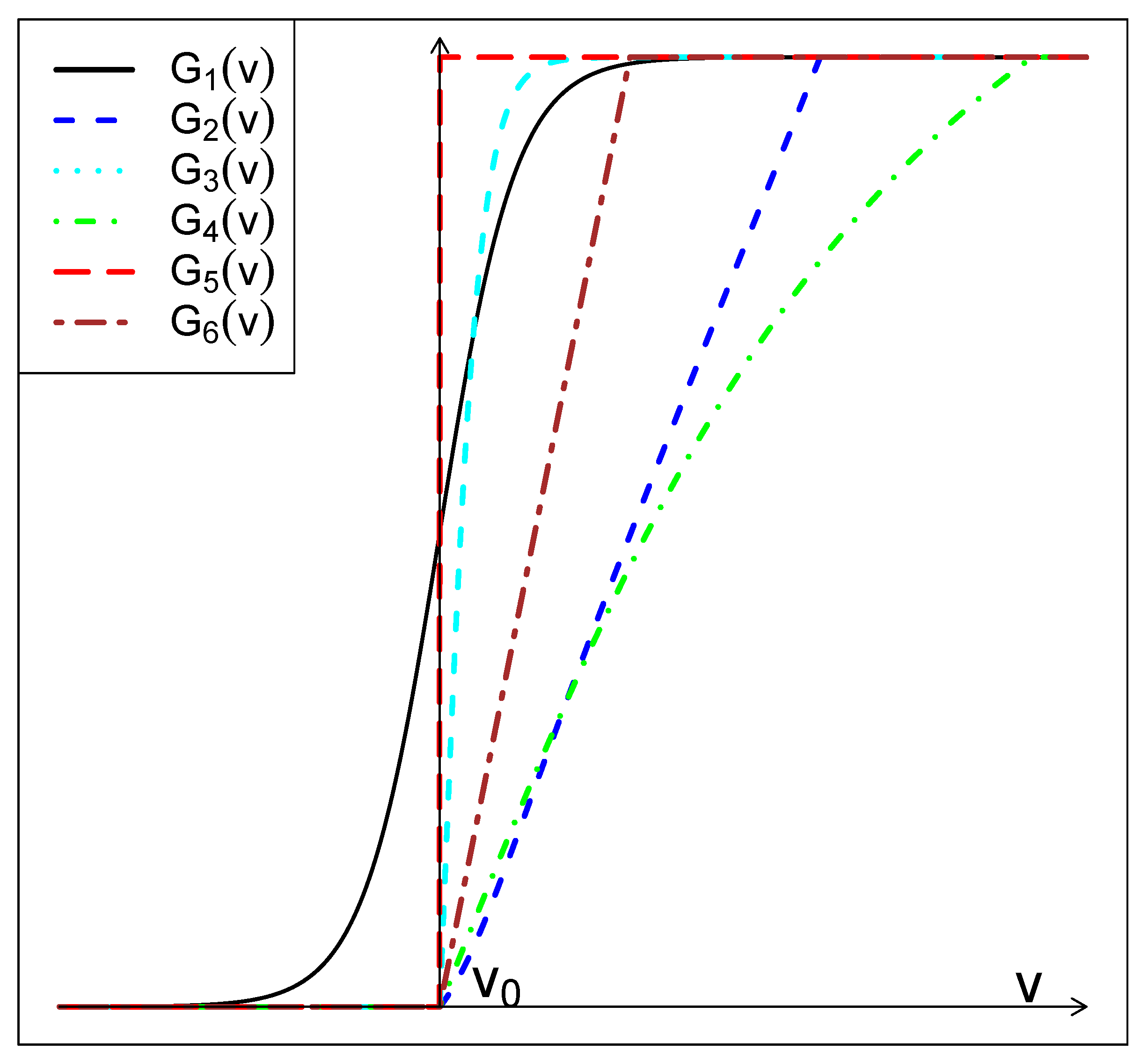


| Name | Formulation | Conditions |
|---|---|---|
| Sigmoid: | 0 | if |
| if | ||
| Weighted Sigmoid: | 0 | if |
| if | ||
| Hyperbolic Tangent: | 0 | if |
| if | ||
| Tangent inverse: | if | |
| 0 | if | |
| Heaviside: | 0 | if |
| 1 | if | |
| Ramp: | 0 | if |
| 1 | if |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwessi, E. A Consistent Estimator of Nontrivial Stationary Solutions of Dynamic Neural Fields. Stats 2021, 4, 122-137. https://doi.org/10.3390/stats4010010
Kwessi E. A Consistent Estimator of Nontrivial Stationary Solutions of Dynamic Neural Fields. Stats. 2021; 4(1):122-137. https://doi.org/10.3390/stats4010010
Chicago/Turabian StyleKwessi, Eddy. 2021. "A Consistent Estimator of Nontrivial Stationary Solutions of Dynamic Neural Fields" Stats 4, no. 1: 122-137. https://doi.org/10.3390/stats4010010
APA StyleKwessi, E. (2021). A Consistent Estimator of Nontrivial Stationary Solutions of Dynamic Neural Fields. Stats, 4(1), 122-137. https://doi.org/10.3390/stats4010010






