Abstract
In sequential tests, typically a (pairwise) multiple comparison procedure (MCP) is performed after an omnibus test (an overall equality test). In general, when an omnibus test (e.g., overall equality of multiple proportions test) is rejected, then we further conduct a (pairwise) multiple comparisons or MCPs to determine which (e.g., proportions) pairs the significant differences came from. In this article, via likelihood-based approaches, we acquire three confidence intervals (CIs) for comparing each pairwise proportion difference in the presence of over-reported binomial data. Our closed-form algorithm is easy to implement. As a result, for multiple-sample proportions differences, we can easily apply MCP adjustment methods (e.g., Bonferroni, Šidák, and Dunn) to address the multiplicity issue, unlike previous literatures. We illustrate our procedures to a real data example.
1. Introduction
As a part of sequential tests, an omnibus test is used to test the overall significance among parameters (of the same type). The following are some examples of omnibus tests (but not limited to): Equality of means, equality of proportions, equality of multiple regression coefficients, equality/parallelism of survival curves/distributions, etc. Generally, when an omnibus test (e.g., overall equality of multiple proportions test) is rejected, then one could further conduct a multiple (pairwise) comparisons to determine which (e.g., proportions) pairs the significant differences came from.
As another part of sequential tests, multiple comparisons are the comparisons of two or more groups (sometimes called treatments). Such multiple groups may be treatments of a disease, groups of subjects, or computer systems, for example. Statistical multiple comparison methods are used heavily in research, education, business, and industry to analyze data. Hsu in 1996 [1], Edwards and Hsu in 1983 [2], Hsu and Edwards in 1983 [3], and Hsu in 1982 [4] present the theory behind all the multiple (pairwise) comparisons, giving statistical methods for inference in terms of confidence intervals, illustrate applications with real data, and point out methods empowered by modern computers. In addition, Shiraishi in 2011 [5] proposes multiple tests based on arcsin transformation in multi-sample models with Bernoulli responses.
Hence, in general, an omnibus test is used to test the overall significance, while multiple comparisons test (or procedure) is to find which pair(s) contribute to the significant differences; i.e., the purpose of multiple comparisons procedures (MCPs) is not to test the overall significance, but to test individual (pairwise) effects for significance (while controlling the experiment-wise error rate), at an error-rate of α level.
However, the above MCP-pioneer references are MCP methods without any presence of misclassifications (i.e., false-positive, false-negative, nor both). On the hand, there are literatures which discussed misclassified binomial data, for one-sample and two-sample binomial data, with one-type or both-type of misclassifications, Bayesian or frequentist (i.e., likelihood-based) methods, but none of them are with the multiplicity adjustments for (pairwise) MCPs, either; for example, Rahardja in 2019 [6] reviewed such literature. Additionally, there are past papers which studied various ways to analyze binomial data, but they did not include misclassifications nor multiplicity adjustments for (pairwise) MCPs; for example, among many papers, Gianinetti in 2020 [7], Giles and Fiori in 2019 [8], Hodge and Vieland in 2017 [9].
Stamey, et al. in 2004 [10] proposed multiple comparison method for comparing Poisson rate parameters where counts are subject to misclassification. However, the method is for Poisson data, not for binomial data. Hence, to date, there is no statistical inference method which are easily obtainable/available for (pairwise) MCP of proportion differences, in the presence of binomial misclassifications (over-reported or under-reported binomial data). Hence in this article, we proposed such likelihood-based estimation methods with multiplicity adjusted methods (MCP for proportion differences) in the presence of one-type of misclassified (over-reported or under-reported) binomial data, using a double sampling scheme. The multiplicity adjusted method means to control the experiment-wise (Type I) error rate, to remain at the originally intended error-rate of α level (i.e., not inflated above α level, nor deflated below α level, after testing subgroups multiple times).
Therefore, this article will be valuable and helpful for researchers and practitioners in their applied fields such as business, social sciences, psychology, manufacturing, medicine, industry, etc. to compare multiple proportions subgroups via MCP in the presence of one-type of misclassified binary data and still maintaining unbiased estimation (i.e., preserving a proper level of Type-I error rate, α level).
In the first stage (see Section 2, Section 3, Section 4 and Section 5), we first device three likelihood-based (i.e., frequentist) methods to compare a proportional difference (i.e., just one pair) between two independent binomial samples that have been coded as distinct variables, in the presence of over/under-reported misclassified binary data. For example, people typically interested in comparing gender (proportion) difference in the commonness of disease such as cancer, diabetes, pain and depression, etc. The grouping variables (males/females) are mostly error-free, while the response variable (disease/not) is often misclassified (error-prone). In the terminal disease scenario, under-reporting (false negatives) occurs when a person (male/female) dies due to terminal illness, but the cause of death is not reflected on the official records.
In the midst of various researchers, Bross in 1954 [11], Zelen and Haitovsky in 1991 [12], Rahardja and Yang in 2015 [13], pointed out that studies which are ignorant to account for misclassification (i.e., excluding false-positive and false-negative counts) may result in severely biased estimation. On the other hand, correcting the bias by including false-positive and false-negative parameters in models can lead to another issue which involves fitting models with more parameters than available number of sufficient statistics. Here, we implement a double sampling scheme as a means of gaining more information and ensuring that a model is identifiable as well as unbiased.
Previous literature recommends the merits of using a double sample (Rahardja et al. in 2015 [14]; Rahardja & Yang in 2015 [13]; Tenenbein in 1970 [15]. To incorporate such double sample merit into the MCP problem, using maximum likelihood estimation approach, basically, the Rahardja of 2019 [6] paper has summarized the concept (in Section 1) using a Bayesian approach. Numerous literatures in past studies have previously been listed in Rahardja of 2019 [6] manuscript and hence are not re-listed here.
Note that our ultimate goal (Second/Final Stage, Section 6) is to provide MCP in the presence of multiple-sample over-reported multi-nominal data. The pairwise proportion difference (First Stage, Section 2, Section 3, Section 4 and Section 5) method is just an intermediate step. The methods proposed in the past literature reviews (Rahardja of 2019 [6]) were not able to easily reach MCP adjustment (Second/Final Stage) due to difficult, complex, and non-closed-form algorithms. However, since our closed-form algorithm is easy to implement, consequently, we are able to easily apply MCP adjustment methods (e.g., Bonferroni, Šidák, and Dunn) to address the multiplicity issue.
Here in this manuscript, we device three likelihood-based approaches to make inference on MCP for multiple-sample proportional differences in doubly sampled data subject to only one type of misclassification. In the following sections, we describe the data (Section 2) prior to obtaining three likelihood-based confidence intervals (CIs) in Section 3. We then illustrate the tests using real data (Section 4). We perform simulations study in Section 5.
In the second stage (see Section 6), in making inferences for such over-reported multiple-sample binomial data and to account for the multiplicity effect, we then utilize three MCP methods (Bonferroni, Šidák, and Dunn) to adjust the CI width (from the first stage, in Section 2, Section 3, Section 4 and Section 5). Finally, we test whether zero is in the interval (for each pair’s difference) or not. If zero falls in any of the intervals, then such subgroup pairs do not contribute the significant difference at the corresponding adjusted Type-I error significance level. Next, using real data we then illustrate the MCP and discuss the conclusion of this work.
2. Data
The data structure for the original study and the validation sub study serve as the basis for all analyses performed. Therefore, starting with group i (where i = 1, 2), we define mi and ni as the number of observations in the original study and the sub study, respectively. Next, we denote Ni = mi + ni as the total sample size for group i.
For the jth unit in the ith group, where i = 1, 2 and j = 1,…, Ni, we denote Fij and Tij be the binary response variables by the error-prone and error-free classifiers, respectively. We utilize Fij = 1 if the result is positive by the error-prone classifier and Fij = 0 otherwise. In the same manner, we utilize Tij = 1 if the result is truly positive by the error-free classifier and Tij = 0 otherwise. Note that Fij is observed for all units in both the original study and the validation substudy, while Tij is observed for units in the validation substudy but not in the original study. It is clear that misclassification occurs when Fij ≠ Tij.
In the validation study, for i = 1, 2, j = 0, 1, and k = 0, 1, we used nijk as the number of units in group i classified as j and k by the error-free and the error-prone classifiers, respectively. In the original study, we denoted xi and yi to be the number of positive and negative classifications in group i by the error-prone classifier, respectively. The summary counts in both the original study and the validation substudy for group i are tabulated in Table 1.

Table 1.
Data for group i.
In what follows, we define the parameters for group i. Without Loss of Generality (WLOG) we consider data with one type of misclassification (false positive) only. Here, we denote that the true proportion parameter of interest be , the proportion parameter of the error-prone classifier be , and the false positive rate of the error-prone classifier be . Note that πi is not an additional unique parameter because it is a function of other parameters. Specifically, using the law of total probability, we have
where qi = 1 − pi. For the summary counts displayed in Table 1, the corresponding cell probabilities are shown in Table 2.

Table 2.
Cell Probabilities for group i.
Therefore, in this step, we aim to generate a statistical inference on one pair of proportional difference (say, the proportion difference between group 1 and group 2, among multiple groups, g) and then expand the method to include adjustment for the MCP. Here, we denote the proportion difference of a pair of interest is
3. Model
In this section, we aim to make statistical inference on the proportion difference in Equation (2). Specifically, we intend to construct a point and interval estimation or confidence interval (CI) for the proportion difference in Equation (2).
The data under consideration is presented in Table 1. Then, for group i, the observed counts from the validation substudy have a Trinomial distribution with total size ni and associated probabilities tabulated in an upper right 2 × 2 submatrix in Table 2, i.e.,
Additionally, the observed counts (xi, yi) in the original study have the following binomial distribution:
Since and are independent for group i and these cell counts are independent across groups, up to a constant, the full likelihood function is
where .
It is not a straightforward task to directly maximize Equation (3) with respect to η, as it requires iterative numerical methods. In place of direct enumeration, a reparameterization of η is utilized and hence a closed-form solution is obtainable. Here, we specifically define
The new parameter set are denoted to be . Using Equation (3), the full log likelihood function in γ is
The corresponding score vector has the following form:
Setting the above score vector to 0, the Maximum Likelihood Estimator (MLE) for γ can be obtained as and . By solving Equations (1) and (4) together with the invariance property of MLE, the MLE for η are and
Utilizing Equation (5) above, the expected Fisher information matrix is a diagonal matrix with the displayed diagonal elements as:
The regularity conditions can be checked and are satisfied for this model. Therefore, the MLE has an asymptotic multivariate normal distribution with mean γ and covariance matrix , which is a diagonal matrix with the diagonal elements as below:
Hence, asymptotically, we have
In addition, are asymptotically independent.
Since and are asymptotically independent, by the Delta method, the variance of is expressed as:
A consistent estimator of is
Since a consistent estimator of is . A naïve 100(1−α)% Wald (nWald) CI for δ is , where is the upper α/2th quantile of the standard normal distribution. We term this CI as naïve Wald CI because this CI could be outside the interval between −1 and 1 and this CI tends to be unnecessarily narrow for small samples.
In order to improve the naïve Wald test, we define a transformation . The MLE for is . Using the Delta method, we have .
Then, a consistent estimator for is
Therefore, a 100(1−α)% CI for is Finally, a 100(1−α)% CI for δ is obtained by applying function g on , where is the inverse transformation. We name this CI as modified Wald (mWald) CI.
For small sample size, Wald-type CIs are known to perform under-nominal coverage. A common remedy approach is to add small counts to the data and apply Wald intervals to the resulting new data. Depending on the specific dataset, this kind of small counts addition to the data is not unique. Agresti and Coull in 1998 [16] conducted a similar procedure and recommended adding a count of two to cells for one-sample binomial problems. They arrived at the number two by examining the relationship between Wald CI and Score CI. In a related investigation concerning one-sample misclassified binary data subject to one type of misclassification only, Lee and Byun in 2008 [17] also verified to add either one or two to the cell counts. Our justification for adding the small amount to cells in this study was similar to the argument made by Lee and Byun in 2008 [17]. Subsequently, we call this approach as mWald.2 method.
4. Example
As an example to illustrate obtaining a pair of proportion difference in Equation (2), we utilize the automobile accident dataset described in Hochberg in 1977 [18], which contains both types of misclassifications. For simplicity and illustration, we merge the ni01 (false-positive) counts into the ni00 counts, as we only evaluate false-negatives. The intention here is to contrast the risk of injury between males’ high car damages (Group A) and females’ high car damages (Group B), since the two groups experienced similar severity levels of their car damage. We categorize accidents as either with injuries (1) or without injuries (0). Since the original study is based on 1974 police reports of automobile accidents in North Carolina, we denote the error-prone classifier as the police classifier, and the error-free classifier as the non-police classifier. The validation substudy is based on accidents that occurred in North Carolina during an unspecified short period in early 1975. Table 3 showed such datasets.

Table 3.
North Carolina traffic accident data.
In this specific example, we denote p1 and p2 as the probabilities of injuries for males and females (both high damage accident), respectively. Table 4 display the 90% CI for proportion difference δ by all three likelihood-based methods. As shown in Table 4, all three methods produce similar CIs (between the AB pair) for this specific dataset.

Table 4.
nWald, mWald, mWald.2 90% confidence intervals (CIs) and CI lengths (between Group A and B pair) for North Carolina traffic accident data.
5. Simulation
Simulation studies were demonstrated to evaluate and compare the performances of all three CI approaches under different scenarios. Performance was measured in terms of CI coverage probabilities (CPs) and average lengths (ALs), using two-sided 90% CIs. For presentation simplicity, the overall sample sizes were set as N1 = N2 = N, substudy sample sizes n1 = n2 = n, and false positive rates φ1 = φ2 = φ.
For our simulations, the performance of all CI approaches are evaluated by varying total sample sizes. In these simulations, we select the following:
- False positive rate φ = 0.1.
- Ratio of substudy sample size versus the total sample size s = n/N = 0.2.
- Total sample sizes N: From 100 to 400 with increments of 10.
- True proportion parameters of interest (p1, p2) = (0.4, 0.6) and (0.1, 0.2), which correspond to proportions difference of −0.2 and −0.1, respectively.
For each simulation setting with a combination of fixed (p1, p2), φ, n/N, and N, the simulation of K = 10,000 datasets are performed.
The graphs of CPs and ALs of all CI methods versus N for (p1, p2) = (0.4, 0.6) and (p1, p2) = (0.1, 0.2), are shown in Figure 1 and Figure 2, respectively. When the proportion parameters of interest are close to 0.5 (i.e., close to ‘fair-coin’ or ‘best-case’ scenario), in this case (p1, p2) = (0.4, 0.6), the behavior of the binomial distributions is approximately symmetric around their means, and for this reason, we expected the CI methods to cooperate well. As anticipated, and despite of the sample sizes range selected in this study, Figure 1 demonstrates that all three CIs have close-to-nominal CPs. The mWald.2 CIs are more conservative than the other two CIs. For all CI methods, the ALs are similar. In contrast, when the proportion parameters of interest are further away from ‘fair-coin’, in this case (p1, p2) = (0.1, 0.2), the distributions are skewed and the behavior of binomial distributions do not cooperate. Hence, in contrast, in all similar scenarios we would not expect the CI functions to perform well for small samples.
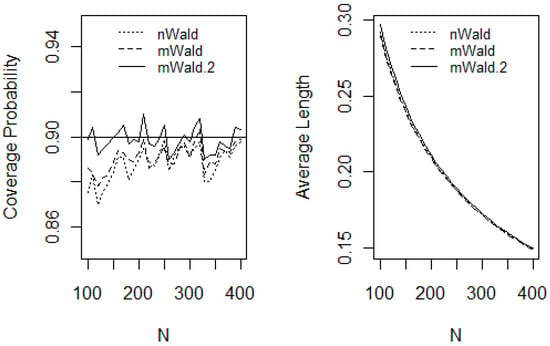
Figure 1.
Coverage probabilities and average lengths versus total sample sizes N where (p1, p2) = (0.4, 0.6). The false positive rate is φ = 0.1 and the ratio of substudy sample size versus the total sample size s = n/N = 0.2.
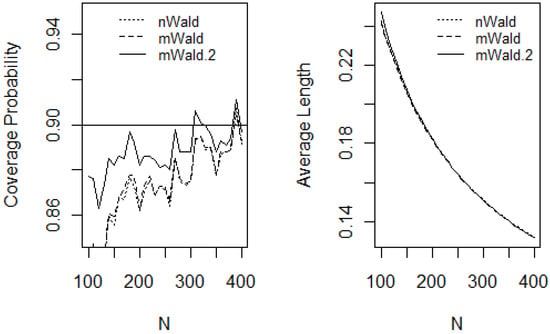
Figure 2.
Coverage probabilities and average lengths versus total sample sizes N where (p1, p2) = (0.1, 0.2). The false positive rate is φ = 0.1 and the ratio of substudy sample size versus the total sample size s = n/N = 0.2.
The plots in Figure 2 display that both the nWald and mWald CIs have very poor CPs for small samples. The CPs for nWald and mWald are close to nominal when sample sizes are large. Impressively, the mWald.2 CIs have considerably good coverage for small and large samples. The ALs for all three methods are similar.
In the following, we provide some guidance where the range of the sample sizes when the three confidence intervals are valid. For mWald.2 CI, when (p1, p2) = (0.4, 0.6) are close to ‘fair-coin’ (best-case scenario), the CPs are close to nominal (here, approximately between 89% and 91% CPs, for a Nominal 90% CI) and the sample size range can be as small as N > 100; and N > 150 when (p1, p2) = (0.1, 0.2) are further-away from ‘fair-coin’ scenarios (here, approximately between 88% and 91% CPs). For the other two CI methods (nWald and mWald), when (p1, p2) = (0.4, 0.6), in order to reach close to Nominal 90% CP (here, between 88% to 91% CPs), both methods need at least N > 175; and N > 375 when (p1, p2) = (0.1, 0.2).
Our simulations conclude that mWald.2 CI approach achieves the best performance among the three CIs because it consistently demonstrates close to nominal coverage, even for relatively smaller sample size. Hence, our simulations study concurs with Agresti and Coull in 1998 [16] and Lee and Byun in 2008 [17] findings and recommendations.
6. Multiple Comparison Procedure (MCP) with the Over-Reported Binomial Data
When we have over-reported binomial data for more than two groups for pairwise comparisons, as described in Section 2, Section 3, Section 4 and Section 5 then there is multiplicity issue generated from multiple times comparing each pairs of g groups of data. Such a multiple comparisons (hypothesis testing or confidence interval) issue is a well-known statistical problem. Hence, it is necessary to adjust such multiplicity issue. The usual goal is to control the family-wise error rate (FWER), the chance/probability of making at least one Type-I error in any of the comparisons, which, therefore, the FWER should be controlled at a desired overall level, called α. To control FWER, there are various MCP methods (such as Bonferroni, Šidák, Dunn, etc.) in the literature. These MCP adjustment methods differ in the way they adjust the value of alpha to compensate for multiple comparisons.
In this article, we employ three adjustment methods (Bonferroni, Šidák, and Dunn) to the differences of proportions parameters in the presence of either under/over-reported multiple-sample binomial data, into the final CIs calculation.
Note that when there is g grouping, then the unique (i.e., permutations, not combinations) number of comparison pairs is
Note also that when comparing with a control group, the number of comparisons we make is only
Hence when ≠ 1 pair, it is therefore no longer a fair/valid comparison to test each pair at an overall level of α = 0.05. For each pair of comparison, the α level must be adjusted. The adjustment methods are as follows.
6.1. Bonferroni Adjustment of CI for Over-Reported Binomial Data
In machine learning literature, Salzberg in 1997 [19] mentions a general solution for the problem of multiple testing is the Bonferroni (Hochberg of 1988 [20]; Holland of 1991 [21]; and Hommel of 1988 [22] correction. Salzberg in 1997 [19] also notes that the Bonferroni correction is usually very conservative (i.e., slow to reject the null hypothesis of equality test) and weak since it assumes the independence of the hypotheses. However, the Bonferroni correction is the first in the literature, and the simplest to understand multiple testing, we therefore prescribed it first, in the presence of over/under-reported binomial data. The Bonferroni correction is a single step procedure, meaning all CIs are compared to the same CI threshold for every zero tested in the m adjusted intervals (Holland and Copenhaver in 1987 [23]; Hochberg and Tamhane in 1987 [24]).
In order to have an overall confidence level of (1−α) × 100%, this (single step) Bonferroni adjustment/correction procedure for each m individual CI for δ is
where m is from Equation (6). If zero is in the (adjusted) interval in Equation (8), then we do not reject equality of the pair’s proportion. Else, if zero is not in the (adjusted) interval (8) then there is significant difference between the pair’s proportion, at each (Bonferroni adjusted) α/m level of significance.
Applying Bonferroni adjustment in Equation (8), with m in Equation (6) to the North Carolina Traffic Data for g = 4 groups (A = Male High Damage, B = Female High Damage, C = Male Low Damage, and D = Female Low Damage), we obtain the resulting m = 6 (mWald.2) CIs, as shown in Table 5.

Table 5.
mWald.2 method for an overall 90% CIs (i.e., Bonferroni 98.33% CI or Šidák 98.26% CI for each group’s pair) for North Carolina under-reported traffic accident data.
As shown on Table 5, using the Bonferroni adjustment method in Equation (8), the significant difference come from the pairs: AC, AD, BC, and BD, because zero is outside these four Bonferroni-adjusted intervals. In order to achieve an overall 90% CI (or α = 0.1), such single-step Bonferroni adjustment method results in 98.33% Bonferroni CI for each of the m = 6 (mWald.2) CIs.
6.2. Šidák Adjustment of CI for Over-Reported Binomial Data
Similar to Bonferroni correction, the Šidák of 1967 [25] correction is another common single step procedure of multiple testing adjustment to control the FWER, but only when the tests are independent or positively dependent. Again, a single step procedure means that all CIs are compared to the same CI threshold for every zero tested in the m adjusted intervals.
In order to have an overall confidence level of (1−α) × 100%, this (single step) Šidák adjustment/correction procedure for each m individual CI for δ is
where m is from Equation (6). If zero is in the (adjusted) interval in Equation (9), then we do not reject equality of the pair’s proportion. Else, if zero is not in the (adjusted) interval (9), then there is significant difference between the pair’s proportion, at each (Šidák adjusted) level of significance.
Applying Šidák adjustment in Equation (9), with m in Equation (6), to the North Carolina Traffic Data for g = 4 groups (A = Male High Damage, B = Female High Damage, C = Male Low Damage, and D = Female Low Damage), we obtain the resulting m = 6 (mWald.2) CIs, as shown in Table 5.
As shown on Table 5, using Šidák adjustment method in Equation (9), the significant difference come from the pairs: AC, AD, BC, and BD—here, in this (traffic data) case, the concluded results are consistent with the results using Bonferroni adjustment method in Equation (8). In order to achieve an overall 90% CI (or α = 0.1), such single-step Šidák adjustment method results in 98.26% Šidák CI for each of the m = 6 (mWald.2) CIs.
6.3. Dunn Adjustment of CI for Over-Reported Binomial Data
Another common single step adjustment/correction method is the Dunn method (Dunn of 1961 [26]) which controls the FWER by dividing α by m, the number of comparisons made, with m in Equation (7). Hence, treating one group as the control group and comparing the remaining of the groups with the one control group. The rest of this procedure is easy to implement because it is the same as the previously discussed (single step) Bonferroni method in Equation (8) of Section 6.1, but with using m from Equation (7).
Here, we do not apply this adjustment/correction method to the traffic data because we are not treating any one of these four groups (A, B, C, and D) as a control (placebo) group, as in the drug development (pharmaceutical study) scenario.
7. Discussion
In this article, we utilized likelihood-based approaches (in the first stage, Section 2, Section 3, Section 4 and Section 5) to obtain a proportional difference of two-sample binary data subject to one type of misclassification. Then (in the second stage, Section 6), we easily adjusted the interval width to account for the multiplicity effect in the MCP because of our easy-to-implement closed-form algorithm.
In the first stage (Section 2, Section 3, Section 4 and Section 5), a double sampling scheme was utilized as a means of obtaining more information, ensuring model identifiability and reducing bias. While applying these procedures, reparameterization of the original full likelihood function was performed because it was computationally unattainable. After doing so, a closed-form new likelihood function is then obtainable. As a result, such closed-form expressions for the MLE and the corresponding three CI approaches (nWald, mWald, and mWald.2) were attainable when calculating the proportional difference. As an example (for the first stage), we demonstrate the three CI methods to the Hochberg of 1977 [18] large sample dataset, for group A (Male and High Car Damage) and B (Female and High Car Damage). As expected, the three methods demonstrated similar CIs because the Hochberg of 1977 [18] dataset have large sample sizes. We note that the past studies of Agresti & Coull in 1998 [16] and Lee & Byun in 2008 [17] have concluded that adding one or two counts to the cell counts for small sample size of binomial data will correct the bias. Similarly, our simulations conclude the same. Hence, among the above three likelihood methods, the mWald.2 method will perform best, even for a small sample size.
In the second stage (Section 6), to account for the multiplicity effect in the MCP, we prescribed three adjustment methods (Bonferroni, Šidák, and Dunn) to the differences of proportions parameters in the presence of either under/over-reported multiple-sample binomial data, into the adjusted CIs calculation. Note that unlike those difficult non-closed-form algorithms proposed in the previously reviewed literature in Rahardja of 2019 [6], this second stage (MCP stage) is easily attainable because of our closed-form algorithm, which is easy to implement, and subsequently, doable to directly invert the adjusted CI methods (Bonferroni, Šidák, and Dunn).
As an illustration (for the second stage) to the pairwise comparison using MCPs, we demonstrate the adjustment methods to Hochberg of 1977 [18] large sample dataset, for the four groups: Group A (Male and High Car Damage) and B (Female and High Car Damage), C (Male and Low Car Damage), and D (Female and Low Car Damage). In that example, using Bonferroni and Šidák adjustment methods, one can see which pairs contributed the significant differences.
In conclusion, we have prescribed likelihood-based estimation approaches to acquire confidence intervals (CIs) for comparing pairwise proportions differences under three MCPs (Bonferroni, Šidák, and Dunn) in the presence of under/over-reported multiple-sample binomial data via a double-sampling scheme. Such prescribed MCP methods will be useful to practitioners and researchers in the binomial misclassification field.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank the Editor and two anonymous referees for their insightful comments and constructive suggestions which have improved the presentations of this manuscript.
Conflicts of Interest
The author declare no conflict of interest.
Dedications
The author dedicates this manuscript for her parents. As a Statistician, having been observing and analyzing big data from all aspects of human beings (psychologically, sociologically, health-wise, religious-wise, etc.), the author is very grateful for her father, Djohan Rahardja, and her mother, Ismajati Kiswojo, who recently passed away († 24 May 2019). They both have been raising her very responsibly, to provide-and-protect, and lovingly to care-and-nurture. There would not be the best-version of her today, without her parents. ~Soli Deo Gloria~
References
- Hsu, J.C. Multiple Comparisons: Theory and Methods; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York City, NY, USA; Washington, DC, USA, 1996; ISBN1 0-41298-281-1. ISBN2 978-0412982811. ISBN3 0412982811. Available online: https://www.asc.ohio-state.edu/hsu.1//mc.html (accessed on 3 May 2019).
- Edward, D.G.; Hsu, J.C. Multiple comparisons with the best treatment. J. Am. Stat. Assoc. 1983, 78, 965–971. [Google Scholar] [CrossRef]
- Hsu, J.C.; Edwards, D.G. Sequential multiple comparisons with the best. J. Am. Stat. Assoc. 1983, 78, 958–964. [Google Scholar] [CrossRef]
- Hsu, J.C. Simultaneous inference with respect to the best treatment in block designs. J. Am. Stat. Assoc. 1982, 77, 461–467. [Google Scholar] [CrossRef]
- Shiraishi, T. Multiple tests based on arcsin transformation in multi-sample models with Bernoulli responses. Jpn. J. Appl. Stat. 2011, 40, 1–17. [Google Scholar] [CrossRef]
- Rahardja, D. Bayesian inference for the difference of two proportion parameters in over-reported two-sample binomial data using the doubly sample. Stats 2019, 2, 9. [Google Scholar] [CrossRef] [Green Version]
- Gianinetti, A. Basic features of the analysis of germination data with generalized linear mixed models. Data 2020, 5, 6. [Google Scholar] [CrossRef] [Green Version]
- Giles, S.N.; Fiori, S. Glomerular filtration rate estimation by a novel numerical binning-less isotonic statistical bivariate numerical modeling method. Information 2019, 10, 100. [Google Scholar] [CrossRef] [Green Version]
- Hodge, S.E.; Vieland, V.J. Information loss in binomial data due to data compression. Entropy 2017, 19, 75. [Google Scholar] [CrossRef] [Green Version]
- Stamey, J.D.; Bratcher, T.L.; Young, D.M. Parameter subset selection and multiple comparisons of Poisson rate parameters with misclassification. Comput. Stat. Data Anal. 2004, 45, 467–479. [Google Scholar] [CrossRef]
- Bross, I. Misclassification in 2 × 2 tables. Biometrics 1954, 10, 478–486. [Google Scholar] [CrossRef]
- Zelen, M.; Haitovsky, Y. Testing hypotheses with binary data subject to misclassification errors: Analysis and experimental design. Biometrika 1991, 78, 857–865. [Google Scholar] [CrossRef]
- Rahardja, D.; Yang, Y. Maximum likelihood estimation of a binomial proportion using one-sample misclassified binary data. Stat. Neerl. 2015, 69, 272–280. [Google Scholar] [CrossRef]
- Rahardja, D.; Yang, Y.; Qu, Y. Maximum likelihood estimation for a binomial parameter using double sampling with one type of misclassification. Am. J. Math. Manag. Sci. 2015, 34, 184–196. [Google Scholar] [CrossRef]
- Tenenbein, A. A double sampling scheme for estimating from binomial data with misclassifications. J. Am. Stat. Assoc. 1970, 65, 1350–1361. [Google Scholar] [CrossRef]
- Agresti, A.; Coull, B.A. Approximate is better than “exact” for interval estimation of binomial proportions. Am. Stat. 1998, 52, 119–126. [Google Scholar]
- Lee, S.C.; Byun, J.S. A Bayesian approach to obtain confidence intervals for binomial proportion in a double sampling scheme subject to false-positive misclassification. J. Korean Stat. Soc. 2008, 37, 393–403. [Google Scholar] [CrossRef]
- Hochberg, Y. On the use of double sampling schemes in analyzing categorical data with misclassification errors. J. Am. Stat. Assoc. 1977, 72, 914–921. [Google Scholar]
- Salzberg, S.L. On comparing classifiers: Pitfalls to avoid and a recommended approach. Data Min. Knowl. Discov. 1997, 1, 317–328. [Google Scholar] [CrossRef]
- Hochberg, Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika 1988, 75, 800–803. [Google Scholar] [CrossRef]
- Holland, B. On the application of three modified Bonferroni procedures to pairwise multiple comparisons in balanced repeated measures designs. Comput. Stat. Q. 1991, 6, 219–231. [Google Scholar]
- Hommel, G. A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika 1988, 75, 383–386. [Google Scholar] [CrossRef]
- Holland, B.S.; Copenhaver, M.D. An improved sequentially rejective Bonferroni test procedure. Biometrics 1987, 43, 417–423. [Google Scholar] [CrossRef]
- Hochberg, Y.; Tamhane, A. Multiple Comparison Procedures; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Šidák, Z.K. Rectangular confidence regions for the means of multivariate normal distributions. J. Am. Stat. Assoc. 1967, 62, 626–633. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple comparisons among means. J. Am. Stat. Assoc. 1961, 56, 52–64. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).