Application of the Modified Shepard’s Method (MSM): A Case Study with the Interpolation of Neogene Reservoir Variables in Northern Croatia
Abstract
1. Introduction
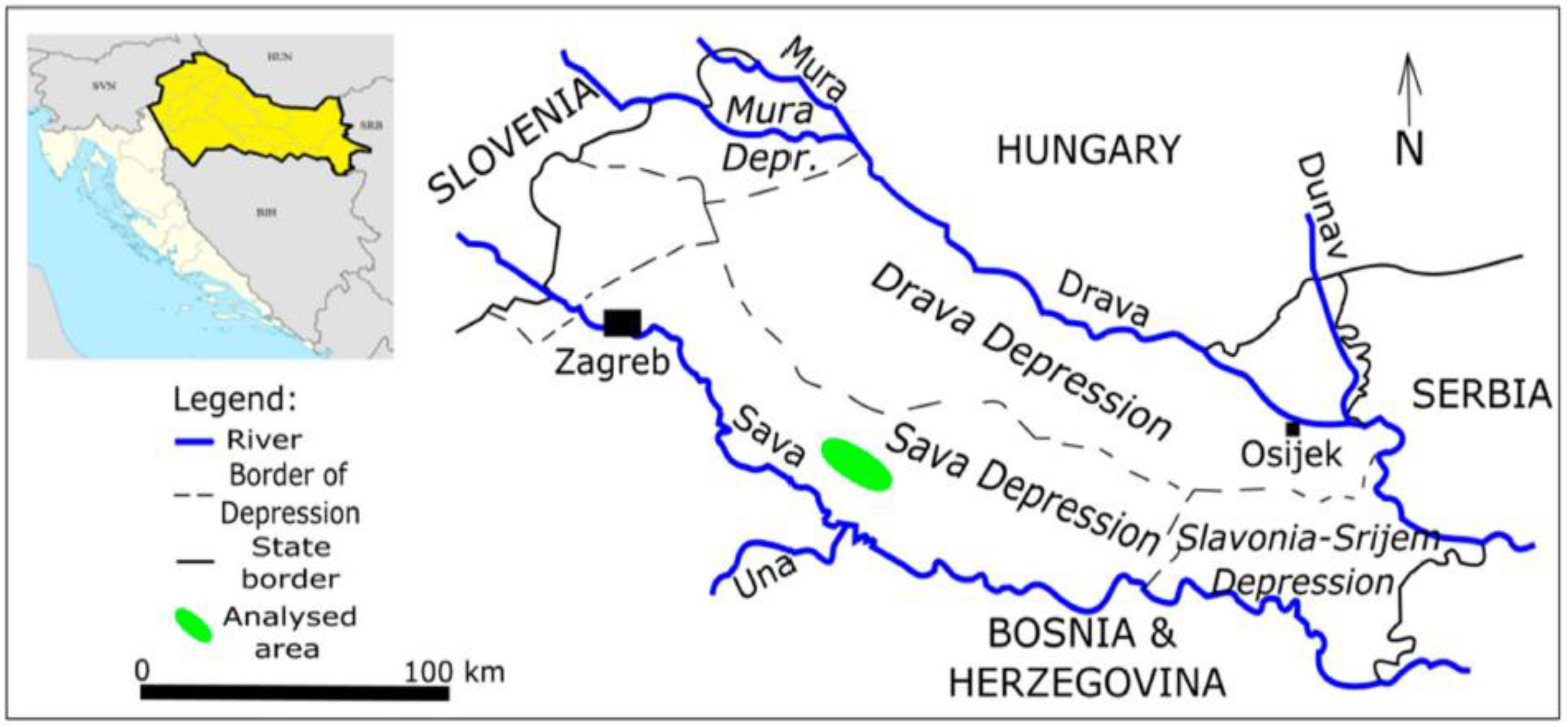
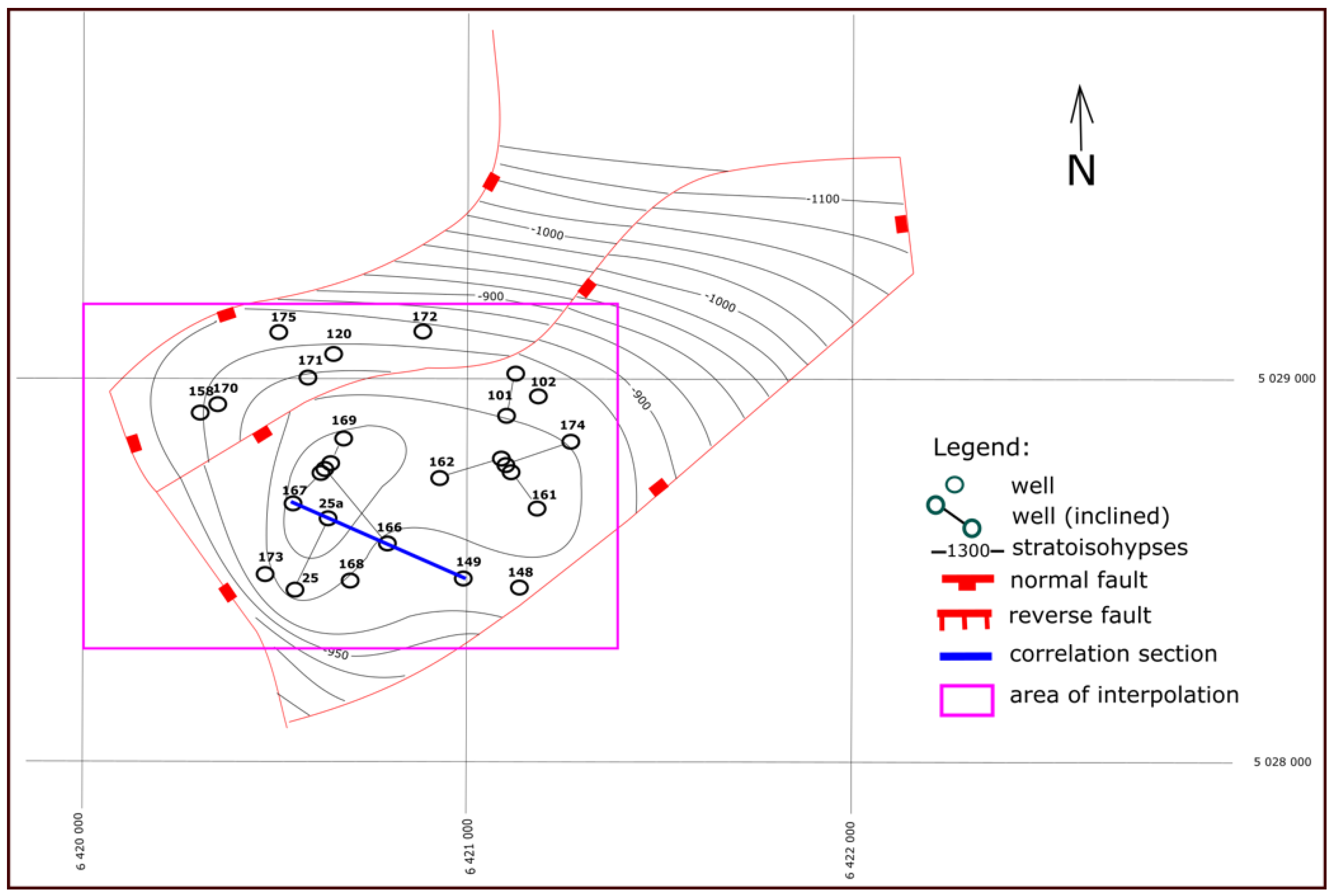
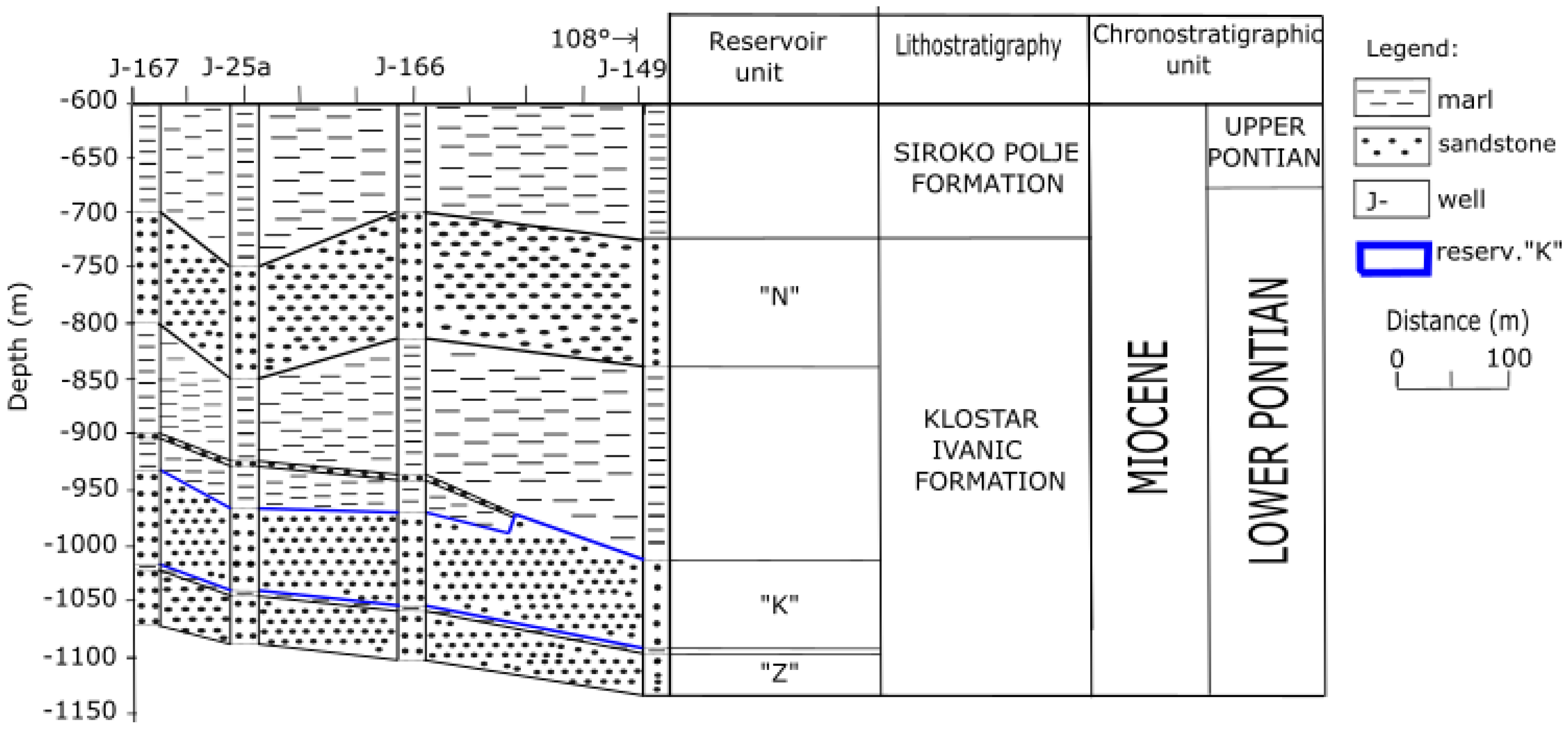
2. Geological Settings of the Analysed Field “B” (Sava Depression, Northern Croatia)
3. Basics of the Applied Interpolation Methods
3.1. Inverse Distance Weighting (IDW)
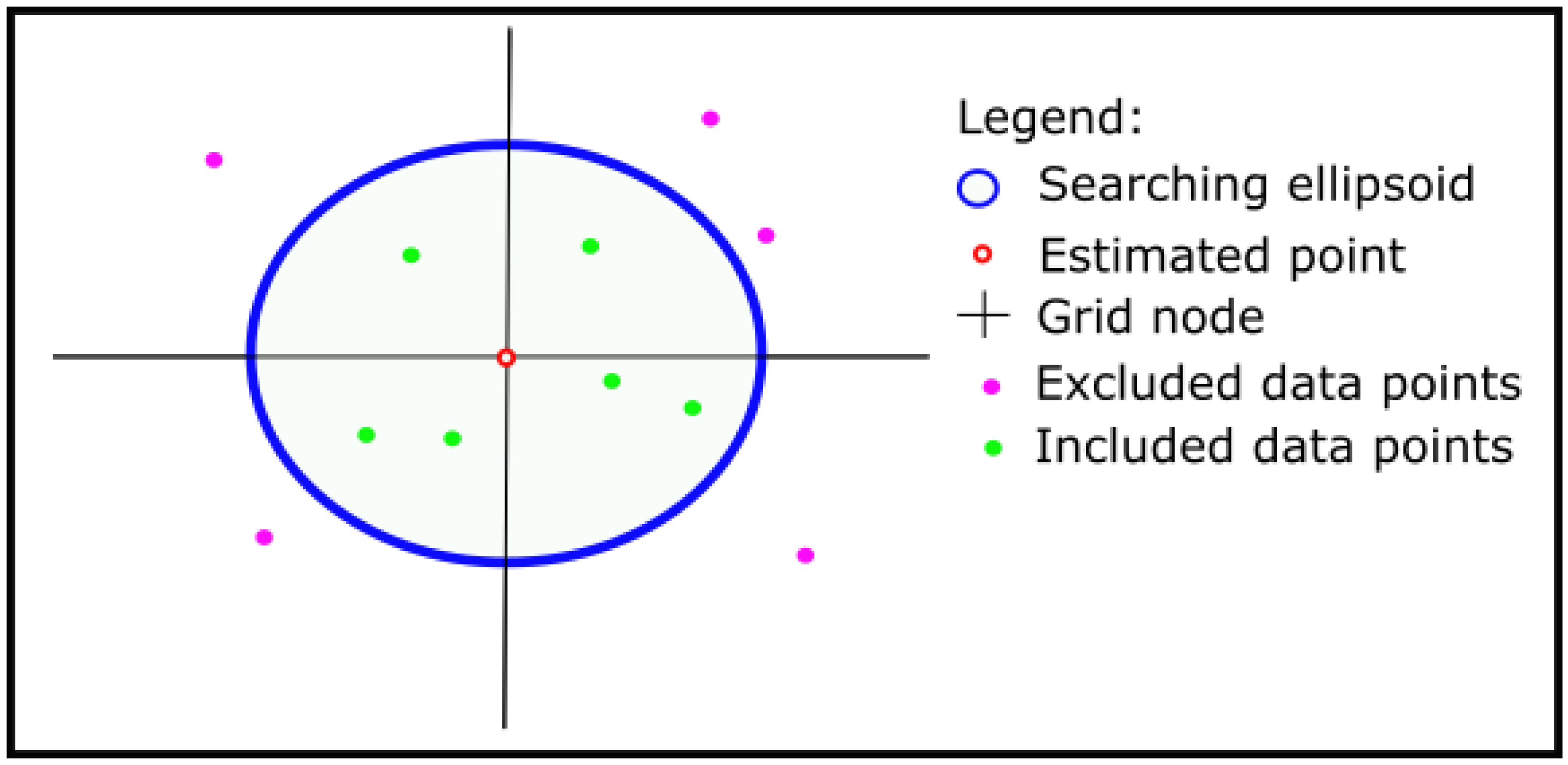
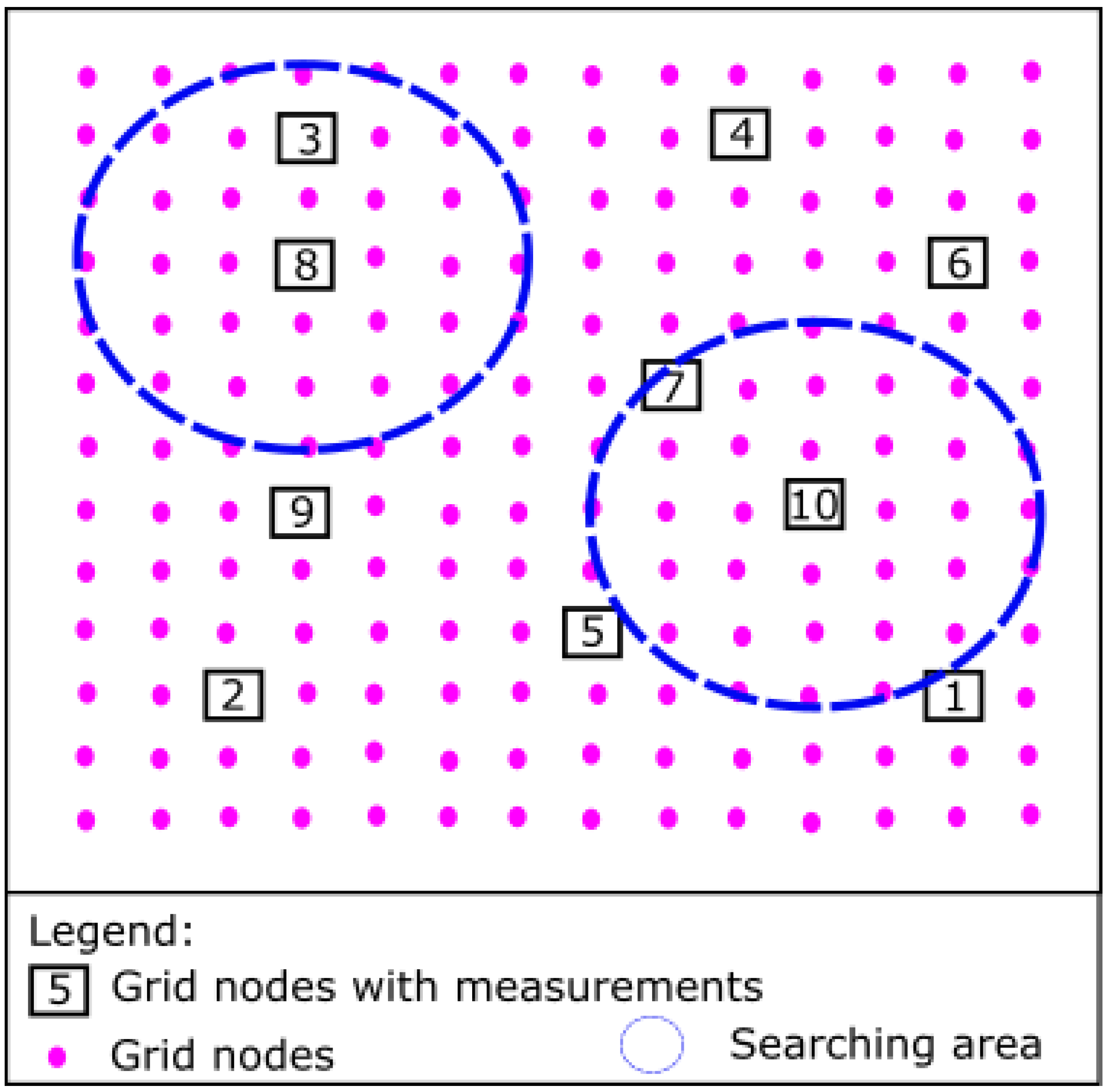
3.2. Modified Shepard’s Method (MSM)
3.3. Cross-Validation (CV)
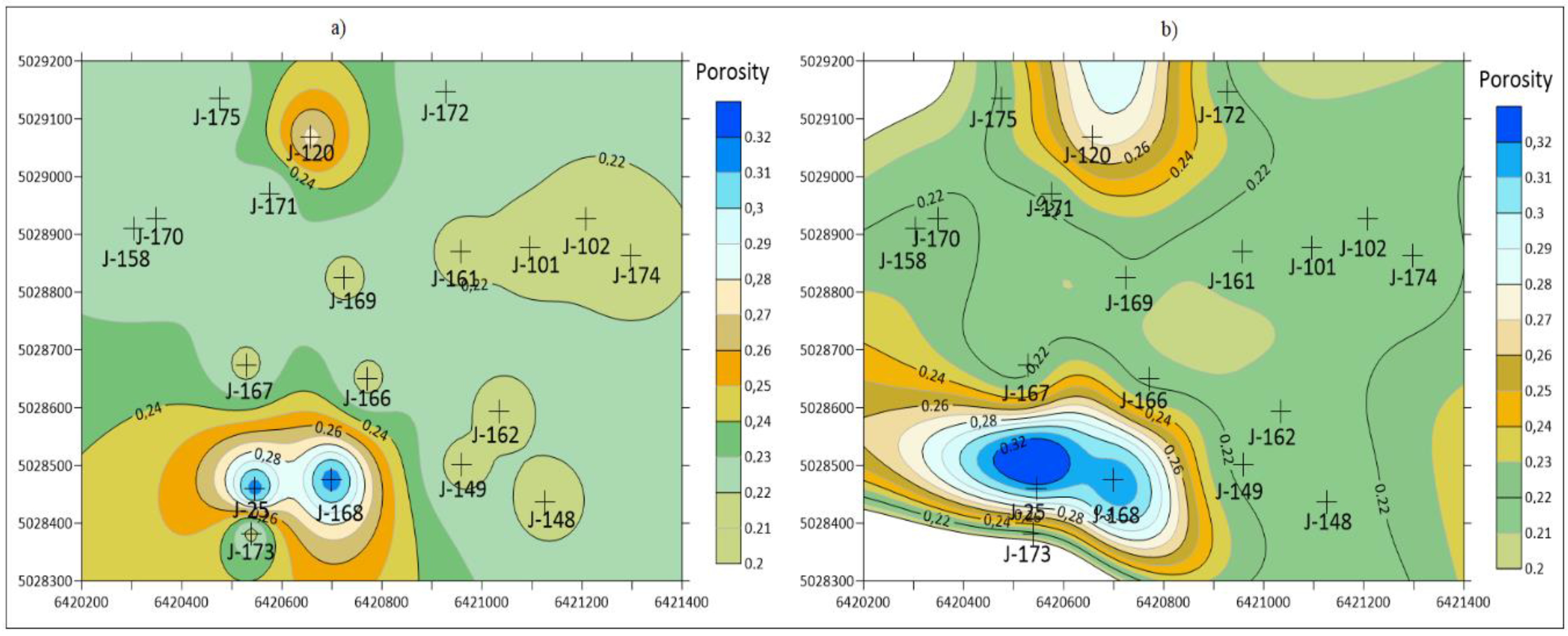
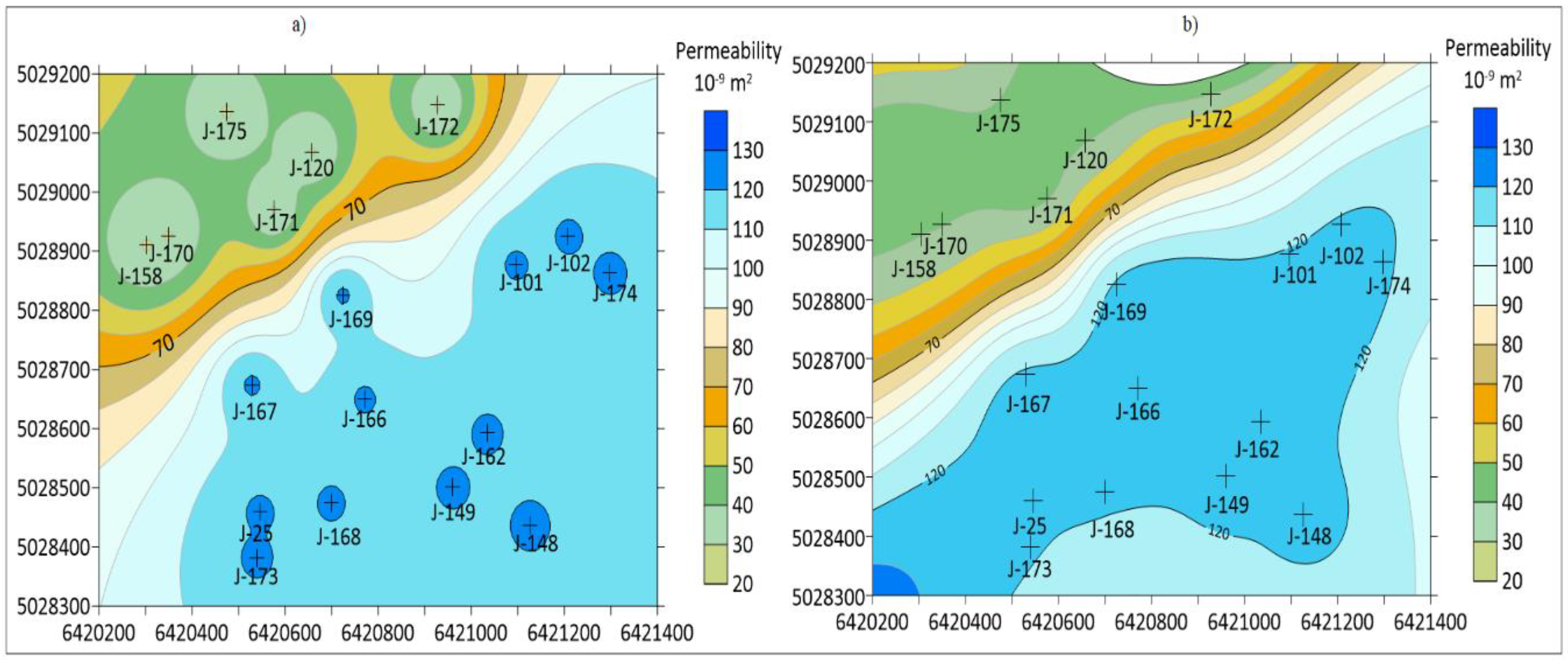
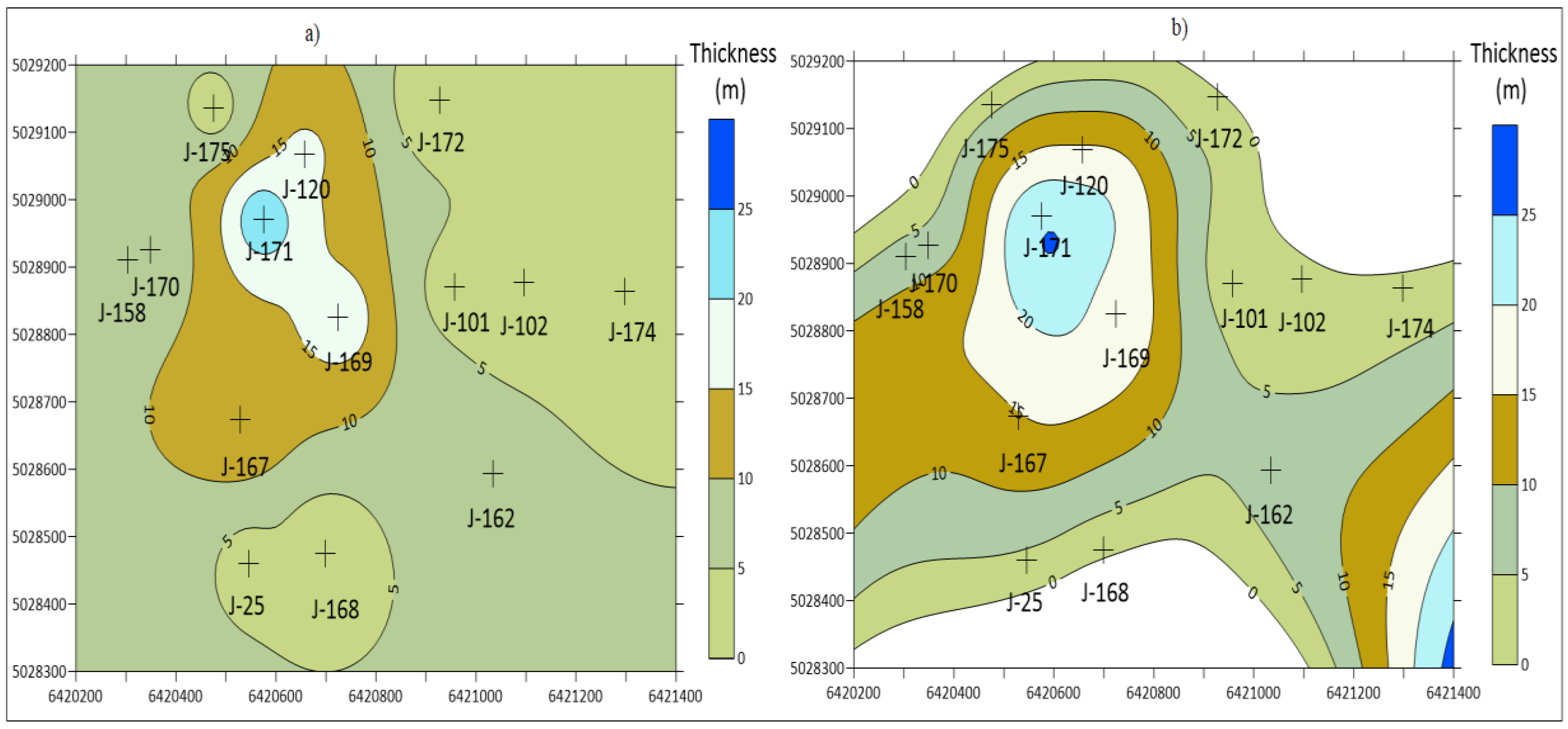
4. Interpolation Results in Reservoir “K” for Variables of Porosity, Thickness and Permeability
5. Discussion
6. Conclusions
- The MSM could be recommended for subsurface geological mapping of Neogene deposits in northern Croatia;
- This method is valid for datasets smaller than 20 measured values, i.e., for the early exploration phase of hydrocarbon reservoirs or the later development phase when the number of measurements of a selected property is small, but quick insight in the spatial distribution of such variables is necessary;
- The selected variables could be porosity, permeability and thickness, measured in Neogene lithostratigraphic units by laboratory analysed well data (cores) or interpreted logs;
- The interpreters need to be aware of: (a) the IDW method resulted in the lowest cross-validation of all applied methods without a spatial model (variogram), i.e., namely the Nearest neighbourhood and the Natural neighbour, (b) the MSM interpolation eliminated all the unwanted geological features and did not result in a cross-validation 250 % higher than in the IDW, for the same variable.
- Based on the visual (geometric) criteria, the sets with less than five measured points are too small for interpolation (using the IDW or MSM methods), and they are only appropriate for zonal estimation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mesić Kiš, I.; Malvić, T. Zonal estimation and interpolation as simultaneous approaches in the case of small input data set (Šandrovac field, northern Croatia). Min. Geol. Pet. Eng. Bull. 2014, 29, 9–16. [Google Scholar]
- Malvić, T. History of geostatistical analyses performed in the Croatian part of the Pannonian Basin System. Nafta 2012, 63, 223–235. [Google Scholar]
- Malvić, T.; Ivšinović, J.; Velić, J.; Rajić, R. Interpolation of small datasets in the sandstone hydrocarbon reservoirs, case study of the Sava Depression, Croatia. Geosciences 2019, 9, 201. [Google Scholar] [CrossRef]
- Malvić, T.; Đureković, M. Application of methods: Inverse distance weighting, ordinary kriging and collocated cokriging in porosity evaluation, and comparison of results on the Beničanci and Stari Gradac fields in Croatia. Nafta 2003, 54, 331–340. [Google Scholar]
- Smoljanović, S.; Malvić, T. Improvements in reservoir characterization applying geostatistical modelling (estimation & stochastic simulations vs. standard interpolation methods), Case study from Croatia. Nafta 2005, 56, 57–63. [Google Scholar]
- Balić, D.; Velić, J.; Malvić, T. Selection of the most appropriate interpolation method for sandstone reservoirs in the Kloštar oil and gas field. Geol. Croat. 2008, 61, 27–35. [Google Scholar]
- Ivšinović, J. Deep mapping of hydrocarbon reservoirs in the case of a small number of data on the example of the Lower Pontian reservoirs of the western part of Sava Depression. In Proceedings of the 2nd Croatian congress on geomathematics and geological terminology, Zagreb, Croatia, 6 October 2018; Malvić, T., Velić, J., Rajić, R., Eds.; University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering: Zagreb, Croatia, 2018; pp. 59–65. [Google Scholar]
- Ivšinović, J. Odabir i Geomatematička Obradba Varijabli za Skupove Manje od 50 Podataka pri Kreiranju Poboljšanoga Dubinskogeološkoga Modela na Primjeru iz Zapadnoga Dijela Savske Depresije (Selection and Geomathematical Calculation of Variables for Sets with Less than 50 Data Regarding the Creation of an Improved Subsurface Model, Case Study from the Western Part of the Sava Depression). Ph.D. Thesis, University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering, Zagreb, Croatia, 2019. [Google Scholar]
- Yang, C.S.; Kao, S.P.; Lee, F.B.; Hung, P.S. Twelve different interpolation methods: A case study of Surfer 8.0. In Proceedings of the XXth ISPRS Congress, Instabul, Turkey, 12–23 July 2004; pp. 778–785. [Google Scholar]
- Rap, A.; Ghosh, S.; Smith, M. Shepard and hardy multiquadric interpolation methods for multicomponent aerosol-cloud parameterization. J. Atmos. Sci. 2009, 66, 105–115. [Google Scholar] [CrossRef]
- Pál, L.; Oláh-Gál, R.; Mako, Z. Shepard interpolation with stationary points. Acta Univ. SapientiaeInform. 2009, 1, 5–13. [Google Scholar]
- Bronowicka-Mielniczuk, U.; Mielniczuk, J.; Obroślak, R.; Przystupa, W. A comparison of some interpolation techniques for determining spatial distribution of nitrogen compounds in groundwater. Int. J. Environ. Res. 2019, 13, 679–687. [Google Scholar] [CrossRef]
- Huang, X.; Chen, W.; Hu, Z.; Zheng, X.; Jin, S.; Zhang, X. Application research of an efficient and stable boundary processing method for the SPH method. Water 2019, 11, 1110. [Google Scholar] [CrossRef]
- Wojciech, M. Kriging method optimization for the process of DTM creation based on huge data sets obtained from MBESs. Geosciences 2018, 8, 433. [Google Scholar] [CrossRef]
- Kuo, P.-H.; Chen, H.-C.; Huang, C.-J. Solar radiation estimation algorithm and field verification in Taiwan. Energies 2018, 11, 1374. [Google Scholar] [CrossRef]
- Arseni, M.; Voiculescu, M.; Georgescu, L.P.; Iticescu, C.; Rosu, A. Testing different interpolation methods based on single beam echosounder river surveying. Case study: Siret River. ISPRS Int. J. Geo Inf. 2019, 8, 507. [Google Scholar] [CrossRef]
- Salekin, S.; Burgess, J.H.; Morgenroth, J.; Mason, E.G.; Meason, D.F. A comparative study of three non-geostatistical methods for optimising digital elevation model interpolation. ISPRS Int. J. Geo Inf. 2018, 7, 300. [Google Scholar] [CrossRef]
- Malvić, T.; Ivšinović, J.; Velić, J.; Rajić, R. Kriging with a small number of data points supported by Jack-Knifing, a case study in the Sava depression (Northern Croatia). Geosciences 2019, 9, 36. [Google Scholar] [CrossRef]
- Malvić, T.; Velić, J. Neogene tectonics in Croatian part of the Pannonian Basin and reflectance in hydrocarbon accumulations. In New Frontiers in Tectonic Research: At the Midst of Plate Convergence; Schattner, U., Ed.; Tech: Rijeka, Croatia, 2011; pp. 215–238. [Google Scholar]
- Šimunić, A.; Pikija, M.; Hećimović, I.; Šimunić, A. Basic Geological Map of SFR Yugoslavia; 1:100.000; Geology for Varaždin Sheet L33-69.-Geological Survey Zagreb; Federal Geological Survey: Belgrade, Serbia, 1981. (In Croatian) [Google Scholar]
- Pettijohn, F.J.; Potter, P.E.; Siever, R. Sand and Sandstones; Springer: Berlin, Germany, 1972. [Google Scholar]
- Ivšinović, J. The relationship between sandstone depositional environment and water injection system, a case study from the Upper Miocene hydrocarbon reservoir in northern Croatia. In Proceedings of the 2nd Croatian Scientific Congress from Geomathematics and Terminology in Geology, Zagreb, Croatia, 6 October 2018; Malvić, T., Velić, J., Rajić, R., Eds.; University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering: Zagreb, Croatia, 2018; pp. 65–75. [Google Scholar]
- Ivšinović, J. The cost analysis of the separation of produced formation water from the hydrocarbon reservoir using the example of the Upper Miocene sandstone deposits of the Sava Depression. Rud. Geološko Naft. Zb. (Min. Geol. Pet. Eng. Bull.) 2018, 35, 35–43. [Google Scholar]
- Malvić, T. Geological maps of Neogene sediments in the Bjelovar Subdepression (northern Croatia). J. Maps 2011, 7, 304–317. [Google Scholar] [CrossRef]
- Malvić, T.; Jović, G. Thickness maps of Neogene and Quaternary sediments in the Kloštar Field (Sava Depression, Croatia). J. Maps 2012, 8, 260–266. [Google Scholar] [CrossRef]
- Novak Zelenika, K.; Cvetković, M.; Malvić, T.; Velić, J.; Sremac, J. Sequential Indicator Simulations maps of porosity, depth and thickness of Miocene clastic sediments in the Kloštar Field, Northern Croatia. J. Maps 2013, 9, 550–557. [Google Scholar] [CrossRef]
- Špelić, M.; Malvić, T.; Saraf, V.; Zalović, M. Remapping of depth of e-log markers between Neogene basement and Lower/Upper Pannonian border in the Bjelovar Subdepression. J. Maps 2016, 12, 45–52. [Google Scholar] [CrossRef]
- Mesić Kiš, I.; Malvić, T. The Universal Kriging mapping of the Neogene EL-markers Rs5 and Δ, Northern Croatia. RMZ Mater. Geoenviron. 2018, 65, 187–198. [Google Scholar]
- Malvić, T. Primjena Geostatistike u Analizi geoloških Podataka (Application of Geostatistics in Geological Data Analysis); INA-Industrija nafte d.d.: Zagreb, Croatia, 2008. [Google Scholar]
- Ly, S.; Charles, C.; Degré, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation for irregularly spaced data function. In Proceedings of the 1968 ACM national conference, New York, NY, USA, 27–29 August 1968; Blue, R.B., Rosenberg, A.M., Eds.; Association for Computing Machinery: New York, NY, USA; pp. 517–523. [Google Scholar]
- Franke, R.; Nielson, G. Smooth interpolation of large sets of scattered data. Int. J. Numer. Methods Eng. 1980, 15, 1691–1704. [Google Scholar] [CrossRef]
- Renka, R.J. Multivariate interpolation of large sets of scattered data. ACM Trans. Math. Softw. 1988, 14, 139–148. [Google Scholar] [CrossRef]
- Basso, K.; Zingano, P.; Freitas, C. Interpolation of scattered data: Investigating alternatives for the modified Shepard method. In Proceedings of the XII Brazilian Symposium on Computer Graphics and Image Processing (SIBGRAPI ’99), Campinas, Brazil, 17–20 October 1999; Stolfi, J., Tozzi, C.L., Eds.; Universidade Estadual de Campinas (INICAMP) & Sociedade Brasileira de Computasilo (SBC): Campinas, Brazil, 1999; pp. 39–48. [Google Scholar]
- Davis, B. Uses and abuses of cross validation in geostatistics. Math. Geol. 1987, 19, 241–248. [Google Scholar] [CrossRef]
- Husanović, E.; Malvić, T. Review of deterministic geostatistical mapping methods in Croatian hydrocarbon reservoirs and advantages of such approach. Nafta 2014, 65, 57–63. [Google Scholar]
- Castañón, C.; Arias, D.; Diego, I.; Martin-Izard, A.; Ruiz, Y. Minerals Resource and reserve calculation in seam-shaped mineral deposits; A new approach: The pentahedral method. Minerals 2017, 7, 72. [Google Scholar]


| Description | No Data | Min | Max | Mean |
|---|---|---|---|---|
| Porosity | 19 | 0.217 | 0.315 | 0.232 |
| Permeability (10−9 m2) | 18 | 29.6 | 121.2 | 85.7 |
| Thickness (m) | 14 | 1 | 24 | 7.7 |
| Well’s No. | Surface X | Surface Y | Porosity (Parts of Unit) | Thickness (m) | Permeability (mD) |
|---|---|---|---|---|---|
| J-101 | 6,421,096 | 5,028,877 | 0.217 | 1 | 121.2 |
| J-120 | 6,420,658 | 5,029,068 | 0.272 | 15.7 | 29.6 |
| J-161 | 6,420,957 | 5,028,870 | 0.217 | 3 | 29.6 |
| J-162 | 6,421,034 | 5,028,593 | 0.217 | 6.5 | 121.2 |
| J-167 | 6,420,529 | 5,028,674 | 0.217 | 14.8 | 121.2 |
| J-168 | 6,420,699 | 5,028,475 | 0.315 | 1 | 121.2 |
| J-169 | 6,420,724 | 5,028,825 | 0.217 | 18.4 | 121.2 |
| J-170 | 6,420,349 | 5,028,926 | 0.223 | 7 | 29.6 |
| J-174 | 6,421,298 | 5,028,863 | 0.217 | 1.1 | 29.6 |
| J-175 | 6,420,475 | 5,029,136 | 0.223 | 3.2 | 121.1 |
| J-158 | 6,420,303 | 5,028,910 | 0.223 | 7.3 | 29.6 |
| J-171 | 6,420,576 | 5,028,970 | 0.223 | 24 | 29.6 |
| J-172 | 6,420,928 | 5,029,147 | 0.223 | 0.5 | 29.6 |
| J-102 | 6,421,208 | 5,028,926 | 0.217 | 121.2 | |
| J-148 | 6,421,126 | 5,028,437 | 0.217 | ||
| J-149 | 6,420,959 | 5,028,501 | 0.217 | 121.2 | |
| J-166 | 6,420,771 | 5,028,650 | 0.217 | 121.2 | |
| J-25 | 6,420,546 | 5,028,460 | 0.315 | 3.8 | 121.2 |
| J-173 | 6,420,539 | 5,028,382 | 0.217 | 121.2 |
| Description | No Data | Cross-Validation | |
|---|---|---|---|
| Inverse Distance (IDW) | Modified Shepard’s Method (MSM) | ||
| Porosity | 19 | 0.00119 | 0.00345 |
| Permeability | 18 | 480.8 | 516.1 |
| Thickness | 14 | 40.7 | 60.5 |
| Number of Data | Applicability of Interpolation Method | ||
|---|---|---|---|
| Inverse Distance Weighting | Nearest Neighbourhood | Natural Neighbour | |
| 1–5 | Yes | Yes | No |
| 6–10 | Yes | Yes | Yes |
| 11–19 | Yes | Yes | Yes |
| Number of Data | Applicability of Interpolation Method | |
|---|---|---|
| Inverse Distance Weighting | Modified Shepard’s Method | |
| Criteria |
|
|
| 5–20 | Yes | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malvić, T.; Ivšinović, J.; Velić, J.; Sremac, J.; Barudžija, U. Application of the Modified Shepard’s Method (MSM): A Case Study with the Interpolation of Neogene Reservoir Variables in Northern Croatia. Stats 2020, 3, 68-83. https://doi.org/10.3390/stats3010007
Malvić T, Ivšinović J, Velić J, Sremac J, Barudžija U. Application of the Modified Shepard’s Method (MSM): A Case Study with the Interpolation of Neogene Reservoir Variables in Northern Croatia. Stats. 2020; 3(1):68-83. https://doi.org/10.3390/stats3010007
Chicago/Turabian StyleMalvić, Tomislav, Josip Ivšinović, Josipa Velić, Jasenka Sremac, and Uroš Barudžija. 2020. "Application of the Modified Shepard’s Method (MSM): A Case Study with the Interpolation of Neogene Reservoir Variables in Northern Croatia" Stats 3, no. 1: 68-83. https://doi.org/10.3390/stats3010007
APA StyleMalvić, T., Ivšinović, J., Velić, J., Sremac, J., & Barudžija, U. (2020). Application of the Modified Shepard’s Method (MSM): A Case Study with the Interpolation of Neogene Reservoir Variables in Northern Croatia. Stats, 3(1), 68-83. https://doi.org/10.3390/stats3010007







