Abstract
Quantum-secure cryptography is a dynamic field due to its crucial role in various domains. This field aligns with the ongoing efforts in data security. Post-quantum encryption (PQE) aims to counter the threats posed by future quantum computers, highlighting the need for further improvement. Based on the learning with error (LWE) system, this paper introduces a novel asymmetric encryption technique that encrypts entire messages of n bits rather than just 1 bit. This technique offers several advantages including an additive homomorphic cryptosystem. The robustness of the proposed lightweight public key encryption method, which is based on a new version of LWE, ensures that private keys remain secure and that original data cannot be recovered by an attacker from the ciphertext. By improving encryption and decryption execution time—which achieve speeds of 0.0427 ms and 0.0320 ms, respectively—and decreasing ciphertext size to 708 bits for 128-bit security, the obtained results are very promising.
1. Introduction
Alongside advancements in homomorphic encryption (HE), the field of post-quantum encryption (PQE) is rapidly evolving due to the impending threat quantum computing poses to current cryptographic standards [1]. PQE aims to develop techniques capable of withstanding the computational power of future quantum computers, which could potentially compromise widely used encryption schemes such as RSA and elliptic curve cryptography (ECC). These traditional encryption methods are prevalent in numerous critical domains, including encryption, authentication, data integrity, IoT applications, secure measurement, and cloud computing applications. For instance, RSA and ECC are integral to the encryption protocols used to safeguard sensitive data during transmission. Similarly, these cryptographic techniques underpin authentication processes, ensuring that only authorized users can access specific systems or information [2]. Moreover, maintaining data integrity through these methods is crucial, as it verifies that data has not been tampered with or altered during storage or transmission [3].
The importance of PQE extends to the rapidly growing Internet of Things (IoT) sector, where secure communication between connected devices is paramount to prevent unauthorized access and cyber-attacks [4]. In secure measurement systems, robust encryption is necessary to protect sensitive data collected from various sensors and devices, ensuring its confidentiality and accuracy. Furthermore, the shift towards cloud computing has highlighted the need for enhanced cryptographic methods to protect data stored and processed in the cloud from potential quantum threats. The development and implementation of PQE are essential for ensuring the security and integrity of digital communication and data in the quantum era [5]. As quantum computing continues to advance, the urgency to adopt PQE measures increases, aiming to preemptively address the vulnerabilities that quantum computers could exploit. This proactive approach is vital for safeguarding the digital infrastructure that underpins modern society, including financial systems, healthcare data, governmental communications, and personal information. One of these strategies is learning with errors (LWE).
LWE is a fundamental problem in computational mathematics that underpins many cryptographic constructions believed to be secure against quantum attacks [6]. The principle behind LWE-based encryption techniques involves introducing controlled errors into computations, making decryption possible only with the secret key. Without the key, these errors render it computationally infeasible to recover the original message. Essentially, the LWE problem requires solving linear equations obscured by small random errors [7], making the original system of equations difficult to decipher. This complexity is what makes LWE an attractive foundation for cryptographic schemes in the quantum era [8], as quantum computers are expected to break many traditional cryptographic protocols but not those based on LWE [9].
Fully homomorphic encryption, another application of LWE, permits computations to be carried out on encrypted data without needing to decrypt it first, thereby preserving data confidentiality throughout the processing stages. This capability is particularly valuable for cloud computing services, where data is often processed and stored on remote servers [10]. Digital signatures based on LWE provide a way to verify the authenticity and integrity of digital messages or documents, ensuring that they have not been altered and are indeed from the purported sender. The robustness of these signatures against quantum attacks makes them essential for secure online communications and transactions.
Many LWE-based approaches are not yet compatible with homomorphic encryption (HE). This limitation has posed significant challenges for integrating LWE-based cryptographic methods with the capabilities of HE, which allows computations to be performed on encrypted data without needing to decrypt it first. Despite the robust security that LWE offers against quantum attacks, its incompatibility with HE has restricted its application in scenarios where data privacy and computational capabilities need to coexist seamlessly.
This paper introduces a new quantum-resistant, lightweight public cryptosystem that bridges this gap. The proposed cryptosystem is designed to be quantum resistant, leveraging the security advantages of LWE while ensuring compatibility with HE. This compatibility enables an untrusted third party to perform operations on encrypted data, maintaining the confidentiality of the data throughout the computational process. The innovation lies in the ability of this system to facilitate secure and private computations without exposing the underlying data, thereby enhancing its applicability in various real-world scenarios.
Moreover, the cryptosystem provides mechanisms for the data owner to easily verify the integrity of the results obtained from the third party. This verification process is crucial, as it ensures that the operations performed on the encrypted data yield accurate and reliable outcomes, despite being handled by an untrusted entity. The lightweight nature of this cryptosystem makes it particularly suitable for applications where computational efficiency and resource constraints are critical considerations.
The development of this new cryptosystem represents a significant advancement in the field of post-quantum cryptography. By addressing the compatibility issues between LWE and HE, it opens up new possibilities for secure data processing in environments such as cloud computing, where data often needs to be processed by external servers while remaining protected against potential breaches. Additionally, the ability to verify the correctness of results enhances trust and reliability in outsourced computations, making it a valuable tool for industries that require high levels of data integrity and security.
In summary, this paper’s contribution lies in presenting a novel solution that combines the advantages of LWE and HE, providing a quantum-resistant, efficient, and verifiable cryptographic framework. This advancement not only bolsters the security of encrypted data against quantum threats but also extends the practical utility of LWE-based encryption by decreasing ciphertext size and execution time.
The rest of the paper is structured as follows: Section 2 presents the related work to the field, while Section 3 highlights the quantum key distribution solutions and their shortcomings. In Section 4, the proposed LWE cryptosystem is presented, while in Section 5, a security analysis is conducted. Finally, in Section 6, the conclusions of this work are presented.
2. Related Work
LWE has become a fundamental strategy for post-quantum cryptography, supporting the development of secure encryption, secure multiparty computation, fully homomorphic encryption, and digital signatures. These cryptographic constructs are crucial for securing communications, data storage, and digital transactions in the quantum era. For instance, secure encryption based on LWE ensures that sensitive information remains confidential even in the face of quantum computing advances, providing a robust defense against potential decryption attempts by powerful quantum algorithms. Additionally, LWE-based secure multiparty computation allows multiple parties to jointly compute a function over their inputs while keeping those inputs private, enabling collaborative data analysis without compromising individual privacy [11].
In the sector of homomorphic encryption and post-quantum cryptography, the authors in [12] introduced a privacy-protective method for data collection via the mobile cloud, allowing individuals to securely submit personal information. This technique ensures the safe storage of user data, minimizing the risk of unauthorized modifications by employing an advanced privacy-preserving homomorphic encryption system as described in [13]. Although this scheme has a lower computational complexity, it is still based on a factorization problem, rendering it vulnerable to quantum computer attacks.
In [14], a homomorphic encryption scheme was presented, which was tailored to meet the requirements of the cryptosystem of Paillier. The public key is determined as the least common prime factor of the Euler’s totient function values for two large prime numbers p and q. The issue with this technique is its reliance on the discrete logarithm (DL) problem’s difficulty, which renders it ineffective in the quantum era.
In [15], Iqra et al. introduced a lattice-based RSA (LB-RSA) designed for IoT-based cloud applications to secure data and information sharing. This technique was implemented in a 60-dimensional space. The key size is approximately 115,200 bits, with a generation time of 0.8 h. Despite these features, the research has a significant drawback: It requires the use of a parallel Gauss–Sieve algorithm [16] to find the shortest vector, an NP-hard problem. The problem here is the size and execution time.
The authors of [17] proposed a single-bit public key encryption technique based on a new variant of learning parity with noise (LPN). They extended the technique to a multi-bit public key encryption system. Even though the encoding error rate of this scheme is negligible, it is based on single-bit encryption. The paper [18] demonstrated that non-black-box schemes are not necessary for basic laconic cryptography primitives. The authors presented a completely algebraic construction of laconic encryption, a concept that they introduced; it served as the cornerstone of their model.
In [19], the authors presented a new family of public key encryption (PKE) and key encapsulation mechanism (KEM) techniques based on LWE. Two new design schemes were adopted and named SCloud (sampling method and the error-reconciliation mechanism). The scheme is secure against dual attacks. Afterwards, an error-reconciliation approach was constructed by combining the binary linear codes and Gray codes. Despite that, the implementation has to be a constant time in order to avoid timing attacks, which will slightly affect the efficiency.
In [20], the authors presented a multi-bit leveled FHE technique by utilizing multivariate polynomial evaluations. The security of this technique depends on the robustness of the LWE problem. Unfortunately, the addition and multiplication are conducted bitwise, which increases the computation cost ().
To counter some of the eavesdropping attacks, the authors in [21] utilized a coherently driven quantum dot to illustrate a modified Ekert QKD protocol with two quantum channel manners: a 250 m-long single-mode fiber both in free space and linking two buildings. However, the extreme requirements of the photon source have limited its use.
The authors of [22] presented an encryption technique based on the multiplication of the plaintext by a dynamic key making a one-time pad system [23]. The technique uses probabilistic and linear encryption. Assuming that the cloud is a non-trust entity, this technique ensures data integrity within homomorphic operations. The drawback of this system is that it relies on factorization problem hardness, which makes it vulnerable to quantum computers.
To address these issues, including quantum vulnerability due to relying on factorization/discrete logarithm problems, non-feasibility due to the large size of the key/ciphertext, and effects on efficiency due to the increased computation cost or implementation in a constant time, etc., this work introduces a lightweight post-quantum encryption technique based on the LWE system, which has proven its efficiency for the quantum era. One of the most important factors in the proposed method is encrypting the entire message in one ciphertext rather than each bit separately.
3. Quantum Key Distribution (QKD) Solutions and Its Shortcomings
Quantum key distribution is a cryptographic protocol designed for establishing a shared secret between two parties communicating over an unsecured channel. This shared secret typically serves to create a common cryptographic key, enabling the parties to secure their communications with symmetric encryption. Unlike traditional cryptographic protocols, which rely on the presumed difficulty of certain computational problems, quantum key distribution derives its security from the fundamental principles of quantum p hysics [24]. A key aspect of this method is the no-cloning theorem, which states that it is impossible to perfectly copy a particle in an unknown state, thus potentially allowing for the detection of interception attempts. This approach forms a specific branch of quantum cryptography [25].
3.1. Quantum Key Exchange Protocols
The BB84 protocol, introduced in 1984 by Charles Bennett and Gilles Brassard [26], marked the first quantum key exchange method. It operates on a “preparation and measurement” basis, where a quantum object, such as a photon, is prepared in a secret state (often a polarization state) by one participant. The other participant, or a potential adversary, guesses the state and measures it. Due to the collapse of the wave packet during measurement, the original state cannot be restored, and any interference by an adversary leads to detectable disturbances. This allows participants to either halt communication or use techniques to amplify the signal and create a secure key despite the adversary’s partial knowledge [27].
In contrast, the E91 protocol, developed by Artur Ekert in 1991 [28], leverages quantum entanglement. Here, the exchanged quantum objects are always in a state of superposition, with their specific states kept confidential. While the exact polarization state cannot be determined when photons are used, statistical correlations remain intact unless an adversary intervenes. Such an intervention disrupts these correlations, detectable through the violation of Bell’s inequalities, indicating potential eavesdropping [21].
3.2. Implementations
Quantum key exchange depends on the rapid generation, measurement, and transmission of quantum objects in specific states over considerable distances. A notable milestone was reached in 2015 when polarized photons were transmitted through optical fiber over a distance of 307 km at a rate of 12.7 kbit/s [29]. Further advancements were showcased in June 2017 by the QUESS experiment, which successfully demonstrated key exchange over distances exceeding 1000 km using satellites [30]. Noteworthy achievements include the DARPA QKD network with ten nodes since 2004, NIST’s 2007 success with an optical fiber reaching 148.7 km [31], and the SECOCQ QKD network using 200 km of standard optical fibers implemented in 2008 [32].
However, these achievements are not sufficient due to the material constraints and difficulty of implementation, as creating such secure lines is not available to everyone, as is the case in the exchange of keys based on computational power.
3.3. Protocol Security
The security of quantum key exchange protocols primarily relies on the no-cloning theorem of quantum physics, which prevents adversaries from copying the state of a quantum particle before its measurement. This contrasts with traditional key exchange protocols, which depend on the mathematical complexity of problems. However, quantum key exchange protocols face vulnerabilities due to practical limitations in device performance, decoherence phenomena, and potential auxiliary channels that attackers might exploit. Some vulnerabilities are fundamental and potentially affect all quantum key exchange protocols [33]:
- Without proper authentication, all quantum key exchange protocols are susceptible to man-in-the-middle attacks. Even with authentication, there remains a risk that an adversary may not be detected, appearing merely as noise in the system.
- Denial of service attacks are a risk for all quantum key exchange protocols since the communication channel can be disrupted by an adversary. Standard countermeasures like data copying and redundancy, which help preserve data integrity in traditional systems, are not applicable in quantum systems due to the need to maintain the integrity of the quantum state.
- Attacks exploiting the detection of measurement states are a concern, particularly in protocols like BB84 where polarizing filters are used. An attacker might use back-propagation techniques to determine the polarization axis, thereby predicting the quantum states being communicated [34].
- Quantum key exchange protocols that depend on random bit sequences can be compromised if the randomness source lacks sufficient entropy or predictability. Employing a hardware-based random number generator is a common countermeasure.
- Protocol-specific attacks also exist, such as the photon number-splitting (PNS) attack, which exploits photon generation devices that occasionally emit multiple photons with identical polarization. This allows an attacker to intercept photons without detection [35].
- Some attacks manipulate the communication channel itself, involving phase manipulation, timing shifts, or the insertion of false quantum states. These tactics have been demonstrated against some commercial quantum key exchange systems [36,37,38].
It can be noted here that most of these types of attacks cannot be applied to techniques that rely on computational power.
4. LWE Cryptosystem
4.1. Original LWE Technique
The learning with errors (LWE) cryptosystem is a post-quantum cryptographic scheme based on the difficulty of solving linear equations with noisy terms. In LWE, the security relies on the difficulty of distinguishing between randomly generated linear equations and those with small, deliberately introduced errors. This problem is believed to be resistant to attacks by both classical and quantum computers, making LWE a strong candidate for secure communication in a post-quantum world. The basic Ring-LWE encryption can be described as follows:
4.1.1. Basic Setup
- LWE Problem Definition: Given a vector in and a noisy inner product , where
- is a random vector from ;
- is a secret vector from ;
- e is a small error sampled from a discrete Gaussian distribution or another error distribution over ;
- q is a prime modulus.
- Search Problem: The goal of LWE is to find the secret vector given several pairs .
- Decision Problem: The decision version of LWE is to distinguish between pairs generated as described above and pairs where is uniformly random in .
4.1.2. LWE Encryption Scheme
- Key Generation:
- Choose a secret vector .
- The public key consists of several pairs where
- -
- is an matrix with entries from ;
- -
- ;
- -
- is a small error vector from a discrete Gaussian distribution.
- Encryption:
- To encrypt a bit ,
- -
- Choose a random binary vector .
- -
- Compute .
- -
- Compute .
- -
- The ciphertext is .
- Decryption:
- Given ciphertext ,
- -
- Compute .
- -
- If is closer to 0 than to , decrypt as 0; otherwise, decrypt as 1.
4.1.3. Security
The security of the LWE cryptosystem relies on the difficulty of the LWE problem, which is believed to be hard for both classical and quantum computers. Specifically, the problem can be reduced to certain worst-case lattice problems, such as the shortest vector problem (SVP) and the bounded distance-decoding (BDD) problem, which are conjectured to be difficult.
4.2. Proposed LWE Cryptosystem
Table 1 illustrates the used notations.

Table 1.
Used Notations.
The proposed cryptosystem replaces the small errors and in with two random fragments of m, which are and (Equation (1)).
Key Generation:
The key generation process in the proposed technique is similar to that used in the basic LWE system. This function generates the number a and the secret keys s and e, then computes the public key as shown in Equation (2).
therefore the public key is .
Encryption:
To encrypt a plaintext m, the system generates and randomly fragments m to and , multiplies r by a and b in u and v, respectively, then adds and as follows:
Enc(m):
Therefore, the ciphertext of a t-bit binary plaintext is represented by only one pair , where u, .
The cryptosystem in this representation is vulnerable to the chosen ciphertext attack (CCA) as illustrated below.
In the hypothesis that the attacker has , it is enough to add a value x to v (or subtract x from u) to get . Therefore, the attacker can easily distinguish between the encryptions of any two chosen messages.
. So .
Therefore, the new representation of the ciphertext is . Algorithm 1 describes the encryption function.
| Algorithm 1 Encryption |
|
Decryption:
The decryption process is shown in Algorithm 2.
| Algorithm 2 Decryption |
function Dec
|
4.3. Parameter Selection
To insure correct decryption and prevent the enemy from getting any sensitive information, the following conditions must be satisfied. We will see that any breach of these conditions will affect the performance of the proposal.
- : This is to get from .In decryption, we have , then ; if , . Suppose that ; it might give because m is fragmented randomly. To get , it must compute , meaning , which will not give a correct . Therefore, m must be less than s.
- : This is to get from .Suppose that , so will not give exactly , which we need to extract and . The same thing occurs when computing ; it leads to setting .
- : This is to get r and from z.If , we cannot extract exactly , so z must be less than p in order to neglect , and it is enough to put .
- : This is to make sense for the modulus when calculating .If , b will be less than p because , so b will be exactly equal to without mod, which makes it more vulnerable, and the attacker might get one of these secret values due to modulus operation increasing the computational complexity.
4.4. Enc-Dec Correctness
To eliminate the value which is hidden in both u and v, the function starts with computing z as follows:
as a result, ;
then, it starts to extract values r, , and .
- Since , ;
we put
compute .
- Since , .
Compute
- .
Finally, is obtained.
4.5. Homomorphic Addition
An encryption scheme supports homomorphic addition if there exists an operation ⊕ on ciphertexts such that for any plaintext m and n with their respective ciphertexts and , it holds that (Equation (5))
where Dec is the decryption function, is the secret key, and + denotes the addition operation in the plaintext space.
Let m and n be two messages.
We have and , then , so . Therefore, the proposed technique supports the homomorphic addition property.
5. Security Analysis and Performance
Learning with errors (LWE) is a foundational problem in post-quantum cryptography. The security of LWE-based cryptographic schemes hinges on the presumed hardness of the LWE problem, which remains difficult even for quantum computers. Considering the hardness assumption, lattice problems like SVP and GapSVP are believed to be difficult for both classical and quantum computers, providing a strong foundation for the difficulty of LWE. The objective is to achieve IND-CCA security.
5.1. IND-CCA Security Definition
An encryption scheme is said to be IND-CCA secure (indistinguishability under chosen ciphertext attack) if an adversary cannot distinguish between the encryptions of any two chosen plaintexts, even with access to a decryption oracle, except for the challenge ciphertext.
5.2. Security Game
- Setup:
- The challenger generates a key pair .
- The public key is given to the adversary.
- Phase 1 (Decryption Queries):
- The adversary can query the decryption oracle with any ciphertext c except for the challenge ciphertext .
- The oracle returns the plaintext m such that .
- Challenge:
- The adversary chooses two plaintexts m and .
- The challenger randomly selects a value and computes the challenge ciphertext .
- The challenge ciphertext is given to the adversary.
- Phase 2 (Decryption Queries):
- The adversary can continue to query the decryption oracle with any ciphertext c except .
- Guess:
- The adversary outputs a guess .
- The adversary wins if .
The encryption scheme is IND-CCA secure if for any probabilistic polynomial-time adversary , the probability of winning the above game is at most negligibly better than , i.e.,
where is a negligible function in the security parameter n.
To reach a successful attack, let us suppose the following scenario:
Initially, the attacker needs to know , the first fragment of the challenger’s randomly selected value , knowing that the attacker has only the given ciphertext computed by the challenger. By multiplying w by , x is a number chosen by the attacker. He can get , then he can easily add x to v as ; finally, he gets valid decryption. Therefore, without knowing exactly , the random fragment of b, it is impossible to calculate a correct and then to make a successful attack.
Figure 1 (u-CCA and v-CCA) shows that the Dec algorithm always returns 0 because w is different from , then even for any polynomial q, the scheme is semantically secure against a q-bounded CCA2 attack (for q queries). Return to Phase 2 (decryption queries) in the security game, where the adversary can continue to query the decryption oracle with any ciphertext c except . The attacker has to try all possibilities of fragments of m to reach a probability of because he does not know b is m and , so the attacker cannot tell if the decryption of a ciphertext concerns m or , with a probability of more than . As a result, the proposed technique is IND-CCA secure.
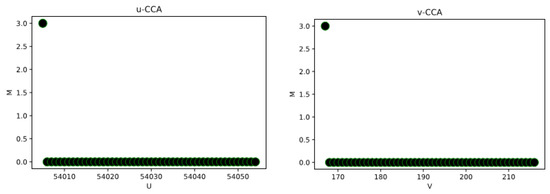
Figure 1.
Illustration of uv-CCA.
For quantum CCA security (qCCA), ensuring privacy in the presence of quantum decryption queries, when an adversary can query a superposition of ciphertexts and receive a superposition of their decryption, Navid and Varun [39] proved that “the single-bit qCCA-secure scheme is sufficient to realize a multi-bit scheme with qCCA security”. Therefore, the proposal is IND-qCCA.
Primal attacks construct a lattice with the unique shortest vector from an instance of an LWE system and then use the BKZ algorithm to solve the unique shortest vector problem. With our variant of LWE, the attacker cannot construct a d-dimensional lattice, and the BKZ algorithm cannot be used.
In the Ajtai–Dwork Theorem, the LWE problem can be reduced from certain worst-case lattice problems such as the shortest vector problem (SVP) and the gap shortest vector problem (GapSVP). This reduction implies that an efficient algorithm solving LWE would also solve these hard lattice problems. Regarding the proposal, smaller errors and in were replaced by relatively large values [40]. This means that efficient algorithms solving LWE would not solve the proposed version of lattice problems.
Against classical attacks, in lattice reduction attacks, techniques like the LLL algorithm and BKZ reduction are used to attempt to solve the underlying lattice problem. However, the parameter choices for LWE (Section 4.3) are set to ensure these lattice reduction algorithms remain inefficient. In distinguishing attacks, given the difficulty of the decision LWE problem, distinguishing between LWE samples and random noise is computationally impossible (Figure 1 and Figure 2) [41].
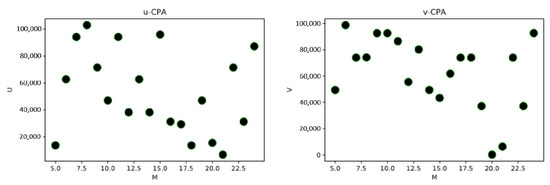
Figure 2.
Illustration of uv-CPA.
The security of LWE is specifically designed to withstand quantum attacks. Known quantum algorithms like Grover’s search or Shor’s algorithm do not provide efficient solutions to LWE. In quantum reduction, the worst-case to average-case reduction for LWE holds in the quantum setting as well, implying that LWE remains hard for quantum computers under standard assumptions. Hybrid attacks combine classical and quantum techniques, like using quantum algorithms to speed up parts of classical lattice reduction methods. Despite these advancements, the parameter settings for LWE can be adjusted to maintain security against such hybrid attacks. Besides selecting the true random numbers generator, an illustrated parameter selection in Section 4.3, the proposed technique realizes a high level of security. It should be noted that the most efficient way to obtain a true RNG is by employing a quantum-RNG, whereas pseudo-RNGs offer in principle the possibility, for Eve, of retrieving the generation algorithm. Therefore, we suggest the employment of QRNGs, which are inherently random and therefore non-replicable [42,43,44].
Compared with the classical LWE version, the authors’ proposal does not rely on increasing the dimension of n or on error distribution. In basic LWE, larger dimensions increase security but affect the size; also, the choice of the error distribution (often Gaussian) and its parameters must ensure sufficient noise to prevent easy solving of the equations but not too much to make the scheme impractical.
The security of the proposed LWE-based encryption method is supported by reductions from worst-case lattice problems, making them robust against both classical and quantum attacks. The careful selection of parameters and consideration of implementation strategies ensure their practical security and efficiency.
Table 2 shows the chosen settings for comparison. Reference [17] used 128-bit security and . Reference [19] chose the following parameters: public key(bit) = , secret key(bit) = , and message(bit) = 256; and Reference [45] chose the following parameters: message size = 128 bits and ciphertext degree .

Table 2.
Parameter sizes and conditions.
Table 3 provides a comprehensive comparison between the encryption and decryption times as well as the ciphertext sizes of the proposed technique and those found in other studies employing the LWE (learning with errors) method. Notably, the proposed technique significantly outperforms its peers in terms of efficiency. It records an encryption time of merely 0.0427 ms compared to substantially higher times of 102.10 ms in Reference [17] and ms in Reference [19]. Similarly, for decryption, the proposed technique achieves a rapid 0.0320 ms, starkly faster than the 0.258 ms of Reference [17] and again, the exceedingly slower ms in Reference [19].

Table 3.
Performance comparison of different techniques.
The proposed encryption technique not only advances performance in terms of execution speed but also makes significant strides in reducing the size of the ciphertext, a critical aspect of cryptographic efficiency. The results illustrate that the technique compresses the ciphertext to a mere 708 bits. This represents a profound improvement when juxtaposed with the sizes reported in other studies: bits in Reference [17], which can grow exponentially with the parameter n; 82,000 bits in Reference [19]; and 60 kilobits in Reference [45]. Such reductions in ciphertext size are pivotal, especially in contexts where bandwidth and storage are at a premium.
This remarkable decrease in ciphertext size not only implies a more efficient use of storage space but also enhances the speed at which encrypted data can be transmitted across networks. Smaller ciphertexts mean that less data needs to be sent over the network, reducing transmission time and potentially decreasing the likelihood of transmission errors. This becomes increasingly important in environments like mobile computing and Internet of Things (IoT) devices, where bandwidth and storage capabilities are often limited. Moreover, the reduction in ciphertext size contributes directly to lowering the computational overhead involved in the encryption and decryption processes. By producing smaller encrypted outputs, the proposed technique alleviates the burden on system resources, thereby facilitating quicker processing and less energy consumption. This is particularly beneficial for battery-operated devices and for applications that require real-time or near-real-time data processing.
The substantial gains in both time and space efficiency stem from the methodological innovation of encrypting the entire message as a whole rather than encrypting each bit individually. This holistic approach reduces the computational burden by minimizing the number of necessary calculations. Consequently, this leads to faster execution times and results in much smaller ciphertexts, thus enhancing the overall performance and practicality of the encryption technique. These results demonstrate the effectiveness of the proposed method in leveraging the strengths of the LWE method while mitigating its computational demands and storage requirements.
6. Conclusions
This paper introduces a lightweight encryption technique that utilizes random fragmentation of messages and linear arithmetic operations. The proposed cryptosystem has several key advantages, notably its ability to perform homomorphic addition on encrypted data, making it highly applicable in critical areas such as data mining. A standout feature of the proposal is its resistance against quantum computers, achieved through a new learning with errors (LWE) variant. This paper provided comprehensive details of the proposed technique. The results obtained are very promising, as encryption/decryption times equal to 0.0427 ms and 0.0320 ms, respectively, were achieved, with a ciphertext size of 708 bits corresponding to a message of 64 bits and 128 bits security.
Author Contributions
Conceptualization, M.K.; methodology, K.K.; validation, G.P.; formal analysis, M.H. and M.A.; writing, M.K., K.K., G.P., M.H., and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, S.; Chen, Y.; Chen, L.; Liao, J.; Kuang, C.; Li, K.; Liang, W.; Xiong, N. Post-Quantum Security: Opportunities and Challenges. Sensors 2023, 23, 8744. [Google Scholar] [CrossRef]
- Kara, M.; Karampidis, K.; Sayah, Z.; Laouid, A.; Papadourakis, G.; Abid, M.N. A Password-Based Mutual Authentication Protocol via Zero-Knowledge Proof Solution. In Proceedings of the International Conference on Applied CyberSecurity, Dubai, United Arab Emirates, 29 April 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 31–40. [Google Scholar]
- Chait, K.; Kara, M.; Laouid, A.; Hammoudeh, M.; Bounceur, A. One Digit Checksum for Data Integrity Verification of Cloud-executed Homomorphic Encryption Operations. In Proceedings of the 7th International Conference on Future Networks and Distributed Systems, Dubai, United Arab Emirates, 21–22 December 2023; pp. 71–75. [Google Scholar]
- Medileh, S.; Kara, M.; Laouid, A.; Bounceur, A.; Kertiou, I. A Secure Clock Synchronization Scheme in WSNs Adapted for IoT-based Applications. In Proceedings of the 7th International Conference on Future Networks and Distributed Systems, Dubai, United Arab Emirates, 21–22 December 2023; pp. 674–681. [Google Scholar]
- Ajao, L.A.; Agajo, J.; Adedokun, E.A.; Karngong, L. Crypto hash algorithm-based blockchain technology for managing decentralized ledger database in oil and gas industry. J 2019, 2, 300–325. [Google Scholar] [CrossRef]
- Ananth, P.; Poremba, A.; Vaikuntanathan, V. Revocable cryptography from learning with errors. In Proceedings of the Theory of Cryptography Conference, Taipei, Taiwan, 29 November–2 December 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 93–122. [Google Scholar]
- Kuka, C.S.; Hu, Y.; Xu, Q.; Chandler, J.; Alkahtani, M. A Novel True Random Number Generator in Near Field Communication as Memristive Wireless Power Transmission. J 2021, 4, 764–783. [Google Scholar] [CrossRef]
- Topaloglu, R.O. Quantum logic locking for security. J 2023, 6, 411–420. [Google Scholar] [CrossRef]
- Gao, W.; Yang, L.; Zhang, D.; Liu, X. Quantum identity-based encryption from the learning with errors problem. Cryptography 2022, 6, 9. [Google Scholar] [CrossRef]
- Pouly, A.; Shen, Y. Provable dual attacks on learning with errors. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zurich, Switzerland, 26–30 May 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 256–285. [Google Scholar]
- Montag, C.; Baumeister, H.; Kannen, C.; Sariyska, R.; Meßner, E.M.; Brand, M. Concept, possibilities and pilot-testing of a new smartphone application for the social and life sciences to study human behavior including validation data from personality psychology. J 2019, 2, 102–115. [Google Scholar] [CrossRef]
- Oh, E.N.; Baharon, M.R.; Yassin, S.; Idris, A.; MacDermott, A. Preserving data privacy in mobile cloud computing using enhanced homomorphic encryption scheme. J. Phys. Conf. Ser. 2022, 2319, 012024. [Google Scholar] [CrossRef]
- Baharon, M.R.; Shi, Q.; Llewellyn-Jones, D. A new lightweight homomorphic encryption scheme for mobile cloud computing. In Proceedings of the 2015 IEEE International Conference on Computer and Information Technology; Ubiquitous Computing and Communications; Dependable, Autonomic and Secure Computing; Pervasive Intelligence and Computing, Liverpool, UK, 26–28 October 2015; pp. 618–625. [Google Scholar]
- Pang, H.; Wang, B. Privacy-preserving association rule mining using homomorphic encryption in a multikey environment. IEEE Syst. J. 2020, 15, 3131–3141. [Google Scholar] [CrossRef]
- Mustafa, I.; Khan, I.U.; Aslam, S.; Sajid, A.; Mohsin, S.M.; Awais, M.; Qureshi, M.B. A lightweight post-quantum lattice-based RSA for secure communications. IEEE Access 2020, 8, 99273–99285. [Google Scholar] [CrossRef]
- Ishiguro, T.; Kiyomoto, S.; Miyake, Y.; Takagi, T. Parallel Gauss sieve algorithm: Solving the SVP challenge over a 128-dimensional ideal lattice. In Proceedings of the Public-Key Cryptography–PKC 2014: 17th International Conference on Practice and Theory in Public-Key Cryptography, Buenos Aires, Argentina, 26–28 March 2014; Proceedings 17. Springer: Berlin/Heidelberg, Germany, 2014; pp. 411–428. [Google Scholar]
- Yu, Z.; Gao, C.z.; Jing, Z.; Gupta, B.B.; Cai, Q. A practical public key encryption scheme based on learning parity with noise. IEEE Access 2018, 6, 31918–31923. [Google Scholar] [CrossRef]
- Döttling, N.; Kolonelos, D.; Lai, R.W.; Lin, C.; Malavolta, G.; Rahimi, A. Efficient laconic cryptography from learning with errors. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Lyon, France, 23 April 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 417–446. [Google Scholar]
- Zheng, Z.; Wang, A.; Fan, H.; Zhao, C.; Liu, C.; Zhang, X. Scloud: Public key encryption and key encapsulation mechanism based on learning with errors. Cryptol. Eprint Arch. 2020. Available online: https://eprint.iacr.org/2020/095 (accessed on 3 August 2024).
- Dowerah, U.; Krishnaswamy, S. Towards an efficient LWE-based fully homomorphic encryption scheme. IET Inf. Secur. 2022, 16, 235–252. [Google Scholar] [CrossRef]
- Basso Basset, F.; Valeri, M.; Roccia, E.; Muredda, V.; Poderini, D.; Neuwirth, J.; Spagnolo, N.; Rota, M.B.; Carvacho, G.; Sciarrino, F.; et al. Quantum key distribution with entangled photons generated on demand by a quantum dot. Sci. Adv. 2021, 7, eabe6379. [Google Scholar] [CrossRef]
- Kara, M.; Karampidis, K.; Papadourakis, G.; Laouid, A.; AlShaikh, M. A Probabilistic Public-Key Encryption with Ensuring Data Integrity in Cloud Computing. In Proceedings of the 2023 International Conference on Control, Artificial Intelligence, Robotics & Optimization (ICCAIRO), IEEE, Crete, Greece, 11–13 April 2023; pp. 59–66. [Google Scholar]
- Kara, M.; Laouid, A.; Bounceur, A.; Hammoudeh, M.; AlShaikh, M. Perfect Confidentiality through Unconditionally Secure Homomorphic Encryption Using OTP With a Single Pre-Shared Key. J. Inf. Sci. Eng. 2023, 39, 183. [Google Scholar]
- Flamini, F.; Spagnolo, N.; Sciarrino, F. Photonic quantum information processing: A review. Rep. Prog. Phys. 2018, 82, 016001. [Google Scholar] [CrossRef]
- Pirandola, S. Composable security for continuous variable quantum key distribution: Trust levels and practical key rates in wired and wireless networks. Phys. Rev. Res. 2021, 3, 043014. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef]
- Korzh, B.; Lim, C.C.W.; Houlmann, R.; Gisin, N.; Li, M.J.; Nolan, D.; Sanguinetti, B.; Thew, R.; Zbinden, H. Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat. Photonics 2015, 9, 163–168. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.H.; Liao, S.K.; Zhang, L.; Ren, J.G.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; et al. Satellite-based entanglement distribution over 1200 kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef]
- Hiskett, P.A.; Rosenberg, D.; Peterson, C.G.; Hughes, R.J.; Nam, S.; Lita, A.; Miller, A.; Nordholt, J. Long-distance quantum key distribution in optical fibre. New J. Phys. 2006, 8, 193. [Google Scholar] [CrossRef]
- Peev, M.; Pacher, C.; Alléaume, R.; Barreiro, C.; Bouda, J.; Boxleitner, W.; Debuisschert, T.; Diamanti, E.; Dianati, M.; Dynes, J.; et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 2009, 11, 075001. [Google Scholar] [CrossRef]
- Das, S.; Bäuml, S.; Winczewski, M.; Horodecki, K. Universal limitations on quantum key distribution over a network. Phys. Rev. X 2021, 11, 041016. [Google Scholar] [CrossRef]
- Jain, N.; Anisimova, E.; Khan, I.; Makarov, V.; Marquardt, C.; Leuchs, G. Trojan-horse attacks threaten the security of practical quantum cryptography. New J. Phys. 2014, 16, 123030. [Google Scholar] [CrossRef]
- Brassard, G.; Lütkenhaus, N.; Mor, T.; Sanders, B.C. Limitations on practical quantum cryptography. Phys. Rev. Lett. 2000, 85, 1330. [Google Scholar] [CrossRef]
- Fung, C.H.F.; Qi, B.; Tamaki, K.; Lo, H.K. Phase-remapping attack in practical quantum-key-distribution systems. Phys. Rev. A Atomic, Mol. Opt. Phys. 2007, 75, 032314. [Google Scholar] [CrossRef]
- Zhao, Y.; Fung, C.H.F.; Qi, B.; Chen, C.; Lo, H.K. Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A At. Mol. Opt. Phys. 2008, 78, 042333. [Google Scholar] [CrossRef]
- Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Kurtsiefer, C.; Makarov, V. Full-field implementation of a perfect eavesdropper on a quantum cryptography system. Nat. Commun. 2011, 2, 349. [Google Scholar] [CrossRef]
- Alamati, N.; Maram, V. Quantum CCA-Secure PKE, Revisited. In Proceedings of the IACR International Conference on Public-Key Cryptography, Sydney, Australia, 15–17 April 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 193–226. [Google Scholar]
- Cini, V.; Ramacher, S.; Slamanig, D.; Striecks, C. CCA-secure (puncturable) KEMs from encryption with non-negligible decryption errors. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Seoul, Republic of Korea, 7–11 December 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 159–190. [Google Scholar]
- Zong, C. The Mathematical Foundation of Post-Quantum Cryptography. arXiv 2024, arXiv:2404.19186. [Google Scholar]
- Herrero-Collantes, M.; Garcia-Escartin, J.C. Quantum random number generators. Rev. Mod. Phys. 2017, 89, 015004. [Google Scholar] [CrossRef]
- Cao, Z.; Zhou, H.; Yuan, X.; Ma, X. Source-independent quantum random number generation. Phys. Rev. X 2016, 6, 011020. [Google Scholar] [CrossRef]
- Mannalatha, V.; Mishra, S.; Pathak, A. A comprehensive review of quantum random number generators: Concepts, classification and the origin of randomness. Quantum Inf. Process. 2023, 22, 439. [Google Scholar] [CrossRef]
- Subramaniyaswamy, V.; Jagadeeswari, V.; Indragandhi, V.; Jhaveri, R.H.; Vijayakumar, V.; Kotecha, K.; Ravi, L. Somewhat homomorphic encryption: Ring learning with error algorithm for faster encryption of IoT sensor signal-based edge devices. Secur. Commun. Netw. 2022, 2022, 2793998. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).