A Comprehensive Approach to Quantitative Risk Assessment of Rockfalls on Buildings Using 3D Model of Rockfall Runout
Abstract
1. Introduction
1.1. Definition and Generalities
1.2. Risk Assessment Methods
1.3. Quantitative Risk Assessment
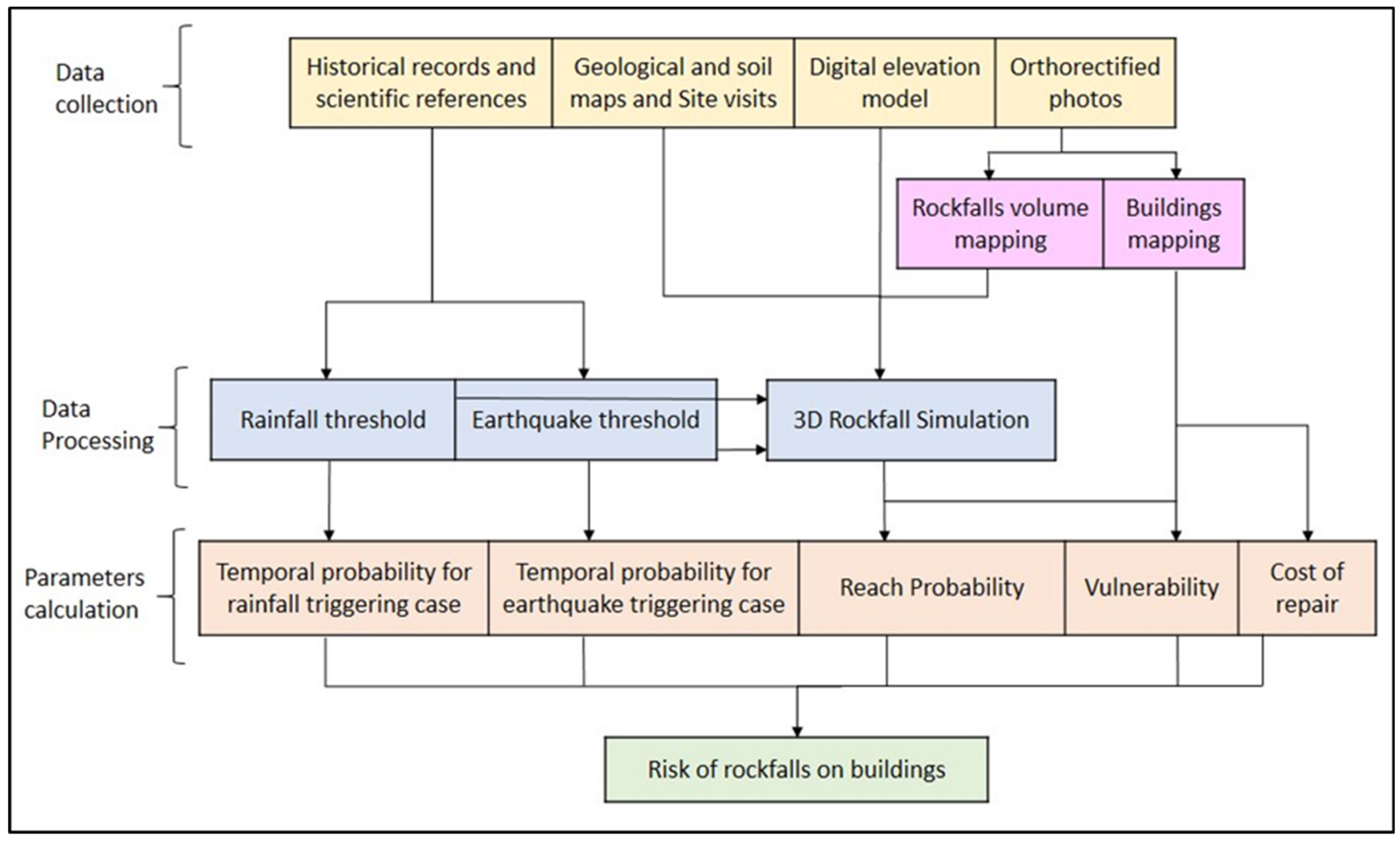
2. Methodology
2.1. Study Area
2.2. Runout Simulations
2.2.1. Case of Earthquake
2.2.2. Case of Rainfall
2.2.3. Collection and Calculation Risk Equation Parameters
2.2.4. Probability of Occurrence—P(Mi)
2.2.5. Reach Probability—P (Xj|Mi)
2.2.6. Probability of the Element Being at Point X at the Time of the Rockfall Occurrence P (T|Xj)
2.2.7. Physical Vulnerability—(Vij)
2.2.8. Value of the Element at Risk
3. Results and Discussion
4. Concluding Remarks and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mourey, J.; Lacroix, P.; Duvillard, P.-A.; Marsy, G.; Marcer, M.; Ravanel, L.; Malet, E. Rockfall and Vulnerability of Mountaineers on the West Face of the Aiguille du Goûter (Classic Route up Mont Blanc, France), an Interdisciplinary Study. Nat. Hazards Earth Syst. Sci. 2021, 1–29. [Google Scholar] [CrossRef]
- Zheng, L.; Wu, Y.; Zhu, Z.; Ren, K.; Wei, Q.; Wu, W.; Zhang, H. Investigating the Role of Earthquakes on the Stability of Dangerous Rock Masses and Rockfall Dynamics. Front. Earth Sci. 2022, 9, 1338. [Google Scholar] [CrossRef]
- Guzzetti, F. Rockfall BT—Encyclopedia of Natural Hazards; Bobrowsky, P.T., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 875–877. ISBN 978-1-4020-4399-4. [Google Scholar]
- Scavia, C.; Barbero, M.; Castelli, M.; Marchelli, M.; Peila, D.; Torsello, G.; Vallero, G. Evaluating rockfall risk: Some critical aspects. Geosciences 2020, 10, 98. [Google Scholar] [CrossRef]
- Briones-Bitar, J.; Carrión-Mero, P.; Montalván-Burbano, N.; Morante-Carballo, F. Rockfall research: A bibliometric analysis and future trends. Geosciences 2020, 10, 403. [Google Scholar] [CrossRef]
- Hantz, D.; Corominas, J.; Crosta, G.B.; Jaboyedoff, M. Definitions and concepts for quantitative rockfall hazard and risk analysis. Geosciences 2021, 11, 158. [Google Scholar] [CrossRef]
- Crosta, G.; Agliardi, F.; Frattini, P.; Lari, S. Key Issues in Rock Fall Modeling, Hazard and Risk Assessment for Rockfall Protection. In Engineering Geology for Society and Territory; Springer: Berlin/Heidelberg, Germany, 2015; pp. 43–58. ISBN 978-3-319-09056-6. [Google Scholar]
- Singh, A.; Kanungo, D.; Singh, P. Site-Specific Risk Assessment of Buildings Exposed to Rock Fall in India—A Case Study. In Understanding and Reducing Landslide Disaster Risk; Springer: Berlin/Heidelberg, Germany, 2021; pp. 475–482. ISBN 978-3-030-60226-0. [Google Scholar]
- Mavrouli, O.; Corominas, J. Rockfall vulnerability assessment for reinforced concrete buildings. Nat. Hazards Earth Syst. Sci. 2010, 10, 2055–2066. [Google Scholar] [CrossRef]
- Lollino, G.; Giordan, D.; Crosta, G.B.; Corominas, J.; Azzam, R.; Wasowski, J.; Sciarra, N. Engineering Geology for Society and Territory—Volume 2: Landslide Processes; Springer: Berlin/Heidelberg, Germany, 2015; Volume 2, ISBN 9783319090573. [Google Scholar]
- Žabota, B.; Kobal, M. A new methodology for mapping past rockfall events: From mobile crowdsourcing to rockfall simulation validation. ISPRS Int. J. Geo-Information 2020, 9, 514. [Google Scholar] [CrossRef]
- Romeo, S.; Cosentino, A.; Giani, F.; Mastrantoni, G.; Mazzanti, P. Combining ground based remote sensing tools for rockfalls assessment and monitoring: The poggio baldi landslide natural laboratory. Sensors 2021, 21, 2632. [Google Scholar] [CrossRef]
- Corominas, J.; Mavrouli, O.; Ruiz-Carulla, R. Rockfall Occurrence and Fragmentation BT—Advancing Culture of Living with Landslides; Sassa, K., Mikoš, M., Yin, Y., Eds.; Springer: Cham, Switzerland, 2017; pp. 75–97. [Google Scholar]
- Bertolo, D. A decision support system (DSS) for critical landslides and rockfalls and its application to some cases in the Western Italian Alps. Nat. Hazards Earth Syst. Sci. 2017, 1–31. Available online: https://nhess.copernicus.org/preprints/nhess-2017-396/ (accessed on 3 March 2024).
- Farvacque, M.; Lopez-Saez, J.; Corona, C.; Toe, D.; Bourrier, F.; Eckert, N. Quantitative risk assessment in a rockfall-prone area: The case study of the Crolles municipality (Massif de la Chartreuse, French Alps). Geomorphol. Reli. Process. Environ. 2019, 25, 7–19. [Google Scholar] [CrossRef]
- Wang, X.; Frattini, P.; Crosta, G.B.; Zhang, L.; Agliardi, F.; Lari, S.; Yang, Z. Uncertainty assessment in quantitative rockfall risk assessment. Landslides 2014, 11, 711–722. [Google Scholar] [CrossRef]
- Mavrouli, O.C.; Abbruzzese, J.; Corominas, J.; Labiouse, V. Review and advances in methodologies for rockfall hazard and risk assessment. Adv. Nat. Technol. Hazards Res. 2014, 34, 179–199. [Google Scholar] [CrossRef] [PubMed]
- Corominas, J.; Mavrouli, O.C. Quantitative Risk Assessmenent for Buildings due to Rock-Falls: Some Achievements and Challenges. 2011. Available online: https://api.semanticscholar.org/CorpusID:819582 (accessed on 3 March 2024).
- Ferrari, F.; Giacomini, A.; Thoeni, K. Qualitative Rockfall Hazard Assessment: A Comprehensive Review of Current Practices. Rock Mech. Rock Eng. 2016, 49, 2865–2922. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B.; Frattini, P. Integrating rockfall risk assessment and countermeasure design by 3D modelling techniques. Nat. Hazards Earth Syst. Sci. 2009, 9, 1059–1073. [Google Scholar] [CrossRef]
- Baecher, G.; Christian, J. Reliability and Statistics in Geotechnical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Corominas, J.; Westen, C.J.; Frattini, P.; Cascini, L.; Malet, J.-P.; Fotopoulou, S.; Catani, F.; Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Corominas, J.; Copons, R.; Moya, J.; Vilaplana, J.M.; Altimir, J.; Amigó, J. Quantitative assessment of the residual risk in a rockfall protected area. Landslides 2005, 2, 343–357. [Google Scholar] [CrossRef]
- Fell, R.; Ho, K.; Lacasse, S.; Leroi, E. A Framework for Landslide Risk Assessment and Management; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Moos, C.; Fehlmann, M.; Trappmann, D.; Stoffel, M.; Dorren, L. Integrating the mitigating effect of forests into quantitative rockfall risk analysis—Two case studies in Switzerland. Int. J. Disaster Risk Reduct. 2018, 32, 55–74. [Google Scholar] [CrossRef]
- Corominas, J.; Mavrouli, O. Rockfall Quantitative Risk Assessment. In Rockfall Engineering; Wiley: Hoboken, NJ, USA, 2013; pp. 255–301. ISBN 9781118601532. [Google Scholar]
- Dussauge-Peisser, C.; Helmstetter, A.; Grasso, J.R.; Hantz, D.; Desvarreux, P.; Jeannin, M.; Giraud, A. Probabilistic approach to rock fall hazard assessment: Potential of historical data analysis. Nat. Hazards Earth Syst. Sci. 2002, 2, 15–26. [Google Scholar] [CrossRef]
- Dubertert, L. Geological Maps of Syria and Lebanon at 1.50.000; No. 21 Sheets with Explicative Note; Minister of Public Affairs: Beiru, Lebanon, 1953.
- Al-Shaar, M.; Gérard, P.-C.; Faour, G.; Al-Shaar, W.; Adjizian-Gérard, J. Comparison of Earthquake and Moisture Effects on Rockfall-Runouts Using 3D Models and Orthorectified Aerial Photos. Geographies 2023, 3, 110–129. [Google Scholar] [CrossRef]
- Nasrallah, H.; Shukor, M.; Ghandour, A.J. Sci-Net: Scale-invariant model for buildings segmentation from aerial imagery. Signal Image Video Process 2023, 17, 2999–3007. [Google Scholar] [CrossRef]
- Khatiwada, D.; Dahal, R.K. Rockfall hazard in the Imja Glacial Lake, eastern Nepal. Geoenviron. Disasters 2020, 7, 29. [Google Scholar] [CrossRef]
- Jones, C.L.; Higgins, J.D.; Andrew, R.D. Colorado Rockfall Simulation Program Version 4.0 Manual. In Colorado Department of Transportation, Denver, CO; Institute of Agricultural Economics: Belgrade, Serbia, 2000; p. 80222. ISBN 3037579749. [Google Scholar]
- Luuk Dorren, A.K. Rockyfor3D (v5.2) Revealed—Transparent Description of the Complete 3D Rockfall Model. ecorisQ Pap. 2015, 1–37. Available online: https://www.ecorisq.org/docs/Rockyfor3D_v5_2_EN.pdf (accessed on 25 September 2022).
- Elias, A.R. Short Notice on Earthquake Hazard in Lebanon; Geology Department, American University of Beirut: Beirut, Lebanon, 2012; pp. 1–4. [Google Scholar]
- Harajli, M.; Sadek, S.; Asbahan, R. Evaluation of the seismic hazard of Lebanon. J. Seismol. 2002, 6, 257–277. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J.; Wartman, J. Methodology to evaluate rock slope stability under seismic conditions at Solá de Santa Coloma, Andorra. Nat. Hazards Earth Syst. Sci. 2009, 9, 1763–1773. [Google Scholar] [CrossRef]
- Saroglou, C.; Asteriou, P.; Zekkos, D.; Tsiambaos, G.; Clark, M.; Manousakis, J. UAV-based mapping, back analysis and trajectory modeling of a coseismic rockfall in Lefkada island, Greece. Nat. Hazards Earth Syst. Sci. 2018, 18, 321–333. [Google Scholar] [CrossRef]
- Faour, G. Forest Fire Fighting in Lebanon Using Remote Sensing and GIS. 2004. Available online: https://www.researchgate.net/publication/310796768_FOREST_FIRE_FIGHTING_IN_LEBANON_USING_REMOTE_SENSING_AND_GIS (accessed on 17 January 2024).
- Darwish, T.; Khawlie, M.; Daher, M.; Jomaa, I.; Awad, M.; Masri, T.; Shaban, A.; Faour, G.; Abdallah, C.; Kheir, R.; et al. Soil Map of Lebanon 1:50000; CNRS, Remote Sensing Center: Beirut, Lebanon, 2006. [Google Scholar]
- Rabat, Á.; Tomás, R.; Cano, M.; Pérez-Rey, I.; Siles, J.S.; Alejano, L.R. Influence of water content on the basic friction angle of porous limestones—Experimental study using an automated tilting table. Bull. Eng. Geol. Environ. 2022, 81, 223. [Google Scholar] [CrossRef]
- Aboushook, M.; EL-Sohby, M.; Mazen, O. Slope degradation and analysis of Mokattam plateau, Egypt. In Proceedings of the 2nd International Conference on Geotechnical Site Characterization (ISC-2), Porto, Portugal, 30 March 2004; pp. 1081–1887. [Google Scholar]
- Mary Vick, L.; Zimmer, V.; White, C.; Massey, C.; Davies, T. Significance of substrate soil moisture content for rockfall hazard assessment. Nat. Hazards Earth Syst. Sci. 2019, 19, 1105–1117. [Google Scholar] [CrossRef]
- Asteriou, P.; Saroglou, H.; Tsiambaos, G. Rockfall: Scaling factors for the coefficient of restitution. In ISRM EUROCK; ISRM: Lisbon, Portugal, 2013; pp. 195–200. [Google Scholar] [CrossRef]
- Klein, C.; Carmichael, R.S. General Considerations Rock Types. Rock. Encycl. Br. 2021, 1–30. Available online: https://www.britannica.com/science/rock-geology (accessed on 25 September 2022).
- Jaiswal, P.; van Westen, C.J. Estimating temporal probability for landslide initiation along transportation routes based on rainfall thresholds. Geomorphology 2009, 112, 96–105. [Google Scholar] [CrossRef]
- Coe, J.; Michael, J.; Crovelli, R.; Savage, W.; Laprade, W.; Nashem, W. Probabilistic Assessment of Precipitation-Triggered Landslides Using Historical Records of Landslide Occurrence, Seattle, Washington. Environ. Eng. Geosci. 2004, 10, 103–122. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Higgins, J.D.; Andrew, R.D.; By, E.; Keith Turner, A.; Jayaprakash, G.P. Rockfall Types and Causes. In Rockfall: Characterization and Control. Transp. Res. Board. 2013, 284, 21–55. [Google Scholar] [CrossRef]
- Wyllie, D.C. Rock Fall Engineering, 1st ed.; Taylor & Francis Group: Abingdon, UK, 2014. [Google Scholar] [CrossRef]
- Wieczorek, G.F. Landslides: Investigation and mitigation. Chapter 4-Landslide triggering mechanisms. Transp. Res. Board Spec. Rep. 1996, 247, 76–90. [Google Scholar]
- Brax, M.; Albini, P.; Beauval, C.; Jomaa, R.; Sursock, A. An Earthquake Catalog for the Lebanese Region. Seismol. Res. Lett. 2019, 90, 2236–2249. [Google Scholar] [CrossRef]
- El Kadri, S.; Beauval, C.; Brax, M.; Bard, P.Y.; Vergnolle, M.; Klinger, Y. A Fault-Based Probabilistic Seismic Hazard Model for Lebanon, Controlling Parameters and Hazard Levels; Springer: Dordrecht, The Netherlands, 2023; Volume 21, ISBN 0123456789. [Google Scholar]
- Arango, M.C.; Lubkowski, Z.A. Seismic hazard assessment and design requirements for Beirut, Lebanon. In Proceedings of the 15th World Conference in Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; Volume 11266, pp. 1–10. [Google Scholar]
- Leyva, S.; Cruz-Pérez, N.; Rodríguez-Martín, J.; Miklin, L.; Santamarta, J.C. Rockfall and Rainfall Correlation in the Anaga Nature Reserve in Tenerife (Canary Islands, Spain). Rock Mech. Rock Eng. 2022, 55, 2173–2181. [Google Scholar] [CrossRef]
- NASA. Earthdata; NASA: Washington, DC, USA, 2023. Available online: https://search.earthdata.nasa.gov/ (accessed on 29 June 2023).
- Dorren, L.; Berger, F.; Bourrier, F.; Eckert, N.; Saroglou, C.; Schwarz, M.; Stoffel, M.; Trappmann, D.; Utelli, H.-H.; Moos, C. Delimiting rockfall runout zones using reach probability values simulated with a Monte-Carlo based 3D trajectory model. Nat. Hazards Earth Syst. Sci. Discuss. 2022, 1–23. [Google Scholar]
- Glade, T. Vulnerability assessment in landslide risk analysis. Beitrag zur Erdsystemforsch 2003, 134, 123–146. [Google Scholar]
- Uzielli, M.; Nadim, F.; Lacasse, S.; Kaynia, A. A conceptual framework for quantitative estimation of physical vulnerability to landslides. Eng. Geol. 2008, 102, 251–256. [Google Scholar] [CrossRef]
- Caleca, F.; Tofani, V.; Segoni, S.; Raspini, F.; Rosi, A.; Natali, M.; Catani, F.; Casagli, N. A methodological approach of QRA for slow-moving landslides at a regional scale. Landslides 2022, 19, 1539–1561. [Google Scholar] [CrossRef]
- UNDP/UNESCO. Vulnerability and Seismic Hazard. Vulnerability Analysis in the Balkan Region. Project RER/79/014 WG.B Final Report. 1982. Available online: https://www.iitk.ac.in/nicee/wcee/article/8_vol7_647.pdf (accessed on 2 March 2024).
- Li, Z.; Nadim, F.; Huang, H.; Uzielli, M.; Lacasse, S. Quantitative vulnerability estimation for scenario-based landslide hazards. Landslides 2010, 7, 125–134. [Google Scholar] [CrossRef]
- Lateltin, O.; Haemmig, C.; Raetzo, H.; Bonnard, C. Landslide risk management in Switzerland. Landslides 2005, 2, 313–320. [Google Scholar] [CrossRef]
- Wei, L.; Hu, K.; Hu, X.; Wu, C.; Zhang, X. Quantitative multi-hazard risk assessment to buildings in the Jiuzhaigou valley, a world natural heritage site in Western China. Geomat. Nat. Hazards Risk 2022, 13, 193–221. [Google Scholar] [CrossRef]
- Al-Shaar, W. (National Council for Scientific Research (CNRS), Beirut, Lebanon). Interview with Walid Al-Shaar. Personal Interview. 2023. [Google Scholar]
- Rafiei Sardooi, E.; Azareh, A.; Mesbahzadeh, T.; Soleimani Sardoo, F.; Parteli, E.J.R.; Pradhan, B. A hybrid model using data mining and multi-criteria decision-making methods for landslide risk mapping at Golestan Province, Iran. Environ. Earth Sci. 2021, 80, 487. [Google Scholar] [CrossRef]
- Kamal, A.S.M.M.; Hossain, F.; Ahmed, B.; Rahman, M.Z.; Sammonds, P. Assessing the effectiveness of landslide slope stability by analysing structural mitigation measures and community risk perception. Nat. Hazards 2023, 117, 2393–2418. [Google Scholar] [CrossRef]

| Rockfall Intensity | Kinetic Energy: E (KJ) | Proposed I Value |
|---|---|---|
| Low | Less than 30 | 0.2 |
| Moderate | 30–300 | 0.6 |
| High | More than 300 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Shaar, M.; Gerard, P.-C.; Faour, G.; Al-Shaar, W.; Adjizian-Gérard, J. A Comprehensive Approach to Quantitative Risk Assessment of Rockfalls on Buildings Using 3D Model of Rockfall Runout. J 2024, 7, 183-203. https://doi.org/10.3390/j7020011
Al-Shaar M, Gerard P-C, Faour G, Al-Shaar W, Adjizian-Gérard J. A Comprehensive Approach to Quantitative Risk Assessment of Rockfalls on Buildings Using 3D Model of Rockfall Runout. J. 2024; 7(2):183-203. https://doi.org/10.3390/j7020011
Chicago/Turabian StyleAl-Shaar, Mohammad, Pierre-Charles Gerard, Ghaleb Faour, Walid Al-Shaar, and Jocelyne Adjizian-Gérard. 2024. "A Comprehensive Approach to Quantitative Risk Assessment of Rockfalls on Buildings Using 3D Model of Rockfall Runout" J 7, no. 2: 183-203. https://doi.org/10.3390/j7020011
APA StyleAl-Shaar, M., Gerard, P.-C., Faour, G., Al-Shaar, W., & Adjizian-Gérard, J. (2024). A Comprehensive Approach to Quantitative Risk Assessment of Rockfalls on Buildings Using 3D Model of Rockfall Runout. J, 7(2), 183-203. https://doi.org/10.3390/j7020011








