Abstract
The construction industry consumes over 32% of the annually excavated natural resources worldwide. Additionally, it is responsible for 25% of the annually generated solid waste. To become a more sustainable industry, a circular economy is necessary: resources are kept in use as long as possible, aiming to reduce and recirculate natural resources. In this paper, the investigation focuses on pedestrian truss bridges of the types Warren and Howe. Many pedestrian bridges currently find themselves in their end-of-life phase and most commonly these bridges are demolished and rebuilt, thus needing a lot of new materials and energy. The aim is thus first and foremost to reduce the amount of necessary new materials. For this reason, a design tool will be created, using the software ‘Matlab’, in which truss bridges can be evaluated and compared in the conceptual design stage. The tool is based on the theory of morphological indicators: the volume indicator, displacement indicator, buckling indicator and first natural frequency indicator. These allow a designer to determine the most material efficient Warren or Howe truss bridge design with user-defined constraints concerning deflection, load frequency, buckling and overall dimension. Subsequently, the tool was tested and compared to calculations made in the finite element modelling software Diamonds. In total, 72 steel bridge structures were tested. From these it could be concluded that the manual calculations in Diamonds in general confirmed the results obtained with the automated design tool based on morphological indicators. As such, it allows a designer to converge more quickly towards the best performing structure, thus saving time, materials, and corresponding costs and energy.
1. Introduction
In the current linear economy, the excavation rate of non-renewable materials is alarming. If this trend continues, the annual extraction of non-renewable resources will reach 170–184 billion tonnes by 2050, which will quickly result in their depletion [1]. A way to limit the excavation is by changing from a linear economy model, where the idea is based on a ‘take, make and dispose’ model, to a circular economy (CE) model [2]. The essence of the CE can be brought back to the 4R’s—Reduce, Reuse, Recycle, Recover—signifying the desired order of the value retention of products and materials [3,4]. As such, the first step is always to ‘Reduce’ the amount of required material. This can be done by designing with material-efficiency in mind. Additionally, the product should be designed in a way that its components can be easily disassembled and ‘Reused’. Alternatively, the materials should be ‘Recycled’ when the components are not reusable anymore. Lastly, when the materials cannot be recycled, the embedded energy in the material should be ‘Recovered’ in heat and power plants. The latter is mostly reserved for the bioeconomy.
This study will focus on pedestrian bridges. Many concrete pedestrian bridges ranging from 30 to 50 years in age, presently need to be replaced as they reached their end-of-life phase and appear to be in a severe condition of disrepair [5,6,7]. This also corresponds to the typical design working life that is mentioned in e.g., the Eurocodes [8,9]. Typically, these bridges are not just being demolished, they are replaced by new ones. However, a CE oriented design methodology for pedestrian and cycling bridges is non-existent. Hence, a design methodology that incorporates the 4R principle needs to be developed. The R’s Reuse and Recycle have been extensively researched, as they directly correspond to Design for Adaptability and Design for Disassembly (e.g., [10,11,12,13,14,15]). The R of Recover is covered in the bioeconomy. Yet, the first R of Reduce, the most important R in the CE, is generally neglected and severely underestimated. Even in the current Eurocodes there is no mention of structural optimisation. Traditionally, the engineer’s role is to calculate the bridge structure according to the 3S principle: Strength, Stiffness, Stability. The aim is always to design the structure so it is fully stressed and stripped of all redundant material. Vandenbergh and De Wilde explain that this is of great importance, because low material consumption limits the structure’s energetic impact, and decreases procurement, transportation and construction costs. This thus lowers the environmental footprint and post-use waste, and leads to a more sustainable structure by and large [16]. However, engineers are usually involved in the design process after the architects have finished the conceptual design. This often leads to lots of additional design iterations in order to somewhat optimise the structural system [17,18,19,20,21]. Hence, engineers design an optimised structure for an architectural concept that may be far from ideal from a structural point of view. Unfortunately, less efficient structures require more material, even when they are designed to be fully stressed.
The calculation method for a structure is well defined, but the method for choosing the most optimal structural design is usually vague and subjective. Often, structural engineers generate conceptual designs based on intuitive knowledge and experience, which means that only few possible alternatives are considered [17,20].
A structural geometry can also be generated with computational methods like topology optimisation. This allows an engineer to obtain a lightweight design with maximum stiffness for a given set of boundary conditions [22]. However, this can be computationally expensive and often requires lots of post-processing in order to translate the generated morphology into a practical one [23]. Some studies also incorporate principles of life cycle assessment and life cycle costing analysis for the development of new optimisation and decision-making methodologies for the design of different structural members [24,25,26,27,28,29,30]. These optimisation and decision-making tools will then find the most optimal parameters -resulting in the lowest CO2 emissions and economic costs- for a certain type of structural member. Hence, these optimisation tools allow to improve the sustainability of structural components, as they result in lower material consumption. However, they are not suitable for the optimisation of complete structural typologies.
For the optimisation of complete structures, the theory of the Morphological Indicators (MI) was developed as a means to formalise the search for the most efficient-fully stressed- structural typology in the conceptual design stage [31]. Considering the morphology of structures, it was in the work of Zalewski and Kus [32] that the link between the geometrical slenderness L/H and both the volume and displacement of trusses was demonstrated for the first time. This concept was developed further by Samyn [33] in a methodical study of the volume and displacement of structures. He also introduced the term ‘MI’. Van Steirteghem defines MI as dimensionless numbers that represent a geometrical property or a physical performance of a structure which can be used as a design tool to optimise structures in the conceptual design stage [34]. In addition to Samyn’s work, multiple MI have been developed such as the buckling indicator, self-weight indicator and the first natural frequency indicator. Where the choice of the structural typology used to be a guess based on experience, the idea of the MI is that they should easily allow to make a better guess, actually leading to material savings. However, the problem with these MI is that they are all inter-connected and their practical application has become very complex. Hence, they are barely used.
The goal is to develop a CE oriented design methodology for pedestrian and cycling bridges. This paper optimises the application process of the MI by means of an automated algorithm. In doing so, the MI can become a standard procedure in the conceptual design stage in order to formalise material reduction in the envisaged design methodology.
In the subsequent sections, the applied method to construct the algorithm will be explained. Subsequently, the MI that will be incorporated in the algorithm and the actual algorithm are shown. Lastly, the algorithm is tested and discussed, followed by a conclusion and further research recommendations.
2. Conceptual Design According to Morphological Indicators
The MI are to be used in the conceptual design stage. They allow the optimisation of structures based on certain criteria. There are two kinds of MI: primary indicators and secondary indicators, which are both dimensionless. The secondary indicators represent the physical quantities: the quantity of material, the displacement, the rotation, the stresses, etc. Examples of primary indicators are the slenderness, the form coefficient, or the buckling indicator. Secondary indicators are implicitly dependent on one or more primary indicators. The most important secondary indicator is the volume indicator (W) [31].
Initially, the theory on MI only considered design for strength with the volume of used materials as the objective function. This strategy often resulted in a lightweight structure with a questionable lack of stiffness, which implicates a significant increase of material volume in the final design to meet the stiffness criteria [35,36]. Therefore, additional indicators like the indicators of buckling Ψ and displacement ∆ were introduced, improving the results obtained with the volume indicator.
The indicator of volume W allows the designer to compare the necessary material volume for different structures. It is defined as follows: ‘The volume of a structure of identical shape with a unity span of 1 m, loaded with a unit force of 1 N with a material of allowable stress of 1 Pa’ [35,37]. In its most simple form, only considering design for strength with all elements fully stresses, thus ignoring buckling, the equation for the indicator of volume is: [34].
With:
- W the indicator of volume
- σ the allowable stress of the constituent material of the structure [N/m²]
- V the total volume of the structure [m³]
- F the total force acting upon the structure [N]
- L the span of the structure [m]
- li/L the ratio of the length of member i to the total length of the structure
- ki the portion of the load F present in member i
The indicator of buckling Ψ [38], is developed to indicate the tendency to buckling of a compressed element in a structure. The higher Ψ, the higher the risk of buckling. The primary indicator Ψ should be used in combination with the secondary indicators like the indicator of volume W, the indicator of displacement ∆ and the indicator of first natural frequency Θ. The indicator of buckling Ψ is defined as [35]:
With:
- Ψ the indicator of buckling
- L the span
- q a form factor defining the cross section of the bars
- E the modulus of elasticity of the material
- σ the allowable stress to which at least one section is dimensioned
- F the total resultant force
- µ the proportion of the buckling length of the compression bars to their geometrical length, depending on the connection type
When the buckling indicator Ψ is considered, it is possible to take the buckling of the members into account. For this reason, the lengths li and member forces fi need to be expressed as a function of the overall slenderness L/H. Latteur [31,38] illustrates in his work that with a given Ψ, a value L/H exists with a minimal value of W. This means the volume indicator is not only dependent on the slenderness L/H anymore but is also dependent on the buckling indicator Ψ. Latteur [38] shows that for every structure with a total length L, composed of a material which is fully stressed σ, loaded with a resultant force F working on elements i with a length li and following the Rankine buckling curve, W becomes:
This equation can be used for both Warren structures with an even and an odd number of panels. However, for both cases, the portion of loads, ki, in the members i will be different. For more information about the theory behind the calculation of these portions of loads, one can consult the scientific literature on MI. The portion of loads ki will be the same for an even and odd truss structure except for the middle panel, where the portion of loads in the diagonals will be 0 for a Warren truss with an odd number of panels.
The equation is divided into members subjected to tension and members subjected to compression. If Ψ = 0, i.e., when buckling in the members in compression is ignored, the same result is obtained as with Equation (1).
The displacement indicator compares the displacement of different truss structure systems. It is the maximum displacement of an isomorphic structure with a unit span of 1 m, with a material with a unit Young’s modulus of 1 GPa and an allowable stress of 1 N/mm², subjected to a system load with a unit force of 1 N [35].
In its most simple form, considering only the slenderness L/H, thus ignoring buckling, the equation for the indicator of displacement is [31,34,38]:
With:
- ∆ the indicator of displacement
- E the modulus of elasticity of the used material [N/mm²]
- δ the maximum displacement of the structure [mm]
- σ the allowable stress of the material used for the structure [N/mm²]
- L the span of the structure [mm]
- li/L the ratio of the length of member i to the total length of the structure
- ni the portion of the unitary force, applied in a node j, present in member i
When considering Ψ, it is possible to take the buckling of each member into account. First of all, not only the portion of loads ki, but also the portion of unitary loads ni need to be addressed. When ∆ is no longer solely dependent on L/H but also on Ψ, the equation for calculating the displacement indicator ∆ for a Warren truss becomes [33,34,38]:
Equation (5) can be used to calculate both even and uneven Warren trusses.
Until now, Latteur [38] and Samyn [33] introduced the volume and displacement indicator taking buckling into consideration. However, a structure optimised with respect to strength often does not meet the necessary stiffness requirements. Lightweight structures in which all components are optimised to be fully stressed may lack resistance to vibrations occurring during use. Therefore, it is necessary to extend the morphological indicators to include the natural frequencies of the structure. These should not coincide with the frequencies of the applied load. For this reason, the indicator of first natural frequency is introduced [34]:
This indicator is directly linked with the displacement indicator ∆. Hence, it is also dependent on the buckling indicator Ψ.
The indicator of the first natural frequency is defined as “the natural frequency of a structure with a unit length (L = 1 m) composed of members working at a unit stress (σ = 1 Pa, β = 1) and with a unit Young’s modulus (E = 1 Pa) for which the ratio of the co-vibrating loads to the total load is equal to z* = 1 in SLS” [17].
As apparent above, a hierarchy between W and ∆ exists, as ‘design for strength’, i.e., the volume of material, is taken as the point of departure. Both Samyn [9] and Latteur [38] strive for the minimization of volume. Even though efficiency curves for ∆ have been established, these are customarily used to verify afterwards if the displacement, i.e., the stiffness, does not exceed the normative constraints imposed by the design code. In addition, Van Steirteghem [34] proved that if buckling is considered, the displacements are smaller than when buckling is ignored. Both Samyn and Latteur proved that the slenderness optimised through the volume of material (W) is rarely equal to the slenderness that minimises the displacement (∆). However, minimising ∆ is only important to the extent that it does not exceed the normative criteria. When the indicator of first natural frequency is introduced in the optimisation, a constraint that considers the dynamic behaviour of the structure is added. Therefore, the general optimisation procedure can be formulated as follows:
- σ* (≈ is the stress level in the structure in SLS
- are the natural frequencies of the structure that must be adequately far from the excitation frequencies of the external load.
If this constraint is rewritten in an interval of first natural frequencies that should be avoided, in terms of the indicator of displacement, this interval will become [34]:
or
or
The parameter is used to define the safety interval around the first natural frequency of the structure. This constraint yields an interval on the slenderness determined by the indicator of displacement. The indicator of volume is not explicitly present in the constraint. However, the first concern is to limit the volume of material, meaning that the stress level is to be maximised. Thus, the indicator of volume is indirectly present in the formula.
3. Design of the Software
The morphological indicators, designed to be a simple conceptual design tool, have paradoxically grown into a complex system. Their practical use is therefore limited to non-existent. Hence, in this study the previously described morphological indicators will be programmed into an automated algorithm. The platform used to create the software is MATLAB [39], and more specifically the ‘app-designer’ function. The latter was chosen in order to increase the user-friendliness, taking into account the norm ISO 25010:2011 [40,41]. The aim is to create a user-friendly design tool which will determine the most optimal structure based on some user-defined constraints. The development of this tool needs to conform to the Eurocode ‘NBN EN 1991-2—part 2: traffic loads on bridges’ [42].
The design tool is divided into four sections: Home, Limits, Results and Advanced settings, as shown in Figure 1, Figure 2, Figure 3 and Figure 4. Home is where the type of truss, the dimensions of the bridge, the material specifications and the loads acting upon the bridge can be defined. Limits is where the user can specify the constraints. The adjustable constraints are the pavement length, height, deflection and first natural frequency. Results is where the user determines if buckling needs to be considered, and where the result is calculated. The final tab, Advanced settings, is where the user is able to change parameters that in most cases would be a standard fixed value or to give certain values in a different form (e.g., displacement in mm instead of L/x). This prevents that the critical path to get a result, is cluttered with input options.
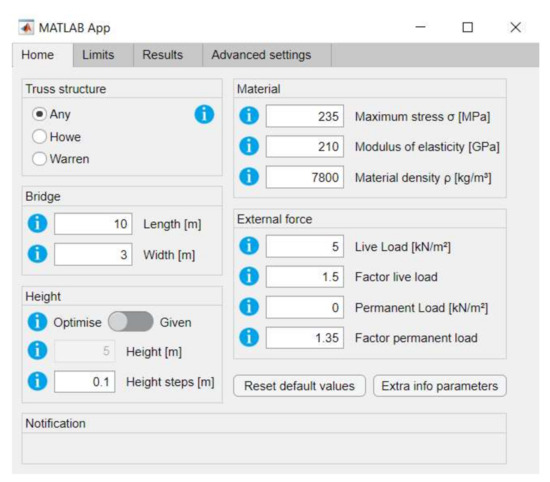
Figure 1.
Software home tab.
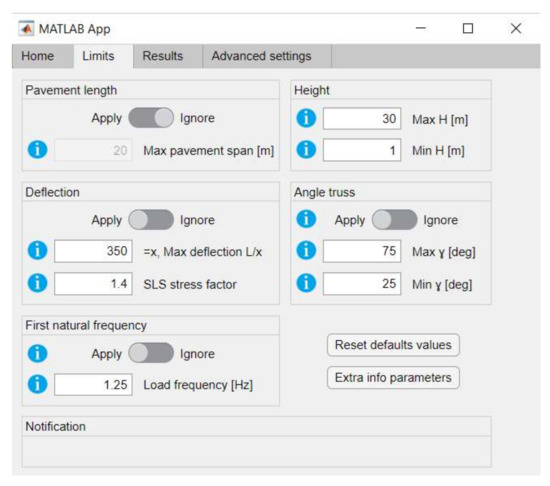
Figure 2.
Software limits tab.
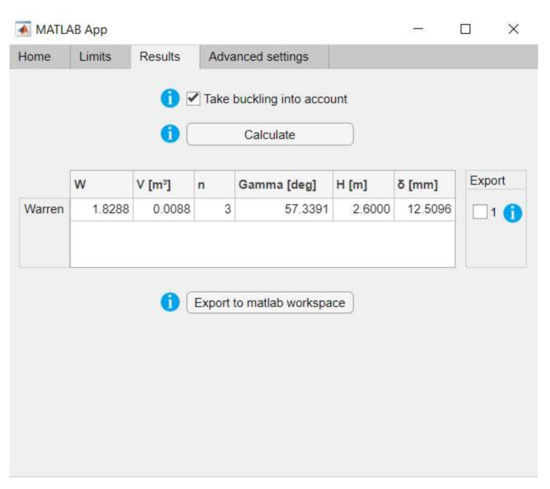
Figure 3.
Software results tab.
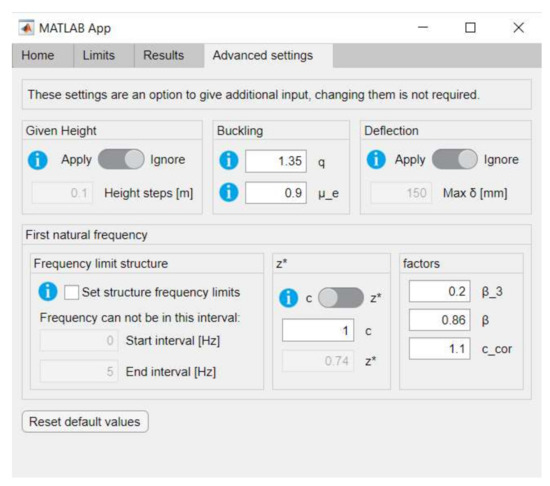
Figure 4.
Software advanced settings tab.
The result consists of six parameters: the volume indicator W, the volume V in cubic meters (derived from W), the number of panels n, the angle g that the first diagonal makes with the lower horizontal chord, the height H and the deflection d in millimetres. If the height is fixed there can be up to three results: the first is the optimal layout for the given height; the second is the absolute optimum with the optimal height; the third is the layout where the height is minimal but where the volume indicator is equal to or lower than that for the given height. If the optimal height is to be determined there will only be a single solution, the absolute optimum for the given span. The essential steps that the software runs through to calculate the result is depicted as a flowchart in Figure 5 and Figure 6.
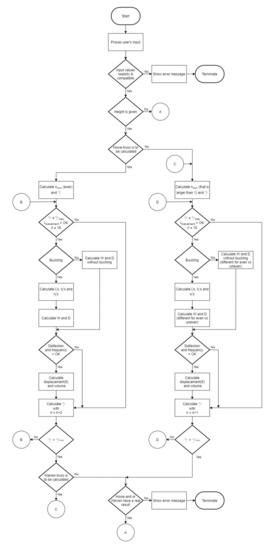
Figure 5.
Flowchart software, part 1.
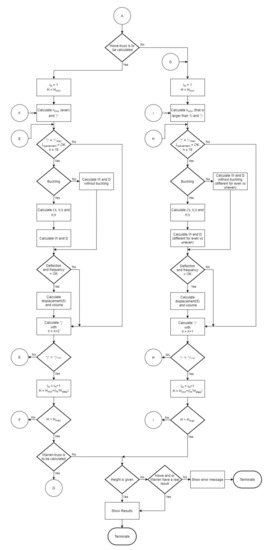
Figure 6.
Flowchart software, part 2.
4. Results and Discussion
In order to check the tool’s performance, a comparison is made using the finite element modelling software ‘Diamonds’ [43]. In this software, truss bridges are drawn with the same input parameters as the ones used in the design tool based on morphological indicators. This means that the bridges are drawn with the same span “L”, height “H” and number of panels “n”. Several bridge spans were tested, but some parameters were fixed: the bridge width is 3 m; the structural material is normal construction steel with a yield stress of 235 MPa, Young’s modulus of 210 GPa and density of 7800 kg/m³; the service load on the bridge is 5 kN/m² with a safety factor of 1.5, both as prescribed in the Eurocode; the maximum vertical deformation is limited to L/350.
The aim is not to obtain the same volume as indicated in the developed design tool. Rather, the structural calculations in Diamonds serve as confirmation of the indicated most optimal structure according to the design tool. The results are shown in Table 1 and Table 2. When reviewing the results, it can be concluded that both Diamonds and the design tool follow the same trend, independent of the span-to-height ratio. The most optimal result according to the software tool is indicated in bold, the results in Diamonds that deviate are highlighted in yellow. There are some important remarks to be made. The morphological indicators do not consider actual cross sections for the different bars in the truss. They consider a form factor which is equal for all bars, and which expresses the efficiency of the cross section. In the software tool, a highly efficient cross section is assumed. One can understand that in a truss, where the internal forces are all normal forces, this form factor is only important for bars in compression, thus bars susceptible to buckling. Additionally, regardless of the bars’ susceptibility to buckling, the morphological indicators assume that all bars are dimensioned so that they are all fully stressed, 100%. When this was translated to a realistic structure in Diamonds, only standard profile sections were used, corresponding to the considered form factor. Thus, for all bars in compression, profiles of type CHS with standard dimensions available in the European Union and the United Kingdom were chosen. The diagonals in tension were appointed L-shaped sections, because these are available in very small sizes and can thus approximate a fully stressed state. For the bars in the lower beam of the truss, it was chosen to use standard I-shaped sections, because the lower bars are also very susceptible to bending considering their self-weight. Some examples are shown in Figure 7 and Figure 8.

Table 1.
Warren trusses (The most optimal result according to the software tool is indicated in bold, the results in Diamonds that deviate are highlighted in yellow).

Table 2.
Howe trusses (The most optimal result according to the software tool is indicated in bold, the results in Diamonds that deviate are highlighted in yellow).

Figure 7.
Warren truss, span L = 40 m, height H = 7 m, number of panels n = 5, optimal standard sections are indicated.

Figure 8.
Howe truss, span L = 40 m, height H = 6 m, number of panels n = 6, optimal standard sections are indicated.
The use of standard profile sections implicates that there is only a limited number of profiles from which one can choose. This means that a fully stressed condition of each bar is not possible, because there may not be a standard profile section with the necessary dimensions to reach this fully stressed state. This is especially the case for compression bars, as these are optimised for buckling and will rarely be fully stressed. Additionally, for these compression bars it may even be that there is no standard profile section with the necessary dimensions to reach a 100% optimisation for buckling, again reducing the optimisation rate. These remarks are important, because they explain why the results in Diamonds sometimes deviate from the results obtained with the design tool. Nonetheless, the best performing structures according to the design tool were mostly confirmed in Diamonds. The design tool based on the morphological indicators thus proves to be useful in the conceptual design stage. It allows an engineer to converge more quickly towards the best performing structure, thus saving time, materials, and corresponding costs and energy. However, it is important to stress once again that this cannot be decoupled from an earlier involvement of engineers, preferably already in the conceptual design stage.
In this study, only pedestrian bridges were considered. However, the design tool based on morphological indicators can also be used when designing heavier bridge structures for regular traffic or trains. The major difference in the conceptual design stage is the increased load that needs to be considered.
The calculations of the 72 bridges were executed in a 2D design space, both in the design tool based on the morphological indicators and in Diamonds. This means that only local buckling of truss components was considered, while global buckling of the trusses was neglected. Additionally, imperfections that could affect the trusses’ susceptibility to buckling were not considered. Tomei et al. investigated these buckling phenomena for grid shell structures [44]. Their research may serve a s starting point for a future investigation of the effect of global buckling phenomena on W.
The major limitation of the design tool in its current form is that it only considers Warren and Howe truss bridges. In the future, other types of structures should be integrated in the software tool as well. Important bridge typologies to be considered are arch bridges, suspension bridges and cable-stayed bridges.
Additionally, the reuse of components in the end-of-life stage of a construction not only corresponds to DfA and DfD, but also to standardisation. In this sense, the use of standard profile sections is a start, but in order to enable the reuse of components, also the standardisation of their lengths becomes important [45] whilst maintaining a balance between architectural freedom and standardisation [3]. Hence, another challenge for improving the design tool will be to incorporate standardisation to improve the applicability and concreteness of the conceptual design results.
Another parameter that can be implemented is a parameter for non-homogenous materials, as the software tool can only work with homogenous materials. Finally, higher frequencies can be implemented in the software as well to take into account other types of external frequencies, such as wind and earthquakes.
5. Conclusions
The goal is to develop a CE oriented design methodology for pedestrian and cycling bridges, a design methodology that incorporates the 4R principle. The R’s of Reuse and Recycle have been extensively researched. The R of Recover is covered in the bioeconomy. Yet, the first R of Reduce, the most important R in the CE, is generally neglected and severely underestimated. This paper optimises the application process of the MI by means of an automated algorithm. This developed design tool allows the user to quickly obtain the best structural typology, Warren or Howe, to be used for a given span. The user can also introduce additional boundary conditions, e.g., height, number of panels, fixed typology (Warren or Howe), etc. This allows the user to find alternative, but sub-optimal solutions. The design tool was tested and compared to calculations made in the FEM software Diamonds. In total, 72 steel bridge structures were tested. From these it could be concluded that the manual calculations in Diamonds mostly confirmed the results obtained with the design tool based on morphological indicators. However, some important remarks are to be considered. The theory of morphological indicators starts with the assumption that all components in a structure are dimensioned so they are fully stressed, 100%. In reality, this is very difficult to achieve as usually standard profile sections are used. This means there is a limited number of sections from which the designer can choose. Hence, especially for compression elements, the profile section is optimised for buckling, rather than stress. As a result, the calculations in Diamonds result in higher material volumes.
Important to note is that only local buckling of truss components was considered in this study. In future work, the effect of global buckling phenomena on W can be investigated.
In its current form, the design tool only considers Warren and Howe truss bridges. The most important challenge in the further development of the design tool is therefore to integrate other types of structures. Important bridge typologies to be considered are arch bridges, suspension bridges and cable-stayed bridges. Another challenge for improving the design tool will be to incorporate standardisation to improve the applicability and concreteness of the conceptual design results, and this whilst maintaining a balance between architectural freedom and standardisation.
To conclude, the design tool based on the morphological indicators proves to be useful in the conceptual design stage. It allows a designer to converge more quickly towards the best performing structure by automating the selection of the optimal structural typology, thus saving time, materials, and corresponding costs and energy. Hence, it allows the R of Reduce to be formalised in the CE oriented design methodology.
Author Contributions
Conceptualization, K.A. and J.B.; Formal analysis, K.A., T.L. and J.M.; Investigation, K.A.; Methodology, K.A. and J.B.; Resources, A.A. and J.B.; Supervision, K.A. and J.B.; Writing—original draft, K.A., T.L. and J.M.; Writing—review & editing, K.A., A.A. and J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| 3S | Strength, Stiffness, Stability |
| 4R’s | Reduce, Reuse, Recycle, Recover |
| A | section area |
| B | width of the bridge |
| ccor | correction factor |
| CE | Circular Economy |
| CHS | Circular Hollow Sections |
| DfA | Design for Adaptability |
| DfD | Design for Disassembly/Deconstruction |
| E | modulus of elasticity |
| fe,i | excitation frequencies of the external load |
| fi | natural frequencies of the structure |
| f1 | the first natural frequency of the structure |
| F | total resultant Force |
| FD* | co-vibrating load |
| FEM | Finite Element Modelling |
| g | gravitational acceleration |
| GPa | GigaPascal |
| H | Height of a truss |
| i | the index of an element |
| I | second moment of inertia |
| j | the index of a node |
| k | static stiffness |
| ki | portion of load F present in member i |
| kN | kiloNewton |
| li | length of member I [m] |
| L | span of a truss |
| m | meter |
| mm | millimeter |
| MI | Morphological Indicator(s) |
| MPa | MegaPascal |
| n | number of panels of a truss |
| ni | the portion of the unitary force, applied in node j, present in member i |
| Pa | Pascal |
| q | formfactor |
| qfk | standard uniform characteristic load for pedestrian found in ‘NBN EN 1991-2—part 2’ |
| SLS | Serviceability Limit State |
| ULS | Ultimate Limit State |
| V | Volume |
| V(T) | Volume of the members in tension |
| V(C) | Volume of the members in compression |
| W | volume indicator |
| W(T) | morphological indicator of volume of the members in tension |
| W(C) | morphological indicator of volume of the members in compression |
| z* | ratio of the co-vibrating load in service limit state to the total load in ultimate limit state |
| β | parameter for the stress level in the structure in the calculation of the displacement and first natural frequency indicators |
| β3 | parameter to define the safety interval around the first natural frequency of the structure |
| δ | the maximum displacement in the middle of the truss |
| ∆ | morphological indicator of displacement |
| Θ | morphological indicator of the first natural frequency |
| µ | proportion of the buckling length of compression bars over their geometrical length, depending on its connection type |
| σ | allowable stress |
| σ* | stress level in the structure |
| morphological indicator of buckling |
References
- De Wit, M.; Hoogzaad, J.; Ramkumar, S.; Friedl, H.; Douma, A. The Circularity Gap Report—An Analysis of the Circular State of the Global Economy; Circle Economy: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Benachio, G.L.F.; do Carmo Duarte Freitas, M.; Tavares, S.F. Circular economy in the construction industry: A systematic literature review. J. Clean. Prod. 2020, 260, 121046. [Google Scholar] [CrossRef]
- Anastasiades, K.; Blom, J.; Buyle, M.; Audenaert, A. Translating the Circular Economy into Bridge Construction: Lessons Learnt from a Critical Literature Review. Renew. Sustain. Energy Rev. 2020, 117. [Google Scholar] [CrossRef]
- Kirchherr, J.; Reike, D.; Hekkert, M. Conceptualizing the Circular Economy: An Analysis of 114 Definitions. Resour. Conserv. Recycl. 2017, 127, 221–232. [Google Scholar] [CrossRef]
- Shuck-Britson; Snyder & Associates. Structural Evaluation Report—Pedestrian Bridge Structural Evaluation; 2015. Available online: https://businessdocbox.com/82967608-Construction/Structural-evaluation-report.html (accessed on 15 March 2019).
- City of Ottawa Harmer Avenue Pedestrian Bridge Replacement. Available online: https://ottawa.ca/en/city-hall/public-engagement/projects/harmer-avenue-pedestrian-bridge-replacement#public-information-boards-march-27-2018 (accessed on 15 March 2019).
- CTV News Calgary City Inspections Determine Two Pedestrian Bridges Need to Be Replaced; 2018. Available online: https://calgary.ctvnews.ca/city-inspections-determine-two-pedestrian-bridges-need-to-be-replaced-1.3845829 (accessed on 15 March 2019).
- CEN. Eurocode: Basis of Structural Design; CEN: Brussels, Belgium, 2002. [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Kissel, M.; Schrieverhoff, P.; Lindemann, U. Design for Adaptability—Identifying Potential for Improvement on an Architecture Basis. In Proceedings of the NordDesign Conference 2012, Aalborg, Denmark, 22–24 August 2012. [Google Scholar]
- Kasarda, M.E.; Terpenny, J.P.; Inman, D.; Precoda, K.R.; Jelesko, J.; Sahin, A.; Park, J. Design for adaptability (DFAD)—A new concept for achieving sustainable design. Robot. Comput. Integr. Manuf. 2007, 23, 727–734. [Google Scholar] [CrossRef]
- Schrieverhoff, P.; De Neufville, R.; Lindemann, U. Valuation of product adaptability in architecture design. In Proceedings of the 13th International Design Conference, DESIGN, Dubrovnik, Croatia, 19–22 May 2014; pp. 373–384. [Google Scholar]
- Soh, S.L.; Ong, S.K.; Nee, A.Y.C. Design for disassembly for remanufacturing: Methodology and technology. Procedia CIRP 2014, 15, 407–412. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, S.; Saitou, K. Design for Optimal End-of-Life Scenario Via Product-Embedded Disassembly. In Proceedings of the LCE2006, Leuven, Belgium, 31 May–2 June 2006; pp. 423–428. [Google Scholar]
- Yoga Mule, J. Design for Disassembly Approaches on Product Development Jaykumar Yoga Mule. Int. J. Sci. Eng. Res. 2012, 3, 1–5. [Google Scholar]
- Vandenbergh, T.; De Wilde, W.P. A review on conceptual design with morphological indicators. Int. J. Struct. Eng. 2010, 1, 280–298. [Google Scholar] [CrossRef]
- Hamidavi, T.; Abrishami, S.; Hosseini, M.R. Towards intelligent structural design of buildings: A BIM-based solution. J. Build. Eng. 2020, 32, 101685. [Google Scholar] [CrossRef]
- Mujumdar, P.; Maheswari, J.U. Design iteration in construction projects—Review and directions. Alex. Eng. J. 2018, 57, 321–329. [Google Scholar] [CrossRef]
- Christensen, P.W.; Klarbring, A. An Introduction to Structural Optimization; Springer Science + Business Media: Linköping, Sweden, 2009; ISBN 978-1-4020-8665-6. [Google Scholar]
- Vandenbergh, T.; De Wilde, W.P.; Latteur, P. Optimisation at the conceptual design stage with morphological indicators: Design for strength or design for stiffness. WIT Trans. Built Environ. 2008, 97, 401–410. [Google Scholar] [CrossRef] [Green Version]
- Park, P.; Gilbert, M.; Tyas, A.; Popovic-Larsen, O. Potential use of structural layout optimization at the conceptual design stage. Int. J. Archit. Comput. 2012, 10, 13–32. [Google Scholar] [CrossRef] [Green Version]
- Stangl, T.; Pribek, M.; Wartzack, S. Integration of structural optimization in the engineering design process. In Proceedings of the 13th International Design Conference, DESIGN, Dubrovnik, Croatia, 19–22 May 2014; pp. 1989–1998. [Google Scholar]
- He, L.; Gilbert, M.; Johnson, T.; Pritchard, T. Conceptual design of AM components using layout and geometry optimization. Comput. Math. Appl. 2019, 78, 2308–2324. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Martí, J.V.; Alcalá, J. Optimization of Concrete I-Beams Using a New Hybrid Glowworm Swarm Algorithm. Lat. Am. J. Solids Struct. 2014, 11, 1190–1205. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T. Cost and CO2 Emission Optimization of Precast-Prestressed Concrete U-Beam Road Bridges by a Hybrid Glowworm Swarm Algorithm. Autom. Constr. 2015, 49, 123–134. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Alcalá, J.; Pérez-López, E. Hybrid Harmony Search for Sustainable Design of Post-Tensioned Concrete Box-Girder Pedestrian Bridges. Eng. Struct. 2015, 92, 112–122. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design. Sustainability 2016, 8, 1295. [Google Scholar] [CrossRef] [Green Version]
- García-Segura, T.; Yepes, V. Multiobjective Optimization of Post-Tensioned Concrete Box-Girder Road Bridges Considering Cost, CO2 Emissions, and Safety. Eng. Struct. 2016, 125, 325–336. [Google Scholar] [CrossRef]
- García-Segura, T.; Penadés-Plà, V.; Yepes, V. Sustainable Bridge Design by Metamodel-Assisted Multi-Objective Optimization and Decision-Making under Uncertainty. J. Clean. Prod. 2018, 202, 904–915. [Google Scholar] [CrossRef]
- García-segura, T.; Yepes, V.; Frangopol, D.M.; Yang, D.Y. Lifetime Reliability-Based Optimization of Post-Tensioned Box-Girder Bridges. Eng. Struct. 2017, 145, 381–391. [Google Scholar] [CrossRef]
- Latteur, P. Eléments d’optimisation structurale. In Calculer une Structure: De la Théorie à L’exemple; L’Harmattan/Academia Editors: Louvain-la-Neuve, Belgium, 2016; pp. 411–463. ISBN 9782806102706. [Google Scholar]
- Zalewski, W.; Kus, S. Shaping structures for least-weight. In Proceedings of the IASS Symposium, Conceptual Design of Structures, Stuttgart, Germany, 7–11 October 1996. [Google Scholar]
- Samyn, P. Etude Comparée du Volume et du Déplacement de Structures Bidimensionnelles, Sous Charges Verticales Entre Deux Appuis, Vers un Outil D’évaluation et de Prédimensionnement des Structures; Université de Liège: Liège, Belgium, 1999. [Google Scholar]
- Van Steirteghem, J. A Contribution to the Optimisation of Structures Using Morphological Indicators. Ph.D. Thesis, Vrije Universiteit Brussel, Brussels, Belgium, 2006. [Google Scholar]
- Vandenbergh, T.; De Wilde, W.P.; Latteur, P.; Verbeeck, B.; Ponsaert, W.; Van Steirteghem, J. Influence of stiffness constraints on optimal design of trusses using morphological indicators. In Proceedings of the WIT Transactions on the Built Environment—High Performance Structures and Materials III; WIT Press: Southampton, UK, 2006; Volume 85, pp. 31–40. [Google Scholar]
- De Wilde, W.P. Conceptual design of lightweight structures: The role of morphological indicators and the structural index. In Proceedings of the WIT Transactions on the Built Environment—High Performance Structures and Materials III; WIT Press: Southampton, UK, 2006; Volume 85, pp. 3–12. [Google Scholar]
- Verbeeck, B.; Van Steirteghem, J.; De Wilde, W.P.; Samyn, P. The use of genetic algorithms and morphological indicators in the optimization of 2D trusses. In Proceedings of the WIT Transactions on the Built Environment—High Performance Structures and Materials II; Brebbia, C.A., De Wilde, W.P., Eds.; WIT Press: Southampton, UK, 2004; Volume 7, pp. 571–577. [Google Scholar]
- Latteur, P. Optimisation et Prédimensionnement des Treillis, Arcs, Poutres et Câbles sur Base D’indicateurs Morphologiques—Application Aux Structures Soumises en Partie ou en Totalité au Flambement. Ph.D. Thesis, Vrije Universiteit Brussel, Ixelles, Belgium, 2000. [Google Scholar]
- Mathworks Matlab. Available online: https://nl.mathworks.com/products/matlab.html (accessed on 22 December 2021).
- International Organization for Standardization; International Electrotechnical Commission. Systems and Software Engineering—Systems and Software Quality Requirements and Evaluation (SQuaRE)—System and Software Quality Models; International Organization for Standardization; International Electrotechnical Commission: London, UK, 2011. [Google Scholar]
- Estdale, J.; Georgiadou, E. Applying the ISO/IEC 25010 Quality Models to Software Product. In Proceedings of the Systems, Software and Services Process Improvement. EuroSPI 2018. Communications in Computer and Information Science; Larrucea; Larrucea, X., Santamaria, I., O’Connor, R., Messnarz, R., Eds.; Springer: Cham, Switzerland, 2018; Volume 896, pp. 492–503. [Google Scholar]
- European Committe for Standardisation. Eurocode 1: Actions on Structures—Part 2: Traffic Loads on Bridges; European Committe for Standardisation: Bruxelles, Belgium, 2010. [Google Scholar]
- Buildsoft Diamonds. Available online: https://buildsoft.eu/en/product/diamonds (accessed on 22 December 2021).
- Tomei, V.; Grande, E.; Imbimbo, M. Influence of geometric imperfections on the efficacy of optimization approaches for grid-shells. Eng. Struct. 2021, 228. [Google Scholar] [CrossRef]
- Anastasiades, K.; Goffin, J.; Rinke, M.; Buyle, M.; Audenaert, A.; Blom, J. Standardisation: An essential enabler for the circular reuse of construction components? A trajectory for a cleaner European construction industry. J. Clean. Prod. 2021, 298, 126864. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).