Research on K-Value Selection Method of K-Means Clustering Algorithm
Abstract
:1. Introduction
2. The K-means Algorithm
3. Research on K-Value Selection Algorithm
3.1. An Elbow Method Algorithm
| Algorithm 1: Silhouette Coefficient |
| Input: iris = datasets.load_iris(), X = iris.data [:, 2 :] |
| Output: d, k |
| 1: d = []; |
| 2: for k = 1, k in rang (1, 9) do |
| ; |
| 4: return d, k; |
3.2. The Gap Statistic Algorithm
| Algorithm 2: Gap Statistic |
| Input: iris = datasets.load_iris(), X = iris.data [:, 2 :] |
| Output: k |
| 1: def SampleNum, P, MaxK, u, sigma; |
| 2: SampleSet = []; |
| 3: size (u) = [uM, ]; |
| 4: for i = 1 : uM do 5: SampleSet = [SampleSet; mvnrnd(u(i, :), sigma, fix(SampleNum/uM))]; |
| 6: Wk = log(CompuWk(SampleSet, MaxK)); |
| 7: for b = 1 : P do 8: Wkb = log(CompuWk(RefSet(:, :, b), MaxK)); |
| 9: for k = 1 : MaxK, OptimusK = 1 do 10: Gapk = (); |
| 11: Gapk <= Gapk−1 + s(k), OptimusK == 1; |
| 12: OptimusK = k – 1; |
| 13: retuern k; |
3.3. The Silhouette Coefficient Algorithm
| Algorithm 3: Silhouette Coefficient |
| Input: iris = datasets.load_iris(), X = iris.data [:, 2 :] |
| Output: S(i), k |
| 1: def i in X, C, D; |
| ; |
| CDdo |
| ; |
| ; 6: if a(i) = b(i), S(i) = 0; ; |
| 8: for k = 2, 3, 4, 5, 6 do 9: lables = KMeans(n_clusters = k).fix(x).lables_; |
| 10: retuern S(i), k; |
3.4. The Canopy Algorithm
| Algorithm 4: Canopy |
| Input: iris = datasets.load_iris(), X = iris.data [:, 2 :] |
| Output: k |
| 1: def T1, T2, T1 > T2; delete_X = []; Canopy_X = []; |
| Xdo |
| ; |
| 4: if d < T2 then 5: delete_X = [d]; 6: else Canopy_X = [d]; |
| 7: until X = Φ; 8: end; |
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Zhai, D.; Yu, J.; Gao, F.; Lei, Y.; Feng, D. K-means text clustering algorithm based on centers selection according to maximum distance. Appl. Res. Comput. 2014, 31, 713–719. [Google Scholar]
- Sun, J.; Liu, J.; Zhao, L. Clustering algorithm research. J. Softw. 2008, 19, 48–61. [Google Scholar] [CrossRef]
- Li, X.; Yu, L.; Hang, L.; Tang, X. The parallel implementation and application of an improved k-means algorithm. J. Univ. Electron. Sci. Technol. China 2017, 46, 61–68. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 0–892. [Google Scholar] [CrossRef]
- Wagstaff, K.; Cardie, C.; Rogers, S.; Schrödl, S. Constrained k-means clustering with background knowledge. In Proceedings of the Eighteenth International Conference on Machine Learning, Williamstown, MA, USA, 28 June–1 July 2001; pp. 577–584. [Google Scholar]
- Huang, Z. Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min. Knowl. Discov. 1998, 24, 283–304. [Google Scholar] [CrossRef]
- Narayanan, B.N.; Djaneye-Boundjou, O.; Kebede, T.M. Performance analysis of machine learning and pattern recognition algorithms for Malware classification. In Proceedings of the 2016 IEEE National Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS), Dayton, OH, USA, 25–29 July 2016; pp. 338–342. [Google Scholar]
- Narayanan, B.N.; Hardie, R.C.; Kebede, T.M.; Sprague, M.J. Optimized feature selection-based clustering approach for computer-aided detection of lung nodules in different modalities. Pattern Anal. Appl. 2019, 22, 559–571. [Google Scholar] [CrossRef]
- Narayanan, B.N.; Hardie, R.C.; Kebede, T.M. Performance analysis of a computer-aided detection system for lung nodules in CT at different slice thicknesses. J. Med. Imag. 2018, 5, 014504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Wang, C.; Feng, Z.; Ye, J. Review of K-means clustering algorithm. Electron. Des. Eng. 2012, 20, 21–24. [Google Scholar]
- Ravindra, R.; Rathod, R.D.G. Design of electricity tariff plans using gap statistic for K-means clustering based on consumers monthly electricity consumption data. Int. J. Energ. Sect. Manag. 2017, 2, 295–310. [Google Scholar]
- Han, L.; Wang, Q.; Jiang, Z.; Hao, Z. Improved K-means initial clustering center selection algorithm. Comput. Eng. Appl. 2010, 46, 150–152. [Google Scholar]
- UCI. UCI Machine learning repository. Available online: http://archive.ics.uci.edu/ml/ (accessed on 30 March 2019).
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Statist. Soc. Ser. B (Statist. Methodol.) 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Xiao, Y.; Yu, J. Gap statistic and K-means algorithm. J. Comput. Res. Dev. 2007, 44, 176–180. [Google Scholar]
- Kaufmn, I.; Rousseeuw, P.J. Finding Groups in Data an Introduction to Cluster Analysis; New York John Wiley&Sons: Hoboken, NY, USA, 1990. [Google Scholar]
- Esteves, K.M.; Rong, C. Using Mahout for clustering Wikipedia’s latest articles: A comparison between K-means and fuzzy c-means in the cloud. In Proceedings of the 2011 Third IEEE International Conference on Science, Cloud Computing technology and IEEE Computer Society, Washington, DC, USA, 29 November–1 December 2011; pp. 565–569. [Google Scholar]
- Yu, C.; Zhang, R. Research of FCM algorithm based on canopy clustering algorithm under cloud environment. Comput. Sci. 2014, 41, 316–319. [Google Scholar]
- Mccallum, A.; Nigam, K.; Ungar, I.H. Efficient clustering of high-dimensional data sets with application to reference matching. In Proceedings of the Sixth ACM SIUKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 169–178. [Google Scholar]
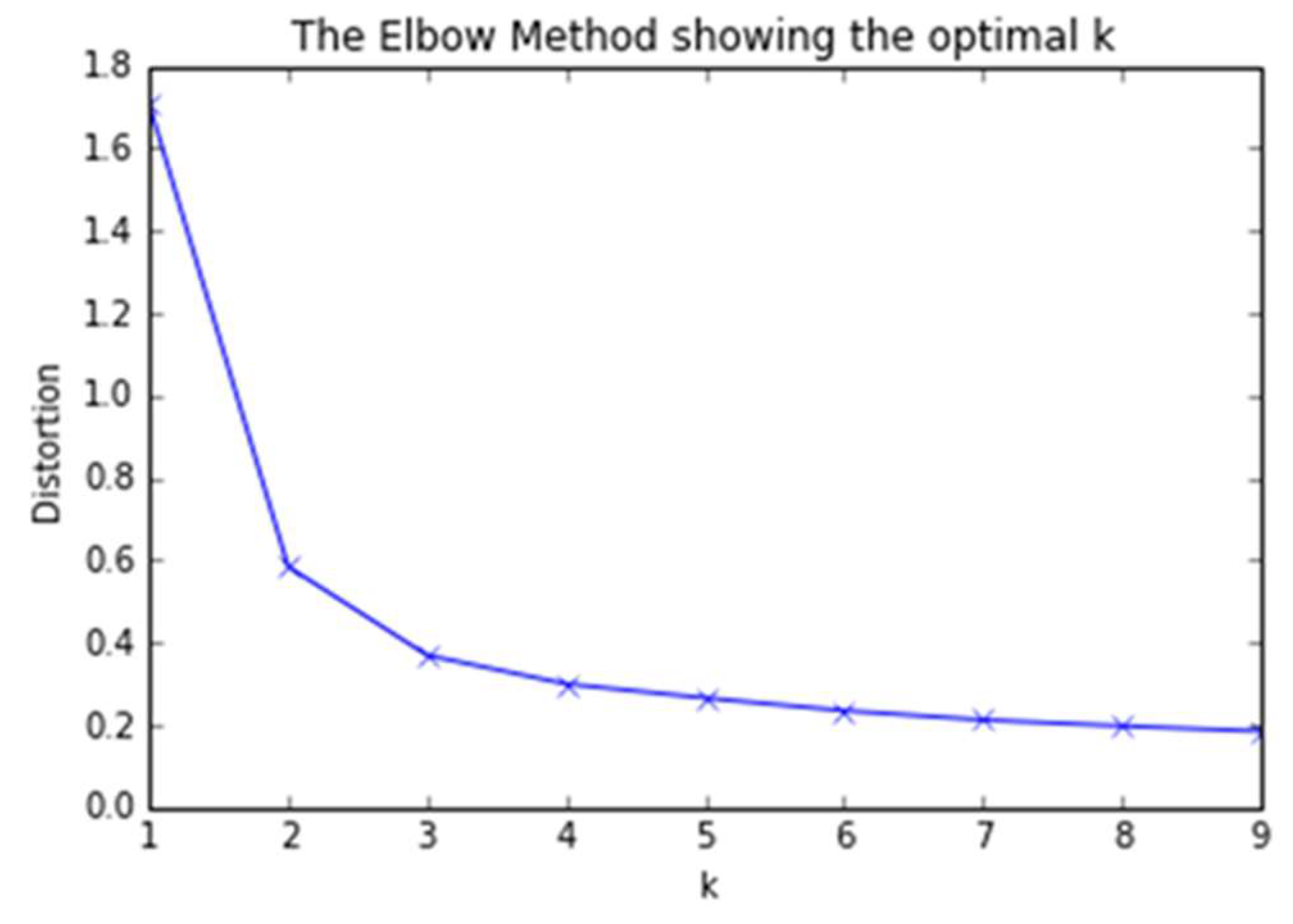
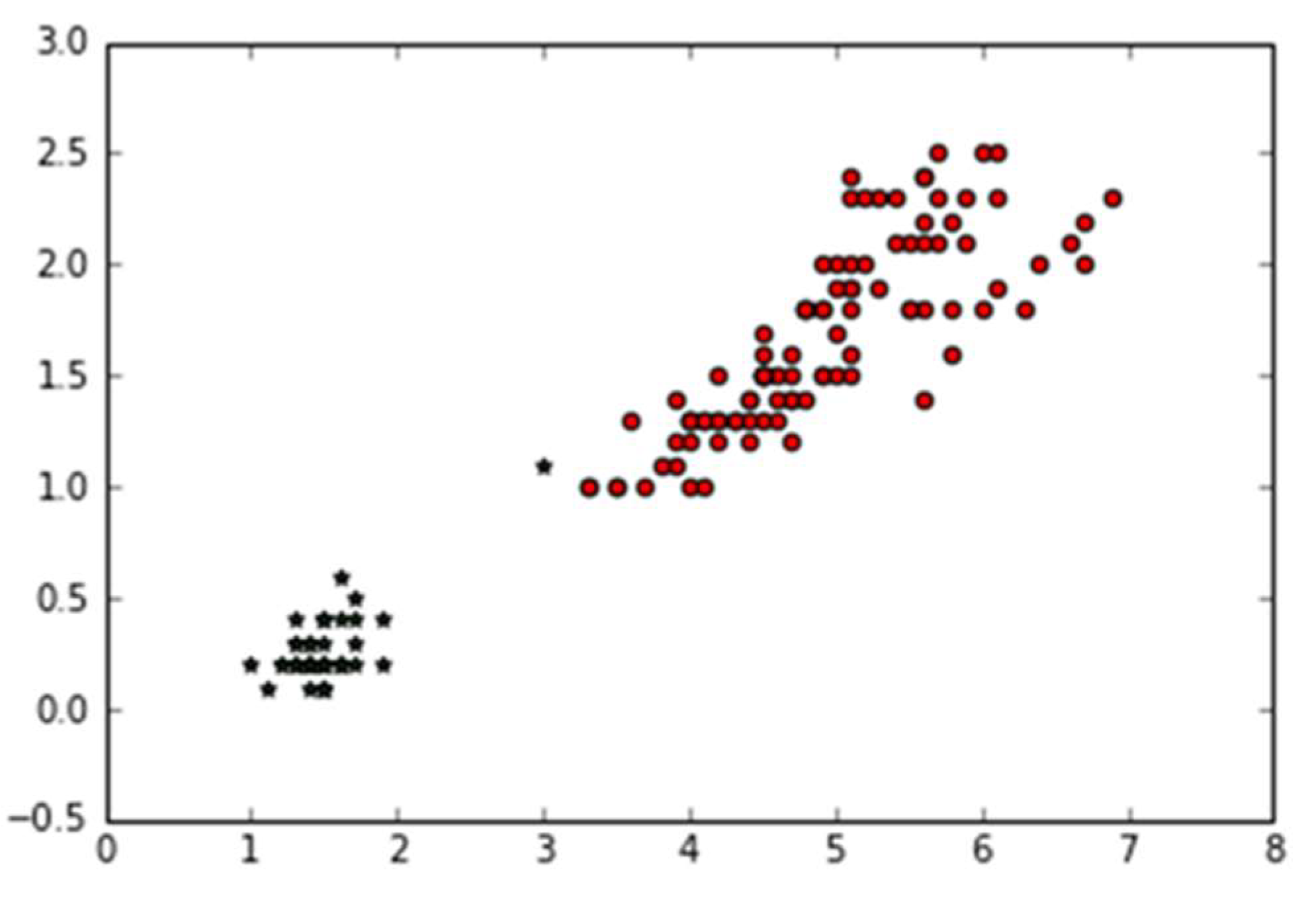

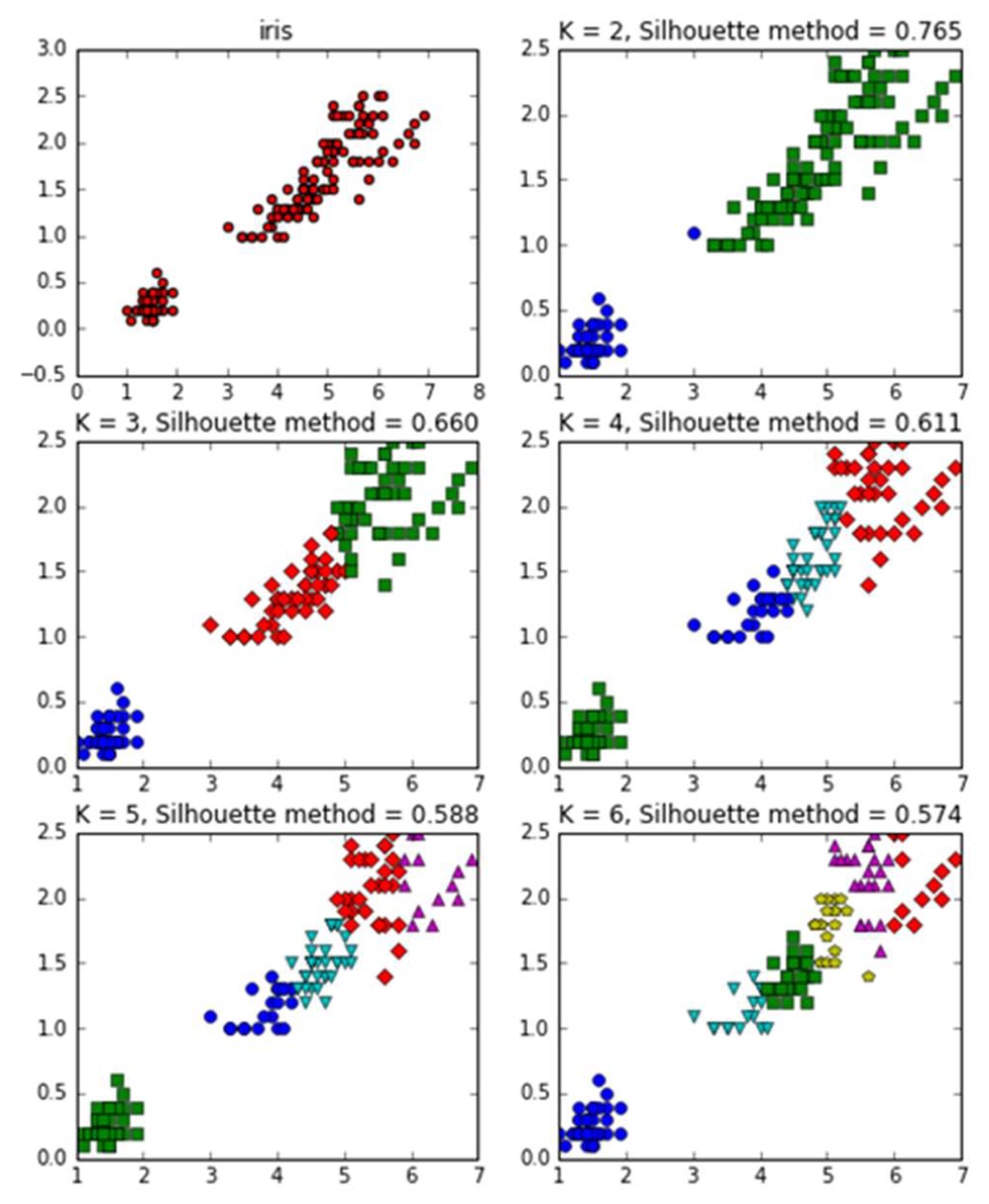
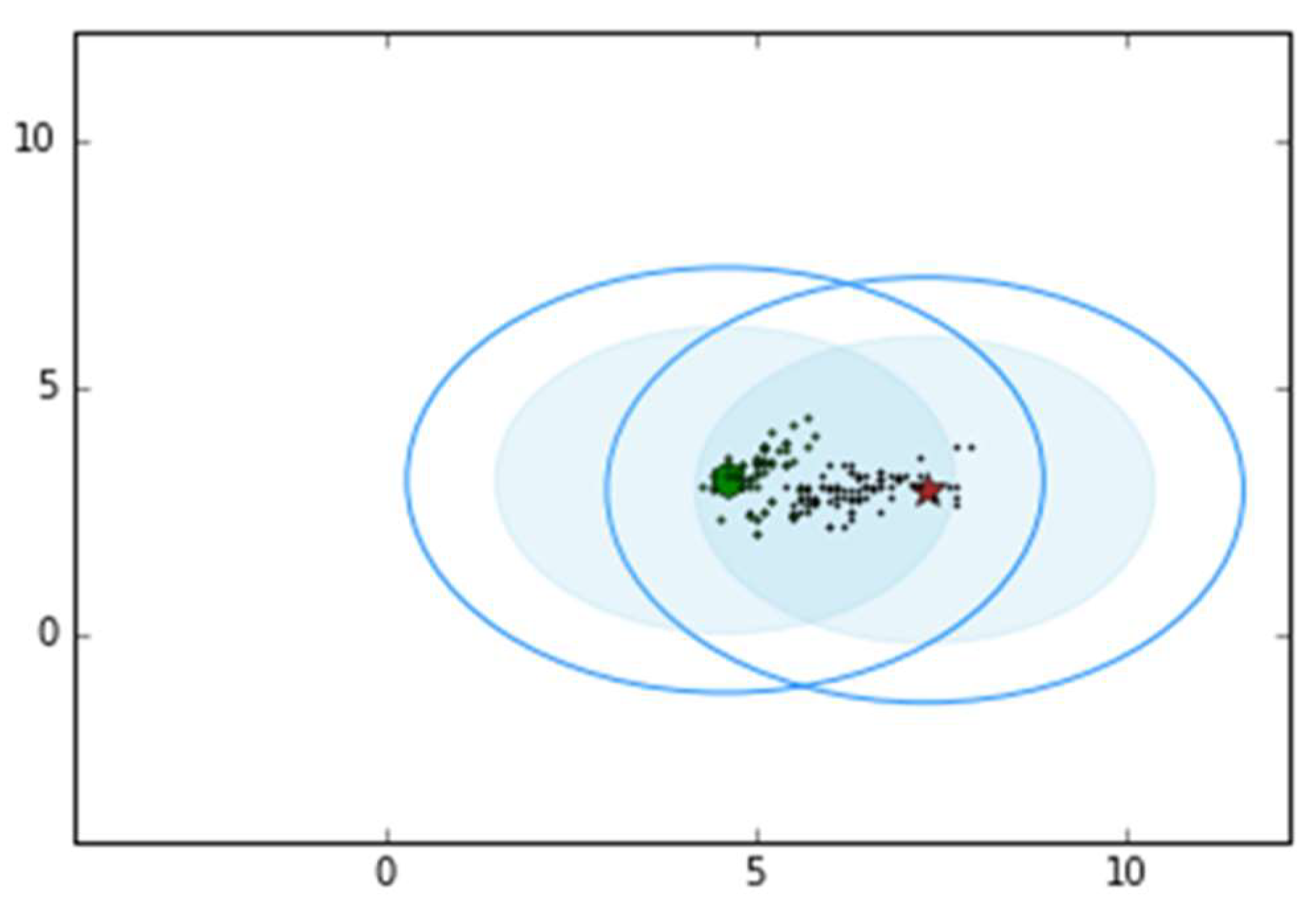
| No. | Name | K value | Execution Time |
|---|---|---|---|
| 1 | Elbow Method | 2 | 1.830 s |
| 2 | Gap Statistic | 2 | 9.763 s |
| 3 | Silhouette Coefficient | 2 | 8.648 s |
| 4 | Canopy | 2 | 2.120 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, C.; Yang, H. Research on K-Value Selection Method of K-Means Clustering Algorithm. J 2019, 2, 226-235. https://doi.org/10.3390/j2020016
Yuan C, Yang H. Research on K-Value Selection Method of K-Means Clustering Algorithm. J. 2019; 2(2):226-235. https://doi.org/10.3390/j2020016
Chicago/Turabian StyleYuan, Chunhui, and Haitao Yang. 2019. "Research on K-Value Selection Method of K-Means Clustering Algorithm" J 2, no. 2: 226-235. https://doi.org/10.3390/j2020016
APA StyleYuan, C., & Yang, H. (2019). Research on K-Value Selection Method of K-Means Clustering Algorithm. J, 2(2), 226-235. https://doi.org/10.3390/j2020016





