Genetic diversity of germplasm is assessed by collecting key information, especially: (i) Allele number per locus; (ii) genotype number per locus; (iii) gene diversity; (iv) PIC (polymorphism information content) values; (v) observed and expected heterozygosity; (vi) partition of the diversity into its components within and between populations; and (vii) the genetic distance among the analyzed populations. The analyses are usually performed using a variety of molecular markers grouped into two categories: Co-dominant markers, such as SSR (single sequence repeat) and SNP (single nucleotide polymorphism), which are able to identify the allelic situation at each locus, and dominant markers, such as ISSR (inter simple sequence repeats), RAPD (random amplified polymorphic DNA), and AFLP (amplified fragment length polymorphism), which usually have a multi-band pattern and are unable to recognize allelic variants [
1]. The latter produce a series of bands with unknown relationships (i.e., could be allelic variants of the same genes or mark different genome regions). Hence, without knowing the allelic situation, each band is recorded as a locus with two possible alleles’ band presence (scored as 1) or band absence (scored as 0) and the relative 0/1 matrix is used in statistical analyses. The papers reviewed here comprise data based on co-dominant markers that were often wrongly recorded as the presence/absence of possible bands, leading to a loss of information on allelic variance and the presence of heterozygosity (observed heterozygosity, Ho).
The present paper offers a short and simple guide to the principles that form the base of the most common analyses. It focuses on some of the most widely-used computer programs in population genetics, run under Windows, to highlight the advantages and disadvantages of the various software packages, thus facilitating appropriate selection and use.
1.1. Hardy–Weinberg Principle
Most of the statistical computations use parameters based on the Hardy–Weinberg principle [
2,
3]. Here, the basis of the principle and its applications are highlighted. As it is widely known, the Hardy–Weinberg principle considers the genetic and genotype frequency for a single locus in a population and states: “
allele and genotype frequencies in a population will remain constant from generation to generation in the absence of other evolutionary influences”. These potential evolutionary forces include: (i) Migration, (ii) mutation, (iii) selection, (iv) population size sufficient to avoid drift, and (v) random mating. Unfortunately, this definition of the Hardy–Weinberg does not sufficiently focus on other important consequences of the principle such as: “
if a population is in equilibrium it is possible to compute the allele frequencies knowing the genotype frequencies and vice-versa by the formula of binomial square development i.e., (
p +
q)
2 =
p2 +
q2 + 2
pq = 1”, where
p2 is the frequency of the AA genotype,
q2 indicates the aa genotype frequency, 2
pq the Aa genotype frequency,
p the A allele frequency, and
q the a allele frequency. This equation is true only for a population in the Hardy–Weinberg equilibrium where it is possible to compute allele frequencies from knowing the genotype frequencies and vice versa. The above is if only two alleles, A and a, are possible for that locus. If, instead, three alleles may occur at a locus, the formula would be a trinomial square development ((
p +
q +
r)
2 =
p2 +
q2 +
r2 + 2
pq + 2
pr + 2
qr = 1) and so on for higher numbers of alleles. It should be noted that the square terms (i.e.,
p2 +
q2 +
r2, etc.) are homozygote frequencies while the others (i.e., 2
pq + 2
pr + 2
qr, etc.) are heterozygotes. Considering several alleles,
I, with a frequency,
pi, the homozygote frequency is Ʃ
pi2 and heterozygote frequency can be calculated as the complementary difference from the homozygote frequency (i.e., 2
pq = 1 − (
p2 +
q2) or 1 − Ʃ
pi2).
1.2. Genetic Diversity
The gene diversity index is calculated for each locus and population according to Nei [
4], utilizing the Hardy–Weinberg formula,
, hereafter simplified as
He = 1 − Ʃ
pi2, which is the heterozygosity expected if the population is in Hardy–Weinberg equilibrium. In analogy, the genetic identity (
J) is Ʃ
pi2 (homozygotes). However, since
He could be computed for all populations, including non-random mating systems (e.g., autogamus, which, by definition, will not in Hardy–Weinberg equilibrium being a pure line with homozygosity for all loci), the terminology for
He is thus
gene diversity, rather than
expected heterozygosity.
In a small population, the alleles per locus can be skewed, especially when compared to large populations [
5]. Unbiased heterozygosity is as for the above-mentioned heterozygosity multiplied by the factor, 2
n/(2
n − 1) [
6]. As a result, the larger the population, the lower are the differences between the biased and unbiased expected heterozygosity. This detail is often not sufficiently elaborated upon in the literature, as many papers do not mention whether unbiased or biased
He is used.
The variability between and within populations can be calculated according to Nei [
4] by taking into account different allele frequencies in whole populations or only in subpopulations. The nomenclature used is:
HT for total observed diversity;
HS for within-population diversity; and
DST for the between-population diversity, with
HT =
HS +
DST.
Similarly, the Wright’s fixation indices,
FIS,
FST, and
FIT [
7], are often used, also the F-statistics are based on the expected level of heterozygosity. The measures describe the different levels of population structures, such as variance of allele frequencies within populations (
FIS), variance of allele frequencies between populations (
FST), and an inbreeding coefficient of an individual relative to the total population (
FIT), all of which are related to heterozygosity at various levels of population structure. The terms mentioned above are represented by the formula, 1 −
FIT = 1 −
FIS + 1 −
FST, where
I is the individual,
S the subpopulation, and
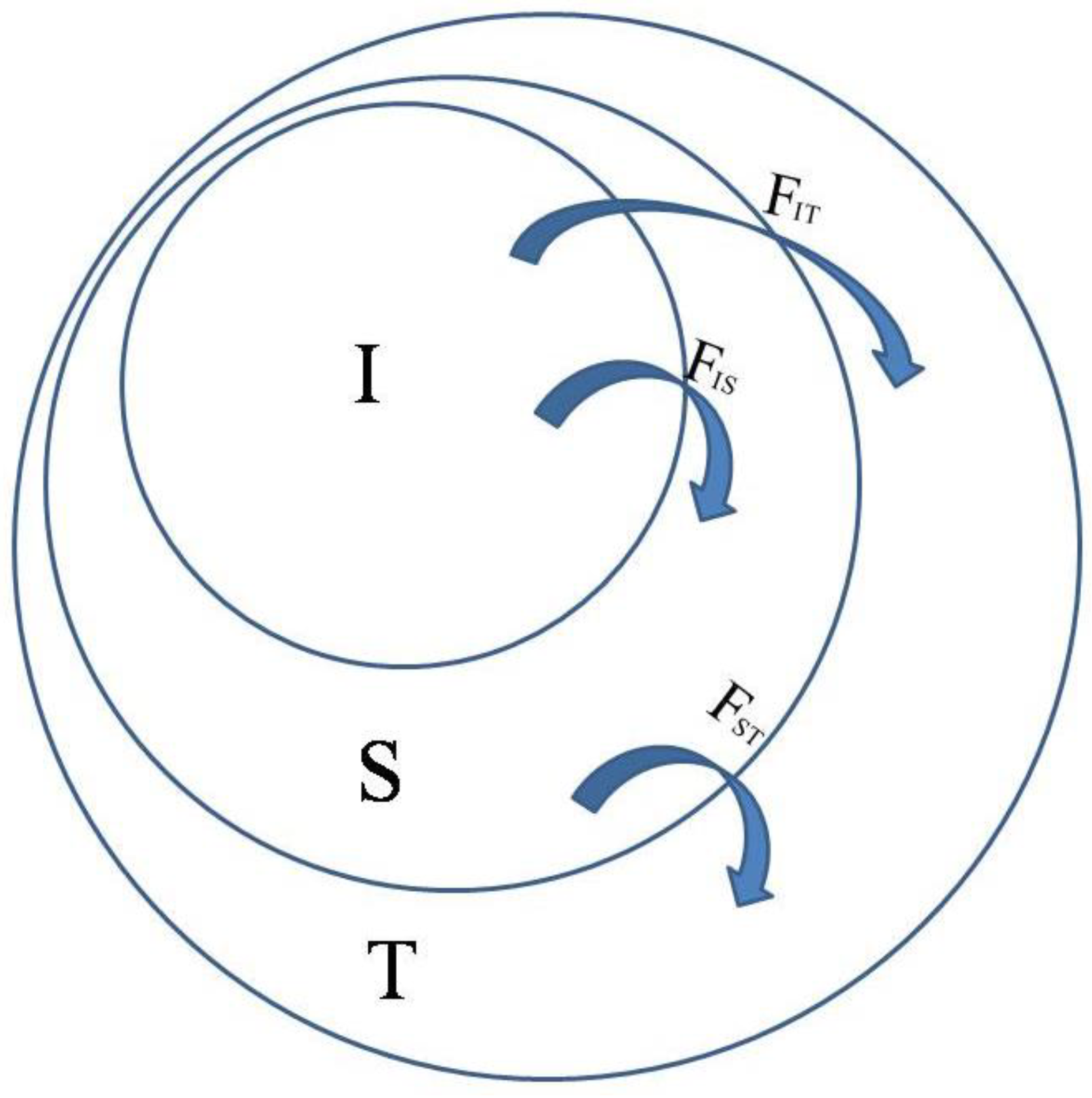
T the total population.
FIT thus refers to the individual in comparison with the total,
FIS is the individual in comparison with the subpopulation, and
FST is the subpopulation in comparison with the total. As shown in
Figure 1, total
F, indicated by
FIT, can be partitioned into
FIS (or
f) and
FST (or
θ).
FST can be calculated using the formula: FST = (HT − HS)/HT, where HT is the proportion of the heterozygotes in the total population and HS the average proportion of heterozygotes in subpopulations.
In a series of loci, l, in n populations and using the complementary sum of allele frequency (1 − Ʃpi2), different figures can be obtained. In particular:
For each locus and each population, He = (1 − Ʃpi(lg)2), where pi(lg) is the ith allele frequency of the lth locus in the gth population.
The average of the above He over populations gives the genetic diversity within a population for each locus, while the average of all the loci within a population diversity gives HS. The formula can thus be written as: HS = (Ʃl(Ʃg(1 − Ʃpi(lg)2)/g)/l), where (1 − Ʃpi(lg)2) indicates the expected heterozygosity for each locus in each population, g indicates the number of populations, and l the loci number.
The total genetic diversity, HT, is calculated using the allele frequency, pi(l), for each locus over all populations and calculating the mean over loci: HT = Ʃ(1 − Ʃpi(l)2)/l).
The between population component of diversity is calculated using the formula: DST = HT − HS.
The between population component may also be expressed in relation to the total genetic diversity (for each locus and overall loci) as
GST =
HT/
DST [
4].
Table 1 shows an example extracted from Turpeinen et al. [
8], where different parameters for three populations were analyzed using two markers. The
HT for each locus corresponds to the polymorphic information content (PIC) of that locus, which in other words, consists in the capacity of that locus (or better a marker) to assess polymorphism and diversity. Botstein et al. [
9] proposed an adjustment of this value as:
where
pi and
pj are the population frequency of the
ith and
jth alleles. The PIC proposed by Botstein and colleagues [
9] subtracts from the
He value an additional probability (ƩƩ2
pi2pj2) due to the fact that linked individuals do not add information to the overall variation.
1.3. Genetic Distance
Genetic diversity (
He) and genetic identity (
J or
Ho) are also used to estimate the genetic distance within and between populations, since two populations with high identity in their genes are closer than two with high diversity. If
Jx = Ʃ
pxi2 is the probability of identity in population
x with
pxi the frequency of the
i-th allele and
Jy = Ʃ
pyi2 is the probability of identity in population
y, the probability of identity in both populations is
Jxy = Ʃ
pxipyi as described by Nei [
10,
11]. The probability of identity in population
x for all normalized loci is
I =
Jxy/√(
JxJy) and, in turn, the genetic distance is
D = −
LnI = −
Ln (
Jxy/√(
JxJy)). In a small sample set with many loci, any biases can be corrected using
Ď = −
Ln Gxy/√(
GxGy), where
Gx and
Gy are (2
nxJx − 1)/(2
nx − 1) and (2
nyJy − 1)/(2
ny − 1) over the l loci studied, respectively, and
Gxy =
Jxy [
12]. In this case,
Ď could be negative, due to sampling errors, and hence considered as zero.
Various software packages can be used to calculate the above-mentioned parameters; they often use different parameters and have their own advantages and disadvantages. In general, for the analyses of genetic diversity, characteristics required in statistical software are: (i) Precision (no bugs), accuracy, and reproducibility; (ii) user friendliness (e.g., do not need command line scripts); (iii) clear output in terms of graphical options; and (iv) that it is open access. This paper compares some software packages that run using Microsoft Windows, which are generally used to calculate population genetic analyses. The software packages assessed are:
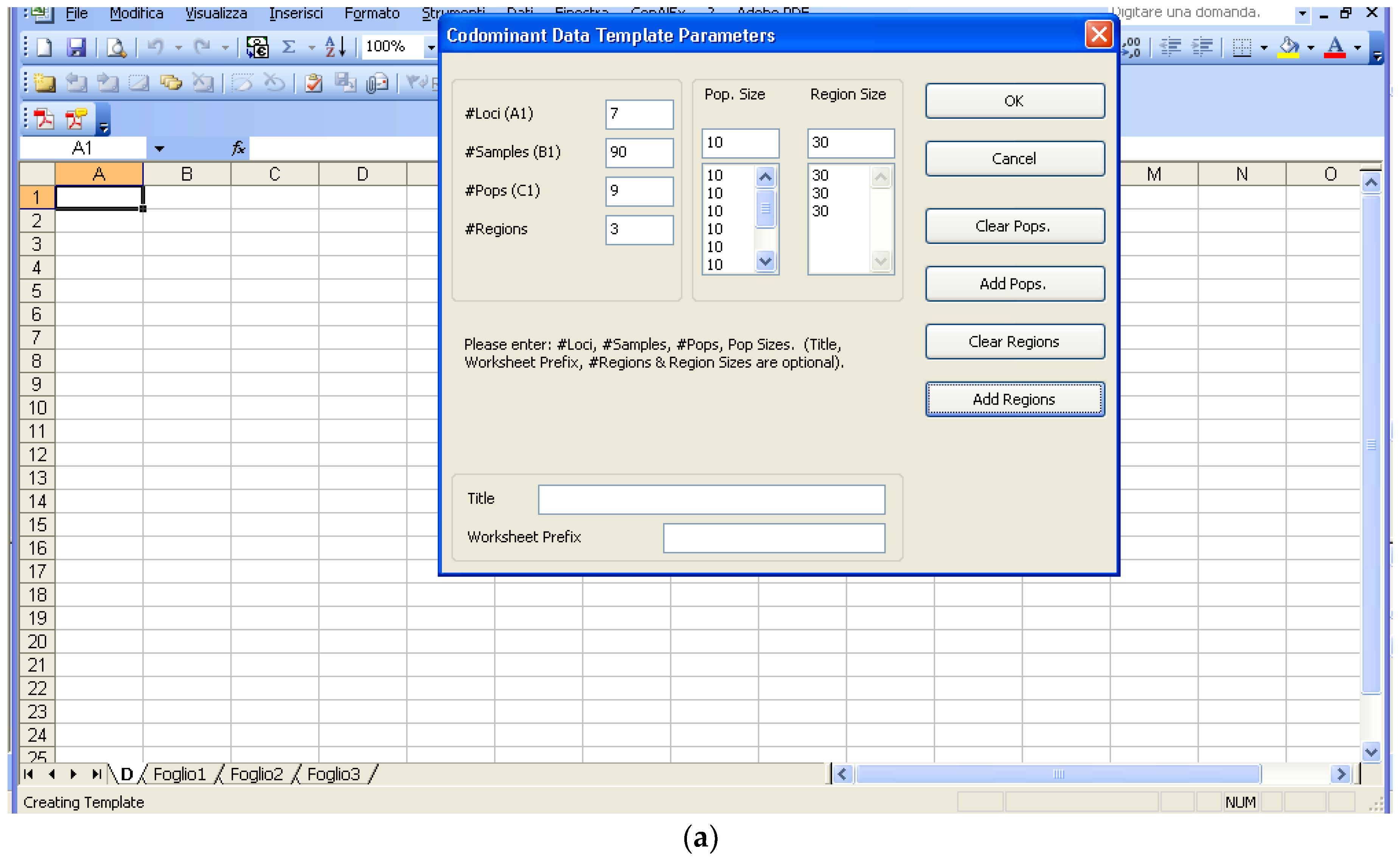
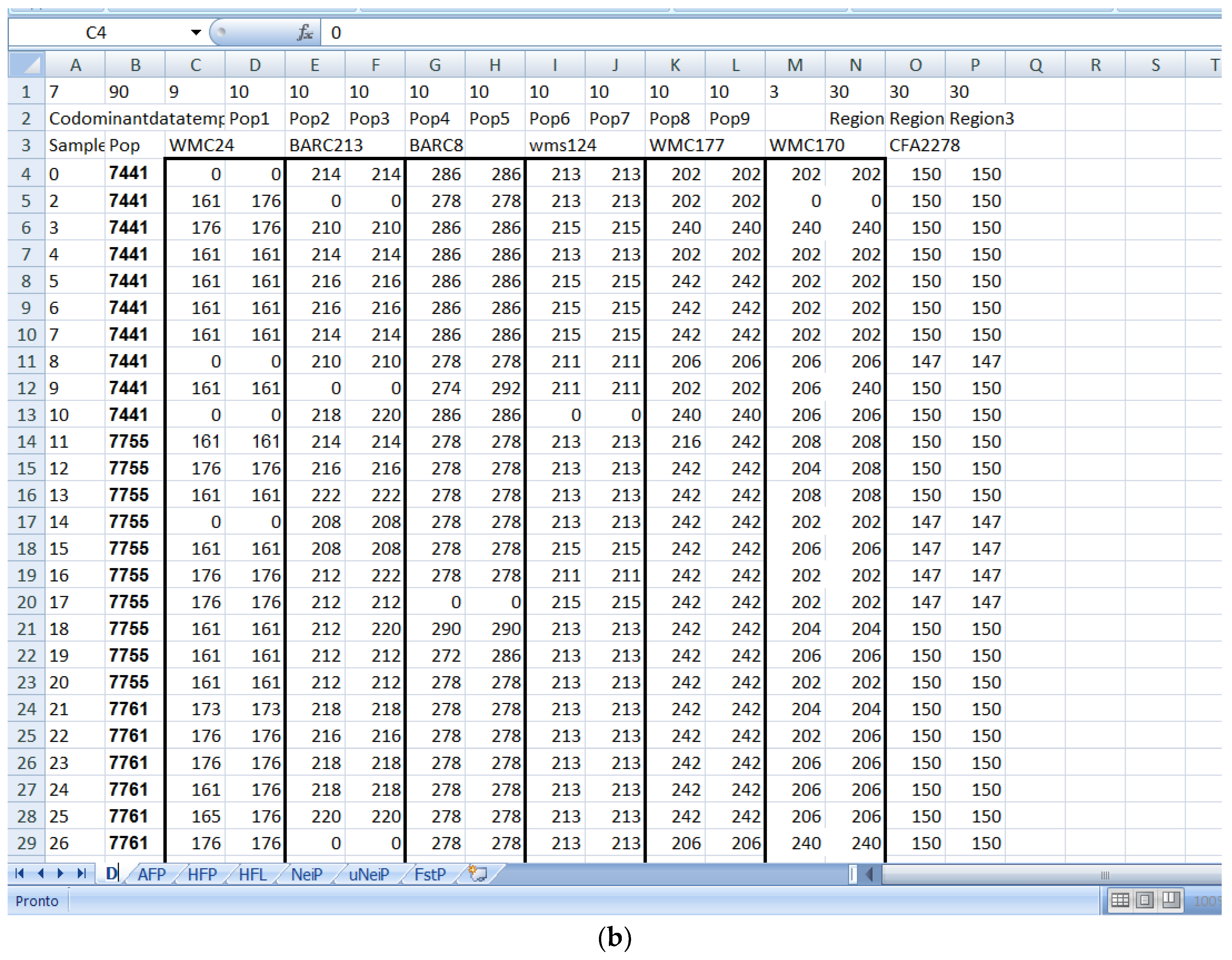
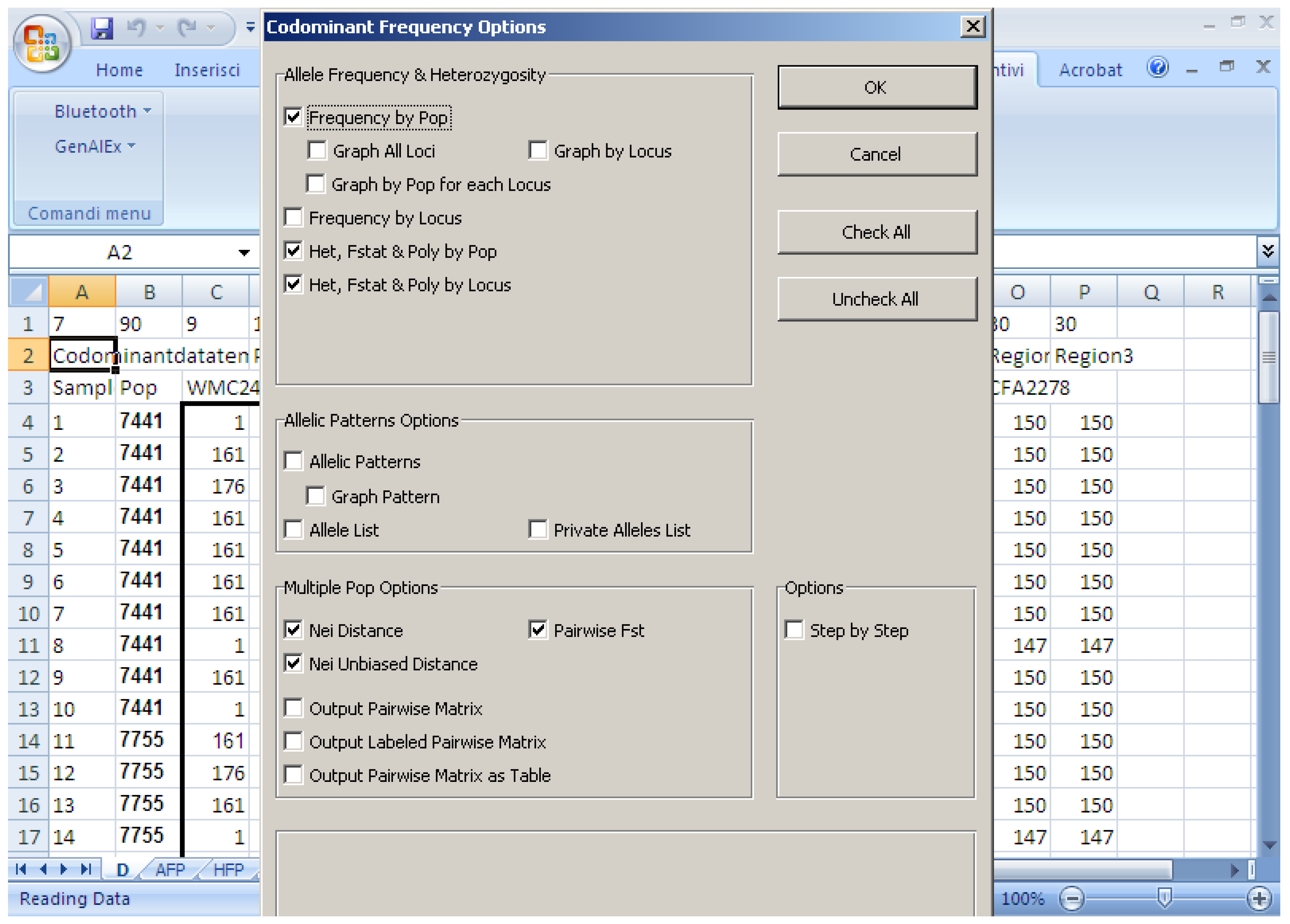
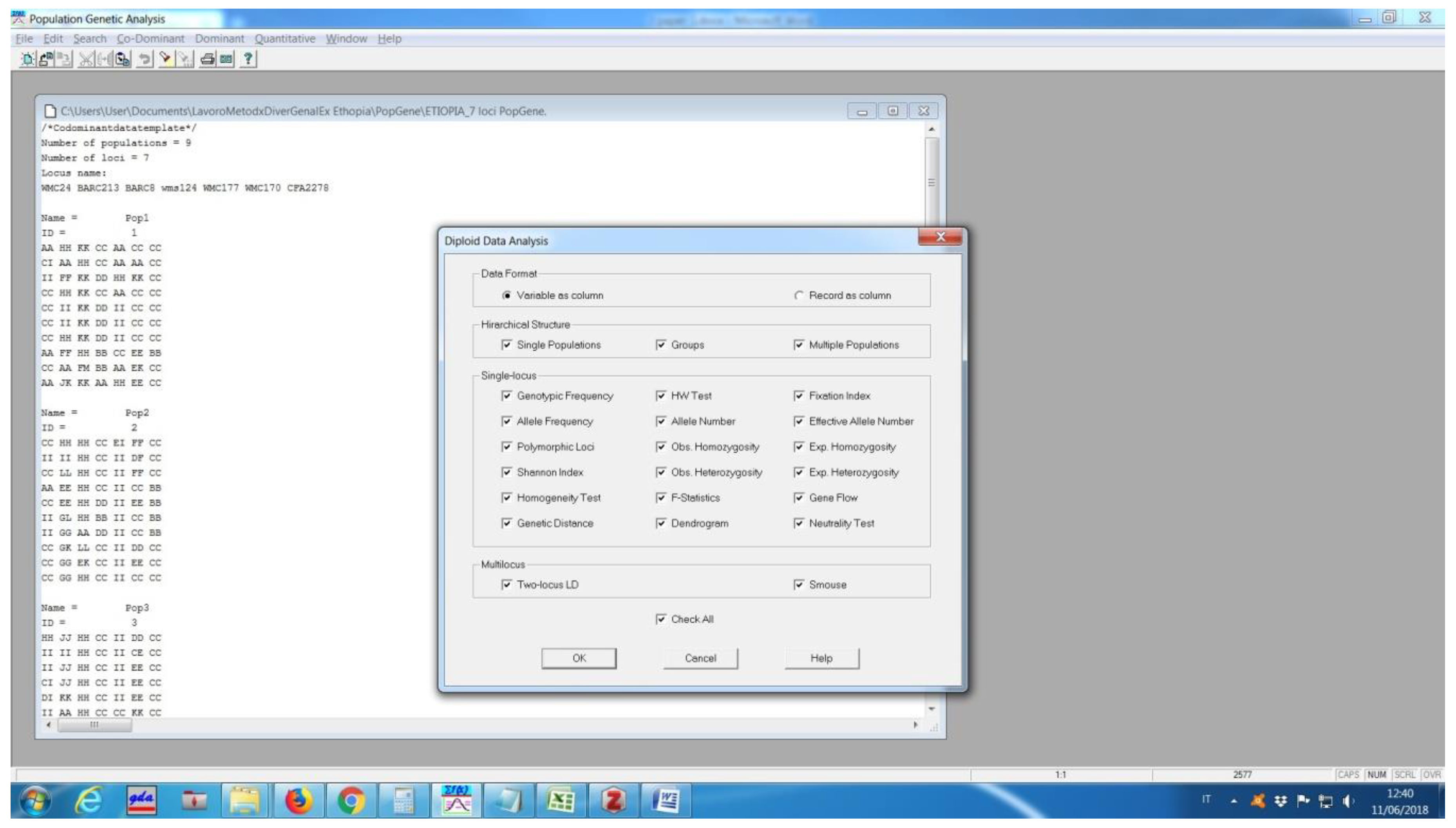
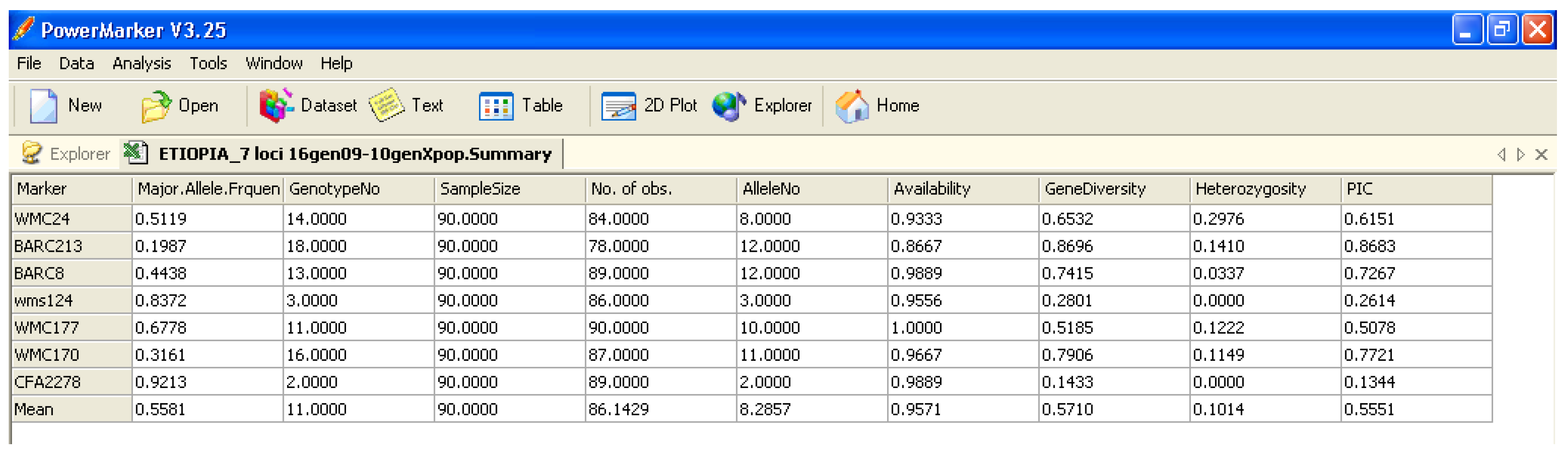
Software description and comparison is carried out using examples of data obtained with SSR markers (hence, co-dominant) on nine durum wheat populations from three Ethiopian regions as described by Mondini et al. [
20]. For the purpose of this assessment, the analyses of 10 genotypes per population are reported.