First Assessment of the Thryssa vitrirostris (Engraulidae) Beach Seine Fishery in Northeastern Mozambique
Abstract
:1. Introduction
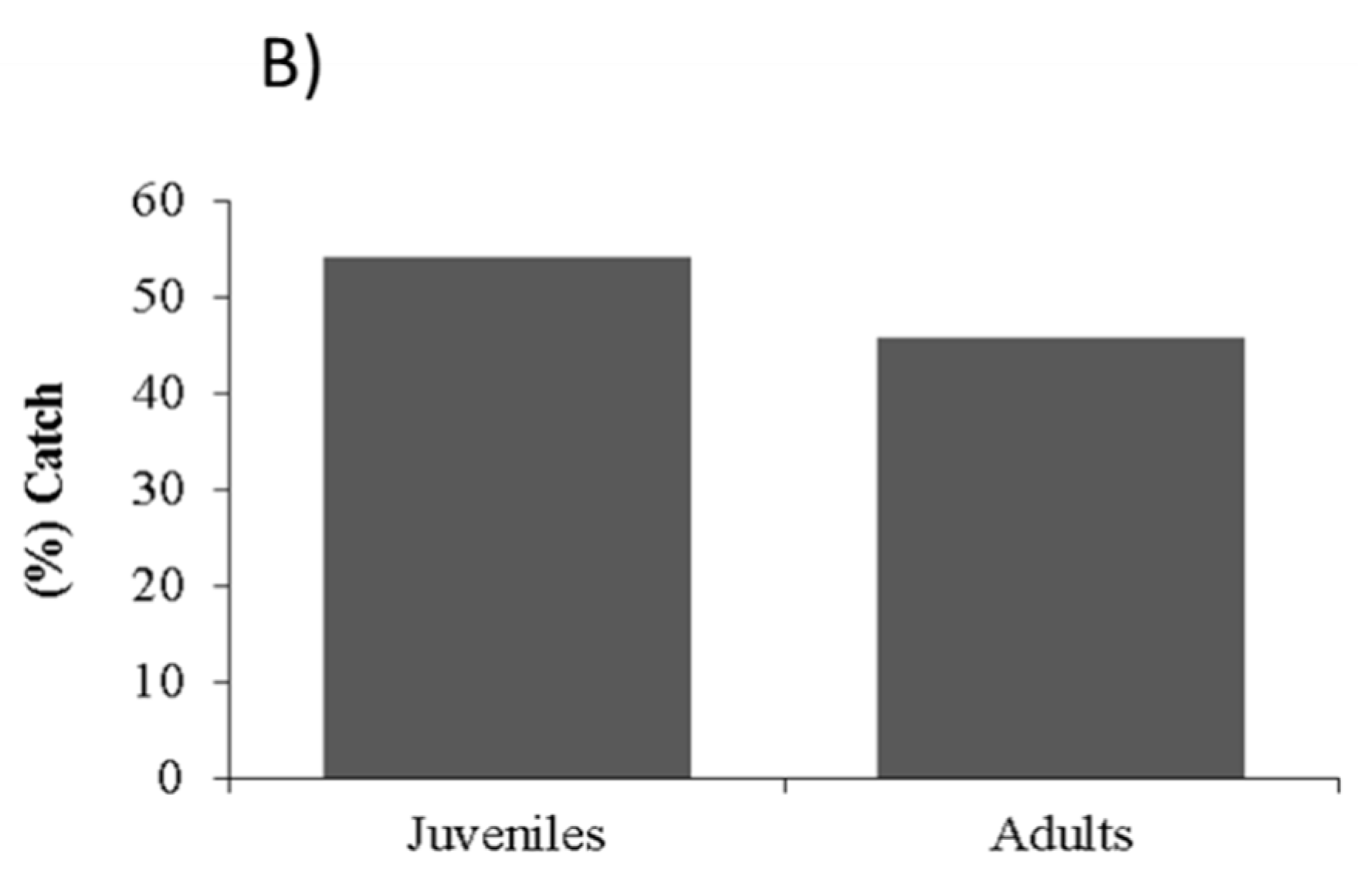
2. Results
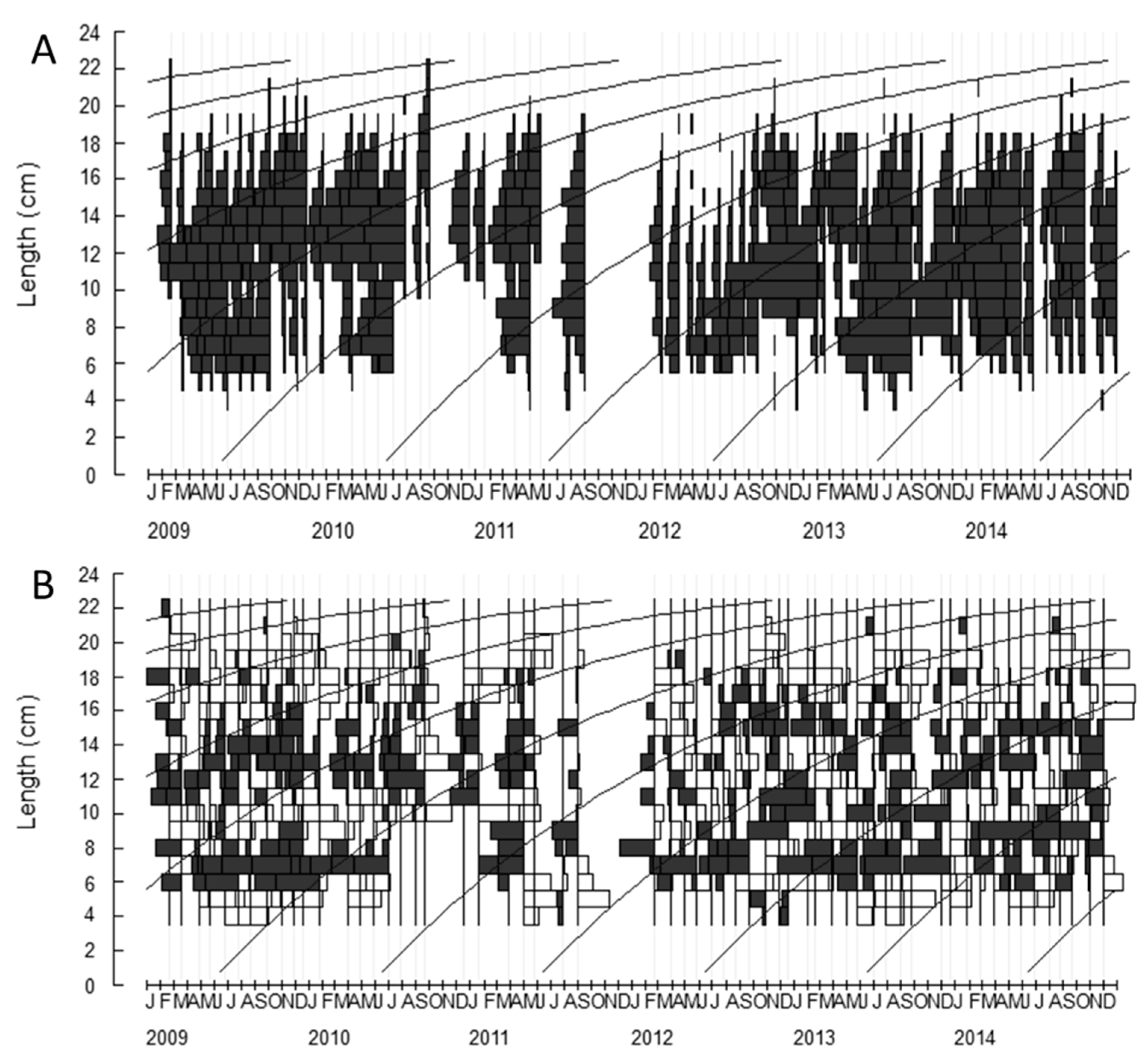
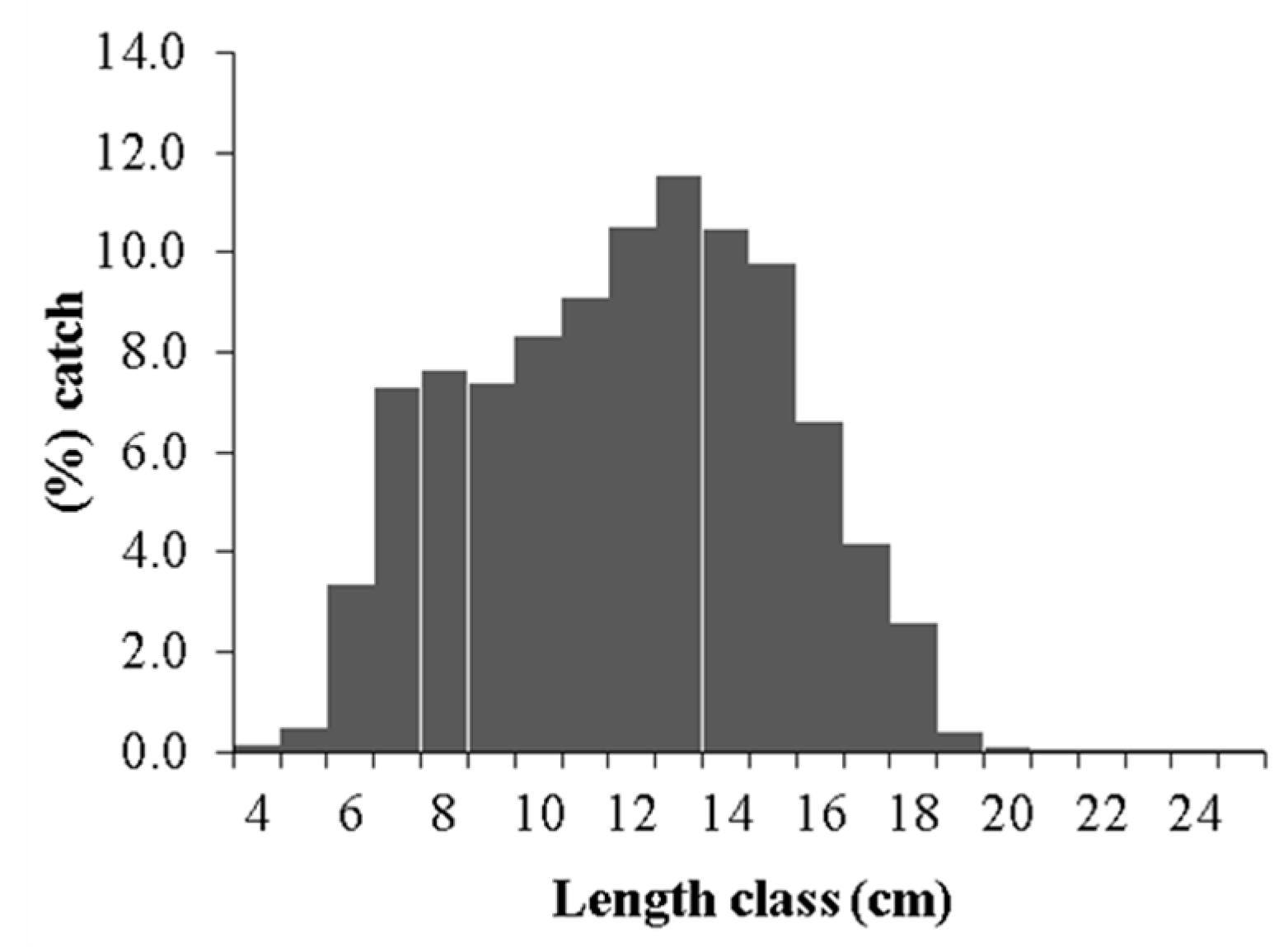
2.1. Growth Parameters
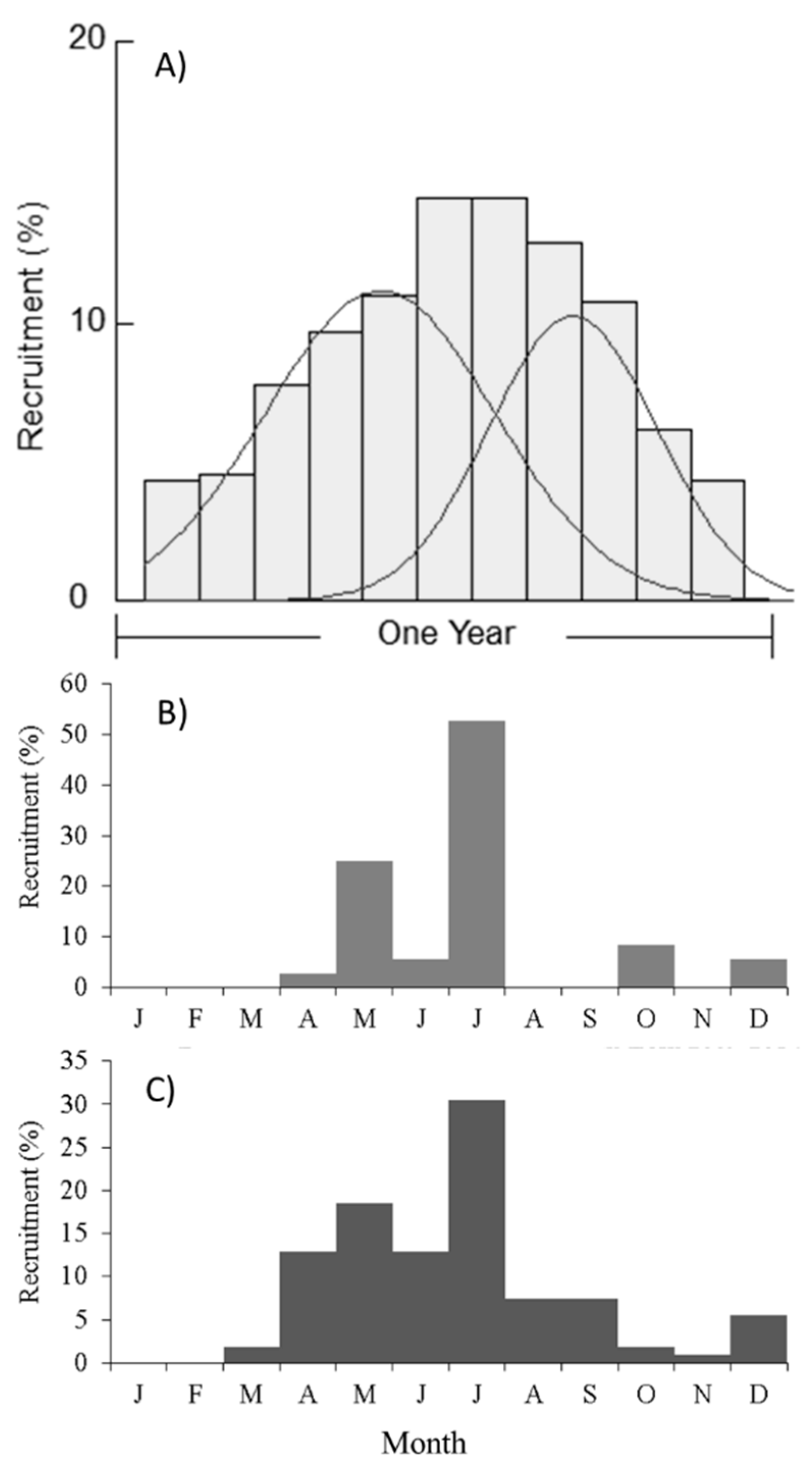
2.2. Recruitment Patterns
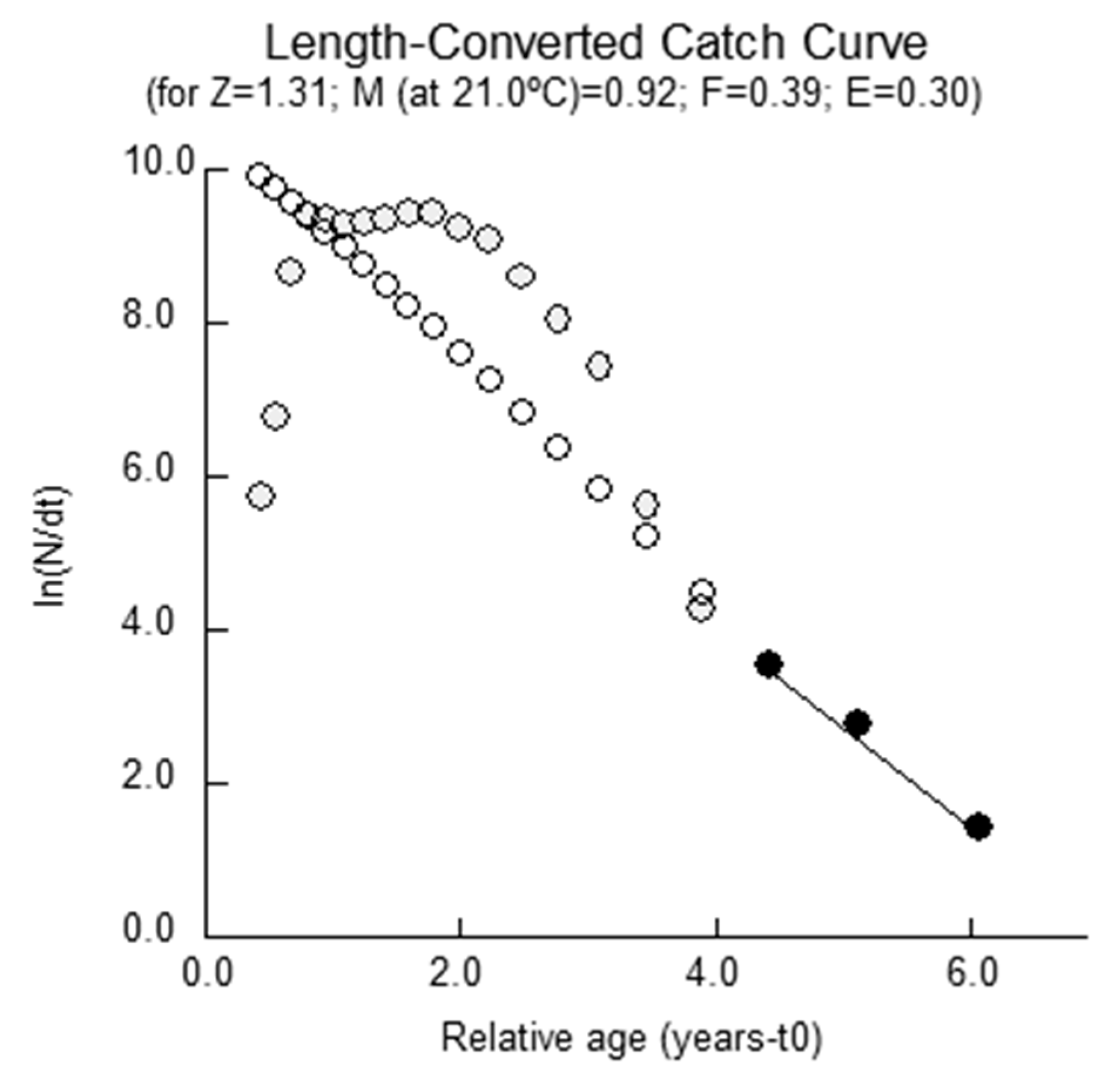
2.3. Mortality Parameters
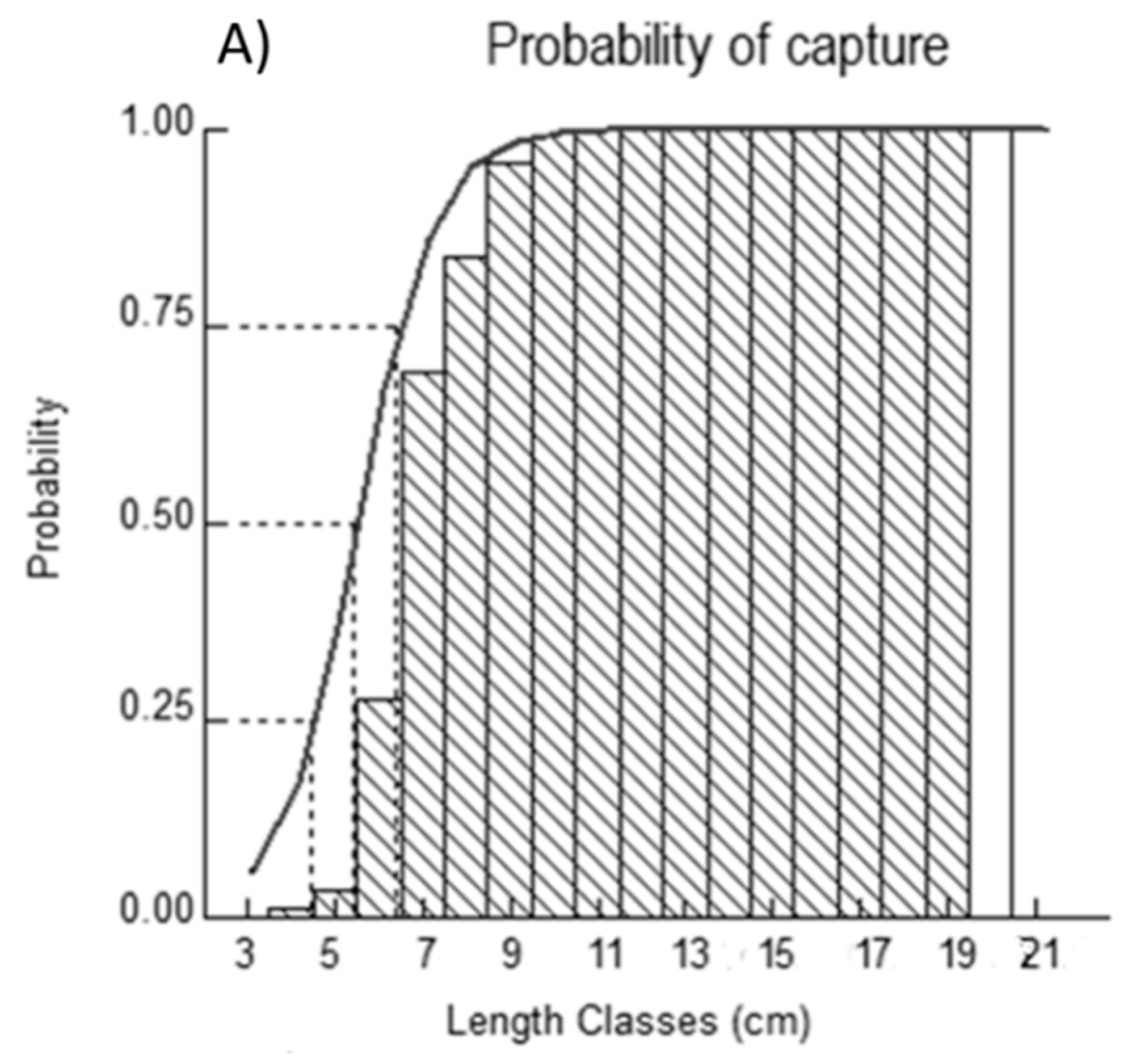
2.4. Probabilities of Capture
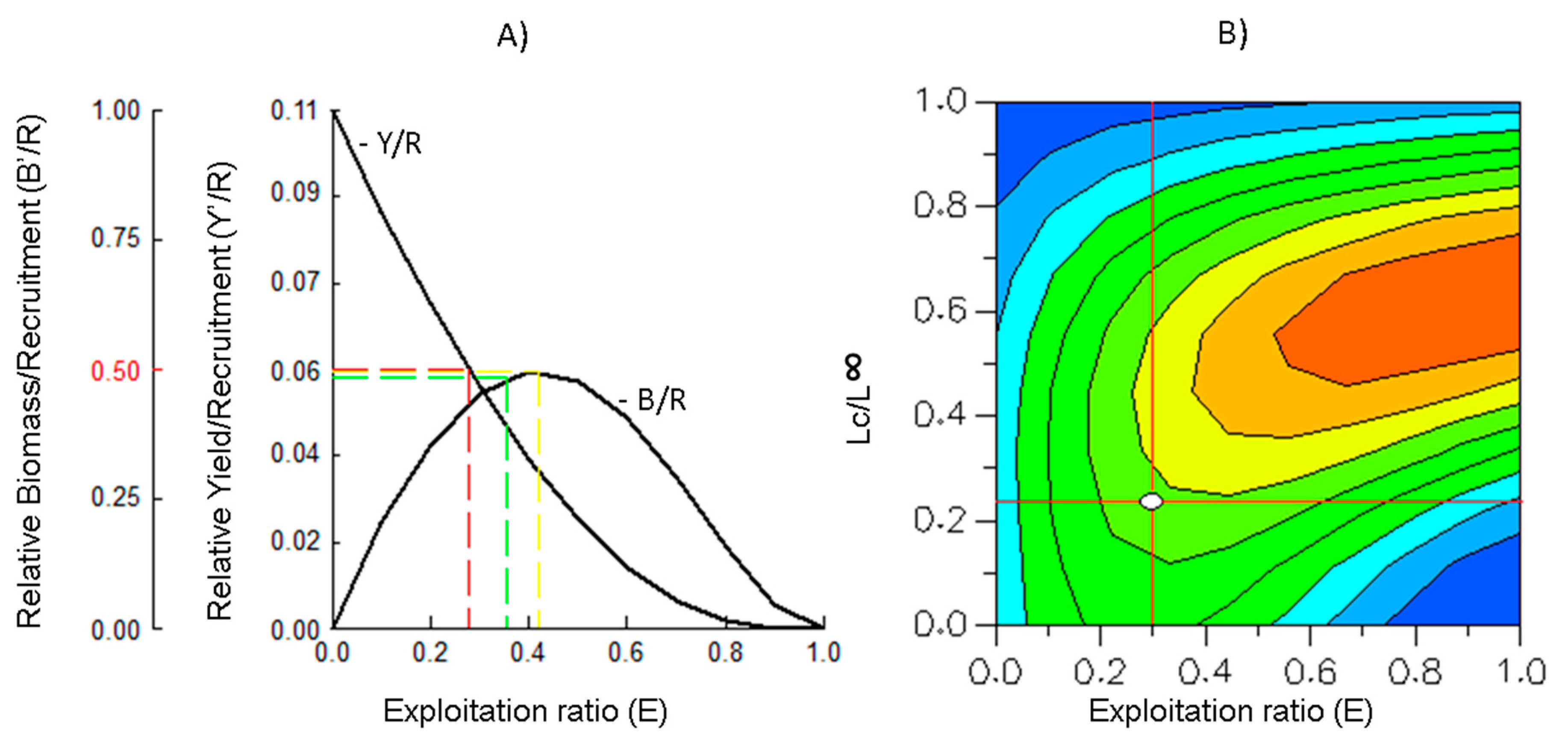
2.5. Relative Yield per Recruit (Y’/R) and Relative Biomass per Recruit (B’/R)
2.6. Yield Isopleths
3. Discussion
4. Materials and Methods
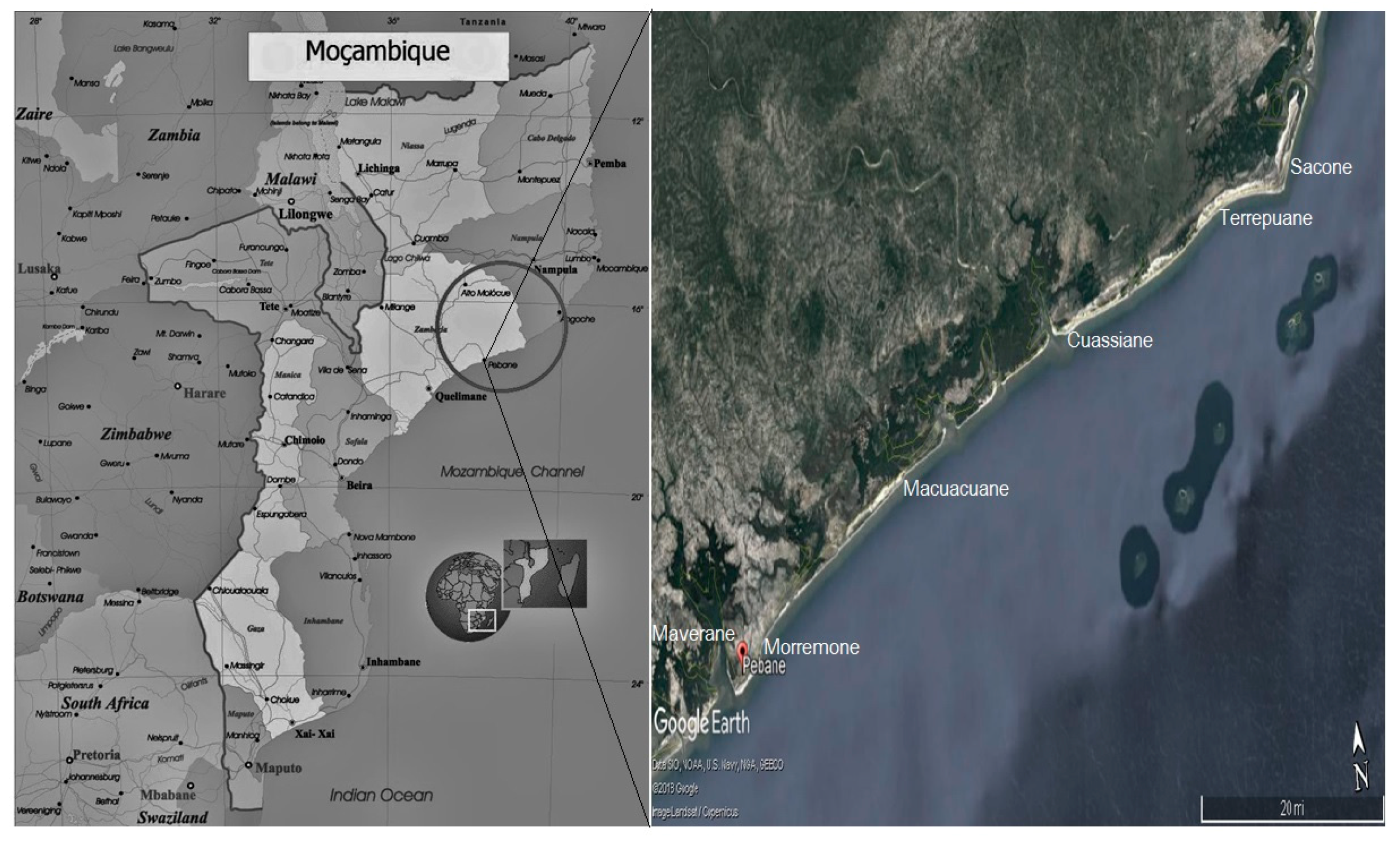
4.1. Study Area
4.2. Data Collection
4.3. Data Analysis
4.3.1. Growth Parameters
- (i)
- The Powell–Wetherall plot method was used to obtain an initial estimate of (L∞ = 27.11 cm). This method takes into consideration the distribution of length frequency, pooled against the midlength [26,44], allowing for verification of the behavior or variation of the individual sizes in relation to L∞. The mathematical model of this method is described below:Lmiddle – L′ = a + b·L′Lmiddle—is the mean length of all fish (≥L′) and was calculated as:L′ is the cutoff length, the length that once reached, the individual has maximum probability of being caught by fishing, L∞ = −a/b and Z/K = −(1 + b)/b.
- (ii)
- L∞ required for “seed” L∞ in VBF Equation (1) was determined based on the maximum length ratio observed (Lmax./0.95) in the original length frequency data (maximum observed length-class = 25 cm) according to [45].
- (iii)
- At last, the L∞ value from length frequency data was estimated using the response value routine in ELEFAN. Using the latter approach (iii), and removing the two higher length-classes, that showed an irregular distribution (frequency occurrence very low), we were able to get a good fit for the VBF growth Equation (1) and for both mortality rates and catch plot curves.
4.3.2. Growth Parameters (L∞) and Model Selection
4.3.3. Recruitment Patterns
4.3.4. Mortality Parameters
Natural Mortality
Total Mortality
4.4. Probabilities of Capture
4.5. Relative Yield per Recruit (Y’/R) and Relative Biomass per Recruit (B’/R)
4.6. Yield Isopleths
Author Contributions
Funding
Conflicts of Interest
References
- Jacquet, J.; Fox, H.; Motta, H.; Ngusaru, A.; Zeller, D. Few data but many fish: Marine small-scale fisheries catches for Mozambique. Afr. J. Mar. Sci. 2010, 32, 197–206. [Google Scholar] [CrossRef]
- Halare, A.I. Relação entre Parâmetros ambientais e distribuição temporal de dois pequenos peixes pelágicos Decapterus russelli (Rüpelli, 1930) e Amblygaster sirm (Walbaum, 1792) na Baia de Inhambane. Revista Moçambicana de Investigação Pesqueira 2012, 31, 2–22. [Google Scholar]
- Morgado, F.; Farooq, H.; Silva, I.M.; Soares, A. Artes de Pesca Artesanal e Peixes De Interesse Comercial Da Baia de Pemba; Afrontamento, Ediçoes, Ed.; Departamento de Biologia, Universidade de Aveiro: Aveiro, Portugal, 2015. [Google Scholar]
- United Nations Environment Programme (UNEP). Eastern Africa Atlas of Coastal Resources: Tanzania; United Nations Environment Programme (UNEP): Nairobi, Kenya, 2001. [Google Scholar]
- Doherty, B.; McBride, M.M.; Brito, A.J.; Le Manache, F.; Sousa, L.; Chauca, I.; Zeller, D. Marine fisheries in Mozambique: Catches updated to 2010 and taxonomic disaggregation. In Fisheries Catches Reconstruction in the Western Indian Ocean, 1950–2010; Le Manache, L., Pauly, D., Eds.; Fisheries Centre Research Report; Fisheries Centre, University of British Columbia: Vancouver, BC, Canada, 2015; Volume 23, pp. 67–82. [Google Scholar]
- Mualeque, D.; Santos, J. Biology, fisheries and distribution of Thryssa vitrirostris (Gilchrist &Thompson 1908) and other Engraulidae along the coast of the Sofala Bank, western Indian Ocean. Afr. J. Mar. Sci. 2011, 33, 127–137. [Google Scholar]
- Mualeque, D.O. Distribuição e Biologia de Ocar de Cristal (Thryssa Vitrirostris) nos Distritos de Angoche e Moma. Master’s Thesis, Universidade Apolitécnica, Maputo, Mozambique, 2008; p. 83. [Google Scholar]
- Sjösted, M.; Sundström, A. Overfishing in Southern Africa: A Comparative Account of Regime Effectiveness and National Capacities. J. Comp. Policy Anal. 2013, 15, 415–431. [Google Scholar] [CrossRef]
- Sætre, R.; de Paula e Silva, R. The Marine Fish Resources of Mozambique; Reports on surveys with the R/V Dr Fridtjof Nansen; Geological-Geophysical Atlas of the Indian Ocean (Bergen); Serviço de Investigações Pesqueiras: Maputo, Mozambique; Institute of Marine Research: Bergen, Norway, 1979; p. 134. [Google Scholar]
- Fischer, W.; Sousa, I.; Silva, C.; De Freitas, A.; Poutiers, J.M.; Schneider, W.; Borges, T.C.; Féral, J.P.; Massinga, A. Guia de Campo das Espécies Comerciais Marinhas e de Águas Salobras de Moçambique; Fichas FAO de Identificação de Espécies para Actividades de Pesca; FAO: Rome, Italy, 1990. [Google Scholar]
- FishBase. World Wide Web Electronic Publication. 2018. Available online: www.fishbase.org (accessed on 2 June 2018).
- Johnsen, E.; Krakstad, J.O.; Ostrowski, M.; Serigstad, B.; Strømme, T.; Alvheim, O.; Olsen, M.; Zaera, D.; André, E.R.; Dias, N.; et al. Surveys Of The Living Marine Resources Of Mozambique: Ecosystem Survey and Special Studies. 27 September–21 December 2007; Institute of Marine Research: Bergen, Norway, 2008. [Google Scholar]
- Sousa, M.I. Relatório do cruzeiro realizado no Banco de Sofala pelo navio “Pantikapey” de 7-23/Junho/1981: Peixes pelágicos e fauna acompanhante de Carapau e Cavala. Revista de Investigaçāo Pesqueira 1983, 4, 33–66. [Google Scholar]
- Gislason, H.; Sousa, M.I. Biology, stock size and catch of Small Pelagic Fish along the cost of Mozambique. Revista Moçambicana de Investigação Pesqueira 1985, 13, 27–81. [Google Scholar]
- Sousa, M.I.; Gjøsaeter, J. A revision of growth parameters of some commercially exploited fishes from Mozambique. Revista de Investigação Pesqueira 1987, 16, 19–40. [Google Scholar]
- Whitehead, P.J.; Nelson, G.J.; Wongratana, T. An Annotated and Illustrated Catalogue of the Herrings, Sardines, Pilchards, Sprats, Shads, Anchovies and Wolf-Herrings; Clupeoid Fishes of the World (Suborder Clupeoidei); FAO Fisheries Synopsis; FAO: Rome, Italy, 1988; p. 283. [Google Scholar]
- Wolf, M. A proposed method for standardization of the selection of class interval for length-frequency analysis. Fishbyte 1989, 7, 5. [Google Scholar]
- Hilbron, R.; Walters, C.J. Quantitative Fisheries Stock Assessment: Choice, Dynamics, and Uncertainty; Chapman & Hall: New York, NY, USA, 1992. [Google Scholar]
- Mandara, A.W.; Halare, A.I. Distribuição Temporal, Crescimento e Biologia Reprodutiva da Thryssa vitrirostris (Gilchrist and Thompson, 1908) na Praia de Zalala. Bachelor’s Thesis, Universidade Eduardo Mondlane, Maputo, Mozambique, 2010; p. 43. [Google Scholar]
- Pauly, D.; Pullin, R.S.V. Hatching time and spherical, pelagic, marine fish eggs in response to temperature and egg size. Environ. Biol. Fishes 1988, 22, 261–271. [Google Scholar] [CrossRef]
- Pepin, P. Effect of temperature and size on development, mortality, and survival rates of the pelagic early life history stages of marine fish. Can. J. Fish. Aquat. Sci. 1991, 48, 503–518. [Google Scholar] [CrossRef]
- Leitão, F.; Alms, V.; Erzini, K. A multi-model approach to evaluate the role of environmental variability and fishing pressure in sardine fisheries. J. Mar. Syst. 2014, 139, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Malauene, B.S. Shelf Edge Upwelling Off Northern Mozambique. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2010; p. 102. [Google Scholar]
- Santos, R. Fisheries in Angoche, Moma and Pebane: A Preliminary Description; WWF: Maputo, Mozambique, 2007. [Google Scholar]
- Pauly, D. Tropical fishes: Patterns and propensities. J. Fish Biol. 1998, 53, 1–17. [Google Scholar]
- Enin, U.I. First estimates of growth mortality and recruitment parameters of Macrobrachium macrobrachium Herklots 1985 in the cross River estuary. Dana 1995, 11, 29–38. [Google Scholar]
- Etim, L.; Sankare, Y. Growth and mortality, recruitment and yield of the fresh-water shrimp, Macrobrachium vollenhovenii, Herklots 1851 (Crustacea, Palaemonidae) in the Fahe reservoir, Côte d’Ivoire, West Africa. Fish. Res. 1998, 38, 211–223. [Google Scholar] [CrossRef]
- Costalago, D.; Potter, P.; Paula, P.; Strydom, N.A. Influence of environmental variables on the larval stages of anchovy, Engraulis encrasicolus, and sardine, Sardinops sagax, in Algoa Bay, South Africa. Environ. Biol. Fish 2018, 101, 225–236. [Google Scholar] [CrossRef]
- Houde, E.D.; Zastrow, C.E. Ecosystem- and taxon-specific dynamic and Energetics properties of larval Fish assemblages. Bull. Mar. Sci. 1993, 53, 290–335. [Google Scholar]
- Ismen, A. Growth, mortality and yield per recruit model of picarel (Spicara smaris L.) on the eastern Turkish Black Sea coast. Fish. Res. 1995, 22, 299–308. [Google Scholar] [CrossRef]
- Silva, J.P.C.; Santos, R.S.; Costa, M.R.; Araujo, F.G. Parâmetros de crescimento e mortalidade de Eucinostomus Argenteus (Baird & Girard, 1854) capturados no manguezal de guaratiba, Baía de Sepetiba, Rio de Janeiro. Boletim do Instituto de Pesca 2014, 40, 657–667. [Google Scholar]
- Beverton, R.J.H.; Holt, S.J. Manual of Methods for Fish Stock Assessment—Part 2: Tables of Yield Function. FAO Fisheries Technical Paper; FAO: Rome, Italy, 1966; Volume 38, pp. 7–29. [Google Scholar]
- Beverton, R.J.H.; Holt, S.J. On the Dynamics of Exploited Fish Populations; Fishery Investigation: London, UK, 1957; Volume 2, pp. 1–533. [Google Scholar]
- Pauly, D.; Soriano, M.I. Some pratical extensions to Beverton and Holt’s relative yiel-per-recruit model. In The First Asian Fisheries Forum; Maclean, J.L., Dizon, L.B., Hosillos, L.V., Eds.; Asiam Fisheries Society: Manila, Philippines, 1986; pp. 491–495. [Google Scholar]
- International Council for the Expoloration of the Sea (ICES). Report of the Working Group on Southern Horse Mackerel, Anchovy and Sardine (WGHANSA), 24–29 June 2017, Bilbao, Spain; ICES CM 2017/ACOM: 17; ICES: Copenhagen, Denmark, 2017; p. 602. [Google Scholar]
- Souto, M. Governação e Crescimento Partilhado das Pescas no Sudoeste do Oceano Índico em Moçambique (SWIOFish); Quadro de Gestão ambiental e Social (QGAS); Ministerio das Pescas: Maputo, Mozambique, 2014. [Google Scholar]
- Hoguane, A.M. Perfil Diagnóstico da Zona Costeira de Moçambique. Revista de Gestão Costeira Integrada 2007, 7, 69–82. [Google Scholar] [CrossRef]
- Instituto Nacional De Investigação Pesqueira (IIP). Manual do Amostrador da Pesca Artesanal; National Institute of Fisheries Research (IIP): Maputo, Mozambique, 2006. [Google Scholar]
- Gayanilo, F.C., Jr.; Sparre, P.; Pauly, D. FAO-ICLARM Stock Assessment Tools II (FiSAT II): User’s Guide; FAO Computerized Information Series (Fisheries); FAO: Rome, Italy, 2005; No. 8. [Google Scholar]
- Pauly, D.; David, N. Elefan—I, a Basic Program for the Objective Extraction of Growth Parameters from Length-Frequency Data. Meeresforschung 1981, 28, 205–211. [Google Scholar]
- Pauly, D.; Gaschuètz, G. A Simple Method for Fitting Oscillating Length Growth Data with a Program for Pocket Calculators; 1979/G/24; ICES Demersal Fish Committee: Copenhagen, Denmark, 1979. [Google Scholar]
- Amponsah, S.K.K.; Danson, P.K.; Nunoo, F.K.E. Fishing regime, growth, mortality and exploitation rates of Scomber Japonicus (Houttuyn, 1782) from catches landed along the eastern coastline of Ghana. Int. J. Fish. Aquat. Res. 2016, 1, 5–10. [Google Scholar]
- Gayanilo, F.C., Jr.; Pauly, D. Fisat: FAO-ICLARM Stock Assessment Tools, Reference Manual; FAO Computerized Information Series Fisheries; FAO: Rome, Italy, 1997; pp. 41–47. [Google Scholar]
- Pauly, D. A simple method for estimating the food consumption of fish populations from growth data and food conversion experiments. Fish. Bull. 1986, 84, 827–842. [Google Scholar]
- Pauly, D. Some Simple Methods for the Assessment of Tropical Fish Stocks; FAO Fisheries Technical Paper; FAO: Rome, Italy, 1983; Volume 234, pp. 1–52. [Google Scholar]
- Pauly, D. A Review of the ELEFAN System for Analysis of Length-Frequency Data in Fish and Aquatic Invertebrates; International Center for Living Aquatic Resources Management: Manila, Philippines; Kuwait Institute for Scientific Research: Safat, Kuwait, 1987; pp. 7–34. [Google Scholar]
- Zar, J.H. Biostatistical Analysis, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996; 662p. [Google Scholar]
- Pauly, D. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. ICES J. Mar. Sci. 1980, 39, 175–192. [Google Scholar] [CrossRef]
- Peixer, J.; Catella, A.C.; Petrere, M., Jr. Yield per recruit of the pacu Piaractus mesopotamicus (Holmberg, 1887) in the pantanal of Mato Grosso do Sul, Brazil. Braz. J. Biol. 2007, 67, 561–567. [Google Scholar] [CrossRef] [PubMed]
- Dinh, Q.M. Population Dynamics of Boleophthalmus bodarti in the Mekong Delta Vietnan. J. Anim. Plant Sci. 2017, 27, 603–610. [Google Scholar]
| Method | L∞ (cm) | K (cm) | Rn | Z/K | Z (year−1) | M (year−1) | F (year−1) | Eest. (year−1) | Emax. (year−1) | M/K | Lc/L∞ | r |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Powell Wetheral (4–25 cm) | 27.11 | 0.34 | 0.17 | 1.14 | 0.64 | 0.79 | −0.15 | −0.24 | 0.41 | 2.30 | 0.15 | −0.95 |
| Powell Wetheral (4–23 cm) | 21.71 | 2.20 | 0.12 | 3.16 | 5.12 | 2.87 | 2.25 | 0.44 | 0.48 | 1.30 | 0.34 | −0.95 |
| Maximum length (4–25 cm) | 26.25 | 0.37 | 0.16 | 7.00 | 0.62 | 0.85 | −0.23 | −0.37 | 0.42 | 2.30 | 0.16 | −0.72 |
| Maximum length (4–23 cm) | 24.15 | 0.45 | 0.14 | 3.16 | 1.12 | 0.99 | 0.14 | 0.12 | 0.48 | 2.20 | 0.24 | −0.95 |
| Response Surface (4–25 cm) | 28.20 | 0.31 | 0.17 | 7.00 | 0.65 | 0.74 | −0.09 | −0.14 | 0.42 | 0.03 | 0.15 | −0.72 |
| Response Surface (4–23 cm) | 25.10 | 0.41 | 0.15 | 3.16 | 1.31 | 0.92 | 0.39 | 0.30 | 0.48 | 2.20 | 0.24 | −0.95 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manuessa, B.; Morais, E.; Cerveira Borges, T.; Teodósio, M.A.; Leitão, F. First Assessment of the Thryssa vitrirostris (Engraulidae) Beach Seine Fishery in Northeastern Mozambique. J 2018, 1, 116-132. https://doi.org/10.3390/j1010012
Manuessa B, Morais E, Cerveira Borges T, Teodósio MA, Leitão F. First Assessment of the Thryssa vitrirostris (Engraulidae) Beach Seine Fishery in Northeastern Mozambique. J. 2018; 1(1):116-132. https://doi.org/10.3390/j1010012
Chicago/Turabian StyleManuessa, Bonifácio, Eurico Morais, Teresa Cerveira Borges, Maria Alexandra Teodósio, and Francisco Leitão. 2018. "First Assessment of the Thryssa vitrirostris (Engraulidae) Beach Seine Fishery in Northeastern Mozambique" J 1, no. 1: 116-132. https://doi.org/10.3390/j1010012
APA StyleManuessa, B., Morais, E., Cerveira Borges, T., Teodósio, M. A., & Leitão, F. (2018). First Assessment of the Thryssa vitrirostris (Engraulidae) Beach Seine Fishery in Northeastern Mozambique. J, 1(1), 116-132. https://doi.org/10.3390/j1010012







