Heat Recovery Potential in a Semi-Closed Greenhouse for Tomato Cultivation
Abstract
1. Introduction
2. Materials and Methods
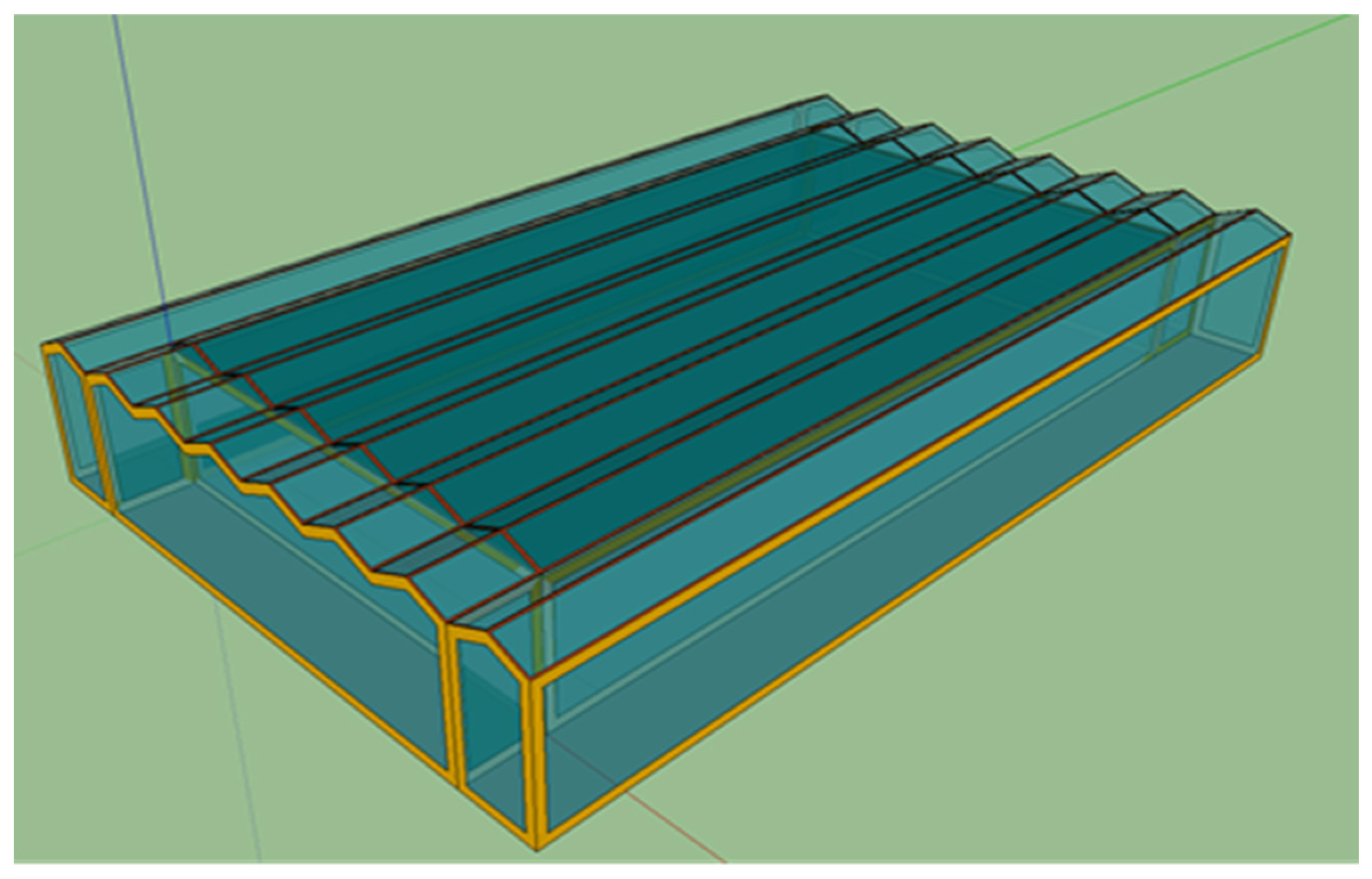
2.1. Greenhouse Geometry and Materials
2.2. Modeling of Specific Phenomena
- The convection heat exchange coefficient with outdoor air for transparent walls (the heat exchange by thermal infrared radiation being low because of the high reflectivity of the glass greenhouse surfaces, no specific coefficient is needed);
- The evapotranspiration by plants as heat and moisture gain;
- The air infiltrations in a greenhouse-type structure and the voluntary ventilation by a specific management of the openings.
2.2.1. External Heat Exchange Coefficient by Convection
- = ;
- = the vertical component of the wind speed (m/s);
- a = 2.38 on the windward side and a = 2.86 on the leeward side;
- b = 0.89 on the windward side and b = 0.62 on the leeward side.
2.2.2. Evapotranspiration
- A = 0.58 during the day;
- B = 17.2 W·m−2·kPa−1 during the night;
- A = irrelevant during the night (Ri = 0);
- B = 11.6 during the night.
2.2.3. Infiltration and Voluntary Ventilation
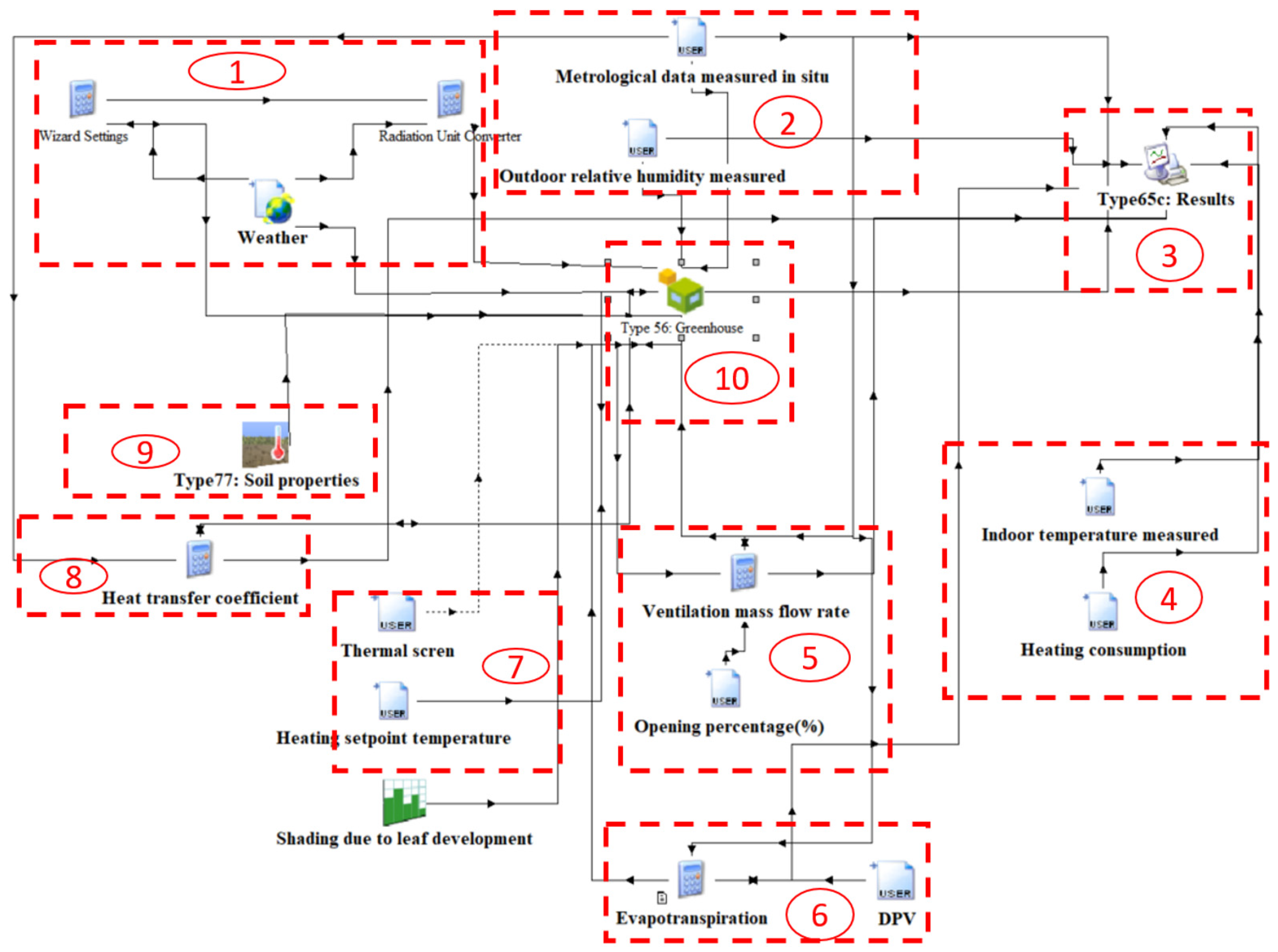
2.3. Simulation Model
2.3.1. Modeling Procedure
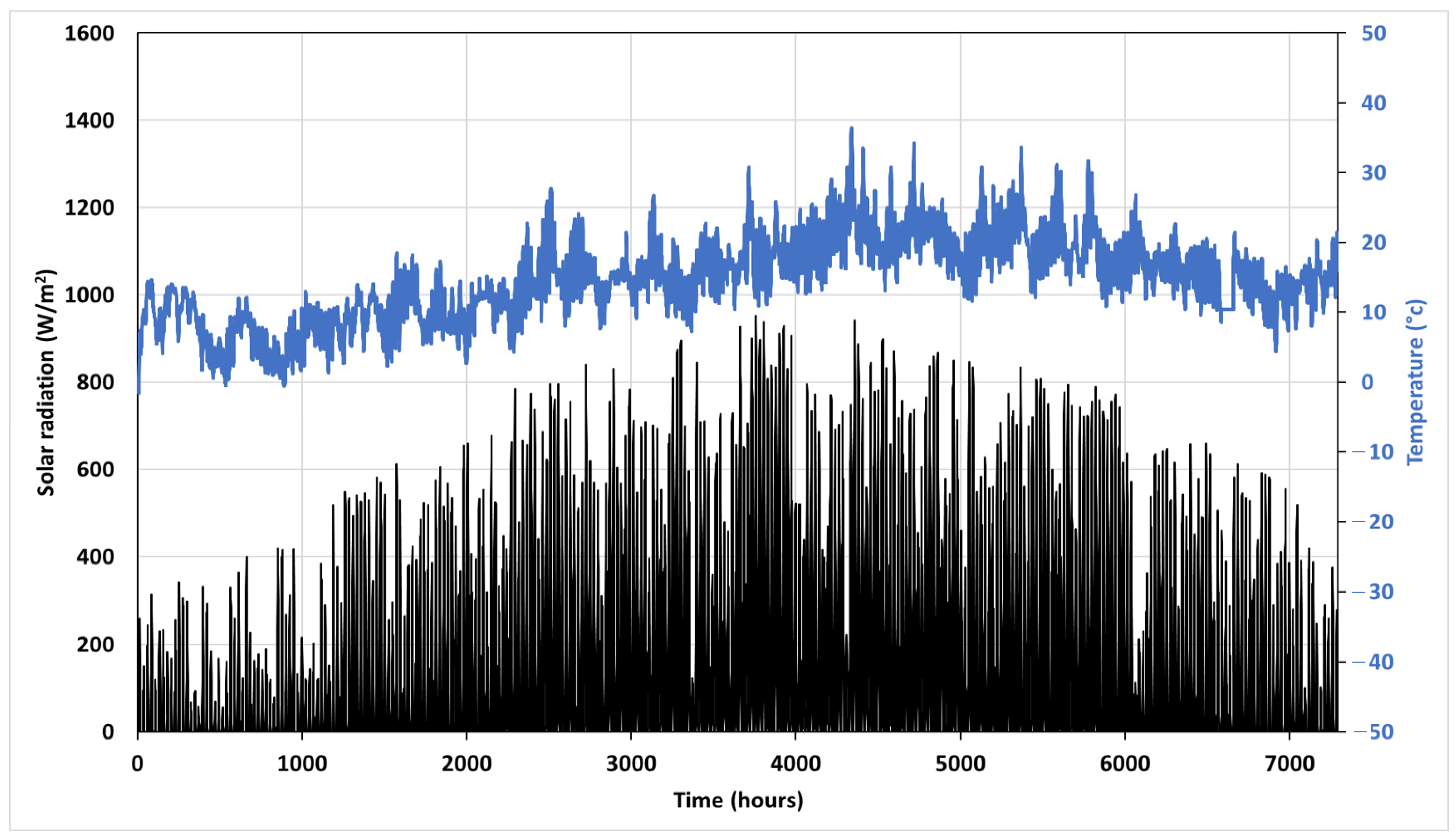
2.3.2. Weather Data File
3. Results and Discussion
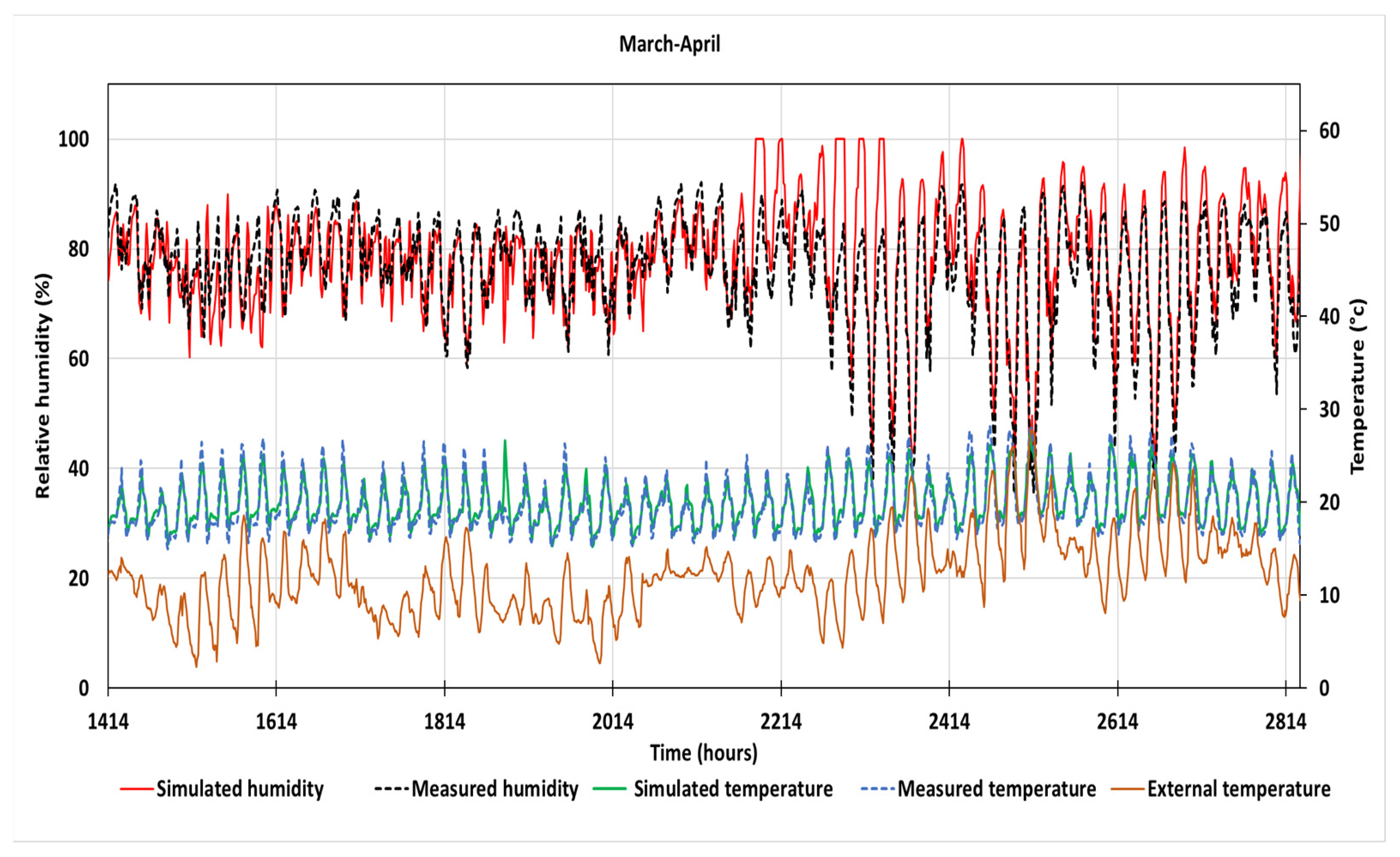
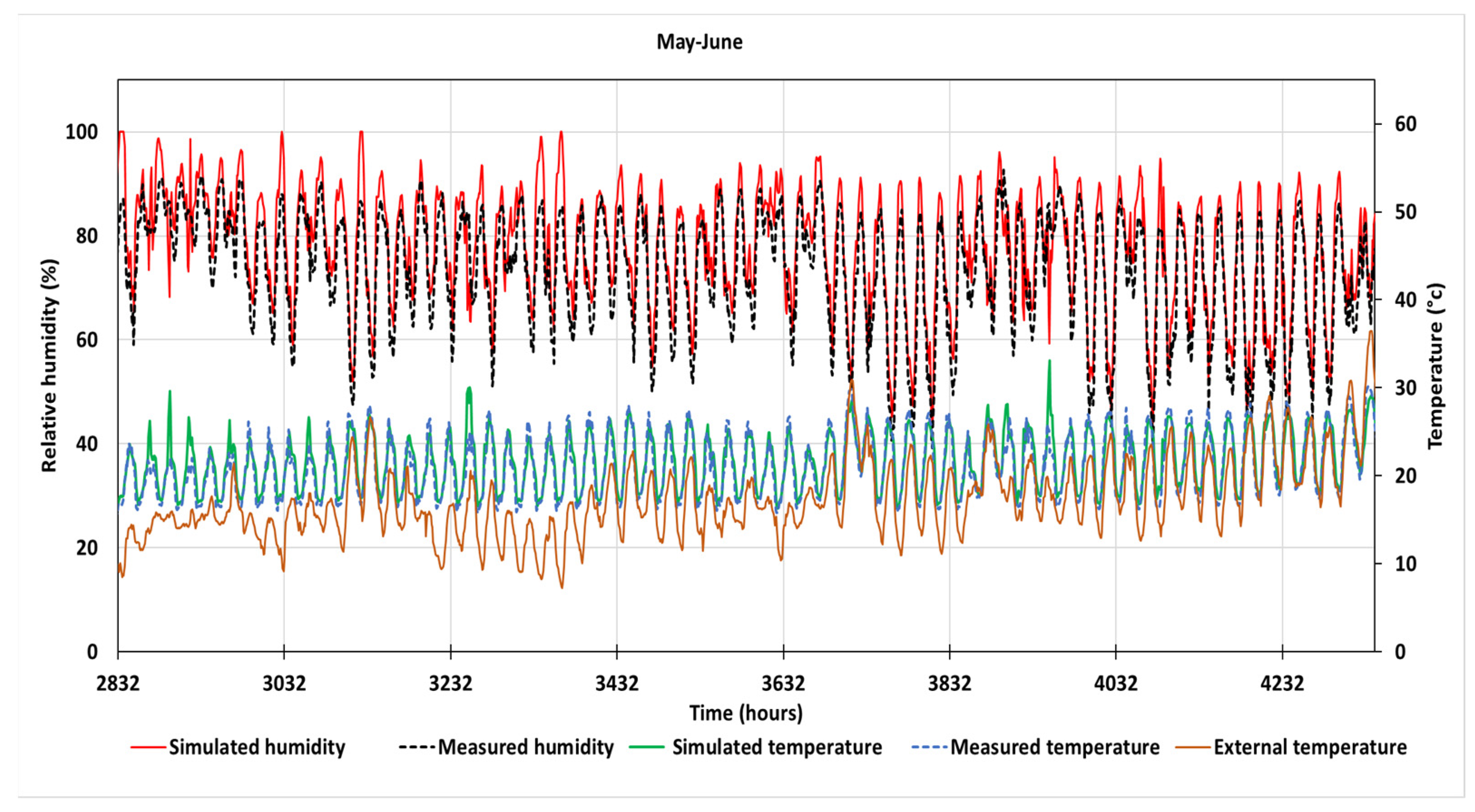
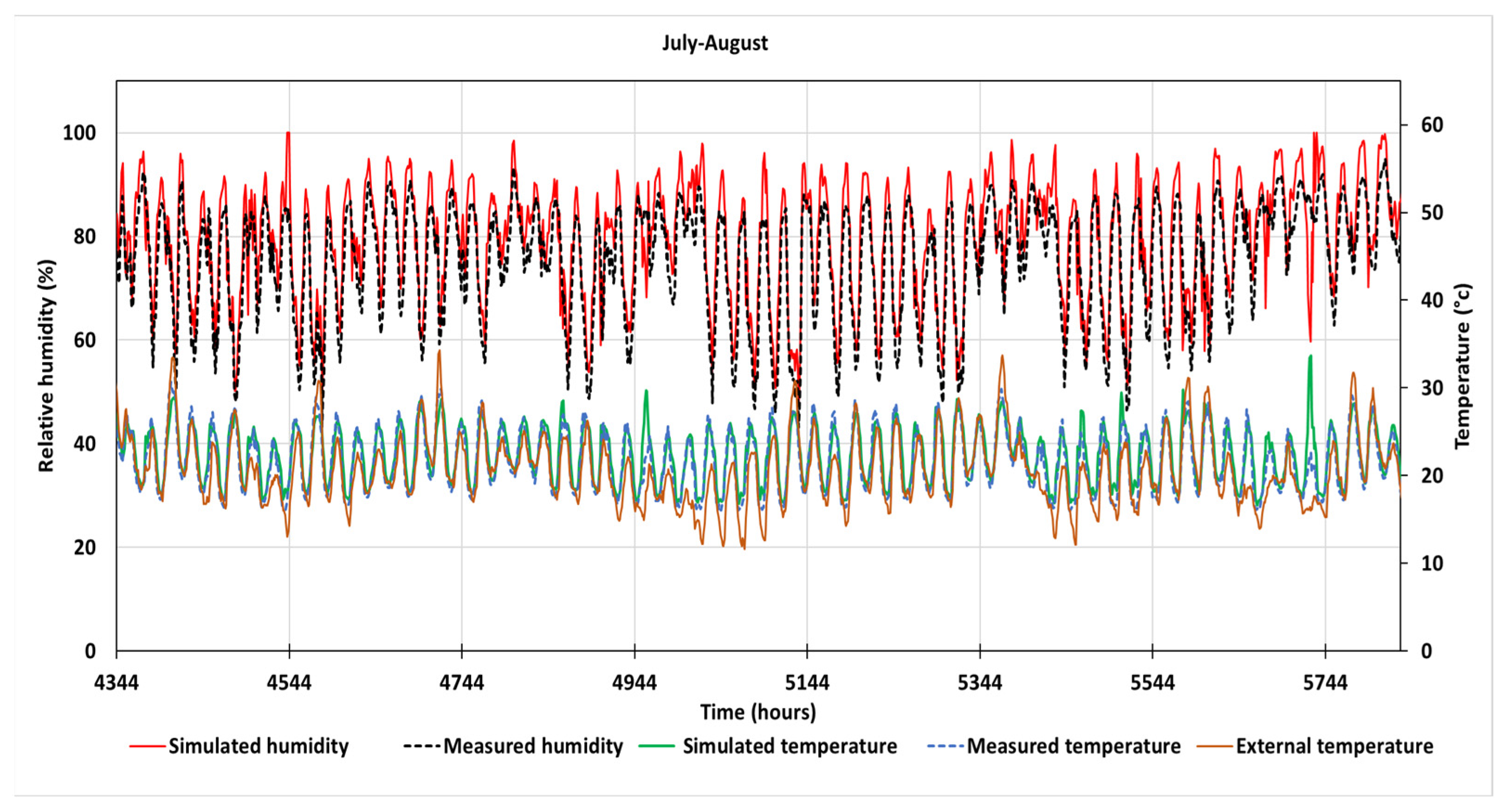
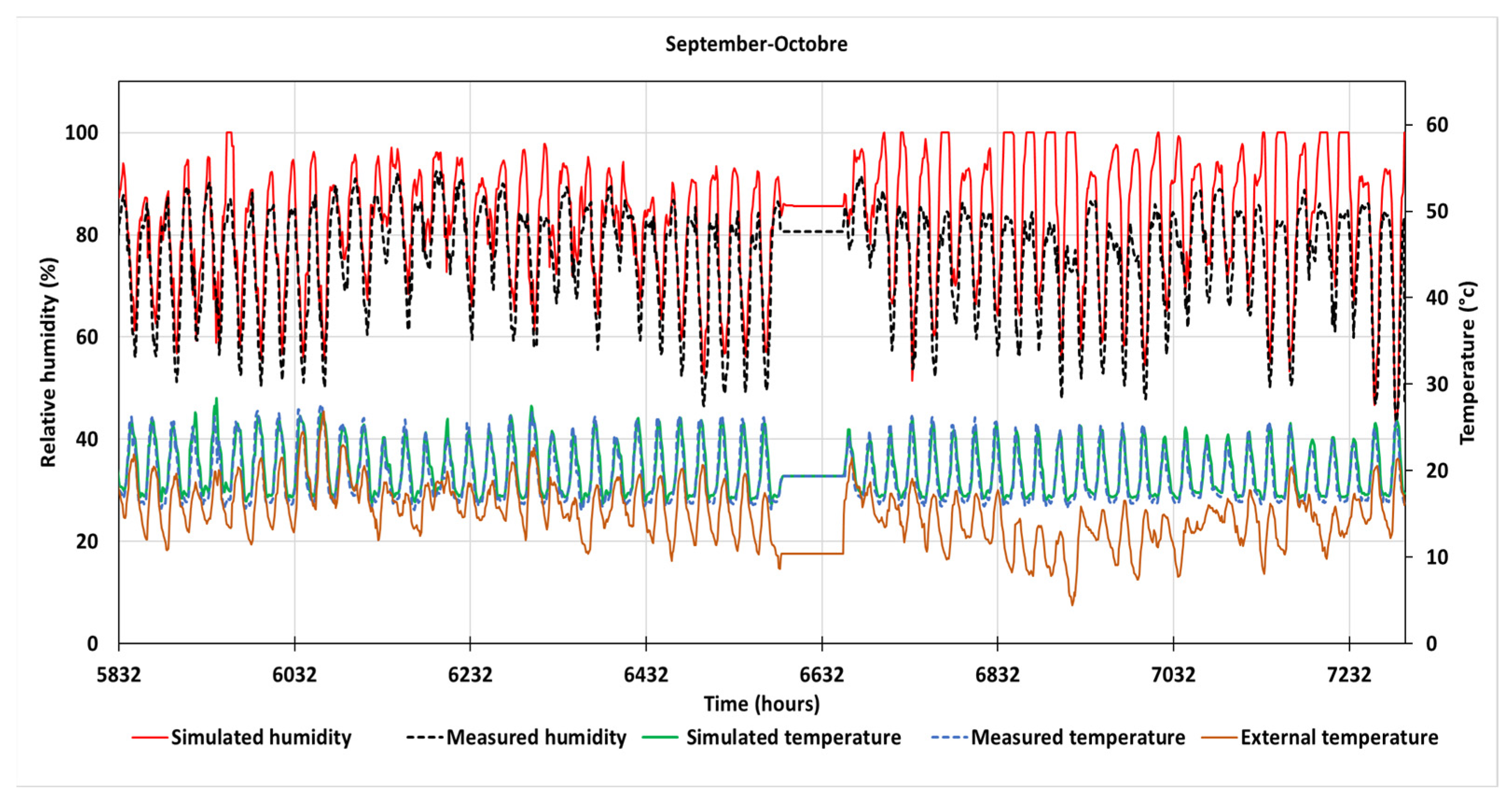
3.1. Model Validation by Comparison of Simulated and Experimental Results
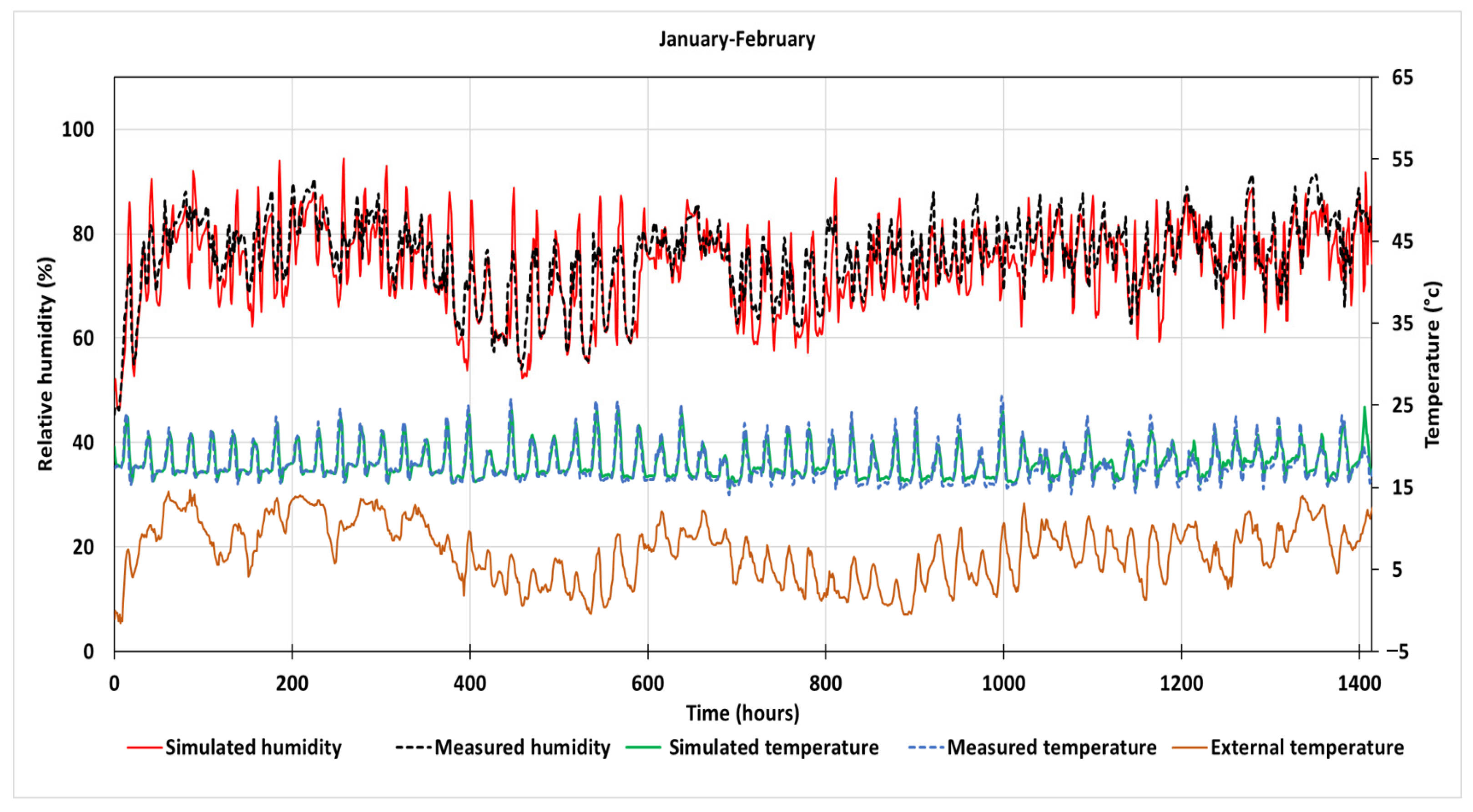
3.1.1. Experimental Data
3.1.2. Model Validation
3.2. Parametric Study
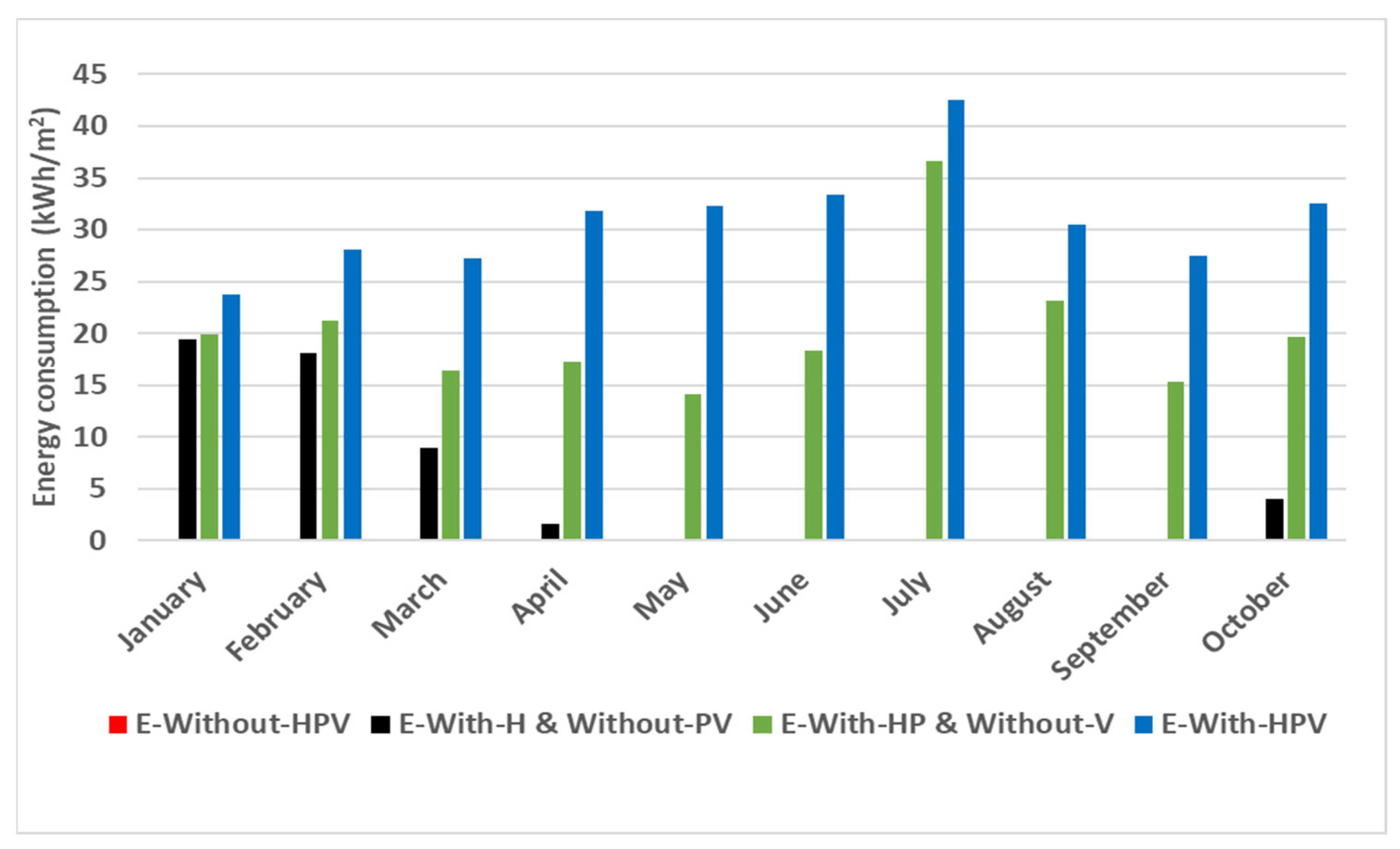
3.2.1. Identification of Different Contributions in Energy Consumption
- Envelope in free evolution without heating, plants, and ventilation (E-Without-HPV);
- Envelope with heating to maintain real CTIFL annual air temperature variation, without plants and ventilation (E-With-H&Without-PV);
- Envelope with heating to maintain real CTIFL annual air temperature variation, with plants and without ventilation (E-With-HP&Without-V);
- Envelope with heating to maintain real CTIFL annual air temperature variation, with plants and ventilation (E-With-HPV).
3.2.2. Effect of Glazing Type
3.2.3. Effect of Thermal Inertia
3.2.4. Effect of Thermal Buffer Zone
3.2.5. Effect of Thermal and Shading Screens
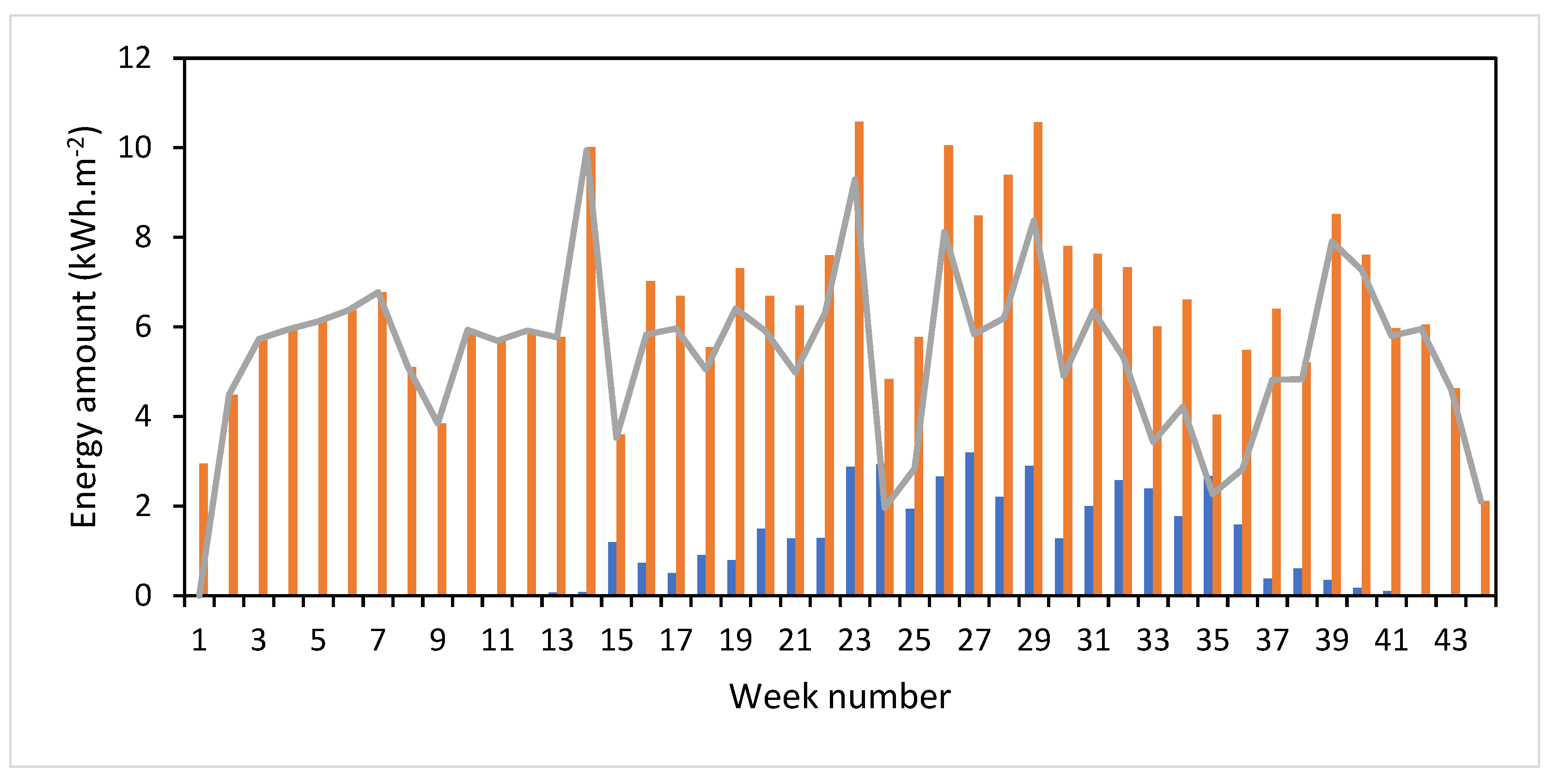
3.3. Heat Recovery Potential
4. Conclusions
- The properties of glazed surfaces;
- The presence of a thermal buffer zone;
- The heat exchange by convection with the outdoor air;
- The ventilation rate;
- The evapotranspiration of plants.
- The inert mass inside the greenhouse;
- The internal lighting gains, LED technology being assumed;
- The internal electric gains due to equipment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin letters: | |
| A0 | Total openings area (m2) |
| B | Thermal expansion coefficient (K−1) |
| C | Specific heat capacity (J·Kg−1·K−1) |
| Cl | Leakage coefficient |
| VPD | Vapor pressure deficit (kPa) |
| fl | Leakage flow rate (m3·s−1·m−2) |
| G | Gravitational acceleration (m·s−2) |
| g-value | Glass total solar energy transmittance (-) |
| H | Heating |
| hci | Internal connective heat transfer convection (W·m−2·K−1) |
| hce | External connective heat transfer convection (W·m−2·K−1) |
| LAI | Leaf area index per m2 of ground surface |
| Re | External radiation (W·m−2) |
| Ri | Indoor radiation (W·m−2) |
| T | Temperature (°C) |
| Tr | Evapotranspiration rate (W·m−2) |
| U-value | Overall heat transfer coefficient (W·m−2·K−1) |
| Vz | Vertical component of the wind speed (m/s) |
| Greek letters: | |
| α | Leeward openings angle |
| β | Windward openings angle |
| ϕl(α) | Leeward openings percentage |
| ϕopenings | Total opening mass flow rate (m3·s−1) |
| ϕt | Opening mass flow rate due to wind effect (m3·s−1) |
| ϕv | Opening mass flow rate due to thermal effect (m3·s−1) |
| ϕw(β) | Windward openings percentage |
| λ | Thermal conductivity (W·m−1·K−1) |
| ρ | Density (kg·m−3) |
| ρsol | Glass reflectivity of the solar radiation (-) |
| τL | Glass thermoluminescence (-) |
| τsol | Glass transmissivity of the solar radiation (-) |
References
- Sanchez, E.A.; Retureta, G.L.; Flores, E.P.; Velazquez, A.L. Evaluation of thermal behavior for an asymmetric greenhouse by means of dynamic simulations. Dyna-Colomb. 2014, 81, 152–159. [Google Scholar] [CrossRef]
- Altes-Buch, Q.; Quoilin, S.; Lemort, V. A modeling framework for the integration of electrical and thermal energy systems in greenhouses. Build. Simul. 2022, 15, 779–797. [Google Scholar] [CrossRef]
- Yohannes, T.; Fath, H. Novel agriculture greenhouse that grows its water and power: Thermal analysis. In Proceedings of the 24th Canadian Congress of Applied Mechanics (CANCAM 2013), Saskatoon, SK, Canada, 2–6 June 2013. [Google Scholar]
- Mashonjowa, E.; Ronsse, F.; Milford, J.R.; Pieters, J. Modelling the thermal performance of a naturally ventilated greenhouse in Zimbabwe using a dynamic greenhouse climate model. Sol. Energy 2013, 91, 381–393. [Google Scholar] [CrossRef]
- Hou, Y.; Li, A.; Li, Y. Analysis of microclimate characteristics in solar greenhouses under natural ventilation. Build. Simul. 2021, 14, 1811–1821. [Google Scholar] [CrossRef]
- Klein, S.A. TRNSYS 18: A Transient System Simulation Program; Solar Energy Laboratory, University of Wisconsin: Madison, WI, USA, 2017; Available online: http://sel.me.wisc.edu/trnsys (accessed on 3 October 2022).
- Rasheed, A.; Kwak, C.S.; Kim, H.T.; Lee, H.W. Building Energy and Simulation Model for Analysing Energy Saving Options of Multi-Span Greenhouses. Appl. Sci. 2020, 10, 6884. [Google Scholar] [CrossRef]
- Rasheed, A.; Na, W.H.; Lee, J.W.; Kim, H.T.; Lee, H.W. Optimisation of Greenhouse Thermal Screens for Maximized Energy Conservation. Energies 2019, 12, 3592. [Google Scholar] [CrossRef]
- Patil, R.; Atre, U.; Nicklas, M.; Bailey, G.; Power, G. An Integrated Sustainable Food Production and Renewable Energy System with Solar & Biomass CHP; American Solar Energy Society: Austin, TX, USA, 2013. [Google Scholar]
- Chargui, R.; Sammouda, H.; Farhat, A. Geothermal heat pump in heating mode: Modeling and simulation on TRNSYS. Int. J. Refrig. 2012, 35, 1824–1832. [Google Scholar] [CrossRef]
- Candy, S.; Moore, G.; Freere, P. Design and modeling of a greenhouse for a remote region in Nepal. Procedia Eng. 2012, 49, 152–160. [Google Scholar] [CrossRef][Green Version]
- Banakar, A.; Montazeri, M.; Ghobadian, B.; Pasdarshahri, H.; Kamrani, F. Energy analysis and assessing heating and cooling demands of closed greenhouse in Iran. Therm. Sci. Eng. Prog. 2021, 25, 101042. [Google Scholar] [CrossRef]
- Chahidi, L.O.; Fossa, M.; Priarone, A.; Mechaqrane, A. Greenhouse cultivation in Mediterranean climate: Dynamic energy analysis and experimental validation. Therm. Sci. Eng. Prog. 2021, 26, 101102. [Google Scholar] [CrossRef]
- Rodríguez, F.; Yebra, L.J.; Berenguel, M.; Dormido, S. Modelling and simulation of greenhouse climate using Dymola. In IFAC Proceedings Volumes (IFAC-PapersOnline); IFAC Secretariat: Laxenburg, Austria, 2002; pp. 79–84. [Google Scholar]
- Costantino, A.; Comba, L.; Sicardi, G.; Bariani, M.; Fabrizio, E. Energy performance and climate control in mechanically ventilated greenhouses: A dynamic modelling-based assessment and investigation. Appl. Energy 2021, 288, 116583. [Google Scholar] [CrossRef]
- Taki, M.; Ajabshirchi, Y.; Faramarz Ranjbar, S.; Rohani, A.; Matloobi, M. Modeling and experimental validation of heat transfer and energy consumption in an innovative greenhouse structure. Inf. Process. Agric. 2016, 3, 157–174. [Google Scholar] [CrossRef]
- van Beveren, P.J.M.; Bontsema, J.; van Straten, G.; van Henten, E.J. Minimal heating and cooling in a modern rose greenhouse. IFAC Proc. Vol. 2013, 46, 282–287. [Google Scholar] [CrossRef]
- Esen, M.; Yuksel, T. Experimental evaluation of using various renewable energy sources for heating a greenhouse. Energy Build. 2013, 65, 340–351. [Google Scholar] [CrossRef]
- Hepbasli, A. Low exergy modelling and performance analysis of greenhouses coupled to closed earth-to-air heat exchangers (EAHEs). Energy Build. 2013, 64, 224–230. [Google Scholar] [CrossRef]
- Kumar, K.S.; Madan, K.; Jha, K.N.; Tiwari, A.P. Singh, Modeling and evaluation of greenhouse for floriculture in subtropics. Energy Build. 2010, 42, 1075–1083. [Google Scholar] [CrossRef]
- Berroug, F.; Lakhal, E.K.; El Omari, M.; Faraji, M.; El Qarnia, H. Thermal performance of a greenhouse with a phase change material north wall. Energy Build. 2011, 43, 3027–3035. [Google Scholar] [CrossRef]
- Mobtaker, H.G.; Ajabshirchi, Y.; Ranjbar, S.F.; Matloobi, M. Simulation of thermal performance of solar greenhouse in north-west of Iran: An experimental validation. Renew. Energy 2019, 135, 88–97. [Google Scholar] [CrossRef]
- Byrne, P.; Lalanne, P. Parametric study of a long-duration energy storage using pumped-hydro and carbon dioxide transcritical cycles. Energies 2021, 14, 4401. [Google Scholar] [CrossRef]
- Rahman, M.M.; Gemechu, E.; Oni, A.O.; Kumar, A. The development of a techno-economic model for the assessment of the cost of flywheel energy storage systems for utility-scale stationary applications. Sustain. Energy Technol. Assess. 2021, 47, 101382. [Google Scholar] [CrossRef]
- Barnhart, C.J.; Benson, S.M. On the importance of reducing the energetic and material demands of electrical energy storage. Energy Environ. Sci. 2013, 6, 1083–1092. [Google Scholar] [CrossRef]
- Odukomaiya, A.; Abu-Heiba, A.; Gluesenkamp, K.R.; Abdelaziz, O.; Jackson, R.K.; Daniel, C.; Graham, S.; Momen, A.M. Thermal analysis of near-isothermal compressed gas energy storage system. Appl. Energy 2016, 179, 948–960. [Google Scholar] [CrossRef]
- Hunt, J.D.; Zakeri, B.; Lopes, R.; Barbosa, P.S.F.; Nascimento, A.; De Castro, N.J.; Brandão, R.; Smith Schneider, P.; Wada, Y. Existing and new arrangements of pumped-hydro storage plants. Renew. Sustain. Energy Rev. 2020, 129, 109914. [Google Scholar] [CrossRef]
- Cavazzini, G.; Houdeline, J.B.; Pavesi, G.; Teller, O.; Ardizzon, G. Unstable behaviour of pump-turbines and its effects on power regulation capacity of pumped-hydro energy storage plants. Renew. Sustain. Energy Rev. 2018, 94, 399–409. [Google Scholar] [CrossRef]
- Pujades, E.; Willems, T.; Bodeux, S.; Orban, P.; Dassargues, A. Underground pumped storage hydroelectricity using abandoned works (deep mines or open pits) and the impact on groundwater flow. Hydrogeol. J. 2016, 24, 1531–1546. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Finn, P.; Mathiesen, B.V.; Leahy, M. Practical operation strategies for pumped hydroelectric energy storage (PHES) utilising electricity price arbitrage. Energy Policy 2011, 39, 4189–4196. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.A.; Alami, A.H. Compressed air energy storage systems: Components and operating parameters—A review. J. Energy Storage 2021, 34, 102000. [Google Scholar] [CrossRef]
- Tallini, A.; Vallati, A.; Cedola, L. Applications of micro-CAES systems: Energy and economic Analysis. Proceedings of the 70th Conference of the ATI Engineering Association. Energy Procedia 2015, 82, 797–804. [Google Scholar] [CrossRef]
- Bi, J.; Jiang, T.; Chen, W.; Ma, X. Research on Storage Capacity of Compressed Air Pumped Hydro Energy Storage Equipment. Energy Power Eng. 2013, 5, 26–30. [Google Scholar] [CrossRef]
- Dib, G.; Haberschill, P.; Rullière, R.; Perroit, Q.; Davies, S.; Revellin, R. Thermodynamic simulation of a micro advanced adiabatic compressed air energy storage for building application. Appl. Energy 2020, 260, 114248. [Google Scholar] [CrossRef]
- Kandezi, M.S.; Naeenian, S.M.M. Investigation of an efficient and green system based on liquid air energy storage (LAES) for district cooling and peak shaving: Energy and exergy analyses. Sustain. Energy Technol. Assess. 2021, 47, 101396. [Google Scholar]
- Georgiou, S.; Shah, N.; Markides, C.N. A thermo-economic analysis and comparison of pumped-thermal and liquid-air electricity storage systems. Appl. Energy 2018, 226, 1119–1133. [Google Scholar] [CrossRef]
- Steinmann, W.D.; Bauer, D.; Jockenhöfer, H.; Johnson, M. Pumped thermal energy storage (PTES) as smart sector-coupling technology for heat and electricity. Energy 2019, 183, 185–190. [Google Scholar] [CrossRef]
- Mercangöz, M.; Hemrle, J.; Kaufmann, L.; Z’Graggen, A.; Ohler, C. Electrothermal energy storage with transcritical CO2 cycles. Energy 2012, 45, 407–415. [Google Scholar] [CrossRef]
- McTigue, J.D.; White, A.J.; Markides, C.N. Parametric studies and optimisation of pumped thermal electricity storage. Appl. Energy 2015, 137, 800–811. [Google Scholar] [CrossRef]
- Siemens-Gamesa Electric Thermal Energy Storage. Available online: https://deepresource.wordpress.com/2019/06/17/siemens-gamesa-electric-thermal-energy-storage (accessed on 17 October 2020).
- Hu, G.; Chen, C.; Lu, H.T.; Wu, Y.; Liu, C.; Tao, L.; Men, Y.; He, G.; Li, K.G. A review of technical advances, barriers, and solutions in the Power to Hydrogen (P2H) roadmap. Engineering 2020, 6, 1364–1380. [Google Scholar] [CrossRef]
- Yazdanian, M.; Klems, J.H. Measurement of the exterior convective film coefficient for windows in low-rise buildings. ASHRAE Trans. 1993, 100 Pt 1, LBL-34717. [Google Scholar]
- Hamer, P.J.C. Validation of a model used for irrigation control of a greenhouse crop. Acta Hortic. 1998, 458, 75–82. [Google Scholar] [CrossRef]
- Boulard, T.; Jemaa, R. Greenhouse tomato crop transpiration model application to irrigation control. Acta Hortic. 1993, 335, 381–388. [Google Scholar] [CrossRef]
- Jemaa, R.; Boulard, T.; Baille, A. Apport des modèles de transpiration d’une culture de tomate sous serre au pilotaghe de l’irrigation. Cah. Options Mediterr. 1999, 31, 203–214. [Google Scholar]
- Medrano, E.; Lorenzo, P.; Sanchez-Guerrero, M.C.; Garcia, M.L.; Caparros, I.; Gimenez, M. Influence of an external greenhouse mobile shading on tomato crop transpiration. Acta Hortic. 2004, 659, 195–199. [Google Scholar] [CrossRef]
- Vanthoor, B.H.E.; Stanghellini, C.; van Henten, E.J.; de Visser, P.H.B. A methodology for model-based green-house design: Part 1, a greenhouse climate model for a broad range of designs and climates. Biosyst. Eng. 2011, 110, 363–377. [Google Scholar] [CrossRef]
- De Zwart, H.F. Analyzing Energy-Saving Options in Greenhouse Cultivation Using a Simulation Model; Land-Bouw Universitet te Wageningen: Wageningen, The Netherlands, 1996. [Google Scholar]
- Gavilán, P.; Ruiz, N.; Lozano, D. Daily forecasting of reference and strawberry crop evapotranspiration in greenhouses in a Mediterranean climate based on solar radiation estimates. Agric. Water Manag. 2015, 159, 307–317. [Google Scholar] [CrossRef]
- Rabiu, A.; Na, W.; Akpenpuun, T.D.; Rasheed, A.; Adesanya, M.A.; Ogunlowo, Q.O.; Kim, H.T.; Lee, H. Determination of overall heat transfer coefficient for greenhouse energy-saving screen using Trnsys and hotbox. Biosyst. Eng. 2022, 217, 88–101. [Google Scholar] [CrossRef]
- Ahamed, M.S.; Guo, H.; Tanino, K. Energy saving techniques for reducing the heating cost of conventional greenhouses. Biosyst. Eng. 2019, 178, 9–33. [Google Scholar] [CrossRef]








| Authors | Case Study | Numerical Model | Experimental Validation and Presented Measurements |
|---|---|---|---|
| Rasheed et al. [7,8] | Building energy and simulation model for analyzing energy-saving options of multi-span greenhouses | Transient model using TRNSYS | 20 days 20–29 August, 1–10 December |
| Banakar et al. [12] | Energy performance investigation of three types of greenhouses: conventional, semi-closed, and closed | Transient model using TRNSYS | 4 days 17 January, 15 May, 17 July, and 14 November |
| Chahidi et al. [13] | Study of a greenhouse equipped by a ground with heat pump and photovoltaic panels in roof | Simulations with EnergyPlus | 56 days 1–31 March, 20 August to 13 September |
| Costantino et al. [15] | Energy consumption of a new fully mechanical ventilation-controlled greenhouse | Model workflow | 31 days July |
| Taki et al. [16] | Six geometries of semi-solar greenhouse are analyzed | MATLAB software | 2 days 2 November and 30 November |
| Van Beveren et al. [17] | Development and validation of a dynamic air temperature model for greenhouse in order to optimize energy consumption | PROPT–MATLAB Optimal Control Software | 7 days 13 to 20 April |
| Mobtaker et al. [22] | Analysis of the greenhouse shape effect on heat losses and solar radiation gains | MATLAB Software | 1 day 29 November |
| Storage Time | Article | System | Power | Energy Storage Capacity | Round-Trip Efficiency |
|---|---|---|---|---|---|
| Very low | Rahman et al. [24] | Flywheel | 20 MW | 5 MWh | 90% |
| Barnhart and Benson [25] | Batteries | Not provided | 4–12 h | 75–90% | |
| Odukomaiya et al. [26] | Batteries | kW–MW scale | 180–1800 MJ/m3 | 63–90% | |
| Barnhart and Benson [25] | Flow batteries | Not provided | 4–12 h | 64–71% | |
| Low | Hunt et al. [27] | PHES | 100 MW | 1 day to several years | Not provided |
| Cavazzini [28] | PHES | Over 7400 MW | Not provided | 65–80% | |
| Pujades et al. [29] | PHES | Not provided | Up to 2 days | Not provided | |
| Connolly et al. [30] | PHES | 360 MW pump 300 MW turbine | 2 GWh | 85% (92% pumping 92% generating) | |
| Odukomaiya et al. [26] | PHES | GW scale | 0.72–7.2 MJ/m3 | 65–87% | |
| Medium | Olabi et al. [31] | CAES | 3 kW to 1 GW | 100 kWh–1 GWh | 40–70% |
| Odukomaiya et al. [26] | CAES | kW–GW scale | 7.2–21.6+ MJ/m3 | 30–70% | |
| Tallini et al. [32] | CAES | 33–100 kW | Not provided | Not provided | |
| Bi et al. [33] | CAES-PHES | Not provided | Not provided | 21.7–22.6% | |
| Odukomaiya et al. [26] | CAES-PHES | 3 kW | 2.46–3.59 MJ/m3 | 66–82% | |
| Dib et al. [34] | AA-CAES | 23.5 kW | 188 kWh 54.6 MJ/m3 | 33.7% | |
| Kandezi et al. [35] | LAES | 5300 kW | 762 MJ/m3 | 65.7% | |
| Georgiou et al. [36] | LAES | 12 MW | 50 MWh | 55% | |
| Steinmann et al. [37] | PTES | Multi-MW | Up to 200,000 m3 | 70% | |
| Mercangöz et al. [38] | PTES | 50 MW | 1 MWh | 65% | |
| McTigue et al. [39] | PTES | 2 MW | 200 MJ/m3 | 70% | |
| Georgiou et al. [36] | PTES | 2 MW | 11.5 MWh | 75% | |
| Siemens Gamesa [40] | PTES | 100 MW | 130 MWh | 50% | |
| High | Hu et al. [41] | Hydrogen and synthetized gas | 7 kW to 1 MW | 2360–4600 MJ/m3 | 19–45% |
| Element | Composition | Thickness (m) | Properties | |
|---|---|---|---|---|
| Frame wall | Aluminum | 0.05 | ρ = 2700 kg·m−3 C = 860 J·kg−1·K−1 λ = 256 W·m−1·K−1 hci = 3 W·m−2·K−1 hce =17 W·m−2·K−1 | |
| Window | Glass tempered | 0.004 | g-value = 0.9 τsol = 0.896 ρsol = 0.080 τL= 0.907 hci = 3 W·m−2·K−1 hce = f(V, Text,Tglass) as presented in Section 2.2.1 | |
| Concrete floor | Concrete | 0.250 | ρ = 2200 kg·m−3 C = 880 J·kg−1·K−1 λ = 0.331 W·m−1·K−1 hci = 3 W·m−2·K−1 | |
| Ground floor | Soil White tarpaulin | 0.250 0.005 | For soil ρ = 3200 kg·m−3 C = 840 J·kg−1·K−1 λ = 2.4 W·m−1·K−1 | For tarpaulin ρ = 120 kg·m−3 C = 484 J·kg−1·K−1 λ = 0.04 W·m−1·K−1 |
| hci = 3 W·m−2·K−1 | ||||
| Themal screen XLS-10 ULTRA REVOULUX | Aluminium strips | 0.004 | Energy savings = 47% Direct light transmission = 85% Diffuse light transmission = 76% | |
| Shading screen XLS-35F HARMONY REVOULUX | Polyster | 0.004 | Energy savings = 15% Direct light transmission = 65% Diffuse light transmission = 63% | |
| Coefficient | Day | Night | References |
|---|---|---|---|
| A | 0.7 | 0.15 | Boulard and Jemaa [44] |
| B (W·m−2·kPa−1) | 88 | 55 | Boulard and Jemaa [44] |
| A | 0.6 | 0.2 | Jemaa et al. [45] |
| B (W·m−2·kPa−1) | 100–140 | 40–60 | Jemaa et al. [45] |
| Month | Mean Monthly External Temperature (°C) | Mean Monthly External Solar Radiation (W/m2) | ||||
|---|---|---|---|---|---|---|
| TRNSYS File | Experimental Data | Absolute Deviation | TRNSYS File | Experimental Data | Relative Deviation | |
| January | 7.9 | 5.2 | 2.7 | 41.8 | 42.6 | −1.9% |
| February | 6.5 | 5.8 | 0.6 | 74.0 | 79.1 | −6.4% |
| March | 10.2 | 8.0 | 2.3 | 119.4 | 118.8 | 0.5% |
| April | 14.3 | 10.1 | 4.3 | 177.4 | 185.2 | −4.2% |
| May | 15.6 | 13.6 | 1.9 | 201.6 | 202.2 | −0.3% |
| June | 19.6 | 16.6 | 3.1 | 248.6 | 264.1 | −5.9% |
| July | 20.6 | 19.1 | 1.5 | 243.6 | 217.9 | 11.8% |
| August | 20.8 | 18.5 | 2.3 | 211.3 | 191.0 | 10.6% |
| September | 16.6 | 16.2 | 0.4 | 157.9 | 166.7 | −5.3% |
| October | 13.4 | 12.8 | 0.6 | 94.1 | 96.3 | −2.3% |
| Sensor Type | Measuring Range | Uncertainty | |
|---|---|---|---|
| Temperature | PT100 | −10 to 50 °C | 0.1 °C |
| Relative humidity | HMP110 | 0 to 100% | 1.5% |
| VPD | Infra-red OPTRIS (OPTCTLT 15 CFCB8) | −50 °C to 975 °C | 1 °C |
| Month | Mean Monthly Temperature (°C) | Mean Monthly Relative Humidity (%) | ||||
|---|---|---|---|---|---|---|
| Simulation Results | Experimental Data | Absolute Deviation (K) | Simulation Results | Experimental Data | Relative Deviation (%) | |
| January | 18.1 | 18.0 | 0.1 | 72.7 | 74.2 | 2% |
| February | 18.0 | 17.7 | 0.3 | 75.0 | 77.1 | 3% |
| March | 19.4 | 19.2 | 0.2 | 77,2 | 78.8 | 2% |
| April | 20.5 | 20.3 | 0.2 | 79.5 | 73.7 | 8% |
| May | 21.0 | 20.4 | 0.6 | 80,3 | 75.7 | 6% |
| June | 22.3 | 22.0 | 0.3 | 74.4 | 70.3 | 6% |
| July | 22.4 | 21.8 | 0.6 | 78.9 | 74.6 | 6% |
| August | 22.3 | 21.6 | 0.7 | 79.7 | 75.7 | 5% |
| September | 20.4 | 19.8 | 0.6 | 80.8 | 75.8 | 7% |
| October | 19.6 | 19.1 | 0.5 | 84.5 | 75.7 | 12% |
| Mean Temperature (°C) | Mean Relative Humidity (%) | |||||
|---|---|---|---|---|---|---|
| Simulation Results | Experimental Data | Absolute Deviation (K) | Simulation Results | Experimental Data | Relative Deviation (%) | |
| 15 January | 18.2 | 18.2 | 0.0 | 76.8 | 76.9 | 0% |
| 15 April | 22.4 | 22.2 | 0.2 | 61.6 | 62.1 | −1% |
| 15 July | 23.3 | 23.0 | 0.4 | 79.0 | 75.6 | 4% |
| Energy Consumption (kWh·m−2) | Heat Loss Parts | Value (kWh·m−2) | |
|---|---|---|---|
| E-With-H&Without-PV | 56 | Heat loss envelope compensation | 56 |
| E-With-HP&Without-V | 211 | Heat loss envelope compensation | 56 |
| Heat loss evapotranspiration compensation | 155 | ||
| E-With-HPV | 310 | Heat loss envelope compensation | 56 |
| Heat loss evapotranspiration compensation | 155 | ||
| Heat loss ventilation compensation | 99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Labihi, A.; Byrne, P.; Meslem, A.; Collet, F.; Prétot, S. Heat Recovery Potential in a Semi-Closed Greenhouse for Tomato Cultivation. Clean Technol. 2023, 5, 1159-1185. https://doi.org/10.3390/cleantechnol5040058
Labihi A, Byrne P, Meslem A, Collet F, Prétot S. Heat Recovery Potential in a Semi-Closed Greenhouse for Tomato Cultivation. Clean Technologies. 2023; 5(4):1159-1185. https://doi.org/10.3390/cleantechnol5040058
Chicago/Turabian StyleLabihi, Abdelouhab, Paul Byrne, Amina Meslem, Florence Collet, and Sylvie Prétot. 2023. "Heat Recovery Potential in a Semi-Closed Greenhouse for Tomato Cultivation" Clean Technologies 5, no. 4: 1159-1185. https://doi.org/10.3390/cleantechnol5040058
APA StyleLabihi, A., Byrne, P., Meslem, A., Collet, F., & Prétot, S. (2023). Heat Recovery Potential in a Semi-Closed Greenhouse for Tomato Cultivation. Clean Technologies, 5(4), 1159-1185. https://doi.org/10.3390/cleantechnol5040058







