Spatial Variability and Temporal Changes of Soil Properties Assessed by Machine Learning in Córdoba, Argentina
Abstract
1. Introduction
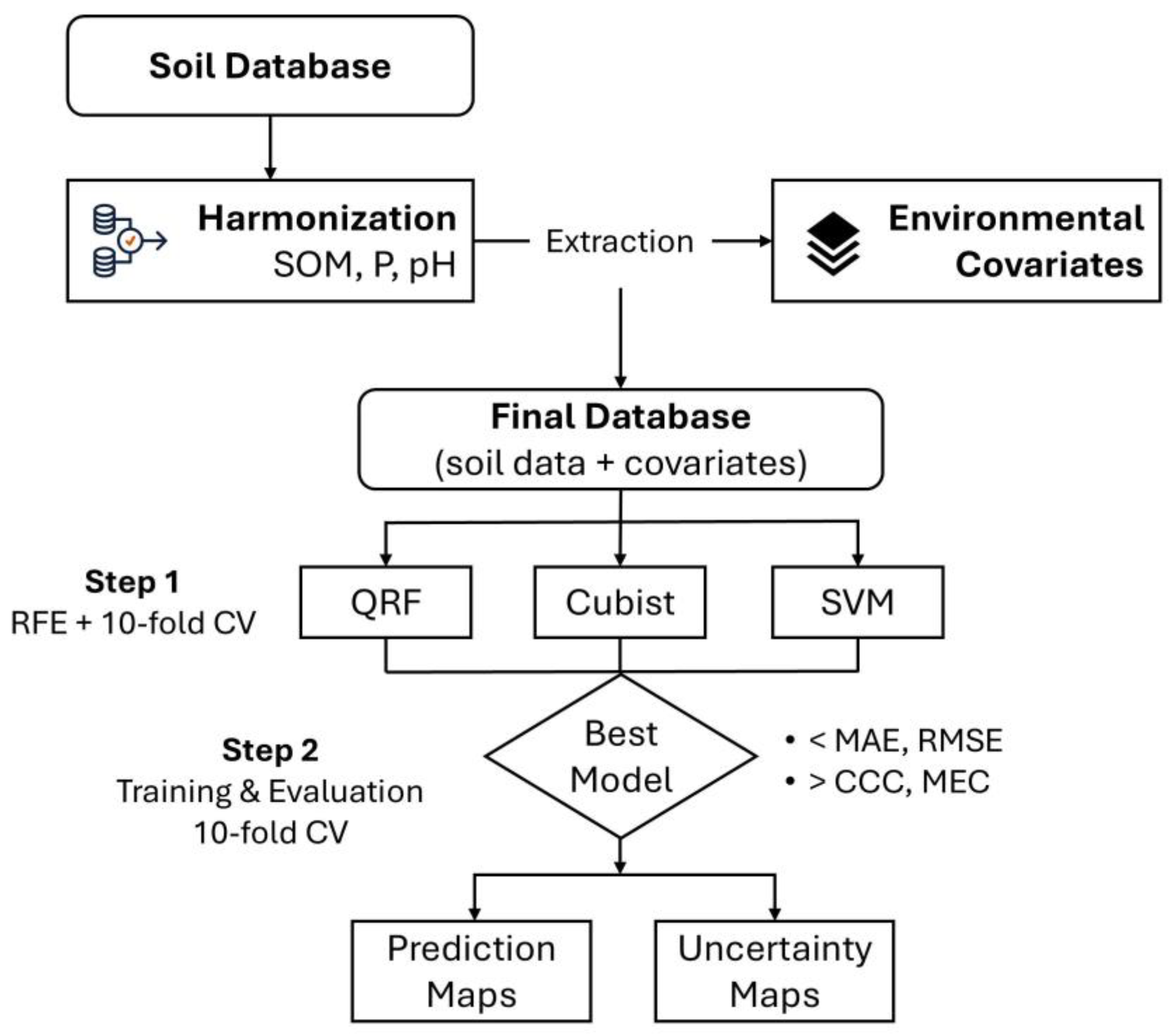
2. Materials and Methods
2.1. Study Area
2.2. Soil Data
2.3. Environmental Covariates
2.4. Machine Learning (ML) Algorithms
2.4.1. Quantile Regression Forest (QRF)
2.4.2. Cubist
2.4.3. Support Vector Machine (SVM)
2.5. Assessment of ML Algorithms
2.6. Temporal Changes in Soil Properties
3. Results
3.1. Soil Properties
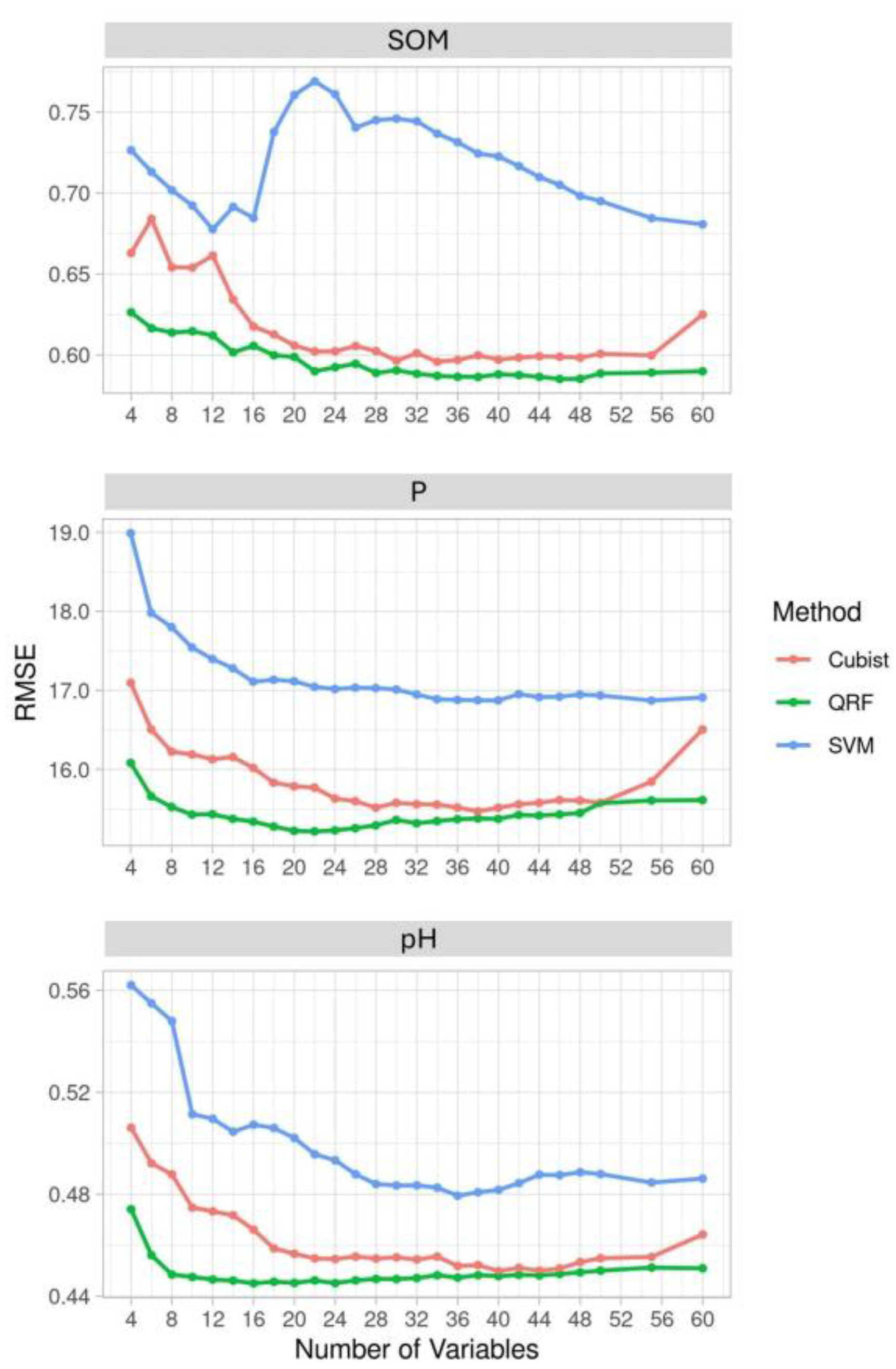
3.2. Performance of ML Models
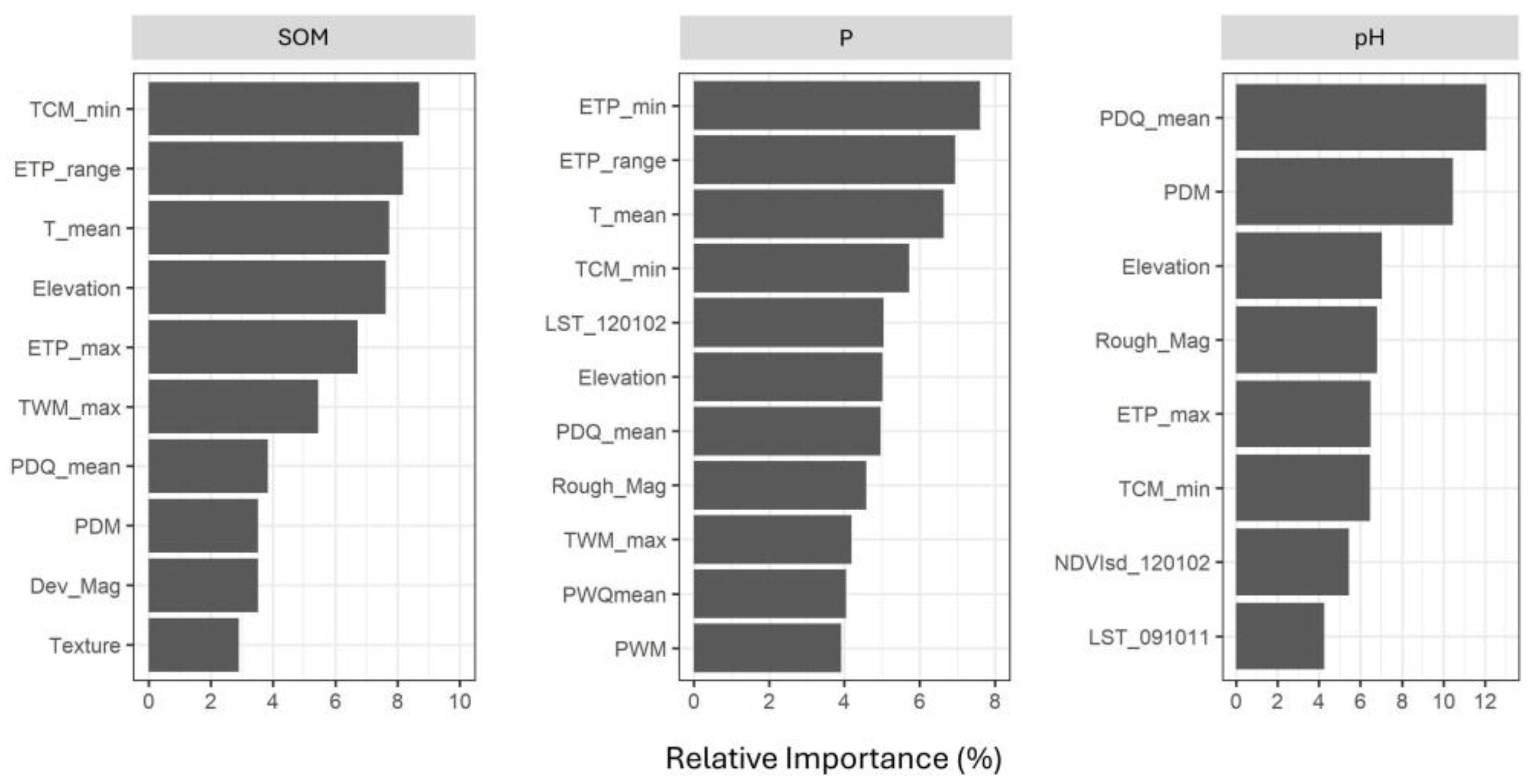
3.3. Relative Importance of Covariates
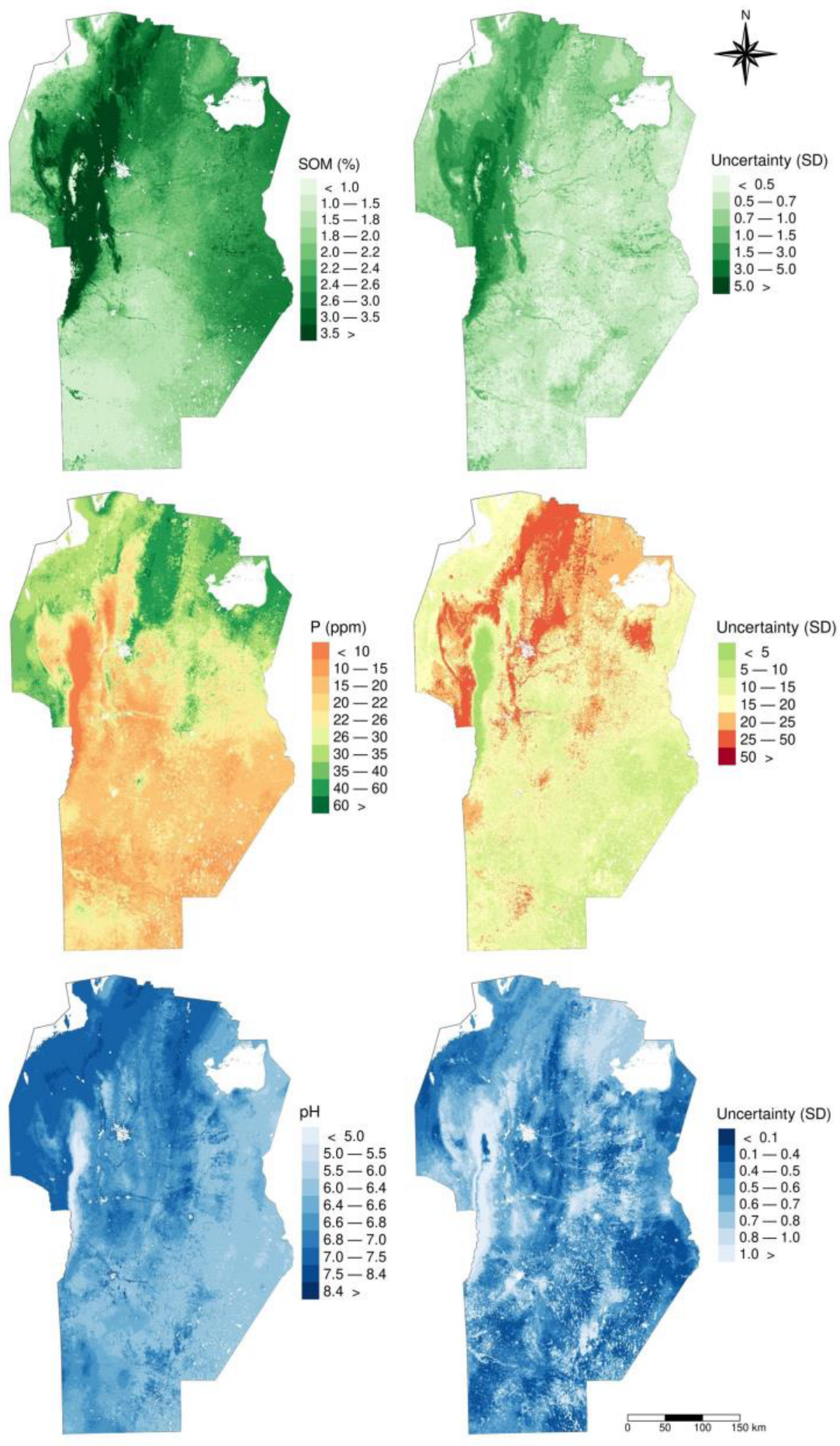
3.4. Prediction and Uncertainty Maps of Soil Properties
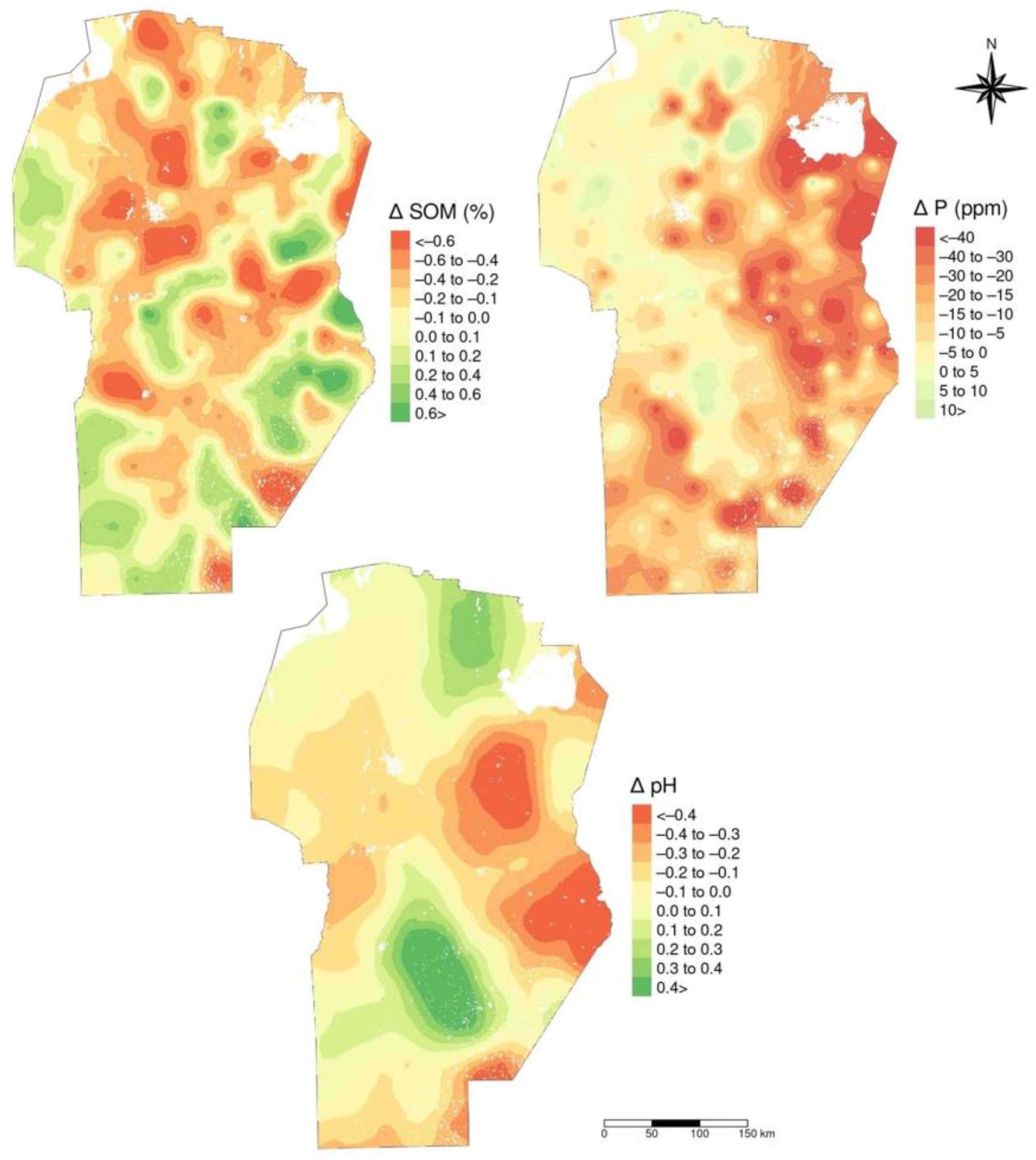
3.5. Temporal Variation in Soil Properties Across Land-Uses
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| ANN | artificial neural networks |
| CCC | Lin’s Concordance Correlation Coefficient |
| CV | coefficient of variation |
| DL | deep learning |
| DSM | digital soil mapping |
| ETP_range | annual range of monthly potential evapotranspiration |
| fPAR | fraction of photosynthetically active radiation absorbed by vegetation |
| LST | land surface temperature |
| LST_120102 | mean land surface temperature from December to February |
| MAE | mean absolute error |
| MEC | modeling efficiency coefficient |
| ML | machine learning |
| NDVI | normalized vegetation index |
| P | extractable phosphorus |
| PDQ_mean | mean monthly precipitation amount of the driest quarter |
| PDM | precipitation amount of the driest month |
| QRF | quantile regression forest |
| RF | random forest |
| RT | regression Tree |
| RFE | recursive feature elimination |
| RMSE | root mean square error |
| SD | standard deviation |
| SVM | Support Vector Machine |
| SOC | soil organic carbon |
| SOM | soil organic matter |
| SWIR | shortwave infrared |
| TCM_min | mean daily minimum air temperature of the coldest month |
| T_mean | mean annual air temperature |
References
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital Mapping of Soil Properties Using Multiple Machine Learning in a Semi-Arid Region, Central Iran. Geoderma 2019, 338, 445–452. [Google Scholar] [CrossRef]
- Wang, Q.; Le Noë, J.; Li, Q.; Lan, T.; Gao, X.; Deng, O.; Li, Y. Incorporating Agricultural Practices in Digital Mapping Improves Prediction of Cropland Soil Organic Carbon Content: The Case of the Tuojiang River Basin. J. Environ. Manag. 2023, 330, 117203. [Google Scholar] [CrossRef]
- Läuchli, A.; Grattan, S.R. Plant Stress under Non-Optimal Soil PH. In Plant Stress Physiology; CABI: Oxfordshire, UK, 2017; pp. 201–216. [Google Scholar]
- Khan, F.; Siddique, A.B.; Shabala, S.; Zhou, M.; Zhao, C. Phosphorus Plays Key Roles in Regulating Plants’ Physiological Responses to Abiotic Stresses. Plants 2023, 12, 2861. [Google Scholar] [CrossRef]
- Hart, M.R.; Quin, B.F.; Nguyen, M.L. Phosphorus Runoff from Agricultural Land and Direct Fertilizer Effects: A Review. J. Environ. Qual. 2004, 33, 1954–1972. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.C.; Minasny, B.; McBratney, A.B. Machine Learning for Digital Soil Mapping: Applications, Challenges and Suggested Solutions. Earth Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- Akkem, Y.; Biswas, S.K.; Varanasi, A. Smart Farming Using Artificial Intelligence: A Review. Eng. Appl. Artif. Intell. 2023, 120, 105899. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital Soil Mapping: A Brief History and Some Lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Gomes, L.C.; Faria, R.M.; de Souza, E.; Veloso, G.V.; Schaefer, C.E.G.R.; Filho, E.I.F. Modelling and Mapping Soil Organic Carbon Stocks in Brazil. Geoderma 2019, 340, 337–350. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Khaledian, Y.; Miller, B.A. Selecting Appropriate Machine Learning Methods for Digital Soil Mapping. Appl. Math. Model. 2020, 81, 401–418. [Google Scholar] [CrossRef]
- Qu, L.; Lu, H.; Tian, Z.; Schoorl, J.M.; Huang, B.; Liang, Y.; Qiu, D.; Liang, Y. Spatial Prediction of Soil Sand Content at Various Sampling Density Based on Geostatistical and Machine Learning Algorithms in Plain Areas. Catena 2024, 234, 107572. [Google Scholar] [CrossRef]
- Quinlan, J.R. Combining Instance-Based and Model-Based Learning. In Machine Learning Proceedings 1993; Elsevier: Amsterdam, The Netherlands, 1993; pp. 236–243. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Meinshausen, N. Quantile Regression Forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. Adv. Neural Inf. Process Syst. 1997, 9, 155–161. [Google Scholar]
- Vaysse, K.; Lagacherie, P. Using Quantile Regression Forest to Estimate Uncertainty of Digital Soil Mapping Products. Geoderma 2017, 291, 55–64. [Google Scholar] [CrossRef]
- Diks, C.G.H.; Vrugt, J.A. Comparison of Point Forecast Accuracy of Model Averaging Methods in Hydrologic Applications. Stoch. Environ. Res. Risk Assess. 2010, 24, 809–820. [Google Scholar] [CrossRef]
- Baltensweiler, A.; Walthert, L.; Hanewinkel, M.; Zimmermann, S.; Nussbaum, M. Machine Learning Based Soil Maps for a Wide Range of Soil Properties for the Forested Area of Switzerland. Geoderma Reg. 2021, 27, e00437. [Google Scholar] [CrossRef]
- Parvizi, Y.; Fatehi, S. Geospatial Digital Mapping of Soil Organic Carbon Using Machine Learning and Geostatistical Methods in Different Land Uses. Sci. Rep. 2025, 15, 4449. [Google Scholar] [CrossRef]
- Bulmer, C.; Paré, D.; Domke, G.M. A New Era of Digital Soil Mapping across Forested Landscapes. In Developments in Soil Science; Elsevier: Amsterdam, The Netherlands, 2019; pp. 345–371. [Google Scholar]
- Lal, R. Managing Soils for Resolving the Conflict between Agriculture and Nature: The Hard Talk. Eur. J. Soil Sci. 2020, 71, 1–9. [Google Scholar] [CrossRef]
- Koritschoner, J.J.; Whitworth Hulse, J.I.; Cuchietti, A.; Arrieta, E.M. Spatial Patterns of Nutrients Balance of Major Crops in Argentina. Sci. Total Environ. 2023, 858, 159863. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.B.; Gifford, R.M. Soil Carbon Stocks and Land Use Change: A Meta Analysis. Glob. Change Biol. 2002, 8, 345–360. [Google Scholar] [CrossRef]
- Apezteguia, H.; Izaurralde, R.; Sereno, R. Simulation Study of Soil Organic Matter Dynamics as Affected by Land Use and Agricultural Practices in Semiarid Córdoba, Argentina. Soil Tillage Res. 2009, 102, 101–108. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 13th ed.; USDA Natural Resources Conservation Service: Washington, DC, USA, 2022.
- Jarsún, B.; Gorgas, J.; Zamora, E.; Bosnero, H.; Lovera, E.; Ravelo, A.; Tassile, J. Los Suelos de Córdoba; Agencia Córdoba Ambiente e Instituto Nacional de Tecnología Agropecuaria, EEA Manfredi: Córdoba, Argentina, 2006. [Google Scholar]
- Bozzer, C. Cambios de Uso y Degradacion de Los Suelos En La Pampa Medanosa Cordobesa: Evolucion Impactos y Escenarios Futuros. Ph.D. Thesis, Universidad Nacional de Río Cuarto, Córdoba, Argentina, Universidad Federal Rural Do Rio de Janeiro, Rio de Janeiro, Brazil, 2021. [Google Scholar]
- Bongiovanni, M.D. Contenido de Carbono Orgánico En Relación al Uso de Suelos Pertenecientes a Las Cuencas Del Rio Cuarto y Arroyos Menores Del Sur de Córdoba: Establecimiento de Un Modelo Descriptivo Simple de Balance de Carbono. Ph.D. Thesis, Universidad Nacional del sur, Bahía Blanca, Argentina, 2022. [Google Scholar]
- Malone, B.P.; McBratney, A.B.; Minasny, B.; Laslett, G.M. Mapping Continuous Depth Functions of Soil Carbon Storage and Available Water Capacity. Geoderma 2009, 154, 138–152. [Google Scholar] [CrossRef]
- Bray, R.; Kurtz, L. Determination of Total, Organic and Available Form of Phosphorus in Soil. Soil. Sci. 1945, 59, 360–361. [Google Scholar] [CrossRef]
- Walkley, A.J.; Black, I.A. Estimation of Soil Organic Carbon by the Chromic Acid Titration Method. Soil. Sci. 1934, 47, 29–38. [Google Scholar] [CrossRef]
- Karger, D.N.; Wilson, A.M.; Mahony, C.; Zimmermann, N.E.; Jetz, W. Global Daily 1 km Land Surface Precipitation Based on Cloud Cover-Informed Downscaling. Sci. Data 2021, 8, 307. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Myneni, R.; Knyazikhin, Y.; Park, T. MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V061; NASA EOSDIS Land Processes Distributed Active Archive Center (DAAC): Sioux Falls, SD, USA, 2021.
- Amatulli, G.; McInerney, D.; Sethi, T.; Strobl, P.; Domisch, S. Geomorpho90m, Empirical Evaluation and Accuracy Assessment of Global High-Resolution Geomorphometric Layers. Sci. Data 2020, 7, 162. [Google Scholar] [CrossRef]
- Keys, R. Cubic Convolution Interpolation for Digital Image Processing. IEEE Trans. Acoust. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. An Introduction to Feature Selection. In Applied Predictive Modeling; Springer: New York, NY, USA, 2013; pp. 487–519. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Breiman, L. Manual on Setting Up, Using, and Understanding Random Forests v3.1; University of California Berkeley: Berkeley, CA, USA, 2002. [Google Scholar]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood Susceptibility Assessment Using GIS-Based Support Vector Machine Model with Different Kernel Types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Janssen, P.H.M.; Heuberger, P.S.C. Calibration of Process-Oriented Models. Ecol. Modell. 1995, 83, 55–66. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation Importance: A Corrected Feature Importance Measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional Variable Importance for Random Forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Hang, S.B.; Negro, G.J.; Becerra, M.A.; Rampoldi, E.A. Suelos de Córdoba: Variabilidad de Las Propiedades Del Horizonte Superficial; The National University of Córdoba: Córdoba, Argentina, 2015. [Google Scholar]
- IDECOR. Mapa de Cobertura y Uso de Suelo de La Provincia de Córdoba 2022–2023; IDECOR: Córdoba, Argentina, 2023. [Google Scholar]
- Córdoba, M.; Paccioretti, P.; Balzarini, M. A New Method to Compare Treatments in Unreplicated On-Farm Experimentation. Precis. Agric. 2025, 26, 4. [Google Scholar] [CrossRef]
- Hengl, T.; Leenaars, J.G.B.; Shepherd, K.D.; Walsh, M.G.; Heuvelink, G.B.M.; Mamo, T.; Tilahun, H.; Berkhout, E.; Cooper, M.; Fegraus, E.; et al. Soil Nutrient Maps of Sub-Saharan Africa: Assessment of Soil Nutrient Content at 250 m Spatial Resolution Using Machine Learning. Nutr. Cycl. Agroecosyst 2017, 109, 77–102. [Google Scholar] [CrossRef]
- FAO. Country Guidelines and Technical Specifications for Global Soil Nutrient and Nutrient Budget Maps; FAO: Rome, Italy, 2022; ISBN 978-92-5-136795-7. [Google Scholar]
- Guo, J.; Wang, K.; Jin, S. Mapping of Soil PH Based on SVM-RFE Feature Selection Algorithm. Agronomy 2022, 12, 2742. [Google Scholar] [CrossRef]
- McKearnan, S.B.; Vock, D.M.; Marai, G.E.; Canahuate, G.; Fuller, C.D.; Wolfson, J. Feature Selection for Support Vector Regression Using a Genetic Algorithm. Biostatistics 2023, 24, 295–308. [Google Scholar] [CrossRef]
- Veronesi, F.; Schillaci, C. Comparison between Geostatistical and Machine Learning Models as Predictors of Topsoil Organic Carbon with a Focus on Local Uncertainty Estimation. Ecol. Indic. 2019, 101, 1032–1044. [Google Scholar] [CrossRef]
- Schmidinger, J.; Heuvelink, G.B.M. Validation of Uncertainty Predictions in Digital Soil Mapping. Geoderma 2023, 437, 116585. [Google Scholar] [CrossRef]
- Gupta, S.; Hasler, J.K.; Alewell, C. Mining Soil Data of Switzerland: New Maps for Soil Texture, Soil Organic Carbon, Nitrogen, and Phosphorus. Geoderma Reg. 2024, 36, e00747. [Google Scholar] [CrossRef]
- Falahatkar, S.; Hosseini, S.M.; Ayoubi, S.; Salmanmahiny, A. Predicting Soil Organic Carbon Density Using Auxiliary Environmental Variables in Northern Iran. Arch. Agron. Soil. Sci. 2016, 62, 375–393. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Kerry, R. Digital Mapping of Soil Organic Carbon at Multiple Depths Using Different Data Mining Techniques in Baneh Region, Iran. Geoderma 2016, 266, 98–110. [Google Scholar] [CrossRef]
- Vaieretti, M.V.; Conti, G.; Poca, M.; Kowaljow, E.; Gorné, L.; Bertone, G.; Cingolani, A.M.; Pérez-Harguindeguy, N. Plant and Soil Carbon Stocks in Grassland Patches Maintained by Extensive Grazing in the Highlands of Central Argentina. Austral Ecol. 2021, 46, 374–386. [Google Scholar] [CrossRef]
- Fernández-Catinot, F.; Pestoni, S.; Gallardo, N.; Vaieretti, M.V.; Pérez Harguindeguy, N. No Detectable Upper Limit When Predicting Soil Mineral-Associated Organic Carbon Stabilization Capacity in Temperate Grassland of Central Argentina Mountains. Geoderma Reg. 2023, 35, e00722. [Google Scholar] [CrossRef]
- Cabido, M.; Breimer, R.; Vega, G. Plant Communities and Associated Soil Types in a High Plateau of the Cordoba Mountains, Central Argentina. Mt. Res. Dev. 1987, 7, 25. [Google Scholar] [CrossRef]
- Koritschoner, J.; Giannini Kurina, F.; Hang, S.; Balzarini, M. Site-Specific Modelling of Short-Term Soil Carbon Mineralization in Central Argentina. Geoderma 2022, 406, 115487. [Google Scholar] [CrossRef]
- Bongiovanni, M.D.; Marzari, R.; Ron, M. Fósforo Disponible En Suelos Agrícolas Del Sur de Córdoba y Sudeste de San Luis. In Proceedings of the XXII Congreso Argentino de la Ciencia del Suelo, Rosario, Argentina, 31 May–4 June 2010. [Google Scholar]
- Ortiz, J.; Faggioli, V.S.; Ghio, H.; Boccolini, M.F.; Ioele, J.P.; Tamburrini, P.; Garcia, F.; Gudelj, V. Impacto a Largo Plazo de La Fertilización Sobre La Estructura y Funcionalidad de La Comunidad Microbiana Del Suelo. Cienc. Suelo 2020, 38, 45–55. [Google Scholar]
- Alvarez, R.; Gimenez, A.; Pagnanini, F.; Recondo, V.; Gangi, D.; Caffaro, M.; De Paepe, J.L.; Berhongaray, G. Soil Acidity in the Argentine Pampas: Effects of Land Use and Management. Soil Tillage Res. 2020, 196, 104434. [Google Scholar] [CrossRef]
- Liu, H.; Yin, Y.; Tian, Y.; Ren, J.; Wang, H. Climatic and Anthropogenic Controls of Topsoil Features in the Semi-arid East Asian Steppe. Geophys. Res. Lett. 2008, 35, L04401. [Google Scholar] [CrossRef]
- Wei, J.-B.; Xiao, D.-N.; Zeng, H.; Fu, Y.-K. Spatial Variability of Soil Properties in Relation to Land Use and Topography in a Typical Small Watershed of the Black Soil Region, Northeastern China. Environ. Geol. 2008, 53, 1663–1672. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.-L.; Sun, Y.-J.; Zhao, Y.-G.; Li, D.-C. Mapping the Three-Dimensional Distribution of Soil Organic Matter across a Subtropical Hilly Landscape. Soil Sci. Soc. Am. J. 2013, 77, 1241–1253. [Google Scholar] [CrossRef]
- Penuelas, J.; Coello, F.; Sardans, J. A Better Use of Fertilizers Is Needed for Global Food Security and Environmental Sustainability. Agric. Food Secur. 2023, 12, 5. [Google Scholar] [CrossRef]
- Cabrini, S.M.; Portela, S.I.; Cano, P.B.; López, D.A. Heterogeneity in Agricultural Land Use Decisions in Argentine Rolling Pampas: The Effects on Environmental and Economic Indicators. Cogent Environ. Sci. 2019, 5, 1667709. [Google Scholar] [CrossRef]
- Portela, S.I.; Reixachs, C.; Torti, M.J.; Beribe, M.J.; Giannini, A.P. Contrasting Effects of Soil Type and Use of Cover Crops on Nitrogen and Phosphorus Leaching in Agricultural Systems of the Argentinean Pampas. Agric. Ecosyst. Environ. 2024, 364, 108897. [Google Scholar] [CrossRef]
- Kebebew, S.; Bedadi, B.; Erkossa, T.; Yimer, F.; Wogi, L. Effect of Different Land-Use Types on Soil Properties in Cheha District, South-Central Ethiopia. Sustainability 2022, 14, 1323. [Google Scholar] [CrossRef]
- De la Casa, A.; Ovando, G.; Díaz, G.; Díaz, P.; Soler, F.; Clemente, J.P. Assessment of Land Use Change in the Dryland Agricultural Region of Córdoba, Argentina, between 2000 and 2020 Based on NDVI Data. AgriScientia 2024, 41, 27–43. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M. Uncertainty and Uncertainty Propagation in Soil Mapping and Modelling. In Pedometrics; Springer: Cham, Switzerland, 2018; pp. 439–461. [Google Scholar]
- Sainz Rozas, H.; Reussi Calvo, N.; Wyngaard, N.; Eyherabide, M.; Angelini, H.; Larrea, G.; Garello, F.; Avila Manotoba, O.; Orcellet, J.; González San Juan, F.; et al. Impacto de la Agricultura Sobre la Fertilidad de los Suelos de la Región Pampeana Argentina. In Proceedings of the Simposio Fertilidad 2025, Ferilizar Asociación Civil, Buenos Aires, Argentina, 7 May 2025; p. 3. [Google Scholar]



| Variable | Mean | CV | Min. | Max. | P(05) | P(95) |
|---|---|---|---|---|---|---|
| SOM (%) | 2.19 | 50 | 0.10 | 13.20 | 1.00 | 3.56 |
| P (ppm) | 26.54 | 85 | 0.05 | 152.00 | 5.68 | 72.19 |
| pH | 6.53 | 10 | 4.10 | 11.00 | 5.70 | 7.71 |
| Variable | ML Method | MAE | RMSE | CCC | MEC |
|---|---|---|---|---|---|
| SOM | QRF | 0.380 | 0.581 | 0.846 | 0.715 |
| Cubist | 0.388 | 0.593 | 0.838 | 0.702 | |
| SVM | 0.437 | 0.678 | 0.786 | 0.611 | |
| P | QRF | 9.715 | 15.197 | 0.743 | 0.551 |
| Cubist | 9.769 | 15.486 | 0.732 | 0.534 | |
| SVM | 10.251 | 16.846 | 0.679 | 0.448 | |
| pH | QRF | 0.298 | 0.444 | 0.743 | 0.552 |
| Cubist | 0.304 | 0.451 | 0.734 | 0.537 | |
| SVM | 0.324 | 0.478 | 0.695 | 0.479 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Córdoba, M.A.; Hang, S.B.; Bozzer, C.; Alvarez, C.; Faule, L.; Kowaljow, E.; Vaieretti, M.V.; Bongiovanni, M.D.; Balzarini, M.G. Spatial Variability and Temporal Changes of Soil Properties Assessed by Machine Learning in Córdoba, Argentina. Soil Syst. 2025, 9, 109. https://doi.org/10.3390/soilsystems9040109
Córdoba MA, Hang SB, Bozzer C, Alvarez C, Faule L, Kowaljow E, Vaieretti MV, Bongiovanni MD, Balzarini MG. Spatial Variability and Temporal Changes of Soil Properties Assessed by Machine Learning in Córdoba, Argentina. Soil Systems. 2025; 9(4):109. https://doi.org/10.3390/soilsystems9040109
Chicago/Turabian StyleCórdoba, Mariano A., Susana B. Hang, Catalina Bozzer, Carolina Alvarez, Lautaro Faule, Esteban Kowaljow, María V. Vaieretti, Marcos D. Bongiovanni, and Mónica G. Balzarini. 2025. "Spatial Variability and Temporal Changes of Soil Properties Assessed by Machine Learning in Córdoba, Argentina" Soil Systems 9, no. 4: 109. https://doi.org/10.3390/soilsystems9040109
APA StyleCórdoba, M. A., Hang, S. B., Bozzer, C., Alvarez, C., Faule, L., Kowaljow, E., Vaieretti, M. V., Bongiovanni, M. D., & Balzarini, M. G. (2025). Spatial Variability and Temporal Changes of Soil Properties Assessed by Machine Learning in Córdoba, Argentina. Soil Systems, 9(4), 109. https://doi.org/10.3390/soilsystems9040109







