Estimating Soil Erodible Fraction Using Multivariate Regression and Proximal Sensing Data in Arid Lands, South Egypt
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
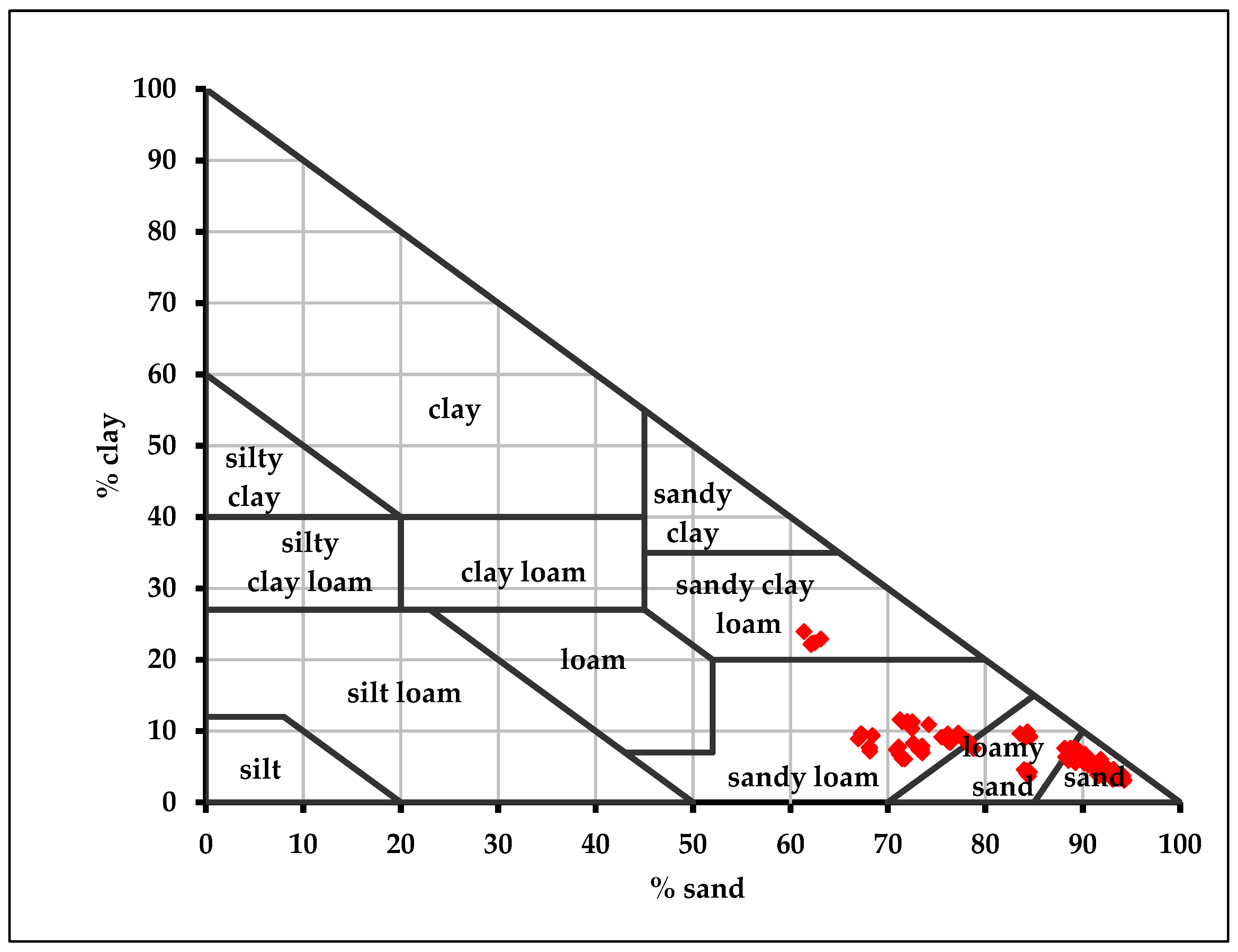
2.2. Sampling Strategy and Laboratory Analyses
2.3. The Wind Erodible Fraction (EF-Factor)
2.4. Spectral Vis-NIR Measurements Data
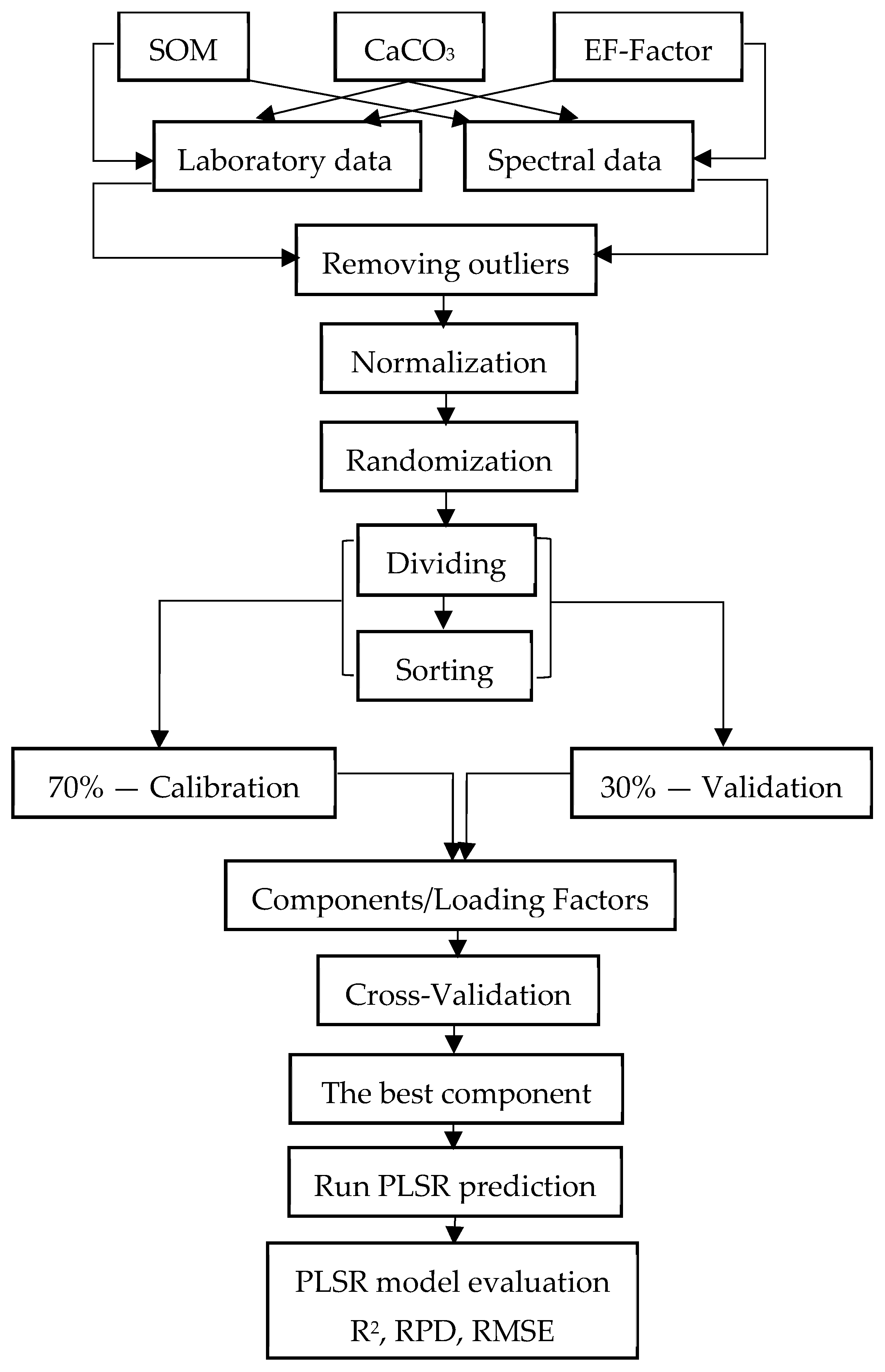
2.5. Soil Spectral Data Processing and Analysis
2.5.1. Preparing the Ground: Enhancing Spectral Data for Precise Analysis
2.5.2. Advanced Statistical Analysis and Innovative Model Development
2.5.3. Partial Least-Squares Regression (PLSR) Model
Selection of the Optimal PLSR Calibration Model
PLSR Model (Calibration-Validation Models)
Data Transformation Methods
- Box–Cox transformation
2.5.4. Support Vector Machine (SVM) Model
2.5.5. Variables Selection Methods
- (i)
- Monte Carlo approach: In this initial step, 80% of the samples from the calibration set are randomly selected;
- (ii)
- Exponentially decreasing function (EDF): In this stage, less significant variables are systematically eliminated. The proportion of variables to be retained is determined using the EDF formula presented in Equation (11):
- (i)
- Adaptive reweighted sampling (ARS): Following the initial elimination based on the EDF, ARS is applied to further remove variables in a competitive manner. ARS operates on the principle of ‘survival of the fittest’ inspired by Darwin’s theory of natural selection. Variables with weights exceeding a specified threshold are retained;
- (ii)
- Assessment of RMSE values: The n subsets generated are evaluated based on their respective RMSE values. The subset that yields the lowest error is selected as the preferred choice.
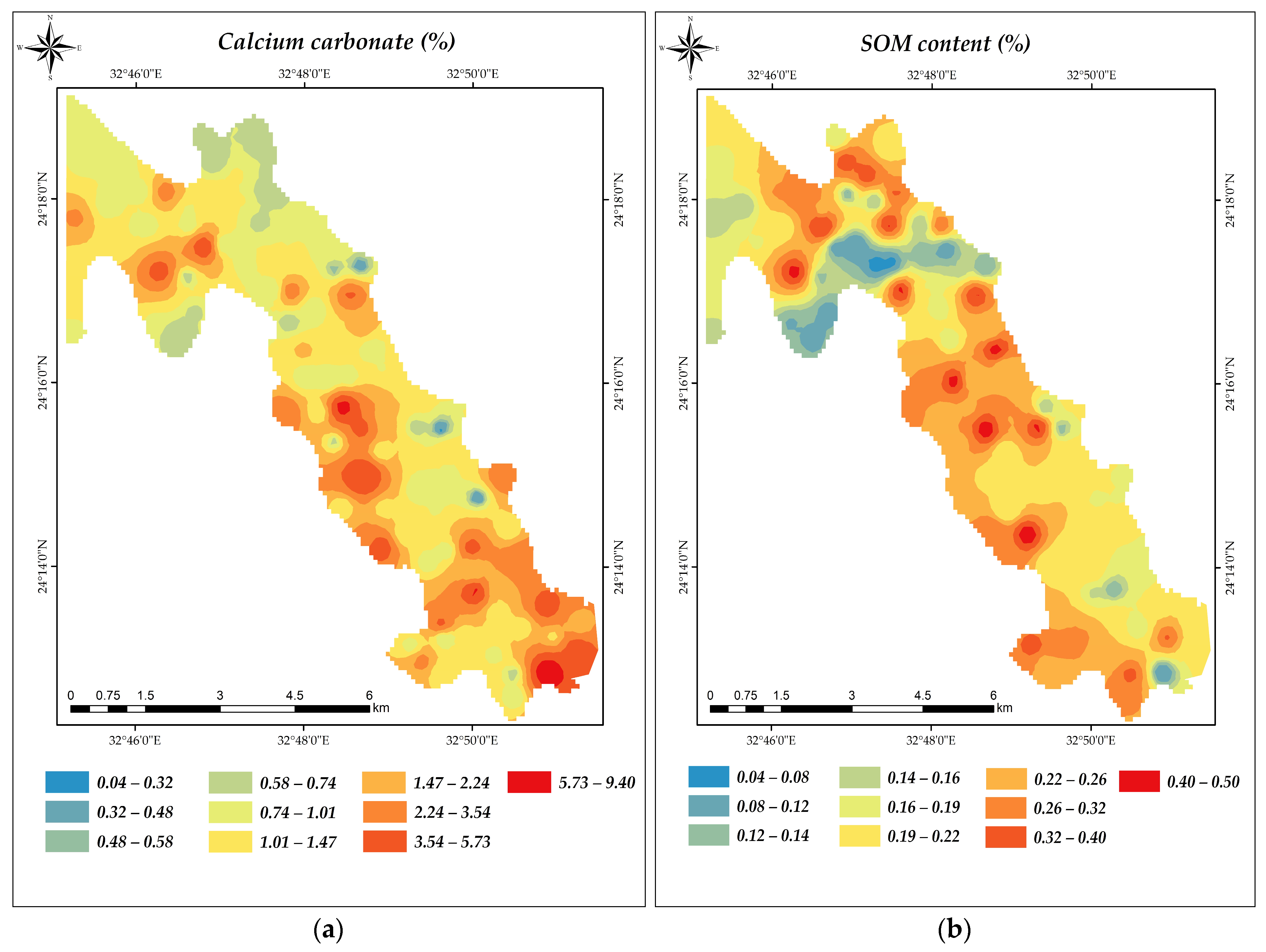
2.6. Mapping of the Spatial Variability Distribution of Soil Properties
3. Results
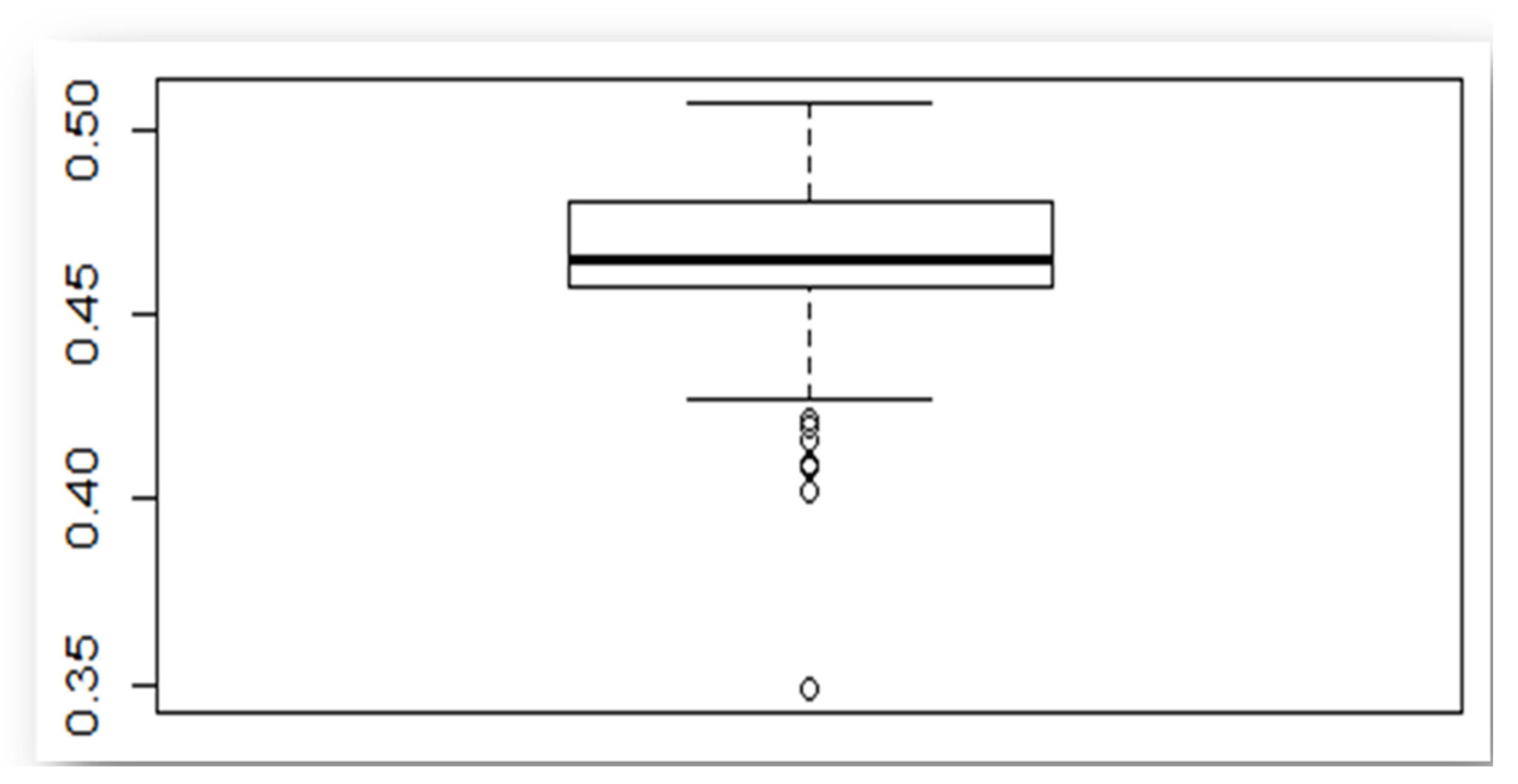
3.1. Description of Soil Properties
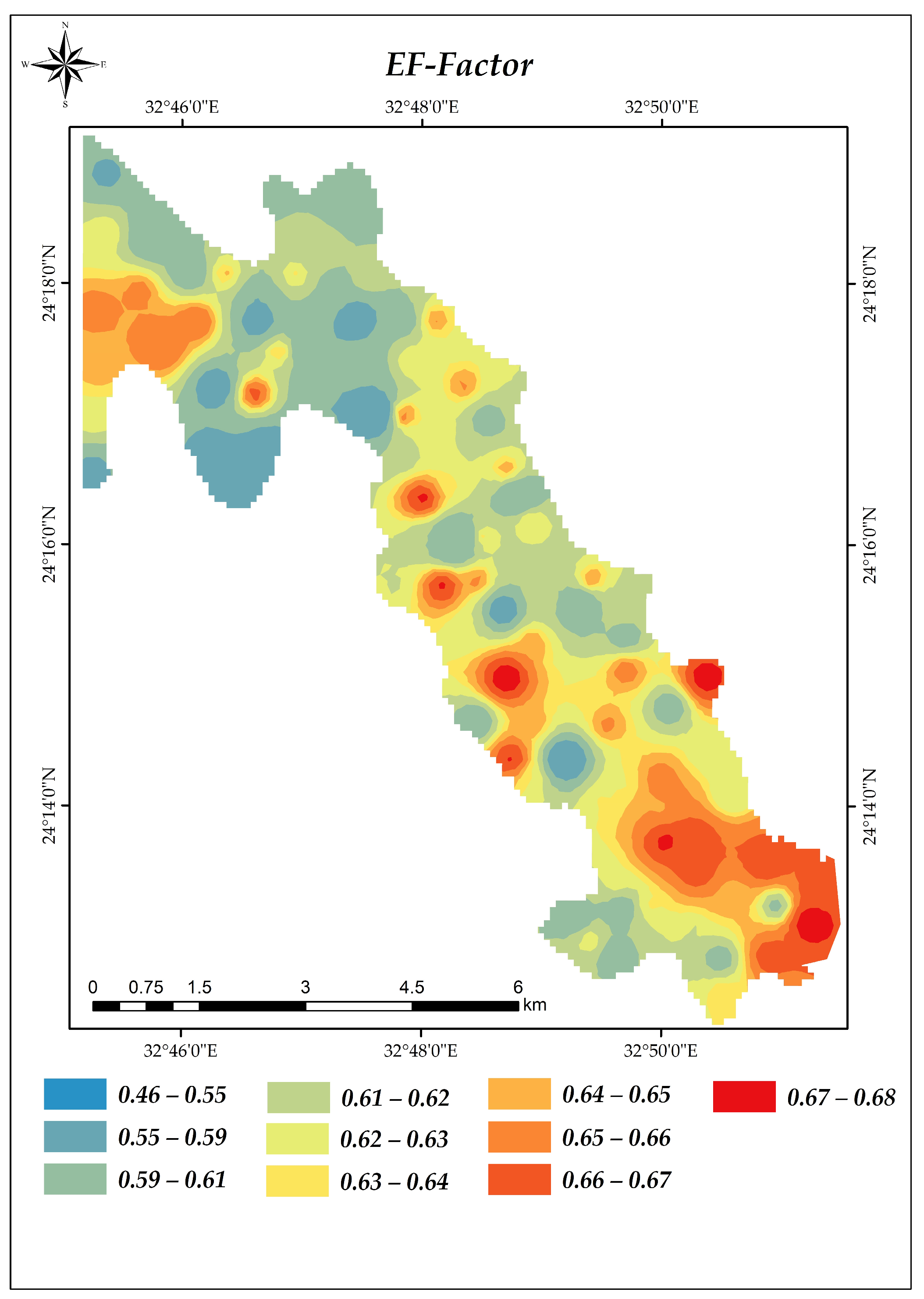
3.2. Wind-Erodible Fraction (EF-Factor) Calculation Using the Fryrear Equation
3.3. Correlation between Soil Properties and EF-Factor
3.4. Soil Spectra Analysis
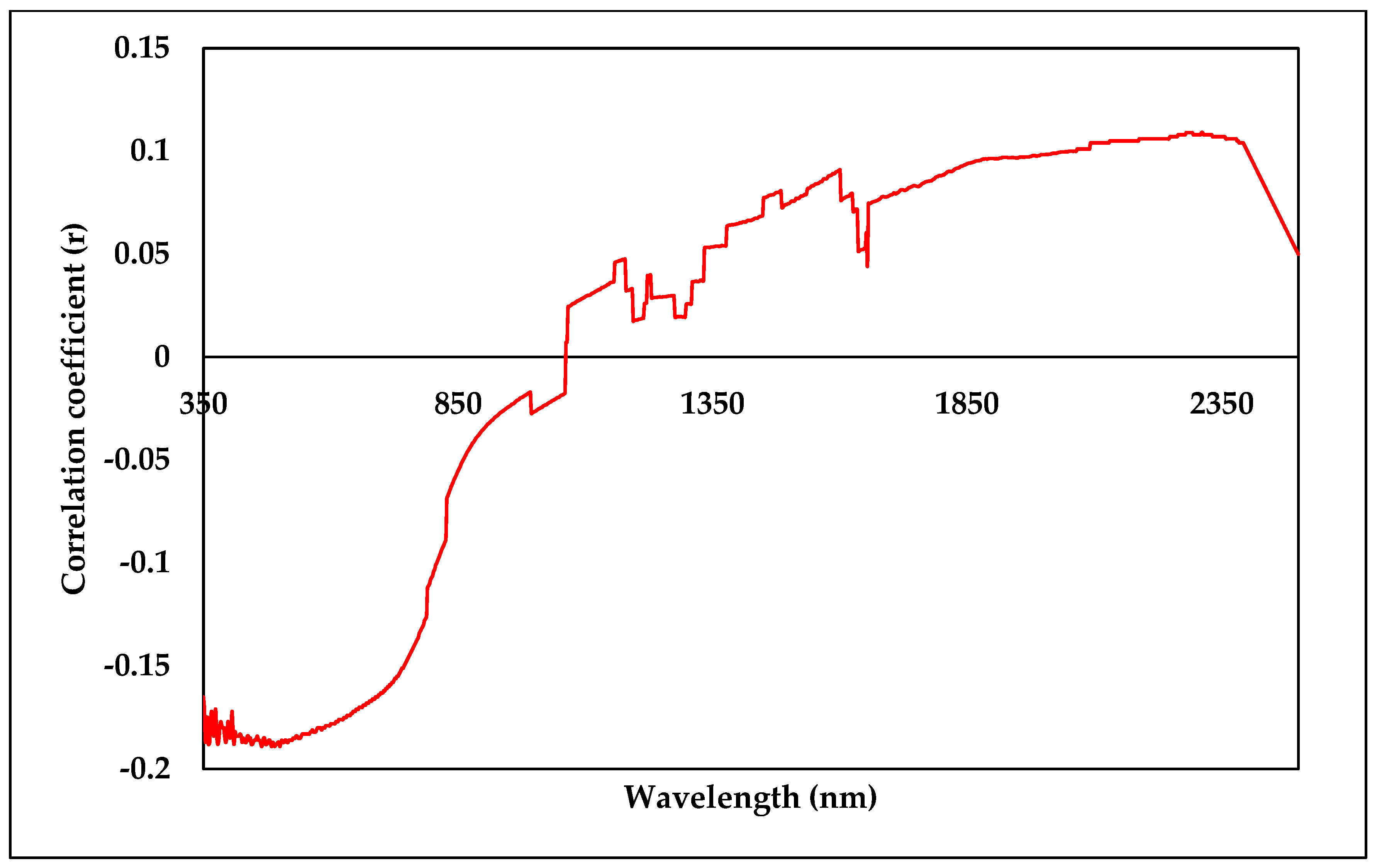
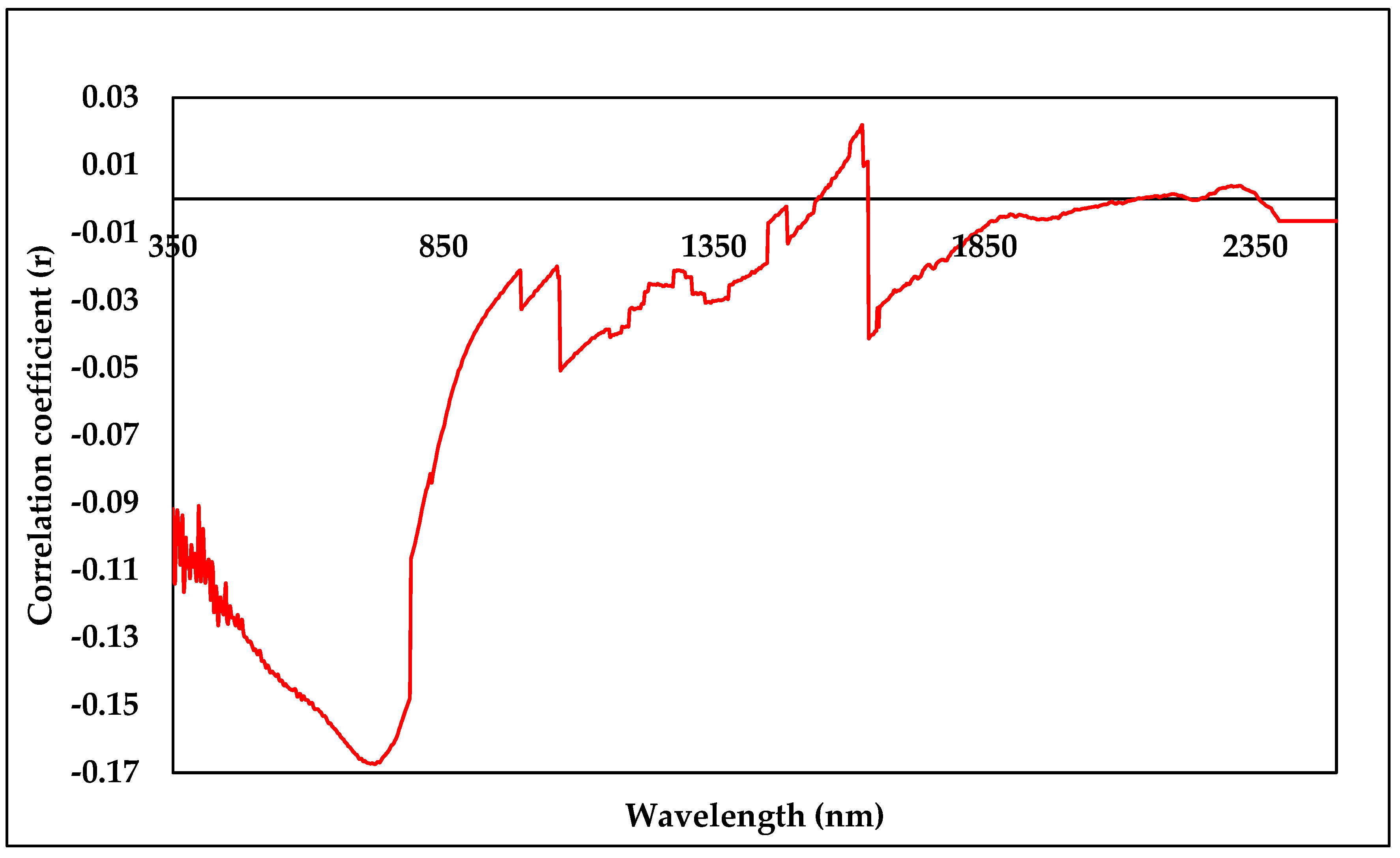
3.5. Correlation between Spectral Reflectance and EF-Factor
3.6. Model Development
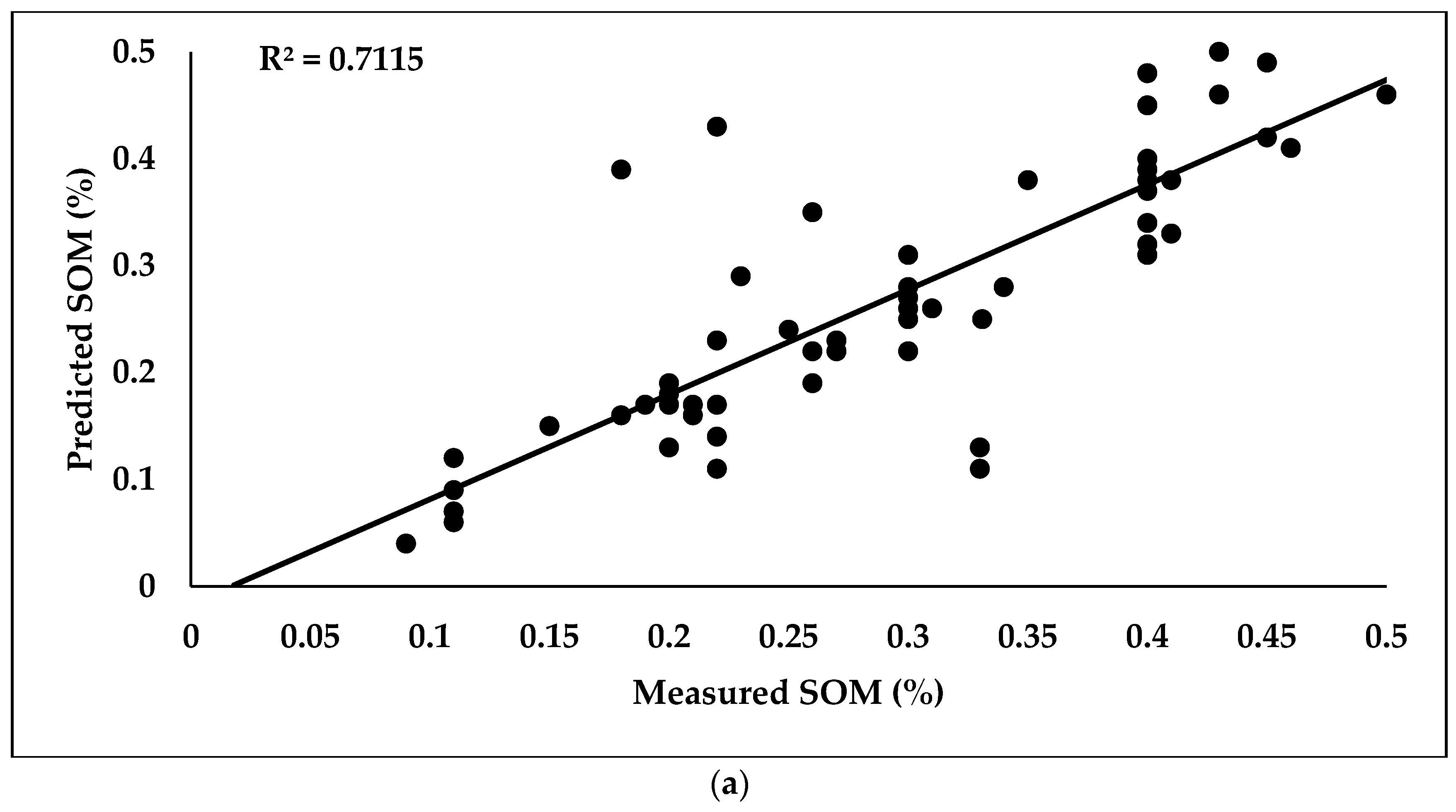
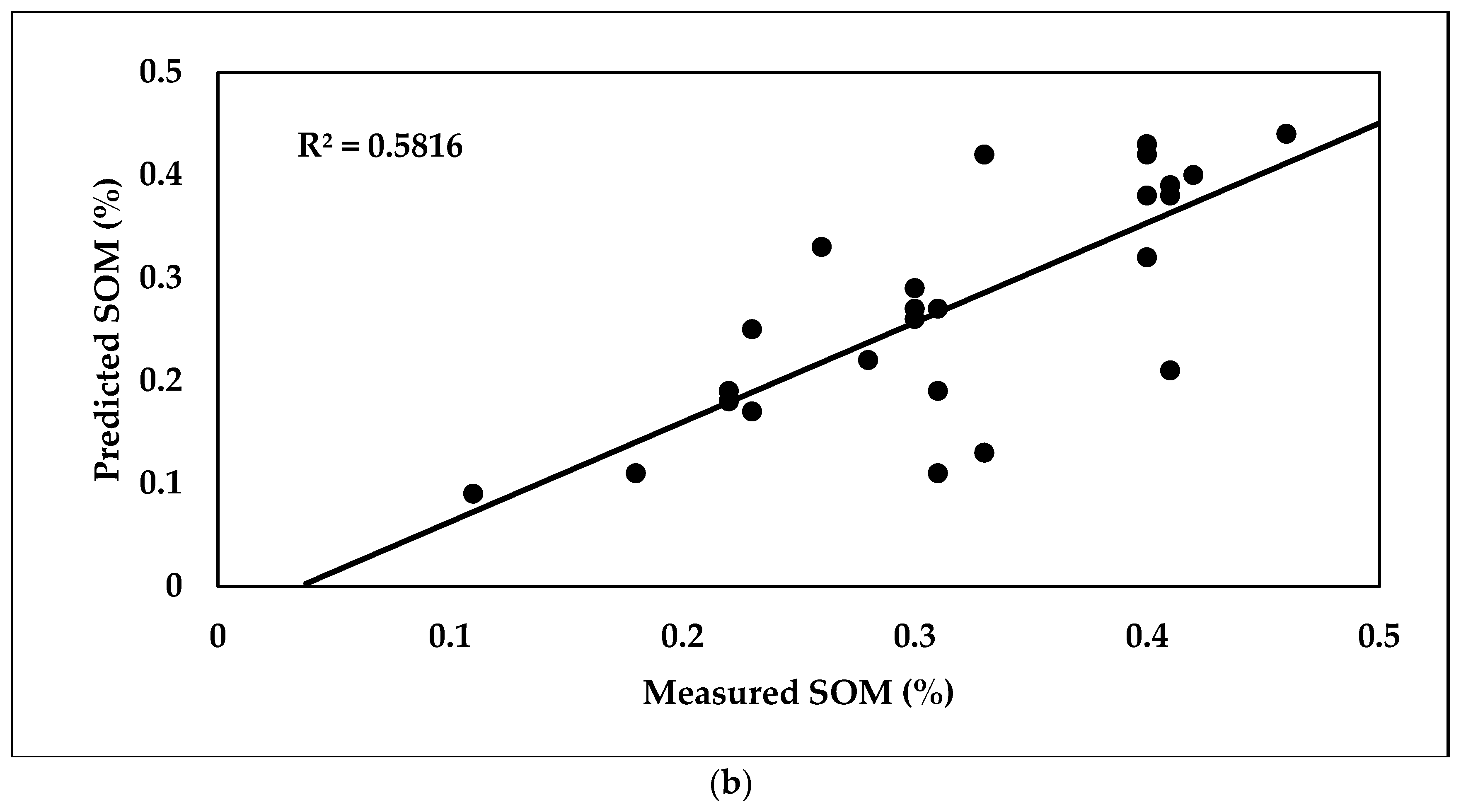
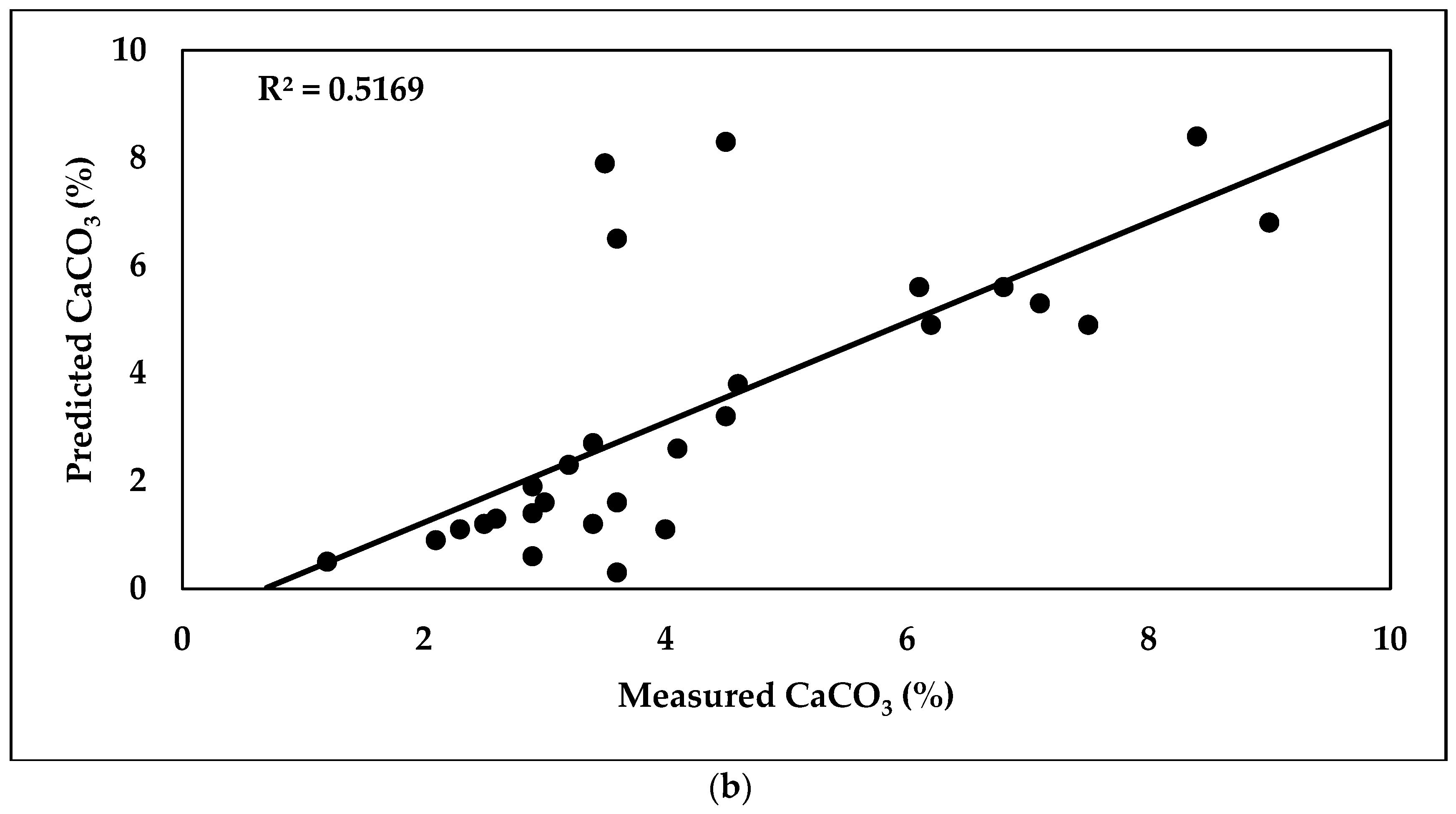
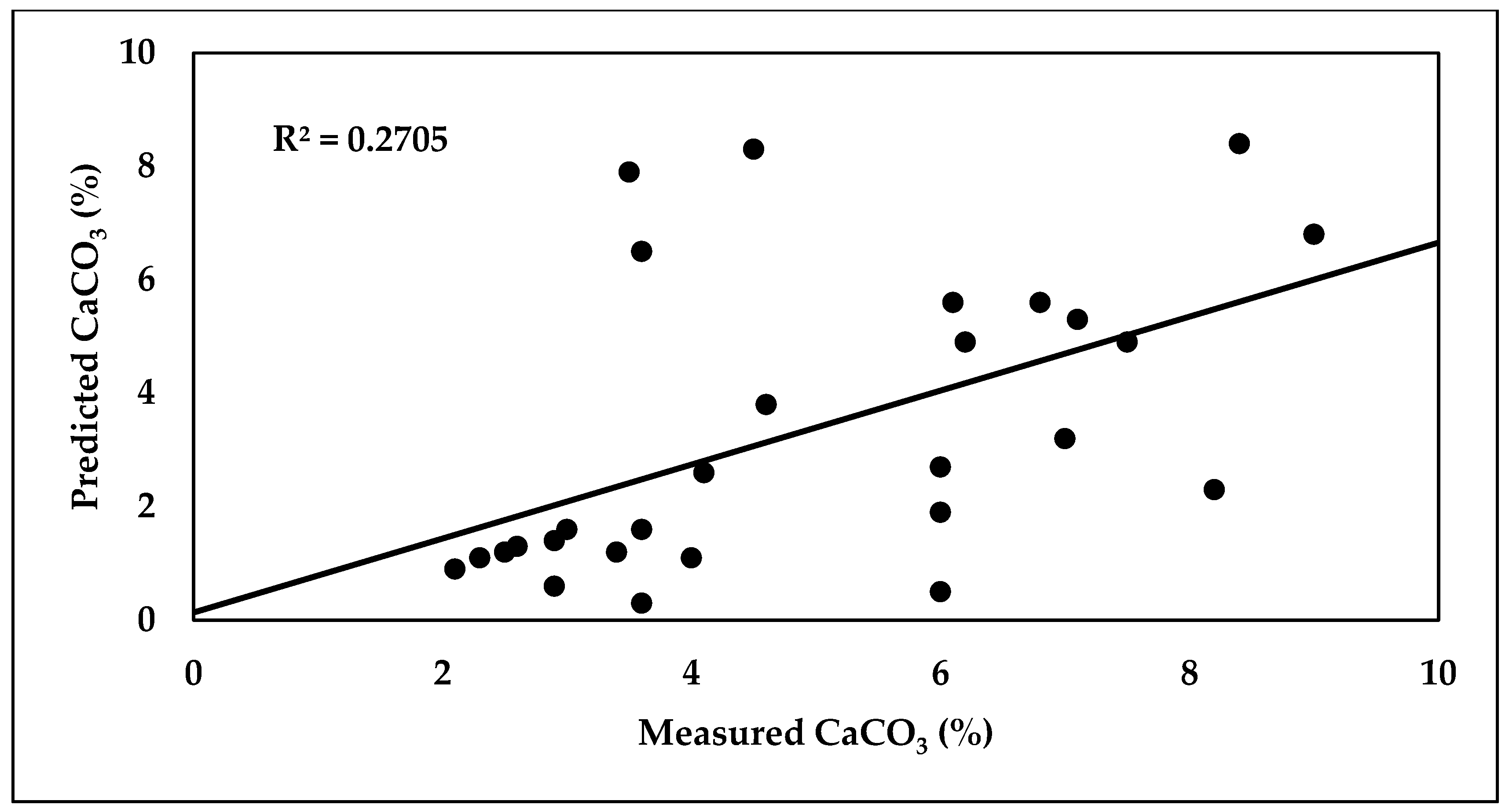
3.6.1. Prediction of SOM and CaCO3 Using PLSR Model
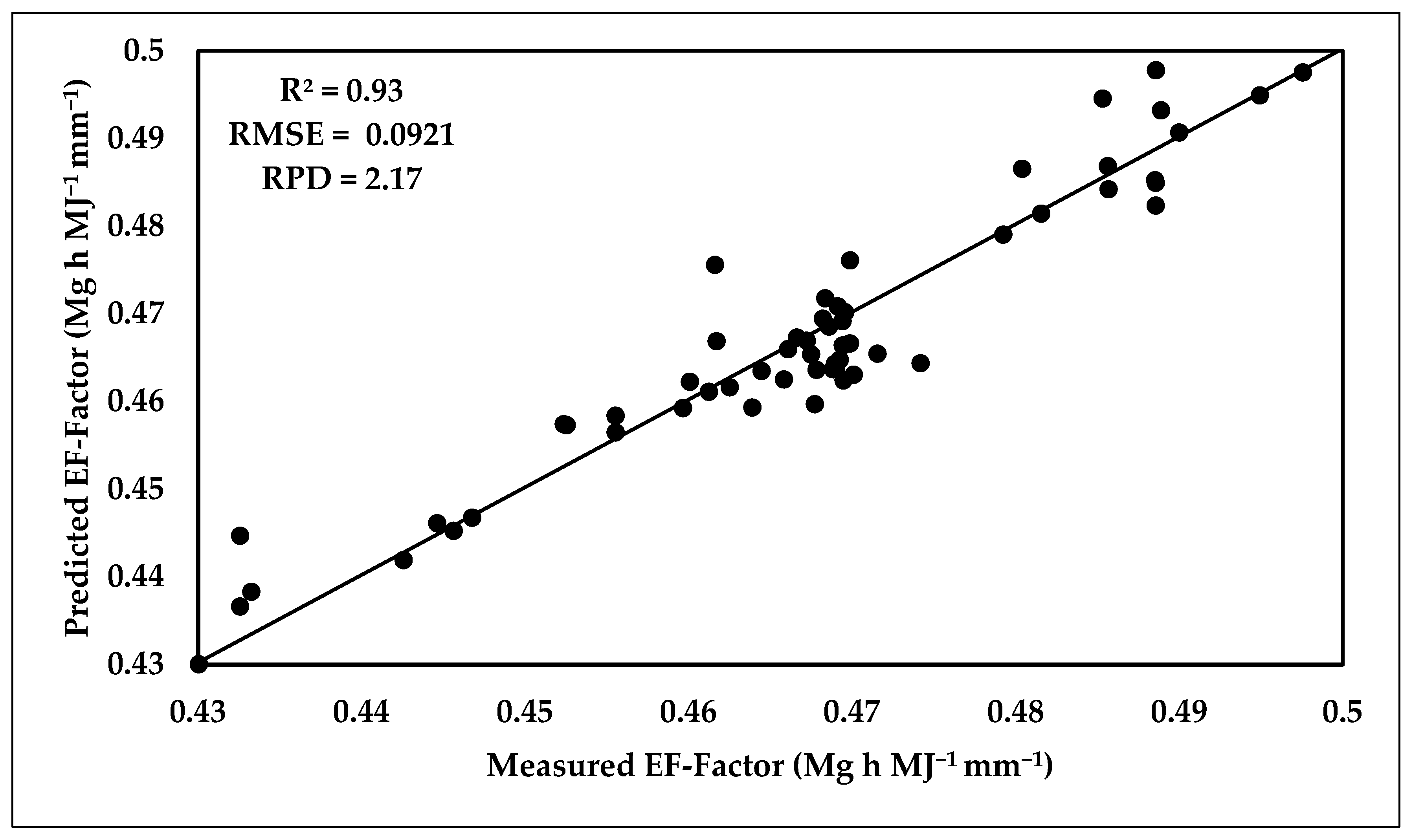
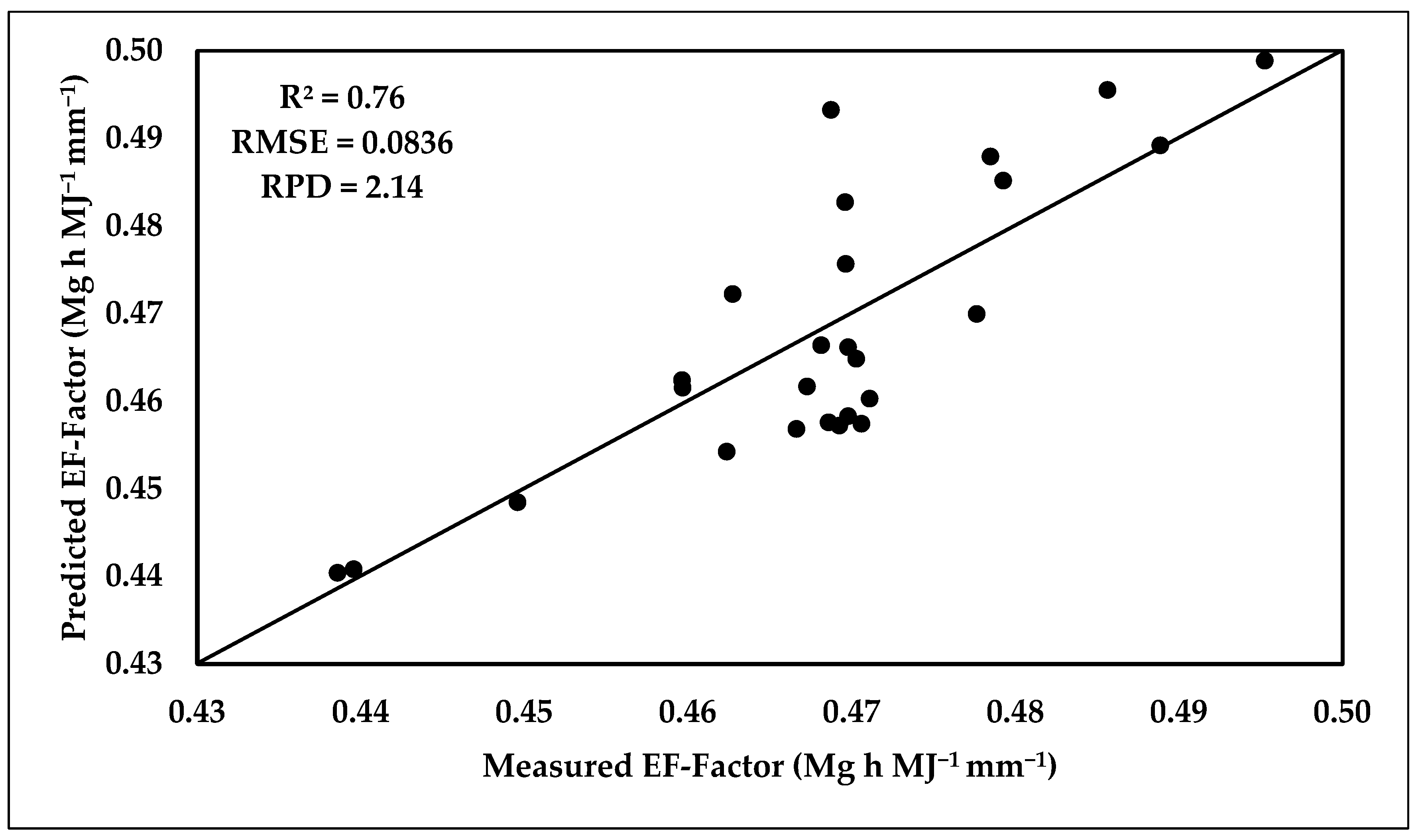
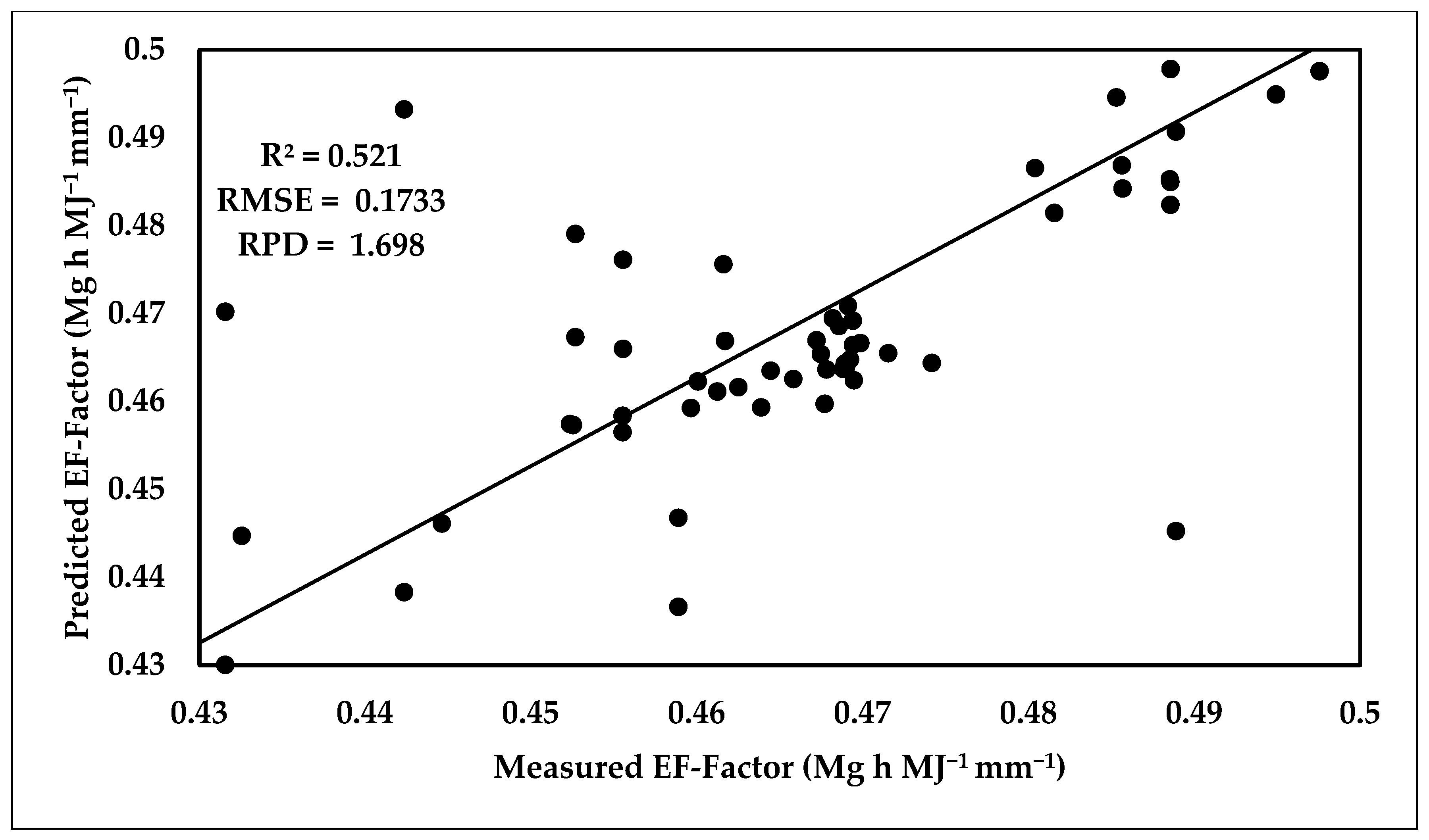
3.6.2. Prediction of EF-Factor Using PLSR Model
3.6.3. Model Validation
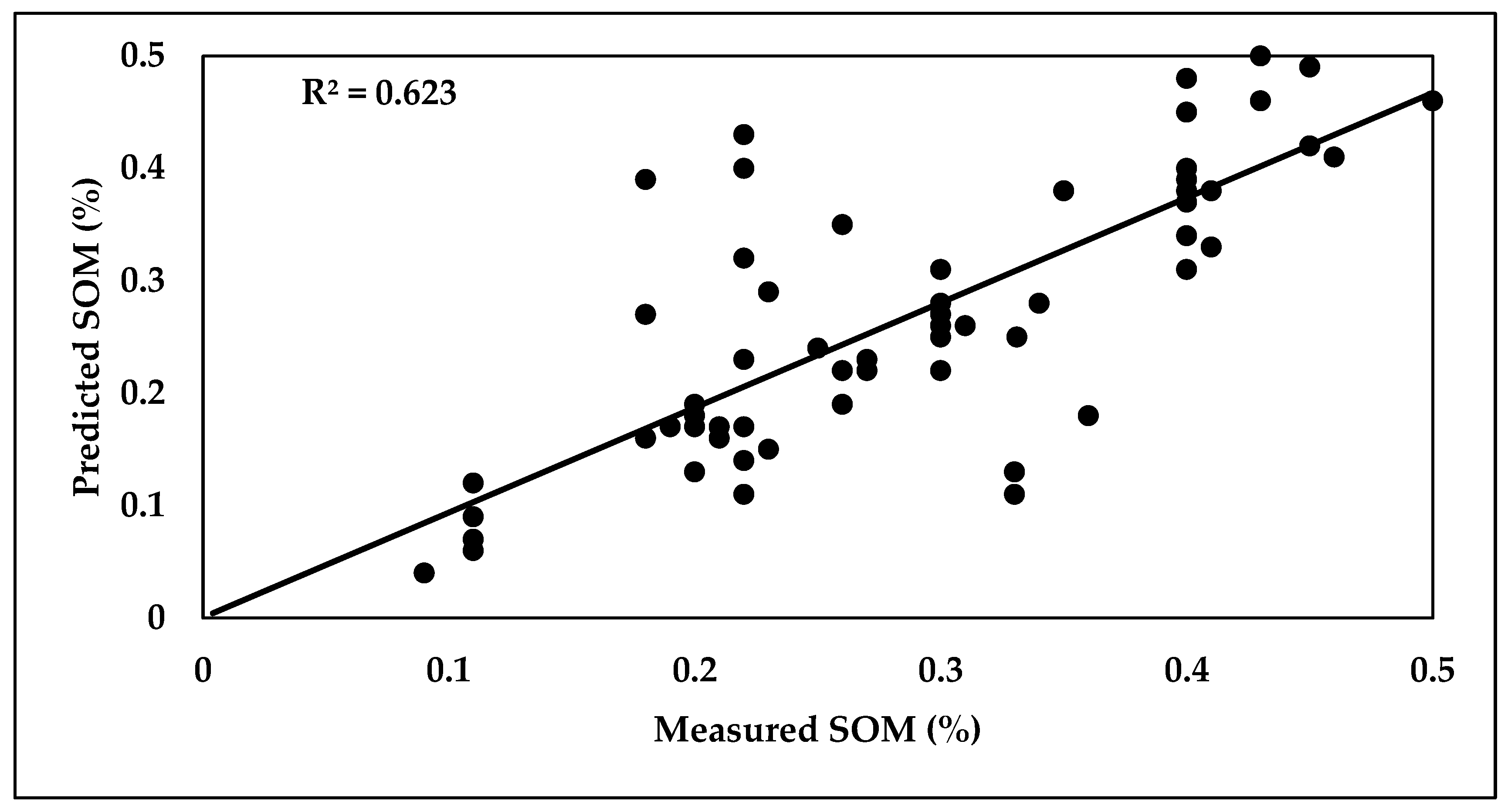
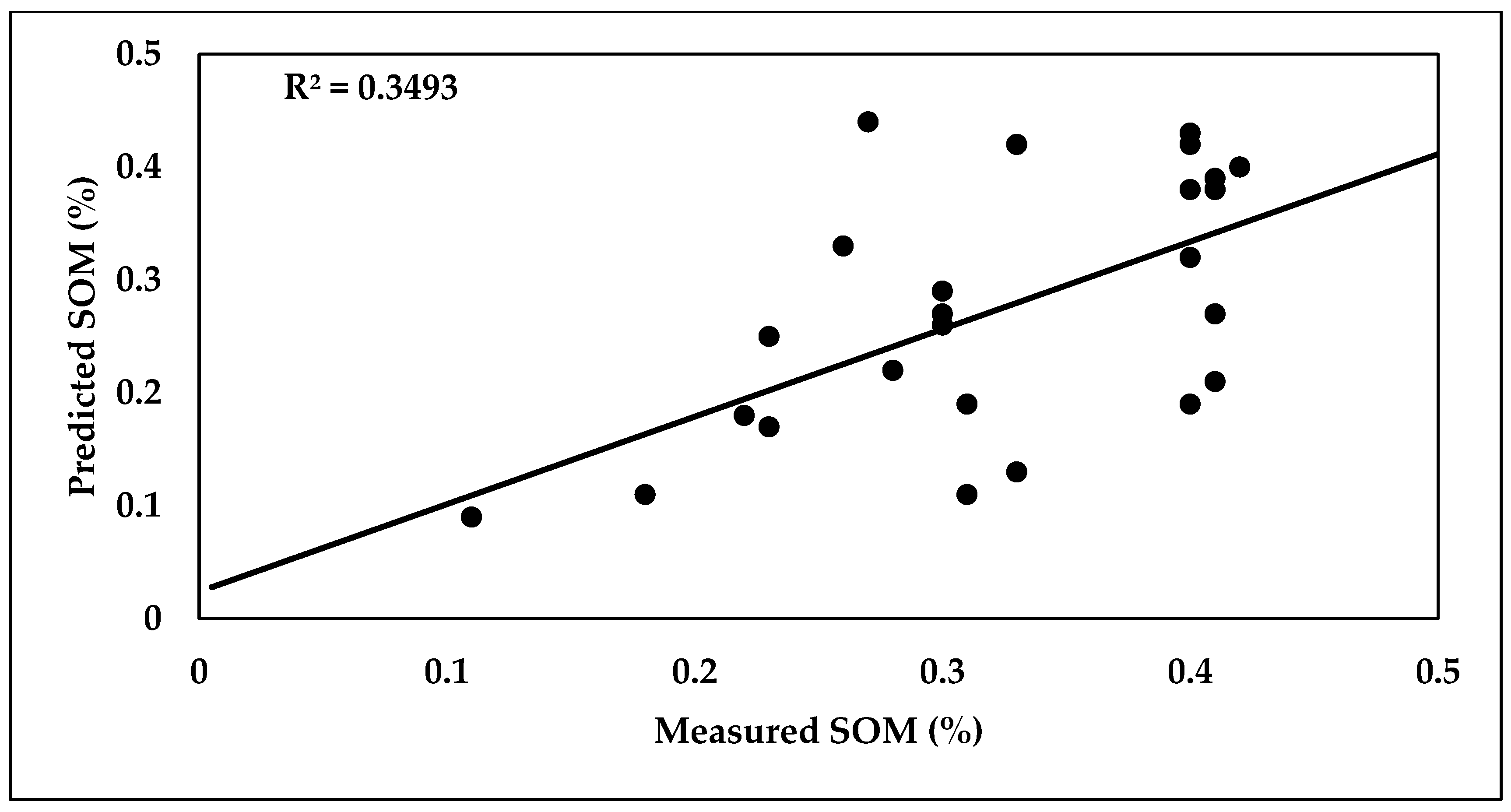
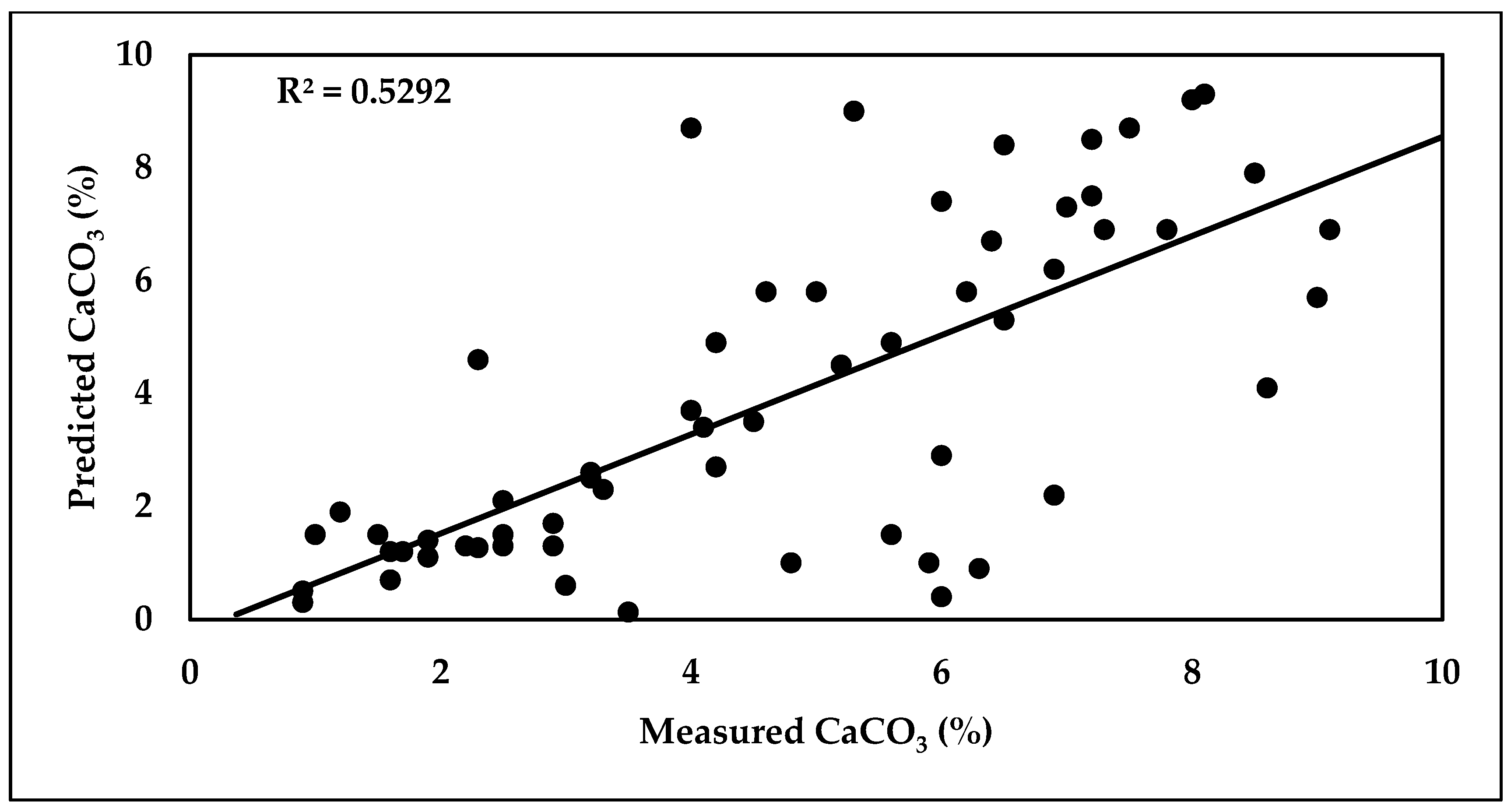
3.6.4. Prediction of SOM, CaCO3, and EF-Factor Using the SVM Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riedel, F.; Denk, M.; Müller, I.; Barth, N.; Gläßer, C. Prediction of soil parameters using the spectral range between 350 and 15,000 nm: A case study based on the Permanent Soil Monitoring Program in Saxony, Germany. Geoderma 2018, 315, 188–198. [Google Scholar] [CrossRef]
- Rossel, R.V.; McGlynn, R.; McBratney, A. Determining the composition of mineral-organic mixes using UV–vis–NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Renard, K.G. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); US Department of Agriculture, Agricultural Research Service: Beltsville, MD, USA, 1997.
- Millward, A.A.; Mersey, J.E. Adapting the RUSLE to model soil erosion potential in a mountainous tropical watershed. Catena 1999, 38, 109–129. [Google Scholar] [CrossRef]
- Selmy, S.A.; Abd Al-Aziz, S.H.; Jiménez-Ballesta, R.; García-Navarro, F.J.; Fadl, M.E. Soil quality assessment using multivariate approaches: A case study of the dakhla oasis arid lands. Land 2021, 10, 1074. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978.
- Nikseresht, F.; Honarbakhsh, A.; Ostovari, Y.; Afzali, S.F. Model development to predict CEC using the intelligence data mining approaches. Commun. Soil Sci. Plant Anal. 2019, 50, 2178–2189. [Google Scholar] [CrossRef]
- Mirzaee, S.; Ghorbani-Dashtaki, S.; Kerry, R. Comparison of a spatial, spatial and hybrid methods for predicting inter-rill and rill soil sensitivity to erosion at the field scale. Catena 2020, 188, 104439. [Google Scholar] [CrossRef]
- Wang, G.; Fang, Q.; Teng, Y.; Yu, J. Determination of the factors governing soil erodibility using hyperspectral visible and near-infrared reflectance spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 48–63. [Google Scholar] [CrossRef]
- Afriyie, E.; Verdoodt, A.; Mouazen, A.M. Potential of visible-near infrared spectroscopy for the determination of three soil aggregate stability indices. Soil Tillage Res. 2022, 215, 105218. [Google Scholar] [CrossRef]
- de Santana, F.B.; de Souza, A.M.; Poppi, R.J. Visible and near infrared spectroscopy coupled to random forest to quantify some soil quality parameters. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 191, 454–462. [Google Scholar] [CrossRef] [PubMed]
- Kim, I.; Pullanagari, R.; Deurer, M.; Singh, R.; Huh, K.; Clothier, B. The use of visible and near-infrared spectroscopy for the analysis of soil water repellency. Eur. J. Soil Sci. 2014, 65, 360–368. [Google Scholar] [CrossRef]
- Afriyie, E.; Verdoodt, A.; Mouazen, A.M. Data fusion of visible near-infrared and mid-infrared spectroscopy for rapid estimation of soil aggregate stability indices. Comput. Electron. Agric. 2021, 187, 106229. [Google Scholar] [CrossRef]
- Ostovari, Y.; Ghorbani-Dashtaki, S.; Bahrami, H.-A.; Abbasi, M.; Dematte, J.A.M.; Arthur, E.; Panagos, P. Towards prediction of soil erodibility, SOM and CaCO3 using laboratory Vis-NIR spectra: A case study in a semi-arid region of Iran. Geoderma 2018, 314, 102–112. [Google Scholar] [CrossRef]
- Khayamim, F.; Khademi, H.; Stenberg, B.; Wetterlind, J. Capability of vis-NIR spectroscopy to predict selected chemical soil properties in Isfahan Province. JWSS-Isfahan Univ. Technol. 2015, 19, 81–92. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; McBratney, A. Near-infrared (NIR) and mid-infrared (MIR) spectroscopic techniques for assessing the amount of carbon stock in soils–Critical review and research perspectives. Soil Biol. Biochem. 2011, 43, 1398–1410. [Google Scholar] [CrossRef]
- Dufréchou, G.; Grandjean, G.; Bourguignon, A. Geometrical analysis of laboratory soil spectra in the short-wave infrared domain: Clay composition and estimation of the swelling potential. Geoderma 2015, 243, 92–107. [Google Scholar] [CrossRef]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Continuum removal versus PLSR method for clay and calcium carbonate content estimation from laboratory and airborne hyperspectral measurements. Geoderma 2008, 148, 141–148. [Google Scholar] [CrossRef]
- Chabrillat, S.; Goetz, A.F.; Krosley, L.; Olsen, H.W. Use of hyperspectral images in the identification and mapping of expansive clay soils and the role of spatial resolution. Remote Sens. Environ. 2002, 82, 431–445. [Google Scholar] [CrossRef]
- Lin, C.; Zhou, S.-L.; Wu, S.-H. Using hyperspectral reflectance to detect different soil erosion status in the Subtropical Hilly Region of Southern China: A case study of Changting, Fujian Province. Environ. Earth Sci. 2013, 70, 1661–1670. [Google Scholar] [CrossRef]
- Sayed, Y.A.; Fadl, M.E. Agricultural sustainability evaluation of the new reclaimed soils at Dairut Area, Assiut, Egypt using GIS modeling. Egypt. J. Remote Sens. Space Sci. 2021, 24, 707–719. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service; Agriculture Department (Eds.) Keys to Soil Taxonomy; Government Printing Office: Washington, DC, USA, 2010. [Google Scholar]
- Embabi, N.S. The karstified carbonate platforms in the Western Desert. In Landscapes and Landforms of Egypt: Landforms and Evolution; Springer: Cham, Switzerland, 2018; pp. 85–104. [Google Scholar] [CrossRef]
- Jahn, R.; Blume, H.; Asio, V.; Spaargaren, O.; Schad, P. Guidelines for Soil Description, 4th ed.; FAO: Rome, Italy, 2006; p. 109. [Google Scholar]
- Staff, S.S. Keys to Soil Taxonomy; United States Department of Agriculture: Washington, DC, USA, 2014.
- Gee, G.W.; Or, D. 2.4 Particle-size analysis. Methods Soil Anal. Part 4 Phys. Methods 2002, 5, 255–293. [Google Scholar]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Wischmeier, W.H. A rainfall erosion index for a universal soil-loss equation. Soil Sci. Soc. Am. J. 1959, 23, 246–249. [Google Scholar] [CrossRef]
- Fryrear, D.; Krammes, C.; Williamson, D.; Zobeck, T. Computing the wind erodible fraction of soils. J. Soil Water Conserv. 1994, 49, 183–188. [Google Scholar]
- Weidong, L.; Baret, F.; Xingfa, G.; Qingxi, T.; Lanfen, Z.; Bing, Z. Relating soil surface moisture to reflectance. Remote Sens. Environ. 2002, 81, 238–246. [Google Scholar] [CrossRef]
- Rossel, R.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Banin, A. Near-infrared analysis as a rapid method to simultaneously evaluate several soil properties. Soil Sci. Soc. Am. J. 1995, 59, 364–372. [Google Scholar] [CrossRef]
- Jiang, Q.; Chen, Y.; Hu, J.; Liu, F. Use of visible and near-infrared reflectance spectroscopy models to determine soil erodibility factor (K) in an ecologically restored watershed. Remote Sens. 2020, 12, 3103. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Oak Brook, IL, USA, 2021; p. 704. [Google Scholar]
- Martens, H.; Naes, T. Multivariate Calibration; John Wiley and Sons: Chichester, UK, 1992. [Google Scholar]
- Malone, B.P.; Minasny, B.; Odgers, N.P.; McBratney, A.B. Using model averaging to combine soil property rasters from legacy soil maps and from point data. Geoderma 2014, 232, 34–44. [Google Scholar] [CrossRef]
- Diks, C.G.; Vrugt, J.A. Comparison of point forecast accuracy of model averaging methods in hydrologic applications. Stoch. Environ. Res. Risk Assess. 2010, 24, 809–820. [Google Scholar] [CrossRef]
- Dondeyne, S.; Vanierschot, L.; Langohr, R.; Van Ranst, E.; Deckers, S. The Soil Map of the Flemish Region Converted to the 3rd Edition of the World Reference Base for Soil Resources. 2014. Available online: https://scholar.google.com/citations?view_op=view_citation&hl=en&user=Aeo6mzgAAAAJ&citation_for_view=Aeo6mzgAAAAJ:NhqRSupF_l8C (accessed on 25 March 2024).
- Granger, C.W.; Ramanathan, R. Improved methods of combining forecasts. J. Forecast. 1984, 3, 197–204. [Google Scholar] [CrossRef]
- Bates, J.M.; Granger, C.W. The combination of forecasts. J. Oper. Res. Soc. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial (with comments by M. Clyde, David Draper and EI George, and a rejoinder by the authors. Stat. Sci. 1999, 14, 382–417. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Rossel, R.V.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Box, G.E.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Stat. Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Enders, A.; North, N.; Clark, J.; Allen, H. Saccharide concentration prediction from proxy-sea surface microlayer samples analyzed via ATR-ATR-FTIR spectroscopy and quantitative machine learning. Anal. Chem. 2023, preprint. [Google Scholar] [CrossRef]
- Stenberg, B. Effects of soil sample pretreatments and standardized rewetting as interacted with sand classes on Vis-NIR predictions of clay and soil organic carbon. Geoderma 2010, 158, 15–22. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000; p. 314. [Google Scholar] [CrossRef]
- De Brabanter, K.; De Brabanter, J.; Gijbels, I.; De Moor, B. Derivative estimation with local polynomial fitting. J. Mach. Learn. Res. 2013, 14, 281–301. [Google Scholar]
- Stone, M. Cross-validation and multinomial prediction. Biometrika 1974, 61, 509–515. [Google Scholar] [CrossRef]
- Suykens, J.A.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Jobson, J.D. Applied Multivariate Data Analysis: Regression and Experimental Design; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Li, S.; Ji, W.; Chen, S.; Peng, J.; Zhou, Y.; Shi, Z. Potential of VIS-NIR-SWIR spectroscopy from the Chinese Soil Spectral Library for assessment of nitrogen fertilization rates in the paddy-rice region, China. Remote Sens. 2015, 7, 7029–7043. [Google Scholar] [CrossRef]
- El-Sayed, M.A.; Abd-Elazem, A.H.; Moursy, A.R.; Mohamed, E.S.; Kucher, D.E.; Fadl, M.E. Integration Vis-NIR Spectroscopy and Artificial Intelligence to Predict Some Soil Parameters in Arid Region: A Case Study of Wadi Elkobaneyya, South Egypt. Agronomy 2023, 13, 935. [Google Scholar] [CrossRef]
- Bonilla, C.A.; Johnson, O.I. Soil erodibility mapping and its correlation with soil properties in Central Chile. Geoderma 2012, 189, 116–123. [Google Scholar] [CrossRef]
- Rossel, R.V. Robust modelling of soil diffuse reflectance spectra by “bagging-partial least squares regression”. J. Near Infrared Spectrosc. 2007, 15, 39–47. [Google Scholar] [CrossRef]
- Bowers, S.A. Reflection of Radiant Energy from Soils; Kansas State University: Manhattan, AR, USA, 1971. [Google Scholar]
- Selmy, S.A.; Abd Al-Aziz, S.H.; Jiménez-Ballesta, R.; García-Navarro, F.J.; Fadl, M.E. Modeling and assessing potential soil erosion hazards using USLE and wind erosion models in integration with gis techniques: Dakhla oasis, Egypt. Agriculture 2021, 11, 1124. [Google Scholar] [CrossRef]
- Clark, R.N.; Rencz, A.N. Spectroscopy of rocks and minerals, and principles of spectroscopy. Man. Remote Sens. 1999, 3, 3–58. [Google Scholar]
- He, G.; Zhang, Z.; Wu, X.; Cui, M.; Zhang, J.; Huang, X. Adsorption of heavy metals on soil collected from Lixisol of typical karst areas in the presence of CaCO3 and soil clay and their competition behavior. Sustainability 2020, 12, 7315. [Google Scholar] [CrossRef]
- Girard, M.; Girard, C. Télédétection Appliquée: Zones Tempérées et Intertropicales; Elsevier Mason SAS: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Hunt, G.R. Visible and near-infrared spectra of minerals and rocks: III. Oxides and hydro-oxides. Mod. Geol. 1971, 2, 195–205. [Google Scholar]
- Yang, M.; Xu, D.; Chen, S.; Li, H.; Shi, Z. Evaluation of machine learning approaches to predict soil organic matter and pH using Vis-NIR spectra. Sensors 2019, 19, 263. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, E.S.; Baroudy, A.A.E.; El-beshbeshy, T.; Emam, M.; Belal, A.; Elfadaly, A.; Aldosari, A.A.; Ali, A.M.; Lasaponara, R. Vis-nir spectroscopy and satellite landsat-8 oli data to map soil nutrients in arid conditions: A case study of the northwest coast of egypt. Remote Sens. 2020, 12, 3716. [Google Scholar] [CrossRef]
- Zhang, X.; Xue, J.; Xiao, Y.; Shi, Z.; Chen, S. Towards Optimal Variable Selection Methods for Soil Property Prediction Using a Regional Soil Vis-NIR Spectral Library. Remote Sens. 2023, 15, 465. [Google Scholar] [CrossRef]
- Alomar, S.; Mireei, S.A.; Hemmat, A.; Masoumi, A.A.; Khademi, H. Prediction and variability mapping of some physicochemical characteristics of calcareous topsoil in an arid region using Vis–SWNIR and NIR spectroscopy. Sci. Rep. 2022, 12, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Saha, P.; Debnath, P.; Thomas, P. Prediction of fresh and hardened properties of self-compacting concrete using support vector regression approach. Neural Comput. Appl. 2020, 32, 7995–8010. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.G.; Tian, Y.C.; Burrage, K.; Cao, T. Support vector regression with asymmetric loss for optimal electric load forecasting. Energy 2021, 223, 119969. [Google Scholar] [CrossRef]
- Chaibi, M.; Benghoulam, E.M.; Tarik, L.; Berrada, M.; Hmaidi, A.E. An interpretable machine learning model for daily global solar radiation prediction. Energies 2021, 14, 7367. [Google Scholar] [CrossRef]
- Sabzekar, M.; Hasheminejad, S.M.H. Robust regression using support vector regressions. Chaos Solitons Fractals 2021, 144, 110738. [Google Scholar] [CrossRef]
- Afriyie, E.; Verdoodt, A.; Mouazen, A.M. Estimation of aggregate stability of some soils in the loam belt of Belgium using mid-infrared spectroscopy. Sci. Total Environ. 2020, 744, 140727. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]






| Climate Data for Aswan, Egypt | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | Year |
| High Temp * °C | 35.3 | 38.5 | 44 | 46.1 | 47.8 | 50.6 | 51 | 48 | 47.8 | 45.4 | 42.2 | 38.6 | 44.61 |
| Average Temp °C | 22.9 | 25.2 | 29.5 | 34.9 | 38.9 | 41.4 | 41.1 | 40.9 | 39.3 | 35.9 | 29.1 | 24.3 | 33.62 |
| Low Temp °C | 2.4 | 3.8 | 5 | 7.8 | 13.4 | 18.9 | 20 | 20 | 16.1 | 12.2 | 6.1 | 0.6 | 11.26 |
| Average rainfall mm | 0 | 0 | 0 | 0 | 0.1 | 0 | 0 | 0.7 | 0 | 0.6 | 0 | 0 | 0.12 |
| Average relative humidity (%) | 40 | 32 | 24 | 19 | 17 | 16 | 18 | 21 | 22 | 27 | 36 | 42 | 26.17 |
| Soil Properties | ||||||||
|---|---|---|---|---|---|---|---|---|
| Statistical Parameters | % Silt | % Sand | % Clay | % OM | % CaCO3 | pH (1:2.5 w/v) | EC (mS cm−1) | EF-Factor |
| Maximum | 24.67 | 94.26 | 11.59 | 0.50 | 9.40 | 8.67 | 2.65 | 0.68 |
| Minimum | 2.11 | 66.95 | 3.08 | 0.04 | 0.04 | 6.54 | 0.22 | 0.46 |
| Average | 8.93 | 84.38 | 6.69 | 0.22 | 1.60 | 7.97 | 0.70 | 0.59 |
| SD | 6.93 | 8.32 | 2.18 | 0.11 | 1.91 | 0.37 | 0.40 | 0.04 |
| CV | 77.63 | 9.86 | 32.51 | 51.66 | 119.62 | 4.64 | 56.32 | 7.58 |
| Sample Count | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 |
| % Silt | % Sand | % Clay | % OM | % CaCO3 | pH (1:2.5) w/v) | EC (mS cm−1) | EF-Factor | |
|---|---|---|---|---|---|---|---|---|
| Silt (%) | 1 | |||||||
| Sand (%) | −0.934 ** | 1 | ||||||
| Clay (%) | 0.415 ** | −0.754 ** | 1 | |||||
| OM (%) | 0.001 | −0.262 ** | 0.606 ** | 1 | ||||
| CaCO3 (%) | 0.113 | −0.091 | 0.02 | −0.036 | 1 | |||
| pH (1:2.5 w/v) | −0.117 | 0.174 | −0.220 * | −0.382 ** | 0.104 | 1 | ||
| EC (mS/cm) | −0.236 * | 0.236 * | −0.146 | −0.195 | 0.039 | −0.054 | 1 | |
| EF-Factor | 0.191 | 0.541 ** | 0.423 ** | 0.814 ** | 0.780 ** | −0.154 | −0.16 | 1 |
| EF-Factor | |||||||
| r | −0.0151 | −0.0176 | −0.0356 | 0.0457 | −0.0758 | −0.2120 | 0.3720 |
| Wavelengths (nm) | 526 | 688 | 744 | 1418 | 1442 | 2292 | 2374 |
| SOM | |||||||
| r | 0.0181 | 0.0196 | −0.0281 | 0.0540 | −0.0801 | −0.1130 | −0.1210 |
| Wavelengths (nm) | 496 | 658 | 779 | 1089 | 1417 | 1871 | 2423 |
| CaCO3 | |||||||
| r | −0.1850 | −0.1700 | −0.0975 | 0.0459 | 0.0679 | 0.0946 | 0.1070 |
| Wavelengths (nm) | 470 | 649 | 802 | 1161 | 1421 | 1854 | 2362 |
| Soil Parameter | Calibration Data-Set | Validation Data-Set | ||||||
| n | RMSE | RPD | R2 | n | RMSE | RPD | R2 | |
| PLSR Model | ||||||||
| SOM (%) | 65 | 0.0714 | 2.190 | 0.71 | 26 | 0.0683 | 2.137 | 0.58 |
| CaCO3 (%) | 63 | 0.0982 | 2.562 | 0.59 | 28 | 0.4163 | 1.936 | 0.52 |
| EF-Factor (Mg h MJ−1 mm−1) | 62 | 0.0921 | 2.168 | 0.931 | 27 | 0.0836 | 2.147 | 0.76 |
| Soil Parameter | SVM Model | |||||||
| SOM (%) | 67 | 0.0803 | 1.855 | 0.623 | 29 | 0.0827 | 1.101 | 0.35 |
| CaCO3 (%) | 67 | 0.1752 | 1.677 | 0.53 | 29 | 0.5889 | 0.995 | 0.27 |
| EF-Factor (Mg h MJ−1 mm−1) | 67 | 0.1733 | 1.698 | 0.52 | 29 | 0.1903 | 0.860 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-Elazem, A.H.; El-Sayed, M.A.; Fadl, M.E.; Zekari, M.; Selmy, S.A.H.; Drosos, M.; Scopa, A.; Moursy, A.R.A. Estimating Soil Erodible Fraction Using Multivariate Regression and Proximal Sensing Data in Arid Lands, South Egypt. Soil Syst. 2024, 8, 48. https://doi.org/10.3390/soilsystems8020048
Abd-Elazem AH, El-Sayed MA, Fadl ME, Zekari M, Selmy SAH, Drosos M, Scopa A, Moursy ARA. Estimating Soil Erodible Fraction Using Multivariate Regression and Proximal Sensing Data in Arid Lands, South Egypt. Soil Systems. 2024; 8(2):48. https://doi.org/10.3390/soilsystems8020048
Chicago/Turabian StyleAbd-Elazem, Alaa H., Moatez A. El-Sayed, Mohamed E. Fadl, Mohammedi Zekari, Salman A. H. Selmy, Marios Drosos, Antonio Scopa, and Ali R. A. Moursy. 2024. "Estimating Soil Erodible Fraction Using Multivariate Regression and Proximal Sensing Data in Arid Lands, South Egypt" Soil Systems 8, no. 2: 48. https://doi.org/10.3390/soilsystems8020048
APA StyleAbd-Elazem, A. H., El-Sayed, M. A., Fadl, M. E., Zekari, M., Selmy, S. A. H., Drosos, M., Scopa, A., & Moursy, A. R. A. (2024). Estimating Soil Erodible Fraction Using Multivariate Regression and Proximal Sensing Data in Arid Lands, South Egypt. Soil Systems, 8(2), 48. https://doi.org/10.3390/soilsystems8020048











