Reconciling Negative Soil CO2 Fluxes: Insights from a Large-Scale Experimental Hillslope
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site and Environmental Conditions
2.2. Environmental Measurements
2.3. CO2 Flux Estimation
2.4. Statistical Analysis
3. Results
3.1. General Environmental Conditions at LEO
3.2. Diurnal Variability
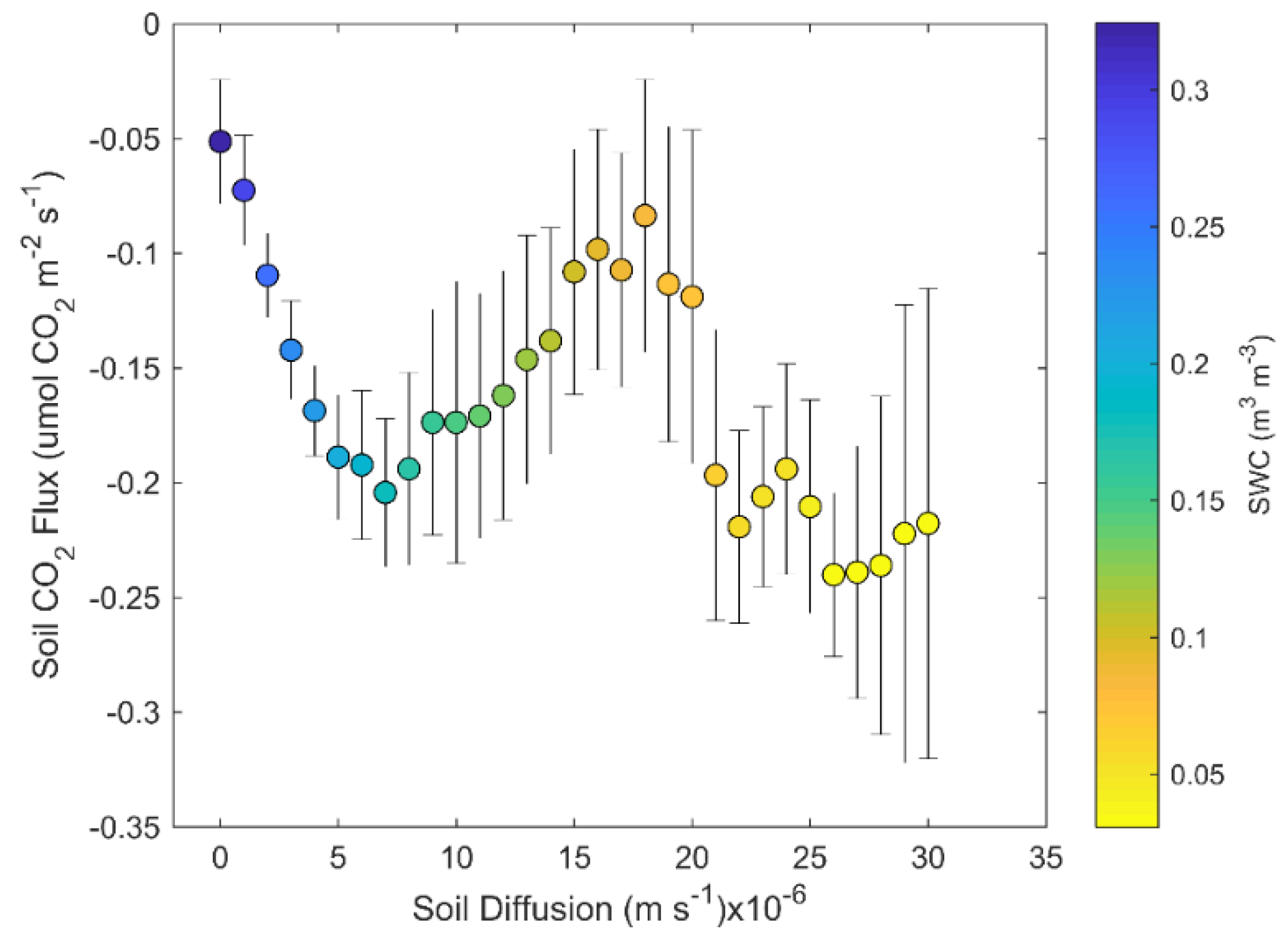
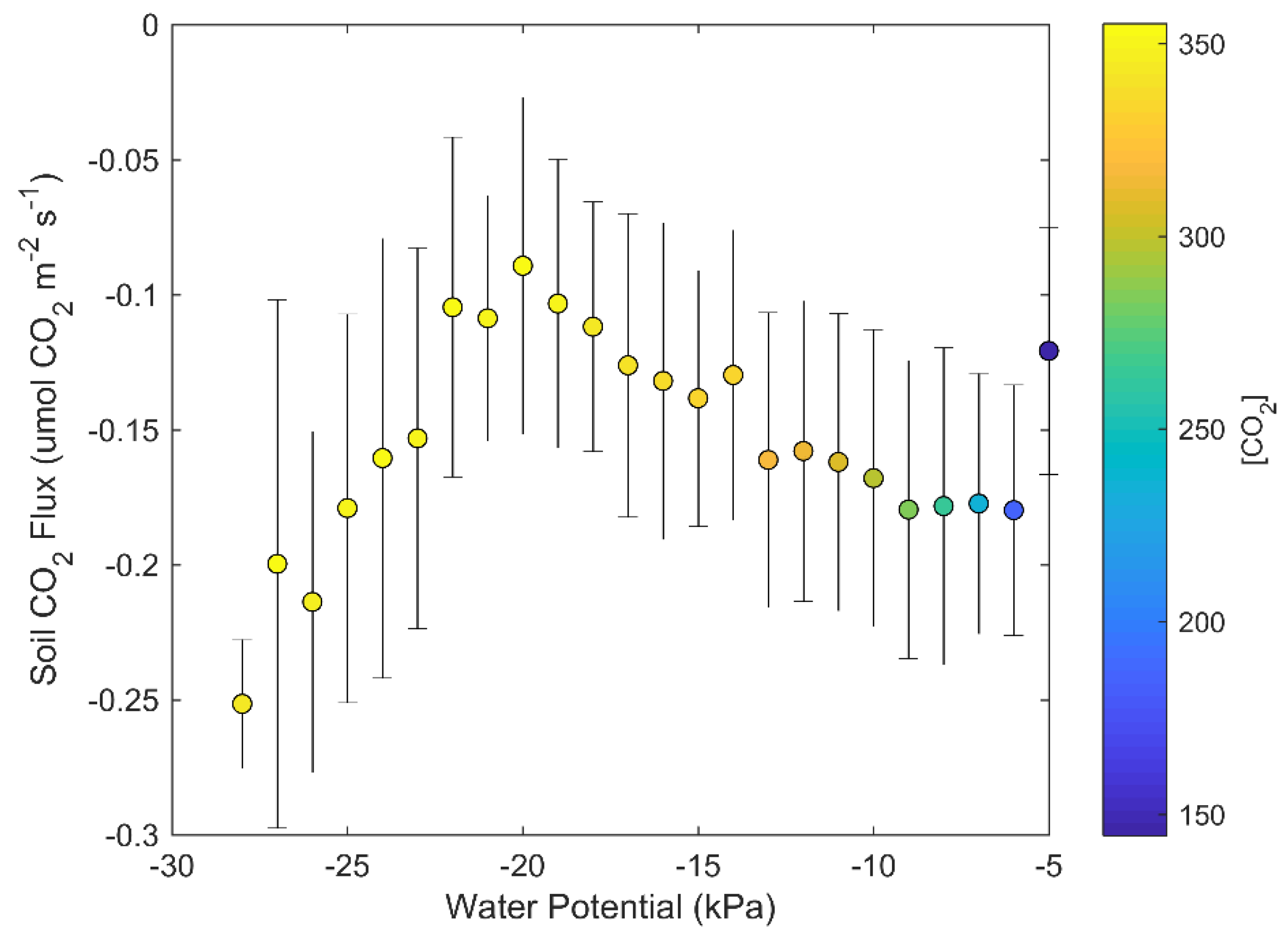
3.3. Physical Drivers of Negative Soil CO2 Fluxes
4. Discussion
4.1. Reversible Flux or Sequestration
4.2. Temporal Variability
4.3. Physical vs. Biological Drivers
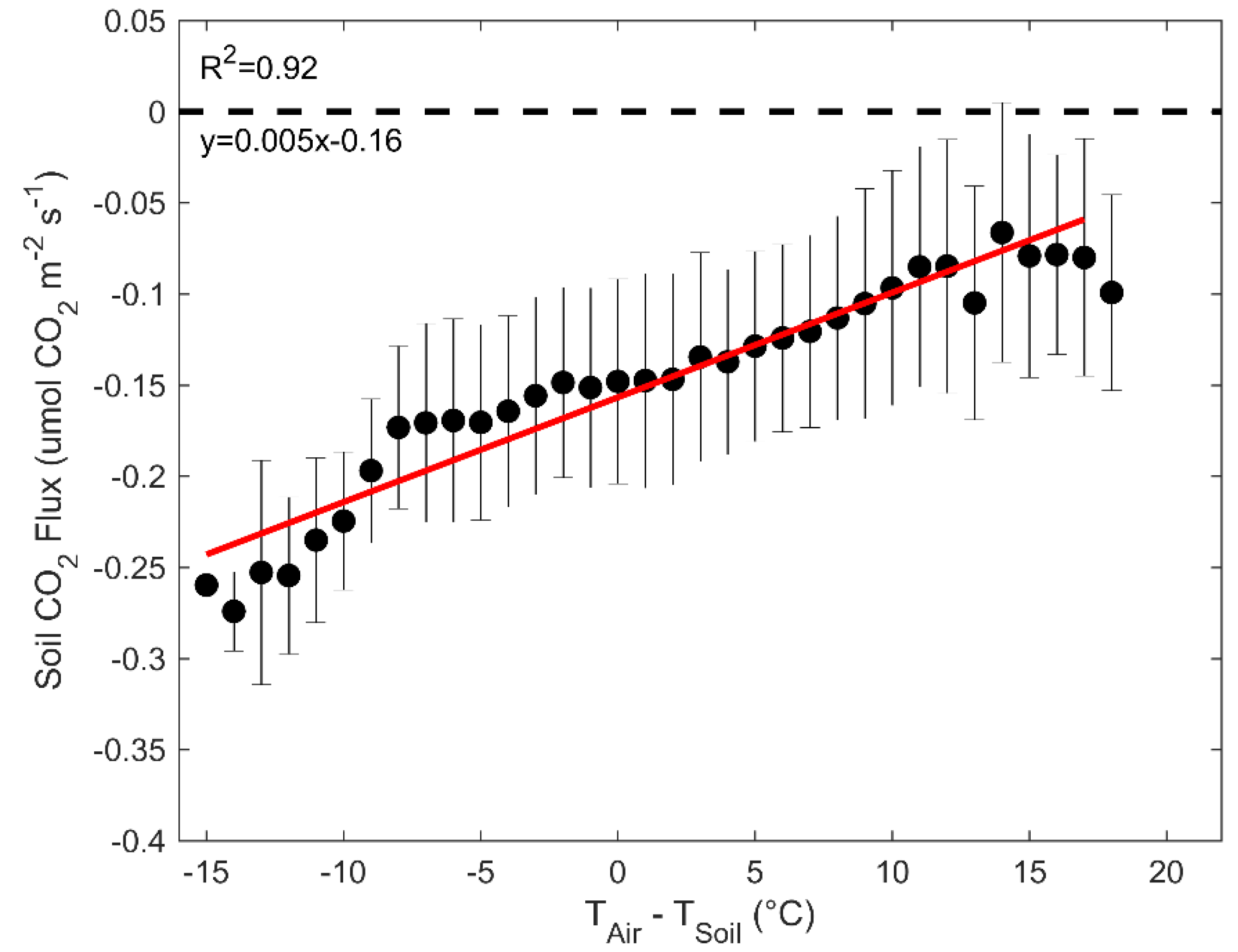
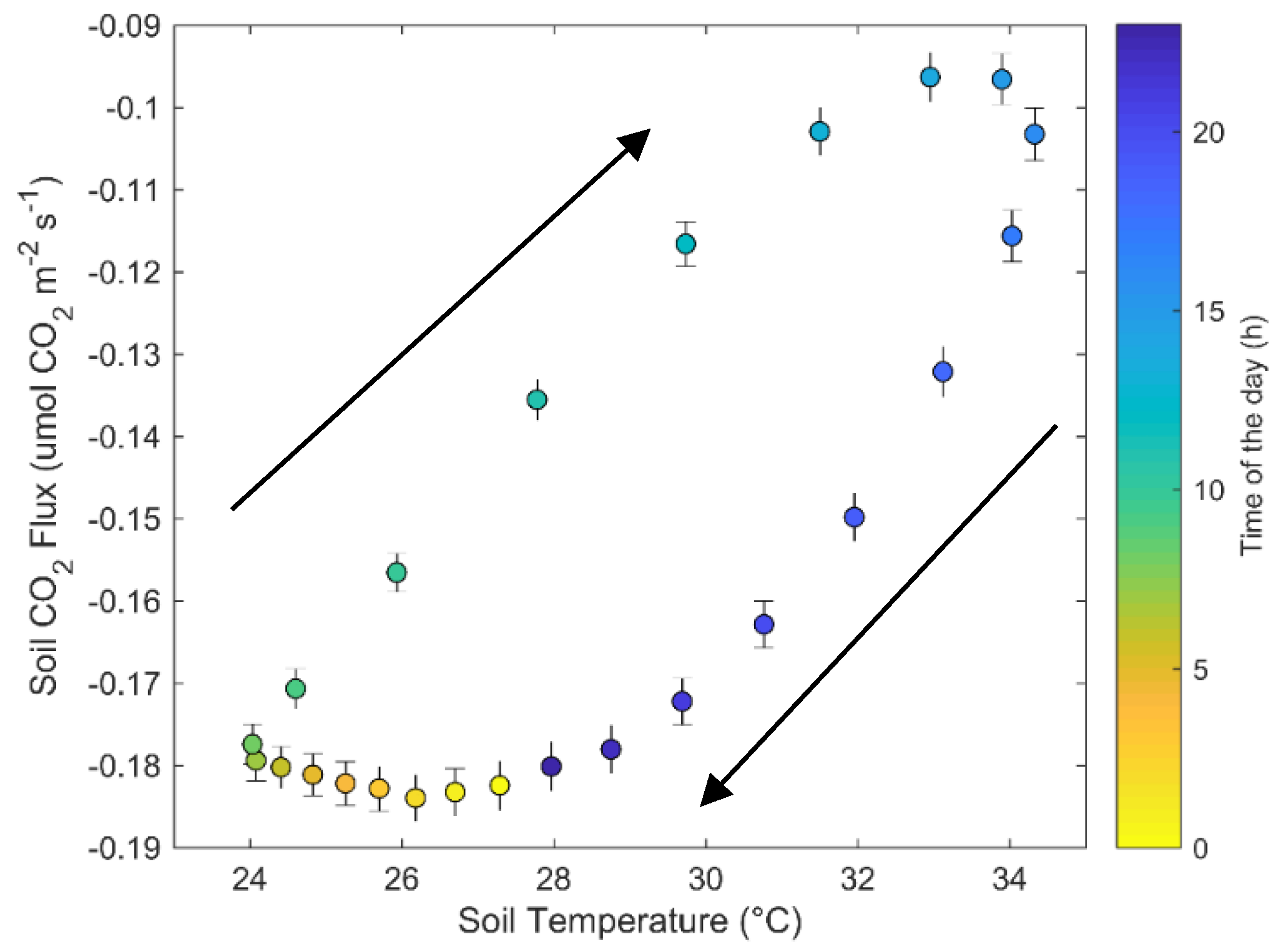
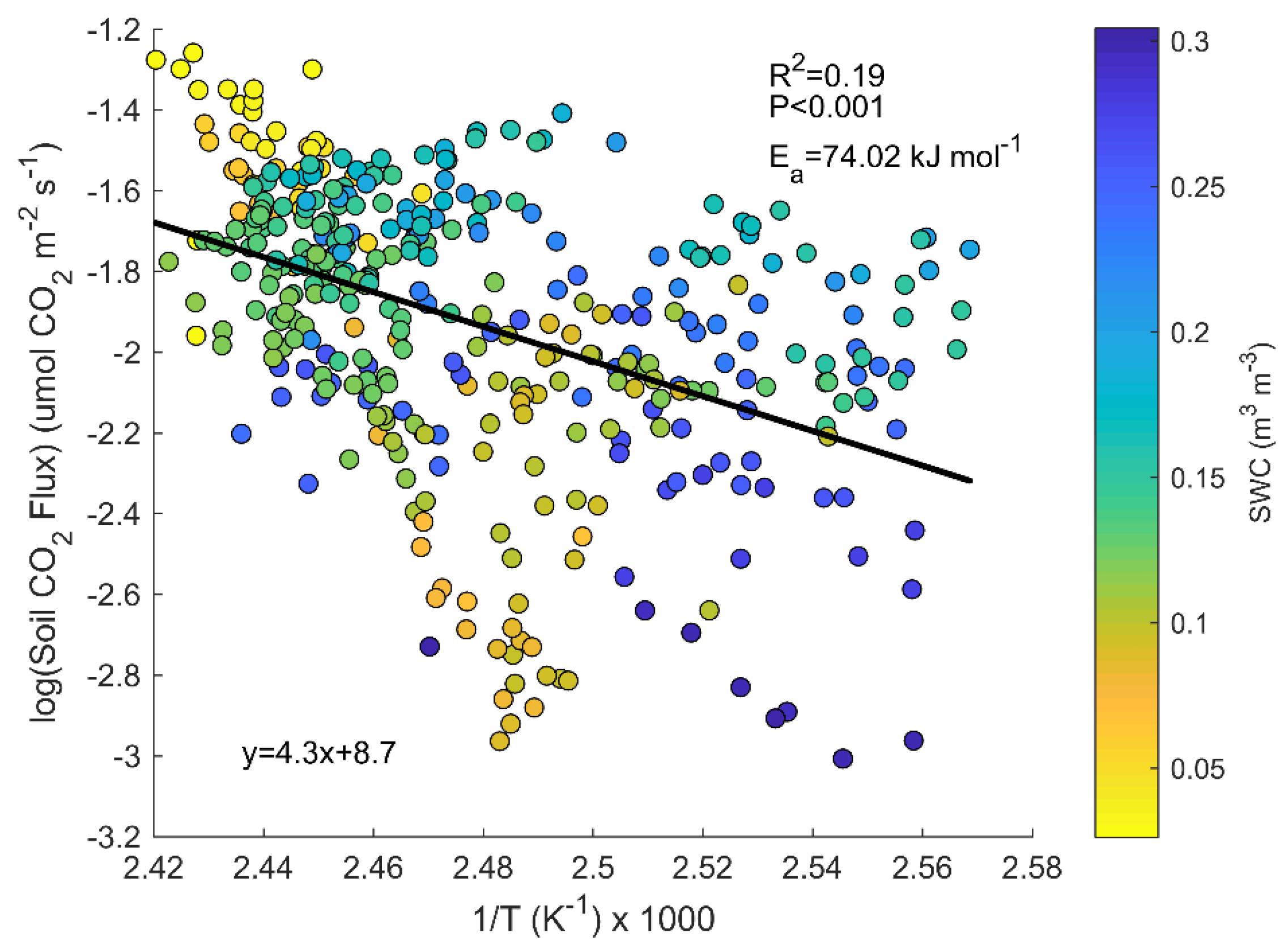
4.4. Temperature Relationship and Hysteresis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahlström, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K.; et al. Carbon cycle. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef] [PubMed]
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y.; et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef]
- Baldocchi, D.; Chu, H.; Reichstein, M. Inter-annual variability of net and gross ecosystem carbon fluxes: A review. Agric. For. Meteorol. 2018, 249, 520–533. [Google Scholar] [CrossRef]
- Reynolds, J.F.; Smith, D.M.S.; Lambin, E.F.; Turner, B.L.; Mortimore, M.; Batterbury, S.P.J.; Downing, T.E.; Dowlatabadi, H.; Fernández, R.J.; Herrick, J.E.; et al. Global desertification: Building a science for dryland development. Science 2007, 316, 847–851. [Google Scholar] [CrossRef]
- Andela, N.; Liu, Y.Y.; van Dijk, A.I.J.M.; de Jeu, R.A.M.; McVicar, T.R. Global changes in dryland vegetation dynamics (1988–2008) assessed by satellite remote sensing: Comparing a new passive microwave vegetation density record with reflective greenness data. Biogeosciences 2013, 10, 6657–6676. [Google Scholar] [CrossRef]
- Noy-Meir, I. Desert Ecosystems: Environment and Producers. Annu. Rev. Ecol. Syst. 1973, 4, 25–51. [Google Scholar] [CrossRef]
- Emmerich, W.E. Carbon dioxide fluxes in a semiarid environment with high carbonate soils. Agric. For. Meteorol. 2003, 116, 91–102. [Google Scholar] [CrossRef]
- Ma, J.; Liu, R.; Tang, L.-S.; Lan, Z.-D.; Li, Y. A downward CO2 flux seems to have nowhere to go. Biogeosci. Discuss. 2014, 11, 6251–6262. [Google Scholar] [CrossRef]
- Ono, K.; Miyata, A.; Yamada, T. Apparent downward CO2 flux observed with open-path eddy covariance over a non-vegetated surface. Theor. Appl. Climatol. 2007, 92, 195–208. [Google Scholar] [CrossRef]
- Schlesinger, W.H. Carbon storage in the caliche of arid soils. Soil Sci. 1982, 133, 247–255. [Google Scholar] [CrossRef]
- Curl, R.L. Carbon Shifted But Not Sequestered. Science 2012, 335, 655. [Google Scholar] [CrossRef] [PubMed]
- Larson, C. Climate change. An unsung carbon sink. Science 2011, 334, 886–887. [Google Scholar] [CrossRef]
- Stone, R. Ecosystems. Have desert researchers discovered a hidden loop in the carbon cycle? Science 2008, 320, 1409–1410. [Google Scholar] [CrossRef] [PubMed]
- Bond-Lamberty, B.; Thomson, A. Temperature-associated increases in the global soil respiration record. Nature 2010, 464, 579–582. [Google Scholar] [CrossRef] [PubMed]
- Raich, J.W.; Potter, C.S. Global patterns of carbon dioxide emissions from soils. Glob. Biogeochem. Cycles 1995, 9, 23–36. [Google Scholar] [CrossRef]
- Reichstein, M.; Beer, C. Soil respiration across scales: The importance of a model–data integration framework for data interpretation. J. Plant Nutr. Soil Sci. 2008, 171, 344–354. [Google Scholar] [CrossRef]
- Ryan, M.G.; Law, B.E. Interpreting, measuring, and modeling soil respiration. Biogeochemistry 2005, 73, 3–27. [Google Scholar] [CrossRef]
- Schindlbacher, A.; Borken, W.; Djukic, I.; Brandstätter, C.; Spötl, C.; Wanek, W. Contribution of carbonate weathering to the CO2 efflux from temperate forest soils. Biogeochemistry 2015, 124, 273–290. [Google Scholar] [CrossRef] [PubMed]
- Schlesinger, W.H.; Belnap, J.; Marion, G. On carbon sequestration in desert ecosystems. Glob. Chang. Biol. 2009, 15, 1488–1490. [Google Scholar] [CrossRef]
- Schlesinger, W.H. An evaluation of abiotic carbon sinks in deserts. Glob. Chang. Biol. 2017, 23, 25–27. [Google Scholar] [CrossRef]
- Hastings, S.J.; Oechel, W.C.; Muhlia-Melo, A. Diurnal, seasonal and annual variation in the net ecosystem CO2 exchange of a desert shrub community (Sarcocaulescent) in Baja California, Mexico. Glob. Chang. Biol. 2005, 11, 927–939. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Fenstermaker, L.F.; Arnone, J.A., III. Large annual net ecosystem CO2 uptake of a Mojave Desert ecosystem. Glob. Chang. Biol. 2008, 14, 1475–1487. [Google Scholar] [CrossRef]
- Rey, A. Mind the gap: Non-biological processes contributing to soil CO2 efflux. Glob. Chang. Biol. 2015, 21, 1752–1761. [Google Scholar] [CrossRef]
- Roland, M.; Serrano-Ortiz, P.; Kowalski, A.S.; Goddéris, Y.; Sánchez-Cañete, E.P.; Ciais, P.; Domingo, F.; Cuezva, S.; Sanchez-Moral, S.; Longdoz, B.; et al. Atmospheric turbulence triggers pronounced diel pattern in karst carbonate geochemistry. Biogeosciences 2013, 10, 5009–5017. [Google Scholar] [CrossRef]
- Dessert, C.; Dupré, B.; Gaillardet, J.; François, L.M.; Allègre, C.J. Basalt weathering laws and the impact of basalt weathering on the global carbon cycle. Chem. Geol. 2003, 202, 257–273. [Google Scholar] [CrossRef]
- Van Haren, J.; Dontsova, K.; Barron-Gafford, G.A.; Troch, P.A.; Chorover, J.; Delong, S.B.; Breshears, D.D.; Huxman, T.E.; Pelletier, J.D.; Saleska, S.R.; et al. CO2 diffusion into pore spaces limits weathering rate of an experimental basalt landscape. Geology 2017, 45, 203–206. [Google Scholar] [CrossRef]
- Lasaga, A.C.; Soler, J.M.; Ganor, J.; Burch, T.E.; Nagy, K.L. Chemical weathering rate laws and global geochemical cycles. Geochim. Cosmochim. Acta 1994, 58, 2361–2386. [Google Scholar] [CrossRef]
- Gislason, S.R.; Oelkers, E.H.; Eiriksdottir, E.S.; Kardjilov, M.I.; Gisladottir, G.; Sigfusson, B.; Snorrason, A.; Elefsen, S.; Hardardottir, J.; Torssander, P.; et al. Direct evidence of the feedback between climate and weathering. Earth Planet. Sci. Lett. 2009, 277, 213–222. [Google Scholar] [CrossRef]
- Aubinet, M. Eddy covariance CO2 flux measurements in nocturnal conditions: An analysis of the problem. Ecol. Appl. 2008, 18, 1368–1378. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Kowalski, A.S.; Serrano-Ortiz, P.; Janssens, I.A.; Sánchez-Moralc, S.; Cuezva, S.; Domingo, F.; Were, A.; Alados-Arboledas, L. Can flux tower research neglect geochemical CO2 exchange? Agric. For. Meteorol. 2008, 148, 1045–1054. [Google Scholar] [CrossRef]
- Brændholt, A.; Larsen, K.S.; Ibrom, A.; Pilegaard, K. Overestimation of closed-chamber soil CO2 effluxes at low atmospheric turbulence. Biogeosciences 2017, 14, 1603–1616. [Google Scholar] [CrossRef]
- Sánchez-Cañete, E.P.; Scott, R.L.; van Haren, J.; Barron-Gafford, G.A. Improving the accuracy of the gradient method for determining soil carbon dioxide efflux. J. Geophys. Res. Biogeosci. 2017, 122, 50–64. [Google Scholar] [CrossRef]
- Barba, J.; Cueva, A.; Bahn, M.; Barron-Gafford, G.A.; Bond-Lamberty, B.; Hanson, P.J.; Jaimes, A.; Kulmala, L.; Pumpanen, J.; Scott, R.L.; et al. Comparing ecosystem and soil respiration: Review and key challenges of tower-based and soil measurements. Agric. For. Meteorol. 2018, 249, 434–443. [Google Scholar] [CrossRef]
- Hill, T.; Chocholek, M.; Clement, R. The case for increasing the statistical power of eddy covariance ecosystem studies: Why, where and how? Glob. Chang. Biol. 2017, 23, 2154–2165. [Google Scholar] [CrossRef] [PubMed]
- Phillips, C.L.; Bond-Lamberty, B.; Desai, A.R.; Lavoie, M.; Risk, D.; Tang, J.; Todd-Brown, K.; Vargas, R. The value of soil respiration measurements for interpreting and modeling terrestrial carbon cycling. Plant Soil 2016, 413, 1–25. [Google Scholar] [CrossRef]
- Hamerlynck, E.P.; Scott, R.L.; Sánchez-Cañete, E.P.; Barron-Gafford, G.A. Nocturnal soil CO2 uptake and its relationship to subsurface soil and ecosystem carbon fluxes in a Chihuahuan Desert shrubland. J. Geophys. Res. Biogeosci. 2013, 118, 1593–1603. [Google Scholar] [CrossRef]
- Pangle, L.A.; DeLong, S.B.; Abramson, N.; Adams, J.; Barron-Gafford, G.A.; Brashears, D.D.; Brooks, P.D.; Chorover, J.; Dietrich, W.E.; Dontsova, K.; et al. The Landscape Evolution Observatory: A large-scale controllable infrastructure to study coupled Earth-surface processes. Geomorphology 2015, 244, 190–203. [Google Scholar] [CrossRef]
- Sengupta, A.; Pangle, L.A.; Volkmann, T.H.M.; Dontsova, K.; Troch, P.A.; Meira-Neto, A.A.; Neilson, J.W.; Hunt, E.A.; Chorover, J.; Zeng, X.; et al. Advancing Understanding of Hydrological and Biogeochemical Interactions in Evolving Landscapes through Controlled Experimentation at the Landscape Evolution Observatory. In Terrestrial Ecosystem Research Infrastructures; Taylor & Francis Group: Milton Park, UK, 2017; pp. 83–118. [Google Scholar]
- Volkmann, T.H.M.; Sengupta, A.; Pangle, L.A.; Dontsova, K.; Barron-Gafford, G.A.; Harman, C.J.; Niu, G.-Y.; Meredith, L.K.; Abramson, N.; Meira Neto, A.A.; et al. Controlled experiments of hillslope coevolution at the Biosphere 2 Landscape Evolution Observatory: Toward prediction of coupled hydrological, biogeochemical, and ecological change. In Hydrology of Artificial and Controlled Experiments; Gu, W.-Z., Ed.; InTech: London, UK, 2018. [Google Scholar]
- Nickerson, N.; Risk, D. Physical controls on the isotopic composition of soil-respired CO2. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Moldrup, P.; Olesen, T.; Yamaguchi, T.; Schjønning, P.; Rolston, D.E. Modeling diffusion and reaction in soils: IX. The buckingham-burdine-campbell equation for gas diffusivity in undisturbed soil. Soil Sci. 1999, 164, 542–551. [Google Scholar] [CrossRef]
- Jones, H.G. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 2013; ISBN 9781107511637. [Google Scholar]
- Vargas, R.; Baldocchi, D.D.; Allen, M.F.; Bahn, M.; Black, T.A.; Collins, S.L.; Yuste, J.C.; Hirano, T.; Jassal, R.S.; Pumpanen, J.; et al. Looking deeper into the soil: Biophysical controls and seasonal lags of soil CO2 production and efflux. Ecol. Appl. 2010, 20, 1569–1582. [Google Scholar] [CrossRef]
- Pumpanen, J.; Ilvesniemi, H.; Hari, P. A Process-Based Model for Predicting Soil Carbon Dioxide Efflux and Concentration. Soil Sci. Soc. Am. J. 2003, 67, 402. [Google Scholar] [CrossRef]
- Pumpanen, J.; Ilvesniemi, H.; Kulmala, L.; Siivola, E.; Laakso, H.; Kolari, P.; Helenelund, C.; Laakso, M.; Uusimaa, M.; Hari, P. Respiration in Boreal Forest Soil as Determined from Carbon Dioxide Concentration Profile. Soil Sci. Soc. Am. J. 2008, 72, 1187. [Google Scholar] [CrossRef]
- Cueva, A.; Bahn, M.; Litvak, M.; Pumpanen, J.; Vargas, R. A multisite analysis of temporal random errors in soil CO2 efflux. J. Geophys. Res. Biogeosci. 2015, 120, 737–751. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Anfang, C.; Bahn, M.; Haslwanter, A.; Newesely, C.; Schmitt, M.; Drösler, M.; Pfadenhauer, J.; Cernusca, A. Quantifying nighttime ecosystem respiration of a meadow using eddy covariance, chambers and modelling. Agric. For. Meteorol. 2005, 128, 141–162. [Google Scholar] [CrossRef]
- Moncrieff, J.B.; Malhi, Y.; Leuning, R. The propagation of errors in long-term measurements of land-atmosphere fluxes of carbon and water. Glob. Chang. Biol. 1996, 2, 231–240. [Google Scholar] [CrossRef]
- Goulden, M.L.; William Munger, J.; Fan, S.-M.; Daube, B.C.; Wofsy, S.C. Measurements of carbon sequestration by long-term eddy covariance: Methods and a critical evaluation of accuracy. Glob. Chang. Biol. 1996, 2, 169–182. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J.A. On the Temperature Dependence of Soil Respiration. Funct. Ecol. 1994, 8, 315. [Google Scholar] [CrossRef]
- Pavelka, M.; Acosta, M.; Marek, M.V.; Kutsch, W.; Janous, D. Dependence of the Q10 values on the depth of the soil temperature measuring point. Plant Soil 2007, 292, 171–179. [Google Scholar] [CrossRef]
- Fa, K.-Y.; Zhang, Y.-Q.; Wu, B.; Qin, S.-G.; Liu, Z.; She, W.-W. Patterns and possible mechanisms of soil CO2 uptake in sandy soil. Sci. Total Environ. 2016, 544, 587–594. [Google Scholar] [CrossRef]
- Parsons, A.N.; Barrett, J.E.; Wall, D.H.; Virginia, R.A. Soil Carbon Dioxide Flux in Antarctic Dry Valley Ecosystems. Ecosystems 2004, 7. [Google Scholar] [CrossRef]
- Risk, D.; Lee, C.K.; MacIntyre, C.; Craig Cary, S. First year-round record of Antarctic Dry Valley soil CO2 flux. Soil Biol. Biochem. 2013, 66, 193–196. [Google Scholar] [CrossRef]
- Luo, H.; Oechel, W.C.; Hastings, S.J.; Zulueta, R.; Qian, Y.; Kwon, H. Mature semiarid chaparral ecosystems can be a significant sink for atmospheric carbon dioxide. Glob. Chang. Biol. 2007, 13, 386–396. [Google Scholar] [CrossRef]
- Xie, J.; Li, Y.; Zhai, C.; Li, C.; Lan, Z. CO2 absorption by alkaline soils and its implication to the global carbon cycle. Environ. Geol. 2008, 56, 953–961. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Amundson, R. Managing for soil carbon sequestration: Let’s get realistic. Glob. Chang. Biol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Cueva, A.; Bullock, S.H.; López-Reyes, E.; Vargas, R. Potential bias of daily soil CO2 efflux estimates due to sampling time. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.-G.; Houghton, R.A.; Tang, L.-S. Hidden carbon sink beneath desert. Geophys. Res. Lett. 2015, 42, 5880–5887. [Google Scholar] [CrossRef]
- Slessarev, E.W.; Lin, Y.; Bingham, N.L.; Johnson, J.E.; Dai, Y.; Schimel, J.P.; Chadwick, O.A. Water balance creates a threshold in soil pH at the global scale. Nature 2016, 540, 567. [Google Scholar] [CrossRef]
- Fa, K.; Zhang, Y.; Lei, G.; Wu, B.; Qin, S.; Liu, J.; Feng, W.; Lai, Z. Underestimation of soil respiration in a desert ecosystem. Catena 2018, 162, 23–28. [Google Scholar] [CrossRef]
- Ma, J.; Wang, Z.-Y.; Stevenson, B.A.; Zheng, X.-J.; Li, Y. An inorganic CO2 diffusion and dissolution process explains negative CO2 fluxes in saline/alkaline soils. Sci. Rep. 2013, 3, 2025. [Google Scholar] [CrossRef] [PubMed]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Castanier, S.; Le Métayer-Levrel, G.; Perthuisot, J.-P. Ca-carbonates precipitation and limestone genesis—The microbiogeologist point of view. Sediment. Geol. 1999, 126, 9–23. [Google Scholar] [CrossRef]
- Douglas, S.; Beveridge, T.J. Mineral formation by bacteria in natural microbial communities. FEMS Microbiol. Ecol. 1998, 26, 79–88. [Google Scholar] [CrossRef]
- Hammes, F.; Verstraete, W. Key roles of pH and calcium metabolism in microbial carbonate precipitation. Rev. Environ. Sci. Technol. 2002, 1, 3–7. [Google Scholar] [CrossRef]
- Berg, I.A.; Kockelkorn, D.; Hugo Ramos-Vera, W.; Say, R.F.; Zarzycki, J.; Hügler, M.; Alber, B.E.; Fuchs, G. Autotrophic carbon fixation in archaea. Nat. Rev. Microbiol. 2010, 8, 447–460. [Google Scholar] [CrossRef]
- Pohlmann, M.; Dontsova, K.; Root, R.; Ruiz, J.; Troch, P.; Chorover, J. Pore water chemistry reveals gradients in mineral transformation across a model basaltic hillslope. Geochem. Geophys. Geosyst. 2016, 17, 2054–2069. [Google Scholar] [CrossRef]
- Yates, E.L.; Detweiler, A.M.; Iraci, L.T.; Bebout, B.M.; McKay, C.P.; Schiro, K.; Sheffner, E.J.; Kelley, C.A.; Tadić, J.M.; Loewenstein, M. Assessing the role of alkaline soils on the carbon cycle at a playa site. Environ. Earth Sci. 2012, 70, 1047–1056. [Google Scholar] [CrossRef]
- Ma, J.; Zheng, X.-J.; Li, Y. The response of CO2 flux to rain pulses at a saline desert. Hydrol. Process. 2012, 26, 4029–4037. [Google Scholar] [CrossRef]
- Xu, L.; Baldocchi, D.D.; Tang, J. How soil moisture, rain pulses, and growth alter the response of ecosystem respiration to temperature. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Manzoni, S.; Katul, G. Invariant soil water potential at zero microbial respiration explained by hydrological discontinuity in dry soils. Geophys. Res. Lett. 2014, 41, 7151–7158. [Google Scholar] [CrossRef]
- Manzoni, S.; Schimel, J.P.; Porporato, A. Responses of soil microbial communities to water stress: Results from a meta-analysis. Ecology 2012, 93, 930–938. [Google Scholar] [CrossRef] [PubMed]
- Tecon, R.; Or, D. Bacterial flagellar motility on hydrated rough surfaces controlled by aqueous film thickness and connectedness. Sci. Rep. 2016, 6, 19409. [Google Scholar] [CrossRef] [PubMed]
- Tecon, R.; Or, D. Biophysical processes supporting the diversity of microbial life in soil. FEMS Microbiol. Rev. 2017, 41, 599–623. [Google Scholar] [CrossRef] [PubMed]
- Moyano, F.E.; Vasilyeva, N.; Bouckaert, L.; Cook, F.; Craine, J.; Curiel Yuste, J.; Don, A.; Epron, D.; Formanek, P.; Franzluebbers, A.; et al. The moisture response of soil heterotrophic respiration: Interaction with soil properties. Biogeosciences 2012, 9, 1173–1182. [Google Scholar] [CrossRef]
- Moyano, F.E.; Manzoni, S.; Chenu, C. Responses of soil heterotrophic respiration to moisture availability: An exploration of processes and models. Soil Biol. Biochem. 2013, 59, 72–85. [Google Scholar] [CrossRef]
- Dalai, T.K.; Krishnaswami, S.; Sarin, M.M. Major ion chemistry in the headwaters of the Yamuna river system: Chemical weathering, its temperature dependence and CO2 consumption in the Himalaya. Geochim. Cosmochim. Acta 2002, 66, 3397–3416. [Google Scholar] [CrossRef]
- Li, G.; Hartmann, J.; Derry, L.A.; West, A.J.; You, C.-F.; Long, X.; Zhan, T.; Li, L.; Li, G.; Qiu, W.; et al. Temperature dependence of basalt weathering. Earth Planet. Sci. Lett. 2016, 443, 59–69. [Google Scholar] [CrossRef]
- Davidson, E.A.; Samanta, S.; Caramori, S.S.; Savage, K. The Dual Arrhenius and Michaelis-Menten kinetics model for decomposition of soil organic matter at hourly to seasonal time scales. Glob. Chang. Biol. 2012, 18, 371–384. [Google Scholar] [CrossRef]
- Parker, L.W.; Miller, J.; Steinberger, Y.; Whitford, W.G. Soil respiration in a Chihuahuan desert rangeland. Soil Biol. Biochem. 1983, 15, 303–309. [Google Scholar] [CrossRef]
- Sierra, C.A. Temperature sensitivity of organic matter decomposition in the Arrhenius equation: Some theoretical considerations. Biogeochemistry 2012, 108, 1–15. [Google Scholar] [CrossRef]
- Shoji, S.; Nanzyo, M.; Shirato, Y.; Ito, T. Chemical kinetics of weathering in young andisols from northeastern japan using soil age normalized to 10 °C. Soil Sci. 1993, 155, 53–60. [Google Scholar] [CrossRef]
- Raymond, P.A. Temperature versus hydrologic controls of chemical weathering fluxes from United States forests. Chem. Geol. 2017, 458, 1–13. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Bailey, V.L.; Chen, M.; Gough, C.M.; Vargas, R. Globally rising soil heterotrophic respiration over recent decades. Nature 2018, 560, 80–83. [Google Scholar] [CrossRef]
- Curiel Yuste, J.; Baldocchi, D.D.; Gershenson, A.; Goldstein, A.; Misson, L.; Wong, S. Microbial soil respiration and its dependency on carbon inputs, soil temperature and moisture. Glob. Chang. Biol. 2007, 13, 2018–2035. [Google Scholar] [CrossRef]
- Davidson, E.A.; Belk, E.; Boone, R.D. Soil water content and temperature as independent or confounded factors controlling soil respiration in a temperate mixed hardwood forest. Glob. Chang. Biol. 1998, 4, 217–227. [Google Scholar] [CrossRef]
- Romero-Mujalli, G.; Hartmann, J.; Börker, J. Temperature and CO2 dependency of global carbonate weathering fluxes—Implications for future carbonate weathering research. Chem. Geol. 2018. [Google Scholar] [CrossRef]
- Barron-Gafford, G.A.; Scott, R.L.; Darrel Jenerette, G.; Huxman, T.E. The relative controls of temperature, soil moisture, and plant functional group on soil CO2 efflux at diel, seasonal, and annual scales. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Riveros-Iregui, D.A.; Emanuel, R.E.; Muth, D.J.; McGlynn, B.L.; Epstein, H.E.; Welsch, D.L.; Pacific, V.J.; Wraith, J.M. Diurnal hysteresis between soil CO2and soil temperature is controlled by soil water content. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Vargas, R.; Allen, M.F. Diel patterns of soil respiration in a tropical forest after Hurricane Wilma. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Phillips, C.L.; Nickerson, N.; Risk, D.; Bond, B.J. Interpreting diel hysteresis between soil respiration and temperature. Glob. Chang. Biol. 2010, 17, 515–527. [Google Scholar] [CrossRef]
- Tang, J.; Baldocchi, D.D.; Xu, L. Tree photosynthesis modulates soil respiration on a diurnal time scale. Glob. Chang. Biol. 2005, 11, 1298–1304. [Google Scholar] [CrossRef]
- Vargas, R.; Baldocchi, D.D.; Bahn, M.; Hanson, P.J.; Hosman, K.P.; Kulmala, L.; Pumpanen, J.; Yang, B. On the multi-temporal correlation between photosynthesis and soil CO2 efflux: Reconciling lags and observations. New Phytol. 2011, 191, 1006–1017. [Google Scholar] [CrossRef]
- Carbone, M.S.; Winston, G.C.; Trumbore, S.E. Soil respiration in perennial grass and shrub ecosystems: Linking environmental controls with plant and microbial sources on seasonal and diel timescales. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Carbone, M.S.; Park Williams, A.; Ambrose, A.R.; Boot, C.M.; Bradley, E.S.; Dawson, T.E.; Schaeffer, S.M.; Schimel, J.P.; Still, C.J. Cloud shading and fog drip influence the metabolism of a coastal pine ecosystem. Glob. Chang. Biol. 2012, 19, 484–497. [Google Scholar] [CrossRef]
- Soper, F.M.; McCalley, C.K.; Sparks, K.; Sparks, J.P. Soil carbon dioxide emissions from the Mojave desert: Isotopic evidence for a carbonate source. Geophys. Res. Lett. 2017, 44, 245–251. [Google Scholar] [CrossRef]
- Cable, J.M.; Ogle, K.; Lucas, R.W.; Huxman, T.E.; Loik, M.E.; Smith, S.D.; Tissue, D.T.; Ewers, B.E.; Pendall, E.; Welker, J.M.; et al. The temperature responses of soil respiration in deserts: A seven desert synthesis. Biogeochemistry 2010, 103, 71–90. [Google Scholar] [CrossRef]
- Maier, M.; Schack-Kirchner, H.; Hildebrand, E.E.; Schindler, D. Soil CO2 efflux vs. soil respiration: Implications for flux models. Agric. For. Meteorol. 2011, 151, 1723–1730. [Google Scholar] [CrossRef]
- Chapin, F.S.; Woodwell, G.M.; Randerson, J.T.; Rastetter, E.B.; Lovett, G.M.; Baldocchi, D.D.; Clark, D.A.; Harmon, M.E.; Schimel, D.S.; Valentini, R.; et al. Reconciling Carbon-cycle Concepts, Terminology, and Methods. Ecosystems 2006, 9, 1041–1050. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Chang. Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Stevenson, B.A.; Verburg, P.S.J. Effluxed CO2-13C from sterilized and unsterilized treatments of a calcareous soil. Soil Biol. Biochem. 2006, 38, 1727–1733. [Google Scholar] [CrossRef]
- Angert, A.; Yakir, D.; Rodeghiero, M.; Preisler, Y.; Davidson, E.A.; Weiner, T. Using O2 to study the relationships between soil CO2 efflux and soil respiration. Biogeosciences 2015, 12, 2089–2099. [Google Scholar] [CrossRef]
- Allison, S.D.; Wallenstein, M.D.; Bradford, M.A. Soil-carbon response to warming dependent on microbial physiology. Nat. Geosci. 2010, 3, 336–340. [Google Scholar] [CrossRef]
- Conrad, R. Soil microorganisms as controllers of atmospheric trace gases (H2, CO, CH4, OCS, N2O, and NO). Microbiol. Rev. 1996, 60, 609–640. [Google Scholar]
- Ogée, J.; Sauze, J.; Kesselmeier, J.; Genty, B.; Van Diest, H.; Launois, T.; Wingate, L. A new mechanistic framework to predict OCS fluxes from soils. Biogeosciences 2016, 13, 2221–2240. [Google Scholar] [CrossRef]
- Meredith, L.K.; Boye, K.; Youngerman, C.; Whelan, M.; Ogée, J.; Sauze, J.; Wingate, L. Coupled biological and abiotic mechanisms driving carbonyl sulfide production in soils. Soil Syst. 2018, 2, 37. [Google Scholar] [CrossRef]
- Petrakis, S.; Barba, J.; Bond-Lamberty, B.; Vargas, R. Using greenhouse gas fluxes to define soil functional types. Plant Soil 2018, 423, 285–294. [Google Scholar] [CrossRef]
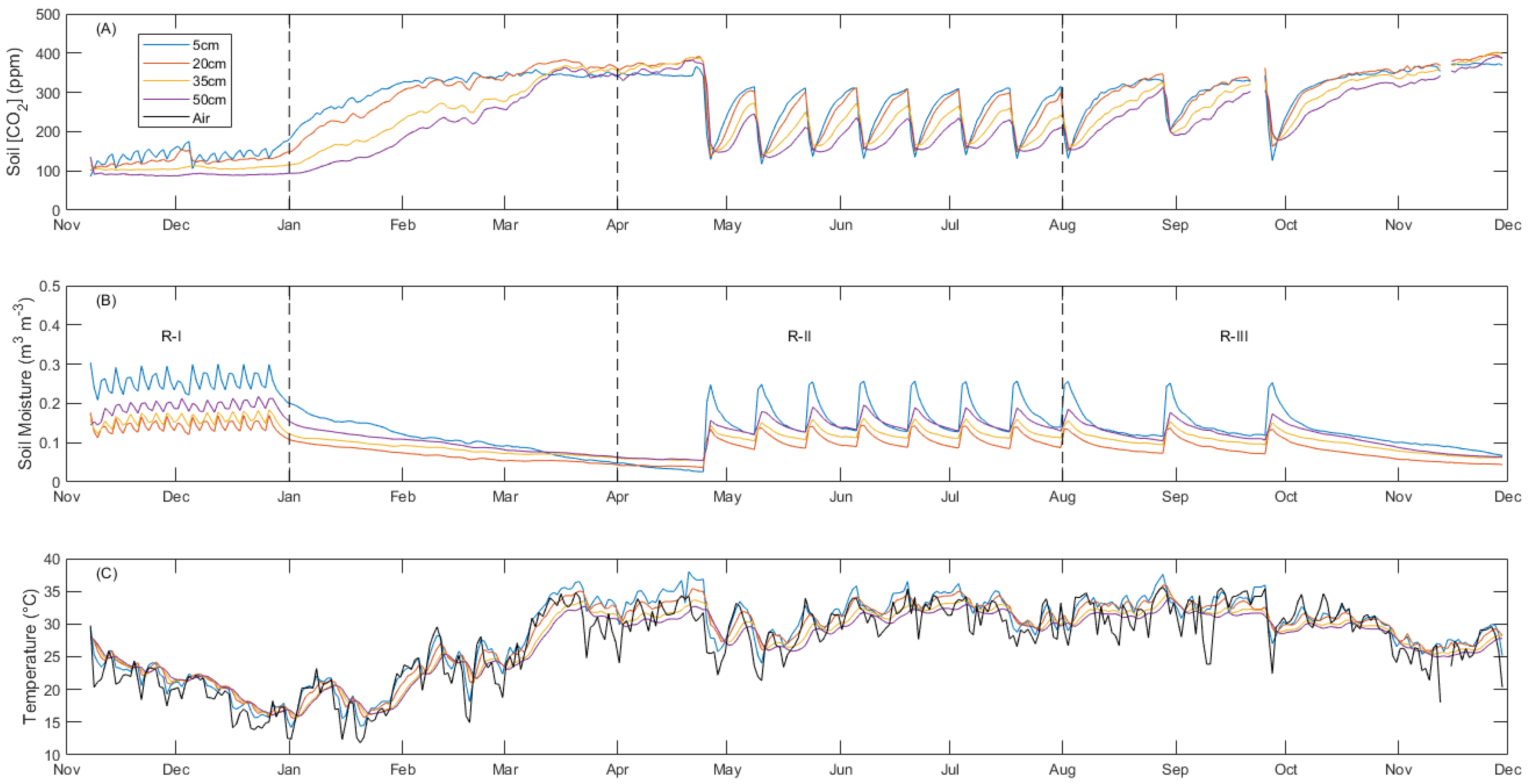
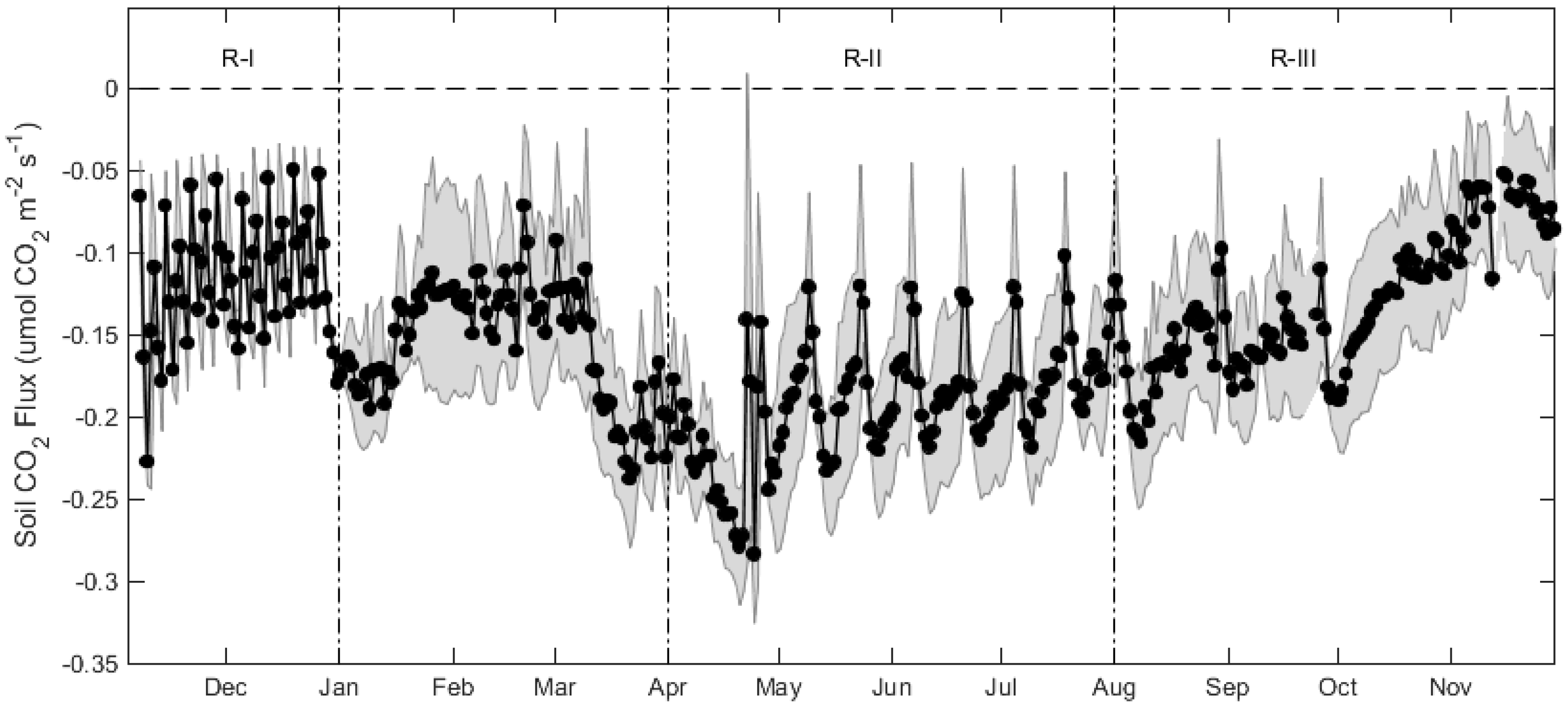
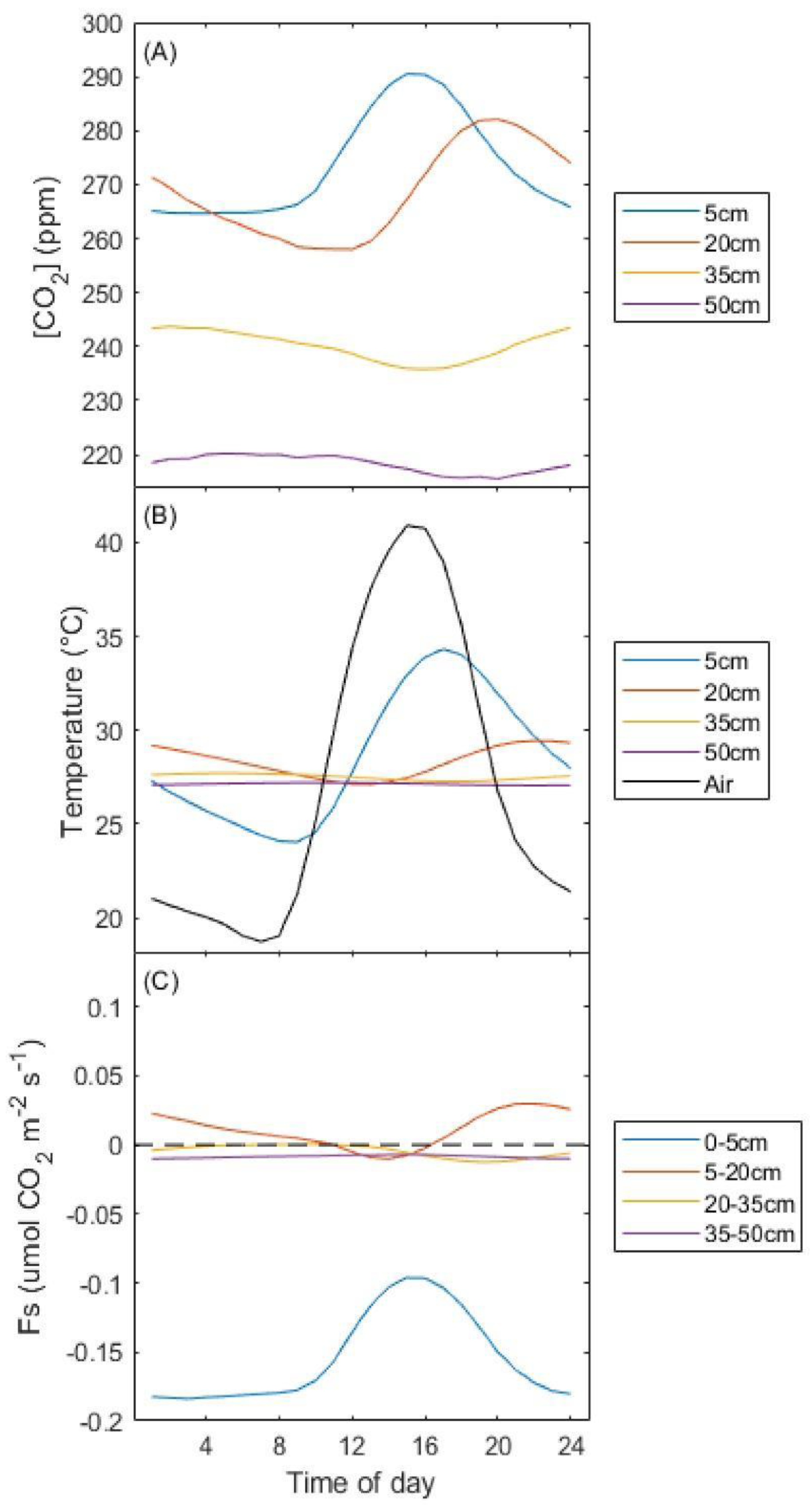
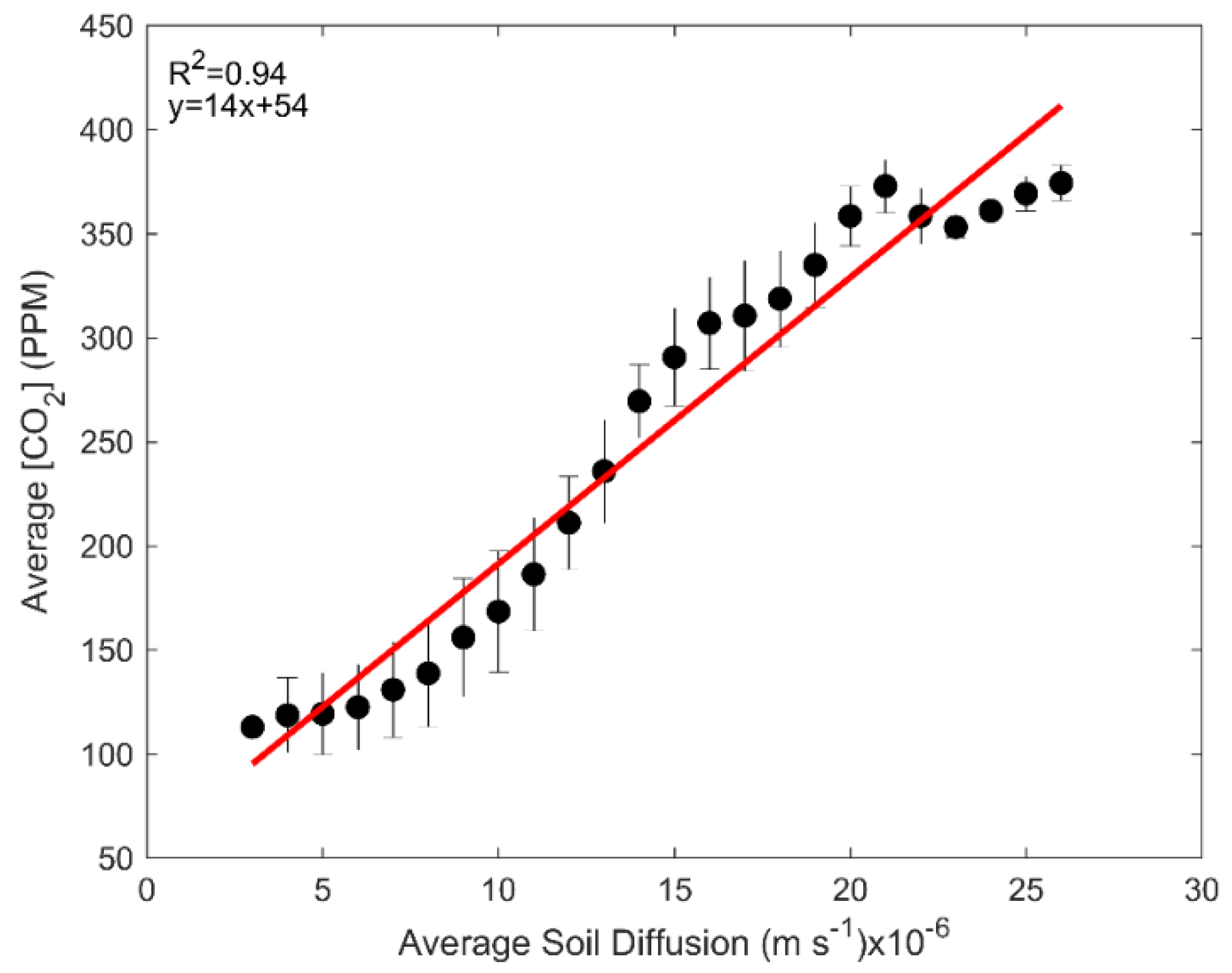
| Temperature (°C) | Moisture (m3 m−3) | [CO2] (ppm) | |
|---|---|---|---|
| Air | 27.13 ± 10.51 | -- | 387.16 ± 28.13 |
| Soil | |||
| 5 cm | 28.56 ± 6.90 | 0.15 ± 0.07 | 273.50 ± 81.08 |
| 20 cm | 28.32 ± 5.42 | 0.09 ± 0.03 | 268.54 ± 88.66 |
| 35 cm | 27.52 ± 5.05 | 0.11 ± 0.03 | 240.17 ± 88.54 |
| 50 cm | 27.14 ± 4.80 | 0.13 ± 0.04 | 218.19 ± 90.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cueva, A.; Volkmann, T.H.M.; van Haren, J.; Troch, P.A.; Meredith, L.K. Reconciling Negative Soil CO2 Fluxes: Insights from a Large-Scale Experimental Hillslope. Soil Syst. 2019, 3, 10. https://doi.org/10.3390/soilsystems3010010
Cueva A, Volkmann THM, van Haren J, Troch PA, Meredith LK. Reconciling Negative Soil CO2 Fluxes: Insights from a Large-Scale Experimental Hillslope. Soil Systems. 2019; 3(1):10. https://doi.org/10.3390/soilsystems3010010
Chicago/Turabian StyleCueva, Alejandro, Till H. M. Volkmann, Joost van Haren, Peter A. Troch, and Laura K. Meredith. 2019. "Reconciling Negative Soil CO2 Fluxes: Insights from a Large-Scale Experimental Hillslope" Soil Systems 3, no. 1: 10. https://doi.org/10.3390/soilsystems3010010
APA StyleCueva, A., Volkmann, T. H. M., van Haren, J., Troch, P. A., & Meredith, L. K. (2019). Reconciling Negative Soil CO2 Fluxes: Insights from a Large-Scale Experimental Hillslope. Soil Systems, 3(1), 10. https://doi.org/10.3390/soilsystems3010010





