Fractional Analytic QCD: The Recent Results
Abstract
1. Introduction
2. Strong Coupling
f-Dependence of the Coupling
3. Fractional Derivatives
4. MA Couplings
4.1. LO
4.2. Beyond LO
4.3. The Case
5. The Behaviors of MA Couplings
5.1. Coupling
5.2. Coupling
5.3. Couplings and
6. MA Coupling : The form Is Convenient for
6.1. LO
6.2. Beyond LO
6.3. The Case
7. Integral Representations for
7.1. Modification of Spectral Functions
7.2. Modification of Polylogarithms
7.3. Discussions
8. Integral Representations for
9. Decay
10. Bjorken Sum Rule
10.1. Results
10.2. Low values
10.3. Photoproduction
10.4. Gerasimov–Drell–Hearn and Burkhardt–Cottingham Sum Rules
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Details of the Evaluation of the Fractional Derivatives
Appendix B. Alternative Form for the Couplings
Appendix C.
References
- Bogolyubov, N.N.; Shirkov, D.V. Introduction to the theory of quantized fields. Intersci. Monogr. Phys. Astron. 1959, 3, 1–720. [Google Scholar] [CrossRef]
- Baikov, P.A.; Chetyrkin, K.G.; Kühn, J.H. Five-Loop Running of the QCD coupling constant. Phys. Rev. Lett. 2017, 118, 082002. [Google Scholar] [CrossRef]
- Herzog, F.; Ruijl, B.; Ueda, T.; Vermaseren, J.A.M.; Vogt, A. The five-loop beta function of Yang-Mills theory with fermions. J. High Energy Phys. 2017, 2017, 90. [Google Scholar] [CrossRef]
- Luthe, T.; Maier, A.; Marquard, P.; Schroder, Y. The five-loop Beta function for a general gauge group and anomalous dimensions beyond Feynman gauge. J. High Energy Phys. 2017, 10, 166. [Google Scholar] [CrossRef]
- Chetyrkin, K.G.; Falcioni, G.; Herzog, F.; Vermaseren, J.A.M. Five-loop renormalisation of QCD in covariant gauges. J. High Energy Phys. 2017, 10, 179. [Google Scholar] [CrossRef]
- Shirkov, D.V.; Solovtsov, I.L. Analytic model for the QCD running coupling with universal αs(0) value. Phys. Rev. Lett. 1997, 79, 1209–1212. [Google Scholar] [CrossRef]
- Shirkov, D.V. Analytic perturbation theory for QCD observables. Theor. Math. Phys. 2001, 127, 409–423. [Google Scholar] [CrossRef]
- Shirkov, D.V. Analytic perturbation theory in analyzing some QCD observables. Eur. Phys. J. C 2001, 22, 331–340. [Google Scholar] [CrossRef]
- Milton, K.A.; Solovtsov, I.L.; Solovtsova, O.P. Analytic perturbation theory and inclusive tau decay. Phys. Lett. B 1997, 415, 104–110. [Google Scholar] [CrossRef]
- Bakulev, A.P.; Mikhailov, S.V.; Stefanis, N.G. QCD analytic perturbation theory: From integer powers to any power of the running coupling. Phys. Rev. D 2005, 72, 074014, Erratum in Phys. Rev. D 2005, 72, 119908. [Google Scholar] [CrossRef]
- Bakulev, A.P.; Mikhailov, S.V.; Stefanis, N.G. Fractional Analytic Perturbation Theory in Minkowski space and application to Higgs boson decay into a b anti-b pair. Phys. Rev. D 2007, 75, 056005, Erratum in Phys. Rev. D 2008, 77, 079901. [Google Scholar] [CrossRef]
- Bakulev, A.P.; Mikhailov, S.V.; Stefanis, N.G. Higher-order QCD perturbation theory in different schemes: From FOPT to CIPT to FAPT. J. High Energy Phys. 2010, 2010, 85. [Google Scholar] [CrossRef]
- Pennington, M.R.; Ross, G.G. Perturbative QCD for Timelike Processes: What Is the Best Expansion Parameter? Phys. Lett. B 1981, 102, 167–171. [Google Scholar] [CrossRef]
- Pennington, M.R.; Roberts, R.G.; Ross, G.G. How to Continue the Predictions of Perturbative QCD From the Space-Like Region Where They Are Derived to the Time-Like Regime Where Experiments Are Performed. Nucl. Phys. B 1984, 242, 69–80. [Google Scholar] [CrossRef]
- Marshall, R. A Determination of the Strong Coupling Constant α−s From e+e− Total Cross-section Data. Z. Phys. C 1989, 43, 595. [Google Scholar] [CrossRef]
- Krasnikov, N.V.; Pivovarov, A.A. The influence of the analytical continuation effects on the value of the qcd scale parameter lambda extracted from the data on charmonium and upsilon hadron decays. Phys. Lett. B 1982, 116, 168–170. [Google Scholar] [CrossRef]
- Radyushkin, A.V. Optimized Λ-Parametrization for the QCD Running Coupling Constant in Space-Like and Time-Like Regions. JINR Rapid Commun. 1996, 78, 9, [hep-ph/9907128]. [Google Scholar]
- Badelek, B.; Kwiecinski, J.; Stasto, A. A Model for F(L) and R = F(L) / F(T) at low x and low Q2. Z. Phys. C 1997, 74, 297–306. [Google Scholar]
- Nikolaev, N.N.; Zakharov, B.G. Color transparency and scaling properties of nuclear shadowing in deep inelastic scattering. Z. Phys. C 1991, 49, 607–618. [Google Scholar] [CrossRef]
- Nikolaev, N.; Zakharov, B.G. Pomeron structure function and diffraction dissociation of virtual photons in perturbative QCD. Z. Phys. C 1992, 53, 331–346. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; de Teramond, G.F. The QCD Running Coupling. Nucl. Phys. 2016, 90, 1. [Google Scholar] [CrossRef]
- Becher, T.; Neubert, M. Drell-Yan Production at Small qT, Transverse Parton Distributions and the Collinear Anomaly. Eur. Phys. J. C 2011, 71, 1665. [Google Scholar] [CrossRef]
- Becher, T.; Neubert, M.; Wilhelm, D. Electroweak Gauge-Boson Production at Small qT: Infrared Safety from the Collinear Anomaly. J. High Energy Phys. 2012, 2012, 124. [Google Scholar] [CrossRef]
- Becher, T.; Neubert, M.; Wilhelm, D. Higgs-Boson Production at Small Transverse Momentum. J. High Energy Phys. 2013, 2013, 110. [Google Scholar] [CrossRef]
- Catani, S.; Grazzini, M. Higgs Boson Production at Hadron Colliders: Hard-Collinear Coefficients at the NNLO. Eur. Phys. J. C 2012, 72, 2013. [Google Scholar] [CrossRef]
- Becher, T.; Neubert, M.; Pecjak, B.D. Factorization and Momentum-Space Resummation in Deep-Inelastic Scattering. J. High Energy Phys. 2007, 01, 76. [Google Scholar] [CrossRef]
- Catani, S.; Mangano, M.L.; Nason, P.; Trentadue, L. The Resummation of soft gluons in hadronic collisions. Nucl. Phys. B 1996, 478, 273–310. [Google Scholar] [CrossRef]
- Ducati, M.B.G.; Halzen, F.; Natale, A.A. Diffraction and the gluon mass. Phys. Rev. D 1993, 48, 2324–2328. [Google Scholar] [CrossRef]
- Mattingly, A.C.; Stevenson, P.M. QCD perturbation theory at low-energies. Phys. Rev. Lett. 1992, 69, 1320–1323. [Google Scholar] [CrossRef]
- Mattingly, A.C.; Stevenson, P.M. Optimization of R(e+ e−) and ‘freezing’ of the QCD couplant at low-energies. Phys. Rev. D 1994, 49, 437–450. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Lipatov, A.V.; Zotov, N.P. The Longitudinal structure function F(L): Perturbative QCD and k(T) factorization versus experimental data at fixed W. J. Exp. Theor. Phys. 2005, 101, 811–816. [Google Scholar] [CrossRef]
- Bogolyubov, N.N.; Logunov, A.A.; Shirkov, D.V. The method of dispersion relations and perturbation theory. Sov. Phys. JETP 1960, 10, 574–581. [Google Scholar]
- Redmond, P.J. Elimination of Ghosts in Propagators. Phys. Rev. 1958, 112, 1404. [Google Scholar] [CrossRef]
- Cvetic, G.; Valenzuela, C. Analytic QCD: A Short review. Braz. J. Phys. 2008, 38, 371–380. [Google Scholar]
- Bakulev, A.P. Global Fractional Analytic Perturbation Theory in QCD with Selected Applications. Phys. Part. Nucl. 2009, 40, 715–756. [Google Scholar] [CrossRef]
- Stefanis, N.G. Taming Landau singularities in QCD perturbation theory: The Analytic approach. Phys. Part. Nucl. 2013, 44, 494–509. [Google Scholar] [CrossRef]
- Nesterenko, A.V. Analytic invariant charge in QCD. Int. J. Mod. Phys. A 2003, 18, 5475–5520. [Google Scholar] [CrossRef]
- Nesterenko, A.V.; Papavassiliou, J. The Massive analytic invariant charge in QCD. Phys. Rev. D 2005, 71, 016009. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Zemlyakov, I.A. Fractional analytic QCD beyond leading order. J. Phys. G 2023, 50, 015001. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Zemlyakov, I.A. Fractional analytic QCD beyond leading order in the timelike region. Phys. Rev. D 2023, 107, 094034. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Zemlyakov, I.A. About Fractional Analytic QCD beyond Leading Order. arXiv 2022, arXiv:2207.01330. [Google Scholar]
- Kotikov, A.V.; Zemlyakov, I.A. About Fractional Analytic QCD. Phys. Part. Nucl. 2023, 54, 942–947. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Zemlyakov, I.A. On Fractional Analytic QCD. Phys. Part. Nucl. 2024, 55, 863–867. [Google Scholar] [CrossRef]
- Gabdrakhmanov, I.R.; Gramotkov, N.A.; Kotikov, A.V.; Volkova, D.A.; Zemlyakov, I.A. Bjorken sum rule with analytic coupling at low Q2 values. JETP Lett. 2023, 118, 478–482. [Google Scholar] [CrossRef]
- Gabdrakhmanov, I.R.; Gramotkov, N.A.; Kotikov, A.V.; Teryaev, O.V.; Volkova, D.A.; Zemlyakov, I.A. Bjorken sum rule with analytic coupling. arXiv 2024, arXiv:2404.01873. [Google Scholar] [CrossRef]
- Gabdrakhmanov, I.R.; Gramotkov, N.A.; Kotikov, A.V.; Teryaev, O.V.; Volkova, D.A.; Zemlyakov, I.A. On Bjorken sum rule with analytic coupling. arXiv 2024, arXiv:2406.20000. [Google Scholar] [CrossRef]
- Shaikhatdenov, B.G.; Kotikov, A.V.; Krivokhizhin, V.G.; Parente, G. QCD coupling constant at NNLO from DIS data. Phys. Rev. D 2010, 81, 034008, Erratum in Phys. Rev. D 2010, 81, 079904. [Google Scholar] [CrossRef]
- Krivokhizhin, V.G.; Kotikov, A.V. A systematic study of QCD coupling constant from deep-inelastic measurements. Phys. Atom. Nucl. 2005, 68, 1873–1903. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 8, 083C01. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C.; et al. Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Chetyrkin, K.G.; Kuhn, J.H.; Sturm, C. QCD decoupling at four loops. Nucl. Phys. B 2006, 744, 121–135. [Google Scholar] [CrossRef]
- Schroder, Y.; Steinhauser, M. Four-loop decoupling relations for the strong coupling. J. High Energy Phys. 2006, 2006, 51. [Google Scholar] [CrossRef]
- Kniehl, B.A.; Kotikov, A.V.; Onishchenko, A.I.; Veretin, O.L. Strong-coupling constant with flavor thresholds at five loops in the anti-MS scheme. Phys. Rev. Lett. 2006, 97, 042001. [Google Scholar] [CrossRef] [PubMed]
- d’Enterria, D.; Rojo, J.; Brambilla, N.; Reichelt, D.; Jamin, M.; Maltman, K.; Sint, S.; Teca, D.; Britzger, D.; Kronfeld, A.S.; et al. The strong coupling constant: State of the art and the decade ahead. arXiv 2022, arXiv:2203.08271. [Google Scholar] [CrossRef]
- Chen, H.M.; Liu, L.M.; Wang, J.T.; Waqas, M.; Peng, G.X. Matching-invariant running of quark masses in quantum chromodynamics. Int. J. Mod. Phys. E 2022, 31, 2250016. [Google Scholar] [CrossRef]
- Illarionov, A.Y.; Kotikov, A.V.; Bermudez, G.P. Small x behavior of parton distributions. A Study of higher twist effects. Phys. Part. Nucl. 2008, 39, 307–347. [Google Scholar] [CrossRef]
- Zeus Collaboration; Chekanov, S. Measurement of the neutral current cross section and structure function for deep inelastic scattering at HERA. Eur. Phys. J. C-Part. Fields 2001, 21, 443–471. [Google Scholar] [CrossRef]
- Cvetic, G.; Valenzuela, C. An Approach for evaluation of observables in analytic versions of QCD. J. Phys. G 2006, 32, L27. [Google Scholar] [CrossRef]
- Cvetic, G.; Valenzuela, C. Various versions of analytic QCD and skeleton-motivated evaluation of observables. Phys. Rev. D 2006, 74, 114030, Erratum in Phys. Rev. D 2011, 84, 019902. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Zemlyakov, I.A. About Derivatives in Analytic QCD. JETP Lett. 2022, 115, 565–569. [Google Scholar] [CrossRef]
- Cvetic, G.; Kogerler, R.; Valenzuela, C. Reconciling the analytic QCD with the ITEP operator product expansion philosophy. Phys. Rev. D 2010, 82, 114004. [Google Scholar] [CrossRef]
- Cvetič, G.; Kotikov, A.V. Analogs of noninteger powers in general analytic QCD. J. Phys. G 2012, 39, 065005. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Lipatov, L.N. NLO corrections to the BFKL equation in QCD and in supersymmetric gauge theories. Nucl. Phys. B 2000, 582, 19–43. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Lipatov, L.N. DGLAP and BFKL equations in the N = 4 supersymmetric gauge theory. Nucl. Phys. B 2003, 661, 19–61. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Lipatov, L.N.; Onishchenko, A.I.; Velizhanin, V.N. Three loop universal anomalous dimension of the Wilson operators in N = 4 SUSY Yang-Mills model. Phys. Lett. B 2004, 595, 521–529. [Google Scholar] [CrossRef]
- Bianchi, L.; Forini, V.; Kotikov, A.V. On DIS Wilson coefficients in N = 4 super Yang-Mills theory. Phys. Lett. B 2013, 725, 394–401. [Google Scholar] [CrossRef]
- Nesterenko, A.V.; Simolo, C. QCDMAPT: Program package for Analytic approach to QCD. Comput. Phys. Commun. 2010, 181, 1769–1775. [Google Scholar] [CrossRef][Green Version]
- Nesterenko, A.V. Electron–positron annihilation into hadrons at the higher-loop levels. Eur. Phys. J. C 2017, 77, 844. [Google Scholar] [CrossRef]
- Pasechnik, R.S.; Shirkov, D.V.; Teryaev, O.V. Bjorken sum rule and perturbative QCD frontier on the move. Phys. Rev. D 2008, 78, 071902. [Google Scholar] [CrossRef]
- Pasechnik, R.S.; Shirkov, D.V.; Teryaev, O.V.; Solovtsova, O.P.; Khandramai, V.L. Nucleon spin structure and pQCD frontier on the move. Phys. Rev. D 2010, 81, 016010. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Shaikhatdenov, B.G. Perturbative QCD analysis of the Bjorken sum rule. Phys. Part. Nucl. 2014, 45, 26–29. [Google Scholar] [CrossRef]
- Khandramai, V.L.; Pasechnik, R.S.; Shirkov, D.V.; Solovtsova, O.P.; Teryaev, O.V. Four-loop QCD analysis of the Bjorken sum rule vs data. Phys. Lett. B 2012, 706, 340–344. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Krivokhizhin, V.G.; Shaikhatdenov, B.G. Analytic and ‘frozen’ QCD coupling constants up to NNLO from DIS data. Phys. Atom. Nucl. 2012, 75, 507–524. [Google Scholar] [CrossRef]
- Sidorov, A.V.; Solovtsova, O.P. The QCD analysis of the combined set for the F3 structure function data based on the analytic approach. Mod. Phys. Lett. A 2014, 29, 1450194. [Google Scholar] [CrossRef]
- Chen, J.P. Spin sum rules and polarizabilities: Results from Jefferson lab. arXiv 2006, arXiv:nucl-ex/0611024. [Google Scholar]
- Chen, J.P.; Deur, A.; Meziani, Z.E. Sum rules and moments of the nucleon spin structure functions. Mod. Phys. Lett. A 2005, 20, 2745–2766. [Google Scholar] [CrossRef]
- Ayala, C.; Cvetic, G.; Kotikov, A.V.; Shaikhatdenov, B.G. Bjorken sum rule in QCD frameworks with analytic (holomorphic) coupling. Int. J. Mod. Phys. A 2018, 33, 1850112. [Google Scholar] [CrossRef]
- Ayala, C.; Cvetič, G.; Kotikov, A.V.; Shaikhatdenov, B.G. Bjorken sum rule in QCD with analytic coupling. J. Phys. Conf. Ser. 2017, 938, 012055. [Google Scholar] [CrossRef]
- Ayala, C.; Cvetič, G.; Kotikov, A.V.; Shaikhatdenov, B.G. Bjorken polarized sum rule and infrared-safe QCD couplings. Eur. Phys. J. C 2018, 78, 1002. [Google Scholar] [CrossRef]
- Ayala, C.; Cvetič, G.; Kotikov, A.V.; Shaikhatdenov, B.G. Bjorken sum rule with analytic QCD coupling. J. Phys. Conf. Ser. 2020, 1435, 012016. [Google Scholar] [CrossRef]
- Broadhurst, D.J.; Kataev, A.L.; Maxwell, C.J. Renormalons and multiloop estimates in scalar correlators: Higgs decay and quark mass sum rules. Nucl. Phys. B 2001, 592, 247–293. [Google Scholar] [CrossRef]
- Chetyrkin, K.G. Correlator of the quark scalar currents and Gamma(tot) (H —> hadrons) at O (alpha-s3) in pQCD. Phys. Lett. B 1997, 390, 309–317. [Google Scholar] [CrossRef]
- Baikov, P.A.; Chetyrkin, K.G.; Kuhn, J.H. Scalar correlator at O(alpha(s)4), Higgs decay into b-quarks and bounds on the light quark masses. Phys. Rev. Lett. 2006, 96, 012003. [Google Scholar] [CrossRef] [PubMed]
- Baikov, P.A.; Chetyrkin, K.G.; Kühn, J.H. Higgs Decay, Z Decay and the QCD Beta-Function. Acta Phys. Polon. B 2017, 48, 2135. [Google Scholar] [CrossRef]
- Chetyrkin, K.G.; Kniehl, B.A.; Sirlin, A. Estimations of order alpha-s3 and alpha-s4 corrections to mass dependent observables. Phys. Lett. B 1997, 402, 359–366. [Google Scholar] [CrossRef]
- Kataev, A.L.; Kim, V.T. The Effects of the QCD corrections to Gamma (H0 —> b anti-b). Mod. Phys. Lett. A 1994, 9, 1309–1326. [Google Scholar] [CrossRef]
- Khan, M.S.A.A. Renormalization group summation and analytic continuation from spacelike to timeline regions. Phys. Rev. D 2023, 108, 014028. [Google Scholar] [CrossRef]
- Wang, S.Q.; Wu, X.G.; Zheng, X.C.; Shen, J.M.; Zhang, Q.L. The Higgs boson inclusive decay channels H→bb and H→gg up to four-loop level. Eur. Phys. J. C 2014, 74, 2825. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Wu, X.G. Scale Setting Using the Extended Renormalization Group and the Principle of Maximum Conformality: The QCD Coupling Constant at Four Loops. Phys. Rev. D 2012, 85, 034038, Erratum in Phys. Rev. D 2012, 86, 079903. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Wu, X.G. Eliminating the Renormalization Scale Ambiguity for Top-Pair Production Using the Principle of Maximum Conformality. Phys. Rev. Lett. 2012, 109, 042002. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Giustino, L.D. Setting the Renormalization Scale in QCD: The Principle of Maximum Conformality. Phys. Rev. D 2012, 86, 085026. [Google Scholar] [CrossRef]
- Mojaza, M.; Brodsky, S.J.; Wu, X.G. Systematic All-Orders Method to Eliminate Renormalization-Scale and Scheme Ambiguities in Perturbative QCD. Phys. Rev. Lett. 2013, 110, 192001. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Mojaza, M.; Wu, X.G. Systematic Scale-Setting to All Orders: The Principle of Maximum Conformality and Commensurate Scale Relations. Phys. Rev. D 2014, 89, 014027. [Google Scholar] [CrossRef]
- Shen, J.M.; Zhou, Z.J.; Wang, S.Q.; Yan, J.; Wu, Z.F.; Wu, X.G.; Brodsky, S.J. Extending the Predictive Power of Perturbative QCD Using the Principle of Maximum Conformality and Bayesian Analysis. arXiv 2023, arXiv:2209.03546. [Google Scholar] [CrossRef]
- Yan, J.; Wu, Z.F.; Shen, J.M.; Wu, X.G. Precise perturbative predictions from fixed-order calculations. arXiv 2023, arXiv:2209.13364. [Google Scholar] [CrossRef]
- de Florian, D.; Fontes, D.; Quevillon, J.; Schumacher, M.; Llanes-Estrada, F.J.; Gritsan, A.V.; Vryonidou, E.; Signer, A.; de Castro Manzano, P.; Pagani, D.; et al. Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector. arXiv 2016, arXiv:1610.07922. [Google Scholar]
- Aaboud, M.; Aad, G.; Abbott, B.; Abeloos, B.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Observation of H→bb decays and VH production with the ATLAS detector. Phys. Lett. B 2018, 786, 59–86. [Google Scholar]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Erö, J.; Escalante Del Valle, A.; et al. Observation of Higgs boson decay to bottom quarks. Phys. Rev. Lett. 2018, 121, 121801. [Google Scholar]
- Tsukerman, I.I. Study of the Standard Model Higgs Boson in the ATLAS and CMS Experiments at the LHC. Phys. Atom. Nucl. 2020, 83, 219–227. [Google Scholar] [CrossRef]
- Bjorken, J.D. Applications of the Chiral U(6) × (6) Algebra of Current Densities. Phys. Rev. 1966, 148, 1467–1478. [Google Scholar] [CrossRef]
- Bjorken, J.D. Inelastic Scattering of Polarized Leptons from Polarized Nucleons. Phys. Rev. D 1970, 1, 1376–1379. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; Téramond, G.F.D. The Spin Structure of the Nucleon. arXiv 2018, arXiv:1807.05250. [Google Scholar] [CrossRef]
- Kuhn, S.E.; Chen, J.P.; Leader, E. Spin Structure of the Nucleon—Status and Recent Results. Prog. Part. Nucl. Phys. 2009, 63, 1–50. [Google Scholar] [CrossRef]
- Pasechnik, R.S.; Soffer, J.; Teryaev, O.V. Nucleon spin structure at low momentum transfers. Phys. Rev. D 2010, 82, 076007. [Google Scholar] [CrossRef]
- Shuryak, E.V.; Vainshtein, A.I. Theory of Power Corrections to Deep Inelastic Scattering in Quantum Chromodynamics. 2. Q4 Effects: Polarized Target. Nucl. Phys. B 1982, 201, 141. [Google Scholar] [CrossRef]
- Balitsky, I.I.; Braun, V.M.; Kolesnichenko, A.V. Power corrections 1/Q2 to parton sum rules for deep inelastic scattering from polarized targets. Phys. Lett. B 1990, 242, 245–250, Erratum in Phys. Lett. B 1993, 318, 648. [Google Scholar] [CrossRef]
- Teryaev, O. Analyticity and higher twists. Nucl. Phys. B Proc. Suppl. 2013, 245, 195–198. [Google Scholar] [CrossRef]
- Khandramai, V.L.; Teryaev, O.V.; Gabdrakhmanov, I.R. Infrared modified QCD couplings and Bjorken sum rule. J. Phys. Conf. Ser. 2016, 678, 012018. [Google Scholar] [CrossRef]
- Gabdrakhmanov, I.R.; Teryaev, O.V.; Khandramai, V.L. Infrared models for the Bjorken sum rule in the APT approach. J. Phys. Conf. Ser. 2017, 938, 012046. [Google Scholar] [CrossRef]
- Baikov, P.A.; Chetyrkin, K.G.; Kuhn, J.H. Adler Function, Bjorken Sum Rule, and the Crewther Relation to Order in a General Gauge Theory. Phys. Rev. Lett. 2010, 104, 132004. [Google Scholar] [CrossRef]
- Ayala, C.; Pineda, A. Bjorken sum rule with hyperasymptotic precision. Phys. Rev. D 2022, 106, 056023. [Google Scholar] [CrossRef]
- Ayala, C.; Castro-Arriaza, C.; Cvetič, G. Evaluation of Bjorken polarised sum rule with a renormalon-motivated approach. Phys. Lett. B 2024, 848, 138386. [Google Scholar] [CrossRef]
- Ayala, C.; Castro-Arriaza, C.; Cvetic, G. Renormalon-based resummation of Bjorken polarised sum rule in holomorphic QCD. Nucl. Phys. B 2024, 1007, 116668. [Google Scholar] [CrossRef]
- Ayala, C.; Castro-Arriaza, C.; Cvetič, G. Renormalon structure in Bjorken sum rule. Nucl. Part. Phys. Proc. 2024, 343, 94–98. [Google Scholar] [CrossRef]
- Kotlorz, D.; Mikhailov, S.V. Optimized determination of the polarized Bjorken sum rule in pQCD. Phys. Rev. D 2019, 100, 056007. [Google Scholar] [CrossRef]
- Ayala, C.; Cvetic, G. Towards unifying perturbative and Holographic Light-Front QCD via holomorphic coupling. J. High Energy Phys. 2024, 12, 074. [Google Scholar] [CrossRef]
- Baikov, P.A.; Chetyrkin, K.G.; Kuhn, J.H. Order alpha4(s) QCD Corrections to Z and tau Decays. Phys. Rev. Lett. 2008, 101, 012002. [Google Scholar] [CrossRef] [PubMed]
- Deur, A.; Chen, J.P.; Kuhn, S.E.; Peng, C.; Ripani, M.; Sulkosky, V.; Adhikari, K.; Battaglieri, M.; Burkert, V.D.; Cates, G.D.; et al. Experimental study of the behavior of the Bjorken sum at very low Q2. Phys. Lett. B 2022, 825, 136878. [Google Scholar] [CrossRef]
- Abe, K.; Akagi, T.; Anthony, P.L.; Antonov, R.; Arnold, R.G.; Averett, T.; Band, H.R.; Bauer, J.M.; Borel, H.; Bosted, P.E.; et al. Measurements of the proton and deuteron spin structure functions g(1) and g(2). Phys. Rev. D 1998, 58, 112003. [Google Scholar] [CrossRef]
- Abe, K.; Akagi, T.; Anderson, B.D.; Anthony, P.L.; Arnold, R.G.; Averett, T.; Band, H.R.; Berisso, C.M.; Bogorad, P.; Borel, H.; et al. Precision determination of the neutron spin structure function g1(n). Phys. Rev. Lett. 1997, 79, 26–30. [Google Scholar] [CrossRef]
- Anthony, P.L.; Arnold, R.G.; Band, H.R.; Borel, H.; Bosted, P.E.; Breton, V.; Cates, G.D.; Chupp, T.E.; Dietrich, F.S.; Dunne, J.; et al. Deep inelastic scattering of polarized electrons by polarized He-3 and the study of the neutron spin structure. Phys. Rev. D 1996, 54, 6620–6650. [Google Scholar] [CrossRef] [PubMed]
- Anthony, P.L.; Arnold, R.G.; Averett, T.; Band, H.R.; Berisso, M.C.; Borel, H.; Bosted, P.E.; Bueltmann, S.L.; Buenerd, M.; Chupp, T.; et al. Measurement of the deuteron spin structure function g1(d)(x) for 1-(GeV/c)**2 < Q**2 < 40-(GeV/c)**2. Phys. Lett. B 1999, 463, 339–345. [Google Scholar]
- Anthony, P.L.; Arnold, R.G.; Averett, T.; Band, H.R.; Berisso, M.C.; Borel, H.; Bosted, P.E.; Bueltmann, S.L.; Buenerd, M.; Chupp, T.; et al. Measurements of the Q**2 dependence of the proton and neutron spin structure functions g(1)**p and g(1)**n. Phys. Lett. B 2000, 493, 19–28. [Google Scholar] [CrossRef]
- Adeva, B.; Ahmad, S.; Arvidson, A.; Badelek, B.; Ballintijn, M.K.; Bardin, G.; Baum, G.; Berglund, P.; Betev, L.; Bird, I.G.; et al. Measurement of the spin dependent structure function g1(x) of the deuteron. Phys. Lett. B 1993, 302, 533–539. [Google Scholar] [CrossRef]
- Adams, D.; Adeva, B.; Akdogan, T.; Arik, E.; Arvidson, A.; Badelek, B.; Ballintijn, M.K.; Bardin, D.; Bardin, G.; Baum, G.; et al. The Spin dependent structure function g(1) (x) of the proton from polarized deep inelastic muon scattering. Phys. Lett. B 1997, 412, 414–424. [Google Scholar]
- Adams, D.; Adeva, B.; Arik, E.; Arvidson, A.; Badelek, B.; Ballintijn, M.K.; Bardin, G.; Baum, G.; Berglund, P.; Betev, L.; et al. Measurement of the spin dependent structure function g1(x) of the proton. Phys. Lett. B 1994, 329, 399–406, Erratum in Phys. Lett. B 1994, 339, 332–333. [Google Scholar] [CrossRef][Green Version]
- Adams, D.; Adeva, B.; Arik, E.; Arvidson, A.; Badelek, B.; Ballintijn, M.K.; Bardin, G.; Baum, G.; Berglund, P.; Betev, L.; et al. A New measurement of the spin dependent structure function g1(x) of the deuteron. Phys. Lett. B 1995, 357, 248–254. [Google Scholar] [CrossRef]
- Adams, D.; Adeva, B.; Arik, E.; Arvidson, A.; Badelek, B.; Ballintijn, M.K.; Bardin, G.; Baum, G.; Berglund, P.; Betev, L.; et al. The Spin dependent structure function g1(x) of the deuteron from polarized deep inelastic muon scattering. Phys. Lett. B 1997, 396, 338–348. [Google Scholar] [CrossRef]
- Adams, D.; Adeva, B.; Arik, E.; Arvidson, A.; Badelek, B.; Ballintijn, M.K.; Bardin, G.; Baum, G.; Berglund, P.; Betev, L.; et al. Spin structure of the proton from polarized inclusive deep inelastic muon-proton scattering. Phys. Rev. D 1997, 56, 5330–5358. [Google Scholar] [CrossRef]
- Ageev, E.S.; Alexakhin, V.Y.; Alexandrov, Y.; Alexeev, G.D.; Amoroso, A.; Badełek, B.; Balestra, F.; Ball, J.; Baum, G.; Bedfer, Y.; et al. Measurement of the spin structure of the deuteron in the DIS region. Phys. Lett. B 2005, 612, 154–164. [Google Scholar] [CrossRef][Green Version]
- Ageev, E.S.; Alexakhin, V.Y.; Alexandrov, Y.; Alexeev, G.D.; Amoroso, A.; Badełek, B.; Balestra, F.; Ball, J.; Baum, G.; Bedfer, Y.; et al. Spin asymmetry A1(d) and the spin-dependent structure function g1(d) of the deuteron at low values of x and Q2. Phys. Lett. B 2007, 647, 330–340. [Google Scholar]
- Alekseev, M.G.; Alexakhin, V.Y.; Alexandrov, Y.; Alexeev, G.D.; Amoroso, A.; Austregesilo, A.; Badełek, B.; Balestra, F.; Ball, J.; Barth, J.; et al. The Spin-dependent Structure Function of the Proton and a Test of the Bjorken Sum Rule. Phys. Lett. B 2010, 690, 466–472. [Google Scholar] [CrossRef]
- Bordalo, P.; Franco, C.; Nunes, A.S.; Quaresma, M.; Quintans, C.; Ramos, S.; Silva, L.; Stolarski, M.; COMPASS collaboration. The spin structure function of the proton and a test of the Bjorken sum rule. Phys. Lett. B 2016, 753, 18–28. [Google Scholar]
- Bordalo, P.; Franco, C.; Nunes, A.S.; Quaresma, M.; Quintans, C.; Ramos, S.; Silva, L.; Stolarski, M.; COMPASS collaboration. Final COMPASS results on the deuteron spin-dependent structure function and the Bjorken sum rule. Phys. Lett. B 2017, 769, 34–41. [Google Scholar]
- Aghasyan, M.; Akhunzyanov, R.; Alexeev, M.G.; Alexeev, G.D.; Amoroso, A.; Andrieux, V.; Anfimov, N.V.; Anosov, V.; Antoshkin, A.; Augsten, K.; et al. Longitudinal double-spin asymmetry and spin-dependent structure function of the proton at small values of x and Q2. Phys. Lett. B 2018, 781, 464–472. [Google Scholar] [CrossRef]
- HERMES Collaboration; Ackerstaff, K.; Airapetian, A.; Akushevich, I.; Akopov, N.; Amarian, M.; Aschenauer, E.C.; Avakian, R.; Avakian, H.; Avetissian, A.; et al. Measurement of the neutron spin structure function g1(n) with a polarized He-3 internal target. Phys. Lett. B 1997, 404, 383–389. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akopov, Z.; Andrus, A.; Aschenauer, E.C.; Augustyniak, W.; Avakian, R.; Avetissian, A.; Avetissian, E.; Belostotski, S.; et al. Measurement of the proton spin structure function g1(p) with a pure hydrogen target. Phys. Lett. B 1998, 442, 484–492. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akopov, Z.; Andrus, A.; Aschenauer, E.C.; Augustyniak, W.; Avakian, R.; Avetissian, A.; Avetissian, E.; Belostotski, S.; et al. Precise determination of the spin structure function g(1) of the proton, deuteron and neutron. Phys. Rev. D 2007, 75, 012007. [Google Scholar] [CrossRef]
- Deur, A.; Bosted, P.E.; Burkert, V.; Cates, G.; Chen, J.P.; Choi, S.; Crabb, D.; de Jager, C.W.; Vita, R.D.; Dodge, G.E.; et al. Experimental determination of the evolution of the Bjorken integral at low Q2. Phys. Rev. Lett. 2004, 93, 212001. [Google Scholar] [CrossRef]
- Deur, A.; Bosted, P.; Burkert, V.; Crabb, D.; Dharmawardane, V.; Dodge, G.E.; Forest, T.A.; Griffioen, K.A.; Kuhn, S.E.; Minehart, R.; et al. Experimental study of isovector spin sum rules. Phys. Rev. D 2008, 78, 032001. [Google Scholar] [CrossRef]
- Deur, A.; Prok, Y.; Burkert, V.; Crabb, D.; Girod, F.X.; Griffioen, K.A.; Guler, N.; Kuhn, S.E.; Kvaltine, N. High precision determination of the Q2 evolution of the Bjorken Sum. Phys. Rev. D 2014, 90, 012009. [Google Scholar] [CrossRef]
- Slifer, K.; Rondón, O.A.; Aghalaryan, A.; Ahmidouch, A.; Asaturyan, R.; Bloch, F.; Boeglin, W.; Bosted, P.; Carasco, C.; Carlini, R.; et al. Probing Quark-Gluon Interactions with Transverse Polarized Scattering. Phys. Rev. Lett. 2010, 105, 101601. [Google Scholar] [CrossRef]
- Kataev, A.L. Infrared renormalons and the relations between the Gross-Llewellyn Smith and the Bjorken polarized and unpolarized sum rules. JETP Lett. 2005, 81, 608–611. [Google Scholar] [CrossRef][Green Version]
- Kataev, A.L. Deep inelastic sum rules at the boundaries between perturbative and nonperturbative QCD. Mod. Phys. Lett. A 2005, 20, 2007–2022. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Teramond, G.F.; Dosch, H.G.; Erlich, J. Light-Front Holographic QCD and Emerging Confinement. Phys. Rep. 2015, 584, 1–105. [Google Scholar] [CrossRef]
- Burkert, V.D.; Ioffe, B.L. On the Q2 variation of spin dependent deep inelastic electron-proton scattering. Phys. Lett. B 1992, 296, 223–226. [Google Scholar] [CrossRef]
- Burkert, V.D.; Ioffe, B.L. Polarized structure functions of proton and neutron and the Gerasimov-Drell-Hearn and Bjorken sum rules. J. Exp. Theor. Phys. 1994, 78, 619–622. [Google Scholar]
- Soffer, J.; Teryaev, O. The Role of g-2 in relating the Schwinger and Gerasimov-Drell-Hearn sum rules. Phys. Rev. Lett. 1993, 70, 3373–3375. [Google Scholar] [CrossRef]
- Soffer, J.; Teryaev, O. QCD radiative and power corrections and generalized GDH sum rules. Phys. Rev. D 2004, 70, 116004. [Google Scholar] [CrossRef]
- Blümlein, J.; Falcioni, G.; Freitas, A.D. The Complete O() Non-Singlet Heavy Flavor Corrections to the Structure Functions (x, Q2), (x, Q2), (x, Q2) and the Associated Sum Rules. Nucl. Phys. B 2016, 910, 568–617. [Google Scholar] [CrossRef]
- Gabdrakhmanov, I.R.; Gramotkov, N.A.; Kotikov, A.V.; Teryaev, O.V.; Volkova, D.A.; Zemlyakov, I.A. Heavy quark contributions in Bjorken sum rule with analytic coupling. arXiv 2024, arXiv:2408.16804. [Google Scholar]
- Gabdrakhmanov, I.R.; Gramotkov, N.A.; Kotikov, A.V.; Volkova, D.A.; Zemlyakov, I.A. On Bjorken Sum Rule with Analytic Coupling at Low Q2 Values. Phys. Atom. Nucl. 2024, 87, 536–540. [Google Scholar] [CrossRef]
- Gabdrakhmanov, I.R.; Gramotkov, N.A.; Kotikov, A.V.; Teryaev, O.V.; Volkova, D.A.; Zemlyakov, I.A. On Bjorken sum rule: Heavy quarks and analytic coupling. arXiv 2025, arXiv:2501.00456. [Google Scholar]
- Magradze, B.A. Analytic approach to perturbative QCD. Int. J. Mod. Phys. A 2000, 15, 2715–2734. [Google Scholar] [CrossRef]
- Magradze, B.A. QCD coupling up to third order in standard and analytic perturbation theories. arXiv 2000, arXiv:hep-ph/0010070. [Google Scholar]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W Function. Adv. Comput. Math. 1996, 5, 329. [Google Scholar] [CrossRef]
- Bakulev, A.P.; Khandramai, V.L. FAPT: A Mathematica package for calculations in QCD Fractional Analytic Perturbation Theory. Comput. Phys. Commun. 2013, 184, 183–193. [Google Scholar] [CrossRef]
- Khandramai, V. On applications of Mathematica Package ‘FAPT’ in QCD. J. Phys. Conf. Ser. 2014, 523, 012062, [arXiv:1310.5983[hep-ph]]. [Google Scholar] [CrossRef]
- Chetyrkin, K.G. Quark mass anomalous dimension to O (alpha-s4). Phys. Lett. B 1997, 404, 161–165. [Google Scholar] [CrossRef]





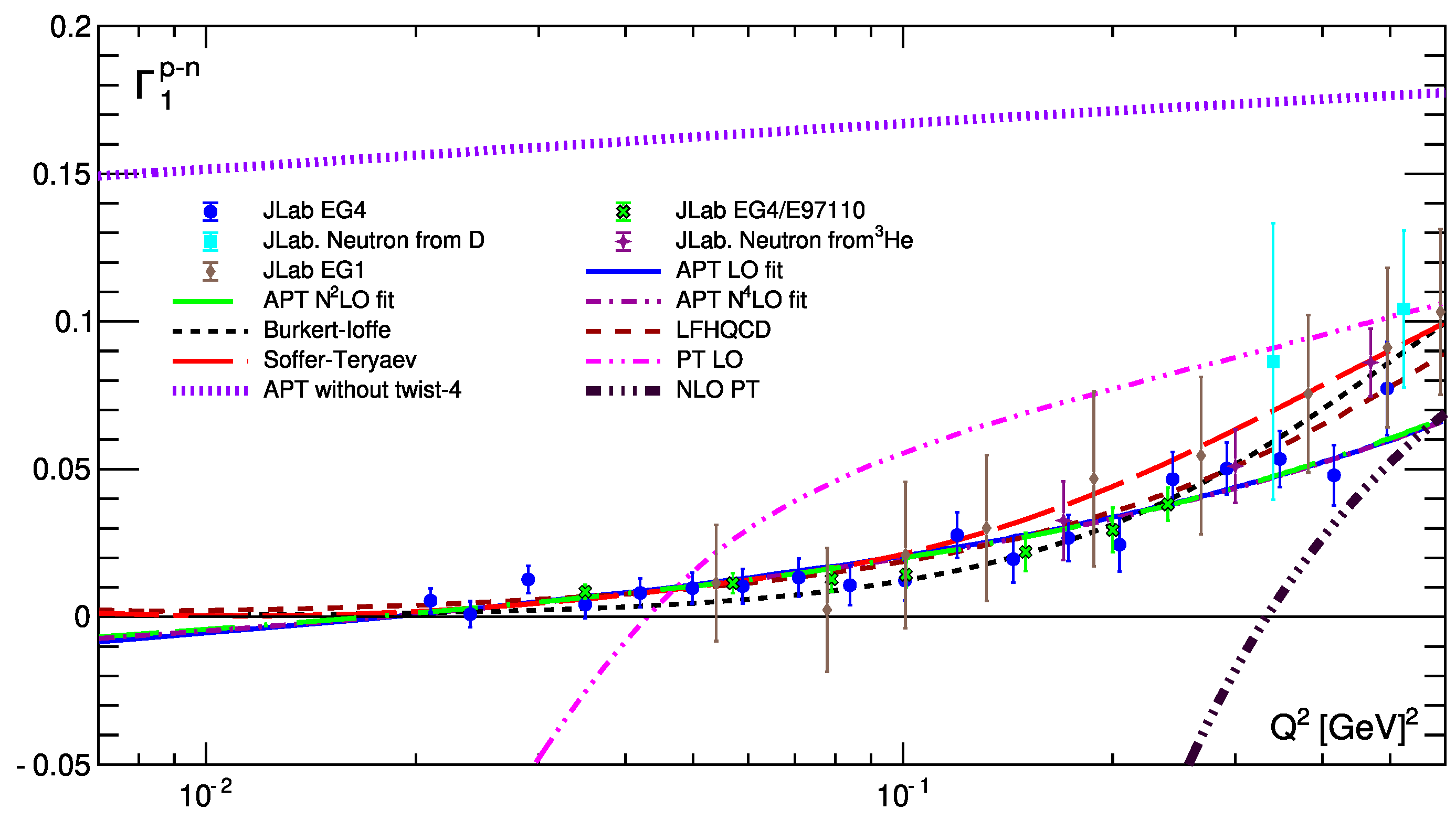

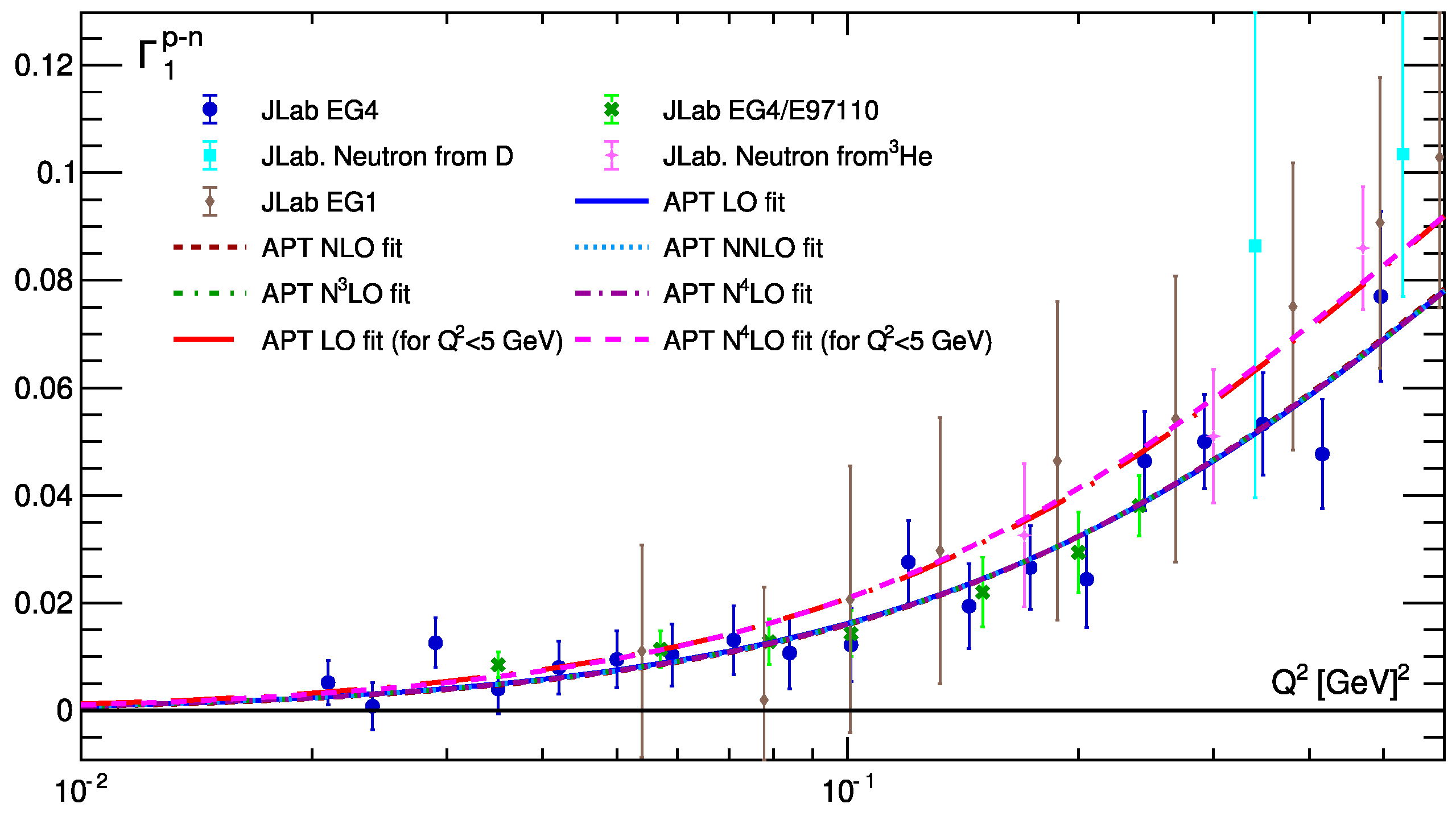
| [] for (for GeV2) | for (for GeV2) | for (for ) | |
|---|---|---|---|
| LO | 0.472 ± 0.035 | −0.212 ± 0.006 | 0.667 |
| (1.631 ± 0.301) | (−0.166 ± 0.001) | (0.789) | |
| NLO | 0.414 ± 0.035 | −0.206 ± 0.008 | 0.728 |
| (1.545 ± 0.287) | (−0.155 ± 0.001) | (0.757) | |
| N2LO | 0.397 ± 0.034 | −0.208± 0.008 | 0.746 |
| (1.417 ± 0.241) | (−0.156 ± 0.002) | (0.728) | |
| N3LO | 0.394 ± 0.034 | −0.209 ± 0.008 | 0.754 |
| (1.429 ± 0.248) | (−0.157 ± 0.002) | (0.747) | |
| N4LO | 0.397 ± 0.035 | −0.208 ± 0.007 | 0.753 |
| (1.462 ± 0.259) | (−0.157 ± 0.001) | (0.754) |
| [] for (for GeV2) | for (for ) | |
|---|---|---|
| LO | 0.383 ± 0.014 (0.576 ± 0.046) | 0.572 (0.575) |
| NLO | 0.394 ± 0.013 (0.464 ± 0.039) | 0.586 (0.590) |
| LO | 0.328 ± 0.014 (0.459 ± 0.038) | 0.617 (0.584) |
| LO | 0.330 ± 0.014 (0.464 ± 0.039) | 0.629 (0.582) |
| LO | 0.331 ± 0.013 (0.465 ± 0.039) | 0.625 (0.584) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabdrakhmanov, I.R.; Gramotkov, N.A.; Kotikov, A.V.; Teryaev, O.V.; Volkova, D.A.; Zemlyakov, I.A. Fractional Analytic QCD: The Recent Results. Particles 2025, 8, 29. https://doi.org/10.3390/particles8010029
Gabdrakhmanov IR, Gramotkov NA, Kotikov AV, Teryaev OV, Volkova DA, Zemlyakov IA. Fractional Analytic QCD: The Recent Results. Particles. 2025; 8(1):29. https://doi.org/10.3390/particles8010029
Chicago/Turabian StyleGabdrakhmanov, Ilnur R., Nikita A. Gramotkov, Anatoly V. Kotikov, Oleg V. Teryaev, Daria A. Volkova, and Ivan A. Zemlyakov. 2025. "Fractional Analytic QCD: The Recent Results" Particles 8, no. 1: 29. https://doi.org/10.3390/particles8010029
APA StyleGabdrakhmanov, I. R., Gramotkov, N. A., Kotikov, A. V., Teryaev, O. V., Volkova, D. A., & Zemlyakov, I. A. (2025). Fractional Analytic QCD: The Recent Results. Particles, 8(1), 29. https://doi.org/10.3390/particles8010029








