Imprints of High-Density Nuclear Symmetry Energy on Crustal Fraction of Neutron Star Moment of Inertia

Abstract

The density dependence of nuclear symmetry energy $E_{\mathrm{sym}}\left(\rho \right)$ remains the most uncertain aspect of the equation of state (EOS) of supradense neutron-rich nucleonic matter. Utilizing an isospin-dependent parameterization of the nuclear EOS, we investigate the implications of the observational crustal fraction of the neutron star (NS) moment of inertia $\Delta I/I$ for the $E_{\mathrm{sym}}\left(\rho \right)$. We find that symmetry energy parameters significantly influence the $\Delta I/I$, while the EOS of symmetric nuclear matter has a negligible effect. In particular, an increase in the slope L and skewness $J_{\mathrm{sym}}$ of symmetry energy results in a larger $\Delta I/I$, whereas an increase in the curvature $K_{\mathrm{sym}}$ leads to a reduction in $\Delta I/I$. Moreover, the $\Delta I/I$ is shown to have the potential for setting a lower limit of symmetry energy at densities exceeding $3{\rho }_0$, particularly when L is constrained to values less than 60 MeV, thereby enhancing our understanding of supradense NS matter.

1. Introduction

The equation of state (EOS) of neutron-rich matter plays a crucial role in determining many properties of neutron stars (NSs). Unfortunately, it still has significant uncertainties, especially at high densities. The high-density behavior of nuclear symmetry energy $E_{\mathrm{sym}}$ has long been recognized as the most uncertain aspect of the EOS of supradense neutron-rich nucleonic matter. This uncertainty stems from our limited understanding of the weak isospin dependence of the strong force, the spin–isospin dependence of three-body nuclear forces, and the tensor-force-induced isospin dependence of short-range nucleon–nucleon correlations in dense matter and is compounded by the challenges of accurately solving nuclear many-body problems [1]. The symmetry energy significantly influences various properties of neutron stars, including their radii, deformations and polarizabilities [2], and moments of inertia, and the crust–core transition density [3,4]. Thus, constraining the EOS or $E_{\mathrm{sym}}$ remains a critical issue for both the nuclear physics and astrophysics communities [5,6,7,8,9,10,11].

Fortunately, terrestrial nuclear experiments and astrophysical observations have provided tighter constraints over the past decades. For example, the mass of the most massive NS observed so far, e.g., the mass of PSR J0740+6620, has recently been updated to $2.08\pm 0.07$ M_⊙ [12,13], with its radius constrained to $R=13.7_{-1.5}^{+2.6}$ km [14] or $R=12.{39}_{-0.98}^{+1.30}$ km [15] by the Neutron Star Interior Composition Explorer (NICER) Collaboration. Additionally, with a significant increase in the dataset, updated analyses of the radius have been reported in refs. [16,17,18]. Furthermore, the tidal deformability of a neutron star with 1.4 M_⊙ (canonical neutron star) has been extracted from the binary neutron star merger event GW170817, yielding $80<{\Lambda }_{1.4}<580$ at the 90% confidence level, as reported by the LIGO and Virgo Collaborations [19]. Although these observations still carry substantial uncertainties, they have been repeatedly employed in various analyses to enhance our understanding of neutron star matter (see, e.g., refs. [20,21,22] for reviews).

In addition to the aforementioned observational data, the glitch phenomenon in pulsars can also serve to constrain the EOS or $E_{\mathrm{sym}}$ [23,24,25,26,27]. This phenomenon, characterized by sudden increases in spin frequency, was first observed in the Vela pulsar [28,29] and has since been detected in approximately 6% of all known pulsars. Glitches occur due to the transfer of angular momentum from the superfluid component of the stellar interior to the solid crust [30,31,32]. Previous studies have indicated that the glitch phenomenon is closely associated with the crustal fraction of the moment of inertia $\Delta I/I$, where I represents the total moment of inertia of the star and $\Delta I$ is the moment of inertia of the crust. By combining glitch data from the Vela pulsar and six other pulsars, ref. [33] established that $\Delta I/I$ in a neutron star must exceed 1.4%. Notably, this constraint does not depend on the mass of the neutron star, leading many references to assume masses of either 1.0 M_⊙ or 1.4 M_⊙, resulting in conditions of ${(\Delta I/I)}_{1.4}\ge 1.0\%$ or ${(\Delta I/I)}_{1.4}\ge 1.4\%$. This lower limit was later increased to 1.6% [34]. While this limit can be met by nearly all EOSs, accounting for the entrainment of superfluid neutrons in the crust raises the constraint to $\Delta I/I\ge 7\%$ [35,36], providing a more stringent condition for constraining the EOS or $E_{\mathrm{sym}}$.

Based on the constraints inferred from analyzing the glitch phenomenon, previous studies have found that a strong correlation exists between the density dependence of symmetry energy and the crustal moment of inertia (see, e.g., [25,26,37]), especially within the framework of microscopic or phenomenological nuclear many-body theories. However, no clear constraints on the EOS or $E_{\mathrm{sym}}$ have been extracted. On the other hand, with the accumulation of more of the NS observations mentioned above, many parameterized EOSs (see, e.g., refs. [38,39,40,41,42]) have been proposed and found very useful due to their flexibility and convenience in generating vastly different EOSs continuously. While not necessarily directly connected with a specific force within a specific many-body theory, such meta-model EOSs have been found very useful in extracting constraints on the EOS or $E_{\mathrm{sym}}$ within either Bayesian analysis [43] or forward modeling [42]. Moreover, results from such an analytical formula and simple physics pictures are consistent with those starting from using different microscopic/phenomenological methods with various interactions (see, e.g., ref. [44], for detailed comparisons).

In our previous study [45], we simultaneously considered the maximum observed mass of PSR J0740+6620, the simultaneous measurement of mass and radius for this pulsar, and the tidal deformability from GW170817 to extract constraints on the EOS and $E_{\mathrm{sym}}$. We found that the $E_{\mathrm{sym}}$ at densities greater than $3{\rho }_0$ still exhibits significant uncertainties, highlighting the need for additional observational data. In this work, we examine prospects of using the crustal fraction of NS moment of inertia $\Delta I/I$ to constrain the EOS and especially $E_{\mathrm{sym}}$ at suprasaturation densities using an isospin-dependent parameterization for the EOS of NS matter.

The remainder of the paper is organized as follows: In the next section, we introduce the meta-model EOSs describing nuclear matter and detail the calculations of $\Delta I/I$ and NS crust–core transition properties. Section 3 discusses symmetry energy effects on the crustal fraction of the NS moment of inertia. Finally, we summarize our findings in Section 4.

2. Theoretical Framework

2.1. Explicitly Isospin-Dependent Meta-Model EOS for Super-Dense Neutron-Rich Nuclear Matter

A meta-model is a model of models. In the present work, we assume the neutron star matter is made of neutron-rich nuclear matter ($npe\mu$) at $\beta$-equilibrium described by a meta-model constructed in ref. [42]. The energy density for $npe\mu$ matter at $\beta$-equilibrium can be calculated from

$$\epsilon (\rho ,\delta )=\rho [E(\rho ,\delta )+M_N]+{\epsilon }_l(\rho ,\delta ),$$

(1)

where the first term donates the energy density of nucleons and ${\epsilon }_l(\rho ,\delta )$ denotes the energy density for leptons (electrons and muons) that can be calculated from, e.g., the noninteracting Fermi gas model [46]. $\delta =({\rho }_n+{\rho }_p)/\rho$ is the isospin asymmetry, $M_N$ represents the average nucleon mass of 938 MeV, and $E(\rho ,\delta )$ is the energy per nucleon of asymmetric nuclear matter, which is a parabolic function of $\delta$ [47]:

$$E(\rho ,\delta )=E_0\left(\rho \right)+E_{\mathrm{sym}}\left(\rho \right)·{\delta }^2+\mathcal{O}\left({\delta }^4\right),$$

(2)

where $E_0\left(\rho \right)$ is the energy per nucleon of symmetric nuclear matter (SNM) and $E_{\mathrm{sym}}\left(\rho \right)$ is nuclear symmetry energy at density $\rho$. Once the energy density is determined, the baryon densities ${\rho }_i$ of particle i can be obtained by solving the $\beta$-equilibrium condition ${\mu }_n-{\mu }_p={\mu }_e={\mu }_{\mu }\approx 4\delta E_{\mathrm{sym}}\left(\rho \right)$ where ${\mu }_i=\partial \epsilon (\rho ,\delta )/\partial {\rho }_i$ and charge neutrality condition ${\rho }_p={\rho }_e+{\rho }_{\mu }$. The pressure of neutron-rich nuclear matter can be calculated from

$$P\left(\rho \right)={\rho }^2{\displaystyle \frac{\mathrm{d}\epsilon (\rho ,\delta (\rho \left)\right)/\rho }{\mathrm{d}\rho }}.$$

(3)

Then, an EOS is obtained. To generate a series of EOSs with continuously variable parameters, we parameterize the $E_0\left(\rho \right)$ and $E_{\mathrm{sym}}\left(\rho \right)$ as

$$E_0\left(\rho \right)=E_0\left({\rho }_0\right)+{\displaystyle \frac{K_0}{2}}{\left({\displaystyle \frac{\rho -{\rho }_0}{3{\rho }_0}}\right)}^2+{\displaystyle \frac{J_0}{6}}{\left({\displaystyle \frac{\rho -{\rho }_0}{3{\rho }_0}}\right)}^3,$$

(4)

$$\begin{array}{ccc}\hfill E_{\mathrm{sym}}\left(\rho \right)& =& E_{\mathrm{sym}}\left({\rho }_0\right)+L\left({\displaystyle \frac{\rho -{\rho }_0}{3{\rho }_0}}\right)\hfill \\ & +& {\displaystyle \frac{K_{\mathrm{sym}}}{2}}{\left({\displaystyle \frac{\rho -{\rho }_0}{3{\rho }_0}}\right)}^2+{\displaystyle \frac{J_{\mathrm{sym}}}{6}}{\left({\displaystyle \frac{\rho -{\rho }_0}{3{\rho }_0}}\right)}^3.\hfill \end{array}$$

(5)

We emphasize that the above parameterizations are different from the Taylor expansions. Our meta-model EOS constructed for neutron stars contains physics about the compositions of neutron star matter. In particular, the proton fraction is determined consistently by the symmetry energy, which plays the most important role in determining the radii of neutron stars. More details about this model can be found in our previous publications [45,48,49,50,51,52,53,54].

Based on the accumulations of terrestrial nuclear experiments and astrophysical observations in past decades, the binding energy $E_0\left({\rho }_0\right)$ and incompressibility $K_0$ of SNM at the saturation density have been tightly constrained to $E_0\left({\rho }_0\right)=-15.9\pm 0.4$ MeV and $K_0=240\pm 20$ MeV [55,56]. Based on surveys of 53 analyses of different kinds of terrestrial and astrophysical data available up to 2016 October, the magnitude $E_{\mathrm{sym}}\left({\rho }_0\right)$ and slope L of symmetry energy at ${\rho }_0$ are constrained to $E_{\mathrm{sym}}\left({\rho }_0\right)=31.7\pm 3.2$ MeV and $L=58.7\pm 28.1$ MeV [9,57], respectively. For the parameters characterizing the medium- or high-density behavior of neutron-rich nuclear matter, the curvature of the symmetry energy is around $K_{\mathrm{sym}}=-100\pm 100$ MeV [22,40,58,59,60], while the skewness of the SNM EOS is constrained to $J_0=-190\pm 100$ MeV [43,44,61] based on terrestrial experiments and astrophysical observations. Few constraints on $J_{\mathrm{sym}}$ have been obtained so far, and it is only very roughly known to be around $-200<J_{\mathrm{sym}}<800$ MeV [62,63,64]. However, as a small $J_{\mathrm{sym}}$ leads to low-mass neutron stars, especially when $J_{\mathrm{sym}}$ is negative, we choose the lower boundary of $J_{\mathrm{sym}}$ to be 200 MeV in the present work. We emphasize that the above parameters can be varied independently within the uncertain ranges given above. In fact, some of the uncertainty ranges are obtained from the marginalized posterior probability distribution functions (PDFs) of individual parameters in Bayesian analyses of NS observables. Nevertheless, once new observables or physics conditions are considered, correlations among the updated posterior EOS parameters may be introduced. In this work, however, all EOS parameters should be considered independent in the current uncertainty ranges given above.

Compared with EOSs from microscopic and/or phenomenological nuclear many-body theories, as well as piecewise polytropes or spectrum functions, here, we want to emphasize the following aspects of the meta-model and justifications for using it. First of all, for microscopic and/or phenomenological nuclear many-body theories of neutron star matter, though numerous fundamental physical details can be included, it is challenging to isolate the individual effects of each parameter on the properties of neutron stars as they typically exhibit correlations. On the contrary, all parameters of our meta-model can be varied independently within their presently known uncertainties. In addition, the meta-model can generate different EOSs that can mimic essentially all existing EOSs predicted by basically all microscopic and/or phenomenological theories by varying the meta-model EOS parameters. Secondly, we emphasize here that our model is different from the Taylor expansions where the convergence problem arises for densities larger than about 1.5${\rho }_0$. The parameters given by Equations (4) and (5) coincide with the Taylor expansion coefficients of the EOS around ${\rho }_0$, but their high-density interpretation is tied to the specific functional form of the parameterization employed here. Specifically, the higher-order terms in these equations are not merely coefficients of a Taylor series but are tied to the analytical structure of the chosen parameterization. As parameterizations, mathematically, they can be valid at any density without the convergence issue even at $(2-3){\rho }_0$ and beyond. Their parameters can be extracted from astrophysical observations or terrestrial experiments. On the other hand, when approaching the saturation density, Equations (4) and (5) are exactly the Taylor expansions up to the third order. The same notation has been consistently adopted in our prior works and more detailed demonstrations can be found in refs. [42,48,53].

At densities below the crust–core transition point, we choose the Negele–Vautherin (NV) EOS [65] for the inner crust and the Baym–Pethick–Sutherland (BPS) EOS [66] for the outer crust. Once the parameters in Equations (4) and (5) are fixed and the transition density is calculated, a unique EOS is obtained. Then, NS properties including masses and radii can be calculated by solving the TOV equations [46,67].

2.2. Crustal Fraction of Neutron Star Moment of Inertia

In the present work, as we want to check how the observation of the crustal fraction of moment of inertia $\Delta I/I$ can constrain the parameters shown in Equations (4) and (5), we calculate the $\Delta I/I$ using the following formalism, given in ref. [33]:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\Delta I}{I}}& =& {\displaystyle \frac{28\pi P_t{R}^3}{3M{c}^2}}{\displaystyle \frac{(1-1.67\xi -0.6{\xi }^2)}{\xi }}\hfill \\ & \times & [1+{\displaystyle \frac{2P_t}{{\rho }_t{m}_b{c}^2}}{{\displaystyle \frac{1+5\xi -14{\xi }^2}{{\xi }^2}}}^{-1}],\hfill \end{array}$$

(6)

where $\xi =GM/R{c}^2$ is the dimensionless compactness, and $m_b=930$ MeV/$c^2$ is the mass of ${}^{12}\mathrm{C}$/12 or ${}^{56}\mathrm{Fe}$/56 [3,4].

As shown in the above equation, the crustal fraction of the moment of inertia of the neutron star is quite sensitive to the crust–core transition density ${\rho }_t$ and the pressure $P_t$ there. The crust–core transition density ${\rho }_t$ can be found by examining when the incompressibility of NS matter in the uniform core vanishes [68,69,70]:

$$\begin{array}{ccc}\hfill K_{\mu }& =& {\rho }^2{\displaystyle \frac{{\mathrm{d}}^2{E}_0}{\mathrm{d}{\rho }^2}}+2\rho {\displaystyle \frac{\mathrm{d}{E}_0}{\mathrm{d}\rho }}+{\delta }^2\hfill \\ & \times & [{\rho }^2{\displaystyle \frac{{\mathrm{d}}^2{E}_{\mathrm{sym}}}{\mathrm{d}{\rho }^2}}+2\rho {\displaystyle \frac{\mathrm{d}{E}_{\mathrm{sym}}}{\mathrm{d}\rho }}-2E_{\mathrm{sym}}^{-1}{\left(\rho {\displaystyle \frac{\mathrm{d}{E}_0}{\mathrm{d}\rho }}\right)}^2]=0.\hfill \end{array}$$

(7)

Once $K_{\mu }$ becomes negative, the speed of sound becomes imaginary. It indicates the onset of the mechanical instability (spinodal decomposition of matter) in the core, leading to the formation of clusters making up the crust. This method has been used extensively in the literature to locate the crust–core transition point using various EOSs (see, e.g., [71,72,73,74]). As the $E_{\mathrm{sym}}$ and $E_0$ appear explicitly in the above equation, it is thus necessary and interesting to explore whether $E_{\mathrm{sym}}$ and $E_0$ have significant effects on the crustal fraction of the NS moment of inertia [75,76]. The flexibility of the meta-model and the very diverse EOSs generated with it enable us to explore possible effects of $E_{\mathrm{sym}}$ and $E_0$ on $\Delta I/I$ more easily and broadly. In particular, we focus on the effects of the high-order coefficients of nuclear symmetry energy ($K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$) that have not been studied yet in the literature. Since the crust–core transition density and pressure are determined by the curvature of NS matter in Equation (7), the $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ are expected to be important for determining the $\Delta I/I$.

3. Results and Discussions

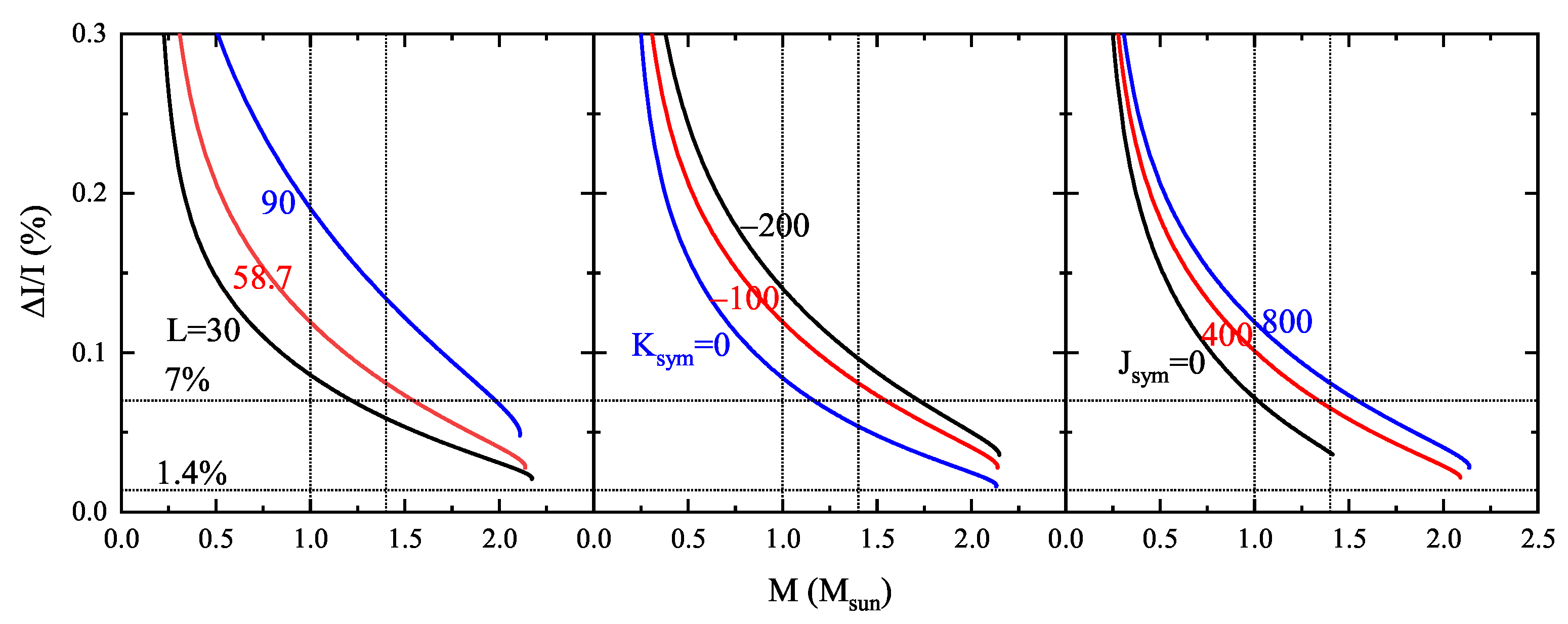
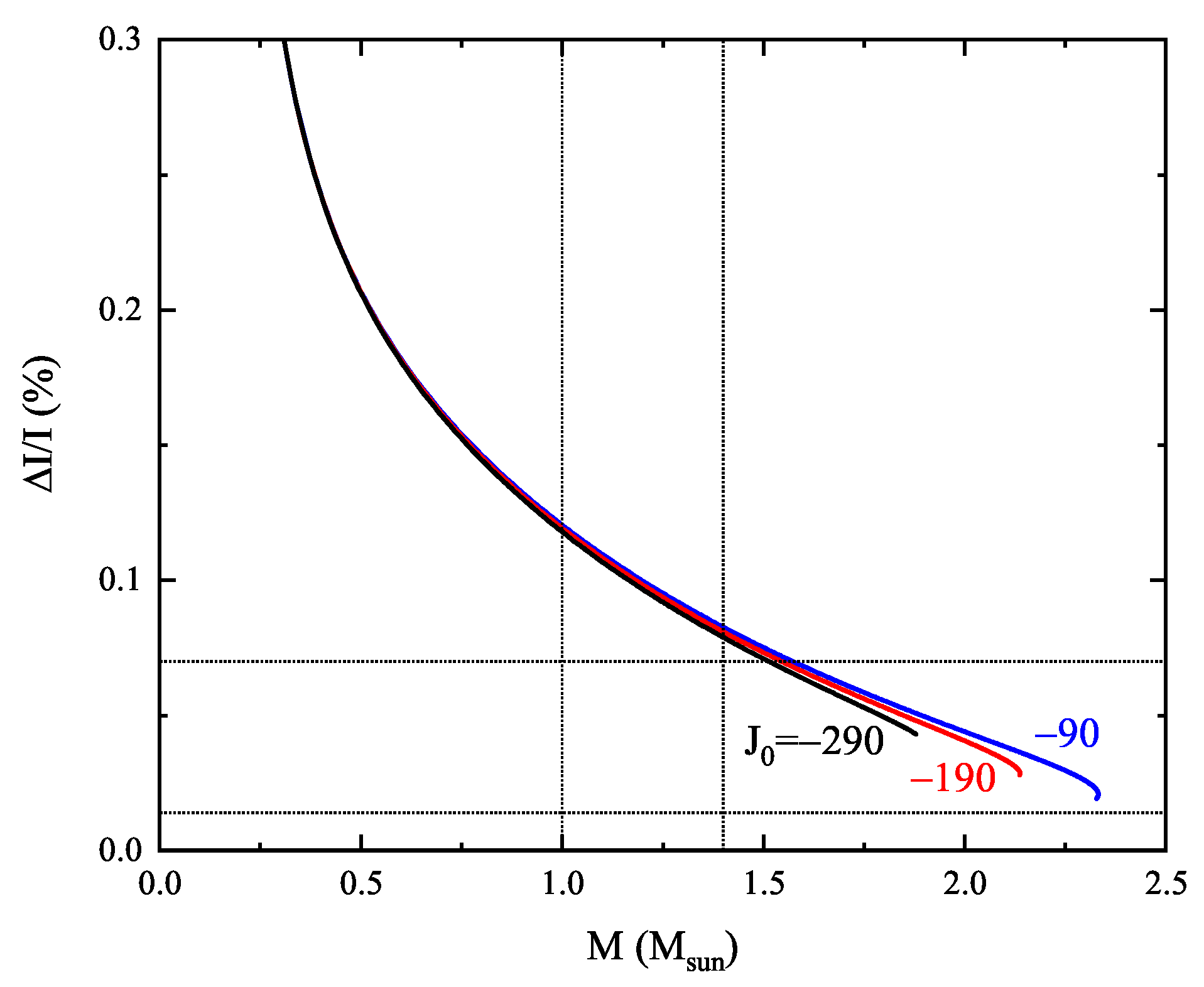
3.1. Effects of Nuclear EOS Parameters on the Crustal Fraction of the NS Moment of Inertia

Effects of the slope L (left plot), curvature $K_{\mathrm{sym}}$ (middle plot), and skewness $J_{\mathrm{sym}}$ (right plot) of nuclear symmetry energy on the crustal fraction of NS moment of inertia $\Delta I/I$ are illustrated in Figure 1. The horizontal dotted lines represent the constraints of 1.4% and 7%, while the vertical dotted lines correspond to neutron star masses of 1.0 and 1.4 M_⊙. Other parameters are kept at the most probable values currently known, as previously mentioned. From the figure, it is evident that the symmetry energy parameters exert minimal influence on the NS maximum mass reached, with the exception of $J_{\mathrm{sym}}=0$, which results in a very soft EOS at high densities. Additionally, all symmetry energy parameters significantly affect the crustal fraction of the NS moment of inertia. More specifically, as L increases, the $\Delta I/I$ consistently increases for a given NS mass. The condition $\Delta I/I>1.4\%$ is easily satisfied, whereas $\Delta I/I>7\%$ is only met when $M<1.21$ M_⊙ for $L=30$ MeV and $M<1.98$ M_⊙ for $L=90$ MeV, respectively. This indicates that the constraint of $\Delta I/I>7\%$ can exclude $L=30$ MeV for neutron stars with masses larger than $1.21$ M_⊙ while favoring larger values of L that allow for a broader mass range to satisfy the $\Delta I/I>7\%$ constraint.

A similar trend is observed for $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$. However, an increase in $K_{\mathrm{sym}}$ leads to a decrease in $\Delta I/I$. This is due to the fact that a higher $K_{\mathrm{sym}}$ results in a lower crust–core transition density, particularly affecting the transition pressure. On the other hand, an increase in L or $J_{\mathrm{sym}}$ raises the crust–core transition density, as shown in Figure 3 of ref. [42]. It is important to note that, since the symmetry energy at saturation density is well constrained, the effects of $E_{\mathrm{sym}}\left({\rho }_0\right)$ are not significant and are thus not depicted here. Consequently, the competition among the symmetry energy parameters ultimately determines the value of $\Delta I/I$ and its mass dependence.

In addition to the effects of nuclear symmetry energy, effects of the skewness $J_0$ of SNM on the crustal fraction of NS moment of inertia $\Delta I/I$ are illustrated in Figure 2. It was seen that $J_0$ has minimal impact on $\Delta I/I$, leading us to fix $J_0=-190$ MeV in the subsequent discussions regarding $\Delta I/I$. However, $J_0$ does significantly influence the maximum mass of neutron stars, which increases from 1.88 to 2.33 M_⊙ as $J_0$ rises from $-290$ MeV to $-90$ MeV. Similar findings have been reported in our previous publications (e.g., refs. [42,48,49]). Likewise, effects of the incompressibility $K_0$ of SNM are not shown here as it is well constrained and has little effect on the $\Delta I/I$.

Based on the discussions above, we conclude that, while the symmetry energy can significantly affect the moment of inertia, the EOS of SNM has minimal impact. Thus, we will focus on the effects of symmetry energy in the following subsection.

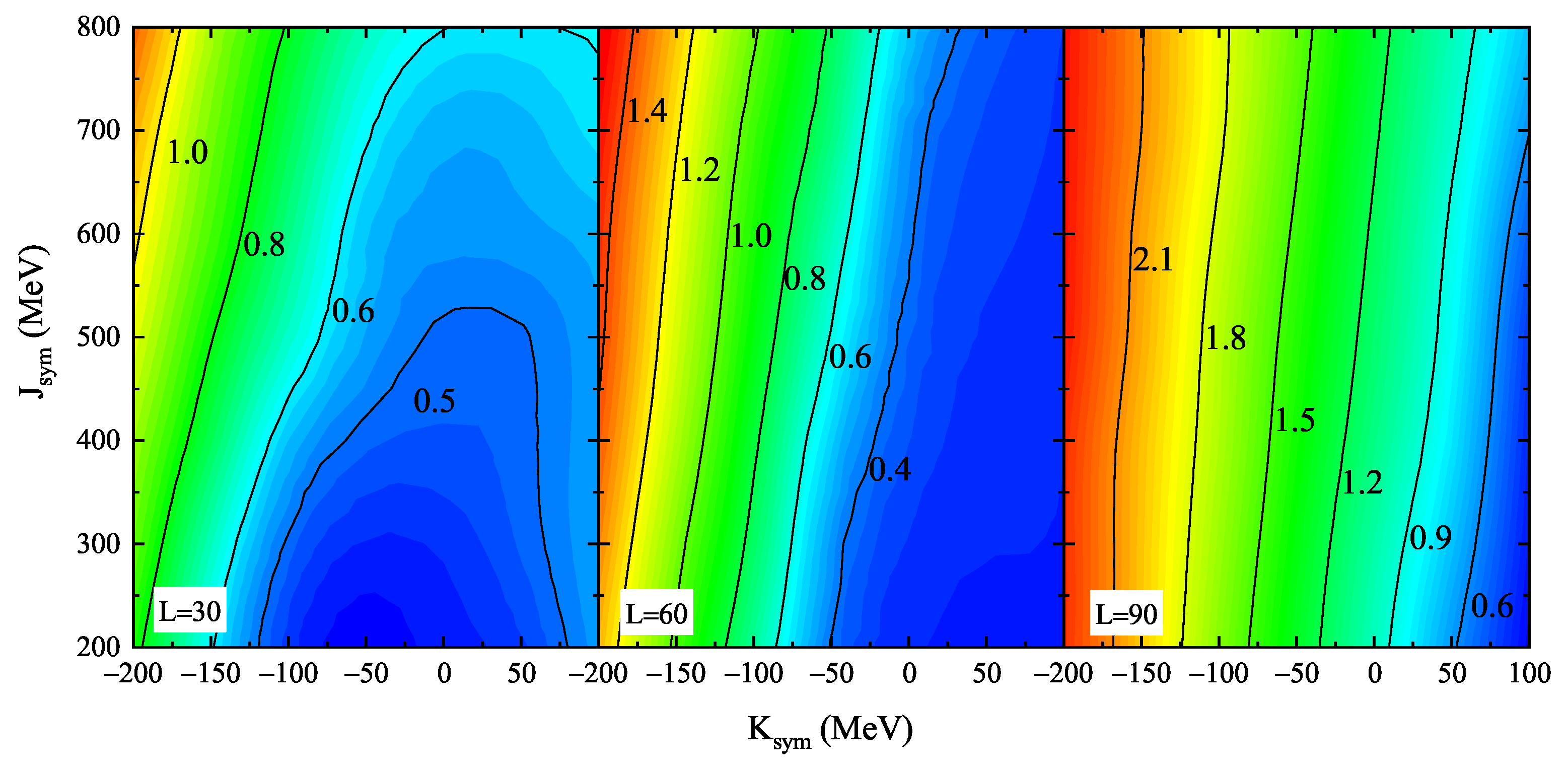
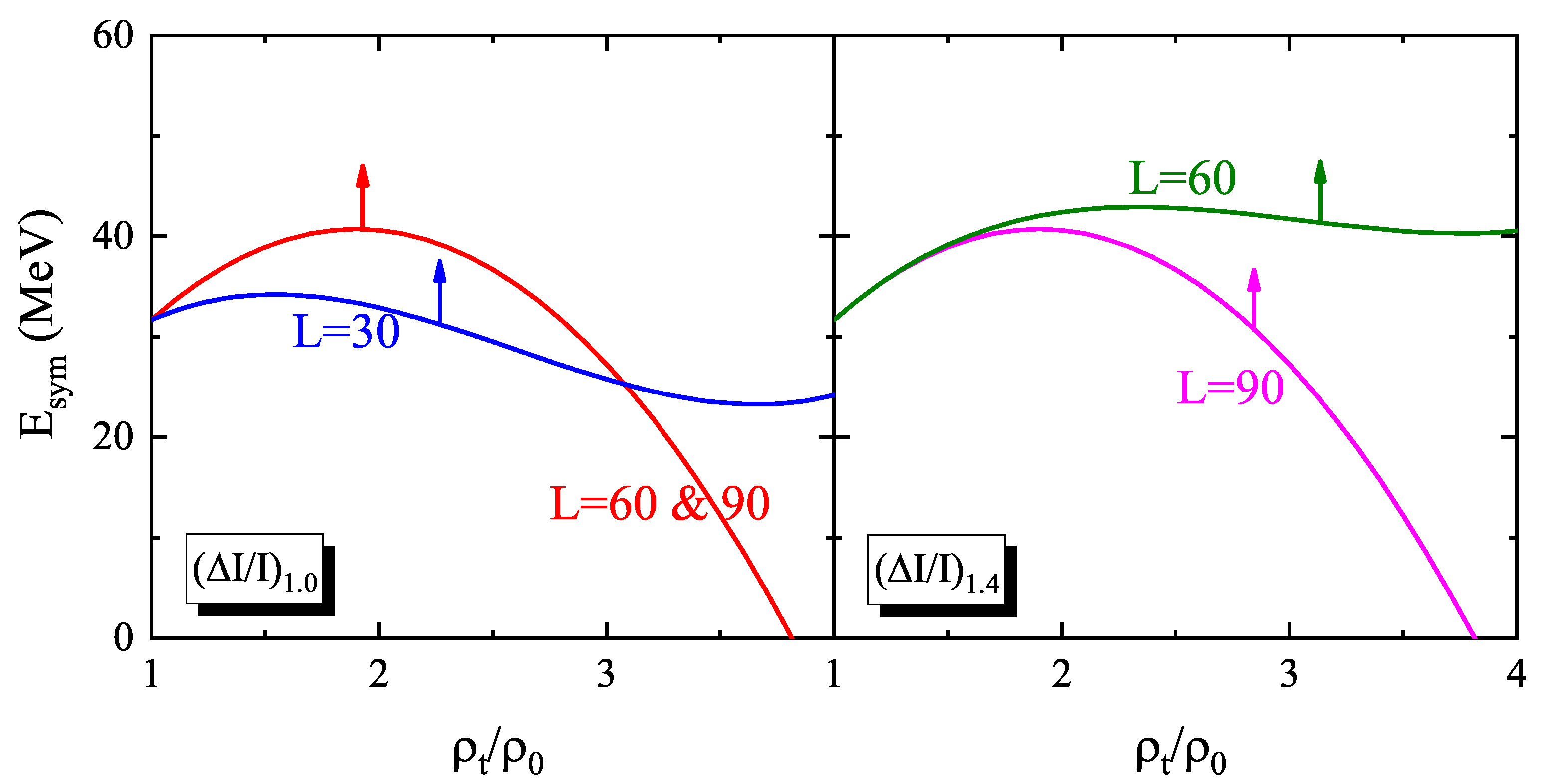
3.2. Constraints on Symmetry Energy Parameters Imposed by Crustal Fraction of NS Moment of Inertia

Currently, the lightest mass of observed NSs is around 1.0 M_⊙, while most NSs have masses around 1.4 M_⊙, and the maximum observed mass is around 2.0 M_⊙. For the integrity of our following discussions, the NSs with masses of 1.0 M_⊙, 1.4 M_⊙, and 2.0 M_⊙ are included as examples.

Fixing the lower mass limit of neutron stars at 1.0 M_⊙, the left plots of Figure 3 present the contour of the crustal fraction of NS moment of inertia $\Delta I/I$ in the $K_{\mathrm{sym}}$ versus $J_{\mathrm{sym}}$ plane for the slope of symmetry energy $L=30$ (upper plot), 60 (middle plot), and 90 MeV (lower plot), respectively. The red lines indicate the constraint of $\Delta I/I=7\%$. It is apparent that $\Delta I/I\ge 7\%$ or $1.4\%$ can be satisfied for all values of L considered. The maximum $\Delta I/I$ appears at $K_{\mathrm{sym}}=-200$ and $J_{\mathrm{sym}}=800$ MeV, as previously shown in Figure 1. $\Delta I/I$ increases with increasing $J_{\mathrm{sym}}$ but decreases with $K_{\mathrm{sym}}$. Additionally, the allowed range expands as L increases.

For $L=30$ MeV, the area below the red line is excluded. Although the individual uncertainties in $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ cannot be narrowed further compared to their initial uncertainties, the combinations of these parameters are significantly constrained. In other words, nearly half of the parameter plane is excluded, particularly when both $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ are small. Furthermore, the relationship between $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ for constant $\Delta I/I$ is not monotonic. As $K_{\mathrm{sym}}$ increases, the curves for fixed $\Delta I/I$ initially rise and then fall. At $K_{\mathrm{sym}}=-200$ MeV, $J_{\mathrm{sym}}$ must exceed 294 MeV, which can be explained by examining the transition density and pressure, as discussed below.

For $L=60$ MeV, the relationship between $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ for constant $\Delta I/I$ becomes monotonic, and the lower-right region of the plane is excluded. The upper limit of $K_{\mathrm{sym}}$ is constrained to be 41 MeV, while $J_{\mathrm{sym}}$ remains unconstrained for $L=60$ MeV. Thus, the crustal fraction of the NS moment of inertia can help constrain the symmetry energy at medium densities characterized by $K_{\mathrm{sym}}$, rather than at high densities, for larger values of L. When L increases to 90 MeV, only a negligible range is excluded to satisfy $\Delta I/I\ge 7\%$ in the lower-right corner. Given that the upper limit of $K_{\mathrm{sym}}$ is constrained to be about 0, symmetry energies with larger values of L cannot be constrained at any density by the $\Delta I/I\ge 7\%$ constraint.

Although a neutron star with 1.0 M_⊙ can achieve $\Delta I/I\ge 7\%$ for any value of L, we find that (1) a larger $J_{\mathrm{sym}}$ is favored for $L=30$ MeV; (2) a smaller $K_{\mathrm{sym}}$ is favored for $L=60$ MeV, while no constraints can be drawn for $J_{\mathrm{sym}}$; and (3) no constraints can be extracted for $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ for $L=90$ MeV. Therefore, the symmetry energy should be treated with caution when calculating the moment of inertia of neutron stars. Additionally, the allowed parameter plane enlarges with L, indicating that a stiffer symmetry energy around saturation density, characterized by L, is more likely to satisfy the constraints imposed by the crustal fraction of the NS moment of inertia.

For a canonical NS with $M=1.4$ M_⊙, the contours of the crustal fraction of NS moment of inertia $\Delta I/I$ in the $K_{\mathrm{sym}}$ versus $J_{\mathrm{sym}}$ plane, with $L=30$ (upper plot), 60 (middle plot), and 90 MeV (lower plot), respectively, are presented in the middle plots of Figure 3. When compared to the left plots of Figure 3, similar features can be observed. However, the parameter plane is clearly more tightly constrained for any value of L as the crustal fraction of the NS moment of inertia decreases with increasing mass. With $L=30$ MeV, no parameter combinations can satisfy the constraint $\Delta I/I\ge 7\%$, indicating that this constraint favors a symmetry energy with a larger slope L. For instance, at $L=60$ MeV, we obtain tighter constraints on $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ compared to a neutron star with $M=1.0$ M_⊙. The lower limit of $J_{\mathrm{sym}}$ is constrained to be 289 MeV, while the upper limit of $K_{\mathrm{sym}}$ is constrained to be $-46$ MeV. This constrained value of $K_{\mathrm{sym}}$ is consistent with findings of previous studies that suggest $K_{\mathrm{sym}}=-100\pm 100$ MeV [22,40,58,59,60]. These constraints on $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ may indicate a relatively stiff symmetry energy at high densities. For $L=90$ MeV, the lower-right corner of the plane is excluded. However, if the upper limit of $K_{\mathrm{sym}}$ is set to 0, the crustal fraction of the NS moment of inertia still cannot effectively constrain the symmetry energy.

For the most massive observed NS with $M\approx 2.0$ M_⊙, the contours of $\Delta I/I$ in the $K_{\mathrm{sym}}$ versus $J_{\mathrm{sym}}$ plane are presented in the right plots of Figure 3. The white regions indicate the excluded parameter sets that cannot support an NS with $M=2.0$ M_⊙. It is clear that the constraint of $\Delta I/I=7\%$ can only be satisfied within a narrow range for $L=90$ MeV.

In short, the constraint $\Delta I/I\ge 7\%$ does not favor symmetry energies with small slopes (such as $L=30$ MeV), and tighter constraints on symmetry energy can be extracted for neutron stars with masses around 1.4 or 2.0 M_⊙. If the neutron star has a significantly larger mass, it is anticipated that only symmetry energies with a considerably larger slope can satisfy this constraint.

From Equation (7), it is evident that the transition pressure $P_t$ plays the most important role in determining the crustal fraction of the moment of inertia, alongside the mass M and radius R of an NS. Notably, the transition density ${\rho }_t$ merely appears in the correction term and thus contributes little to the moment of inertia. Furthermore, lower values of $P_t$ result in a decreased crustal moment of inertia, thereby imposing stricter constraints on the EOS or the symmetry energy $E_{\mathrm{sym}}$. In the thermodynamical approach given in Equation (7), the crust–core transition pressure can be approximated as follows [3,4,70]:

$$P_t={\displaystyle \frac{K_0}{9}}{\displaystyle \frac{{\rho }_t^2}{{\rho }_0}}\left({\displaystyle \frac{{\rho }_t}{{\rho }_0}}-1\right)+{\rho }_t{\delta }_t\left[{\displaystyle \frac{1-{\delta }_t}{2}}{E}_{\mathrm{sym}}\left({\rho }_t\right)+{\left(\rho {\displaystyle \frac{\mathrm{d}{E}_{\mathrm{sym}}\left(\rho \right)}{\mathrm{d}\rho }}\right)}_{{\rho }_t}{\delta }_t\right].$$

(8)

The above equation shows clearly that the relation between $P_t$ and ${\rho }_t$ is complicated. The Pearson correlation coefficient between them is calculated by generating about 39,000 EOSs where all parameters vary within their uncertainties. The resulting Pearson coefficient of 0.92631 indicates a strong and approximately linear correlation between them. Thus, the correlations between either $P_t$ or ${\rho }_t$ and the EOS parameters exhibit a strong similarity. The behavior of the constant crustal fraction of the NS moment of inertia can be explained through the core–crust transition density and pressure. In Figure 3 of ref. [42], we plotted the contours of transition density ${\rho }_t$ and transition pressure $P_t$ in the L and $K_{\mathrm{sym}}$ plane with fixed $J_{\mathrm{sym}}$. We found that, for constant ${\rho }_t$, $K_{\mathrm{sym}}$ exhibits a monotonic relationship with L when $K_{\mathrm{sym}}<-100$ MeV. However, this relationship becomes more complex for larger values of $K_{\mathrm{sym}}$.

To illustrate the effects of $J_{\mathrm{sym}}$ on the transition pressure, we present the contours of transition pressure $P_t$ in the $K_{\mathrm{sym}}$ versus $J_{\mathrm{sym}}$ plane in Figure 4. It is evident that the trends for a constant transition pressure are quite similar to those for the constant moment of inertia shown in Figure 3. Notably, the consistency decreases with increasing neutron star mass, which is understandable since the crust of a neutron star is thicker and constitutes a larger mass percentage in lower-mass stars. Consequently, the core–crust transition properties have a more pronounced effect on low-mass neutron stars.

As L, $K_{\mathrm{sym}}$, and $J_{\mathrm{sym}}$ are the three parameters characterizing the density dependence of nuclear symmetry energy, the constraints on these parameters can be translated into constraints on the symmetry energy itself. The lower boundaries of the symmetry energy for different slopes L of the symmetry energy, corresponding to neutron stars with 1.0 M_⊙ (left plot) and 1.4 M_⊙ (right plot), are illustrated in Figure 5. It is important to note that the lower limit of $E_{\mathrm{sym}}$ is determined by the left bottom corner, specifically, $K_{\mathrm{sym}}=-200$ MeV and $J_{\mathrm{sym}}=200$ MeV within the parameter uncertainties, assuming we do not consider the constraints from the crustal fraction of the NS moment of inertia. With $L=60$ and 90 MeV in the case of the neutron star with 1.0 M_⊙, and for $L=90$ MeV for the neutron star with 1.4 M_⊙, the lower limit of the symmetry energy remains the same, as the left bottom point is not excluded (as shown in Figure 3). As the transition pressure remains almost constant for most combinations of $K_{\mathrm{sym}}$ and $J_{\mathrm{sym}}$ in the left plot of Figure 4 for $L=30$ MeV, a larger $J_{\mathrm{sym}}$ is needed to satisfy $\Delta I/I\ge 7\%$ for the neutron star with 1.0 M_⊙ and $J_{\mathrm{sym}}$ cannot be smaller than 294 MeV (a larger $K_{\mathrm{sym}}$ leads to a smaller $\Delta I/I$). Consequently, the lower limit of symmetry energy along the red line in the upper plot of of left plot of Figure 3 can be extracted, and its lower limit is represented by the blue line in the left plot of Figure 5.

Since no combination of parameters can satisfy $\Delta I/I\ge 7\%$ for neutron stars with 1.4 M_⊙ at $L=30$ MeV, only the lines for $L=60$ MeV and 90 MeV are plotted in the right plot of Figure 5. Focusing on the blue and green lines, it is clear that the symmetry energy remains nearly constant with increasing density, even for densities $\rho >3{\rho }_0$. It is worth noting that the symmetry energy can only be constrained for approximately $\rho <3{\rho }_0$ based on the current observations of NSs by NICER [14,15] and LIGO and Virgo [19] Collaborations, as discussed in our previous study [45]. The present results suggest that the crustal fraction of the NS moment of inertia has the potential to constrain the lower limit of the symmetry energy at densities exceeding $3{\rho }_0$, particularly when L is constrained to values less than 60 MeV.

4. Summary and Conclusions

In summary, using an isospin-dependent NS meta-model EOS, we investigated the implications of the crustal fraction of NS moment of inertia $\Delta I/I$ for NSs with 1.0 M_⊙ or 1.4 M_⊙ on the density dependence of nuclear symmetry energy $E_{\mathrm{sym}}\left(\rho \right)$. We found that an increase in the slope L and skewness $J_{\mathrm{sym}}$ of symmetry energy results in a larger $\Delta I/I$, whereas an increase in the curvature $K_{\mathrm{sym}}$ leads to a reduction in $\Delta I/I$. On the other hand, the SNM EOS was found to have little influence on the $\Delta I/I$. Our findings highlight the significant role of the symmetry energy parameters in determining the crustal fraction of the NS moment of inertia. Moreover, we found that a larger slope L is favored to satisfy the $\Delta I/I\ge 7\%$ constraint, with tighter constraints emerging for neutron stars around 1.4 M_⊙. Furthermore, we extracted the lower boundaries for $E_{\mathrm{sym}}\left(\rho \right)$ from the constraint $\Delta I/I\ge 7\%$ for different L values. Our results indicate that the crustal fraction of the NS moment of inertia has the potential to set a lower limit of symmetry energy at densities exceeding $3{\rho }_0$, particularly when L can be constrained to values less than 60 MeV, reflecting the complex interplay between the core–crust transition properties and the underlying nuclear interactions. These findings emphasize the potential of using the crustal fraction of the NS moment of inertia to refine our understanding of NS physics and the properties of supradense neutron-rich nuclear matter.

Of course, our work has limitations and caveats. First, the crustal moment of inertia is highly sensitive to the crust–core transition density. It is well known that employing different crust models can introduce uncertainty into the radius calculations. However, a quantitative estimate of the associated uncertainty in the predicted NS radius is model dependent, ranging from about 0.1 to 0.7 km (Table I of ref. [77]), while its quantitative effects on the crustal moment of inertia are still unclear. Unified EOSs for both the crust and the core from the same microscopic and/or phenomenological nuclear many-body theories (e.g., refs. [78,79]) could describe the core–crust transition properties more consistently. While our meta-model can mimic some of these uncertainties by varying the EOS parameters as discussed above, investigating the associated microscopic physics in and around the crust–core transition is beyond the ability of our meta-model. Similarly, when deriving the crustal moment of inertia from pulsar observations, the complex dynamics of nucleon superfluidity, which is closely related to the nuclear force, must be considered. Here, we used the observational constraint on the crustal fraction of the neutron star moment of inertia regardless of how it is extracted. Within the framework of our meta-model, we cannot say anything about the microphysics occurring around the interface between the core and the crust of neutron stars. Thirdly, the thermodynamical method (via Equation (7)) suggests larger values of $P_t$ or ${\rho }_t$ (and, consequently, larger values of $\Delta I/I$) compared to the dynamical method, as shown in refs. [71,80]. Therefore, tighter constraints may be obtained if the dynamical method is adopted to calculate the $P_t$ or ${\rho }_t$. Nevertheless, our main qualitative conclusions are not expected to be affected by the above uncertainties.