Black Hole’s Spin-Dependence of γ-Ray and Neutrino Emissions from MAXI J1820+070, XTE J1550-564, and XTE J1859+226
Abstract
1. Introduction
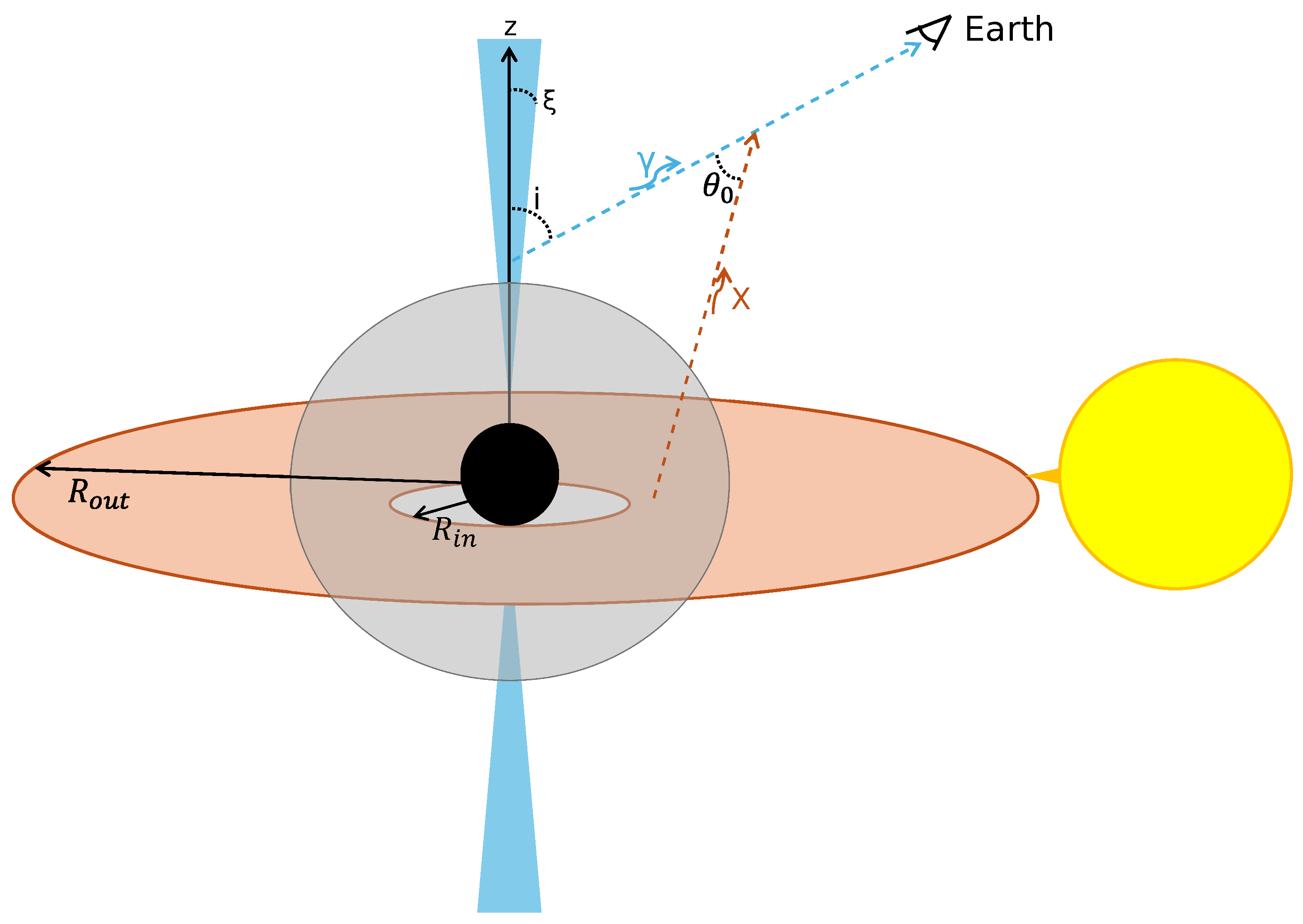
2. Spin-Induced Modifications of the Accretion Disk’s Properties
2.1. Inner Radius of the Accretion Disk around a Kerr Black Hole
2.2. Disk Temperature Profile Derived from the Pseudo-Newtonian Potential
3. The Relativistic Jets in BHXRBs
3.1. Reaction Chains within the Relativistic Jets
3.2. Solution of the Transfer Equation
4. High-Energy Gamma-Ray and Neutrino Emissions
4.1. Intensities and Integral Fluxes
4.2. Absorption from the Accretion Disk
5. Results and Discussion
5.1. MAXI J1820+070
5.2. XTE J1550-564
5.3. XTE J1859+226
6. A New Technique for Measuring the Black Hole’s Spin
7. Conclusions
- The black hole’s spin has no effect on the spectra of neutrino emissions. The intensity and the integral flux of the neutrinos remain the same for any value of .
- The black hole’s spin has a strong effect on the spectra of high-energy -rays. The intensity and the integral flux of high-energy -rays decrease as the spin () increases. This happens because the accretion disk’s attenuation, , increases with ; therefore, a greater part of the -rays is annihilated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BHXRB | Black Hole X-Ray Binary |
| Radius of the Innermost Stable Circular Orbit |
References
- De Rosa, A.; Vignali, C.; Bogdanović, T.; Capelo, P.R.; Charisi, M.; Dotti, M.; Husemann, B.; Lusso, E.; Mayer, L.; Paragi, Z.; et al. The quest for dual and binary supermassive black holes: A multi-messenger view. New Astron. Rev. 2019, 86, 101525. [Google Scholar] [CrossRef]
- Branchesi, M. Multi-messenger astronomy: Gravitational waves, neutrinos, photons, and cosmic rays. J. Phys. Conf. Ser. 2016, 718, 022004. [Google Scholar] [CrossRef]
- Ferrigno, C.; Savchenko, V.; Coleiro, A.; Panessa, F.; Bazzano, A.; Bozzo, E.; Chenevez, J.; Domingo, A.; Doyle, M.; Goldwurm, A.; et al. Multi-messenger astronomy with INTEGRAL. New Astron. Rev. 2021, 92, 101595. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Ackermann, M.; Adams, J.; Aguilar, J.; Ahlers, M.; Allen, M.; Altmann, D.; Andeen, K.; et al. The design and performance of IceCube DeepCore. Astropart. Phys. 2012, 35, 615–624. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Allison, P.; Amin, N.M.; et al. IceCube-Gen2: The window to the extreme Universe. J. Phys. G Nucl. Part. Phys. 2021, 48, 060501. [Google Scholar] [CrossRef]
- Padovani, P.; Alexander, D.M.; Assef, R.J.; De Marco, B.; Giommi, P.; Hickox, R.C.; Richards, G.T.; Smolčić, V.; Hatziminaoglou, E.; Mainieri, V.; et al. Active galactic nuclei: What’s in a name? Astron. Astrophys. Rev. 2017, 25, 2. [Google Scholar] [CrossRef]
- Murase, K. Active Galactic Nuclei as High-Energy Neutrino Sources. In Neutrino Astronomy: Current Status, Future Prospects; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2017; pp. 15–31. [Google Scholar]
- Pagliaroli, G.; Villante, F.L. A multi-messenger study of the total galactic high-energy neutrino emission. J. Cosmol. Astropart. Phys. 2018, 2018, 035. [Google Scholar] [CrossRef]
- Kantzas, D.; Markoff, S.; Lucchini, M.; Ceccobello, C. Black-hole X-ray binaries in the new era of multi-messenger Astronomy. PoS 2021, ICRC2021, 1011. [Google Scholar]
- Shidatsu, M.; Nakahira, S.; Murata, K.L.; Adachi, R.; Kawai, N.; Ueda, Y.; Negoro, H. X-ray and optical monitoring of state transitions in MAXI J1820+ 070. Astrophys. J. 2019, 874, 183. [Google Scholar] [CrossRef]
- Rodi, J.; Tramacere, A.; Onori, F.; Bruni, G.; Sànchez-Fernàndez, C.; Fiocchi, M.; Natalucci, L.; Ubertini, P. A broadband view on microquasar MAXI J1820+ 070 during the 2018 outburst. Astrophys. J. 2021, 910, 21. [Google Scholar] [CrossRef]
- Chaty, S.; Dubus, G.; Raichoor, A. Near-infrared jet emission in the microquasar XTE J1550-564. Astron. Astrophys. 2011, 529, A3. [Google Scholar] [CrossRef]
- Sriram, K.; Rao, A.R.; Choi, C.S. Study of a Sudden QPO Transition Event in the Black Hole Source XTE J1550-564. Astrophys. J. 2016, 823, 67. [Google Scholar]
- Bellm, E.C.; Wang, Y.; van Roestel, J.; Phillipson, R.A.; Coughlin, M.W.; Tomsick, J.A.; Groom, S.L.; Healy, B.; Purdum, J.; Rusholme, B.; et al. An Optically Discovered Outburst from XTE J1859+ 226. Astrophys. J. 2023, 956, 21. [Google Scholar] [CrossRef]
- Farinelli, R.; Amati, L.; Shaposhnikov, N.; Frontera, F.; Masetti, N.; Palazzi, E.; Landi, R.; Lombardi, C.; Orlandini, M.; Brocksopp, C. Spectral evolution of the X-ray nova XTE J1859+ 226 during its outburst observed by BeppoSAX and RXTE. Mon. Not. R. Astron. Soc. 2013, 428, 3295–3305. [Google Scholar] [CrossRef][Green Version]
- Romero, G.E.; Torres, D.F.; Kaufman Bernadó, M.M.; Mirabel, I.F. Hadronic gamma-ray emission from windy microquasars. Astron. Astrophys. 2003, 410, L1–L4. [Google Scholar] [CrossRef]
- Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Simulations of Neutrino and Gamma-Ray Production from Relativistic Black-Hole Microquasar Jets. Galaxies 2021, 9, 67. [Google Scholar] [CrossRef]
- Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Relativistic Magnetized Astrophysical Plasma Outflows in Black-Hole Microquasars. Symmetry 2022, 14, 485. [Google Scholar] [CrossRef]
- Gould, R.J.; Schréder, G.P. Pair production in photon-photon collisions. Phys. Rev. 1967, 155, 1404. [Google Scholar]
- Papavasileiou, T.V.; Kosmas, O.T.; Sinatkas, I. Prediction of gamma-ray emission from Cygnus X-1, SS 433, and GRS 1915+ 105 after absorption. Astron. Astrophys. 2023, 673, A162. [Google Scholar]
- Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Studying the Spectral Energy Distributions Emanating from Regular Galactic XRBs. Universe 2023, 9, 312. [Google Scholar] [CrossRef]
- Kosmas, O.; Papavasileiou, T.; Kosmas, T. Integral Fluxes of Neutrinos and Gamma-Rays Emitted from Neighboring X-ray Binaries. Universe 2023, 9, 517. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.S. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating black holes: Locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Frank, J.; King, A.; Raine, D. Accretion Power in Astrophysics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Mukhopadhyay, B. Description of pseudo-Newtonian potential for the relativistic accretion disks around Kerr black holes. Astrophys. J. 2002, 581, 427. [Google Scholar] [CrossRef]
- Rarras, D.; Kosmas, T.; Papavasileiou, T.; Kosmas, O. Galactic Stellar Black Hole Binaries: Spin Effects on Jet Emissions of High-Energy Gamma-Rays. Particles 2024, 7, 792–804. [Google Scholar] [CrossRef]
- Böttcher, M.; Dermer, C.D. Photon-Photon Absorption of Very High Energy Gamma Rays from Microquasars: Application to LS 5039. Astrophys. J. 2005, 634, L81–L84. [Google Scholar] [CrossRef]
- Cerutti, B.; Dubus, G.; Malzac, J.; Szostek, A.; Belmont, R.; Zdziarski, A.A.; Henri, G. Absorption of high-energy gamma rays in Cygnus X-3. Astron. Astrophys. 2011, 529, A120. [Google Scholar] [CrossRef][Green Version]
- Romero, G.E.; Vila, G.S. The proton low-mass microquasar: High-energy emission. Astron. Astrophys. 2008, 485, 623–631. [Google Scholar] [CrossRef]
- Mannheim, K.; Schlickeiser, R. Interactions of cosmic ray nuclei. Astron. Astrophys. 1994, 286, 983–996. [Google Scholar]
- Papadopoulos, D.A.; Kosmas, O.T.; Ganatsios, S. Modeling Particle Transport in Astrophysical Outflows and Simulations of Associated Emissions from Hadronic Microquasar Jets. Adv. High Energy Phys. 2022, 2022, 8146675. [Google Scholar] [CrossRef]
- Smponias, T.; Kosmas, O.T. Neutrino Emission from Magnetized Microquasar Jets. Adv. High Energy Phys. 2017, 2017, 4962741. [Google Scholar] [CrossRef]
- Zhang, J.F.; Li, Z.R.; Xiang, F.Y.; Lu, J.F. Electron transport with re-acceleration and radiation in the jets of X-ray binaries. Mon. Not. R. Astron. Soc. 2017, 473, 3211–3222. [Google Scholar] [CrossRef]
- Kosmas, O.T.; Leyendecker, S. Phase lag analysis of variational integrators using interpolation techniques. PAMM Proc. Appl. Math. Mech. 2012, 12, 677–678. [Google Scholar]
- Kosmas, O.T.; Leyendecker, S. Family of high order exponential variational integrators for split potential systems. J. Phys. Conf. Ser. 2015, 574, 012002. [Google Scholar] [CrossRef]
- Kosmas, O.T.; Vlachos, D.S. A space-time geodesic approach for phase fitted variational integrators. Phys. Conf. Ser. 2016, 738, 012133. [Google Scholar] [CrossRef]
- Reynoso, M.M.; Romero, G.E.; Christiansen, H.R. Production of gamma rays and neutrinos in the dark jets of the microquasar SS433. Mon. Not. R. Astron. Soc. 2008, 387, 1745–1754. [Google Scholar] [CrossRef][Green Version]
- Reynoso, M.M.; Romero, G.E. Magnetic field effects on neutrino production in microquasars. Astron. Astrophys. 2009, 493, 1–111. [Google Scholar] [CrossRef]
- Kantzas, D.; Markoff, S.; Beuchert, T.; Lucchini, M.; Chhotray, A.; Ceccobello, C.; Tetarenko, A.J.; Miller-Jones, J.C.A.; Bremer, M.; Garcia, J.A.; et al. A new lepto-hadronic model applied to the first simultaneous multiwavelength data set for Cygnus X–1. Mon. Not. R. Astron. Soc. 2021, 500, 2112–2126. [Google Scholar] [CrossRef]
- Carulli, A.M.; Reynoso, M.M.; Romero, G.E. Neutrino production in Population III microquasars. Astropart. Phys. 2021, 128, 102557. [Google Scholar] [CrossRef]
- Stern, B.E.; Poutanen, J. Gamma-ray bursts from synchrotron self-Compton emission. Mon. Not. R. Astron. Soc. 2004, 352, L35–L39. [Google Scholar] [CrossRef]
- Jones, F.C. Calculated spectrum of inverse-Compton-scattered photons. Phys. Rev. 1968, 167, 1159. [Google Scholar] [CrossRef]
- McClintock, J.E.; Narayan, R.; Steiner, J.F. Black hole spin via continuum fitting and the role of spin in powering transient jets. In The Physics of Accretion onto Black Holes; Springer: Berlin/Heidelberg, Germany, 2015; pp. 295–322. [Google Scholar]
- Reynolds, C.S. Measuring black hole spin using X-ray reflection spectroscopy. In The Physics of Accretion onto Black Holes; Springer: Berlin/Heidelberg, Germany, 2015; pp. 277–294. [Google Scholar]
- Ingram, A.; Motta, S. Solutions to the relativistic precession model. Mon. Not. R. Astron. Soc. 2014, 444, 2065–2070. [Google Scholar] [CrossRef]
- Mikołajewska, J.; Zdziarski, A.A.; Ziółkowski, J.; Torres, M.A.P.; Casares, J. The Donor of the Black Hole X-Ray Binary MAXI J1820+ 070. Astrophys. J. 2022, 930, 9. [Google Scholar] [CrossRef]
- Mignard, F. Astronomical distance scales. Comptes Rendus Phys. 2019, 20, 140–152. [Google Scholar] [CrossRef]
- Zhao, X.; Gou, L.; Dong, Y.; Tuo, Y.; Liao, Z.; Li, Y.; Jia, N.; Feng, Y.; Steiner, J.F. Estimating the black hole spin for the X-ray binary MAXI J1820+ 070. Astrophys. J. 2021, 916, 108. [Google Scholar] [CrossRef]
- Draghis, P.A.; Miller, J.M.; Zoghbi, A.; Reynolds, M.; Costantini, E.; Gallo, L.C.; Tomsick, J.A. A systematic view of ten new black hole spins. Astrophys. J. 2023, 945, 19. [Google Scholar] [CrossRef]
- Bhargava, Y.; Belloni, T.; Bhattacharya, D.; Motta, S.; Ponti, G. A timing-based estimate of the spin of the black hole in MAXI J1820+ 070. Mon. Not. R. Astron. Soc. 2021, 508, 3104–3110. [Google Scholar] [CrossRef]
- Poutanen, J.; Veledina, A.; Berdyugin, A.V.; Berdyugina, S.V.; Jermak, H.; Jonker, P.G.; Kajava, J.J.E.; Kosenkov, I.A.; Kravtsov, V.; Piirola, V.; et al. Black hole spin–orbit misalignment in the x-ray binary MAXI J1820+ 070. Science 2022, 375, 874–876. [Google Scholar] [CrossRef]
- Kalogera, V. Spin-orbit misalignment in close binaries with two compact objects. Astrophys. J. 2000, 541, 319. [Google Scholar] [CrossRef]
- Torres, M.A.P.; Casares, J.; Jiménez-Ibarra, F.; Álvarez-Hernández, A.; Muñoz-Darias, T.; Padilla, M.A.; Jonker, P.G.; Heida, M. The binary mass ratio in the black hole transient MAXI J1820+ 070. Astrophys. J. Lett. 2020, 893, L37. [Google Scholar] [CrossRef]
- Atri, P.; Miller-Jones, J.C.A.; Bahramian, A.; Plotkin, R.M.; Deller, A.T.; Jonker, P.G.; Maccarone, T.J.; Sivakoff, G.R.; Soria, R.; Altamirano, D.; et al. A radio parallax to the black hole X-ray binary MAXI J1820+ 070. Mon. Not. R. Astron. Soc. Lett. 2020, 493, L81–L86. [Google Scholar] [CrossRef]
- Zdziarski, A.A.; Tetarenko, A.J.; Sikora, M. Jet Parameters in the Black Hole X-Ray Binary MAXI J1820+ 070. Astrophys. J. 2022, 925, 189. [Google Scholar] [CrossRef]
- Orosz, J.A.; Steiner, J.F.; McClintock, J.E.; Torres, M.A.P.; Remillard, R.A.; Bailyn, C.D.; Miller, J.M. An improved dynamical model for the microquasar XTE J1550- 564. Astrophys. J. 2011, 730, 75. [Google Scholar] [CrossRef]
- Miller-Jones, J.C.A.; Fender, R.P.; Nakar, E. Opening angles, Lorentz factors and confinement of X-ray binary jets. Mon. Not. R. Astron. Soc. 2006, 367, 1432–1440. [Google Scholar] [CrossRef]
- Kaaret, P.; Corbel, S.; Tomsick, J.A.; Fender, R.; Miller, J.M.; Orosz, J.A.; Tzioumis, A.K.; Wijnands, R. X-Ray Emission from the Jets of XTE J1550–564. Astrophys. J. 2003, 582, 945. [Google Scholar] [CrossRef]
- Steiner, J.F.; Reis, R.C.; McClintock, J.E.; Narayan, R.; Remillard, R.A.; Orosz, J.A.; Gou, L.; Fabian, A.C.; Torres, M.A.P. The spin of the black hole microquasar XTE J1550- 564 via the continuum-fitting and Fe-line methods. Mon. Not. R. Astron. Soc. 2011, 416, 941–958. [Google Scholar] [CrossRef]
- Motta, S.E.; Muñoz-Darias, T.; Sanna, A.; Fender, R.; Belloni, T.; Stella, L. Black hole spin measurements through the relativistic precession model: XTE J1550-564. Mon. Not. R. Astron. Soc. Lett. 2014, 439, L56–L69. [Google Scholar] [CrossRef]
- Nandi, A.; Mandal, S.; Sreehari, H.; Radhika, D.; Das, S.; Chattopadhyay, I.; Iyer, N.; Agrawal, V.K.; Aktar, R. Accretion flow dynamics during 1999 outburst of XTE J1859+ 226-modeling of broadband spectra and constraining the source mass. Astrophys. Space Sci. 2018, 363, 90. [Google Scholar] [CrossRef]
- Kimura, M.; Done, C. Evolution of X-ray irradiation during the 1999–2000 outburst of the black hole binary XTE J1859+ 226. Mon. Not. R. Astron. Soc. 2019, 482, 626–638. [Google Scholar] [CrossRef]
- Motta, S.E.; Belloni, T.; Stella, L.; Pappas, G.; Casares, J.; Muñoz-Darias, A.T.; Torres, M.A.P.; Yanes-Rizo, I.V. Black hole mass and spin measurements through the relativistic precession model: XTE J1859+ 226. Mon. Not. R. Astron. Soc. 2022, 517, 1469–1475. [Google Scholar] [CrossRef]
- Yanes-Rizo, I.V.; Torres, M.A.P.; Casares, J.; E Motta, S.; Muñoz-Darias, T.; Rodríguez-Gil, P.; Padilla, M.A.; Jiménez-Ibarra, F.; Jonker, P.G.; Corral-Santana, J.M.; et al. A refined dynamical mass for the black hole in the X-ray transient XTE J1859+ 226. Mon. Not. R. Astron. Soc. 2022, 517, 1476–1482. [Google Scholar] [CrossRef]
- Papavasileiou, T.V.; Kosmas, O.; Kosmas, T.S. A direct method for reproducing fully relativistic spectra from standard accretion disks by modifying their inner boundary. arXiv 2024, arXiv:2408.02415. [Google Scholar]
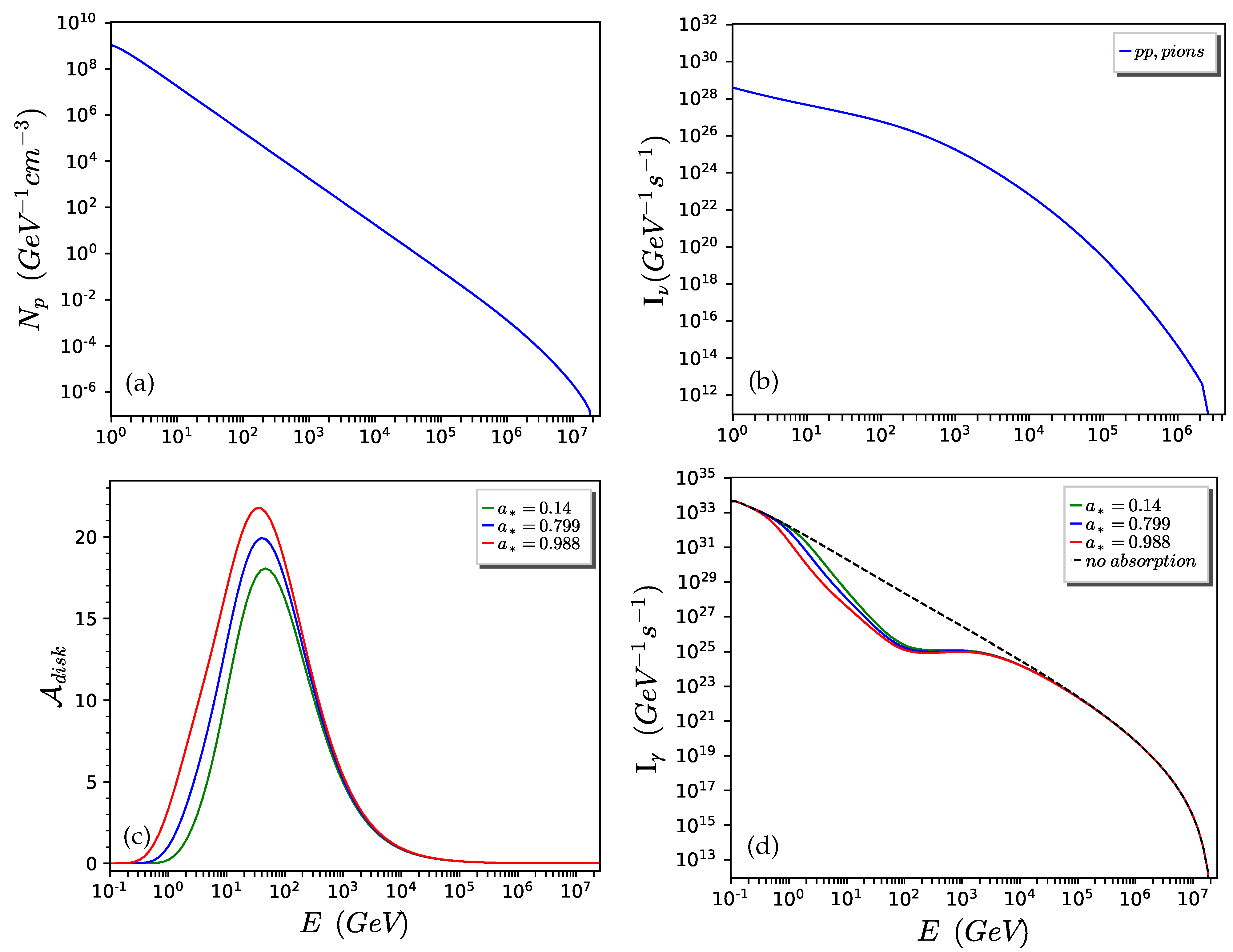
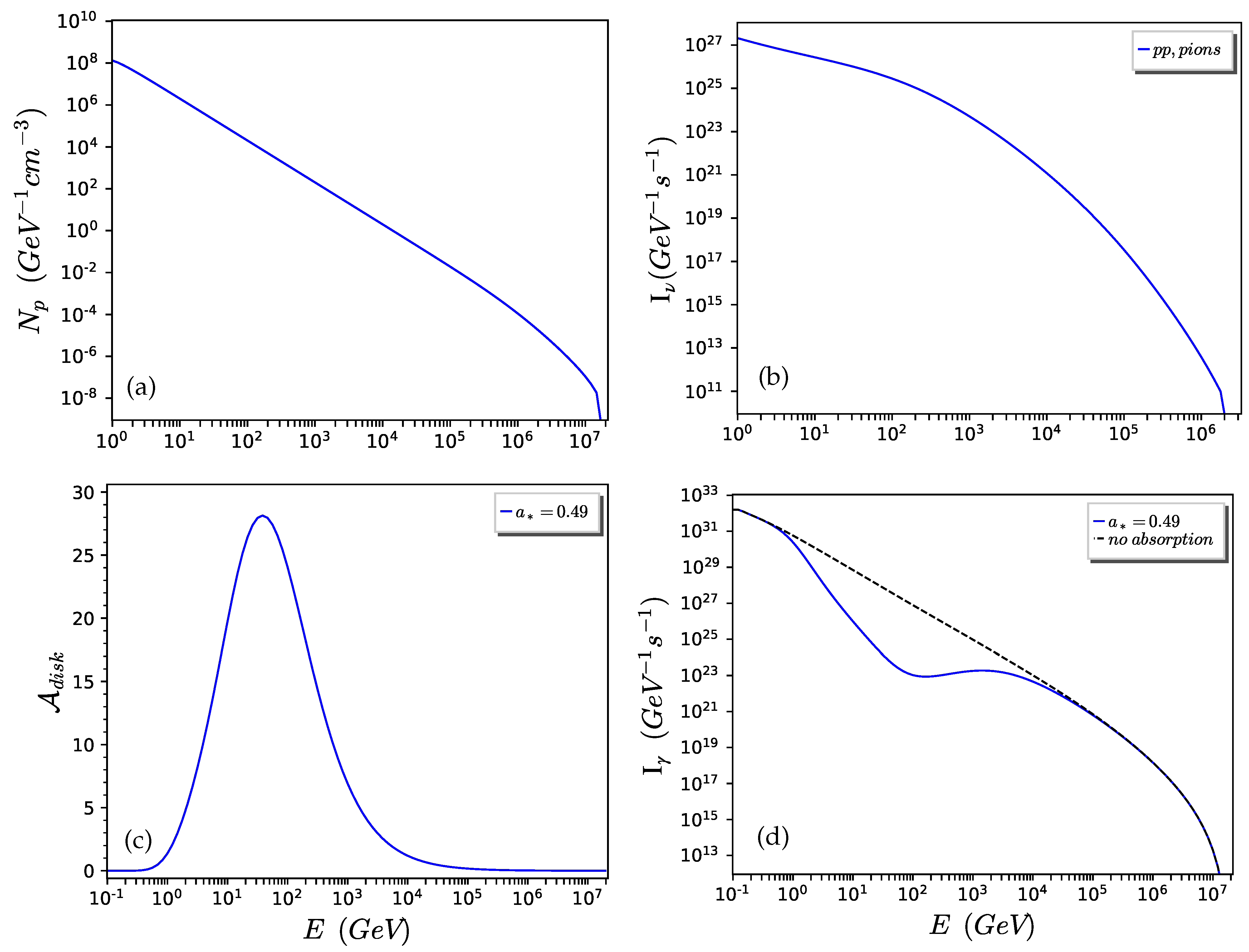
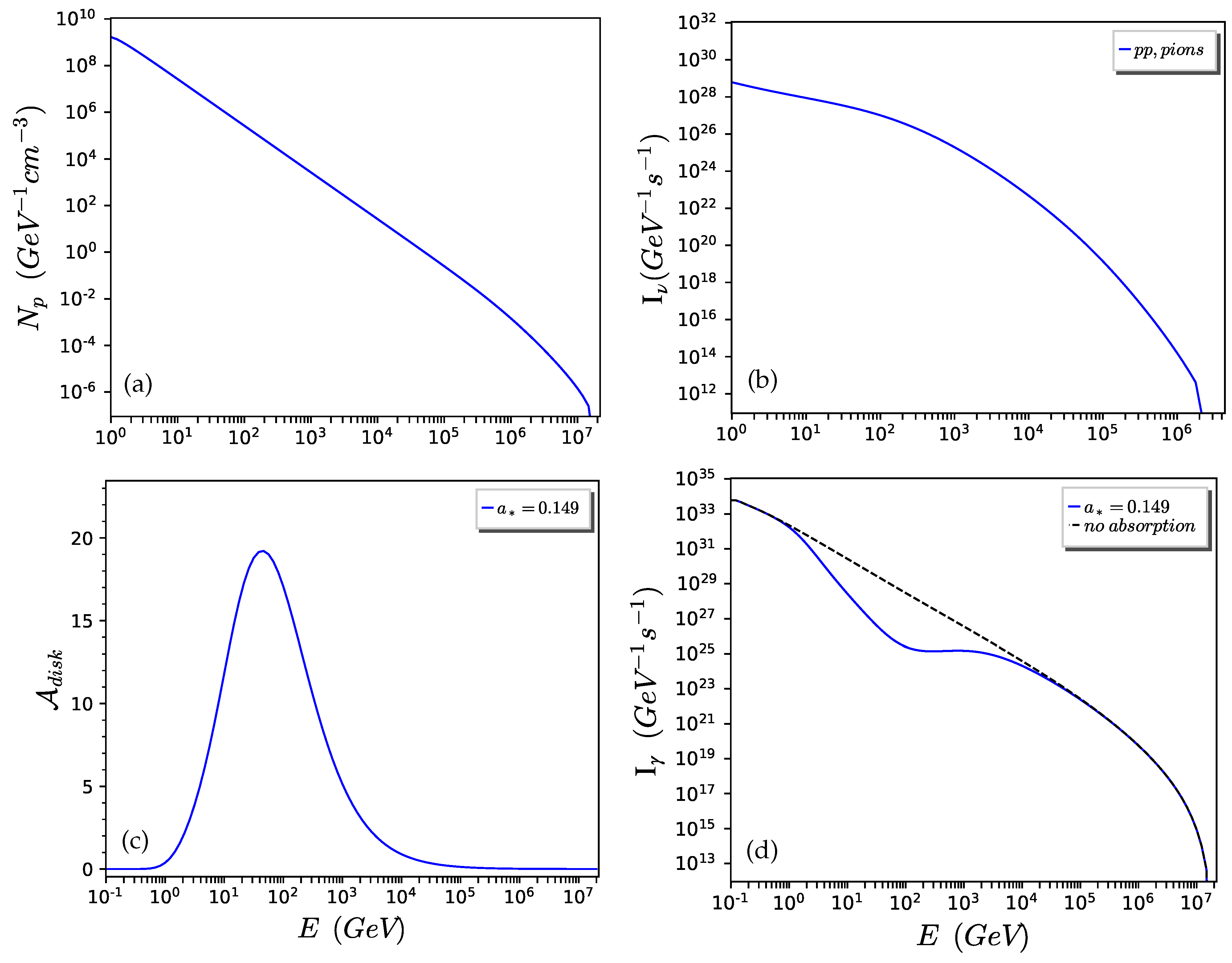
| MAXI J1820+070 | ||||
|---|---|---|---|---|
| d (kpc) | i (°) | (days) | ||
| 8.48 [54] | 0.49 [47] | 2.96 [55] | 63 [55] | 0.68549 [52] |
| (K) | (°) | |||
| 7 | 4200 [47] | 0.89 [55] | 1.5 [56] | 0.14/0.988/0.799 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rarras, D.; Kosmas, O.; Papavasileiou, T.; Kosmas, T. Black Hole’s Spin-Dependence of γ-Ray and Neutrino Emissions from MAXI J1820+070, XTE J1550-564, and XTE J1859+226. Particles 2024, 7, 818-833. https://doi.org/10.3390/particles7030049
Rarras D, Kosmas O, Papavasileiou T, Kosmas T. Black Hole’s Spin-Dependence of γ-Ray and Neutrino Emissions from MAXI J1820+070, XTE J1550-564, and XTE J1859+226. Particles. 2024; 7(3):818-833. https://doi.org/10.3390/particles7030049
Chicago/Turabian StyleRarras, Dimitrios, Odysseas Kosmas, Theodora Papavasileiou, and Theocharis Kosmas. 2024. "Black Hole’s Spin-Dependence of γ-Ray and Neutrino Emissions from MAXI J1820+070, XTE J1550-564, and XTE J1859+226" Particles 7, no. 3: 818-833. https://doi.org/10.3390/particles7030049
APA StyleRarras, D., Kosmas, O., Papavasileiou, T., & Kosmas, T. (2024). Black Hole’s Spin-Dependence of γ-Ray and Neutrino Emissions from MAXI J1820+070, XTE J1550-564, and XTE J1859+226. Particles, 7(3), 818-833. https://doi.org/10.3390/particles7030049







