New Physics Opportunities at the DUNE Near Detector
Abstract
1. Introduction
2. Elastic Neutrino–Electron Scattering in the SM and Beyond
2.1. Standard Model
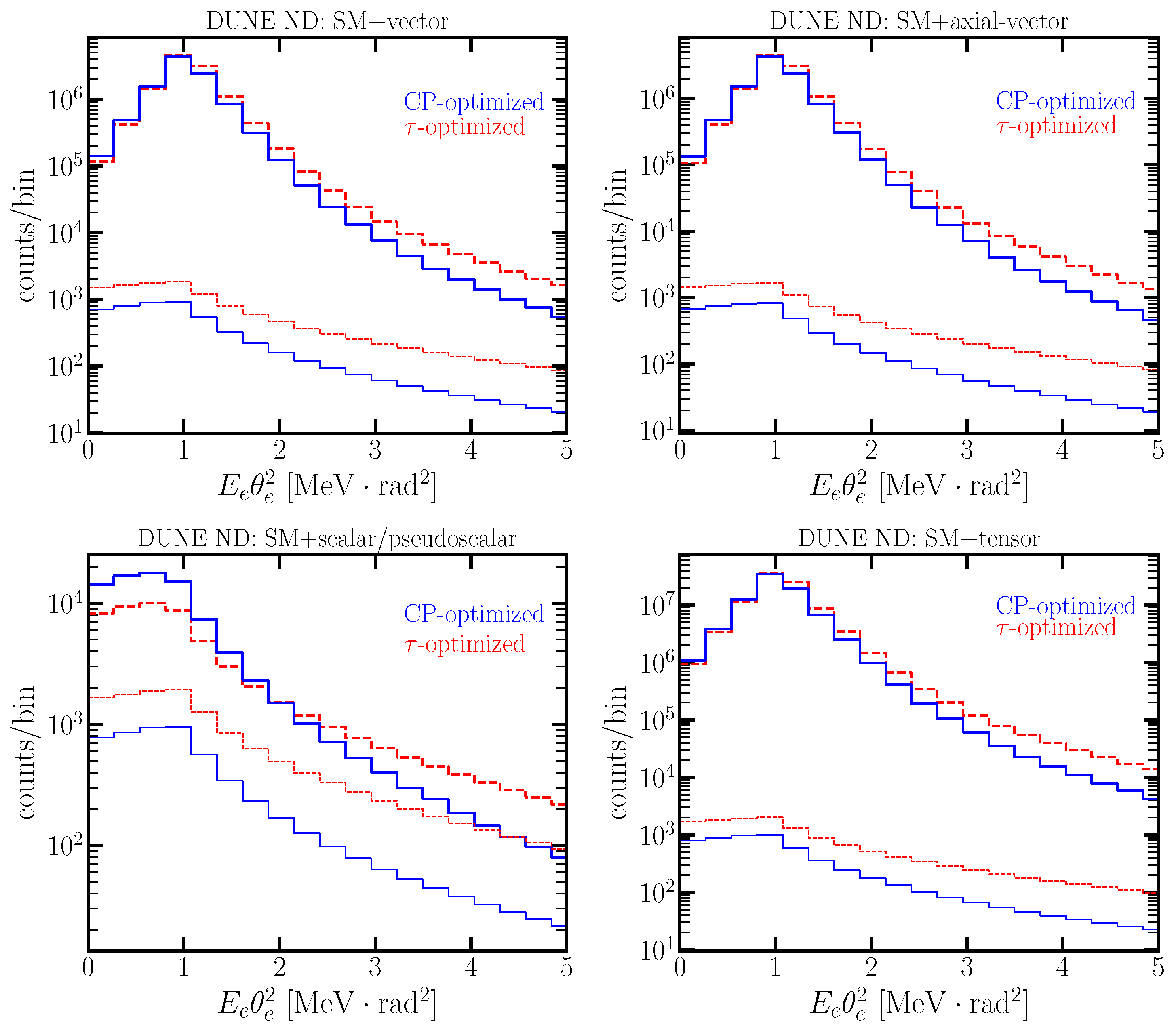
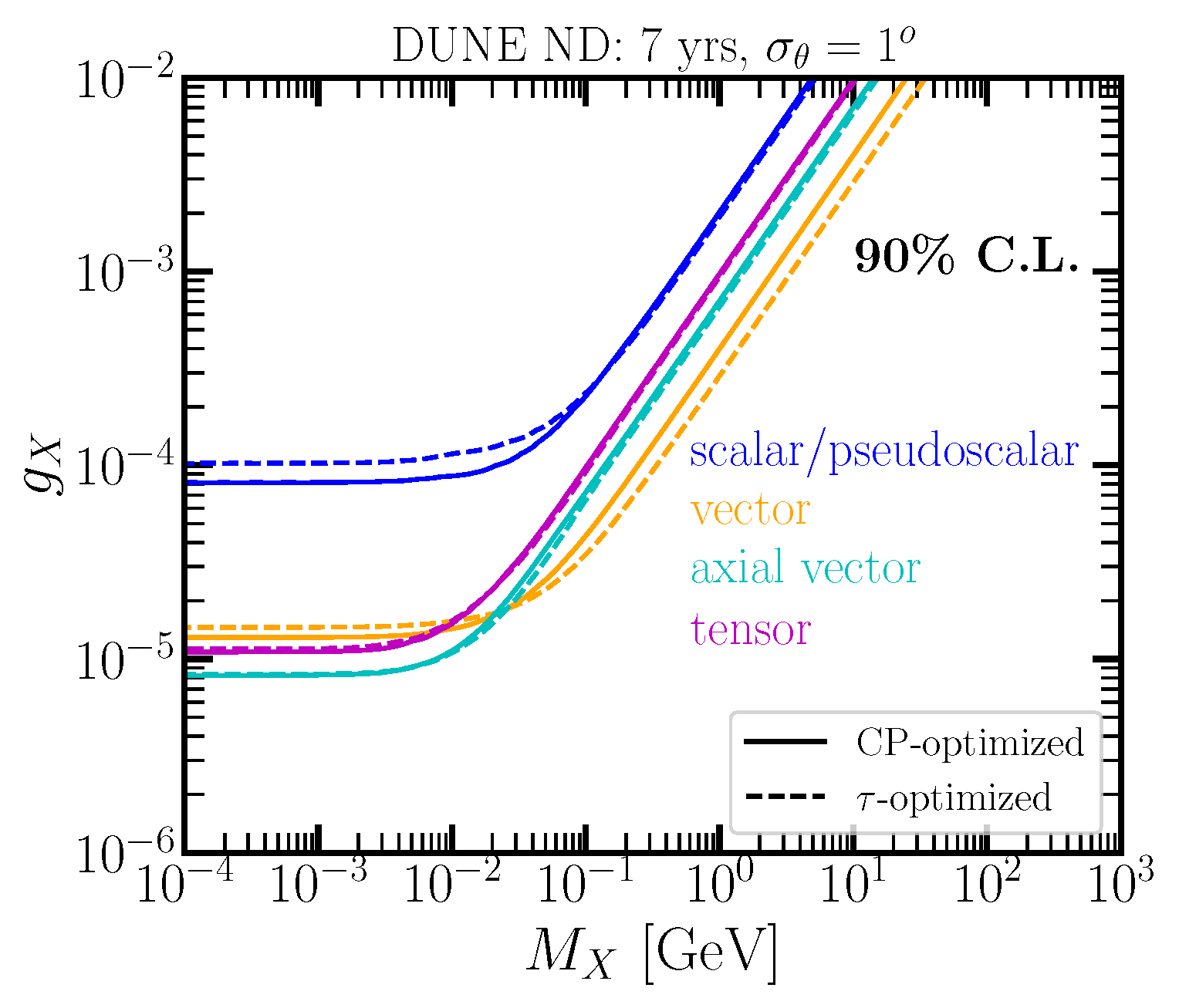
2.2. Neutrino Generalized Interactions (NGIs)
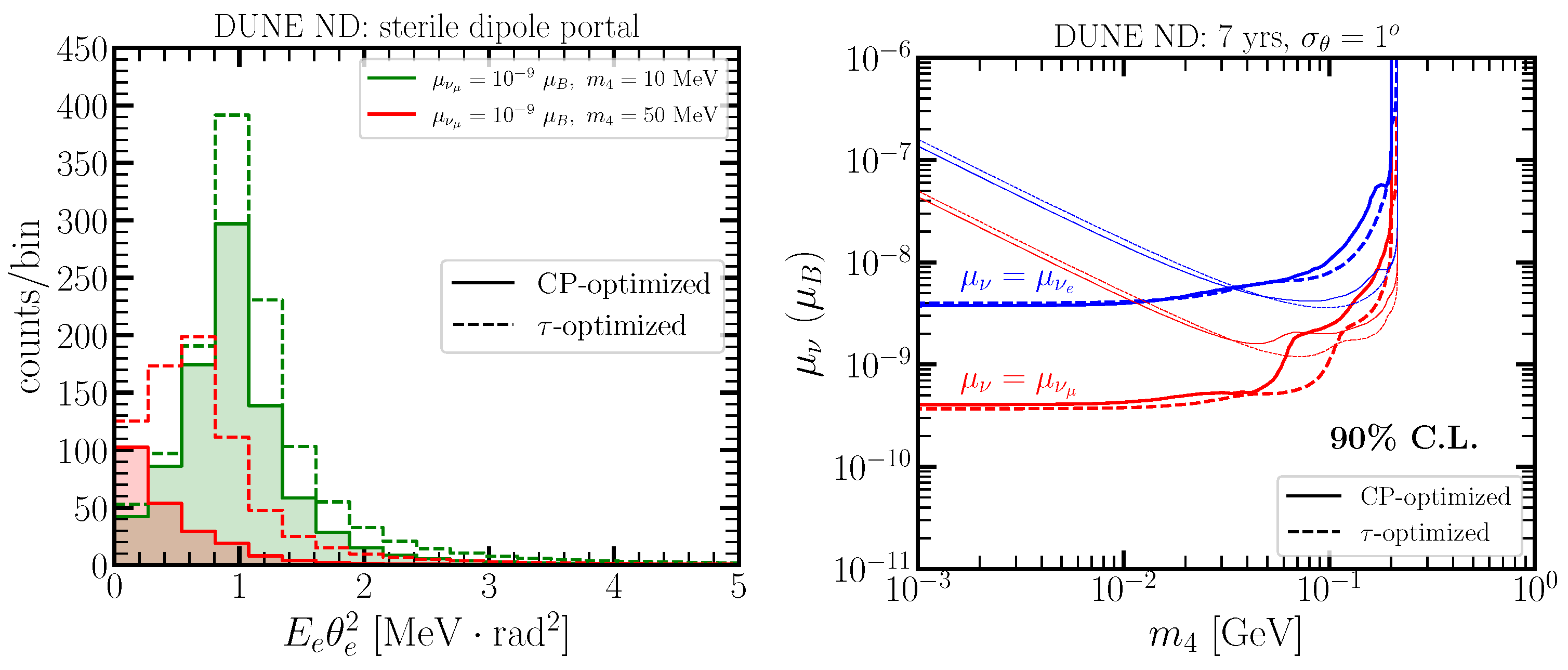
2.3. Sterile Dipole Portal
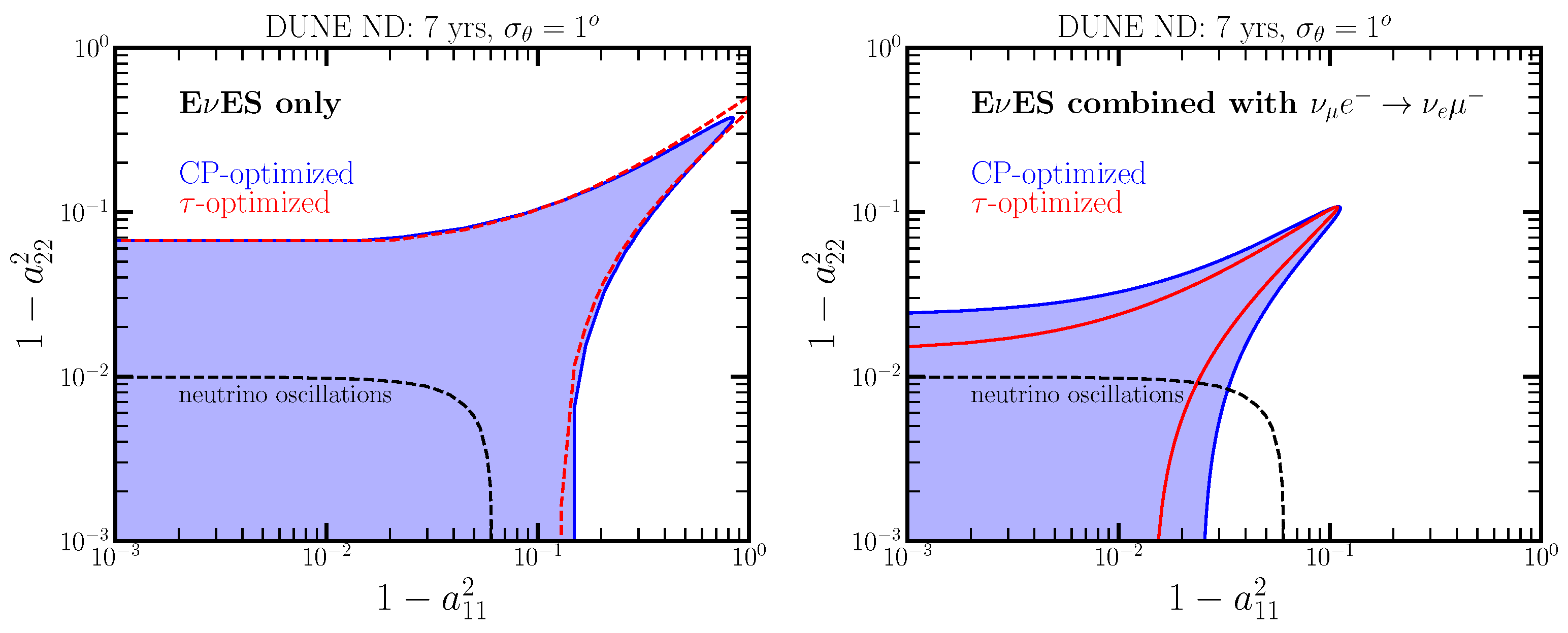
2.4. Non-Unitarity of the Leptonic Mixing Matrix
2.5. Evaluation of the Number of Events
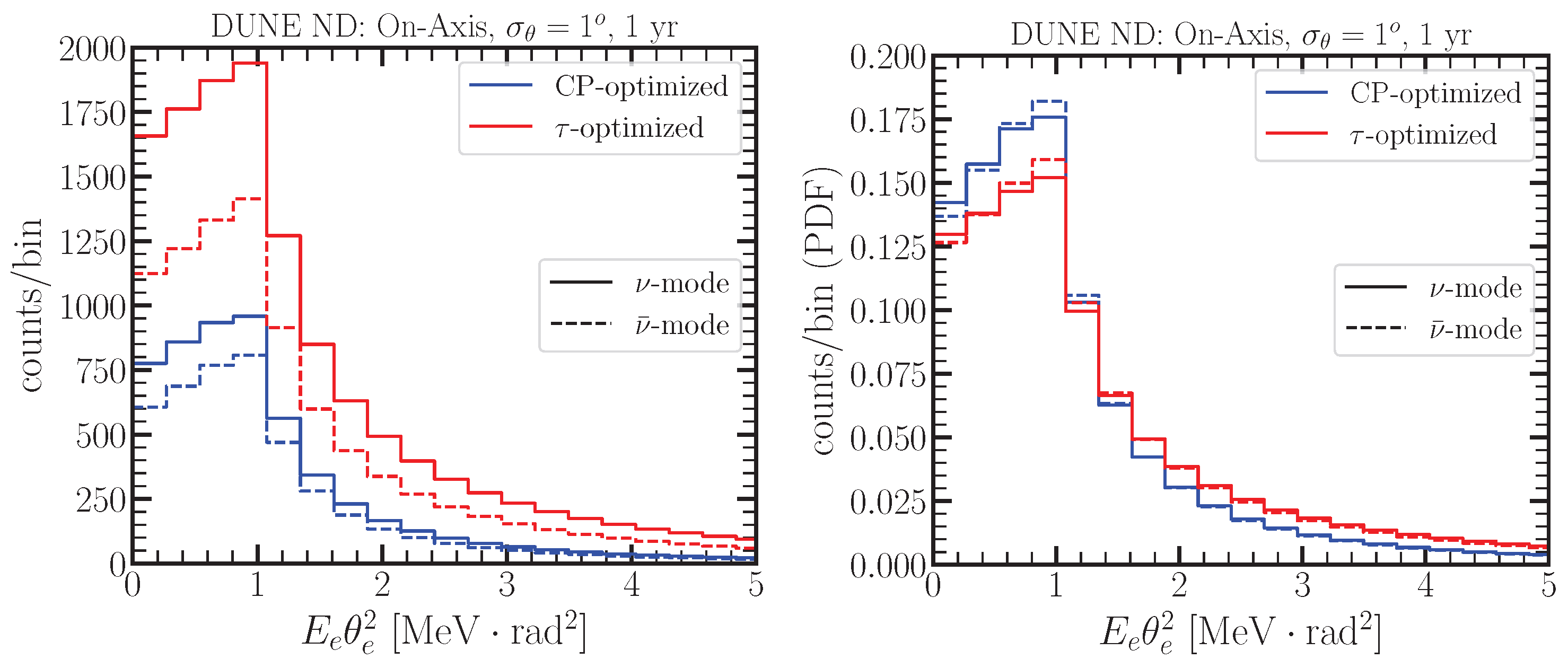
2.6. Signal Reconstruction Method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume I Introduction to DUNE. J. Instrum. 2020, 15, T08008. [Google Scholar] [CrossRef]
- Abi, B.; Acciarri, R.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; Alt, C.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics. arXiv 2020, arXiv:2002.03005. [Google Scholar]
- De Romeri, V.; Fernandez-Martinez, E.; Sorel, M. Neutrino oscillations at DUNE with improved energy reconstruction. J. High Energy Phys. 2016, 9, 30. [Google Scholar] [CrossRef]
- Hewes, V.; Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Aduszkiewicz, A.; Ahmad, Z.; Ahmed, J.; et al. Deep Underground Neutrino Experiment (DUNE) Near Detector Conceptual Design Report. Instruments 2021, 5, 31. [Google Scholar] [CrossRef]
- Abi, B.; Acciarri, R.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; Alt, C.; et al. Prospects for beyond the Standard Model physics searches at the Deep Underground Neutrino Experiment. Eur. Phys. J. C 2021, 81, 322. [Google Scholar] [CrossRef]
- Ballett, P.; Hostert, M.; Pascoli, S.; Perez-Gonzalez, Y.F.; Tabrizi, Z.; Zukanovich Funchal, R. Z’s in neutrino scattering at DUNE. Phys. Rev. D 2019, 100, 055012. [Google Scholar] [CrossRef]
- Melas, P.; Papoulias, D.K.; Saoulidou, N. Probing generalized neutrino interactions with the DUNE Near Detector. J. High Energy Phys. 2023, 7, 190. [Google Scholar] [CrossRef]
- Ballett, P.; Boschi, T.; Pascoli, S. Heavy Neutral Leptons from low-scale seesaws at the DUNE Near Detector. J. High Energy Phys. 2020, 3, 111. [Google Scholar] [CrossRef]
- Beltrán, R.; Günther, J.; Hirsch, M.; Titov, A.; Wang, Z.S. Heavy neutral leptons from kaons in effective field theory. arXiv 2023, arXiv:2309.11546. [Google Scholar] [CrossRef]
- Candela, P.M.; De Romeri, V.; Melas, P.; Papoulias, D.K.; Saoulidou, N. Up-scattering production of a sterile fermion at DUNE: Complementarity with spallation source and direct detection experiments. arXiv 2024, arXiv:2404.12476. [Google Scholar]
- De Romeri, V.; Kelly, K.J.; Machado, P.A.N. DUNE-PRISM Sensitivity to Light Dark Matter. Phys. Rev. D 2019, 100, 095010. [Google Scholar] [CrossRef]
- Breitbach, M.; Buonocore, L.; Frugiuele, C.; Kopp, J.; Mittnacht, L. Searching for physics beyond the Standard Model in an off-axis DUNE near detector. J. High Energy Phys. 2022, 1, 48. [Google Scholar] [CrossRef]
- Kelly, K.J.; Kumar, S.; Liu, Z. Heavy axion opportunities at the DUNE near detector. Phys. Rev. D 2021, 103, 095002. [Google Scholar] [CrossRef]
- Brdar, V.; Dutta, B.; Jang, W.; Kim, D.; Shoemaker, I.M.; Tabrizi, Z.; Thompson, A.; Yu, J. Axionlike Particles at Future Neutrino Experiments: Closing the Cosmological Triangle. Phys. Rev. Lett. 2021, 126, 201801. [Google Scholar] [CrossRef] [PubMed]
- Aristizabal Sierra, D.; De Romeri, V.; Rojas, N. COHERENT analysis of neutrino generalized interactions. Phys. Rev. D 2018, 98, 075018. [Google Scholar] [CrossRef]
- Giunti, C.; Studenikin, A. Neutrino electromagnetic interactions: A window to new physics. Rev. Mod. Phys. 2015, 87, 531. [Google Scholar] [CrossRef]
- Escrihuela, F.J.; Forero, D.V.; Miranda, O.G.; Tortola, M.; Valle, J.W.F. On the description of nonunitary neutrino mixing. Phys. Rev. D 2015, 92, 053009, Erratum in Phys. Rev. D 2016, 93, 119905. [Google Scholar] [CrossRef]
- de Gouvea, A.; Machado, P.A.N.; Perez-Gonzalez, Y.F.; Tabrizi, Z. Measuring the Weak Mixing Angle in the DUNE Near Detector Complex. Phys. Rev. Lett. 2020, 125, 051803. [Google Scholar] [CrossRef] [PubMed]
- Giarnetti, A.; Meloni, D. Probing source and detector nonstandard interaction parameters at the DUNE near detector. Phys. Rev. D 2021, 104, 015027. [Google Scholar] [CrossRef]
- Kayser, B.; Fischbach, E.; Rosen, S.P.; Spivack, H. Charged and Neutral Current Interference in νee Scattering. Phys. Rev. D 1979, 20, 87. [Google Scholar] [CrossRef]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; Amsler, C.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Rosen, S.P. Analog of the Michel Parameter for Neutrino - Electron Scattering: A Test for Majorana Neutrinos. Phys. Rev. Lett. 1982, 48, 842. [Google Scholar] [CrossRef]
- Rodejohann, W.; Xu, X.J.; Yaguna, C.E. Distinguishing between Dirac and Majorana neutrinos in the presence of general interactions. J. High Energy Phys. 2017, 5, 24. [Google Scholar] [CrossRef]
- Miranda, O.G.; Nunokawa, H. Non standard neutrino interactions: Current status and future prospects. New J. Phys. 2015, 17, 095002. [Google Scholar] [CrossRef]
- Babu, K.S.; Gonçalves, D.; Jana, S.; Machado, P.A.N. Neutrino Non-Standard Interactions: Complementarity Between LHC and Oscillation Experiments. Phys. Lett. B 2021, 815, 136131. [Google Scholar] [CrossRef]
- Grimus, W.; Schwetz, T. Elastic neutrino electron scattering of solar neutrinos and potential effects of magnetic and electric dipole moments. Nucl. Phys. B 2000, 587, 45–66. [Google Scholar] [CrossRef][Green Version]
- Aristizabal Sierra, D.; Miranda, O.G.; Papoulias, D.K.; Garcia, G.S. Neutrino magnetic and electric dipole moments: From measurements to parameter space. Phys. Rev. D 2022, 105, 035027. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M. Muon Capture Constraints on Sterile Neutrino Properties. Phys. Rev. D 2010, 82, 113018. [Google Scholar] [CrossRef]
- Vogel, P.; Engel, J. Neutrino Electromagnetic Form-Factors. Phys. Rev. D 1989, 39, 3378. [Google Scholar] [CrossRef]
- Centelles Chuliá, S.; Miranda, O.; Valle, J.W.F. Leptonic neutral-current probes in a short-distance DUNE-like setup. arXiv 2024, arXiv:2402.00114. [Google Scholar] [CrossRef]
- Marshall, C.M.; McFarland, K.S.; Wilkinson, C. Neutrino-electron elastic scattering for flux determination at the DUNE oscillation experiment. Phys. Rev. D 2020, 101, 032002. [Google Scholar] [CrossRef]
- Park, J.; Aliaga, L.; Altinok, O.; Bellantoni, L.; Bercellie, A.; Betancourt, M.; Bodek, A.; Bravar, A.; Budd, H.; Cai, T.; et al. Measurement of Neutrino Flux from Neutrino-Electron Elastic Scattering. Phys. Rev. D 2016, 93, 112007. [Google Scholar] [CrossRef]
- Mathur, V.; Shoemaker, I.M.; Tabrizi, Z. Using DUNE to shed light on the electromagnetic properties of neutrinos. J. High Energy Phys. 2022, 10, 41. [Google Scholar] [CrossRef]
- Acciarri, R.; Acero, M.A.; Adamowski, M.; Adams, C.; Adamson, P.; Adhikari, S.; Ahmad, Z.; Albright, C.H.; Alion, T.; Amador, E.; et al. Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual Design Report, Volume 2: The Physics Program for DUNE at LBNF. arXiv 2015, arXiv:1512.06148. [Google Scholar]
- Machado, P.; Schulz, H.; Turner, J. Tau neutrinos at DUNE: New strategies, new opportunities. Phys. Rev. D 2020, 102, 053010. [Google Scholar] [CrossRef]
- ShivaSankar, K.A.; Majumdar, A.; Papoulias, D.K.; Prajapati, H.; Srivastava, R. Implications of first LZ and XENONnT results: A comparative study of neutrino properties and light mediators. Phys. Lett. B 2023, 839, 137742. [Google Scholar] [CrossRef]
- Miranda, O.G.; Papoulias, D.K.; Sanders, O.; Tórtola, M.; Valle, J.W.F. Low-energy probes of sterile neutrino transition magnetic moments. J. High Energy Phys. 2021, 12, 191. [Google Scholar] [CrossRef]
- Forero, D.V.; Giunti, C.; Ternes, C.A.; Tortola, M. Nonunitary neutrino mixing in short and long-baseline experiments. Phys. Rev. D 2021, 104, 075030. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melas, P.; Papoulias, D.K.; Saoulidou, N. New Physics Opportunities at the DUNE Near Detector. Particles 2024, 7, 623-633. https://doi.org/10.3390/particles7030035
Melas P, Papoulias DK, Saoulidou N. New Physics Opportunities at the DUNE Near Detector. Particles. 2024; 7(3):623-633. https://doi.org/10.3390/particles7030035
Chicago/Turabian StyleMelas, Pantelis, Dimitrios K. Papoulias, and Niki Saoulidou. 2024. "New Physics Opportunities at the DUNE Near Detector" Particles 7, no. 3: 623-633. https://doi.org/10.3390/particles7030035
APA StyleMelas, P., Papoulias, D. K., & Saoulidou, N. (2024). New Physics Opportunities at the DUNE Near Detector. Particles, 7(3), 623-633. https://doi.org/10.3390/particles7030035





