Abstract
We have studied wake effects on the dissociation of heavy quarkonia states J/ψ and Y by introducing an in-medium modification to the inter-quark potential. The wakes in the quark–gluon plasma were modeled using linear response theory using a dynamic dielectric function obtained from kinetic theory (Boltzmann equation) with a Bhatnagar–Gross–Krook (BGK) collision term. The in-medium modified potential was used to investigate the dissociation character depending on various parameters such as the velocity of quarkonium moving through the medium and the collision frequency. We have also calculated critical values of the dissociation temperature. Modifications of the dissociation energy due to wake-field effects were found.
1. Introduction
The investigation of quark–gluon plasma (QGP) has been one of the most significant scientific undertakings and challenges in recent decades. QGP is a state of hot and dense matter at an extremely high temperature above 150 MeV with a density ten times that of nuclear matter, consisting of free quarks and gluons. QGP can only exist in the conditions of the very early universe, up to about 1–5 microseconds after the Big Bang, hypothetically in the centers of neutron star cores, and in heavy ion collision experiments such as in the Super Proton Synchrotron (SPS), the Relativistic Heavy Ion Collider (RHIC), and the Large Hadron Collider (LHC). Quarks and gluons are described by quantum chromodynamics (QCD) and the theory of strong interaction. According to this theory, under normal conditions, these particles cannot be observed in the free state, which is referred to as the confinement problem []. If one tries to separate quarks from each other by applying increasingly more energy, eventually, it becomes more favorable to have a new quark–antiquark pair. However, QCD states that at a sufficiently high temperature, the color charge of quarks and gluons becomes screened [] to the point where they start moving freely in the QGP, which is called “asymptotic freedom” [,]. The formation of QGP cannot be directly detected; therefore, it is challenging to say whether conditions are sufficient to achieve the desired state.
The ultrarelativistic heavy ion collision experiments at the SPS and the RHIC show some promise that strongly coupled QGP might be formed in a hot and dense fireball after nucleus–nucleus collisions []. There are a few signs of QGP formation in the experiments, such as jet quenching, when partons propagate through the fireball [,]. A possible phase transition of dense matter to QGP in the fireball was detected at the RHIC via strong quenching of jets, as well as high hadron spectrum suppression [,]. The suppression of the state of quarkonium was first studied in [], and some calculations were conducted in [].
Quarkonium is a heavy meson consisting of a quark–antiquark pair with the same flavor. Quarks from charm flavor form a meson called charmonium, and quarks with bottom flavor form bottomonium []. These particle systems are similar to positronium, the electron–positron pair system. Charmonium and bottomonium have sparked the interest of scientists because of their huge mass, which is a thousand times heavier that of up and down quarks from which ordinary matter forms. The huge mass of such quarks results in more compact sizes of the system they form compared to light ones. Therefore, quarkonium may survive the phase transition to QGP, being the last that dissolves in a hot and dense state. Hence, when the production of quarkonium stops, we may say with high certainty that QGP is formed. The equations of motion for quarks are described in the framework of QCD theory [].
However, due to the large coupling parameter in the theory of strong interaction, it is impossible to apply methods of perturbative quantum field theory [,]. In addition, there is a problem of confinement, a phenomenon in which the energy of attraction between quarks grows in proportion to the distance between them, which leads to the fact that under normal conditions, quarks cannot exist freely. Therefore, effective theories, which use a certain approximation or constraints, are applied to describe these properties. In this paper, the well-known model of potentials is used [,]. In-medium modification to the quarkonium potential can be introduced via the dielectric function of the media [,]. As the static screening of the potential can be found in [], we mainly focus here on the dynamical screening of inter-quark potential.
There are several works regarding in-medium modification of Cornell potential using dielectric functions obtained from various models, where they also investigate the effect of wake-field on the potential. In paper [], they obtained the dielectric function from viscous chromodynamic equations in the formalism of collision-less kinetic theory for QGP. These equations were solved using the linear response approximation to derive the polarization tensor of the media and the dielectric function. In their subsequent paper [], they used the dielectric function of the viscous QGP model to study wake-field effects on the potential. They also showed how parameters such as shear viscosity affect the wake structure of the potential. In the following papers [], it is proposed that the QGP in the RHIC is strongly coupled. With that in mind, the authors of [] obtained the wake-field potential using the dielectric function from AdS/CFT correspondence. Similarly to [], they also used the framework of linear response theory and introduced an ’R-charged’ particle moving in the strongly coupled super-symmetric Yang–Mills plasma, which induces wake potential along the direction of motion.
Recently, according to the modern effective field theories, there is a result that indicates that the quark–antiquark potential in the medium has to be complex-valued [,]. The potential is derived from the static Wilson loop, with a screened Coulomb part and an imaginary part induced by Landau damping. The process includes the calculation of the lattice QCD correlation function and the reconstruction of their spectral function from lattice data. In papers [,], the authors applied the same methods to investigate the heavy quark–antiquark potential. In paper [], the authors included a non-perturbative contribution to the in-medium potential. The lattice data are prone to statistical errors and discretization effects; therefore, it might be cumbersome to calculate spectral functions. Moreover, not all medium effects can be incorporated into the potential. Therefore, in this paper, we mainly focus on real-valued potentials.
In the following paper [], it was suggested that the motion of partons in the media might lead to a change in attractive potential; hence, the spectrum of bound states and the suppression pattern can be modified. In order to study these changes quantitatively, we use the dielectric function obtained from transport equations, which takes into account collisions [,,].
2. Theory and Methods
The Cornell potential is an effective method to account for the confinement of quarks. It was developed [,] in the 1970s to explain the masses of quarkonium states and account for the relation between the mass and angular momentum of the hadrons. The potential has the following form:
where r is the effective radius of the quarkonium state, is the QCD running coupling, and is the QCD string tension. The value of const. was taken to fit experimental data. Initially, and were merely empirical parameters but with the development of QCD, they can now be calculated using perturbative QCD and lattice QCD, respectively.
There are numerous types of potential models which have been suggested to fit and determine hadron spectra. Those phenomenological models were especially useful when describing the spectra of charmonium and bottomonium because the latter has a huge mass compared to light quarks which ordinary matter is made of. Having a huge mass made it possible to use the non-relativistic Schrödinger equation, since a huge mass implies small velocities. Proposed potentials have the same quality in common: they behave similarly in short and large distances, having a distinction between ranges. At short distances, on account of the one-gluon exchange contribution, it behaves exactly the same as the Coulomb potential:
Consequently, for large distances, there should be a confinement:
The most straightforward and simple method to combine them is to add them together, which leads to the Cornell potential. More complicated potential models leave such asymptotic behavior outside of intermediate region , which is somehow connected in between. Thus, they are also called funnel potentials owing to their shape. One possible way is to connect these two regions using the logarithmic r-dependence as in [,]:
A new heavy quark potential is proposed which incorporates the two concepts of asymptotic freedom and linear quark confinement in a unified manner. It is shown that this potential reproduces the spectra of the triplet -system charmonium and the triplet -system upsilonium (bottomonium). The only parameters other than the scale size are the quark masses. This potential is formulated in momentum space. This potential has the added feature of a minimal number of parameters.
The final remark of general meaning is that one might expect that for heavy constituents that the effect of the relativistic terms amounts to a small correction compared to the effect of the non-relativistic terms in the Hamiltonian. If this is indeed the case, the relativistic corrections may be treated perturbatively. Perturbative treatment means that the Hamiltonian is split up into an unperturbed part and a part that is regarded as a small perturbation. In order to obtain eigenstates, the Schrödinger equation is solved for the unperturbed, in our case, non-relativistic, Hamiltonian. The energy spectrum of the system under consideration is then approximated by the expectation values of the full Hamiltonian taken with respect to the unperturbed eigenstates. Since the non-relativistic Hamiltonian has no means to discriminate between states of different spin, perturbatively, the wavefunctions of the spin-singlet and spin-triplet states, for instance, are identical. In the first place, all of the above models have been designed for the description of heavy-quark systems. It is generally accepted that in this case, a perturbative treatment is justified [].
For simplicity, we use the Cornell potential because we are only going to calculate the ground state of charmoniums and bottomoniums. Moreover, this potential is sufficient to investigate the effect of the wake-field.
We choose the interaction between heavy quarks in charmonium or bottomonium in the form of the well-known Cornell potential []:
For the static case, the form of this potential is given by Karsch et al. []:
where is the inverse of the screening length, also known as the Debye mass. The in-medium modification of the potential can be introduced via the Fourier transform and the longitudinal dielectric function :
The Yukawa-like part of the potential is obtained using the following dielectric function:
To study the dynamical screening case, we consider a particle moving at a constant velocity v through the medium. The motion of the particle with a charge induces the charge density []:
In order to obtain a modified potential, one should take the inverse Fourier transform of the potential :
Here, we only consider a system moving along z-axis, , then the modified potential reads as:
with .
We use the dielectric function, which was studied in [], which was obtained with the Vlasov approach. In order to study collisions, they started with the Boltzmann equation with the BGK collision term []. The advantage of the former is that one can obtain an analytical expression of the dielectric functions []. Such a dielectric function with the BGK collision term was obtained for ordinary plasmas in [], and in spite of color and flavor, it should be valid for the QGP case because both use the same Vlasov approach []. The dielectric function for the collisional quark–gluon plasma is written as follows:
where is the collision term. The dispersion relation for the dielectric function, i.e., longitudinal modes from , is studied in [,,]. The dielectric function used here is highly inspired from works related to classical plasma where a wake-field is induced by flowing ions and electrons. The dielectric equation is obtained from the kinetic equation for the QED case, which is exactly the same except for the color charge. Thus, we treat the collision between point-like constituent partons with a specific color charge , i.e., quarks, antiquark, and gluons without explicit SU(3) symmetry.
In this work, the dissociation of quarkonium, a bound state of heavy quarks, is investigated in the framework of the nonrelativistic potential model. The Hamiltonian of such a system is given as:
where m is the mass of the quark. The Schrödinger equation was used to obtain the spectrum of quarkonium. The application of this formalism is valid because the quarkonium consists of heavy quarks, which has repeatedly been shown in scientific papers [,,].
As the previously obtained potentials for dynamical screening are non-analytic and three-dimensional, the problem of solving the nonrelativistic Schrödinger equation is reduced to the numerical solution of the eigenvalue problem. For this purpose, a finite difference scheme of the three-dimensional differential equation was constructed, and the scientific package SciPy was used. The equation to be solved is given as follows:
where the eigenvalues correspond to the energy levels of the given system and are expressed by the principal quantum number n due to technical difficulties, such as error accumulation with the increasing discretization of the grid size. For the difference scheme here, we have limited ourselves to the ground states of the system at n = 0 (i.e., and states), the charm quark mass GeV, and the bottom quark mass GeV. The final solutions of depend inversely on the Debye mass .
3. Results and Discussion
Since the dielectric functions are nontrivial, the potentials were constructed numerically. In order to obtain them, one has to perform the inverse Fourier transform. For this purpose, the Fast Fourier Transformation (FFT) method was used.
Due to the cylindrical symmetry, the physical z-axis is on the abscissa and the potential itself is on the ordinate. Here, the natural systems of units were used, where and , which is typical for high-energy physics. In these units, length is measured in GeV, and energy is in GeV.
The potentials depend on parameters such as the collision frequency and the velocity of the system v. The following values of the collision frequency were chosen. The potentials were constructed using Equation (12) for and , where c is the speed of light, because those values are usually used in similar papers [,,]. Plots of these potentials are shown in Figure 1 and Figure 2, respectively.
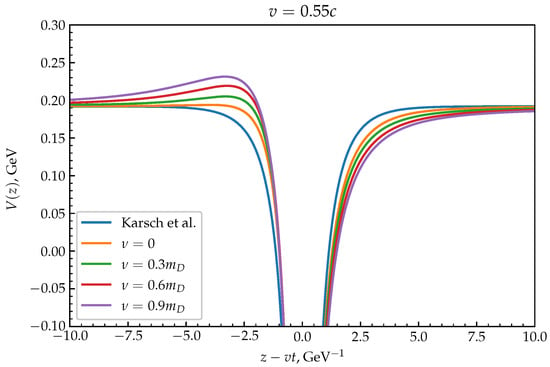
Figure 1.
The behavior of the potential at for different values of the collision frequency.
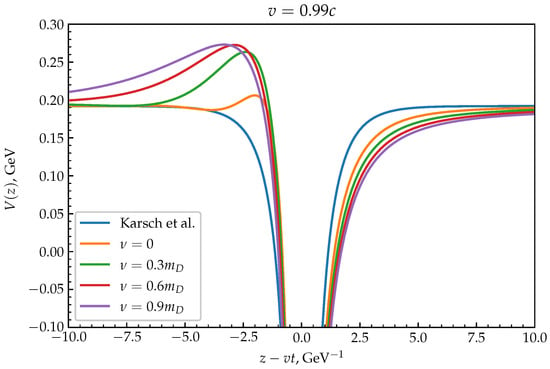
Figure 2.
The behavior of the potential at for different values of the collision frequency.
For visual representation and a better understanding of the behavior of the potential change at the dynamic screening, it is convenient to represent a two-dimensional cross-section of the z–r plane, where the color corresponds to the value of potential energy. Two-dimensional cross sections of the potential are shown in Figure 3 and Figure 4 for different values of the parameters and v.
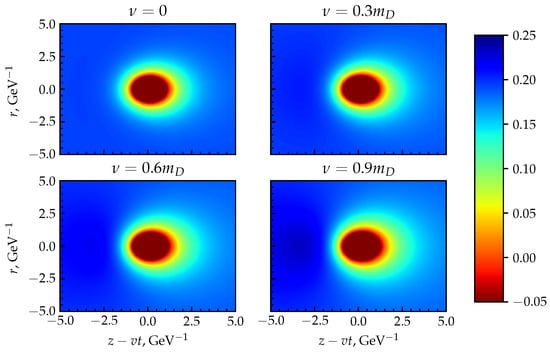
Figure 3.
The behavior of the in-medium heavy quark potential in the plane at for various values of the collision frequency .
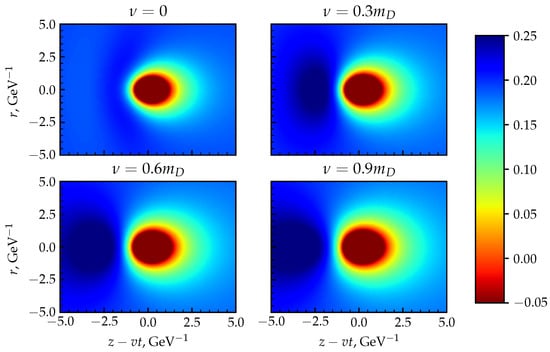
Figure 4.
The behavior of the in-medium heavy quark potential in the plane at for various values of the collision frequency .
It can easily be seen from these graphs that the value of the potential is more intense in front of the particles in the direction of motion and less intense behind these particles. Moreover, the effect is more substantial the greater the velocity of the particle and the collision frequency. A similar phenomenon is observed when a boat moves on a water surface, where it leaves a wake. Therefore, such potentials are called wake-field potentials.
We have represented the amplitudes of the wave function in the presence of the bound state in Figure 5 and Figure 6 for values of and . The amplitudes of the wave functions are normalized. We plotted the wave functions only for the value of the Debye mass GeV and the value of the collision frequency , since the behavior of the wave functions remains the same, except for the magnitude. It can easily be seen that there is an anisotropy in the density distribution of the wave function which is induced by the wake-field.
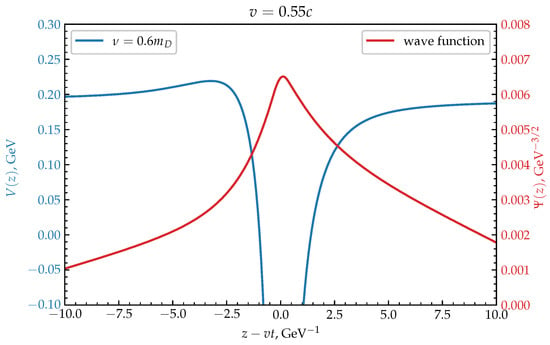
Figure 5.
The behavior of the ground state wave function (red line) and the in-medium heavy quark potential (blue line) in the plane at for the collision frequency of .
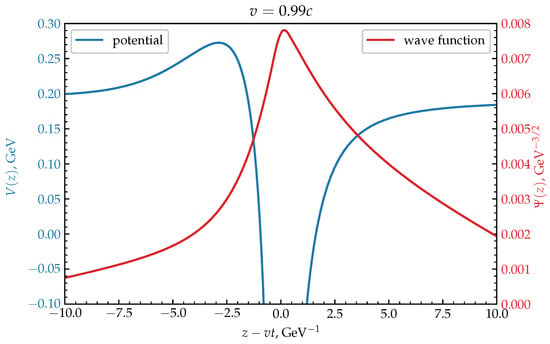
Figure 6.
The behavior of the ground state wave function (red line) and the in-medium heavy quark potential (blue line) in the plane at for the collision frequency of .
A suitable physical quantity by which the moment of decay of quarkonium can be determined is the dissociation energy, given as:
which is positively determined for bound states and negatively determined for free particles. Consequently, the expression
determines the critical value, , at which dissociation occurs. The dissociation energy as a function of for different parameters of the collision frequency and v is depicted in Figure 7 for the -state and in Figure 8 for the -state.
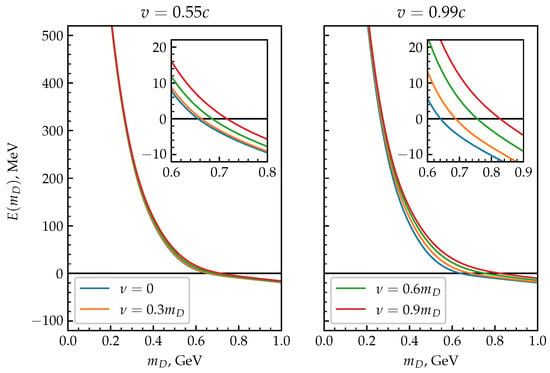
Figure 7.
The dissociation energies for the -state of quarkonium as a function of , the collision frequency , and different velocities: (left) and (right) .
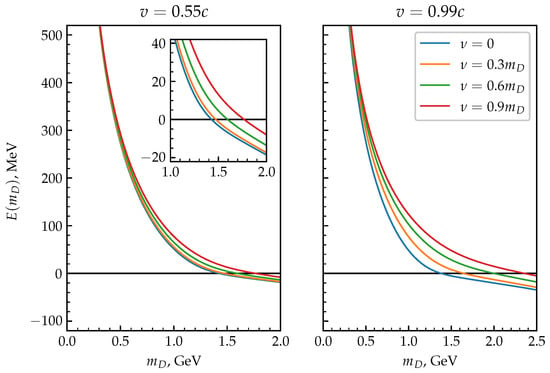
Figure 8.
The dissociation energies for the -state of quarkonium as a function of , the collision frequency , and different velocities: (left) and (right) .
The critical values for were calculated for each set of parameters of the collision frequency and velocity v and can be found in Table 1 and Table 2.

Table 1.
The critical values of the Debye mass (in GeV) for the -state.

Table 2.
The critical values of the Debye mass (in GeV) for the -state.
In order to calculate the critical temperatures of the medium, one might need the expression that relates it to the Debye mass. The perturbation theory of light quarks has the following relation in leading order [,]:
where is the running coupling constant, which depends on temperature T. There is some amount of ambiguity in the coupling constant’s () definition. For simplicity, we have chosen the coupling constant to be . The results for the critical temperatures are shown in Table 3 and Table 4 for the charmonium state. The values for the bottomonium state are in Table 5 and Table 6, for and , respectively.

Table 3.
The critical values of dissociation temperature T (in MeV) at for the -state, .

Table 4.
The critical values of dissociation temperature T (in MeV) at for the -state, .

Table 5.
The critical values of dissociation temperature T (in MeV) at for the -state, .

Table 6.
The critical values of dissociation temperature T (in MeV) at for the -state, .
Unfortunately, there are no directly measured experimental data for the screening length or Debye mass, except for lattice QCD data. However, these results have a considerable degree of diversity. For now, we can just compare our calculation with some values that emerged from lattice QCD in Table 7 [,,].

Table 7.
Debye masses (in GeV) at different temperatures.
Most of the works involving in-medium modification consider a static quark–antiquark potential. Therefore, we restrict ourselves from a direct comparison and treat our results merely as qualitative rather than quantitative. It can be seen from the graph that with increasing collision frequenciees there is a corresponding increase in the critical value of . The same tendency is observed for different values of the parameter and . Consequently, for moving particles the dissociation of quarkonium occurs at a higher effective temperature. Thus, we can conclude that at dynamic screening, the bound states of quarks are more stable than at static screening, which was predicted in [].
4. Conclusions
In this work, the effect of the wake-field on the spectrum and dissociation of quarkonium in a quark–gluon plasma was studied. For this purpose, the quark interaction potential in the gluon medium was constructed by summing the ring diagrams and using the dielectric function from the relativistic Boltzmann equation with the BGK collision integral. It was shown that there is an anisotropy induced by the wake-field in the obtained potentials and in the amplitude of the wave functions as well. The anisotropy is directed along the direction of the quarkonium in the media, and it depends on the velocity of the particle in the medium and the collision frequency. Further, we have analyzed the effect of the wake-field on the spectrum of quarkonium in a quark–gluon plasma. It was demonstrated that for a moving quarkonium in the collisional QGP, dissociation occurs at a much lower screening length and hence at a higher temperature. The collision rate of partons in QGP has an effect on the dissociation of the quarkonium. We have determined the critical plasma temperature corresponding to the dissociation of quarkonium taking into account the wake-field.
Author Contributions
Conceptualization, Y.K. and A.J.; methodology, A.J.; formal analysis, Y.K.; investigation, Y.K.; writing—original draft preparation, Y.K.; writing—review and editing, Y.K. and M.M.; visualization, A.J.; supervision, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant #BR10965191 “Complex research in nuclear and radiation physics, high-energy physics and cosmology for development of the competitive technologies”).
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article and within the references.
Acknowledgments
The authors thank Ramazanov T.S. for thoughtful and stimulating discussions and Baiseitov K.M. for insight into nonrelativistic potentials and dielectric functions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| QGP | Quark–Gluon Plasma |
| SPS | Super Proton Synchrotron |
| RHIC | Relativistic Heavy Ion Collider |
| LHC | Large Hadron Collider |
| QCD | Quantum Chromodynamics |
| BGK | Bhatnagar–Gross–Krook |
References
- Kisslinger, L.S.; Das, D. Review of QCD, quark–gluon plasma, heavy quark hybrids, and heavy quark state production in p–p and A–A collisions. Int. J. Mod. Phys. A 2016, 31, 1630010. [Google Scholar] [CrossRef]
- Shuryak, E.V. Theory of hadron plasma. Sov. Phys.-JETP (Engl. Transl.) 1978, 47. [Google Scholar]
- Sharma, S. Recent theoretical developments on QCD matter at finite temperature and density. Int. J. Mod. Phys. E 2021, 30, 2130003. [Google Scholar] [CrossRef]
- Dzhunushaliev, V.; Makhmudov, A. Scalar model of glueball in nonperturbative quantisation à la Heisenberg. Phys. Sci. Technol. 2015, 1. Available online: https://phst.kaznu.kz/index.php/journal/article/view/35 (accessed on 1 September 2023). [CrossRef]
- Ullrich, T. Zooming in on the quark gluon plasma. Nucl. Phys. A 2007, 783, 1–12. [Google Scholar] [CrossRef]
- Gyulassy, M.; Pliimer, M. Jet quenching in dense matter. Phys. Lett. B 1990, 243, preprint. [Google Scholar] [CrossRef]
- Baier, R.; Schiff, D.; Zakharov, B. Energy loss in perturbative QCD. Annu. Rev. Nucl. Part. Sci. 2000, 50, 37–69. [Google Scholar] [CrossRef]
- Adams, J.; Adler, C.; Aggarwal, M.; Ahammed, Z.; Amonett, J.; Anderson, B.; Anderson, M.; Arkhipkin, D.; Averichev, G.; Badyal, S.; et al. Transverse-Momentum and Collision-Energy Dependence of High-pT Hadron Suppression in Au + Au Collisions at Ultrarelativistic Energies. Phys. Rev. Lett. 2003, 91, 172302. [Google Scholar] [CrossRef] [PubMed]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.; Averbeck, R.; et al. Suppressed π0 Production at Large Transverse Momentum in Central Au + Au Collisions at = 200 GeV. Phys. Rev. Lett. 2003, 91, 072301. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Satz, H. J/ψ suppression by quark-gluon plasma formation. Phys. Lett. B 1986, 178, 416–422. [Google Scholar] [CrossRef]
- Karsch, F.; Mehr, M.T.; Satz, H. Color screening and deconfinement for bound states of heavy quarks. Z. Phys. Part. Fields 1988, 37, 617–622. [Google Scholar] [CrossRef]
- Rapp, R.; Blaschke, D.; Crochet, P. Charmonium and bottomonium in heavy-ion collisions. Prog. Part. Nucl. Phys. 2010, 65, 209–266. [Google Scholar] [CrossRef]
- Nurbakova, G.; Boos, E.; Bunichev, V.; Khabyl, N.; Rustembayeva, S.; Imanova, S. Standard model and predictions for the Higgs boson. Phys. Sci. Technol. 2022, 9, 45–58. [Google Scholar] [CrossRef]
- Dzhunushaliev, V. Gluon field distribution between three infinitely spaced quarks. Phys. Sci. Technol. 2015, 1. [Google Scholar] [CrossRef]
- Lucha, W.; Schöberl, F.F.; Gromes, D. Bound states of quarks. Phys. Rep. 1991, 200, 127–240. [Google Scholar] [CrossRef]
- Rahal, H.; Deutsch, C.; Gombert, M. Temperature-dependent quantum pair potentials and ionization in Helium-like plasmas. Phys. Sci. Technol. 2018, 4, 29–46. [Google Scholar] [CrossRef]
- Agotiya, V.; Chandra, V.; Patra, B.K. Dissociation of quarkonium in a hot QCD medium: Modification of the interquark potential. Phys. Rev. C 2009, 80, 025210. [Google Scholar] [CrossRef]
- Ramazanov, T.; Dzhumagulova, K.; Gabdullin, M.; Moldabekov, Z.; Ismagambetova, T. Development of effective potentials for complex plasmas. Phys. Sci. Technol. 2019, 6, 44–53. [Google Scholar] [CrossRef]
- Jiang, B.F.; Li, J.R. The dielectric function of the viscous quark–gluon plasma. Nucl. Phys. A 2010, 847, 268–282. [Google Scholar] [CrossRef]
- Jiang, B.F.; Li, J.R. The wake potential in the viscous quark–gluon plasma. Nucl. Phys. A 2011, 856, 121–133. [Google Scholar] [CrossRef]
- Liu, L.; Liu, H. Wake potential in a strong coupling plasma from the AdS/CFT correspondence. Phys. Rev. D 2016, 93, 085011. [Google Scholar] [CrossRef]
- Laine, M.; Philipsen, O.; Tassler, M.; Romatschke, P. Real-time static potential in hot QCD. J. High Energy Phys. 2007, 2007, 054. [Google Scholar] [CrossRef]
- Brambilla, N.; Ghiglieri, J.; Vairo, A.; Petreczky, P. Static quark-antiquark pairs at finite temperature. Phys. Rev. D 2008, 78, 014017. [Google Scholar] [CrossRef]
- Rothkopf, A.; Hatsuda, T.; Sasaki, S. Complex heavy-quark potential at finite temperature from lattice QCD. Phys. Rev. Lett. 2012, 108, 162001. [Google Scholar] [CrossRef] [PubMed]
- Burnier, Y.; Kaczmarek, O.; Rothkopf, A. Static quark-antiquark potential in the quark-gluon plasma from lattice QCD. Phys. Rev. Lett. 2015, 114, 082001. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Dong, L.; Pan, J.; Moldes, M.R. Modeling the nonperturbative contributions to the complex heavy-quark potential. Phys. Rev. D 2019, 100, 036011. [Google Scholar] [CrossRef]
- Chakraborty, P.; Mustafa, M.G.; Ray, R.; Thoma, M.H. Wakes in a collisional quark–gluon plasma. J. Phys. G Nucl. Part. Phys. 2007, 34, 2141. [Google Scholar] [CrossRef][Green Version]
- Carrington, M.; Fugleberg, T.; Pickering, D.; Thoma, M. Dielectric functions and dispersion relations of ultra-relativistic plasmas with collisions. Can. J. Phys. 2004, 82, 671–678. [Google Scholar] [CrossRef]
- Moldabekov, Z.A.; Ludwig, P.; Joost, J.P.; Bonitz, M.; Ramazanov, T. Dynamical screening and wake effects in classical, quantum, and ultrarelativistic plasmas. Contrib. Plasma Phys. 2015, 55, 186–191. [Google Scholar] [CrossRef]
- Eichten, E.; Gottfried, K.; Kinoshita, T.; Kogut, J.; Lane, K.D.; Yan, T.M. Spectrum of charmed quark-antiquark bound states. Phys. Rev. Lett. 1975, 34, 369. [Google Scholar] [CrossRef]
- Eichten, E.; Gottfried, K.; Kinoshita, T.; Lane, K.; Yan, T.M. Charmonium: The model. Phys. Rev. D 1978, 17, 3090. [Google Scholar] [CrossRef]
- Bhanot, G.; Rudaz, S. A new potential for quarkonium. Phys. Lett. B 1978, 78, 119–124. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- Schenke, B.; Strickland, M.; Greiner, C.; Thoma, M.H. Model of the effect of collisions on QCD plasma instabilities. Phys. Rev. D 2006, 73, 125004. [Google Scholar] [CrossRef]
- Baiseitov, K.; Moldabekov, Z.; Blaschke, D.; Djienbekov, N.; Ramazanov, T. Surface waves in a collisional quark-gluon plasma. Phys. Part. Nucl. Lett. 2020, 17, 803–808. [Google Scholar] [CrossRef]
- Baiseitov, K.; Blaschke, D.; Ramazanov, T.S. Collective bulk excitations in the QGP: From the weakly non-ideal case to the strong correlation limit. Contrib. Plasma Phys. 2023, 63, e202300015. [Google Scholar] [CrossRef]
- Thompson, E.; Inyang, E.; William, E. Analytical determination of the non-relativistic quantum mechanical properties of near doubly magic nuclei. Phys. Sci. Technol. 2021, 8, 10–21. [Google Scholar] [CrossRef]
- Braaten, E.; Pisarski, R.D. Simple effective Lagrangian for hard thermal loops. Phys. Rev. D 1992, 45, R1827. [Google Scholar] [CrossRef]
- Gross, D.J.; Pisarski, R.D.; Yaffe, L.G. QCD and instantons at finite temperature. Rev. Mod. Phys. 1981, 53, 43. [Google Scholar] [CrossRef]
- DeGrand, T.A.; DeTar, C.E. Static screening lengths in the gluon plasma. Phys. Rev. D 1986, 34, 2469. [Google Scholar] [CrossRef]
- Gale, C.; Kapusta, J. Modification of Debye screening in gluon plasma. Phys. Lett. B 1987, 198, 89–91. [Google Scholar] [CrossRef]
- Laermann, E.; Philipsen, O. Lattice QCD at finite temperature. Annu. Rev. Nucl. Part. Sci. 2003, 53, 163–198. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).