Next Article in Journal
Testing the Paradigm of Nuclear Many-Body Theory
Previous Article in Journal
Mechanisms of Producing Primordial Black Holes and Their Evolution
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Particles
Volume 6
Issue 2
10.3390/particles6020034
particles-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Parameters and Pulsation Constant of Cepheid

by
Sergei V. Sinitsyn
MEPhI, National Research Nuclear University, 115409 Moscow, Russia
Particles 2023, 6(2), 595-610; https://doi.org/10.3390/particles6020034
Submission received: 17 March 2023 / Revised: 22 May 2023 / Accepted: 22 May 2023 / Published: 26 May 2023
Browse Figures
Review Reports Versions Notes

Abstract

:
The analysis of fifty empirical period-radius relations and forty-three empirical period-luminosity relations is performed for the Cepheids. It is found that most of these relations have significant systematic errors. A new metrological method is suggested to exclude these systematic errors using the new empirical metrological relations and the empirical temperature scale of the various samples of the Cepheids. In this regard, the reliable relations between the mass, radius, effective surface temperature, luminosity, absolute magnitude on the one hand, and the pulsation period on the other hand, as well as the reliable dependence of the radius on the mass are determined for the Cepheids of types δ Cephei and δ Scuti from the Galaxy. These reliable relations permit us to accurately determine the empirical value of the pulsation constant for the Cepheids of both types for the first time. It is found that the pulsation constant very weakly depends on the pulsation period of the Cepheid, contrary to the known theoretical calculation. Hence, the Cepheids pulsate almost as a unified whole and homogeneous spherical body in wide ranges of a star’s mass and evolutionary state with an extremely inhomogeneous distribution of stellar substance over its volume. Therefore, it is first suggested that the pulsation of the Cepheid is, first of all, the pulsation of the almost unified whole and homogenous shell of its gravitational mass. This pulsation is triggered by well-known effects; for example, the local optical opacity of the stellar substance and overshooting, using the usual pulsation of the stellar substance.

1. Introduction

In [1], discrete and stepwise gravitational effects were found in the evolutionary expansion and nucleosynthesis of the components of a detached double-lined eclipsing system. In particular, it was found that, in this binary star, the absolute and relative evolutionary expansions of the first and second components are their transitions, respectively, between the areas of the temporal deceleration of the absolutely evolutionary expansion and between the areas of temporarily coordinated evolutionary expansion with temporal localization in them. That is, discrete and stepwise gravitational effects were found in the outer part of a star. In addition, a discrete gravitational effect was found in the nucleosynthesis of the first and second components, namely, along the axis of the relation of the reduced luminosities of these components. That is, a discrete gravitational effect was found in the inner part of a star. In this regard, in this binary star, there are some discrete systems that create these stepwise and discrete effects. It was suggested that these systems are the gravitational masses of the first and second components and the general gravitational mass of the binary star.
In this regard, it is of interest to study further the expansion and compression of the gravitational mass of a star using the example of such variable stars as the Cepheids [2,3,4]. The Cepheids are a type of variable stars that pulsate radially, varying in both diameter and temperature. They change in brightness with a well-defined stable period and amplitude. A strong direct relationship exists between a Cepheid’s luminosity and its pulsation period. The Cepheids are important cosmic benchmarks for scaling galactic and extragalactic distances.
Typical representatives of the Cepheids are the classical Cepheids and, first of all, the Cepheid δ Cephei. Other Cepheids are also known, that is, dwarf Cepheids. The Cepheid δ Scuti is their typical representative. Further, only Galaxy classical Cepheids and Galaxy dwarf Cepheids, that pulsate with fundamental frequency, are analyzed. Hereinafter, the Cepheids of types δ Cephei and δ Scuti are denoted as the Cepheids δCep and δSct, respectively. In [3] it is empirically found that the Cepheids δCep and δSct have common linear relations between the radius and absolute magnitude on the one hand and the pulsation period on the other hand. Moreover, it is namely those Cepheids that pulsate with fundamental frequency [4]. In the Hertzsprung–Russell diagram, these Cepheids form an instability band [5,6]. In the upper and lower parts of the instability band there are the Cepheids δCep and δSct, respectively [4,6]. Some of them are the high-amplitude Cepheids δSct, that is, HADS-Cepheids [7]. The lower and upper parts of the instability band are separated by an area of Cepheid deficiency [4]. According to Figure 1 from [6], in the Hertzsprung–Russell diagram, the instability band is extended from about 4400 K to 8500 K and from about 4 to 105 of the Sun’s luminosities, respectively. Therefore, these variable stars are in a wide range of evolutionary states; that is, from a normal dwarf to almost a red giant and a red supergiant. Moreover, these variable stars are in a wide range of masses; that is, about (1–10) solar masses.
The major parameter of a star’s pulsation is the constant pulsation (Q). For a unified whole and homogeneous pulsating spherical body, it is true that Q = Pρ1/2 [8], where P and ρ are the pulsation period and the volume mass density of this body, respectively. Further, P is the pulsation period of a star. For a pulsating star, Q and P are determined by day. Any pulsating star is not a unified whole and homogeneous pulsating body; therefore, for pulsating star, Q must be dependent on P. However, the variables of type β Cephei [9], the Cepheids of type δ Scuti [10], and the variables of type RR Lyrae [11] have an empirical 〈Q〉 = (0.033–0.036) day for the fundamental frequency of the radial star’s pulsation. It is astonishing since they are very different pulsating stars with extremely inhomogeneous distributions of stellar substance over their volumes [12]. The first two variables are the main sequence stars. The last variables are the very evolved stars. In addition, the first variables are massive stars and the last two variables are small stars. For the fundamental frequency of the Cepheid’s radial pulsation, let us determine the empirical dependence of Q on P; that is, in the range of about (1–10) solar masses and from a normal dwarf to almost a red giant and a red supergiant. Such determination has not been performed till now. However, the theoretical calculations of Q have been performed for the fundamental frequency of the Cepheid’s radial pulsation [13,14].
For the determination of the empirical dependence of Q on P the empirical dependences of Cepheid’s mass and radius on P must be determined. Therefore, in Section 2, the metrological foundation of the determination of Cepheid’s parameters is introduced. The reliability of this foundation is confirmed. In Section 3, the analysis of all empirical period-radius and period-luminosity relations since 1966 are performed for the Cepheids. Significant systematic errors are found in most of these relations. The metrological method of elimination of these systematic errors is suggested. The reliable relations between the radius and the absolute magnitude on the one hand, and the pulsation period on the other hand, are determined for the Cepheids of types δ Cephei and δ Scuti from the Galaxy. In Section 4, the reliable relations between the mass, effective surface temperature, luminosity on the one hand, and the pulsation period on the other hand, as well as the reliable dependence of the radius on the mass, are determined for the Cepheids of types δ Cephei and δ Scuti from the Galaxy. In Section 5, the accurate empirical dependence of Q on P is determined. This dependence is compared with theoretical calculations [13,14] and other empirical data at the end.

2. Parameters of Cepheid

Hereinafter, the index of sol indicates that it belongs to the Sun. M, R, L, Te are the mass, radius, luminosity and effective surface temperature of a star, respectively. Further, only a star’s parameters, averaged over its pulsation period, are considered. The symbol 〈〉 indicates the averaging of such parameters over a sample of stars or the entire volume of a star.
In [1], as the result of the analysis of empirical data from catalogs [15,16,17,18], for the components of detached double-lined eclipsing systems on the main sequence it is found that
L/Lsol = η(M/Msol)γ,
where η and γ are some positive constant parameters. In [19], the analysis of empirical data shows that (1) is valid also for the components of Algol-type binaries on the main sequence. Therefore, let us assume that (1) is valid for the Cepheids. Further, it shows that this assumption is true.
As it is known for a star, it is valid that [20]
L/Lsol = (R/Rsol)2(Te/Tsol)4
MV = Mb(sol) − (5/2)log(L/Lsol) − BCV,
where MV is the absolute magnitude, Mb is the bolometric magnitude, and BCV is the bolometric correction.
In [1], as the result of the analysis of empirical data from catalogs [15,16,17,18], for the components of detached double-lined eclipsing systems at 0.445 ≤ M/Msol < 14.10 it is found that
R/Rsol = κ(M/Msol)ν,
where κ and ν are some positive constant parameters. Therefore, let us assume that (3) is valid for the Cepheids. Further, it shows that this assumption is true.
According to [3,21], log(Te) ≥ 3.64 and log(Te) ≤ 3.93 are valid for the Cepheids δCep and δSct, respectively. Thus, the Cepheids are approximately in the range of 3.64 ≤ log(Te) ≤ 3.93. Several of the dependences of BCV on log(Te) are known for this temperature range [22,23,24,25,26,27]. The dependence of BCV on log(Te) is weak when 3.64 ≤ log(Te) ≤ 3.93. This temperature range (Te ≈ (4400–8500)K) happens to be the critical temperature region at which helium is completely ionized. It is known that Tsol = 5772 K [28]; that is, log(Tsol) = 3.7613. Therefore, let us assume that in the linear approximation at 3.64 ≤ log(Te) ≤ 3.93
BCV = BCV(sol) + bTlog(Te/Tsol),
where bT is some constant coefficient. Further, it shows that this assumption is true.
Note that for the Cepheids (1–4) are the metrological foundation of the determination of their R, M and L. In addition, (1–4) are with respect to the logarithmic axes. Therefore, only log(R/Rsol), log(M/Msol), log(L/Lsol), log(Te/Tsol), log(P), log(Te) are used in further next relations.
According to [3,29,30], for the Cepheids, an empirical linear relation between P and R (PR relation) and an empirical linear relation between P and MV (PMV relation) are valid. The empirical PR relation and PMV relation are determined as, respectively,
log(R/Rsol) = αP + βPlog(P),
MV = AP + BPlog(P)
where αP, βP and AP, BP are some constant coefficients. From (1), (2a), (3) and(5a) it follows that
log(η/κγ/ν) = 4log(Te/Tsol) + [2 − (γ/ν)](αP + βPlog(P))
It is seen that, for the Cepheids, log(Te) is also the function of log(P). From (2b), (4), (5b) and (6) it follows that
AP = Mb(sol) − BCV(sol) − (1/4){(bT + 10) [αP(γ/ν) + log(η/κγ/ν)] − 2αPbT}
BP = −(1/4) [(bT + 10)(γ/ν) − 2bT]βP
Taking into account (5b), the right parts of (7a) and (7b) are constant. Hence, η, γ, κ, ν, aT, bT,αP, βP are constant, too. Thus, (1)–(4) are valid and, thereby, the above assumptions are true. This is important for the metrological foundation of the Cepheids.

3. Radius, Absolute Magnitude and Pulsation Period of Cepheid

Let us analyze the known empirical PR relations and PMV relations. They can be used to find and estimate the systematic errors (δ) of known empirical αP, βP, AP and BP from (5).
At least fifty empirical PR relations [3,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] are known, to date, for the Cepheids from the Galaxy. Figure 1a,b shows the distributions of the PR relations along the axis βP from 1966 to 2009, and since 2009, respectively. Two wide peaks are visible in the range of (0.606–0.679) and (0.706–0.771) in Figure 1a. Two narrow peaks are visible in the range of (0.680–0.698) and (0.740–0.755) in Figure 1b. That is, the first peak shifts towards higher values over time.
At least forty-three empirical PMV relations (PMV) [3,5,29,50,51,55,56,58,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] are known, to date, for the Cepheids from the Galaxy. Figure 2 shows the distribution of the PMV relations along the axis BP since 1988. Three peaks are visible in the range of (−2.689–−2.671), (−2.789–−2.767), and (−2.950–−2.900). Let us determine the values of βP and BP, which are valid, in Figure 1 and Figure 2, respectively.
Figure 3 shows the distribution of the fifty empirical PR relations of (5a). In the first approximation, the PR relations form a linear dependence of αP on βP. This indicates that in most of the PR relations, there is one systematic δ(αP) and one systematic δ(βP), which are connected to each other by a linear law in the first approximation and are significantly larger than any random δ(αP) and δ(βP) and other systematic δ(αP) and δ(βP). This circumstance has not received attention, yet. Let us use it and define the relation between αP and βP in the linear approximation. It notes that the random δ(αP) and δ(βP) are independent and can be comparable to each other. In addition, the other systematic δ(αP) and δ(βP) can be independent and comparable to each other. Therefore, the least square method (LSM) must be used, simultaneously, along both axis αP and axis βP in the linear approximation. That is, the square deviations of empirical data are minimized along both the axis of αP and the axis of βP at the same time, using the linear relation between αP and βP. Moreover, it excludes eight PR relations that differ significantly on βP and αP from others. Then, it follows that
αP = 1.893 − 1.080βP
Figure 3 shows (8). According to Figure 3 and (5a) and (8), most of the fifty PR relations intersect with each other near the point of log(P) = 1.080 and log(R/Rsol) = 1.893. That is, most of these relations differ from each other, first of all, by βP. Therefore, there is a significant systematic δ(βP). The use of (8) allows us to take into account this systematic δ(βP) and, thereby, the significant systematic δ(αP), and also to minimize the random δ(αP) and δ(βP) and the other systematic δ(αP) and δ(βP). Thus, the analysis of the fifty PR relations, from 1966 to 2021, finds significant systematic δ(βP) and δ(αP) in most of these relations.
Figure 4 shows the distribution of the forty-three empirical PMV relations of (5b). In the first approximation, the PMV relations form a linear dependence of AP on BP. This indicates that in most of the PMV relations there is one systematic δ(AP) and one systematic δ(BP), which are connected to each other by a linear law in the first approximation and are significantly larger than any random δ(AP) and δ(BP) and other systematic δ(AP) and δ(BP). This circumstance has not received attention, yet. Let us use it and define the relation between AP and BP in the linear approximation. This notes that the random δ(AP) and δ(BP) are independent and can be comparable to each other. In addition, the other systematic δ(AP) and δ(BP) can be independent and comparable to each other. Therefore, LSM must be used, simultaneously, along both the axis AP and the axis BP in the linear approximation. That is, the square deviations of empirical data are minimized along both the axis of AP and along the axis of BP at the same time, using the linear relation between AP and BP. Moreover, it excludes twelve PMV relations that differ significantly on BP and AP from others. Then, it follows that
AP = −4.999 − 1.308BP
Figure 4 shows (9). According to Figure 4 and (5b) and (9), most of the forty-three PMV relations intersect with each other near the point of log(P) = 1.308 and MV = −4.999. That is, most of these relations differ from each other, first of all, by BP. Therefore, there is significant systematic δ(BP). The use of (9) allows us to take into account this systematic δ(BP) and, thereby, the significant systematic δ(AP), and also to minimize the random δ(AP) and δ(BP) and the other systematic δ(AP) and δ(BP). Thus, the analysis of the forty-three empirical PMV relations, from 1988 to 2021, finds significant systematic δ(AP) and δ(BP) in most of these relations.
The significant systematic δ(αP), δ(βP) and δ(AP), δ(BP) must be excluded. Combining (2), (4), (5), (8) and (9), this obtains the metrological relation between βP and BP, taking into account systematic δ(αP),δ(βP) and δ(AP), δ(BP)
5(1.080 − log(P))βP = −(1.308 − log(P))BP + (10 +bT)log(Te/Tsol) + 4.464 − Mb(sol) + BCV(sol)
The use of (10) allows us to find reliable βP and BP and, thereby, to exclude significant systematic δ(βP) and δ(BP). Further, the use of (8) and (9) allows us to find reliable αP and APand, thereby, to exclude significant systematic δ(αP) and δ(AP). Therefore, only βP and BP are analyzed further.The metrological method, using (8)–(10), has not been used until now.
Note that log(Tsol), Mb(sol), BCV(sol) and log(P), log(Te) must be known to determine βP and BP using (10). It is known that log(Tsol) = 3.7613 (Section 2). According to [87,88], Mb(sol)= (4.7554 ± 0.0004) and BCV(sol) = −(0.107 ± 0.002). The analysis of the temperature dependence of BCV on log(Te) [22,23,24,25,26,27] shows that 〈bT〉 is equal to (2.2–2.8) in the range of 3.64 ≤ log(Te) ≤ 3.93 (Section 2). For the determination of βP and BP, using a sample of the Cepheids is required; that is, 〈log(Te)〉 and 〈log(P)〉 instead of log(Te) and log(P). The use of 〈log(Te)〉 minimizes any random δ(log(Te)). Therefore, the accuracy of the determination of βP and BP increases. Moreover, this sample of the Cepheids must have 〈log(P)〉 as far from 1.080 and 1.308; that is, the values of βP and BP must be sensitive to each other in (10).
At least five relatively large samples [61,89,90,91,92] are known for the Cepheids from the Galaxy. Two and three samples of these are the sample of the Cepheids δCep [61,92] and the Cepheids δSct [89,90,91], respectively. The samples of the Cepheids δCep have a〈log(P)〉 close to 1.108. Therefore, each of these samples is divided into two subsamples. The first and second subsamples for log(P) < 0.93 and log(P) > 0.97 are valid, respectively. The samples and subsamples for 〈log(Te)〉 and 〈log(P)〉 are shown in Table 1. These samples have the same temperature scale in the first approximation. That is, using LSM along the axis log(Te); for these, it is true that
log(Te) = (3.812 ± 0.002) − 0.064log(P)
Here, the deviation of the first coefficient is equal to three standard deviations of the sample mean.
The samples and subsamples deviate from (11) by not more than 0.52% or 30K. Note that the samples were formed from different Cepheids for which their Te were determined from 1972 to 2021 and by different scientists.
In contrast to the Cepheids δCep, for the Cepheids δSct, thePMV relations are mainly in the narrow range along the axis BP, namely, from to −3.00 to −2.89 [73,77,83,85]. Moreover, for the Cepheids δCep and δSct, all general PMV relations [3,29] are also in this range. Therefore, let us determine the βP and BP for the Cepheids δSct first. According to (10), the result of the calculation of BCV(sol) depends on bT.
Particles 06 00034 g005 550
Figure 5. The dependencies of the calculation result of BCV(sol) on bT, according to (10) and the empirical date from Table 1: for the Cepheids of type δScuti at BP = −2.89, βP = 0.736 (a); for the Cepheids of type δCephei at BP = −2.776, βP = 0.7315 (b). The ordinal numbers of these dependencies are according to Table 1.
Figure 5. The dependencies of the calculation result of BCV(sol) on bT, according to (10) and the empirical date from Table 1: for the Cepheids of type δScuti at BP = −2.89, βP = 0.736 (a); for the Cepheids of type δCephei at BP = −2.776, βP = 0.7315 (b). The ordinal numbers of these dependencies are according to Table 1.
Particles 06 00034 g005
In Figure 5a, as an example, at BP = −2.89, the dependences of this result on bT are shown for the samples [89,90,91] when BCV(sol) = −0.109 at bT = 2.2 for the sample [89]. This condition corresponds to βP = 0.736. The other two dependences of the samples [90,91] are shifted to negative values. These shifts are due to the fact that the temperature scales of samples [90,91] are shifted from the temperature scale of sample [89] by 6K and 51K towards higher values, respectively. Using (10) and the data of Table 1, the set of βP is calculated for each sample [89,90,91] at −3.00 ≤ BP ≤ −2.89, 2.2 ≤ bT ≤ 2.8 and −0.109 ≤ BCV(sol) ≤ −0.105. The analysis of these sets shows that −3.00 ≤ BP ≤ −2.89 corresponds to 0.736 ≤ βP ≤ 0.771. Note that, for the Cepheids δCep and δSct, the general PR relations [3,30] are also in this range along the axis βP in Figure 1b. Hence, using (5), (8) and (9), for the Cepheids δSct, it is true that
log(R/Rsol) = (1.079 ± 0.020) + (0.754 ± 0.018)log(P)
MV = −(1.15 ± 0.08) − (2.945 ± 0.055)log(P)
Hereinafter, in any linear relation or dependence the deviations of the first and second coefficients anticorrelate in sign. These coefficients and their deviations determine the upper and lower boundaries of the area in which the reliable relation or the reliable dependence exist. In turn, the coefficient deviations are determined using empirical-metrological (8), (9) and the areas in which the reliable values of βP and BP exist. The last areas are determined using empirical-metrological (10) and the indetermination of bT, and the errors of the temperature scales of samples from Table 1. Thus, in any linear relation or dependence, the coefficient deviations are determined using empirical-metrological (8)–(10) and the indetermination of bT, the errors of the temperature scales of samples from Table 1.
As an example, for the Cepheids δCep, the results of the calculation of BCV(sol) on bT using (10) are shown for the samples [61,92] in Figure 5b when BCV(sol) = −0.105 at bT = 2.8 for the first and second subsamples of the sample [92]. This condition corresponds to βP = 0.7315. For the sample [61], these results are shifted to positive values. This shift is due to the fact that the temperature scale of sample [61] is shifted from the temperature scale of sample [92] by 23K towards smaller values. Note that BP is not fixed here, because two subsamples are used for each sample. Therefore, BP and βP are determined simultaneously using the intersection of two dependences of the calculation results of BCV(sol) on bT for the first and second subsamples. Using (10) and the data of Table 1, the set of βP is calculated for each sample [61,92] at 2.2 ≤ bT ≤ 2.8 and −0.109 ≤ BCV(sol) ≤ −0.105. The analysis of these sets shows that for the sample [61], −2.885 ≤ BP ≤ −2.815 and 0.734 ≤ βP ≤ 0.757 are valid. In addition, the sample [92] −2.783 ≤ BP ≤ −2.717 and 0.713 ≤ βP ≤ 0.735 are valid. Hence, by using (5, 8, 9) and generalizing the calculation results, for the Cepheids δCep, it is true that
log(R/Rsol) = (1.099 ± 0.024) + (0.735 ± 0.022)log(P)
MV = −(1.34 ± 0.12) − (2.80 ± 0.08)log(P)
Note that in (12) and (13), for each coefficient, its δ is determined by using the temperature scale and the range of bT. For example, for the Cepheids δCep at bT = 2.2, BP and βP are equal to (−2.83–−2.72) and (0.713–0.738), respectively. Along with that, at bT = 2.8, BP and βP are equal to (−2.88–−2.77) and (0.732–0.757), respectively. However, for the Cepheids δSct, the dependence of βP on bT is relatively weak. For example, βP is equal to (0.736–0.765) and (0.743–0.771) at abT equal to 2.2 and 2.8, respectively, and −3.00 ≤ BP ≤ −2.89.
According to the above, in Figure 2, for the Cepheids δSct, the peak in the range of (−2.950–−2.900) along the axis BP corresponds to the peaks in the range of (0.706–0.770) and (0.740–0.755) along the axis βP in Figure 1b and 1a, respectively. For the Cepheids δCep, the peak in the range of (−2.789–−2.767) along the axis BP corresponds to the same peaks along the axis βP in Figure 1. Thus, in Figure 1b and 1a along the axis βP, the peaks in the range of (0.706–0.770) and (0.740–0.755) are valid for the Cepheids δSct and δCep. In Figure 2, along the axis BP, the peaks in the range of (−2.950–−2.900) and (−2.789–−2.767) are valid for the Cepheids δSct and δCep, respectively.
In this regard, the Cepheids δCep bT = 2.2 and the temperature scale of sample [92] are more probable than bT = 2.8 and the temperature scale of sample [61], respectively. Therefore, for the Cepheids δCep, it is more probable that log(R/Rsol) = (1.109 ± 0.014) + (0.725 ± 0.012)log(P) and
MV = −(1.370 ± 0.075) − (2.775 ± 0.058)log(P).
Note that the Cepheids δSct and δCep are in extremely different evolutionary states and have significantly different masses. The first variables are a normal dwarf and the second variables are almost a red giant and a red supergiant. However, from the comparison of (12) and (13), it follows that for the Cepheids δSct and δCep, their PR relations are close to each other. Their PMV relations are close to each other, too. Hence, some general PR and PMV relations can be suggested for the Cepheid δSct and δCep in the first approximation. Such relations can be PR and PMV relations [3], namely,
log(R/Rsol) = (1.1116 ± 0.0060) + (0.7385 ± 0.0060)log(P)
MV = −(1.203 ± 0.041) − (2.902 ± 0.030)log(P)
Note that (14a) is very close to (8) and (14b) corresponds to (9) in the limits of its δ.
Thus, the analysis of all known empirical PR relations and PMV relations allows us to find and estimate the significant systematic δ(βP), δ(αP), δ(AP), δ(BP), and to eliminate them, and also decrease random δ(αP), δ(βP), δ(AP), δ(BP). In its turn, this allows us to find reliable empirical PR relations and PMV relations.

4. Radius, Mass, Luminance, Temperature and Pulsation Period of Cepheids

Taking into account the region of the existence of the Cepheids δSct and δCep along the axes BP and βP (Section 3) and using (7b), it follows that, for them, γ/ν is equal to (1.650 ± 0.010) and (1.619 ± 0.011), respectively. According to [1], the analysis of the empirical data [15,16,17,18] shows that γ = 4 at 0.445 ≤ M/Msol < 14.10 for the components of detached double-lined eclipsing systems on the main sequence. In addition, in [19], the analysis of the empirical data shows that γ is equal to (3.92 ± 0.05) and (3.86 ± 0.05) in this mass range for the first and second components of the detached Algol binaries, respectively, on the main sequence. The Cepheids δSct are the main sequence stars at M/Msol ≈ (1.5–2.0) [3]. Therefore, for these Cepheids, γ = 4 is valid. Then, taking into account (7), (12) and (13), for the Cepheids δCep, γ = 4 is valid, too. This condition can be confirmed in another way. For the Cepheids δCep and δSct, −1.408 ≤ log(P) ≤ 1.8378 is valid.The lower and upper limits are from [91] and [68], respectively. Therefore, as follows from (12a), (13a) and(14a), for the Cepheids, log(R/Rsol) increases by (2.3–2.5) when log(P) increases from −1.408 to 1.8378; that is, when M/Msol increases by about an order of magnitude. Hence, taking into account (3), the Cepheids δCep and δSct have ν≈ (2.3–2.5). Further, taking into account γ/ν, the Cepheids have γ≈ (3.72–4.16); that is, about 4. Thus, for the Cepheids δCep and δSct, ν is equal (2.470 ± 0.015) and (2.424 ± 0.015) at γ = 4, respectively. According to [1], the main sequence stars have ν = 3 at 0.445 ≤ M/Msol < 14.10.
For the Cepheids δSct, let us calculate κ using (6) and (12a) and the empirical data of the samples [89,90,91] (Table 1). In this regard, let us assume that the Cepheids δSct have η = 5.31. Further, it shows that this assumption is true. Then, for the Cepheids δSct at η = 5.31 and γ = 4, it follows that
log(R/Rsol) = (0.091 ± 0.012) + (2.424 ± 0.015)log(M/Msol)
Further, taking into account the above calculations, from (1), (12a) and (15) at η = 5.31 and γ = 4 it follows that
log(M/Msol) = (0.407 ± 0.013) + (0.311 ± 0.008)log(P)
log(L/Lsol) = (2.354 ± 0.050) + (1.244 ± 0.031)log(P)
On the other hand, without η and γ from (11) and (12a) it follows that
log(L/Lsol) = (2.360 ± 0.046) + (1.251 ± 0.036)log(P)
The coefficients of (16b) and (17) are the same in the limits of their δ. Therefore, η = 5.31 and γ = 4 are valid for the Cepheids δSct. Hence, the above assumptions are true.
Taking into account the above calculations, from (2a), (12a) and (16b) it follows that
log(Te) = (3.810 ± 0.004) − (0.066 ± 0.002)log(P)
It is seen that the coefficients of (11) and (18) are the same in the limits of their δ.
For the Cepheids δCep, let us calculate κ using (6) and(13a) and the empirical data of the samples [61,92] (Table 1). In this regard, let us assume that the Cepheids δCep have η = 5.31. Further, it shows that this assumption is true. Then, for the Cepheids δCep at η = 5.31 and γ = 4, it follows that
log(R/Rsol) = (0.050 ± 0.014) + (2.470 ± 0.016)log(M/Msol)
Further, taking into account the above calculations, from(1), (13a) and (19) at η = 5.31 and γ = 4 it follows that
log(M/Msol)= (0.424 ± 0.013) + (0.298 ± 0.011)log(P)
log(L/Lsol)= (2.423 ± 0.050) + (1.190 ± 0.043)log(P)
On the other hand, without η and γ from (11) and (13a) it follows that
log(L/Lsol)= (2.400 ± 0.054) + (1.213 ± 0.044)log(P)
The coefficients of (20b) and (21) are the same in the limits of their δ. Therefore, η = 5.31 and γ = 4 are valid also for the Cepheids δCep. Hence, the above assumptions are true.
Taking into account the above calculations, from (2a), (13a) and (20b) it follows that
log(Te) = (3.817 ± 0.002) − (0.070 ± 0.001)log(P)
It is seen that the coefficients of (11) and (22) are very close to each other. Moreover, (15)–(18) and (19)–(22) are close to each other, too. Hence, the Cepheids δSct and δCep are almost unified pulsators. Note, that the first and second variable stars are in extremely different evolutionary states and have significantly different masses. The first variables are a normal dwarf and the second variables are almost a red giant and a red supergiant. Therefore, at the same time, (15)–(18) and (19)–(22) are valid in the different ranges of log(P). According to [51,68,91], the Cepheids δSct and δCep are in the ranges of −1.408 ≤ log(P) ≤ −0.541 and 0.2889 ≤ log(P) ≤ 1.8378, respectively. Then, from (16a) and (20a), it follows that 0.88 ≤ M/Msol ≤ 1.80 and 3.16 ≤ M/Msol ≤ 9.53 for the Cepheids δSct and δCep, respectively.

5. Pulsation Constant of Cepheid

Let us assume that Q = Pρ1/2 (Section 1) is valid for the Cepheid’s pulsation. Then, it follows that
Q = P(M/Msol)1/2/(R/Rsol)3/2
Hence, taking into account (12a, 16a) and (13a, 20a) and also the above calculations (Section 4), it follows that for the Cepheids δSct and δCep, respectively,
log(Q) = −(1.414 ± 0.025) + (0.025 ± 0.023)log(P)
log(Q) = −(1.436 ± 0.030) + (0.046 ± 0.028)log(P),
where Q is determined by day. In (24), the deviations of the first and second coefficients correlate in sign. From (24a,b) it is seen that, for the Cepheids δSct and δCep, Q is very weakly dependent on P, especially for the first of them. Moreover, (24a,b) are very close to each other. However, the first and second variable stars are in extremely different evolutionary states and have significantly different masses. Hence, for these variables and the fundamental frequency, Q depends very weakly on M and the volume distribution of their substance. According to (3), (5a) and (23), it follows that
log(Q) = (1/2ν − 3/2)αP − (1/2ν)log(κ) + [1 − (3/2 − 1/2ν)βP]log(P)
Hence, d(log(Q))/d(log(P)) = 0 if βP = 2/(3 – 1/ν). Then, taking into account (15) and (19), for the Cepheids δSct and δCep, d(log(Q))/d(log(P)) = 0 ifβP is equal to (0.7730 ± 0.0008) and (0.7707 ± 0.0008), respectively. That is, according to (12a) and (13a), along theaxis βP, the upper boundaries of the regions of the existence of the Cepheids δSct and δCep turn out to be very close to the condition of d(log(Q))/d(log(P)) = 0, especially for the first of them.
In [13,14,93,94,95,96], there are the physical foundations and theoretical models of a star pulsation as a stellar substance pulsation. As it follows from (24b), the Cepheids δCep have Q = (0.038 ± 0.002) day at P = 1.95 days. At the same time, according to the theoretical calculation [13] using the formula [93], Q = 0.0364 day at the same value of P. It is seen that the first value of Q coincides with the result of the theoretical calculation. However, in (24b), d(log(Q))/d(log(P)) is about (2–3) times less than according to the theoretical calculations [13], which is important. According to these calculations, d(log(Q))/d(log(P)) = (0.110–0.156) for the Cepheids δCep. In addition, according to another theoretical calculation [14] and taking into account (18) and (22), for the Cepheids δSct, d(log(Q))/d(log(P)) ≈ 0.001, but for the Cepheids δCep, d(log(Q))/d(log(P)) ≈ 0.15, already. Thus, taking into account the results of the theoretical calculations and (24b), at least the pulsation of the Cepheid δCep is not determined by the pulsation of its substance.
In addition, as it follows from (24a), the Cepheids δSct have 〈Q〉 = (0.0366 ± 0.0039) day at 〈P〉 = 0.110 day [97]. They are the main sequence stars at M/Msol≈ (1.5–2.0) [3]. According to [10], for the Cepheids δSct, Q = (0.033 ± 0.006) day as it follows from the empirical data. Hence, (24a) is true. Therefore, (15)–(18) and, thereby, (19)–(22) are true, too. Along with this, on the main sequence, the variables of type β Cephei have 〈Q〉 = 0.033 day for the fundamental frequency but at 8 ≤ M/Msol ≤ 20 and 〈M/Msol〉 = 12 [9]. Hence, for pulsating main sequence stars, the fundamental frequency Q depends also very weakly on M and the volume distribution of their substance.
In addition, according to (24), for the Cepheids δSct, Q increases by (0–10)% when log(P) increases from −1.408 to −0.541. For the Cepheids δCep, Q increases by (7–30)% when log(P) increases from 0.2889 to 1.8378. As it follows from (23) and (24), for the Cepheids, 〈ρ〉∝ 1/P2 is valid. Therefore, for the Cepheids δSct and δCep, Q increases by no more than 10% and 30% when 〈ρ〉 changes by two and three orders of magnitude, respectively. Moreover, for the Cepheids, Q increases by no more than 50% when log(P) increases from −1.408 to 1.8378. Here, 〈ρ〉 changes even by six and a half orders of magnitude. This confirms that the Cepheid δSct and δCep really pulsate almost like a unified whole and a homogeneous spherical body, especially for the first of them. At the same time, the distribution of a substance in a star is extremely inhomogeneous [12].
The above indicates that the pulsation of the Cepheids δCep or δSct is determined by the pulsation of some their almost unified whole and homogeneous elements but not the pulsation of their substance. This element is common to the entire volume of the Cepheid and does not depend on the distribution of the substance in this star. The shell of the star’s gravitational mass should be suggested as such an element.
Then, the pulsation of the Cepheid is determined by the pulsation of the shell of its gravitational mass. The pulsation of the almost unified whole and homogeneous shell of the star’s gravitational mass is triggered by the usual pulsation of the star’s substance. In turn, the usual pulsation of the star’s substance is triggered by the well-known effect of its local optical opacity [94].This effect is created by metal atoms [95].That is, the metallicity of the stellar substance determines the position of the pulsation band with respect to the axes log(Te) and log(L); for example, for RR Lyrae [6,96] or slowly pulsating B-type stars and the variables of type β Cephei [6,94]. In addition, there may be many other factors affecting the formation path and evolution state of variable stars; for example, overshooting [98]. Convective overshoot is not only related to the formation and evolution of pulsating variablestars but also associated with many important celestial bodies and extreme physical processes, such as massive pulsating variable stars [99], white dwarfs [100], X-ray binaries [101], and high-magnetic pulsars [102,103].

6. Conclusions

For the Cepheids δCep and δSct from the Galaxy, the dependence of the radius on the mass and the relations between the mass, radius, effective surface temperature, luminosity, absolute stellar magnitude on the one hand, and the pulsation period on the other hand, are determined. In this regard, it is found that each of these Cepheids pulsates almost like a unified whole and homogeneous spherical body. However, each of these Cepheids has an extremely inhomogeneous distribution of its substance over its volume. This contradiction is valid for wide ranges of a star’s mass and a star’s evolutionary state. Therefore, it is suggested that the pulsation of any Cepheid is, first of all, the pulsation of the almost unified whole and homogenous shell of its gravitational mass. This pulsation is triggered by well-known effects; for example, the local optical opacity of a star’s substance and overshooting, using the usual pulsation of a star’s substance. Thus, the pulsation of a star is, in general, a more complex physical process than was assumed until now.

Funding

This research received no external funding.

Data Availability Statement

All data generated or analyzed during this study are included in this published article.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Sinitsyn, S.V. Gravitational Scale Factor and Discrete Gravitational Effects in Formation, Evolutionary Expansion, and Luminosity of Components of Detached Double-Lined Eclipsing Systems (DDLES’s). Phys. At. Nucl. 2021, 84, 381–388. [Google Scholar] [CrossRef]
  2. Iben, I. The life and times of an intermediate mass star—In isolation/in a close binary, Royal Astronomical Society. Q. J. 1985, 26, 1–39. [Google Scholar]
  3. Fernie, J.D. A new approach to the Cepheid period-luminosity law—Delta Scuti stars as small Cepheids. Astron. J. 1992, 103, 1647. [Google Scholar] [CrossRef]
  4. Fernie, J.D. AC Andromedae: The missing link between Scuti stars and classical Cepheids? Mon. Not. R. Astron. Soc. 1994, 271, L19–L20. [Google Scholar] [CrossRef]
  5. Sandage, A.; Tammann, G.A.; Reindl, B. New period-luminosity and period-color relations of classical Cepheids. II. Cepheids in LMC. Astron. Astrophys. 2004, 424, 43–71. [Google Scholar] [CrossRef]
  6. Kervella, P.; Mérand, A.; Gallenne, A.; Borgniet, S.; Trahin, B.; Nardetto, N.; Pietrzynski, G.; Gieren, W. Interferometry of classical pulsators. Proc. Pol. Astron. Soc. 2018, 6, 201–207. [Google Scholar]
  7. Breger, M. δ Scuti Stars (Review). In Delta Scuti and Related Stars; ASPC: San Francisco, CA, USA; ASP: San Francisco, CA, USA, 2000; Volume 210, pp. 3–42. [Google Scholar]
  8. Eddington, A. The Internal Constitution of the Stars; Cambridge University Press: Cambridge, UK, 1930. [Google Scholar]
  9. Stankov, A.; Handler, G. Catalog of Galactic β Cephei Stars. Astrophys. J. Suppl. Ser. 2005, 158, 193–216. [Google Scholar] [CrossRef]
  10. Handler, G.; Shobbrook, R.R. On the relationship between the δ Scuti and γ Doradus pulsators. Mon. Not. R. Astron. Soc. 2002, 333, 251–261. [Google Scholar] [CrossRef]
  11. Lub, J. RR Lirae calibrations in the light of Gaia DR2. In RR Lyrae/Cepheid 2019: Frontiers of Classical Pulsator; ASPC: San Francisco, CA, USA; ASP: San Francisco, CA, USA, 2021; Volume 529, pp. 33–37. [Google Scholar]
  12. Pols, O.R.; Tout, C.; Eggleton, P.P.; Han, Z. Approximate input physics for stellar modelling. Mon. Not. R. Astron. Soc. 1995, 274, 964–974. [Google Scholar] [CrossRef]
  13. Cox, A.N. Cepheid masses from observations and pulsation theory. Astrophys. J. 1979, 229, 212. [Google Scholar] [CrossRef]
  14. Dornan, V.; Lovekin, C.C. The Effects of Metallicity on Convective Overshoot Behavior in Models of δ Scuti Variable Stars. Astrophys. J. 2022, 924, 130. [Google Scholar] [CrossRef]
  15. Malkov, O.Y. Mass-luminosity relation of intermediate-mass stars. Mon. Not. R. Astron. Soc. 2007, 382, 1073–1086. [Google Scholar] [CrossRef]
  16. Torres, G.; Andersen, J.; Giménez, A. Accurate masses and radii of normal stars: Modern results and applications. Astron. Astrophys. Rev. 2009, 18, 67–126. [Google Scholar] [CrossRef]
  17. Eker, Z.; Bilir, S.; Soydugan, F.; Gökçe, E.Y.; Tüysüz, M.; Şenyüz, T.; Demircan, O. The Catalogue of Stellar Parameters from the Detached Double-Lined Eclipsing Binaries in the Milky Way. Publ. Astron. Soc. Aust. 2014, 31, E024. [Google Scholar] [CrossRef]
  18. Eker, Z.; Soydugan, F.; Bilir, S.; Gökçe, E.Y.; Steer, I.; Tüysüz, M.; Şenyüz, T.; Demircan, O. Main-sequence effective temperatures from a revised mass–luminosity relation based on accurate properties. Astron. J. 2015, 149, 131. [Google Scholar] [CrossRef]
  19. Ibanoǧlu, C.; Soydugan, F.; Dervisoglu, A.; Soydugan, E. Angular momentum evolution of Algol binaries. Mon. Not. R. Astron. Soc. 2006, 373, 435–448. [Google Scholar] [CrossRef]
  20. Bessell, M.S.; Castelli, F.; Plez, B. Model atmospheres broad-band colors, bolometric corrections and temperature calibrations for O-M stars. Astron. Astrophys. 1998, 333, 231–250. [Google Scholar]
  21. Cogan, B.C. The radii and temperatures of classical Cepheids. Astrophys. J. 1978, 221, 635. [Google Scholar] [CrossRef]
  22. Flower, P.J. Transformations from theoretical H-R diagrams to C-M diagrams. Astron. Astrophys. 1977, 54, 31–39. [Google Scholar]
  23. Feast, M.W.; Walker, A.R. Cepheids as Distance Indicators. Annu. Rev. Astron. Astrophys. 1987, 25, 345–375. [Google Scholar] [CrossRef]
  24. Buser, R.; Kurucz, R.L. A library of theoretical stellar flux spectra. I. Synthetic UBVRI photometry and the metallicity scale for F- to K-type stars. Astron. Astrophys. 1992, 264, 557–591. [Google Scholar]
  25. Flower, P.J. Transformations from Theoretical Hertzsprung-Russell Diagrams to Color-Magnitude Diagrams: Effective Temperatures, B-V Colors, and Bolometric Corrections. Astrophys. J. 1996, 469, 355. [Google Scholar] [CrossRef]
  26. Montegriffo, P.; Ferraro, F.R.; Pecci, F.F.; Origlia, L. Towards the absolute planes: A new calibration of the bolometric corrections and temperature scales for Population II giants. Mon. Not. R. Astron. Soc. 1998, 297, 872–884. [Google Scholar] [CrossRef]
  27. Alonso, A.; Arribas, S.; Martínez-Roger, C. The effective temperature scale of giant stars (F0–K5). II. Empirical calibration of Teff versus colours and [Fe/H]. Astron. Astrophys. Suppl. Ser. 1999, 140, 261–277. [Google Scholar] [CrossRef]
  28. Prša, A.; Harmanec, P.; Torres, G.; Mamajek, E.; Asplund, M.; Capitaine, N.; Christensen-Dalsgaard, J.; Depagne, É.; Haberreiter, M.; Hekker, S.; et al. Nominal values for selected solar and planetary quantities: IAU 2015 resolution B3. Astron. J. 2016, 152, 41. [Google Scholar] [CrossRef]
  29. Laney, C.D.; Joner, M.; Schwendiman, L. Dwarf Cepheid radii and the distance scale. In International Astronomical Union Colloquium; ASPC; Cambridge University Press: Cambridge, UK, 2002; Volume 259, pp. 112–115. [Google Scholar]
  30. Laney, C.D.; Joner, M.; Rodriguez, E. HADS, multiple periods, period changes and the PL relation. In Interplay of Periodic, Cyclic and Stochastic Variability in Selected Areas of the HR Diagram; ASPC: San Francisco, CA, USA; Astronomical Society of the Pacific: San Francisco, CA, USA, 2003; Volume 292, pp. 203–209. [Google Scholar]
  31. Johnson, H.L. Astronomical Measurements in the Infrared. Annu. Rev. Astron. Astrophys. 1966, 4, 193–206. [Google Scholar] [CrossRef]
  32. Böhm-Vitense, E. The Effective Temperature Scale. Annu. Rev. Astron. Astrophys. 1981, 19, 295–318. [Google Scholar] [CrossRef]
  33. Sollazzo, C.; Russo, G.; Onnembo, A.; Caccin, B. Cepheid radii and masses by means of VBLUW photometry. Astron. Astrophys. 1981, 99, 66–72. [Google Scholar]
  34. Fernie, J.D. A survey of Cepheid sizes. Astrophys. J. 1984, 282, 641. [Google Scholar] [CrossRef]
  35. Gieren, W. Surface brightness radii, distances, and absolute magnitudes of classical Cepheids. Astrophys. J. 1984, 282, 650–654. [Google Scholar] [CrossRef]
  36. Gieren, W.P. Cepheid radii and masses from the surface-brightness method. Mon. Not. R. Astron. Soc. 1986, 222, 251–260. [Google Scholar] [CrossRef]
  37. Tsvetkov, T.G. Population-I pulsating stars. Part IV. Period–radius and period–gravity relations. Astrophys. Space Sci. 1988, 150, 357–378. [Google Scholar] [CrossRef]
  38. Coulson, I.M.; Caldwell, J.A.R. The radii of 27 southern galactic Cepheids. Mon. Not. R. Astron. Soc. 1989, 240, 285–302. [Google Scholar] [CrossRef]
  39. Gieren, W.P.; Barnes, T.G.; Moffett, T.J. The period-radius relation for classical Cepheids from the visual surface brightness technique. Astrophys. J. 1989, 342, 467–475. [Google Scholar] [CrossRef]
  40. Di Benedetto, G.P. Pulsational parallaxes and calibration of the cosmic distance scale by Cepheid variable stars. Astron. Astrophys. 1994, 285, 819–832. [Google Scholar]
  41. Arellano, E.R.; Ferro, A.A. A new approach to the surface brightness method for Cepheid radii determination. Rev. Mex. Astron. Astrofis. 1994, 29, 148–152. [Google Scholar]
  42. Laney, C.D.; Stobie, R.S. The radii of Galactic Cepheids. Mon. Not. R. Astron. Soc. 1995, 274, 337–360. [Google Scholar] [CrossRef]
  43. Ripepi, V.; Barone, F.; Milano, L.; Russo, G. Cepheid radii and the CORS method revisited. Astron. Astrophys. 1997, 318, 797–804. [Google Scholar]
  44. Gieren, W.P.; Fouque, P.; Gomez, M. Cepheid Period-Radius and Period-Luminosity Relations and the Distance to the Large Magellanic Cloud. Astrophys. J. 1998, 496, 17–30. [Google Scholar] [CrossRef]
  45. Sashkov, E.; Rastorguev, A.S.; Samus, N.N.; Gorynya, N.A. The radii of 62 classical Cepheids. Astron. Lett. 1998, 24, 377–383. [Google Scholar]
  46. Gieren, W.P.; Moffett, T.J.; Iii, T.G.B. Calibrating the Cepheid Period-Radius Relation with Galactic and Magellanic Cloud Cepheids. Astrophys. J. 1999, 512, 553–557. [Google Scholar] [CrossRef]
  47. Ferro, A.A.; Rosenzweig, P. The intermediate-band approach to the surface-brightness method for Cepheid radii and distance determination. Mon. Not. R. Astron. Soc. 2000, 315, 296–306. [Google Scholar] [CrossRef]
  48. Bono, G.; Gieren, W.P.; Marconi, M.; Fouqué, P. On the Pulsation Mode Identification of Short-Period Galactic Cepheids. Astrophys. J. 2001, 552, L141–L145. [Google Scholar] [CrossRef]
  49. Turner, D.G.; Burke, J.F. The Distance Scale for Classical Cepheid Variables. Astron. J. 2002, 124, 2931–2942. [Google Scholar] [CrossRef]
  50. Barnes, T.G.; Jefferys, W.H.; Berger, J.; Mueller, P.J.; Orr, K.; Rodriguez, R. A Bayesian Analysis of the Cepheid Distance Scale. Astrophys. J. 2003, 592, 539–554. [Google Scholar] [CrossRef]
  51. Storm, J.; Carney, B.W.; Gieren, W.P.; Fouqué, P.; Latham, D.W.; Fry, A.M. The effect of metallicity on the Cepheid Period-Luminosity relation from a Baade-Wesselink analysis of Cepheids in the Galaxy and in the Small Magellanic Cloud. Astron. Astrophys. 2004, 415, 531–547. [Google Scholar] [CrossRef]
  52. Ruoppo, A.; Ripepi, V.; Marconi, M.; Russo, G. Improvement of the CORS method for Cepheids radii determination based on Strömgren photometry. Astron. Astrophys. 2004, 422, 253–265. [Google Scholar] [CrossRef]
  53. Kervella, P. Cepheid distances from interferometry. Mem. Soc. Astron. 2006, 77, 227–230. [Google Scholar]
  54. Groenewegen, M. The projection factor, period–radius relation, and surface–brightness colour relation in classical cepheids. Astron. Astrophys. 2007, 474, 975–981. [Google Scholar] [CrossRef]
  55. Segan, S.; Glisovic, P. PR and PL (PMv) relations for classical Cepheids revisited. Serbian Astron. J. 2009, 179, 101–106. [Google Scholar] [CrossRef]
  56. Molinaro, R.; Ripepi, V.; Marconi, M.; Bono, G.; Lub, J.; Pedicelli, S.; Pel, J.W. CORS Baade-Wesselink method in the Walraven photometric system: The period-radius and the period-luminosity relation of classical Cepheids. Mon. Not. R. Astron. Soc. 2011, 413, 942–956. [Google Scholar] [CrossRef]
  57. Pejcha, O.; Kochanek, C.S. A global physical model for Cepheids. Astrophys. J. 2012, 748, 107. [Google Scholar] [CrossRef]
  58. Groenewegen, M.A.T. Baade-Wesselink distances to Galactic and Magellanic Cloud Cepheids and the effect of metallicity. Astron. Astrophys. 2013, 550, A70. [Google Scholar] [CrossRef]
  59. Gallenne, A.; Kervella, P.; Mérand, A.; Pietrzynski, G.; Gieren, W.; Nardetto, N.; Trahin, B. Observational calibration of the projection factor of Cepheids. IV. Period-projection factor relation of Galactic and Magellanic Cloud Cepheids. Astron. Astrophys. 2017, 608, A18. [Google Scholar] [CrossRef]
  60. Lazovik, Y.A.; Rastorguev, A.S. Calibrating the Galactic Cepheid Period–Luminosity Relation from the Maximum-likelihood Technique. Astron. J. 2020, 160, 136. [Google Scholar] [CrossRef]
  61. Trahin, B.; Breuval, L.; Kervella, P.; Mérand, A.; Nardetto, N.; Gallenne, A.; Hocdé, V.; Gieren, W. Inspecting the Cepheid parallax of pulsation using Gaia EDR3 parallaxes. Projection factor and period-luminosity and period-radius relations. Astron. Astrophys. 2021, 656, A102. [Google Scholar] [CrossRef]
  62. Carson, T.R.; Stothers, R.B. Classical bump Cepheids—Reconciliation of theory with observations. Astrophys. J. 1988, 328, 196. [Google Scholar] [CrossRef]
  63. Gieren, W.P. The Galactic Cepheid period-luminosity relation from the visual surface brightness method. Astrophys. J. 1988, 329, 790–796. [Google Scholar] [CrossRef]
  64. Gieren, W.P.; Fouque, P. Comparison of the open cluster and surface-brightness distance scales for galactic classical Cepheids. Astron. J. 1993, 106, 734–739. [Google Scholar] [CrossRef]
  65. Feast, M.W.; Catchpole, R.M. The Cepheid period-luminosity zero-point from Hipparcos trigonometrical parallaxes. Mon. Not. R. Astron. Soc. 1997, 286, L1–L5. [Google Scholar] [CrossRef]
  66. Lanoix, P.; Paturel, G.; Garnier, R. Direct calibration of the Cepheid period-luminosity relation. Mon. Not. R. Astron. Soc. 1999, 308, 969–978. [Google Scholar] [CrossRef]
  67. Fouqué, P.; Storm, J.; Gieren, W. Calibration of the Distance Scale from Cepheids. In Stellar Candles for the Extragalactic Distance Scale; Springer: Berlin/Heidelberg, Germany, 2003; Volume 635, pp. 21–44. [Google Scholar] [CrossRef]
  68. Tammann, G.A.; Sandage, A.; Reindl, B. New Period-Luminosity and Period-Color relations of classical Cepheids: I. Cepheids in the Galaxy. Astron. Astrophys. 2003, 404, 423–448. [Google Scholar] [CrossRef]
  69. Kervella, P.; Bersier, D.; Mourard, D.; Nardetto, N.; Du Foresto, V.C. Cepheid distances from infrared long-baseline interferometry. II. Calibration of the period-radius and period-luminosity relations. Astron. Astrophys. 2004, 423, 327–333. [Google Scholar] [CrossRef]
  70. Benedict, G.F.; McArthur, B.E.; Feast, M.W.; Barnes, T.G.; Harrison, T.E.; Patterson, R.J.; Menzies, J.W.; Bean, J.L.; Freedman, W.L. Hubble Space Telescope Fine Guidance Sensor Parallaxes of Galactic Cepheid Variable Stars: Period-Luminosity Relations. Astron. J. 2007, 133, 1810–1827. [Google Scholar] [CrossRef]
  71. Fouqué, P.; Arriagada, P.; Storm, J.; Barnes, T.G.; Nardetto, N.; Mérand, A.; Kervella, P.; Gieren, W.; Bersier, D.; Benedict, G.F.; et al. A new calibration of Galactic Cepheid period-luminosity relations from B to K bands, and a comparison to LMC relations. Astron. Astrophys. 2007, 476, 73–81. [Google Scholar] [CrossRef]
  72. Fiorentino, G.; Marconi, M.; Musella, I.; Caputo, F. Classical Cepheid pulsation models. XI. Effects of convection and chemical composition on the period-luminosity and period-Wesenheit relations. Astron. Astrophys. 2007, 476, 863–879. [Google Scholar] [CrossRef]
  73. DMcNamara, H.; Clementini, G.; Marconi, M. A δ Scuti distance to the Large Magellanic Cloud. Astron. J. 2007, 133, 2752–2763. [Google Scholar] [CrossRef]
  74. Valle, G.; Marconi, M.; Degl’Innocenti, S.; Moroni, P.G.P. Uncertainties on the theoretical predictions for classical Cepheid pulsational quantities. Astron. Astrophys. 2009, 507, 1541–1554. [Google Scholar] [CrossRef]
  75. Turner, D.G. The PL calibration for Milky Way Cepheids and its implications for the distance scale. Astrophys. Space Sci. 2010, 326, 219–231. [Google Scholar] [CrossRef]
  76. Turner, D.G.; Majaess, D.J.; Lane, D.J.; Rosvick, J.; Henden, A.; Balam, D. The Galactic calibration of the Cepheid period-luminosity relation and its implications for the Universal distance scale. Odessa Astron. Publ. 2010, 23, 119–124. [Google Scholar]
  77. McNamara, D.H. Delta Scuti, SX Phoenicis, and RR Lyrae stars in Galaxies and globular clusters. Astron. J. 2011, 142, 110. [Google Scholar] [CrossRef]
  78. Storm, J.; Gieren, W.; Fouqué, P.; Barnes, T.G.; Pietrzyński, G.; Nardetto, N.; Weber, M.; Granzer, T.; Strassmeier, K.G. Calibrating the Cepheid period-luminosity relation from the infrared surface brightness technique. I. The p-factor, the Milky Way relations, and a universal K-band relation. Astron. Astrophys. 2011, 534, A94. [Google Scholar] [CrossRef]
  79. Anderson, R.I.; Eyer, L.; Mowlavi, N. Cepheids in open clusters: An 8D all-sky census. Mon. Not. R. Astron. Soc. 2013, 434, 2238–2261. [Google Scholar] [CrossRef]
  80. Gaia Collaboration; Clementini, G.; Eyer, L.; Ripepi, V.; Marconi, M.; Muraveva, T.; Garofalo, A.; Sarro, L.M.; Palmer, M.; Luri, X.; et al. Gaia Data Release 1. Testing parallaxes with local Cepheids and RR Lyrae stars. Astron. Astrophys. 2017, 605, A79. [Google Scholar] [CrossRef]
  81. Gieren, W.; Storm, J.; Konorski, P.; Górski, M.; Pilecki, B.; Thompson, I.; Pietrzynski, G.; Graczyk, D.; Barnes, T.G.; Fouqué, P.; et al. The effect of metallicity on Cepheid period-luminosity relations from a Baade-Wesselink analysis of Cepheids in the Milky Way and Magellanic Clouds. Astron. Astrophys. 2018, 620, A99. [Google Scholar] [CrossRef]
  82. Groenewegen, M.A.T. The Cepheid period–luminosity–metallicity relation based on Gaia DR2 data. Astron. Astrophys. 2018, 619, A8. [Google Scholar] [CrossRef]
  83. Ziaali, E.; Bedding, T.R.; Murphy, S.J.; Van Reeth, T.; Hey, D.R. The period–luminosity relation for δ Scuti stars using Gaia DR2 parallaxes. Mon. Not. R. Astron. Soc. 2019, 486, 4348–4353. [Google Scholar] [CrossRef]
  84. Breuval, L.; Kervella, P.; Anderson, R.I.; Riess, A.G.; Arenou, F.; Trahin, B.; Mérand, A.; Gallenne, A.; Gieren, W.; Storm, J.; et al. The Milky Way Cepheid Leavitt law based on Gaia DR2 parallaxes of companion stars and host open cluster populations. Astron. Astrophys. 2020, 643, A115. [Google Scholar] [CrossRef]
  85. Jayasinghe, T.; Stanek, K.Z.; Kochanek, C.S.; Vallely, P.J.; Shappee, B.J.; Holoien, T.W.-S.; A Thompson, T.; Prieto, J.L.; Pejcha, O.; Fausnaugh, M.; et al. The ASAS-SN catalogue of variable stars VI: An all-sky sample of δ Scuti stars. Mon. Not. R. Astron. Soc. 2020, 493, 4186–4208. [Google Scholar] [CrossRef]
  86. Poro, A.; Paki, E.; Mazhari, G.; Sarabi, S.; Alicavus, F.K.; Farahani, F.A.; Guilani, H.; Popov, A.A.; Zubareva, A.M.; Jalalabadi, B.Z.; et al. Observational and Theoretical Studies of 27 δ Scuti Stars with Investigation of the Period–Luminosity Relation. Publ. Astron. Soc. Pac. 2021, 133, 084201. [Google Scholar] [CrossRef]
  87. Mamajek, E.E. On the Age and Binarity of Fomalhaut. Astrophys. J. 2012, 754, L20. [Google Scholar] [CrossRef]
  88. Pecaut, M.; Mamajek, E.E. Intrinsic colors, temperatures, and bolometric corrections of pre-main-sequence stars. Astrophys. J. Suppl. Ser. 2013, 208, 9. [Google Scholar] [CrossRef]
  89. Petersen, J.O.; Jorgensen, H.E. Pulsation of models in the lower part of the Cepheid instability strip and properties of AI Velorum and delta Scuti stars. Astron. Astrophys. 1972, 17, 367–377. [Google Scholar]
  90. de Coca, P.L.; Rolland, A.; Rodriguez, E.; Garrido, R. Empirical P-L-C relationfor delta Scutistars. A catalogue. Astron. Astrophys. Suppl. Ser. 1990, 83, 51–69. [Google Scholar]
  91. McNamara, D. Luminosities of SX Phoenicis, Large-Amplitude Delta Scuti, and RR Lyrae Stars. Publ. Astron. Soc. Pac. 1997, 109, 1221. [Google Scholar] [CrossRef]
  92. Gallenne, A.; Mérand, A.; Kervella, P.; Pietrzyński, G.; Gieren, W.; Hocdé, V.; Breuval, L.; Nardetto, N.; Lagadec, E. Extended envelopes around Galactic Cepheids. V. Multi-wavelength and time-dependent analysis of IR excess. Astron. Astrophys. 2021, 651, A113. [Google Scholar] [CrossRef]
  93. Faulkner, D.J. Cepheid studies. II—A third period in the beat Cepheid TU Cassiopeiae. Astrophys. J. 1977, 218, 209. [Google Scholar] [CrossRef]
  94. Pamyatnykh, A.A. Pulsational instability domains in the upper Main Sequence. Acta Astron. 1999, 49, 119–148. [Google Scholar]
  95. Rogers, F.J.; Iglesias, C.A. The OPAL opacity code: New results. Astron. Soc. Pac. Conf. Ser. 1995, 78, 31–50. [Google Scholar]
  96. Kollath, Z.; Buchler, J.R.; Feuchtinger, M. RR Lyrae: Theory versus Observation. Astrophys. J. 2000, 540, 468–473. [Google Scholar] [CrossRef]
  97. Rodríguez, E.; López-González, M.J.; de Coca, P.L. A revised catalogue of δ Sct stars. Astron. Astrophys. Suppl. Ser. 2000, 144, 469–474. [Google Scholar] [CrossRef]
  98. Deng, Z.-L.; Gao, Z.-F.; Li, X.-D.; Shao, Y. On the Formation of PSR J1640+2224: A Neutron Star Born Massive? Astrophys. J. 2020, 892, 4. [Google Scholar] [CrossRef]
  99. Shi, X.-D.; Qian, S.-B.; Zhu, L.-Y.; Liu, L.; Li, L.-J.; Zang, L. Observational Properties of 155 O- and B-type Massive Pulsating Stars. Astrophys. J. Suppl. Ser. 2023, 265, 33. [Google Scholar] [CrossRef]
  100. Gao, Z.F.; Wang, H.; Zhao, X.J.; Yang, X.F. Equation of state and surface thermal emission of magnetized white dwarfs. Astron. Nachrichten 2023, 344, asna.20220112. [Google Scholar] [CrossRef]
  101. Deng, Z.-L.; Li, X.-D.; Gao, Z.-F.; Shao, Y. Evolution of LMXBs under Different Magnetic Braking Prescriptions. Astrophys. J. 2021, 909, 174. [Google Scholar] [CrossRef]
  102. Gao, Z.F.; Li, X.-D.; Wang, N.; Yuan, J.P.; Wang, P.; Peng, Q.H.; Du, Y.J. Constraining the braking indices of magnetars. Mon. Not. R. Astron. Soc. 2016, 456, 55–65. [Google Scholar] [CrossRef]
  103. Gao, Z.-F.; Wang, N.; Shan, H.; Li, X.-D.; Wang, W. The Dipole Magnetic Field and Spin-down Evolutions of the High Braking Index Pulsar PSR J1640–4631. Astrophys. J. 2017, 849, 19. [Google Scholar] [CrossRef]
Particles 06 00034 g001 550
Figure 1. The distribution of PR relations for the Cepheids from 1966 to 2009 (a) and since 2009 (b).
Figure 1. The distribution of PR relations for the Cepheids from 1966 to 2009 (a) and since 2009 (b).
Particles 06 00034 g001
Particles 06 00034 g002 550
Figure 2. The distribution of the PMV relations for the Cepheids since 1988.
Figure 2. The distribution of the PMV relations for the Cepheids since 1988.
Particles 06 00034 g002
Particles 06 00034 g003 550
Figure 3. The distribution of 50 empirical PR relations according to the empirical data: ○—the Cepheids of type δCephei, ●—the Cepheids of types δCephei and δScuti, _ _ _ _—(8).
Figure 3. The distribution of 50 empirical PR relations according to the empirical data: ○—the Cepheids of type δCephei, ●—the Cepheids of types δCephei and δScuti, _ _ _ _—(8).
Particles 06 00034 g003
Particles 06 00034 g004 550
Figure 4. The distribution of 43 empirical PMV relations according to the empirical data: △—the Cepheids of type δCephei, ●—the Cepheids of types δCephei and δScuti, ○—the Cepheids of type δScuti, _ _ _ _—(9).
Figure 4. The distribution of 43 empirical PMV relations according to the empirical data: △—the Cepheids of type δCephei, ●—the Cepheids of types δCephei and δScuti, ○—the Cepheids of type δScuti, _ _ _ _—(9).
Particles 06 00034 g004
Table
Table 1. The samples of the Cepheids and their parameters.
Table 1. The samples of the Cepheids and their parameters.
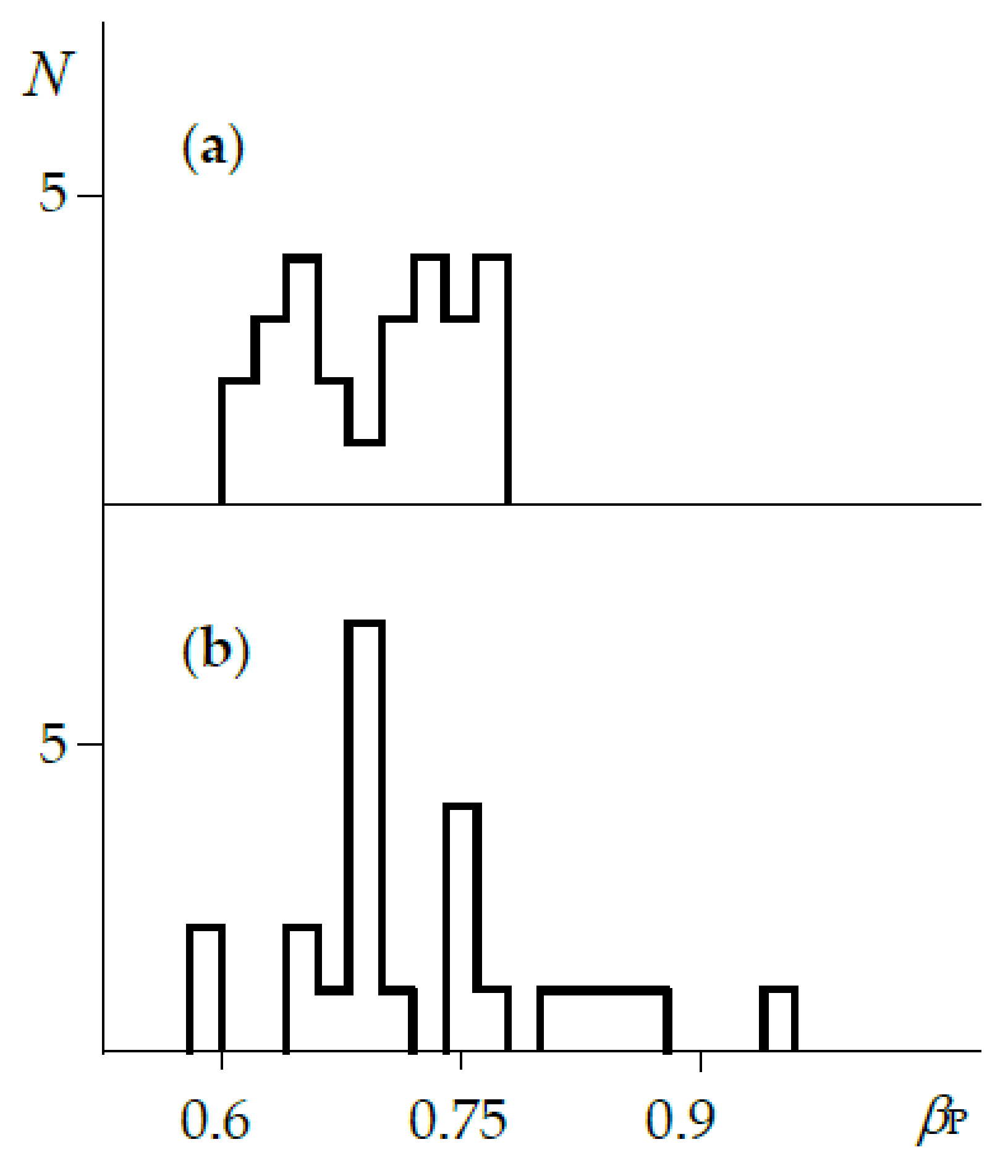
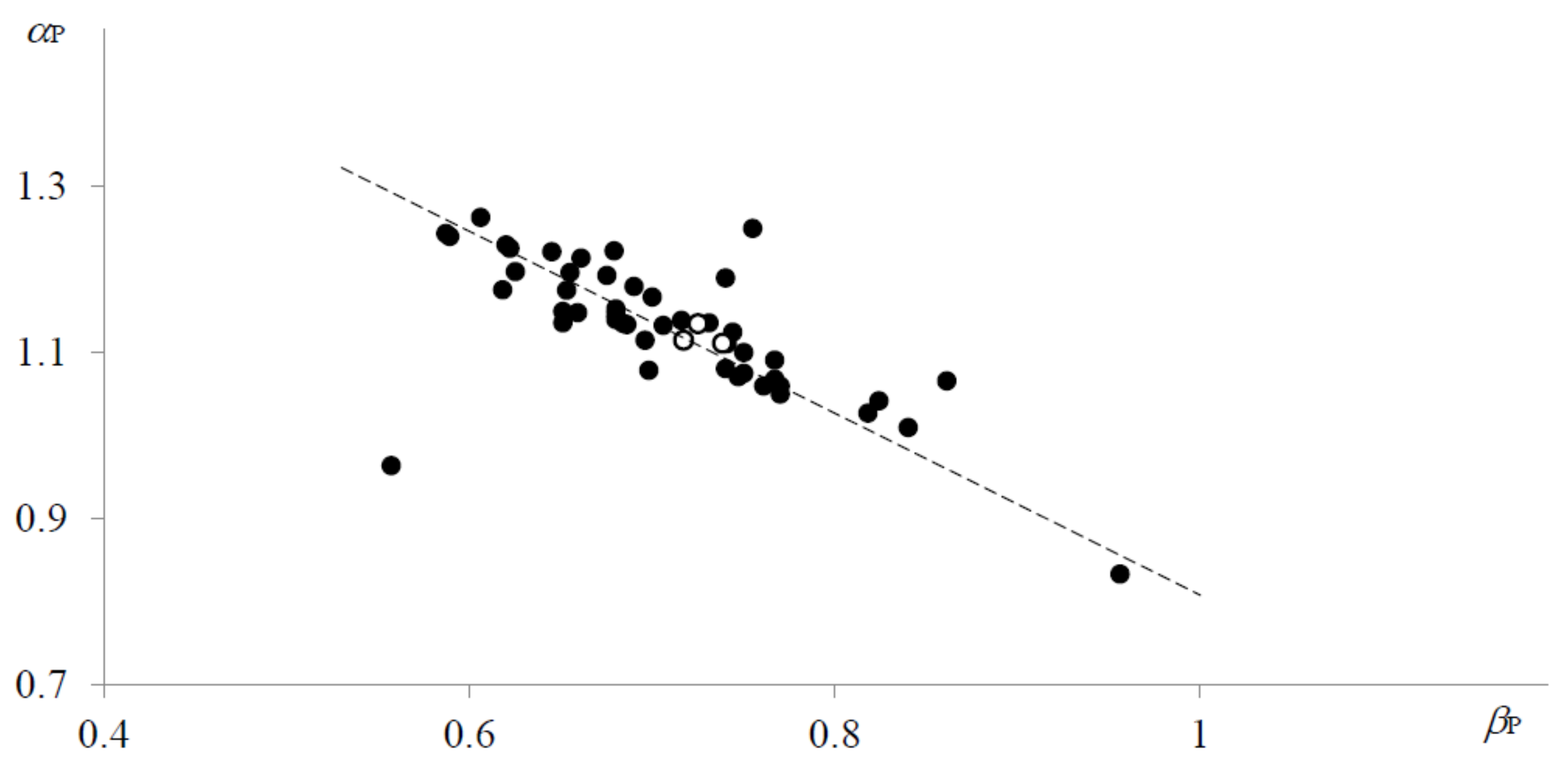
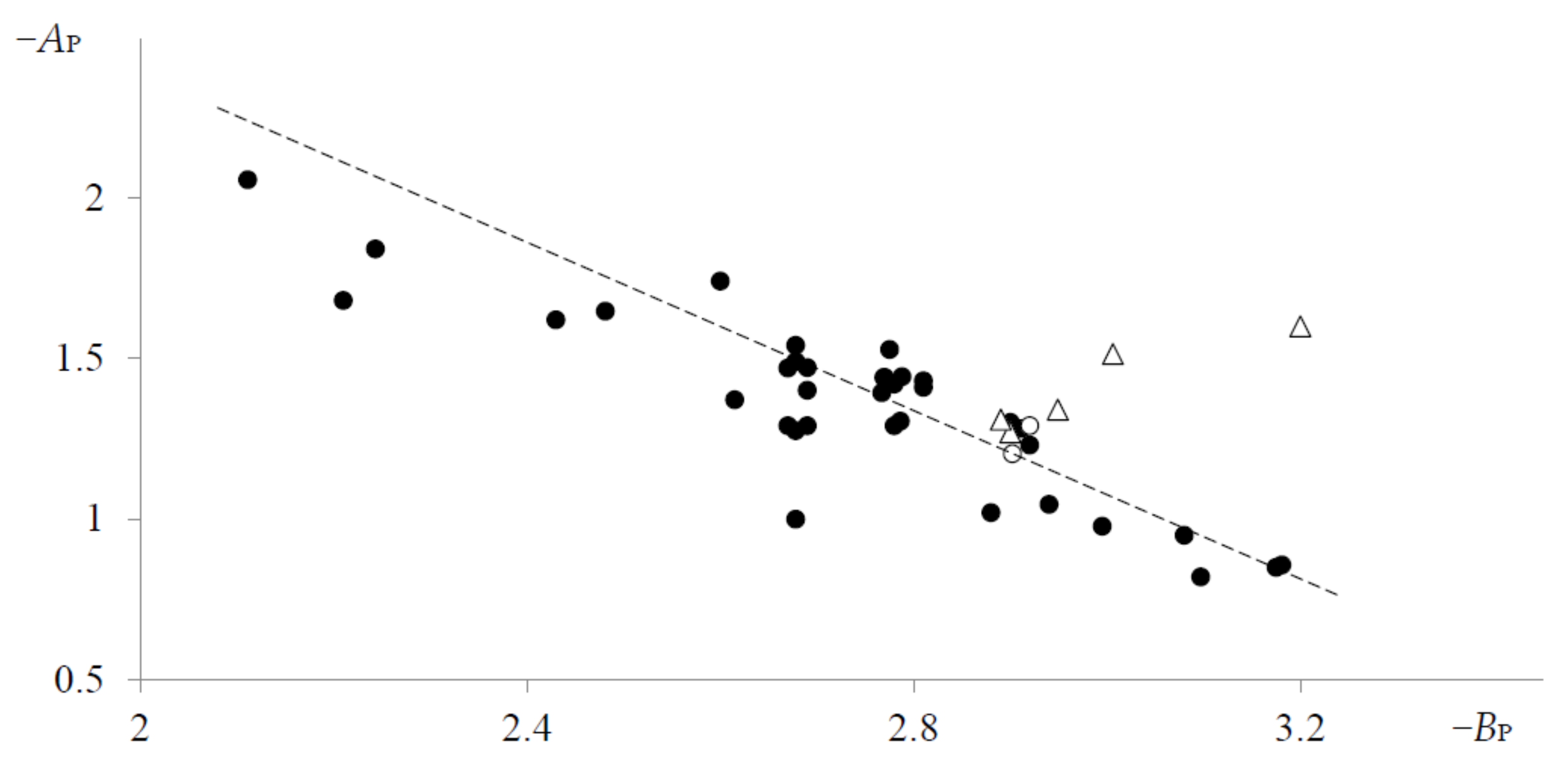
DataN a〈logP〉〈logTe〉№ b
[89]39−1.06533.87901
[90]24−1.03823.87762
[91]26−0.84853.86973
[92]380.94683.7523
210.75543.76564a
171.18313.73584b
[61]530.93313.7515
330.76133.76355a
201.21653.73165b
a The number of the Cepheids in the sample; b The ordinal number of the dependence in Figure 5.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sinitsyn, S.V. Parameters and Pulsation Constant of Cepheid. Particles 2023, 6, 595-610. https://doi.org/10.3390/particles6020034

AMA Style

Sinitsyn SV. Parameters and Pulsation Constant of Cepheid. Particles. 2023; 6(2):595-610. https://doi.org/10.3390/particles6020034

Chicago/Turabian Style

Sinitsyn, Sergei V. 2023. "Parameters and Pulsation Constant of Cepheid" Particles 6, no. 2: 595-610. https://doi.org/10.3390/particles6020034

APA Style

Sinitsyn, S. V. (2023). Parameters and Pulsation Constant of Cepheid. Particles, 6(2), 595-610. https://doi.org/10.3390/particles6020034

Article Metrics

Back to TopTop