Abstract
The multiplicity distribution of charged particles produced from proton–proton collisions at energies = 2.36, 2.76, 5, 7, 8, 10, 13 and 14 TeV were studied in the present work. Furthermore, multiplicity distribution was studied in different pseudorapidity regions ∣∣ < 0.5, 1, 1.5, 2, and 2.5. KNO scaling was studied at the same pseudorapidity regions. This is valid in the pseudorapidity region ∣∣ < 0.5, but with increasing pseudorapidity, the violation increases. The influence of MPI and color reconnection in violation of KNO scaling were studied. The relation between mean multiplicity and collisions energy was explored, noted that it increases with the increasing energy of collisions.
1. Introduction
One of the essential measurements that can be performed at hadron colliders is the exploration of particle production parameters without any selection bias caused by the presence of a hard scattering (a selection known as “minimum bias”). Such events, which occur at low momentum transfers, are impossible to estimate using perturbative quantum chromodynamics (QCD), and for which diffractive scatterings or multiple partonic interactions (MPI) play a significant role, are caused by strong interactions of partons inside hadrons. Theoretical representations of these particle-production components rely on phenomenological models with free parameters modified (“tuned”) to match experimental evidence. Whenever a momentum transfer of many GeV is involved (referred to as a hard process), however, perturbative QCD (pQCD) predictions are often in good agreement with measurements. To fully explain particle production by proton–proton (pp) collisions at the large hadron collider (LHC), it is necessary to understand the transition between hard processes which are estimated by perturbative approaches and soft processes described by nonperturbative models.
The multiplicity distribution means the probability of obtaining a definite number of particles produced from collisions; it contains information about particle correlations. For removing that correlation from data, the average charged particles multiplicity is used instead of multiplicity distribution. The multiplicity distribution of charged particles produced from hadron–hadron (heavy ions) collisions is essential for studying particle production mechanisms and constraints. Cosmic rays, fixed target, and particle colliders experiments were built to study multiplicity distributions. These studies investigated these in greater details to upgrade or discredit models of particle production; most of these models are available in different Monte Carlo (MC) event generators. The multiplicity of charged particle production is considered the key to understanding the particle production mechanism. The probability P(n) of obtaining n charged particles in the final state is related to the particle production mechanism. It obeys Poisson distribution if the particles are produced in a final-state independent way.
Charged particle multiplicity distributions are basic and general observables in modern collider experiments. They contain information about soft QCD processes and hard scattering, thus permitting the exploration of both components and their interactions. Furthermore, the multiplicity distribution of charged particles contains information on many features of the mechanisms of particle production and the hadronization process. Furthermore, in heavy-ion physics, there is a direct correlation between multiplicity and centrality [1,2,3,4], the situation in pp scattering is much less clear. With the recent unequivocal information on collectivity in pp scattering at LHC energies [5], as well as a potentially significant transverse structure of the interaction region, the possible relation between multiplicity and the underlying interaction becomes even more interesting. However, as usual, when dealing with observables of statistical nature, we must always bear in mind that it can be largely independent of the underlying dynamical process. The charged particle multiplicity delivered from pp collisions at high energy is sensitively affected by the number of interactions between gluons and quarks related to the strong interaction and the particle produced by underlying mechanisms. At LHC energies, the production of particles is predominated by soft QCD processes, which are not treated perturbatively and the only modeled phenomenologically. On the other hand, as the colliding energy increases, the contribution of particle production from hard scattering will be increased, which can be treated perturbatively.
In the present work, we compare the distribution of charged particle multiplicity produced from pp collisions at energies of 2.36, 2.76, 5, 7, 8, 10, 13, and 14 TeV, as well as test Koba–Nielsen–Olesen (KNO) scaling at aforementioned these energies. A large Hadron collider operated in some of these energies such as 2.36, 2.76, 7, 8, and 13 TeV so the simulated data can compare with real data. Furthermore, charged particle multiplicities in different eta regions such as < 0.5, 1, 1.5, 2, and 2.5 were studied [6,7,8,9,10,11,12,13,14]. This paper consists of three sections, an introduction to the PYTHIA event generator will be discussed in the first section, the results and discussion in the second section, and the last one is conclusions.
2. PYTHIA Event Generator
The PYTHIA [15] event generator is one of the most popular event generators in particle physics as well as related areas. It is a general-purpose event generator [16] is designed to simulate the collisions between different particles such as proton–proton collisions, which is similar to the collisions that happened in a large hadron collider (LHC) at CERN, p as well as collisions between and collisions.
PYTHIA is based on parton, which simulates interactions of parton and parton showers, the hadronization being handled by using the Lund string fragmentation model.
PYTHIA simulates the collisions between two particles by passing through some steps beginning from hard processes, parton showering of initial- and final-state, and the scattering of multi-parton until the hadronization processes. PYTHIA uses the -ordered approach [17] for modeling the parton shower. PYTHIA employs the original impact parameter model for multi-parton scattering [18]. The hadronization is the last step (fragmentation); in this process, PYTHIA uses the Lund string fragmentation [19,20] and the alternative model.
Inelastic collisions between pp consist of diffractive and non-diffractive, where they are simulated by using PYTHIA8 Monash tune (switching on soft processes) [21,22]. The Monash tune is a method of tuning the Monash parameters to better represent the experimental data at LHC energy, such as minimum-bias charged multiplicity.
PYTHIA is an event generator based on physical models focusing on particle collisions at high energy. For pp collisions, because the approximation of a continuum of enabled final states is utilized in various places in PYTHIA, most notably for the computation of the hadron–hadron cross-section and as the basis for the string-fragmentation model, the energy should be more than 10 GeV. PYTHIA will be inaccurate, when the collision energy reaches the hadronic resonance area at energies below 10 GeV, and such approximations failed. The 10 GeV limit is chosen as a standard scale; it would be possible to go down somewhat for positron–electron annihilation, while the models are not especially trustworthy near the bottom limit for pp collisions. On the other end, we are only aware of specific tests of PYTHIA ’s physics modeling up to approximately 100 TeV CM energies, which corresponds to a fixed-target range pp 10 GeV; see, for example [22,23]. PYTHIA cannot extrapolate except to higher energies recommended for inexperienced users and should be followed by cautious modeling cross-checks and results.
The current software only deals with hadron–hadron or lepton–lepton collisions. The (anti)proton, (anti)neutron, pion, and Pomeron in a specific case are all encompassed by the hadron. There is no support for lepton–hadron collisions or incoming photon beams, but these could be provided in substantial future updates.
Internal facilities to deal with proton–nucleus or nucleus–nucleus collisions are not planned. However, for completeness, we should mention that there are a variety of programs having interfaces with certain PYTHIA physics models, particularly string fragmentation algorithms, Processes of collision and decay. Furthermore, the outgoing particles are produced in a vacuum, and PYTHIA does not include a simulation of the generated particles’ interaction with detector material. The user can write their interfaces to external detector-simulation programs, or they can utilize the HepMC [24] interface. PYTHIA events can always be studied down to the parton or particle level.
Event and Particle Selections
PYTHIA event generator is used to simulate pp collisions; the PYTHIA version used in the present work is 8.245 version. The collisions were simulated at the center of mass energies , , 5, 7, 8, 10, 13 and 14 TeV corresponding to some energies at which the LHC was operated or expected to operate soon. Approximately 20 million events were generated with PYTHIA at each center of mass-energy, Table 1.

Table 1.
The number of events generated by PYTHIA with at least one charged particle and a minimum > 0.1 GeV of and comparison with real data at some energies [6,25].
In the present work, the events are selected according to the following criteria. All QCD soft processes are switched on for simulating the minimum-bias events. Each event must have at least three charged particles in the final state, within the pseudorapidity 2.5 and the whole azimuthal angle .
3. Results and Discussion
3.1. Multiplicity Distribution of Charged Particles
The distribution of charged particles’ multiplicity produced from pp collisions at different energies , , 5, 7, 8, 10, 13 and 14 TeV are shown in Figure 1. Furthermore, the multiplicity of charged particles produced in different eta ranges < 0.5, 1, 1.5, 2 and 2.5 are in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5.
Figure 1.
The charged particle multiplicity distribution in the pseudorapidity interval < 0.5, with 0.1.
Figure 2.
The charged particle multiplicity distribution in the pseudorapidity interval < 1.0, with 0.1 GeV.
Figure 3.
The charged particle multiplicity distribution in the pseudorapidity interval < 1.5, with 0.1.
Figure 4.
The charged particle multiplicity distribution in the pseudorapidity interval < 2.0, with 0.1.
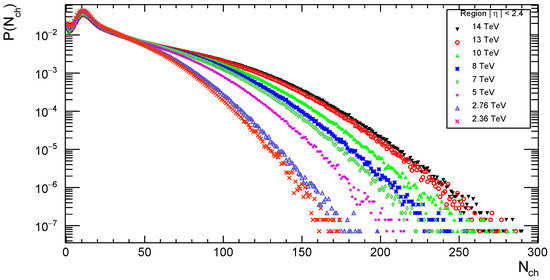
Figure 5.
The charged particle multiplicity distribution in the pseudorapidity interval < 2.4, with 0.1 GeV.
Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show that the number of charged particles produced increase with increasing collision energy and pseudorapidity intervals. The distribution of charged particles’ multiplicity were measured in five different pseudorapidity intervals < 0.5, 1, 1.5, 2 and 2.5 at different energies , , 5, 7, 8, 10, 13 and 14 TeV. In the < 0.5 region, the number of charged particles produced reached approximately 56 at an energy of 2.36 TeV and it increases with energy to reach 114 at an energy of 14 TeV. In the < 1 region, reached 99 with an energy of 2.36 TeV but when the energy was 14 TeV, there were 167 charged particles. In the < 1.5 region, reached 123 with an energy of 2.36 TeV but when the energy was 14 TeV, there were 194 charged particles. In the < 2 region, reached 156 when an energy of 2.36 TeV but when the energy was 14 TeV, there were 252 charged particles. In the < 2.5 region, reached 175 with an energy of 2.36 TeV, but when the energy was 14 TeV, there were 291 charged particles.
There is indeed a shift in slope in P() when > 20 in the maximum pseudorapidity interval of , reflecting a multicomponent structure, as discussed in terms of multiple-soft-Pomeron exchanges in [26,27,28]. Multi-Pomeron exchange contributions are used in Regge Field Theory to explain this expansion. Aside from one Pomeron, contributions from two or more Pomeron exchanges are possible. Because we have a bigger total cross-section at higher energies, we have a higher probability of further rescattering, or additional multiple contacts, defined by the exchange of additional Pomerons; hence, the mean number of Pomeron exchanges grows with energy. As a result, the multiplicity expands. With higher center-of-mass energies, such as at , this feature becomes more noticeable.
Figure 6 shows the multiplicity distribution between the data collected by the compact Muon solenoid (CMS) experiment in LHC at CERN, and the generated Monte Carlo (MC) using the PYTHIA8 Monash tune at the collision energies of 2.36 and 7 TeV [6]. As shown in Figure 6, the data and MC have good agreement.
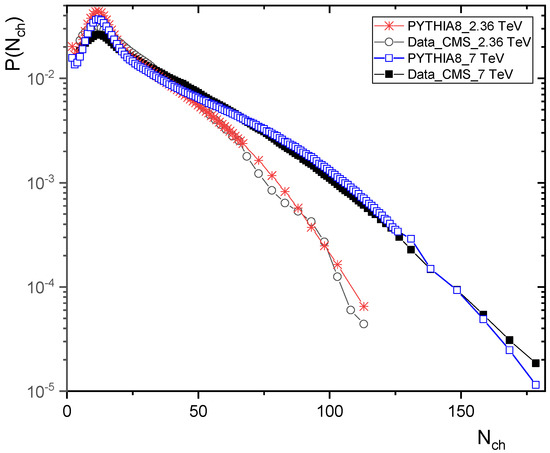
Figure 6.
Comparison between data and PYTHIA8 Monash tune at energies = 2.36 TeV and 7 TeV in region.
3.2. Testing of KNO Scaling at Different Collisions’ Energies
The KNO scaling [29] was initially derived from Feynman scaling [30] for asymptotic energies. Although Feynman scaling was not observed, the KNO scaling was still a practical phenomenological framework for comparing distributions at different energies. The original formulation was:
where is the average multiplicity of charged particles produced from collisions at an energy of . According to the assumption of KNO scaling, the distribution where / is energy independent. That is, the multiplicity distributions are reduced to simple rescaled copies of the universal function (z) with the scaled multiplicity as the only variable. The data points measured at different energies s collapse onto the unique scaling curve, as described by Stanley ().
For hadron–hadron collisions, KNO scaling holds up to ISR energies [31,32], but significant scaling violations occur at = 200 GeV for both whole-phase space and central pseudorapidity range multiplicity distributions [26,33,34,35,36,37]. The UA5 experiment was the first to find a higher than predicted high-multiplicity tail and a shift in slope in pp collisions for wide rapidity ranges [26,38,39,40], which was considered as evidence for a multi-component structure of the final states [27,41]. Strong KNO scaling violations, as well as a change in slope in , were observed at an energy up to = 14 TeV, confirming the previous results at the below energies. This violation comes from multi-parton scattering and Semihard gluon radiation (minijets).
For pp events in PYTHIA, the key aspect is the implementation of multiparton interactions (MPIs), where it is assumed that the impact parameter b between the two protons plays a key role. The small b and large b imply many and few MPIs, respectively. As the energy increases, the average number of MPIs goes up, which means that b can reach larger values. However, the b shape slowly changes with energy, and even less so if rescaling it to the average value. That is, fluctuations around the average scales approximately with energy. This leads to approximate KNO scaling. However, also recall that PYTHIA events, in addition to MPIs, contain a lot of further physics that also affects the final outcome, even if the numbers of MPIs is very important in the overall mix [42].
Color reconnection (CR), a string fragmentation model, was also implemented in PYTHIA, where the final partons are color reconnected in such a way that the entire string length is as small as feasible [43].
According to the multiplicity distributions as in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, the violation of KNO scaling is extreme for but it is still held in the pseudorapidity interval for an energy up to 14 TeV. There is a KNO scaling violation because the tails rise with increasing energy. Furthermore, the violation grows as the pseudorapidity range expands.
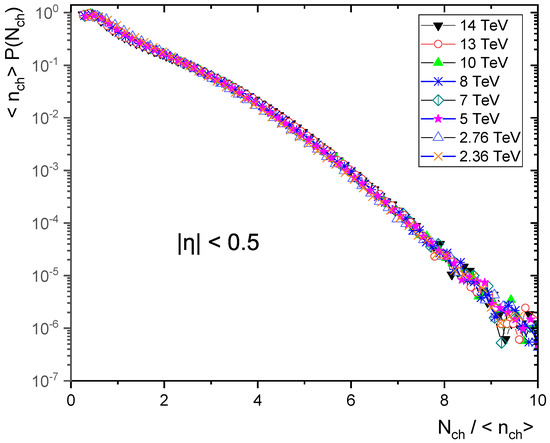
Figure 7.
KNO form of the charged particle multiplicity distribution at different energies in pseudorapidity .
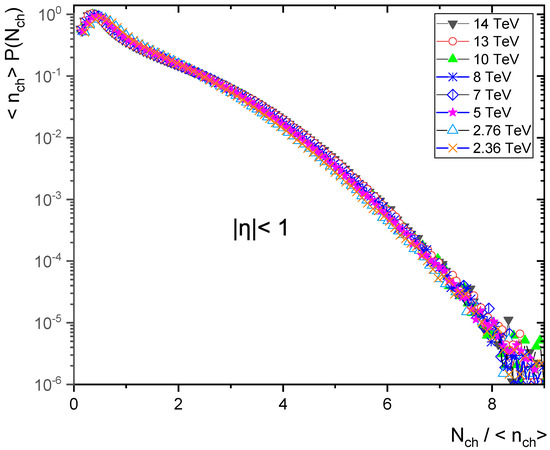
Figure 8.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity .
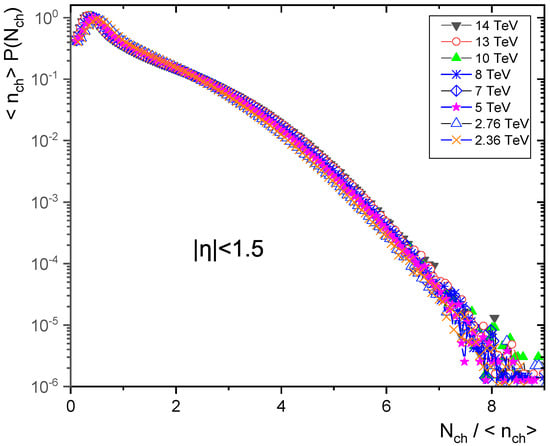
Figure 9.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity .
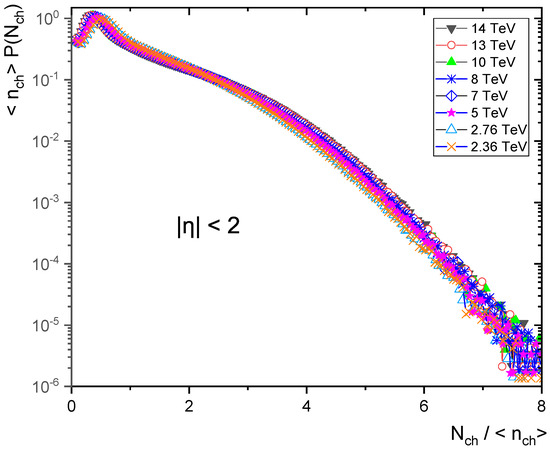
Figure 10.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity .
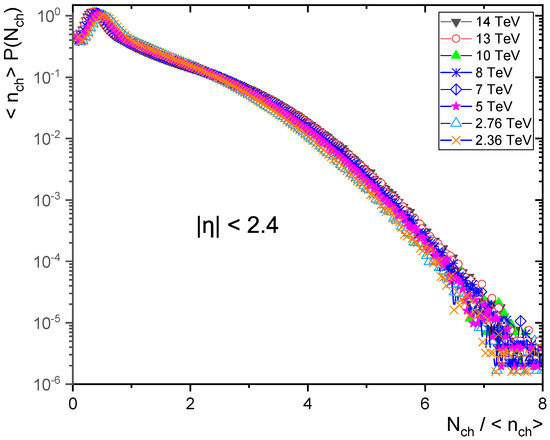
Figure 11.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity .
MPI increases the average multiplicity by three-fold and it has influence in multiplicity distribution to be more wider. Alternatively, CR has a different effect by reducing the average multiplicity by approximately 30% [44]. Additionally, it makes the multiplicity distribution more narrower. The charged particle multiplicity distribution reported at the LHC is rather well reproduced by the entire simulation, which includes both MPI and CR [12].
Some previous work studied the reason for the KNO violation in PYTHIA. In references [45,46], the authors studied the KNO scaling violation in an event-like jet, and they found that the basis of this violation is multiparticle interaction (MPI) and color reconnecting (CR). The microscopic mechanism of CR addresses the interactions that can exist between color fields during the hadronization phase. For testing this violation in minimum bias events, 20 million events were generated by PYTHIA8 without MPI and CR for energies = 5, 7, 10, 13 and 14 TeV and 5 million events were generated with MPI = ON and CR = OFF for energies = 2.36, 2.76, 5, 7, 8, 10, 13 and 14 TeV. As shown in Figure 12 and Figure 13, KNO is almost held when all MPI processes are switched OFF, which can be cleared when comparing them with Figure 7 and Figure 11, KNO scaling fails in the presence of MPI and when CR is OFF. Although CR reduces the mean multiplicity and makes it narrower, the KNO scaling is violated when it is switched OFF, as shown in Figure 12, Figure 13, Figure 14 and Figure 15. It is easy to assume that KNO scaling is violated when the one-to-one connection is cracked by complex QCD processes, such as single and double scatterings of parton linking different hard processes within one event, as well as softer MPI with the beam remnants [46]. We can see that the MPI and CR play essential roles in KNO scaling violations in the high pseudorapidity range.
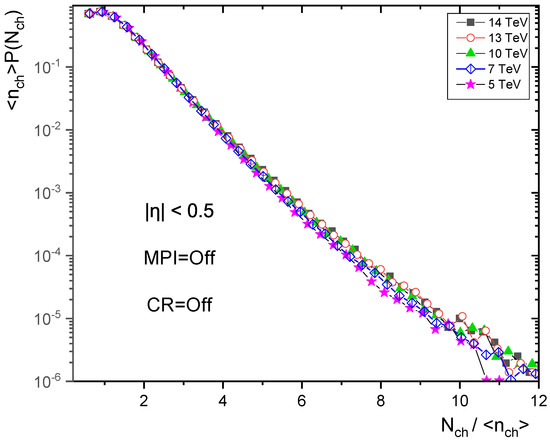
Figure 12.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity with MPI = OFF and CR = OFF.
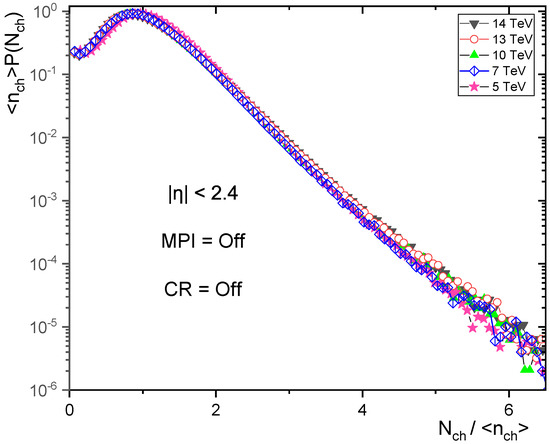
Figure 13.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity with MPI = OFF and CR = OFF.
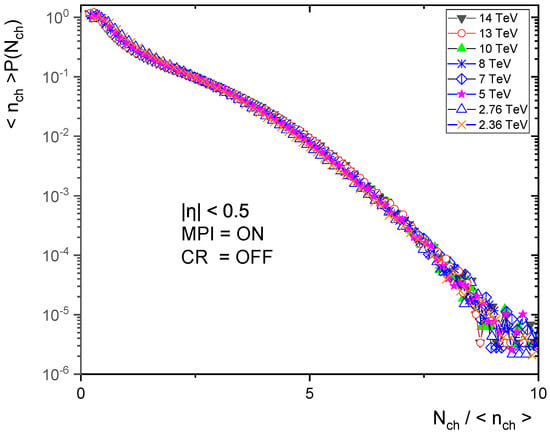
Figure 14.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity with MPI = ON and CR = OFF.
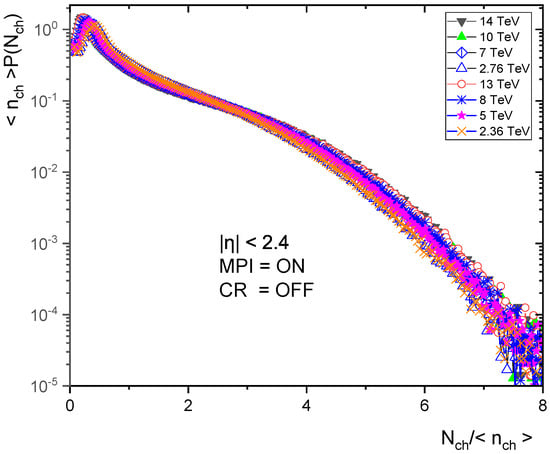
Figure 15.
KNO form of charged particle multiplicity distribution at different energies in pseudorapidity with MPI = ON and CR = OFF.
3.3. Average Multiplicity and Dependence of Energy
The integral of the associated single-particle inclusive density in the interval under consideration is equal to the mean multiplicity, which is the first moment of multiplicity distribution. In hadron–hadron collisions, the mean multiplicity appears to increase with an increasing center-of-mass energy [6,33,38,47,48].
The fitting function of relation between the energy of collisions and mean multiplicity of a charged particle is the polynomial function in the form as shown below in Figure 16, where the values of the parameters are collected in Table 2.
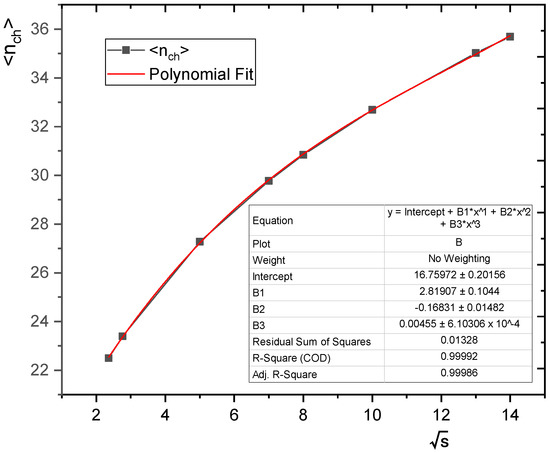
Figure 16.
The relation between the collisions’ energy and the average charged particles when and 0.1 GeV.

Table 2.
Fitting parameters for the relation and in the energy range between 2.36 TeV up to 14 TeV in the pseudorapidity region and 0.1 GeV.
4. Conclusions
The multiplicity distribution of charged particle production from proton–proton collisions at different energies = 2.36, 2.76, 5, 7, 8, 10, 13 and 14 TeV using PYTHIA event generators was presented and studied at different pseudorapidity regions 0.5, 1, 1.5, 2 and 2.5. The average of charged particles produced by the PYTHIA8 Monash tune is close to that measured by LHC experiments at the collisions’ energies = 2.36, 2.76, 7, 8, and 13. KNO scaling was tested in the energy range between = 2.36 TeV and 14 TeV, thus, we conclude that the KNO scaling only holds in the < 0.5 region but with an increased pseudorapidity range, the violation increases. MPI and CR play essential roles in KNO scaling violations in the high pseudorapidity range. The average multiplicity increases with the increase in collisions’ energy with polynomial relations between the energy and mean multiplicity.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Aamodt, K.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z.; Ahmad, N.; et al. Centrality Dependence of the Charged-Particle Multiplicity Density at Midrapidity in Pb-Pb Collisions at = 2.76 TeV. Phys. Rev. Lett. 2011, 106, 032301. [Google Scholar] [CrossRef] [PubMed]
- CMS Collaboration; Chatrchyan, S.; Bäni, L.; Bortignon, P.; Buchmann, M.A.; Casal, B.; Chanon, N.; Deisher, A.; Dissertori, G.; Dittmar, M.; et al. Measurement of the Pseudorapidity and Centrality Dependence of the Transverse Energy Density in Pb-Pb Collisions at = 2.76 TeV. Phys. Rev. Lett. 2012, 109, 152303. [Google Scholar] [CrossRef] [PubMed]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Aiola, S.; et al. Centrality Dependence of the Charged-Particle Multiplicity Density at Midrapidity in Pb-Pb Collisions at = 5.02 TeV. Phys. Rev. Lett. 2016, 116, 222302. [Google Scholar] [CrossRef] [PubMed]
- Parfenov, P.; Idrisov, D.; Luong, V.; Taranenko, A. Relating Charged Particle Multiplicity to Impact Parameter in Heavy-Ion Collisions at NICA Energies. Particles 2017, 4, 275–287. [Google Scholar] [CrossRef]
- CMS Collaboration; Khachatryan, V.; Sirunyan, A.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; et al. Evidence for collectivity in pp collisions at the LHC. Phys. Lett. B 2017, 765, 193–220. [Google Scholar] [CrossRef]
- CMS Collaboration; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; et al. Charged particle multiplicities in pp interactions at = 0.9, 2.36, and 7 TeV. J. High Energy Phys. 2011, 01, 079. [Google Scholar] [CrossRef]
- ALICE Collaboration; Aamodt, K.; Abel, N.; Abeysekara, U.; Abrahantes Quintana, A.; Abramyan, A.; Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; et al. Charged-particle multiplicity measurement in proton–proton collisions at = 7 TeV with ALICE at LHC. Eur. Phys. J. C 2010, 68, 345–354. [Google Scholar] [CrossRef]
- ATLAS Collaboration; Aad, G.; Abbott, B.; Abdallah, J.; Abdelalim, A.A.; Abdesselam, A.; Abdinov, O.; Abi, B.; Abolins, M.; Abramowicz, H.; et al. Charged-particle multiplicities in pp interactions measured with the ATLAS detector at the LHC. New J. Phys. 2011, 13, 053033. [Google Scholar] [CrossRef]
- ALICE Collaboration; Acharya, S.; Adamová, D.; Adolfsson, J.; Aggarwal, M.M.; AglieriRinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, N.; et al. Charged-particle multiplicity distributions over a wide pseudorapidity range in proton-proton collisions at = 0.9, 7, and 8 TeV. Eur. Phys. J. C 2017, 10, 852. [Google Scholar] [CrossRef]
- CMS Collaboration; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Ero, J.; Fabjan, C.; Friedl, M.; et al. Transverse momentum and pseudorapidity distributions of charged hadrons in pp collisions at = 7 TeV. Phys. Rev. Lett. 2010, 105, 022002. [Google Scholar] [CrossRef]
- ATLAS Collaboration; Aad, G.; Abat, E.; Abbott, B.; Abdallah, J.; Abdelalim, A.A.; Abdesselam, A.; Abdinov, O.; Abi, B.; Abolins, M.; et al. Charged-particle multiplicities in pp interactions at = 900 GeV measured with the ATLAS detector at the LHC. Phys. Lett. B 2010, 688, 21–42. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdinov, O.; Abeloos, B.; Aben, R.; Abolins, M.; AbouZeid, O.; Abraham, N.; Abramowicz, H.; et al. Charged-particle distributions in = 13 TeV pp interactions measured with the ATLAS detector at the LHC. Phys. Lett. B 2016, 758, 67–88. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; et al. Multiplicity dependence of π, K, and p production in pp collisions at = 13 TeV. Eur. Phys. J. C 2020, 80, 67–88. [Google Scholar] [CrossRef]
- Acharya, S.; ALICE Collaboration; Adamová, D.; Adhya, S.P.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; et al. Charged-particle production as a function of multiplicity and transverse spherocity in pp collisions at = 5.02 and 13 TeV. Eur. Phys. J. C 2019, 79, 67–88. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Mrenna, S.; Skands, P. PYTHIA 6.4 physics and manual. J. High Energy Phys. 2006, 05, 026. [Google Scholar] [CrossRef]
- Buckley, A.; Butterworth, J.; Gieseke, S.; Grellscheid, D.; Höche, S.; Hoeth, H.; Krauss, F.; Lönnblad, L.; Nurse, E.; Richardson, P.; et al. General-purpose event generators for LHC physics. Phys. Rep. 2011, 504, 145–233. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Skands, P.Z. Transverse-momentum-ordered showers and interleaved multiple interactions. Eur. Phys. J. C 2005, 39, 129–154. [Google Scholar] [CrossRef]
- Sjöstrand, T.; van Zijl, M. A multiple-interaction model for the event structure in hadron collisions. Phys. Rev. D 1987, 36, 2019. [Google Scholar] [CrossRef]
- Andersson, B.; Gustafson, G.; Ingelman, G.; Sjöstrand, T. Parton fragmentation and string dynamics. Phys. Rep. 1983, 97, 31–145. [Google Scholar] [CrossRef]
- Sjöstrand, T. Jet fragmentation of multiparton configurations in a string framework. Nucl. Phys. B 1984, 248, 469–502. [Google Scholar] [CrossRef]
- Corke, R.; Sjöstrand, T. Interleaved parton showers and tuning prospects. J. High Energy Phys. 2011, 3, 32. [Google Scholar] [CrossRef]
- Skands, P.; Carrazza, S.; Rojo, J. Tuning PYTHIA 8.1: The Monash 2013 tune. Eur. Phys. J. C 2014, 74, 3024. [Google Scholar] [CrossRef]
- Skands. Soft-QCD and UE spectra in pp collisions at very high CM energies (a Snowmass white paper). arXiv 2013, arXiv:1308.2813. [Google Scholar]
- Dobbs, M.; Hansen, J.B. The HepMC C++ Monte Carlo event record for High Energy Physics. Comput. Phys. Commun. 2001, 134, 41–46. [Google Scholar] [CrossRef]
- Aggarwal, R.; Kaur, M. Charged particle production in pp collisions at = 8, 7 and 2.76 TeV at the LHC—A case study. Int. J. Mod. Phys. E 2021, 30, 2150005. [Google Scholar] [CrossRef]
- Alexopoulos, T.; Anderson, E.W.; Biswas, N.N.; Bujak, A.; Carmony, D.D.; Erwin, A.R.; Gutay, L.J.; Hirsch, A.S.; Hojvat, C.; Kenney, V.P.; et al. The role of double parton collisions in soft hadron interactions. Phys. Lett. B 1998, 435, 453–457. [Google Scholar] [CrossRef]
- Giovannini, A.; Ugoccioni, R. Soft and semi-hard components structure in multiparticle production in high energy collisions. Nucl. Phys. Proc. Suppl. 1999, 71, 201. [Google Scholar] [CrossRef]
- Schegelsky, V.A.; Martinb, A.D.; Ryskin, M.G.; Khoze, V.A. Pomeron universality from identical pion correlations at the LHC. Phys. Lett. B 2011, 703, 288–291. [Google Scholar] [CrossRef][Green Version]
- Koba, Z.; Nielsen, H.B.; Olesen, P. Scaling of multiplicity distributions in high-energy hadron collisions. Nucl. Phys. B 1972, 40, 317–334. [Google Scholar] [CrossRef]
- Feynman, R.P. Very High-Energy Collisions of Hadrons. Phys. Rev. Lett. 1969, 23, 1415. [Google Scholar] [CrossRef]
- Thomé, W.; Eggert, K.; Giboni, K.; Lisken, H.; Darriulat, P.; Dittmann, P.; Holder, M.; McDonald, K.; Albrecht, H.; Modis, T.; et al. Charged particle multiplicity distributions in p p collisions at ISR energies. Nucl. Phys. B 1977, 129, 365. [Google Scholar] [CrossRef]
- Breakstone, A.; Campanini, R.; Crawley, H.B.; Dallavalle, G.M.; Deninno, M.M.; Doroba, K.; Drijard, D.; Fabbri, F.; Faessler, M.A.; Firestone, A.; et al. Charged multiplicity distribution in p p interactions at ISR energies. Phys. Rev. D 1984, 30, 528. [Google Scholar] [CrossRef]
- EHS/NA22 Collaboration; Adamus, M.; Agababyan, N.M.; Ajinenko, I.V.; Belokopytov, Y.A.; Białkowska, H.; Böttcher, H.; Chliapnikov, P.V.; Crijns, F.; de Roeck, A.; et al. Phase space dependence of the multiplicity distribution in π+ p and p p collisions at 250-GeV/c. Z. Phys. C 1988, 37, 215. [Google Scholar]
- NA22 Collaboration; Adamus, M.; Ajinenko, I.V.; De Almeida, F.M.L., Jr.; Belokopytov, Y.A.; Białkowska, H.; Boettcher, H.; Chliapnikov, P.V.; Crijns, F.; de Roeck, A.; et al. Rapidity dependence of negative and all charged multiplicities in nondiffractive π+ p and p p collisions at 250-GeV/c. Phys. Lett. B 1986, 177, 239. [Google Scholar] [CrossRef]
- CDF Collaboration. Soft and hard interactions in pp collisions at = 1800 GeV and 630 GeV. Phys. Rev. D 2002, 65, 072005. [Google Scholar]
- Capella, A.; Staar, A.; Van, J.T.T. KNO Scaling Violations in the Dual Parton Model. Phys. Rev. D 1985, 32, 2933. [Google Scholar] [CrossRef]
- Bleibel, J.; Bravina, L.V.; Zabrodin, E.E. How many of the scaling the scaling trends in pp collisions will be violated at = 14 TeV?—Predictions from Monte Carlo quark-gluon string model. Phys. Rev. D 2016, 93, 114012. [Google Scholar] [CrossRef]
- Alner, G.; Ansorge, R.; Åsman, B.; Böckmann, K.; Booth, C.; Burow, L.; Carlson, P.; Declercq, C.; Dewolf, R.; Eckart, B.; et al. Scaling violations in multiplicity distributions at 200-GeV and 900-GeV. Phys. Lett. B 1986, 167, 476–480. [Google Scholar] [CrossRef]
- Hegyi, S. KNO scaling 30 years later. Nucl. Phys. Proc. Suppl. 2001, 92, 122–129. [Google Scholar] [CrossRef]
- Bialas, A.; Derado, I.; Stodolsky, L. KNO Scaling Violation and the ’Bremsstrahlung’ Analogy. Phys. Lett. B 1985, 56, 421. [Google Scholar] [CrossRef]
- Matinyan, S.G.; Walker, W.D. Multiplicity distribution and mechanisms of the high energy hadron collisions. Phys. Rev. D 1999, 59, 034022. [Google Scholar] [CrossRef]
- Sjöstrand, T. The Development of MPI Modelling in PYTHIA. Adv. Ser. Direct. High Energy Phys. 2018, 29, 191–225. [Google Scholar]
- Gustafson, G. Multiple Interactions, Saturation and Final States in pp Collisions and DIS. Acta Phys. Pol. B 2009, 40, 1981. [Google Scholar]
- Weber, S.G.; Dubla, A.; Andronic, A.; Morsch, A. Elucidating the multiplicity dependence of J/Ψ production in proton–proton collisions with PYTHIA8. Eur. Phys. J. C 2019, 79, 36. [Google Scholar] [CrossRef]
- Vertesi, R.; Gemes, A.; Barnafoldi, G.G. Koba-Nielsen-Olesen-like scaling within a jet in proton-proton collisions at LHC energies. Phys. Rev. D 2021, 103, L051503. [Google Scholar] [CrossRef]
- Ortiz, A.; Palomo, L.V. Probing color reconnection with underlying event observables at the LHC energies. Phys. Rev. D 2019, 99, 034027. [Google Scholar] [CrossRef]
- Alner, G.; Alpgård, K.; Ansorge, R.; Åsman, B.; Böckmann, K.; Booth, C.; Burow, L.; Carlson, P.; Chevalley, J.-L.; DeClercq, C.; et al. Scaling violation favoring high multiplicity events at 540-GeV CMS energy. Phys. Lett. B 1984, 138, 304–310. [Google Scholar] [CrossRef]
- UA1 Collaboration; Albajar, C.; Albrow, M.G.; Allkofer, O.C.; Andrieu, B.; Ankoviak, K.; Apsimon, R.; Astbury, A.; Aubert, B.; Bacci, C.; et al. A study of the general characteristics of p collisions at = 0.2-TeV to 0.9-TeV. Nucl. Phys. B 1990, 335, 261–287. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).